Abstract
The paper presents a fractional order model of a heating process and a comparison of fractional and standard PI controllers in its closed loop system. Preliminarily, an enhanced fractional order model for the heating process on non-continuous materials has been identified through a fitting algorithm on experimental data. Experimentation has been carried out on a finite length beam filled with three non-continuous materials (air, styrofoam, metal buckshots) in order to identify a model in the frequency domain and to obtain a relationship between the fractional order of the heating process and the different materials’ properties. A comparison between the experimental model and the theoretical one has been performed, proving a significant enhancement of the fitting performances. Moreover the obtained modelling results confirm the fractional nature of the heating processes when diffusion occurs in non-continuous composite materials, and they show how the model’s fractional order can be used as a characteristic parameter for non-continuous materials with different composition and structure. Finally, three different kinds of controllers have been applied and compared in order to keep constant the beam temperature constant at a fixed length.
1. Introduction
The association between non-continuous materials and Fractional Order Systems [1,2,3,4] is an actual research issue involving investigation at the micro- and macroscopic scale [5,6]. This research follows the recent decades’ stream, according to which an increasing interest has arisen for non-continuous, heterogeneous, and composite materials. They are in fact becoming more common in a wide range of functional devices—particularly those involving energy transport and conversion [7]. Their physical properties can be designed as a function of their composition in terms of materials and structure. Modeling and controlling such properties therefore becomes crucial for the optimal materials design.
In particular, the heat transfer model optimization in the frequency domain represents a topic of great interest, considering the common situations of periodic heat flux in engineering problems such as cyclic heating of the cylinder surface of internal combustion engines, diurnal heating and nocturnal cooling of building structures, and periodic (pulse) laser heating of solid surfaces in materials processing [8].
The fractional order calculus was especially useful for modelling thermal processes, as shown in [9,10,11,12,13]. The physics phenomena of such a distributed system model have been approached in literature through different methods: finite difference method by using Grunwald–Letnikov (see [1]), definition for the fractional time derivative [14], and other numerical methods [15,16], such as Podlubny’s matrix approach for discretization of integrals and derivatives of non-integer order [17] and implicit difference approximation to solve the time fractional diffusion equation have been used in [18]. Furthermore, non-Markovian stochastic process—related to a phenomenon of slow anomalous diffusion—have been studied with discrete models of random walk [19].
The aim of this paper is twofold. The first goal is to investigate the fractional order nature of such phenomena in non-continuous, heterogeneous, porous, or composite materials. In particular, the order variation of the heat transfer model has been investigated on non-homogeneous beam heating process by exploiting optimization methods for model identification and validation in the frequency and time domains. The second goal consists of the comparison of classical Proportional Integrative (PI) controllers with the Fractional Order one (FO-PI), keeping constant the beam temperature at a fixed point.
2. Fractional Theoretical Model
Non-continuous material beam heating is associated with the effect of anomalous diffusion, due to the discontinuous interfaces within the material and to part of the heat flux dispersed into the neighbouring environment [8]. Theoretical and experimental models are here presented and compared. The diffusion heat equation applied to a semi-infinite bar is described in Equation (1) in the time domain. Considering the initial condition in Equation (2), the boundary conditions in Equations (3) and (4), and applying the Laplace transform, it is possible to obtain the transfer function in Equation (5), as in [8]. H is the heat flux, T is the temperature, and λ is a normalized distance from the heat source.
temperature along the tube at
heat flux at
temperature at
3. Fractional Experimental Model Identification
3.1. Experimental Setup
The thermal system approximating a semi-infinite beam consists of a steel beam (length cm, outer section diameter cm, inner section diameter cm, thickness mm) filled with different non-continuous materials. The entire experimental setup, schematic and devices, are shown in Figure 1a,b. One end of the metal beam is connected to a Peltier cell (representing the heat source), which is integrated in the heat pump assembly . Such assembly contains a heat sink and the fan: they are used to control the temperature of the cell cold side and to maintain it approximately constant at the ambient temperature. The heat flux out of the Peltier module is controlled by the input current signal coming from a signal generator, and is amplified by a power amplifier . Three temperature sensors are positioned at a fixed distance from the heat source ( at , at , and at ), as detailed in the picture in Figure 1c. Three different experimental setups have been created by varying the beam filling material. The idea was to create composite materials through the composition of granular-shaped materials with air. Such a choice would provide an easy solution for inserting and removing the heterogeneous material from the tube without changing the base of the experimental setup. The maintenance of the basic apparatus, consisting of the metal tube and the Peltier module, ensures the repeatability of the experiments when using different materials. In particular: air, Styrofoam (spheres of 2 mm diameter) and lead buckshot (spheres of 1 mm diameter) have been used in order to investigate how the fractional order of the thermal phenomena varies for the different materials with different thermal conductivity. The lead buckshots filling the tube represent a composite material made of a metal, with good thermal conductivity (35 W/(m·K)), and air, having thermal conductivity of W/(m·K). The Styrofoam spheres, which represent a thermal insulator with thermal conductivity of W/(m·K) with air, represent the second composite materials; while the air filling is used for the control experiment.
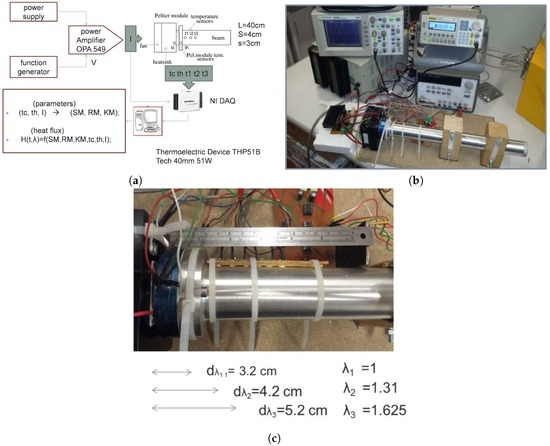
Figure 1.
Experimental setup. (a) Schematic, where (V/K) is the Seebeck coefficient, (Ohm) is the Electrical Resistance, and the Thermal Conductance (W/K) of the Peltier cell. Such parameters where calculated using the Ferrotec method (http://www.ferrotec.com) through measurements of the module input current I, the hot side temperature and the cold side temperature . NI DAQ: National Instrument © Data Acquisition Board; (b) Entire acquisition setup; (c) Beam photo with details on the sensors position.
3.2. Experimental Model
In this paper, an enhanced experimental model for thermal diffusion has been introduced. The theoretical ideal model in Equation (5) has been thus modified, leading to Equation (6) in order to better fit the experimental data. In particular, the fractional order of the system (α) has been left as a parameter to be identified.
The parameter has been included in order to discriminate within the mathematical model the component of the energy transport related to the metal tube. This is important in the parameter identification procedure, in order to decouple the fractional component related to the composite sample from the one related to the experimental setup artifact.
Moreover, the spatial variable λ contribution has been considered in the pole position. Such parameters to be identified are at the basis for the investigation of a possible relationship between the thermal diffusion fractional order and the non-continuous material of the beam.
3.3. Experimental Campaign
Sinusoidal signals at different frequencies have been used for the model identification in the frequency domain. In particular, input current sinusoids with frequencies , , , , , , , , , , , , , , and were used, causing a heat flux peak-to-peak amplitude of about 45 W. For each frequency, the sinusoidal signal has been applied as a current input, and the temperature measurement was collected on three sinusoids when the steady state condition was reached for the output temperature sinusoid off-set. At the end of each sinusoid measurement, the system temperature was allowed to return to the environmental temperature.
Three sets of experimental data acquisition have been conducted by varying the beam filling material: air, Styrofoam, and lead buckshot.
3.4. Identification and Validation Method
Given the spatial dependence of the model, the identification process has been performed in two steps. First, a multi-objective Nelder–Mead simplex optimization algorithm has been used in order to identify the model parameters (, , , α, and ) by fitting the model response (module and phase) to the experimental data for at the normalized distance . The objective function combines the error functions on the module and phase. Then, in order to validate the identified model at different distances from the heat source, the same algorithm was used in order to validate the and parameters by comparing—in the frequency domain—the model output T to the experimental temperature measured, respectively, at distances and . The quality of the identified model on the spatial domain has been measured by comparing estimated distances and (corresponding to the identified and ) with the real ones.
In order to determine the model parameters, the following index error—consisting of the sum of two terms—has been considered. The first term, , is related to the normalized error between the module of the experimental ratio and the simulated one of Equation (6), while the represents the corresponding error for the phase.
with
The minimization of the cost function has been performed sequentially using the Nelder–Mead simplex method [20] implemented via the Matlab function fminsearch [21], see also Figure 2.
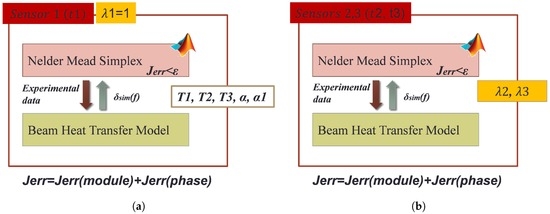
Figure 2.
Nelder–Mead multi-objective optimization algorithm for heat transfer model identification. (a) Identification of model parameters in the frequency domain; (b) Validation of the identified model in the spatial domain.
4. Modelling Results
4.1. Model Identification at sensor1
Three couples of identified models, theoretical and experimental, have been obtained by applying the identification and the validation algorithm on the experimental data acquired at the location on the metal tube filled with the three different materials. The identified parameters are presented in Table 1 and Table 2, respectively, for the theoretical model (, , ) and for the experimental model (, , , α, and ). Comparison between the theoretical model, the experimental model, and the experimental data at the location is performed in the frequency domain through the Bode diagrams—both module and phase—as presented in Figure 3, Figure 4 and Figure 5.

Table 1.
Theoretical model identified parameters at .

Table 2.
Experimental model identified parameters at .
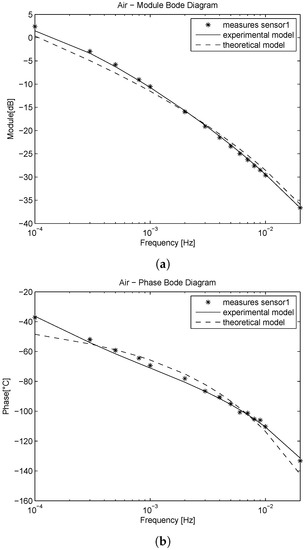
Figure 3.
Metal beam filled with air. Theoretical and experimental model comparison in the frequency domain. (a) Module diagram; (b) Phase diagram.
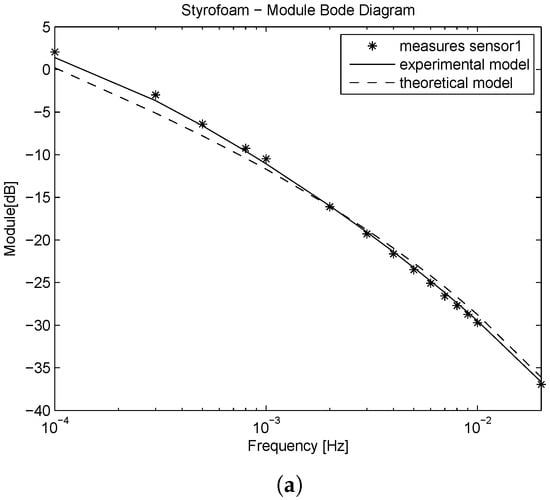
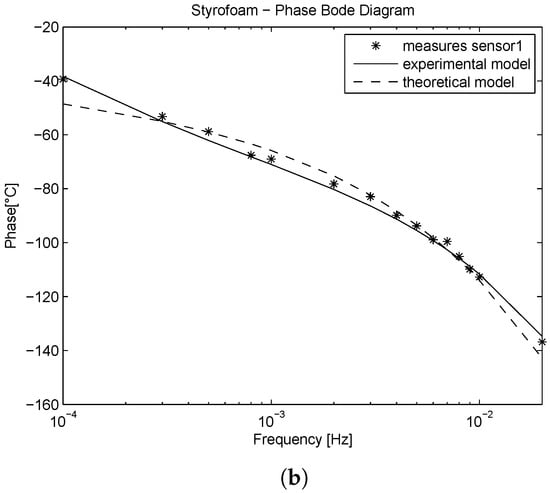
Figure 4.
Metal beam filled with Styrofoam. Theoretical and experimental model comparison in the frequency domain. (a) Module diagram; (b) Phase diagram.
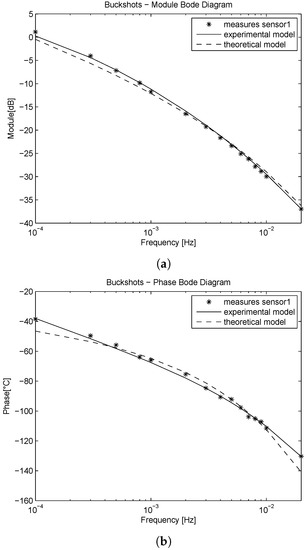
Figure 5.
Metal beam filled with metal buckshots. Theoretical and experimental model comparison in the frequency domain. (a) Module diagram; (b) Phase diagram.
The experimental model’s enhanced performances in fitting experimental data at the location are visible by inspection of the Bode diagrams (see Figure 3, Figure 4 and Figure 5). More evidence of such enhancement is given by the mean square error () calculated between the identified models module and the experimental data at , as shown in Table 3. Moreover, as it is shown in Table 2, the fractional order of the system for the metal buckshots is close to the theoretical value of . The module of the Bode diagram in Figure 5 confirms such evidence, since the theoretical model fits the experimental data with a smaller with respect to the other pipe filling material.

Table 3.
Experimental and theoretical model validation in the spatial domain.
4.2. Time Domain Model Validation at sensor1
The experimental model has been validated in the time domain: the step response analysis has been performed, the steady state value of the heat flux has been measured providing the value of 40 W over a = 100 K of the input step amplitude (see Figure 6). This leads to a static gain of 2.5 K/W for all the materials, which is comparable to the parameter found through experimental model identification, ranging from 2 and 2.5 K/W. Such analysis suggests that the theoretical model in this case fails in fitting the experimental data having a static gainranging from 8 to 13 K/W. It is also worth noticing that the position of the pole for the theoretical model is at a very low frequency, and this affects such a mismatch between the static gains of the two considered models.
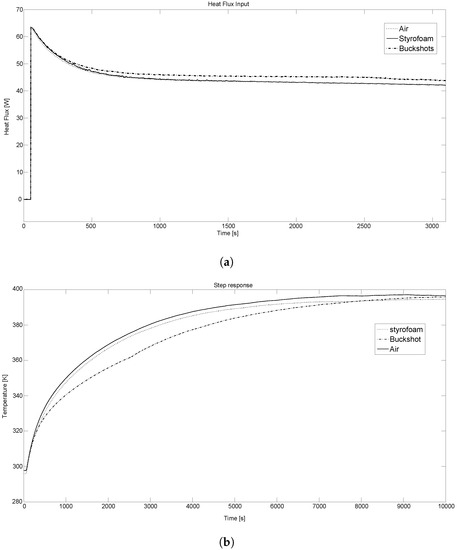
Figure 6.
Step response analysis at (a) Heat flux input; (b) Measured output temperature.
4.3. Model Validation at sensor2 and sensor3
The model validation results in the spatial domain has been presented for the three materials by comparing the estimated distances with the real sensor distances cm, cm. Also in the validation step, the experimental model performs better than the theoretical model.
It is clear how the estimated distances and in Table 3 for the experimental model are closer to the and actual distances with respect to the theoretical model estimated distances.
4.4. Fractional Order and Non-Continuous Materials
The identified values of the fractional order of the experimental model (see Table 4) for the different non-continuous materials suggests that there is a relationship between the material composing the beam and the fractional behavior. This might be due to the multiple interfaces within the material leading to anomalous diffusion. The morphological composition and the relative thermal properties of the non-continuous composite materials can therefore be considered the basis for designing complex materials with desired thermal properties.

Table 4.
Relationship between thermal conductivity of the non-continuous beam material and the experimental fractional order model α.
4.5. Controllers Implementation and Comparison
In this section, the comparison of three different approaches for the control of the temperature of the beam at the distance cm is reported. The control systems have been implemented by using the HIL system DSpace ACE-kit DS1103. Its main features are the PowerPC , 2 MByte local SRAM, 128 MByte global DRAM, 20 ADC channels (16/12 bit), and 8 DAC channels (14 bit).
All the considered controllers have been designed in Matlab/Simulink and then downloaded and tested in real time using the tool as part of the HIL system.
The compared controllers are a conventional PI, an anti-windup PI, and a fractional order (FO) PI controller. The PI has been designed according to the Ziegler–Nichols tuning rules, and the following parameters have been used during the simulation: , ; for the anti-windup controller, see [22]. A feedback gain equal to has been added, while the FO-PI has been designed according to the tuning table given in [23], with , , and the fractional order . In particular, the fractional order controller has been implemented using the Grunwald–Letnikov discrete approximation, as in [1].
As it can be seen in Figure 7, the best performances have been obtained with the fractional controller. This result can be supported by the evidence that a fractional order system can be better controlled with a fractional controller instead of a classical one. The optimization of all the controllers is foreseen as a next step, as well as the implementation and comparison of the control laws on a low-cost microcontroller.
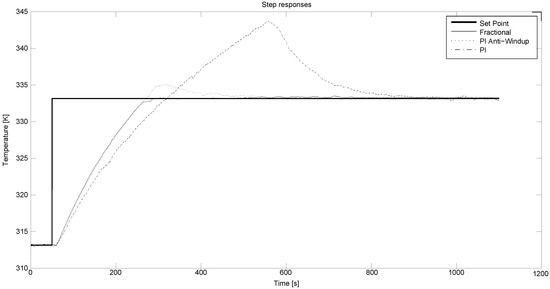
Figure 7.
Step response for the three different controllers: PI, anti-windup PI and FO-PI.
5. Conclusions
In this paper, as a first step, the fractional order of the heat transfer phenomenon on a finite beam made of non-continuous composite materials has been investigated.
An optimized heat transfer model has been obtained by identifying the fractional order by means of a Nelder–Mead optimization algorithm. The model has been identified for three different non-continuous materials: air, Styrofoam, and metal buckshot.
The proposed model is a first step towards a complete enhanced experimental model. The convection analysis is to be included in future models, considering that convective flow can occur in the air and Styrofoam samples. Such an additive effect could affect the fractional order of the model, especially in the case of air and Styrofoam filling.
With this in view, the experimental set-up could be improved taking into account the orientation of the tube to evaluate the effect of the convection and the effect of the tube insulation on the energy transport between the composite sample and the tube itself.
The model optimization paves the way for future work in the design of heating process control for engineering applications. Such results allow us to investigate a simplified thermal model of complex composite materials with a view towards defining the relationship between fabrication parameters, the thermal capacitance and possible mixtures, and the fractional exponent value. This concept opens the way for investigation of the technological control of material thermal properties by composite material structure, concentration, and mixtures, making such design more simple and flexible.
The second step shows the comparison among fractional order and standard PI controllers, outlining a better performance of the fractional one. With respect to the control strategies, future steps consist of the optimization of all the controllers, as well as the implementation and comparison of the control laws on microcontrollers.
Author Contributions
All the authors contributed in the setting up of the experiments, in analyzing the data, getting up the results and writing the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Dover Books: New York, NY, USA, 2006. [Google Scholar]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Petras, I. Fractional Order Systems: Modelling and Control Applications, in Nonlinear Science; Series A; World Scientific: Singapore, 2010; Volume 2. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Caponetto, R.; Graziani, S.; Pappalardo, L.; Sapuppo, F. Experimental Characterization of Ionic Polymer Metal Composite as a Novel Fractional Order Element. Adv. Math. Phys. 2013, 2013, 953695. [Google Scholar] [CrossRef]
- Elshurafa, A.; Mahmoud, N.; Almadhoun, K.; Salama, N.; Alshareef, H. Microscale electrostatic fractional capacitors using reduced graphene oxide percolated polymer composites. Appl. Phys. Lett. 2013, 102, 232901. [Google Scholar]
- Srivastava, I.; Sadasivam, S.; Smith, K.; Fisher, T. Combined Microstructure and Heat Conduction Modeling of Heterogeneous Interfaces and Material. J. Heat Transf. 2013, 135, 061603. [Google Scholar] [CrossRef]
- Kulish, V.; Lage, J. Fractional-Diffusion Solutions for Transient Local Temperature and Heat Flux. Trans. ASME 2000, 122, 372–376. [Google Scholar] [CrossRef]
- Sierociuk, D.; Dzieliski, A.; Sarwas, G.; Petras, I.; Podlubny, I.; Skovranek, T. Modelling heat transfer in heterogeneous media using fractional calculus. Philos. Trans. R. Soc. A 2013, 371, 20120146. [Google Scholar] [CrossRef] [PubMed]
- Gabano, J.; Poinot, T. Fractional modelling applied to heat conductivity and diffusivity estimation. Phys. Scr. 2000, 136, 014015. [Google Scholar] [CrossRef]
- Dzielinski, A.; Sierociuk, D. Fractional order model of beam heating process and its experimental verification. In New Trends in Nanotechnology and Fractional Calculus Applications; Baleanu, D., Guvenc, Z.B., Machado, J.A.T., Eds.; Springer: Berlin, Germany, 2010; pp. 287–294. [Google Scholar]
- Petras, I.; Vinagre, B.; Dorcak, L.; Feliu, V. Fractional digital control of a heat solid: Experimental results. In Proceedings of the 3rd International Carpathian Control Conference ICCC’02, Malenovice, Czech Republic, 27–30 May 2002; pp. 365–370.
- Macias, M.; Sierociuk, D. Fractional order calculus for modelling and fractional PID control of the heating process. In Proceedings of the 13th IEEE International Carpathian Control Conference (ICCC), Podbanske, Slovak Republic, 28–31 May 2012; pp. 452–457.
- Zecova, M.; Terpak, J. Heat conduction modeling by using fractional-order derivatives. Appl. Math. Comput. 2015, 257, 365–373. [Google Scholar]
- Kumar, P.; Agrawal, O. An approximate method for numerical solution of fractional differential equations. Signal Process. 2006, 86, 2602–2610. [Google Scholar] [CrossRef]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the spacetime fractional diffusion equation. Fract. Calc. Appl. Anal. 2001, 4, 153–192. [Google Scholar]
- Podlubny, I.; Skovranek, T.; Vinagre, B.; Petras, I.; Verbitsky, B.; Chen, Y. Matrix approach to discrete fractional calculus III: Non-equidistant grids, variable step length and distributed orders. Philos. Trans. R. Soc. A 2013, 371, 20120153. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, P.; Liu, F. Implicit difference approximation for the time fractional diffusion equation. J. Appl. Math. Comput. 2006, 22, 87–99. [Google Scholar] [CrossRef]
- Gorenflo, P.; Mainardi, F.; Moretti, D.; Paradisi, P. Time fractional diffusion: A discrete random walk approach. Nonlinear Dyn. 2002, 29, 129–143. [Google Scholar] [CrossRef]
- Nelder, J.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 4, 308–313. [Google Scholar] [CrossRef]
- Lagarias, J.; Reeds, J.; Wright, J.; Wright, P. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimension. Siam J. Optim. 2010, 9, 112–147. [Google Scholar] [CrossRef]
- Astrom, K.; Hagglund, T. PID Controllers: Theory, Design, and Tuning, 2nd ed.; The Instrumentation, Systems, and Automation Society: Research Triangle Park, NC, USA, 1995. [Google Scholar]
- Bhaskaran, T.; Chen, Y.Q. Practical tuning of fractional order proportional and integral contrller: Tuning rules deveopment. In Proceedings of the ASME IDETC/CIE 2007, Las Vegas, NV, USA, 4–7 September 2007.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).