Nonlinear Relaxation Phenomena in Metastable Condensed Matter Systems
Abstract
:1. Introduction
2. Short and Long JJ
2.1. Short Graphene JJ—Model
2.1.1. Short Graphene JJ—Results
2.2. Long JJ—The model
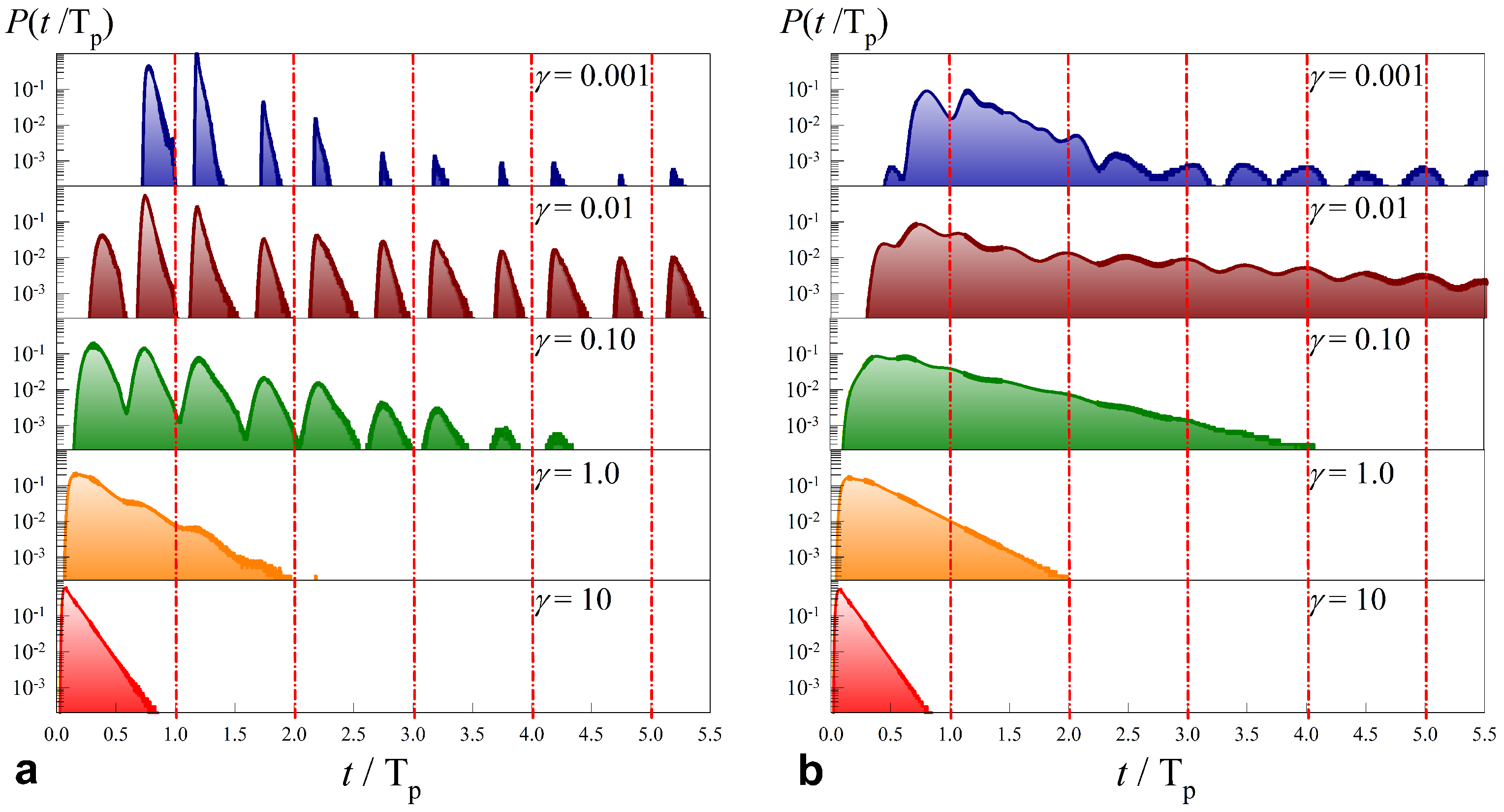
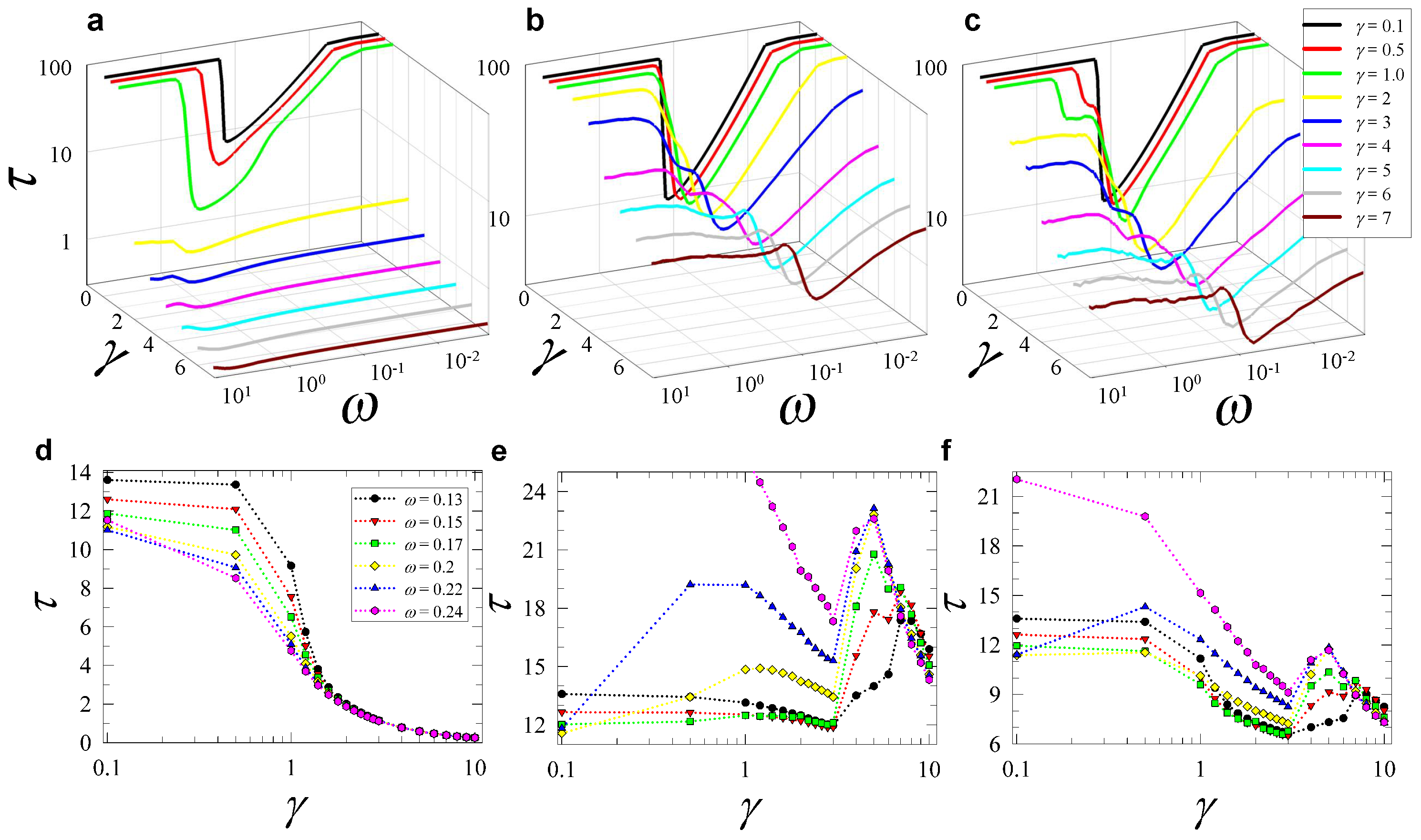
2.2.1. Long JJ—Results
3. Spin Polarised Transport
3.1. The Model
3.2. Monte Carlo Approach and Noise Modelling
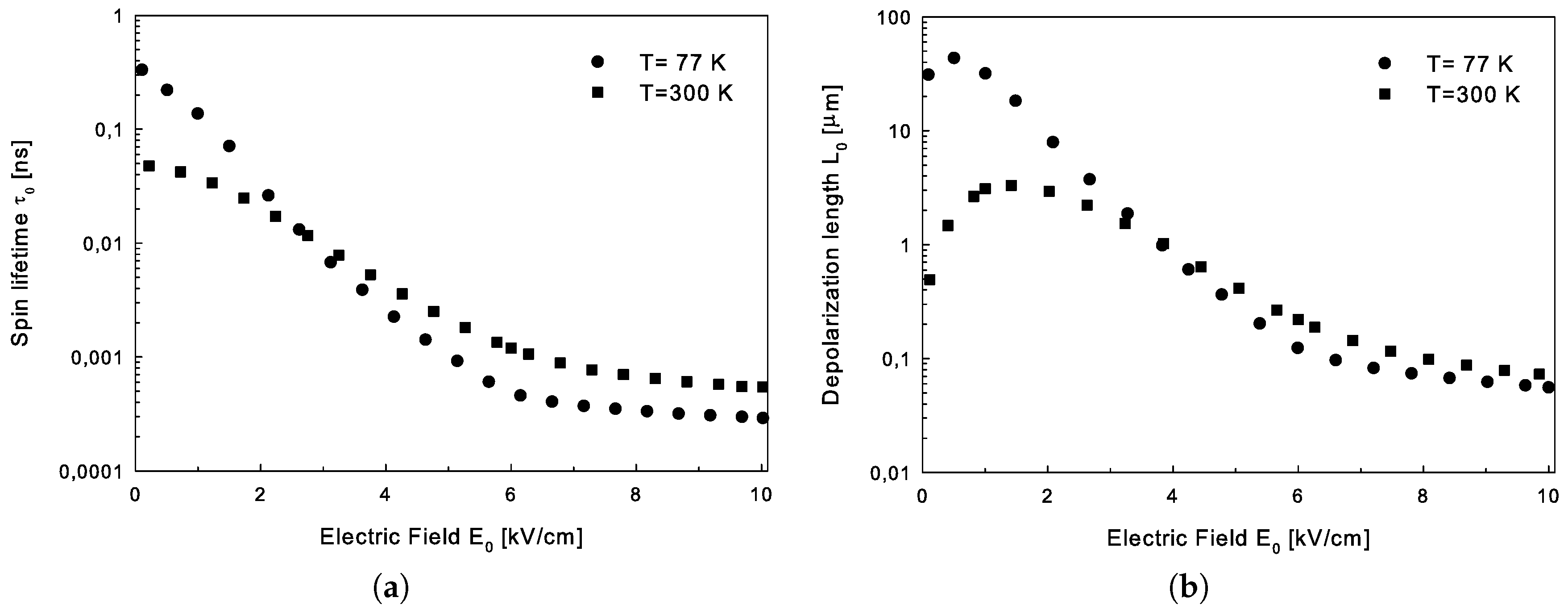
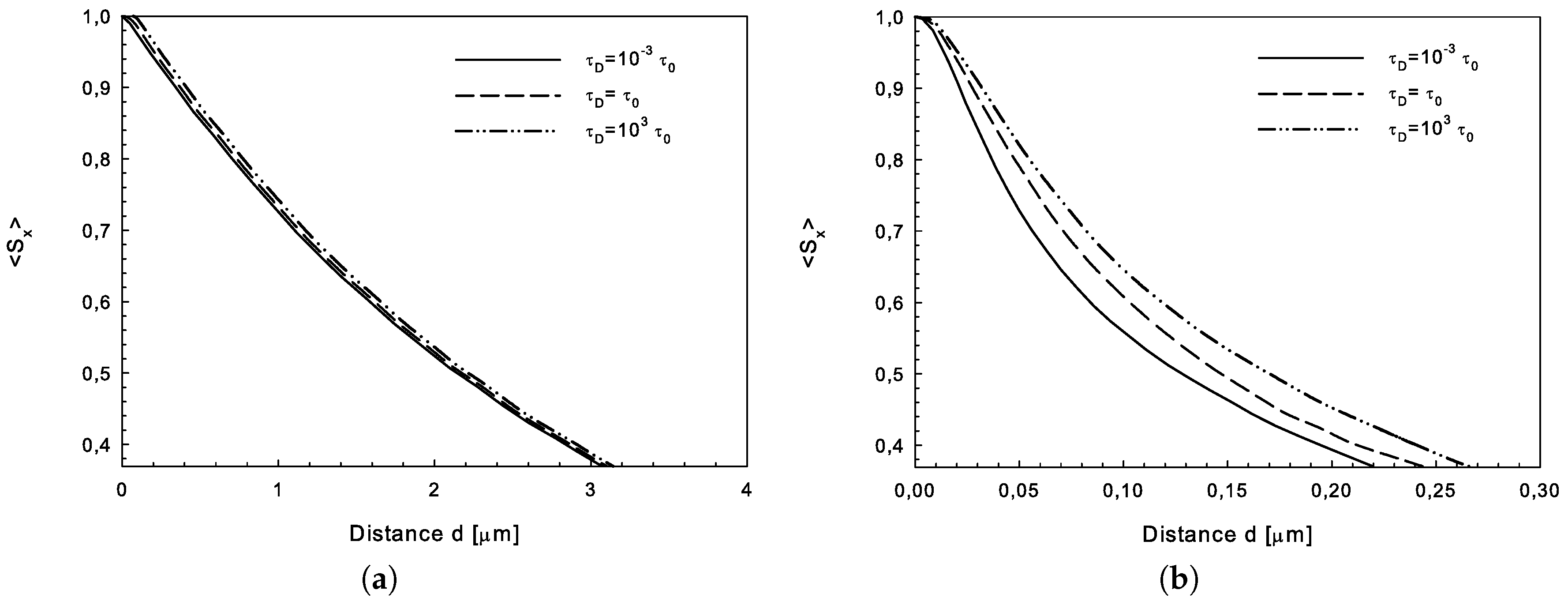
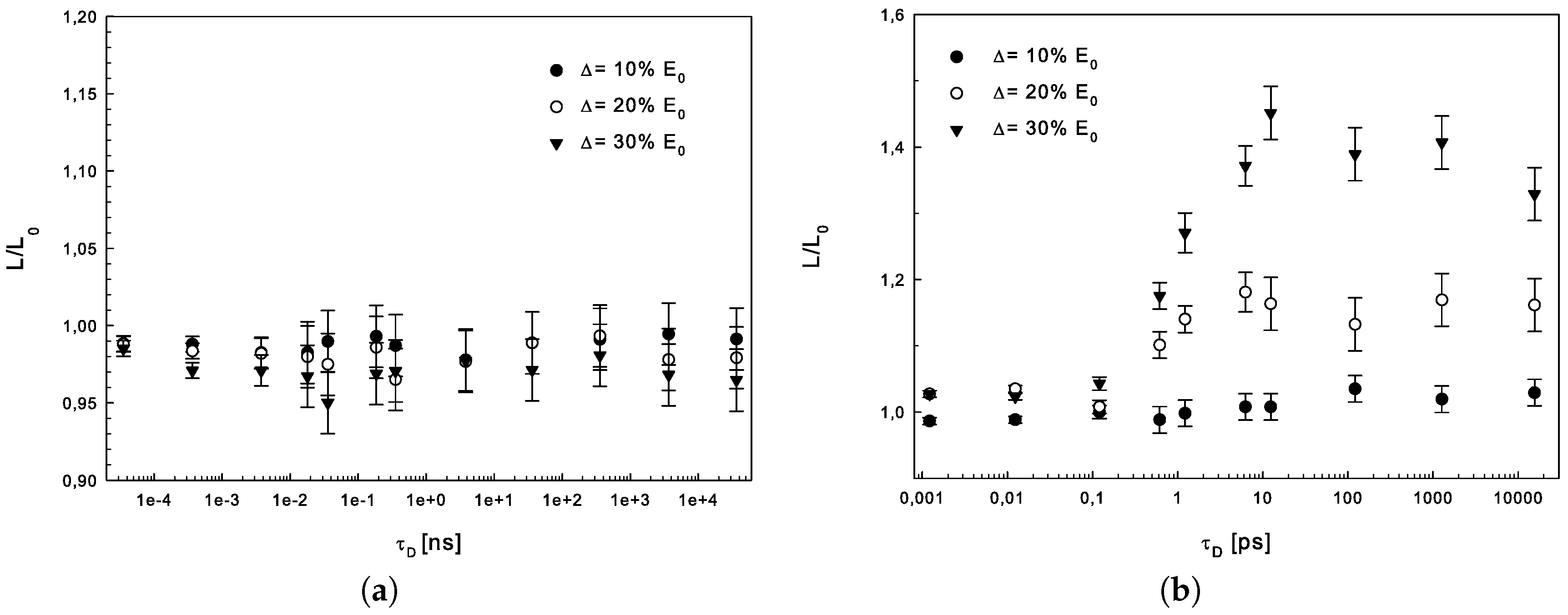
3.3. Numerical Results and Discussion
4. Quantum Metastable State
4.1. The Model
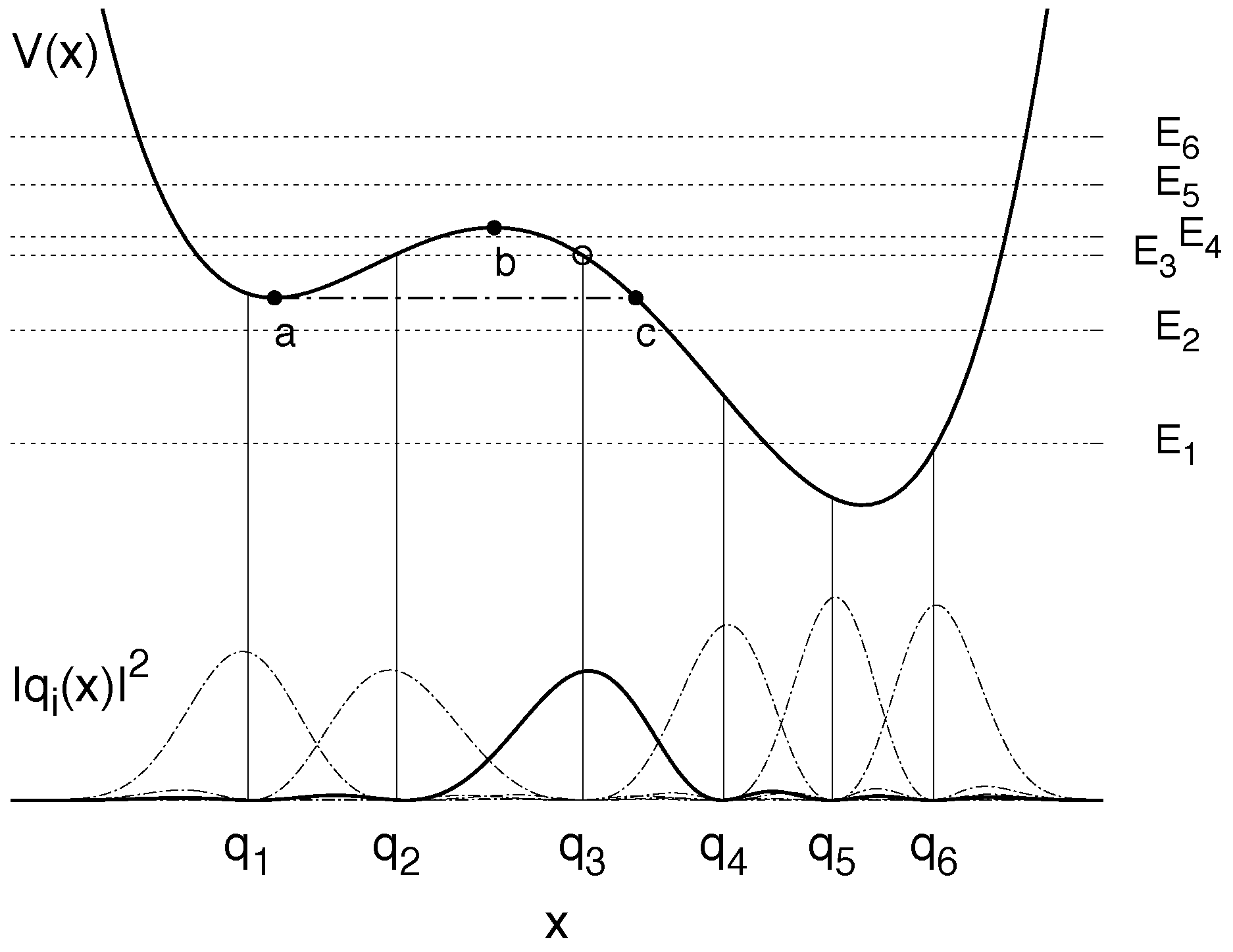
4.2. Discrete Variable Representation
4.3. Strong Dissipation: Analytical Approach
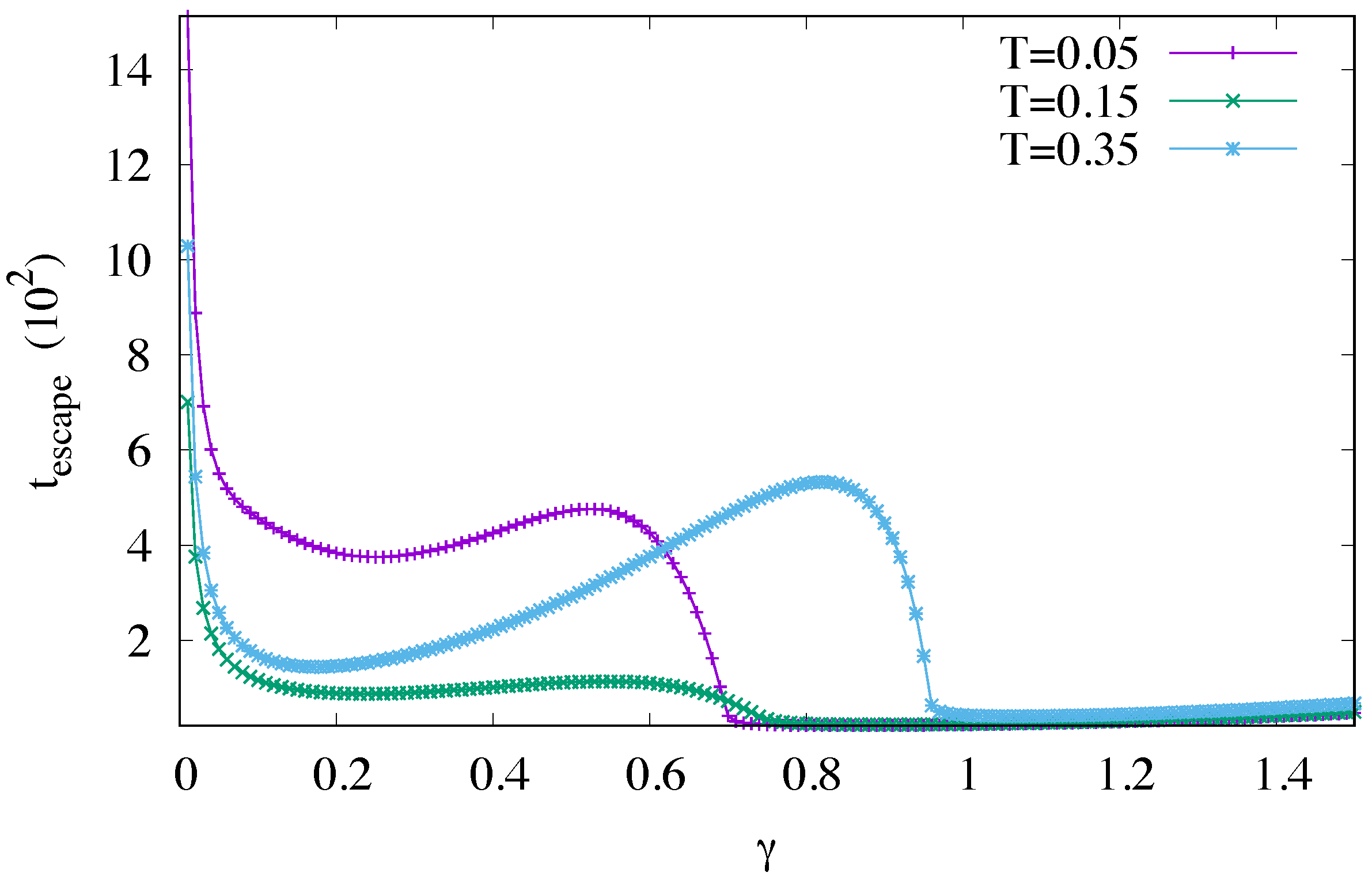
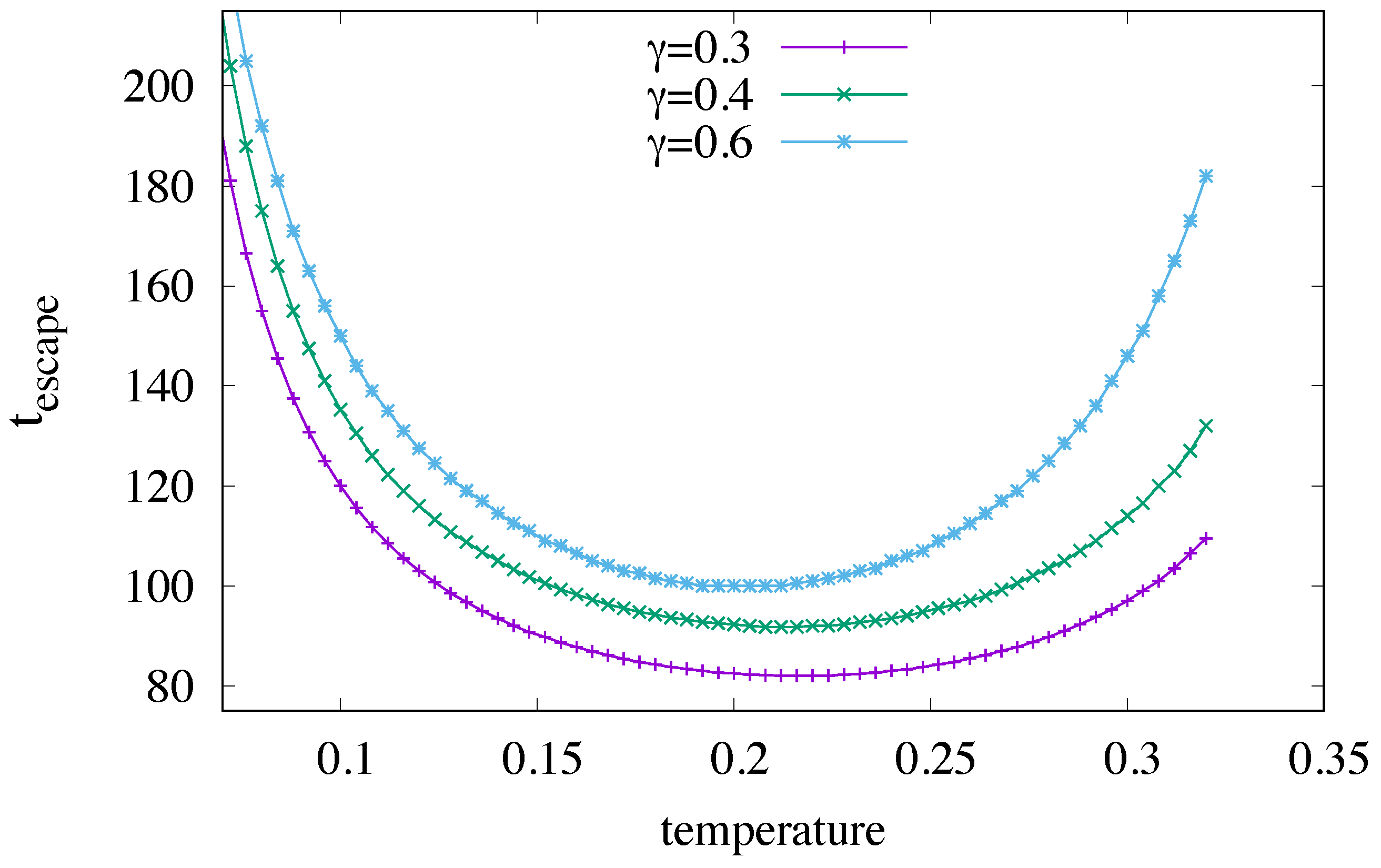
4.4. Escape Time
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bars, I.; Steinhardt, P.J.; Turok, N. Cyclic cosmology, conformal symmetry and the metastability of the Higgs. Phys. Lett. B 2013, 726, 50–55. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Giudice, G.F.; Riotto, A. Cosmological implications of the Higgs mass measurement. J. Cosmol. Astropart. Phys. 2008, 2008. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. A Cyclic Model of the Universe. Science 2002, 296, 1436–1439. [Google Scholar] [CrossRef] [PubMed]
- Steinhardt, P.J.; Turok, N. Cosmic evolution in a cyclic universe. Phys. Rev. D 2002, 65, 126003. [Google Scholar] [CrossRef]
- Bovier, A.; den Hollander, F. Metastability. A Potential-Theoretic Approach; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Serdukova, L.; Zheng, Y.; Duan, J.; Kurths, J. Stochastic basins of attraction for metastable states. Chaos 2016, 26, 073117. [Google Scholar] [CrossRef] [PubMed]
- Valenti, D.; Magazzù, L.; Caldara, P.; Spagnolo, B. Stabilization of quantum metastable states by dissipation. Phys. Rev. B 2015, 91, 235412. [Google Scholar] [CrossRef]
- Menck, P.; Heitzing, J.; Marwan, N.; Kurths, J. How basin stability complements the linear-stability paradigm. Nat. Phys. 2013, 9, 89–92. [Google Scholar] [CrossRef]
- Oliveiri, E.; Vares, M. Large Deviations and Metastability; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Scütte, C.; Sarich, M. Metastability and Markov State Models in Molecular Dynamics; American Mathematical Society: Providence, RI, USA, 2013. [Google Scholar]
- Beltrán, J.; Landim, C. Tunneling and metastability of continuous time Markov chains II, the nonreversible case. J. Stat. Phys. 2012, 149, 598–618. [Google Scholar] [CrossRef]
- Giardina, I. Metastable states in glassy systems. In Les Houches—Session LXXXV: Complex Systems; Bouchaud, J.-P., Mezard, M., Dalibard, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 373–394. [Google Scholar]
- Bouchaud, J.-P.; Mezard, M.; Dalibard, J. (Eds.) Les Houches—Session LXXXV: Complex Systems; Elsevier: Amsterdam, The Netherlands, 2007.
- Dubkov, A.A.; Agudov, N.V.; Spagnolo, B. Noise-enhanced stability in fluctuating metastable states. Phys. Rev. E 2004, 69, 061103. [Google Scholar] [CrossRef] [PubMed]
- Spagnolo, B.; Dubkov, A.A.; Agudov, N.V. Enhancement of stability in randomly switching potential with metastable state. Eur. Phys. J. B 2004, 40, 273–281. [Google Scholar] [CrossRef]
- Augello, G.; Valenti, D.; Spagnolo, B. Non-Gaussian noise effects in the dynamics of a short overdamped Josephson junction. Eur. Phys. J. B 2010, 78, 225–234. [Google Scholar] [CrossRef]
- Valenti, D.; Guarcello, C.; Spagnolo, B. Switching times in long-overlap Josephson junctions subject to thermal fluctuations and non-Gaussian noise sources. Phys. Rev. B 2014, 89, 214510. [Google Scholar] [CrossRef]
- Vilar, J.M.G.; Rubi, J.M. Noise Suppression by Noise. Phys. Rev. Lett. 2001, 86, 950–953. [Google Scholar] [CrossRef] [PubMed]
- Ciuchi, S.; de Pasquale, F.; Spagnolo, B. Nonlinear Relaxation in the presence of an Absorbing Barrier. Phys. Rev. E 1993, 47, 3915–3926. [Google Scholar] [CrossRef]
- Seol, Y.; Visscher, K.; Walton, D.B. Suppression of Noise in a Noisy Optical Trap. Phys. Rev. Lett. 2004, 93, 160602. [Google Scholar] [CrossRef] [PubMed]
- Walton, D.B.; Visscher, K. Noise suppression and spectral decomposition for state-dependent noise in the presence of a stationary fluctuating input. Phys. Rev. E 2004, 69, 051110. [Google Scholar] [CrossRef] [PubMed]
- Valenti, D.; Augello, G.; Spagnolo, B. Dynamics of a FitzHugh-Nagumo system subjected to autocorrelated noise. Eur. Phys. J. B 2008, 65, 443–451. [Google Scholar] [CrossRef]
- Fiasconaro, A.; Spagnolo, B. Stability measures in metastable states with Gaussian colored noise. Phys. Rev. E 2009, 80, 041110. [Google Scholar] [CrossRef] [PubMed]
- Romanczuk, P.; Bär, M.; Ebeling, W.; Lindner, B.; Schimansky-Geier, L. Active Brownian particles. Eur. Phys. J. Spec. Top. 2012, 202, 1–162. [Google Scholar] [CrossRef]
- Sonnenschein, B.; Schimansky-Geier, L. Onset of synchronization in complex networks of noisy oscillators. Phys. Rev. E 2012, 85, 051116. [Google Scholar] [CrossRef] [PubMed]
- Martens, S.; Straube, A.V.; Schmid, G.; Schimansky-Geier, L.; Hänggi, P. Hydrodynamically Enforced Entropic Trapping of Brownian Particles. Phys. Rev. Lett. 2013, 110, 010601. [Google Scholar] [CrossRef] [PubMed]
- Kromer, J.A.; Pinto, R.D.; Lindner, B.; Schimansky-Geier, L. Noise-controlled bistability in an excitable system with positive feedback. Europhys. Lett. 2014, 108, 20007. [Google Scholar] [CrossRef]
- Sonnenschein, B.; Peron, T.K.D.M.; Rodrigues, F.A.; Kurths, J.; Schimansky-Geier, L. Cooperative behavior between oscillatory and excitable units: The peculiar role of positive coupling-frequency correlations. Eur. Phys. J. B 2014, 87, 182. [Google Scholar] [CrossRef]
- Dugaev, V.K.; Inglot, M.; Sherman, E.Y.; Barnas, J. Spin Hall effect and spin current generation in two-dimensional systems with random Rashba spin-orbit coupling. J. Magn. Magn. Mater. 2012, 324, 3573–3575. [Google Scholar] [CrossRef]
- Ghosh, P.; Chattopadhyay, S.; Chaudhuri, J.R. Enhancement of current commensurate with mutual noise-noise correlation in a symmetric periodic substrate: The benefits of noise and nonlinearity. Chem. Phys. 2012, 402, 48–55. [Google Scholar] [CrossRef]
- Sen, M.K.; Ray, S.; Baura, A.; Bag, B.C. Effect of multiplicative noise on the self-induced aggregation kinetics of Brownian particles. Chem. Phys. Lett. 2013, 559, 117–122. [Google Scholar] [CrossRef]
- Yoshimoto, M.; Shirahama, H.; Kurosawa, S. Noise-induced order in the chaos of the Belousov–Zhabotinsky reaction. J. Chem. Phys. 2008, 129, 014508. [Google Scholar] [CrossRef] [PubMed]
- Pizzolato, N.; Fiasconaro, A.; Adorno, D.P.; Spagnolo, B. Resonant activation in polymer translocation: New insights into escape dynamics of molecules driven by an oscillating field. Phys. Biol. 2010, 7, 034001. [Google Scholar] [CrossRef] [PubMed]
- Valenti, D.; Denaro, G.; Adorno, D.P.; Pizzolato, N.; Zammito, S.; Spagnolo, B. Monte Carlo analysis of polymer translocation with deterministic and noisy electric fields. Cent. Eur. J. Phys. 2012, 10, 560–567. [Google Scholar] [CrossRef]
- Pizzolato, N.; Fiasconaro, A.; Adorno, D.P.; Spagnolo, B. Translocation dynamics of a short polymer driven by an oscillating force. J. Chem. Phys. 2013, 138, 054902. [Google Scholar] [CrossRef] [PubMed]
- Atxitia, U.; Chubykalo-Fesenko, O.; Chantrell, R.W.; Nowak, U.; Rebei, A. Ultrafast Spin Dynamics: The Effect of Colored Noise. Phys. Rev. Lett. 2009, 102, 057203. [Google Scholar] [CrossRef] [PubMed]
- Trapanese, M. Noise enhanced stability in magnetic systems. J. Appl. Phys. 2009, 105. [Google Scholar] [CrossRef]
- Adorno, D.P.; Capizzo, M.C.; Zarcone, M. Changes of electronic noise induced by oscillating fields in bulk GaAs semiconductors. Fluct. Noise Lett. 2008, 8, L11–L22. [Google Scholar] [CrossRef]
- Adorno, D.P.; Pizzolato, N.; Spagnolo, B. External Noise Effects on the Electron Velocity Fluctuations in Semiconductors. Acta Phys. Pol. A 2008, 113, 985–988. [Google Scholar] [CrossRef]
- Adorno, D.P.; Pizzolato, N.; Spagnolo, B. Noise influence on electron dynamics in semiconductors driven by a periodic electric field. J. Stat. Mech. Theory Exp. 2009. [Google Scholar] [CrossRef]
- Adorno, D.P.; Pizzolato, N.; Valenti, D.; Spagnolo, B. External noise effects in doped semiconductors operating under sub-THz signals. Rep. Math. Phys. 2012, 70, 171–179. [Google Scholar] [CrossRef]
- Adorno, D.P.; Pizzolato, N.; Alaimo, P.; Spagnolo, B.; Di Paola, B. Electron dynamical response in InP semiconductors driven by fluctuating electric fields. Chaos Soliton Fract. 2015, 81, 425–431. [Google Scholar] [CrossRef]
- Adorno, D.P.; Pizzolato, N.; Spagnolo, B. Noise-induced resonance-like phenomena in InP crystals embedded in fluctuating electric fields. J. Stat. Mech. Theory Exp. 2016, 2016, 054021. [Google Scholar] [CrossRef]
- Lodato, M.A.; Adorno, D.P.; Pizzolato, N.; Spezia, S.; Spagnolo, B. External Noise Effects in Silicon MOS Inversion Layer. Acta Phys. Pol. B 2013, 44, 1163–1172. [Google Scholar] [CrossRef]
- Spagnolo, B.; Dubkov, A.; Pankratov, A.; Pankratova, E.; Fiasconaro, A.; Ochab-Marcinek, A. Lifetime of metastable states and suppression of noise in interdisciplinary physical models. Acta Phys. Pol. B 2007, 38, 1925–1950. [Google Scholar]
- Bonanno, G.; Valenti, D.; Spagnolo, B. Mean escape time in a system with stochastic volatility. Phys. Rev. E 2007, 75, 016106. [Google Scholar] [CrossRef] [PubMed]
- Mankin, R.; Soika, E.; Sauga, A.; Ainsaar, A. Thermally enhanced stability in fluctuating bistable potentials. Phys. Rev. E 2008, 77, 051113. [Google Scholar] [CrossRef] [PubMed]
- Valenti, D.; Spagnolo, B.; Bonanno, G. Hitting time distributions in financial markets. Physica A 2007, 382, 311–320. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Spagnolo, B. Probability distribution of the Residence Times in Periodically Fluctuating Metastable Systems. Int. J. Bifurc. Chaos 1998, 8, 783–790. [Google Scholar] [CrossRef]
- Bonanno, G.; Valenti, D.; Spagnolo, B. Role of Noise in a Market Model with Stochastic Volatility. Eur. Phys. J. B 2006, 53, 405–409. [Google Scholar] [CrossRef]
- Agudov, N.V.; Dubkov, A.A.; Spagnolo, B. Escape from a metastable state with fluctuating barrier. Physica A 2003, 325, 144–151. [Google Scholar] [CrossRef]
- Spagnolo, B.; Agudov, N.V.; Dubkov, A.A. Noise enhanced stability. Acta Phys. Pol. B 2004, 35, 1419–1436. [Google Scholar]
- Mantegna, R.; Spagnolo, B. Noise Enhanced Stability in an Unstable System. Phys. Rev. Lett. 1996, 76, 563–566. [Google Scholar] [CrossRef] [PubMed]
- Agudov, N.V.; Spagnolo, B. Noise-enhanced stability of periodically driven metastable states. Phys. Rev. E 2001, 64, 035102. [Google Scholar] [CrossRef] [PubMed]
- Fiasconaro, A.; Spagnolo, B.; Boccaletti, S. Signatures of noise-enhanced stability in metastable states. Phys. Rev. E 2005, 72, 061110. [Google Scholar] [CrossRef] [PubMed]
- Fiasconaro, A.; Mazo, J.J.; Spagnolo, B. Noise-induced enhancement of stability in a metastable system with damping. Phys. Rev. E 2010, 82, 041120. [Google Scholar] [CrossRef] [PubMed]
- Agudov, N.V.; Malakhov, A.N. Decay of unstable equilibrium and nonequilibrium states with inverse probability current taken into account. Phys. Rev. E 1999, 60, 6333–6342. [Google Scholar] [CrossRef]
- Dan, D.; Mahato, M.C.; Jayannavar, A.M. Mobility and stochastic resonance in spatially inhomogeneous systems. Phys. Rev. E 1999, 60, 6421–6428. [Google Scholar] [CrossRef]
- Wackerbauer, R. When noise decreases deterministic diffusion. Phys. Rev. E 1999, 59, 2872–2879. [Google Scholar] [CrossRef]
- Mielke, A. Noise Induced Stability in Fluctuating, Bistable Potentials. Phys. Rev. Lett. 2000, 84, 818–821. [Google Scholar] [CrossRef] [PubMed]
- Pankratov, A.L.; Spagnolo, B. Suppression of timing errors in short overdamped Josephson junctions. Phys. Rev. Lett. 2004, 93, 177001. [Google Scholar] [CrossRef] [PubMed]
- D’Odorico, P.; Laio, F.; Ridolfi, L. Noise-induced stability in dryland plant ecosystems. Proc. Natl. Acad. Sci. USA 2005, 102, 10819–10822. [Google Scholar] [CrossRef] [PubMed]
- Hurtado, P.I.; Marro, J.; Garrido, P. Metastability, nucleation, and noise-enhanced stabilization out of equilibrium. Phys. Rev. E 2006, 74, 050101. [Google Scholar] [CrossRef] [PubMed]
- Li, J.H.; Łuczka, J. Thermal-inertial ratchet effects: Negative mobility, resonant activation, noise-enhanced stability, and noise-weakened stability. Phys. Rev. E 2010, 82, 041104. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, A.A.; Pankratov, A.L. Influence of the size of uniaxial magnetic nanoparticle on the reliability of high-speed switching. Phys. Rev. B 2010, 82, 132405. [Google Scholar] [CrossRef]
- Jia, Z.-L.; Mei, D.-C. Effects of linear and nonlinear time-delayed feedback on the noise-enhanced stability phenomenon in a periodically driven bistable system. J. Stat. Mech. Theory Exp. 2011, 2011. [Google Scholar] [CrossRef]
- Parker, M.; Kamenev, A.; Meerson, B. Noise-induced stabilization in population dynamics. Phys. Rev. Lett. 2011, 107, 180603. [Google Scholar] [CrossRef] [PubMed]
- Kramers, H.A. Brownian Motion in a Field of Force and the Diffusion Model of Chemical Reactions. Physica 1940, 7, 284–304. [Google Scholar] [CrossRef]
- Hänggi, P.H.; Talkner, P.; Borkovec, M. Reaction Rate Theory: Fifty Years After Kramers. Rev. Mod. Phys. 1990, 62, 251–342. [Google Scholar] [CrossRef]
- Reimann, P.; Van den Broeck, C.; Linke, H.; Hänggi, P.; Rubi, J.; Pérez-Madrid, A. Giant acceleration of free diffusion by use of tilted periodic potentials. Phys. Rev. Lett. 2001, 87, 010602. [Google Scholar] [CrossRef] [PubMed]
- Dubkov, A.A.; Spagnolo, B. Acceleration of diffusion in randomly switching potential with supersymmetry. Phys. Rev. E 2005, 72, 041104. [Google Scholar] [CrossRef] [PubMed]
- Wendin, G.; Shumeiko, V.S. Quantum bits with Josephson junctions. Low Temp. Phys. 2007, 33, 724–744. [Google Scholar] [CrossRef]
- Kim, J.H.; Dhungana, R.P.; Park, K.-S. Decoherence in Josephson vortex quantum bits: Long-Josephson-junction approach to a two-state system. Phys. Rev. B 2006, 73, 214506. [Google Scholar] [CrossRef]
- Szombati, D.B.; Nadj-Perge, S.; Car, D.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Josephson Φ0-junction in nanowire quantum dots. Nat. Phys. 2016, 12, 568–572. [Google Scholar] [CrossRef]
- Levenson-Falk, E.M.; Vijay, R.; Antler, N.; Siddiqi, I. A dispersive nanoSQUID magnetometer for ultra-low noise, high bandwidth flux detection. Supercond. Sci. Technol. 2013, 26, 055015. [Google Scholar] [CrossRef]
- Grabert, H. Theory of a Josephson junction detector of non-Gaussian noise. Phys. Rev. B 2008, 77, 205315. [Google Scholar] [CrossRef]
- Filatrella, G.; Pierro, V. Detection of noise-corrupted sinusoidal signals with Josephson junctions. Phys. Rev. E 2010, 82, 046712. [Google Scholar] [CrossRef] [PubMed]
- Addesso, P.; Filatrella, G.; Pierro, V. Characterisation of escape times of Josephson junctions for signal detection. Phys. Rev. E 2012, 85, 016708. [Google Scholar] [CrossRef] [PubMed]
- Spagnolo, B.; Valenti, D.; Guarcello, C.; Carolllo, A.; Adorno, D.P.; Spezia, S.; Pizzolato, N.; Di Paola, B. Noise-induced effects in nonlinear relaxation of condensed matter systems. Chaos Soliton Fract. 2015, 81, 412–424. [Google Scholar] [CrossRef]
- Guarcello, C.; Valenti, D.; Spagnolo, B. Phase dynamics in graphene-based Josephson junctions in the presence of thermal and correlated fluctuations. Phys. Rev. B 2015, 92, 174519. [Google Scholar] [CrossRef]
- Guarcello, C.; Valenti, D.; Carollo, A.; Spagnolo, B. Effects of Lévy noise on the dynamics of sine-Gordon solitons in long Josephson junctions. J. Stat. Mech. Theory Exp. 2016, 2016. [Google Scholar] [CrossRef]
- Spezia, S.; Adorno, D.P.; Pizzolato, N.; Spagnolo, B. New insights into electron spin dynamics in the presence of correlated noise. J. Phys. Condens. Matter 2012, 24, 052204. [Google Scholar] [CrossRef] [PubMed]
- Spezia, S.; Adorno, D.P.; Pizzolato, N.; Spagnolo, B. Effect of a Fluctuating Electric Field on Electron Spin Dephasing Time in III-V Semiconductors. Acta Phys. Pol. B 2012, 43, 1191–1201. [Google Scholar] [CrossRef]
- Spezia, S.; Adorno, D.P.; Pizzolato, N.; Spagnolo, B. Enhancement of electron spin lifetime in GaAs crystals: The benefits of dichotomous noise. Eur. Phys. Lett. 2013, 104, 47011. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Influence of Dissipation on Quantum Tunneling in Macroscopic Systems. Phys. Rev. Lett. 1981, 46, 211–214. [Google Scholar] [CrossRef]
- Weiss, U. Quantum Dissipative Systems, 4th ed.; World Scientific: Singapore, Singapore, 2012. [Google Scholar]
- Thorwart, M.; Grifoni, M.; Hänggi, P. Strong Coupling Theory for Tunneling and Vibrational Relaxation in Driven Bistable Systems. Ann. Phys. 2001, 293, 15–66. [Google Scholar] [CrossRef]
- Affleck, I. Quantum-Statistical Metastability. Phys. Rev. Lett. 1981, 46, 388–391. [Google Scholar] [CrossRef]
- Grabert, H.; Olschowski, P.; Weiss, U. Quantum decay rates for dissipative systems at finite temperatures. Phys. Rev. B 1987, 36, 1931–1951. [Google Scholar] [CrossRef]
- Barone, A.; Paterno, G. Physics and Applications of the Josephson Effect; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Guarcello, C.; Valenti, D.; Carollo, A.; Spagnolo, B. Stabilization Effects of Dichotomous Noise on the Lifetime of the Superconducting State in a Long Josephson Junction. Entropy 2015, 17, 2862–2875. [Google Scholar] [CrossRef]
- Novotný, T. Josephson junctions as threshold detectors of full counting statistics: Open issues. J. Stat. Mech. Theory Exp. 2009. [Google Scholar] [CrossRef]
- Tobiska, J.; Nazarov, Y.V. Josephson junctions as threshold detectors for full counting statistics. Phys. Rev. Lett. 2004, 93, 106801. [Google Scholar] [CrossRef] [PubMed]
- Sukhorukov, E.V.; Jordan, A.N. Stochastic dynamics of a Josephson junction threshold detector. Phys. Rev. Lett. 2007, 98, 136803. [Google Scholar] [CrossRef] [PubMed]
- Dubkov, A.A.; Spagnolo, B. Langevin Approach to Lévy flights in fixed potentials: Exact results for stationary probability distributions. Acta Phys. Pol. B 2007, 38, 1745–1758. [Google Scholar]
- Ankerhold, J. Detecting charge noise with a Josephson junction: A problem of thermal escape in presence of non-Gaussian fluctuations. Phys. Rev. Lett. 2007, 98, 036601. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.-H.; Jeong, D.; Choi, J.-H.; Doh, Y.-J.; Lee, H.-J. Electrically tunable macroscopic quantum tunnelling in a graphene-based Josephson junction. Phys. Rev. Lett. 2011, 107, 146605. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.-H.; Lee, G.-H.; Park, S.; Jeong, D.; Lee, J.-O.; Sim, H.-S.; Doh, Y.-J.; Lee, H.-J. Complete gate control of supercurrent in graphene p–n junctions. Nat. Commun. 2013, 4, 2525. [Google Scholar] [CrossRef] [PubMed]
- Heersche, H.B.; Jarillo-Herrero, P.; Oostinga, J.B.; Vandersypen, L.M.; Morpurgo, A.F. Bipolar supercurrent in graphene. Nature 2007, 446, 56–59. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Skachko, I.; Andrei, E.Y. Josephson current and multiple Andreev reflections in graphene sns junctions. Phys. Rev. B 2008, 77, 184507. [Google Scholar] [CrossRef]
- Miao, F.; Wijeratne, S.; Zhang, Y.; Coskun, U.C.; Bao, W.; Lau, C.N. Phase-coherent transport in graphene quantum billiards. Science 2007, 317, 1530–1533. [Google Scholar] [CrossRef] [PubMed]
- Jeong, D.; Choi, J.-H.; Lee, G.-H.; Jo, S.; Doh, Y.-J.; Lee, H.-J. Observation of supercurrent in PbIn-graphene- PbIn Josephson junction. Phys. Rev. B 2011, 83, 094503. [Google Scholar] [CrossRef]
- Coskun, U.; Brenner, M.; Hymel, T.; Vakaryuk, V.; Levchenko, A.; Bezryadin, A. Distribution of supercurrent switching in graphene under the proximity effect. Phys. Rev. Lett. 2012, 108, 097003. [Google Scholar] [CrossRef] [PubMed]
- Mizuno, N.; Nielsen, B.; Du, X. Ballistic-like supercurrent in suspended graphene Josephson weak links. Nat. Commun. 2013, 4, 2716. [Google Scholar] [CrossRef] [PubMed]
- Kogan, S. Electronic Noise and Fluctuations in Solids; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Pankratov, E.; Spagnolo, B. Optimization of impurity profile for p-n-junction in heterostructures. Eur. Phys. J. B 2005, 46, 15–19. [Google Scholar] [CrossRef]
- Ustinov, A. Solitons in Josephson junctions. Physica D 1998, 123, 315–329. [Google Scholar] [CrossRef]
- Büttiker, M.; Landauer, R. Nucleation theory of overdamped soliton motion. Phys. Rev. A 1981, 23, 1397–1410. [Google Scholar] [CrossRef]
- McLaughlin, D.W.; Scott, A.C. Perturbation analysis of fluxon dynamics. Phys. Rev. A 1978, 18, 1652–1680. [Google Scholar] [CrossRef]
- Dueholm, B.; Joergensen, E.; Levring, O.; Monaco, R.; Mygind, J.; Pedersen, N.; Samuelsen, M. An analysis of fluxons in long Josephson junctions. IEEE Trans. Magn. 1983, 19, 1196–1200. [Google Scholar] [CrossRef]
- Titov, M.; Beenakker, C.W. Josephson effect in ballistic graphene. Phys. Rev. B 2006, 74, 041401. [Google Scholar] [CrossRef]
- Hagymási, I.; Kormányos, A.; Cserti, J. Josephson current in ballistic superconductor-graphene systems. Phys. Rev. B 2010, 82, 134516. [Google Scholar] [CrossRef]
- Devoret, M.H.; Martinis, J.M.; Esteve, D.; Clarke, J. Resonant activation from the zero-voltage state of a current-biased Josephson junction. Phys. Rev. Lett. 1984, 53, 1260–1263. [Google Scholar] [CrossRef]
- Devoret, M.H.; Martinis, J.M.; Clarke, J. Measurements of macroscopic quantum tunneling out of the zero-voltage state of a current-biased Josephson junction. Phys. Rev. Lett. 1985, 55, 1908–1911. [Google Scholar] [CrossRef] [PubMed]
- Martinis, J.M.; Devoret, M.H.; Clarke, J. Experimental tests for the quantum behavior of a macroscopic degree of freedom: The phase difference across a Josephson junction. Phys. Rev. B 1987, 35, 4682–4698. [Google Scholar] [CrossRef]
- Fiasconaro, A.; Spagnolo, B. Resonant activation in piecewise linear asymmetric potentials. Phys. Rev. E 2011, 83, 041122. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Tan, X.; Yu, Y.; Sun, G.; Kang, L.; Xu, W.; Chen, J.; Wu, P. Resonant activation through effective temperature oscillation in a Josephson tunnel junction. Phys. Rev. E 2009, 79, 030104. [Google Scholar] [CrossRef] [PubMed]
- Mantegna, R.; Spagnolo, B. Numerical simulation of resonant activation in a fluctuating metastable model system. J. Phys. IV (France) 1998, 8, 247–251. [Google Scholar] [CrossRef]
- Fedorov, K.; Pankratov, A.L.; Spagnolo, B. Influence of length on the noise delayed switching of long Josephson junctions. Int. J. Bifurc. Chaos 2008, 18, 2857–2862. [Google Scholar] [CrossRef]
- Fedorov, K.; Pankratov, A. Mean time of the thermal escape in a current-biased long-overlap Josephson junction. Phys. Rev. B 2007, 76, 024504. [Google Scholar] [CrossRef]
- Augello, G.; Valenti, D.; Pankratov, A.L.; Spagnolo, B. Lifetime of the superconductive state in short and long Josephson junctions. Eur. Phys. J. B 2009, 70, 145–151. [Google Scholar] [CrossRef]
- Pankratov, A.L.; Gordeeva, A.V.; Kuzmin, L.S. Drastic Suppression of Noise-Induced Errors in Underdamped Long Josephson Junctions. Phys. Rev. Lett. 2012, 109, 087003. [Google Scholar] [CrossRef] [PubMed]
- Guarcello, C.; Valenti, D.; Augello, G.; Spagnolo, B. The Role of Non-Gaussian Sources in the Transient Dynamics of Long Josephson Junctions. Acta Phys. Pol. B 2013, 44, 997–1005. [Google Scholar] [CrossRef]
- Valenti, D.; Schimansky-Geier, L.; Sailer, X.; Spagnolo, B. Moment equations for a spatially extended system of two competing species. Eur. Phys. J. B 2006, 50, 199–203. [Google Scholar] [CrossRef]
- Valenti, D.; Schimansky-Geier, L.; Sailer, X.; Spagnolo, B.; Iacomi, M. Moment Equations in a Lotka–Volterra Extended System with Time Correlated Noise. Acta Phys. Pol. B 2007, 38, 1961–1972. [Google Scholar]
- Valenti, D.; Spagnolo, B. Stochastic dynamics and mean field approach in a system of three interacting species. Cent. Eur. J. Phys. 2009, 7, 457–471. [Google Scholar] [CrossRef]
- Valenti, D.; Pizzolato, N.; Spagnolo, B. Mean Field Approach and Role of the Coloured Noise in the Dynamics of Three Interacting Species. Acta Phys. Pol. B 2010, 41, 1051–1071. [Google Scholar]
- Doering, C.R.; Gadoua, J.C. Resonant activation over a fluctuating barrier. Phys. Rev. Lett. 1992, 69, 2318–2321. [Google Scholar] [CrossRef] [PubMed]
- Mantegna, R.N.; Spagnolo, B. Experimental investigation of resonant activation. Phys. Rev. Lett. 2000, 84, 3025–3028. [Google Scholar] [CrossRef] [PubMed]
- Pechukas, P.; Hänggi, P. Rates of activated processes with fluctuating barriers. Phys. Rev. Lett. 1994, 73, 2772–2775. [Google Scholar] [CrossRef] [PubMed]
- Marchi, M.; Marchesoni, F.; Gammaitoni, L.; Menichella-Saetta, E.; Santucci, S. Resonant activation in a bistable system. Phys. Rev. E 1996, 54, 3479–3487. [Google Scholar] [CrossRef]
- Fiasconaro, A.; Ochab–Marcinek, A.; Spagnolo, B.; Gudowska–Nowak, E. Monitoring noise-resonant effects in cancer growth influenced by spontaneous fluctuations and periodic treatment. Eur. Phys. J. B 2008, 65, 435–442. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E. Lévy stable noise-induced transitions: Stochastic resonance, resonant activation and dynamic hysteresis. J. Stat. Mech. Theory Exp. 2009. [Google Scholar] [CrossRef]
- Miyamoto, S.; Nishiguchi, K.; Ono, Y.; Itoh, K.M.; Fujiwara, A. Resonant escape over an oscillating barrier in a single-electron ratchet transfer. Phys. Rev. B 2010, 82, 033303. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Arita, M. Escape process and stochastic resonance under noise intensity fluctuation. Phys. Lett. A 2011, 375, 3450–3458. [Google Scholar] [CrossRef]
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; Von Molnár, S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A Spin-Based Electronics Vision for the Future. Science 2001, 294, 1488–1495. [Google Scholar] [CrossRef] [PubMed]
- Žutić, I.; Fabian, J.; Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323–410. [Google Scholar] [CrossRef]
- Fabian, J.; Matos-Abiague, A.; Ertler, C.; Stano, P.; Žutić, I. Semiconductor Spintronics. Acta Phys. Slovaca 2007, 57, 565–907. [Google Scholar] [CrossRef]
- Behin-Aein, B.; Datta, D.; Salahuddin, S.; Datta, S. Proposal for an all-spin logic device with built-in memory. Nat. Nanotechnol. 2010, 5, 266–270. [Google Scholar] [CrossRef] [PubMed]
- Pulizzi, F. Spintronics. Nat. Mater. 2012, 11. [Google Scholar] [CrossRef] [PubMed]
- Salahuddin, S. Solid-state physics: A new spin on spintronics. Nature 2013, 494, 43–44. [Google Scholar] [CrossRef] [PubMed]
- Cadiz, F.; Barate, P.; Paget, D.; Grebenkov, D.; Korb, J.P.; Rowe, A.C.H.; Amand, T.; Arscott, S.; Peytavit, E. All optical method for investigation of spin and charge transport in semiconductors: Combination of spatially and time-resolved luminescence. J. Appl. Phys. 2014, 116, 023711. [Google Scholar] [CrossRef]
- Datta, S.; Das, B. Electronic analog of the electro-optic modulator. Appl. Phys. Lett. 1990, 56, 665–667. [Google Scholar] [CrossRef]
- Awschalom, D.D.; Bassett, L.C.; Dzurak, A.S.; Hu, E.L.; Petta, J.R. Quantum Spintronics: Engineering and Manipulating Atom-Like Spins in Semiconductors. Science 2013, 339, 1174–1179. [Google Scholar] [CrossRef] [PubMed]
- Siegel, G.; Prestgard, M.C.; Teng, S.; Tiwari, A. Robust longitudinal spin-Seebeck effect in Bi-YIG thin films. Sci. Rep. 2014, 4, 4429. [Google Scholar] [CrossRef] [PubMed]
- D’yakonov, M.I. Introduction to spin physics in semiconductors. Physica E 2006, 35, 246–250. [Google Scholar] [CrossRef]
- D’yakonov, M.I.; Perel, V.I. Possibility of Orienting Electron Spins with Current. JETP Lett. 1971, 13, 467–469. [Google Scholar]
- Litvinenko, K.L.; Leontiadou, M.A.; Li, J.; Clowes, S.K.; Emeny, M.T.; Ashley, T.; Pidgeon, C.R.; Cohen, L.F.; Murdin, B.N. Strong dependence of spin dynamics on the orientation of an external magnetic field for InSb and InAs. Appl. Phys. Lett. 2010, 96, 111107. [Google Scholar] [CrossRef]
- Saikin, S.; Shen, M.; Cheng, M.C. Spin dynamics in a compound semiconductor spintronic structure with a Schottky barrier. J. Phys. Condens. Matter 2006, 18, 1535–1544. [Google Scholar] [CrossRef]
- Tong, H.; Wu, M.W. Multivalley spin relaxation in n-type bulk GaAs in the presence of high electric fields. Phys. Rev. B 2012, 85, 075203. [Google Scholar] [CrossRef]
- Fu, J.Y.; Weng, M.Q.; Wu, M.W. Spin-orbit coupling in bulk GaAs. Physica E 2008, 40, 2890–2893. [Google Scholar] [CrossRef]
- Slichter, C.P. Principles of Magnetic Resonance; Lotsch, H.K.V., Ed.; Springer: Berlin, Germany, 1996; p. 399. [Google Scholar]
- Glazov, M.M.; Ivchenko, E.L. Precession spin relaxation mechanism caused by frequent electron-electron collisions. JETP Lett. 2002, 75, 403–405. [Google Scholar] [CrossRef]
- Adorno, D.P. Polarization of the radiation emitted in GaAs semiconductors driven by far-infrared fields. Laser Phys. 2010, 20, 1061–1067. [Google Scholar] [CrossRef]
- Adorno, D.P.; Pizzolato, N.; Fazio, C. Elucidating the electron transport in semiconductors via Monte Carlo simulations: An inquiry-driven learning path for engineering undergraduates. Eur. J. Phys. 2015, 36, 055017. [Google Scholar] [CrossRef]
- Spezia, S.; Adorno, D.P.; Pizzolato, N.; Spagnolo, B. Relaxation of electron spin during high-field transport in GaAs bulk. J. Stat. Mech. Theory Exp. 2010. [Google Scholar] [CrossRef]
- Spezia, S.; Adorno, D.P.; Pizzolato, N.; Spagnolo, B. Temperature dependence of spin depolarization of drifting electrons in n-type GaAs bulk. Acta Phys. Pol. B 2010, 41, 1171–1180. [Google Scholar]
- Adorno, D.P.; Zarcone, M.; Ferrante, G. Far-infrared harmonic generation in semiconductors: A Monte Carlo simulation. Laser Phys. 2000, 10, 310–315. [Google Scholar]
- Peschke, C. The impact of electron-electron interaction on electron transport in GaAs at high electric fields. J. Phys. Condens. Matter 1994, 6, 7027–7044. [Google Scholar] [CrossRef]
- Moško, M.; Mošková, A. Ensemble Monte Carlo simulation of electron-electron scattering: Improvements of conventional methods. Phys. Rev. B 1991, 44, 10794–10803. [Google Scholar] [CrossRef]
- Mošková, A.; Moško, M. Exchange carrier-carrier scattering of photoexcited spin-polarized carriers in GaAs quantum wells: Monte Carlo study. Phys. Rev. B 1994, 49, 7443–7452. [Google Scholar] [CrossRef]
- Bena, I. Dichotomous Markov Noise: Exact Results for Out-of-Equilibrium Systems. Int. J. Mod. Phys. B 2006, 20, 2825–2888. [Google Scholar] [CrossRef]
- Barik, D.; Ghosh, P.K.; Ray, D.S. Langevin dynamics with dichotomous noise; direct simulation and applications. J. Stat. Mech. Theory Exp. 2006. [Google Scholar] [CrossRef]
- Shit, A.; Chattopadhyay, S.; Chaudhuri, J.R. Taming the escape dynamics of nonadiabatic time-periodically driven quantum dissipative system within the frame of Wigner formalism. Chem. Phys. 2014, 431–432, 26–38. [Google Scholar] [CrossRef]
- Shit, A.; Chattopadhyay, S.; Chaudhuri, J.R. Quantum stochastic dynamics in the presence of a time-periodic rapidly oscillating potential: Nonadiabatic escape rate. J. Phys. Chem. A 2013, 117, 8576–8590. [Google Scholar] [CrossRef] [PubMed]
- Devoret, M.H.; Schoelkopf, R.J. Superconducting Circuits for Quantum Information: An Outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef] [PubMed]
- You, J.Q.; Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 2011, 474, 589–597. [Google Scholar] [CrossRef] [PubMed]
- Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Harris, D.O.; Engerholm, G.G.; Gwinn, W.D. Calculation of Matrix Elements for One-Dimensional Quantum-Mechanical Problems and the Application to Anharmonic Oscillators. J. Chem. Phys. 1965, 43, 1515–1517. [Google Scholar] [CrossRef]
- Light, J.C.; Carrington, T. Discrete-Variable Representations and their Utilization. In Advances in Chemical Physics; John Wiley & Sons, Inc.: New York, NY, USA, 2007; Vol. 114, pp. 263–310. [Google Scholar]
- Magazzù, L.; Valenti, D.; Spagnolo, B.; Grifoni, M. Dissipative dynamics in a quantum bistable system: Crossover from weak to strong damping. Phys. Rev. E 2015, 92, 032123. [Google Scholar] [CrossRef] [PubMed]
- Thorwart, M.; Grifoni, M.; Hänggi, P. Strong Coupling Theory for Driven Tunneling and Vibrational Relaxation. Phys. Rev. Lett. 2000, 85, 860–863. [Google Scholar] [CrossRef] [PubMed]
- Grabert, H.; Schramm, P.; Ingold, G.L. Quantum Brownian motion: The functional integral approach. Phys. Rep. 1988, 168, 115–207. [Google Scholar] [CrossRef]
- Leggett, A.J.; Chakravarty, S.; Dorsey, A.T.; Fisher, M.P.A.; Garg, A.; Zwerger, W. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 1987, 59, 1–85. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spagnolo, B.; Guarcello, C.; Magazzù, L.; Carollo, A.; Persano Adorno, D.; Valenti, D. Nonlinear Relaxation Phenomena in Metastable Condensed Matter Systems. Entropy 2017, 19, 20. https://doi.org/10.3390/e19010020
Spagnolo B, Guarcello C, Magazzù L, Carollo A, Persano Adorno D, Valenti D. Nonlinear Relaxation Phenomena in Metastable Condensed Matter Systems. Entropy. 2017; 19(1):20. https://doi.org/10.3390/e19010020
Chicago/Turabian StyleSpagnolo, Bernardo, Claudio Guarcello, Luca Magazzù, Angelo Carollo, Dominique Persano Adorno, and Davide Valenti. 2017. "Nonlinear Relaxation Phenomena in Metastable Condensed Matter Systems" Entropy 19, no. 1: 20. https://doi.org/10.3390/e19010020
APA StyleSpagnolo, B., Guarcello, C., Magazzù, L., Carollo, A., Persano Adorno, D., & Valenti, D. (2017). Nonlinear Relaxation Phenomena in Metastable Condensed Matter Systems. Entropy, 19(1), 20. https://doi.org/10.3390/e19010020








