1. Introduction
Rolling bearing is one of the most important parts of rotating machinery. Its operation state directly determines whether the whole machine is safe, efficient, and reliable. However, due to the influences of transferring load and the additional load by the gear meshing in motor bearing, the fault rate of rolling bearing is always high without decreasing, and even shows an upward trend sometimes. Therefore, it is becoming increasingly important to improve the reliability of rolling bearings and to accurately detect bearing faults in time. When motor bearing faults occur, the periodic pulse impact force is generated, the nonlinear vibration of the mechanical system causes a collected vibration signal that often takes on nonlinear and non-stationary characteristics. At the same time, the fault will rapidly develop and the collected vibration signals often contain a large amount of noise. Moreover, the early fault features of the bearing in the vibration signal is relatively weak, which easily overwhelms the signal due to the noise. It is generally known that the bearing is one of the most vulnerable components in the motor and is where faults occur. Bearing damage constitutes about 44% of the total number of motor faults [
1]. Therefore, accurately extracting fault features from the motor bearing and successfully separating the fault mode has been a serious and difficult problem.
In order to effectively extract fault features of bearing from the vibration signal, many scholars have proposed many effective methods, such as short time Fourier transform (STFT), wavelet transform (WT), Hilbert–Huang transform (HHT), empirical mode decomposition (EMD), ensemble empirical mode decomposition (EEMD), entropy, and so on [
2,
3,
4,
5]. Seker and Ayaz [
6] proposed a new method to extract features from the measured vibration signals in motors subjected to accelerated bearing fluting aging and to detect the effects of bearing fluting at each aging cycle of induction motors. Yang et al. [
7] proposed a fault diagnosis method based on empirical mode decomposition energy entropy according to the non-stationary characteristics of roller bearing fault vibration signals. Cheng et al. [
8] proposed a new fault feature extraction approach based on EMD method and an autoregressive model for roller bearings. Cheng et al. [
9] proposed a local rub-impact fault diagnosis method of a rotor system based on empirical mode decomposition. Immovilli et al. [
10] compared the bearing fault detection capability obtained with the vibration and current signals. These studies contributed to the use of a simple and effective signal processing technique for both current and vibration signals. Lei et al. [
11] proposed an automated and effective fault diagnosis method of a locomotive roller bearing based on ensemble empirical mode decomposition and a wavelet neural network. Wang et al. [
12] proposed a bearing fault diagnosis method (named cyclic spike detection method) to extract weak bearing fault features from a multi-component signal mixture. Liu et al. [
13] proposed frequency band entropy based on short-time Fourier transform to detect hidden periodical components in signals and extract fault features from strong background noises. Wang et al. [
14] proposed a new method for diagnosing faults and assessing the health of bearings by using the Mahalanobis–Taguchi system. Liao and Li [
15] proposed a hybrid fault-feature extraction method by detecting localized defects and analyzing vibration signals of rolling element bearings via customized multi-wavelet packet transform and a swarm fish algorithm. Wang et al. [
16] proposed an early weak fault feature extraction method of a rolling bearing based on ensemble empirical mode decomposition and tunable Q-factor wavelet transform. Ahn et al. [
17] proposed a fault detection method of a roller bearing system by using a wavelet denoising scheme and a proper orthogonal value of an intrinsic mode function covariance matrix. Jiang et al. [
18] proposed a novel approach of condition monitoring and fault diagnosis for rolling element bearings based on an improved ensemble empirical mode decomposition. Zhu et al. [
19] proposed a roller bearing fault diagnosis method based on hierarchical entropy and a support vector machine with a particle swarm optimization algorithm. Gao et al. [
20] proposed a novel time–frequency distribution matrix factorization method based on combining the concepts of a time–frequency distribution with non-negative matrix factorization to enhance representation and identification of bearing faults. Henao et al. [
21] reviewed the trends of diagnostic techniques in fault diagnoses for electrical machines in recent years. The total number of operating electrical machines in the world was around 16.1 billion in 2011. Lucia et al. [
22] proposed a novel technique based on the stray flux measurement in different positions around the electrical machine, and reports an extensive survey on the stray-flux-based fault detection methods for induction motors. Wang et al. [
23] proposed a general sequential Monte Carlo method and a joint posterior probability density function of wavelet parameters by a set of random particles with their associated weights for extracting bearing fault features. He et al. [
24] proposed an ensemble super-wavelet transform based on the combination of tunable Q-factor wavelet transform and Hilbert transform for investigating the vibration features of induction motor bearing faults. Wang et al. [
25] proposed an early weak fault diagnosis method of rolling bearing based on minimum entropy de-convolution and a fast Kurtogram algorithm. Wang et al. [
26] proposed a novel non-negative empirical mode decomposition manifold method for feature extraction from the fault-related intrinsic mode functions in machinery fault diagnosis. Shi et al. [
27] proposed a method of empirical mode decomposition based on a cascaded multi-stable stochastic resonance system. Wang et al. [
28] proposed a novel faint signal extraction method by a time–frequency distribution image dimensionality reduction in order to overcome the shortcomings of the fast Kurtogram method. Li et al. [
29] proposed a new bearing vibration feature extraction method based on self-adaptive time–frequency analysis, multi-scale permutation entropy, and an improved support vector machine based on a binary tree for rolling bearings.
In recent years, many feature extraction methods based on nonlinear dynamics parameters have been proposed, such as fractal dimension, approximate entropy, sample entropy, and so on. They are widely used in signal analysis and processing of machinery and have become new methods for analyzing nonlinear time series. Approximate entropy was proposed by Pincus and applied to analyze physiological time series [
30]. However, the approximate entropy has its matching features [
31]. Richman et al. [
32] proposed sample entropy for compensating approximate entropy defects. Approximate entropy and sample entropy are statistical indexes for measuring the complexity of the signal. When two models are evaluated to be similar or not, the given threshold is used as the criterion. If the distance between two models shows small changes near the threshold parameter, it will cause different discriminated results and affect statistical stability. For this problem, Chen [
33,
34] proposed the fuzzy entropy method. This method used the membership function instead of the hard threshold criterion in fuzzy theory. Fuzzy entropy is used to measure physiological signals and obtain an improved measure effect. On the basis of studies, some new entropy methods are proposed for feature extraction, such as scale entropy [
35], multi-scale entropy [
36,
37], multi-scale permutation entropy [
38,
39,
40], and multi-scale fuzzy entropy [
41]. For the vibration signals of mechanical equipment, the vibration signals of different faults have different complexities, and the probability of generating new models are different. Thus, the entropy values are also different. Moreover, some faults usually appear in a certain frequency band. The fault types are different, as are the corresponding characteristic frequency bands. The signal in the fault frequency band changes, and its complexity will change. Thus, the values of multi-scale fuzzy entropy are used as the fault feature index for the pattern recognition of rolling bearing faults in this paper.
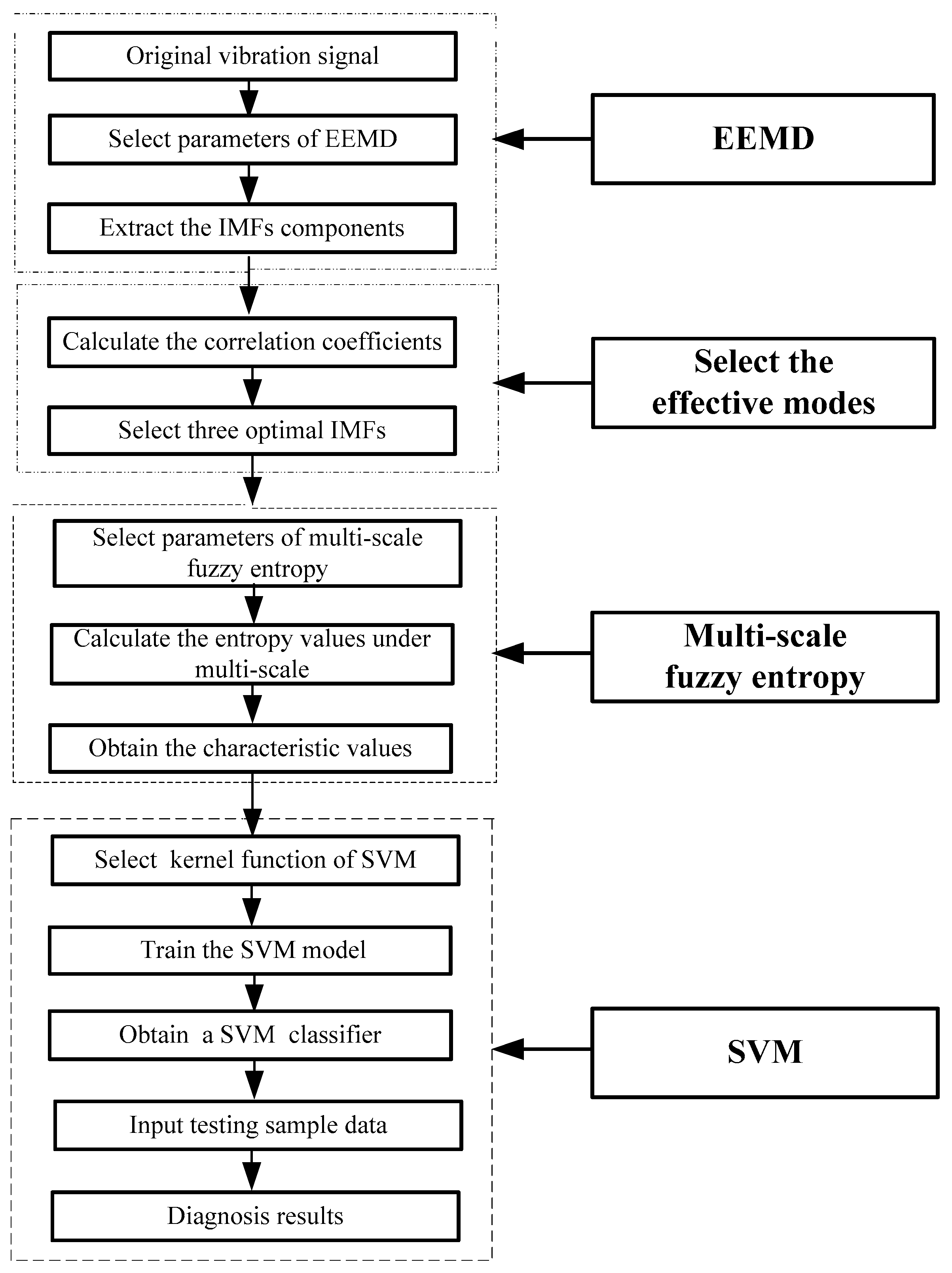
These proposed methods have their own limitations in feature extraction and fault diagnosis for rotating machinery. In a mechanical fault diagnosis, wavelet transform has achieved good results, but it is not clear as to how wavelet function can be chosen with improved time and frequency resolution. The threshold of manual operation needs to be determined. The EMD method has been widely used, but there are problems of mode mixing, end effects, over envelope, under envelope, and so on in the decomposition signal. The EEMD method is an improved EMD method, which can adaptively decompose the signal into a series of IMFs with different time scales according to the characteristics of the signal, and can effectively solve existing problems. Multi-scale fuzzy entropy measures the complexity of the time series under different scales and the probability of generating new information under a new dimension. It is a new method based on multi-scale entropy and fuzzy entropy and takes on the advantages of small data, anti-noise, and relative consistency.
Due to the complexity of the mechanical system, the vibration signal contains related fault information, which is often distributed at different scales. The different fault vibration signals have different complexities, the probability of the generated new model is also different, and the entropy is also different. Thus, the multi-scale analysis method is a valid method for calculating the entropy values to generate the fault feature vector. When the bearing fault occurs, the complexity of the vibration signal will change. For different fault types and severities, the frequencies of the friction and impact are different. The complexities of the corresponding vibration signals are also different. Thus, a new fault feature extraction of the motor bearing based on EEMD, mode selection, and multi-scale fuzzy entropy is proposed in this paper. The EEMD is used to decompose the vibration signal into a series of IMFs with specific physical meanings. Then, three more sensitive IMFs are selected to represent the original signal by using the correlation coefficient method. Moreover, the multi-scale fuzzy entropy is used to extract the features of different faults under different scales. The support vector machine (SVM) classifier is used to classify, identify, and determine the working condition and fault type of the motor bearing. The effectiveness of the proposed method is verified by analyzing and testing the fault signal of a real motor bearing.
5. The Experiment Validation and Result Analysis
5.1. Effectiveness Validation and Comparative Analysis of the Proposed Method
The motor bearing with no-load and a fault diameter of 0.007 in. is selected to validate and analyze the effectiveness of the proposed method in this section.
The original data were divided into segments of samples where each sample covered 2048 data points. Each of the three fault states (the inner race fault, the outer race fault, and the rolling element fault) includes 40 samples. There are 60 samples for training and 60 samples for testing. The dataset consists of 120 data samples of three fault states.
The SVM with small sample classification and the short training time is selected as a classifier here. The obtained values of multi-scale fuzzy entropy are selected as characteristic vectors. That is to say, T = [MFE1, MFE2, MFE3, ..., MFE15] is selected to form characteristic vectors. Then, the characteristic vectors T is input into the SVM model to train the SVM model and obtain the SVM classifier. The diagnosis results of the testing samples are shown in
Table 4.
In order to verify the effectiveness of the proposed EOMSMFD method for feature extraction and fault diagnosis, the EDOFSFD method based on EEMD, mode selection, and fuzzy entropy is selected here. In the EDOFSFD method, the fuzzy entropy is used to replace multi-scale fuzzy entropy. Thus, the flow and steps of the EDOFSFD method is quite similar to the proposed EOMSMFD method. The EDOFSFD method is not described due to the limited space. The comparison results for two fault diagnosis methods are shown in
Table 5.
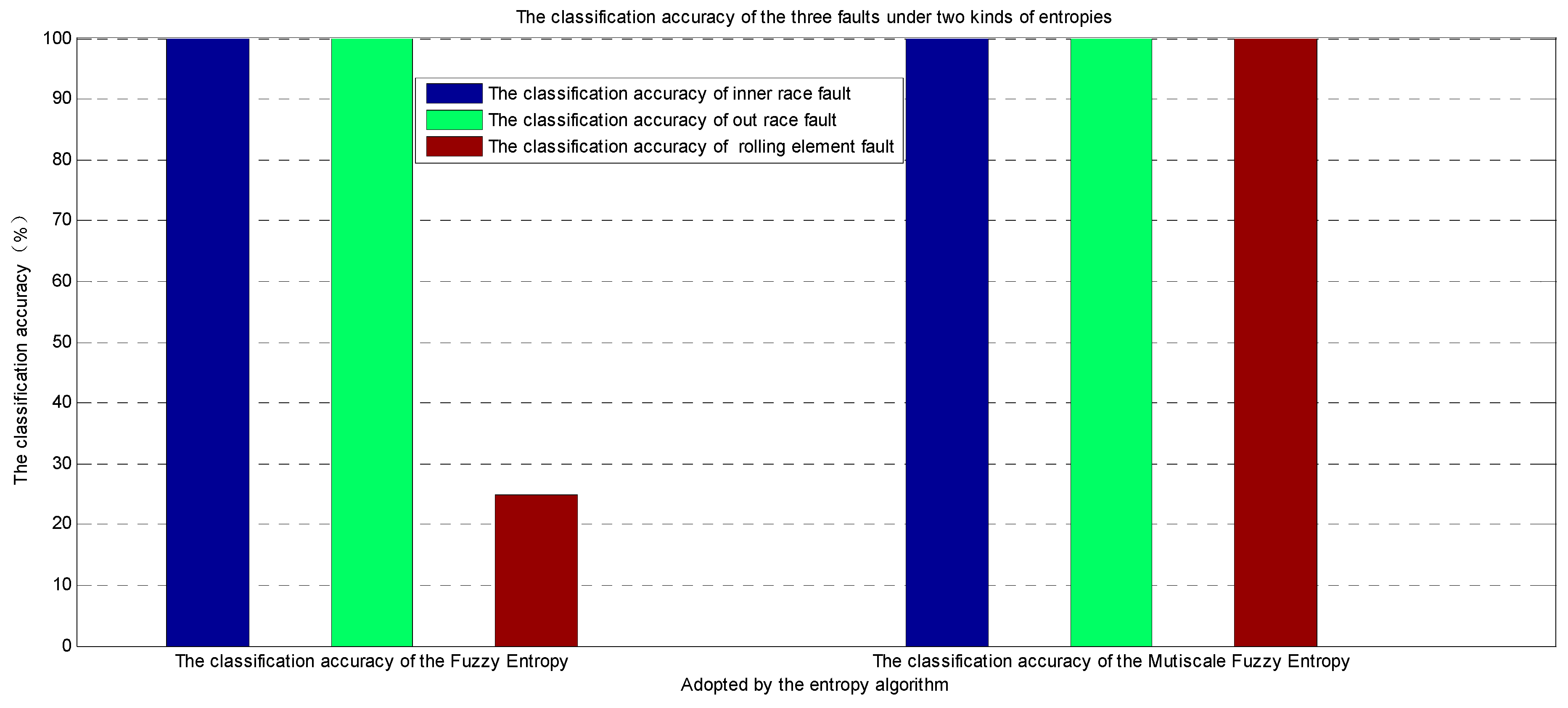
As can be seen from
Table 5 and
Figure 20, for the fault vibration signal of the inner race and the outer race, it can be seen that the proposed EDOFSFD method and the EOMSMFD method can both obtain a diagnosis accuracy of 100%. However, for the fault vibration signal of the rolling element, it can be seen that the test accuracy of the proposed EOMSMFD method and the EDOFSFD method is 100% and 25% in the experiments, respectively. Thus, the proposed EOMSMFD method has a higher diagnosis accuracy than the EDOFSFD method. For the EDOFSFD method and the EOMSMFD method, the EEMD, mode selection, and SVM are the same. Multi-scale fuzzy entropy is used to extract the feature from the vibration signal in the proposed EOMSMFD method, and fuzzy entropy is used to extract the feature from the vibration signal in the proposed EDOFSFD method. This shows that the multi-scale fuzzy entropy can better extract features from the vibration signal than can fuzzy entropy. Thus, the feature extraction and fault diagnosis capabilities of the proposed EOMSMFD method outperform the EDOFSFD method. The EOMSMFD method is the most effective method for extracting the fault feature from the collected vibration signal and for diagnosing the faults.
5.2. Diagnosis Results and Analysis under Different Loads
In order to verify the effectiveness of the proposed EOMSMFD method under load changes, the fault feature extraction and classification of the inner race fault, the outer race fault, and the rolling element fault of the motor bearing under no-load and 3HP loads are studied and analyzed. Fault diameters of 0.007 and 0.021 in. are selected here.
The original data were divided into segments of samples where each sample covered 2048 data points. For each fault under each fault severity and each load, there were 40 samples. Twenty samples were randomly selected as training samples, and the remaining 20 samples were selected as testing samples. Four hundred eighty samples for the motor bearing were obtained here. For each fault diameter, hybrid samples of no-load and 3HP loads were used to diagnose fault type. The diagnosis results are shown in
Table 6.
As can be seen from
Table 6, for the inner race, the outer race, and the rolling element of the motor bearing, the correctness rates of fault diagnosis are 100% for the motors under no-load and the 3HP load and the fault diameters for 0.007 and 0.021 in., respectively. The experiment results show that the proposed method does not have any influence and is very stable for different loads. That is, the proposed method is not sensitive to the load on the motor. It takes on an improved stability and effectiveness in fault diagnosis for the motor under different loads.
5.3. Diagnosis Results and Analysis under Different Fault Severities
In order to verify the effectiveness of the proposed EOMSMFD method for different fault severities, the fault types and fault severities of the inner race, the outer race, and the rolling element of the motor bearing are diagnosed. The motor with fault diameters of 0.007 and 0.021 in. under 3HP load is selected here.
The original data were divided into segments of samples where each sample covered 2048 data points. For each fault type under each fault severity, there were 40 samples. Twenty samples were randomly selected as training samples, and the remaining 20 samples were selected as testing samples. Four hundred eighty samples for the motor bearing were obtained here. The hybrid samples of fault diameters of 0.007 and 0.021 in. were used to diagnose fault type and fault severity. The diagnosis results are shown in
Table 7.
As can be seen from
Table 7, for the inner race and the outer race faults of the motors with 3HP loads and fault diameters of 0.007 and 0.021 in., the correctness rate of classification and the correctness rate of fault severity are 100%, respectively. For the rolling element fault of the motors with 3HP loads and fault diameters of 0.021 in., the correctness rate of classification and the correctness rate of fault severity are both 100%. However, for the rolling element fault of the motors with 3HP loads and fault diameters of 0.007 in., the correctness rate of classification are 95%, and the correctness rate of fault severity is 100%. The experiment results show that the proposed method does not have any influence and is effective for different fault severities on the motor bearing. That is, the proposed method can effectively diagnose the fault for different severities on the motor bearing. Thus, the proposed method is an effective method for realizing the fault types and fault severities of the inner race, the outer race, and the rolling element of the motor bearing.
To summarize, the proposed EOMSMFD method mainly has the following advantages:
(1) The EEMD can effectively decompose the vibration signal into a series of IMFs and residual components. Moreover, it can effectively avoid the mode mixing phenomenon.
(2) The correlation coefficient method can effectively select three corresponding sensitive IMFs to represent the original signal. It can not only extract the effective mode and reduce the workload, but can also avoid dealing with useless modes.
(3) Multi-scale fuzzy entropy can better extract fault features from the vibration signals than can fuzzy entropy. The extracted fault features take on an improved distinguishing ability.
(4) The proposed EOMSMFD method is an effective fault diagnosis method for motor bearings. Moreover, this method does not have any influence on motors with different loads and different fault severities. It can effectively diagnose fault types and fault severities on motor bearings. Moreover, it takes on an improved stability and effectiveness in fault diagnosis for motors under different loads and different fault severities.
6. Conclusions
To perfectly extract the multiple scale characteristics of the vibration signal of the motor bearing and well diagnose its faults, a novel feature extraction (EDOMFE) method is proposed in this paper. The proposed method integrates EEMD, mode selection, and multi-scale fuzzy entropy. Moreover, the SVM is used as a classifier to obtain a fault diagnosis (EOMSMFD) method. The EEMD method is used to decompose the nonlinear and non-stationary vibration signals of the inner ring, the outer ring, and the rolling element of the motor bearing, and the IMFs with small modal mixing are obtained. The correlation coefficient analysis method is used to calculate and determine three improved IMFs, which are close to the original signal. Then, the multi-scale fuzzy entropy is used to calculate the entropy values for the three selected IMFs in order to generate the fault feature vector, which is input into SVM classifier to identify the fault types and fault severities. The effectiveness of the proposed method is fully evaluated by experiments and comparative studies. The experiment results show that the proposed method provides an improved recognition performance under the motor with different loads and different fault severities. The recognition rates of the inner race, the outer race, and the rolling element of the motor bearing, with hybrid samples of no-load and 3HP loads, reach 100% under the fault diameters of 0.007 or 0.021 in., respectively. For the motors with hybrid samples of fault diameters of 0.007 and 0.021 in. under 3HP loads, the recognition rate of classification and the recognition rate of fault severity are 100% for the inner race and the outer race of the motor bearing, and the recognition rate of classification is 95% and the recognition rate of fault severity is 100% for the rolling element of the motor bearing. Moreover, the comparative studies with the other mentioned methods show that the multi-scale fuzzy entropy can extract much more diagnostic information compared with fuzzy entropy, and the proposed method can effectively eliminate the influence of the mode mixing. Thus, the proposed method is found to be an effective method for the fault diagnosis of the motor bearing and has potential application for other rotating machinery.
Due to the lower computational efficiency of the proposed method, in future work, we will attempt to improve the computational efficiency for obtaining the fault feature vector by using multi-scale fuzzy entropy. The goal is to develop a real-time fault diagnosis system for rotating machinery.