Entropy Generation through Non-Equilibrium Ordered Structures in Corner Flows with Sidewall Mass Injection
Abstract
:1. Introduction
2. Selection of Heated Air as the Working Substance
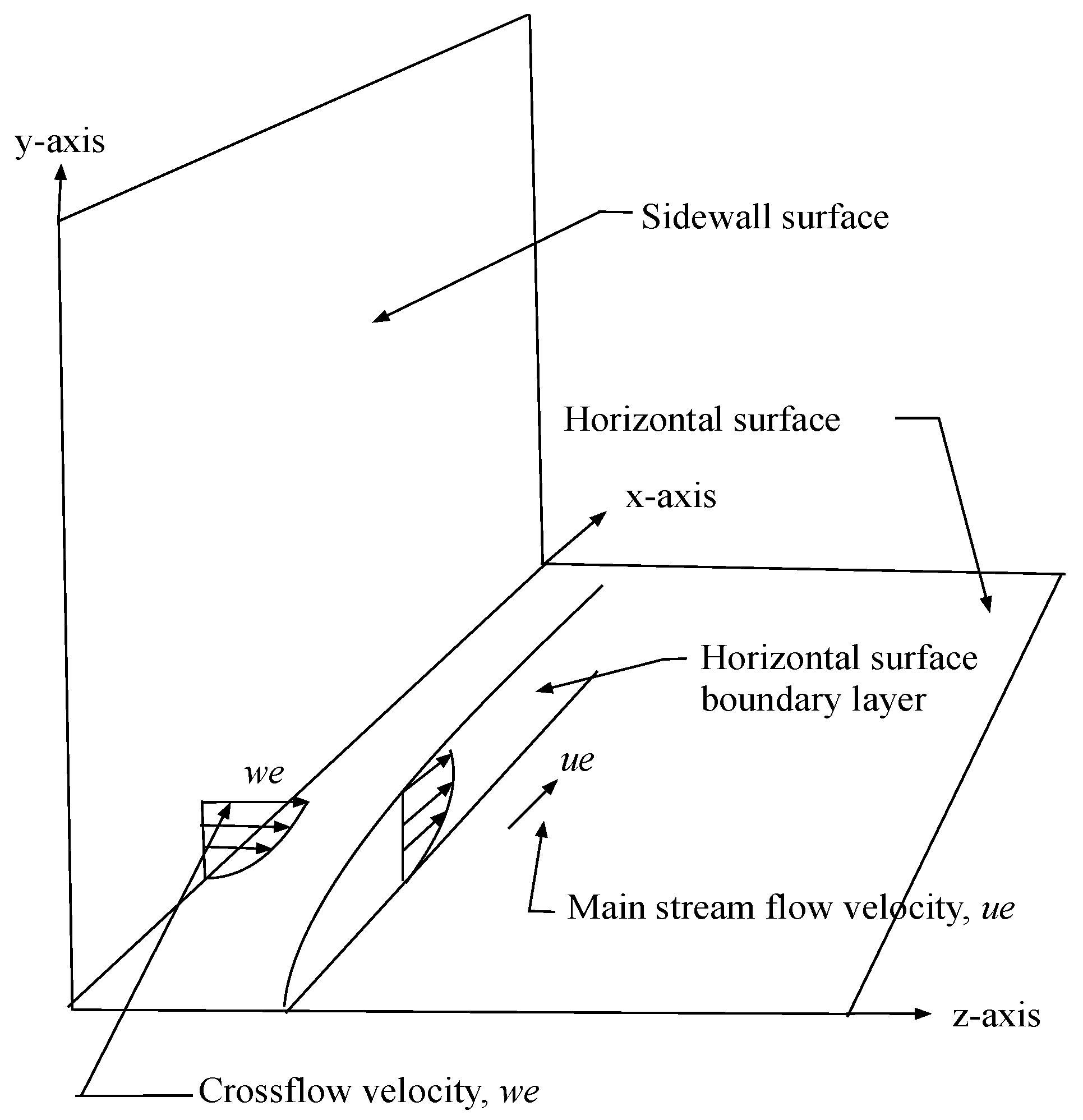
3. Steady-Flow Laminar Boundary-Layer Environment
4. Modified Time-Dependent Lorenz Equations in the Spectral Plane
4.1. Transformation of the Townsend Equations to the Modified Lorenz Format
4.2. Synchronization Properties of the Modified Lorenz Equations
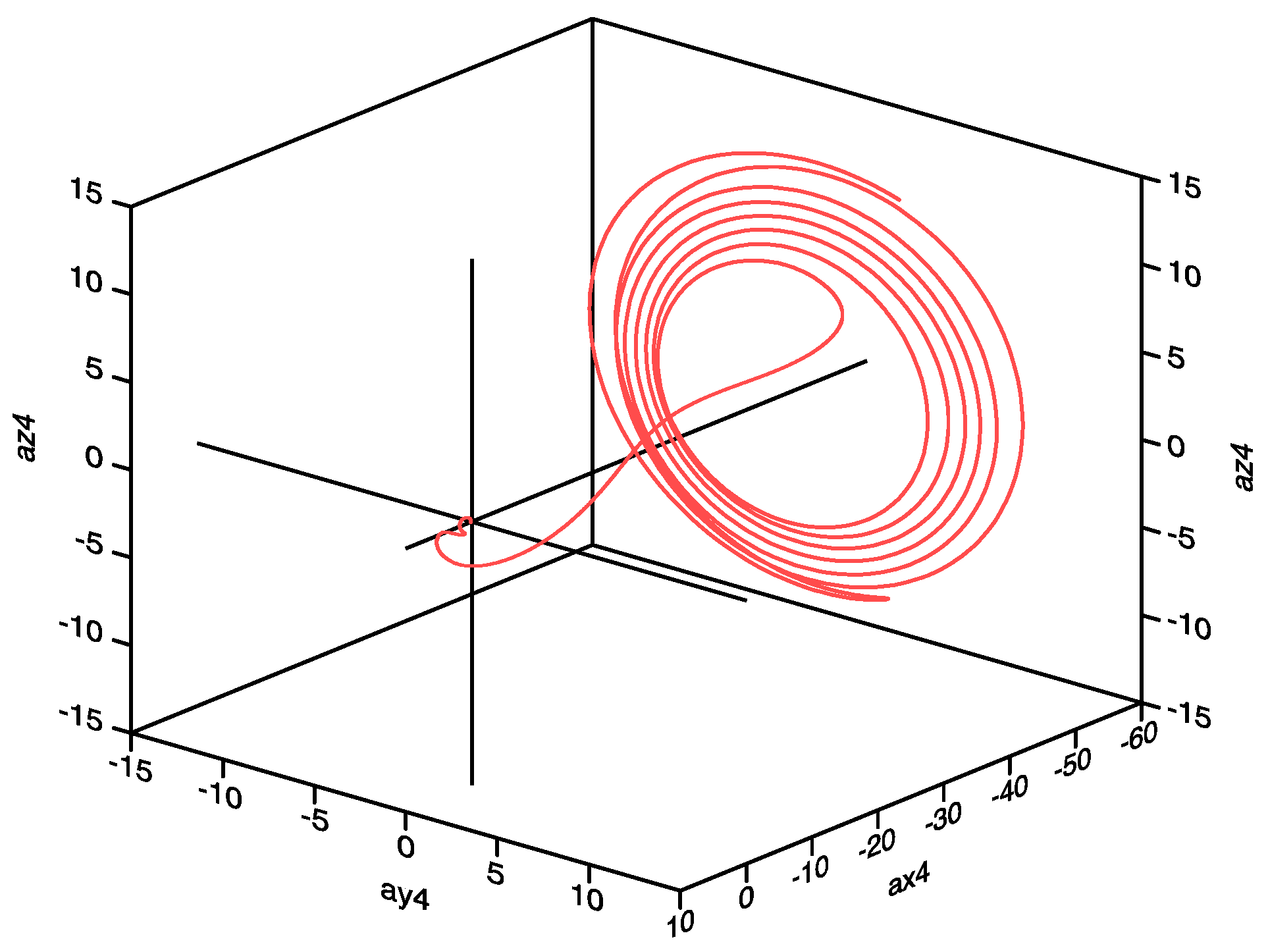
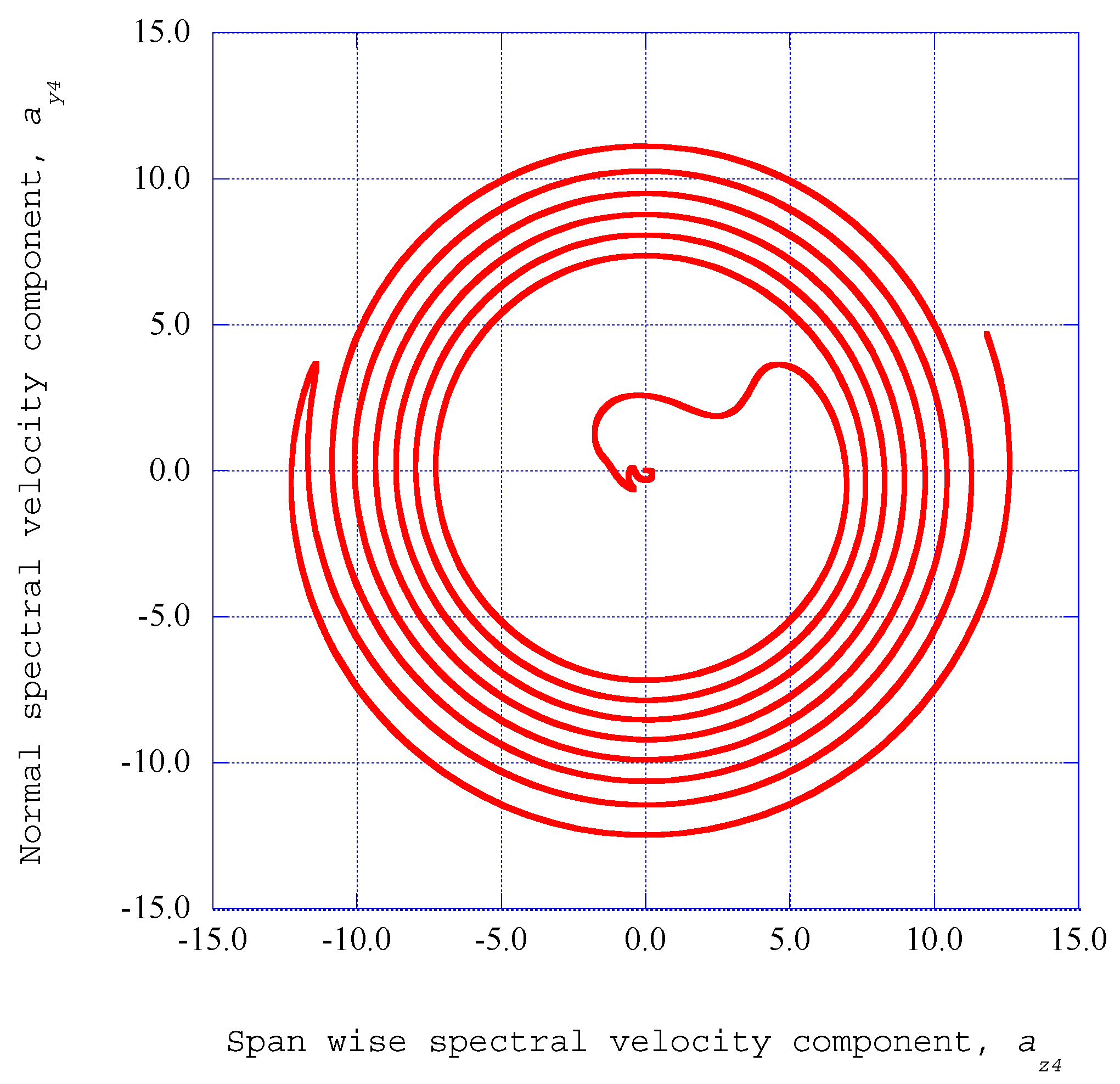
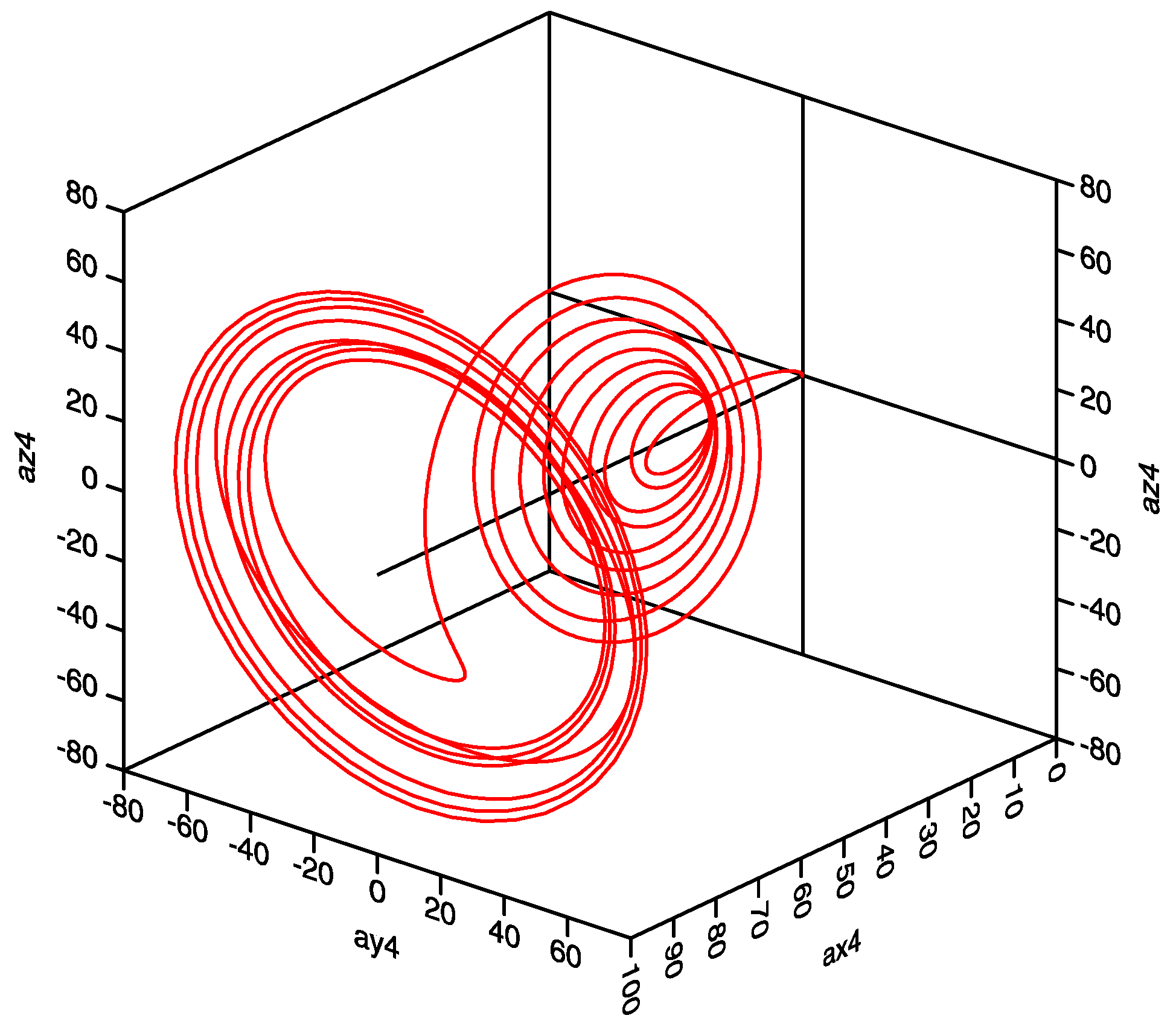
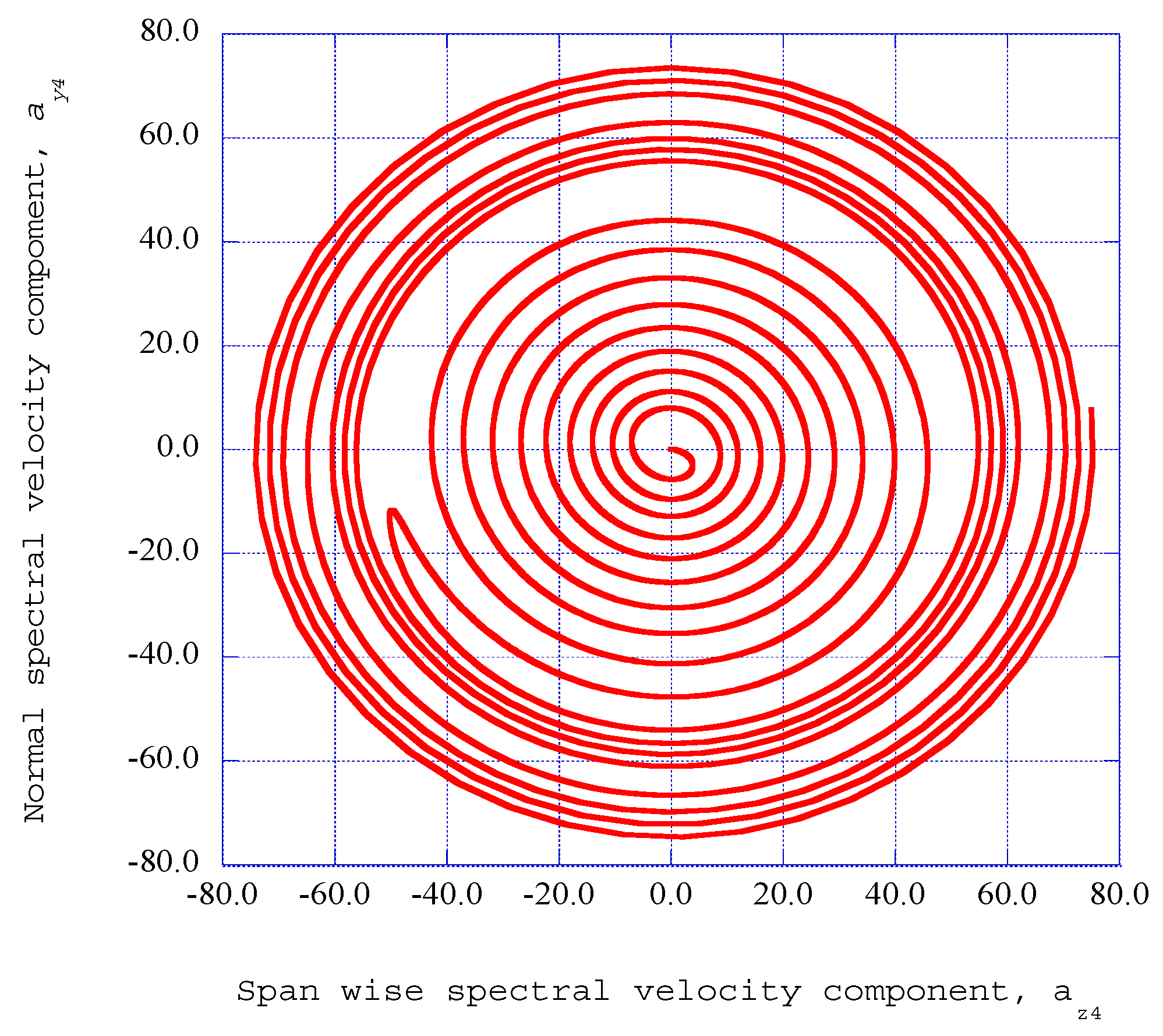
4.3. Deterministic Results for the Modified Lorenz Equations
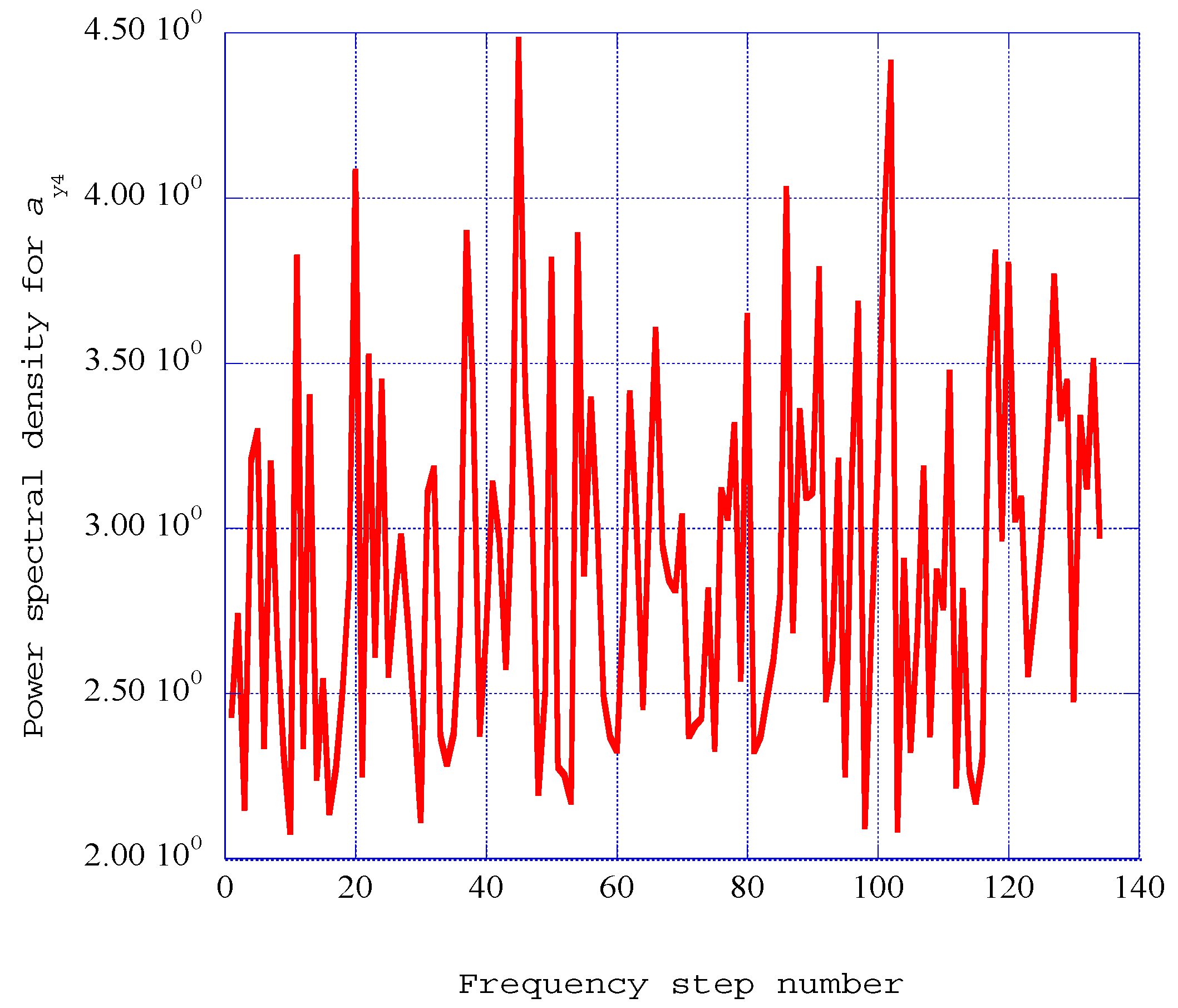
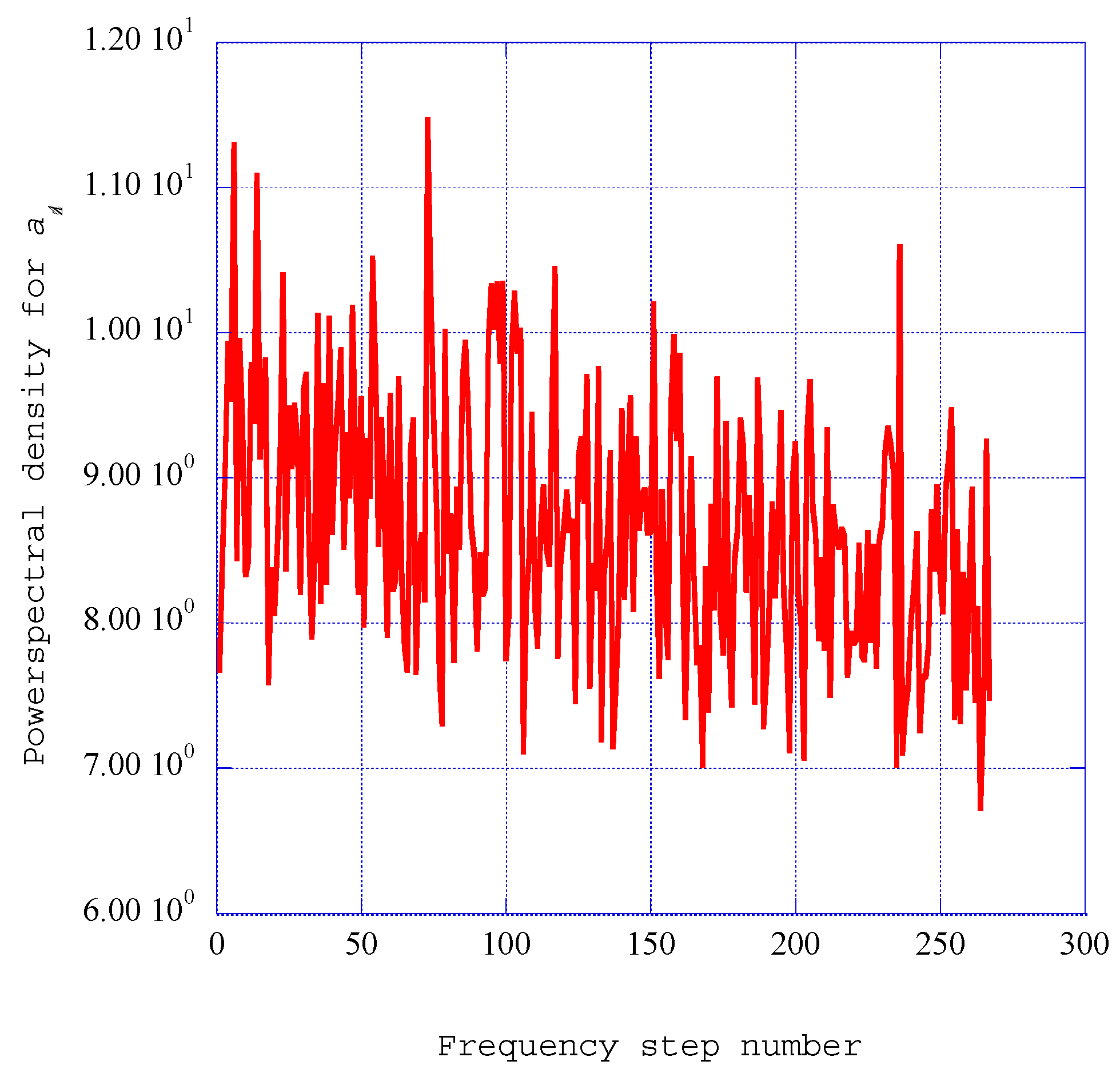
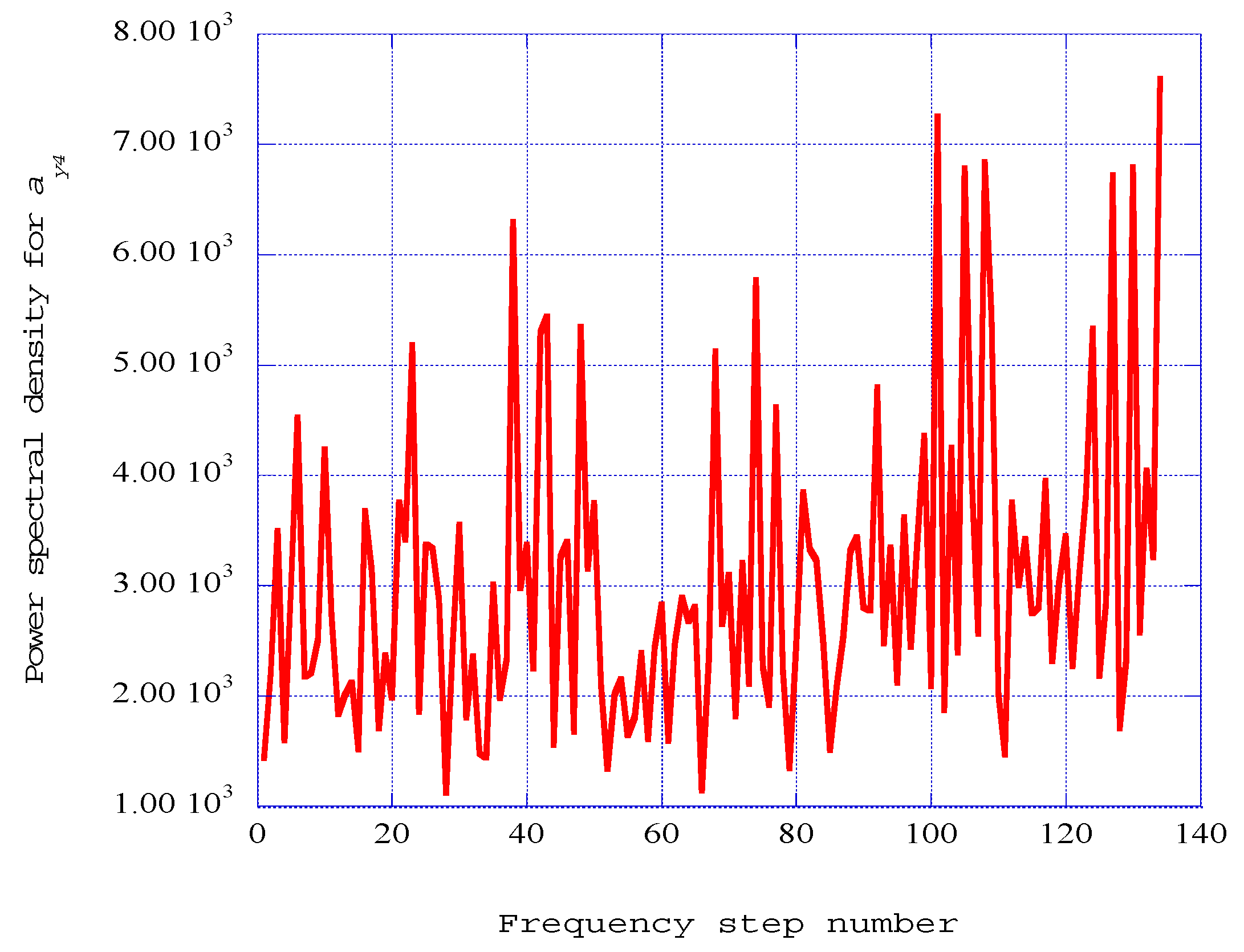
5. Power Spectral Density within the Non-Equilibrium Spectral Velocity Fluctuations
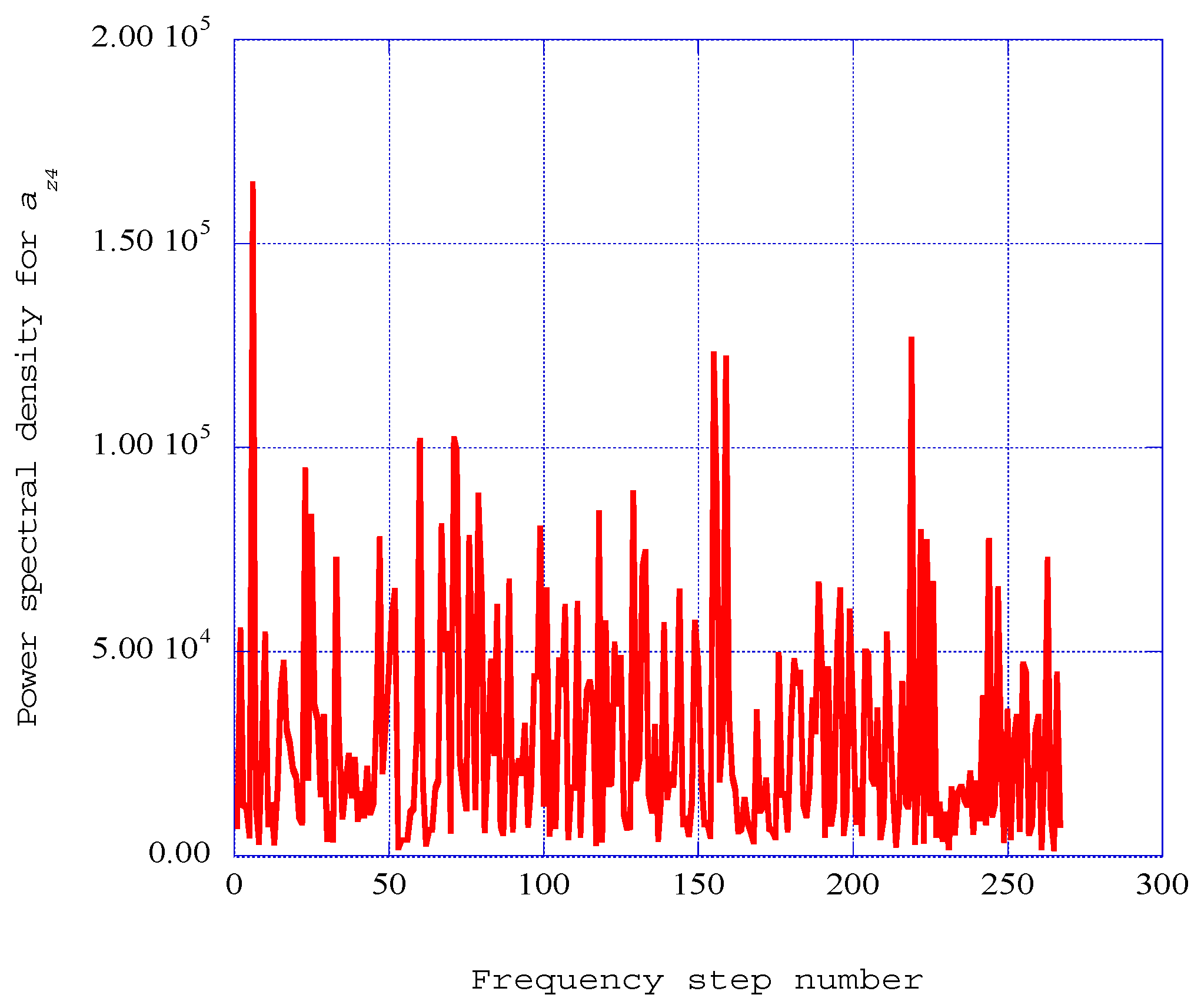
5.1. Power Spectral Densities Indicating Ordered Structures
5.2. Empirical Entropies from Singular Value Decomposition
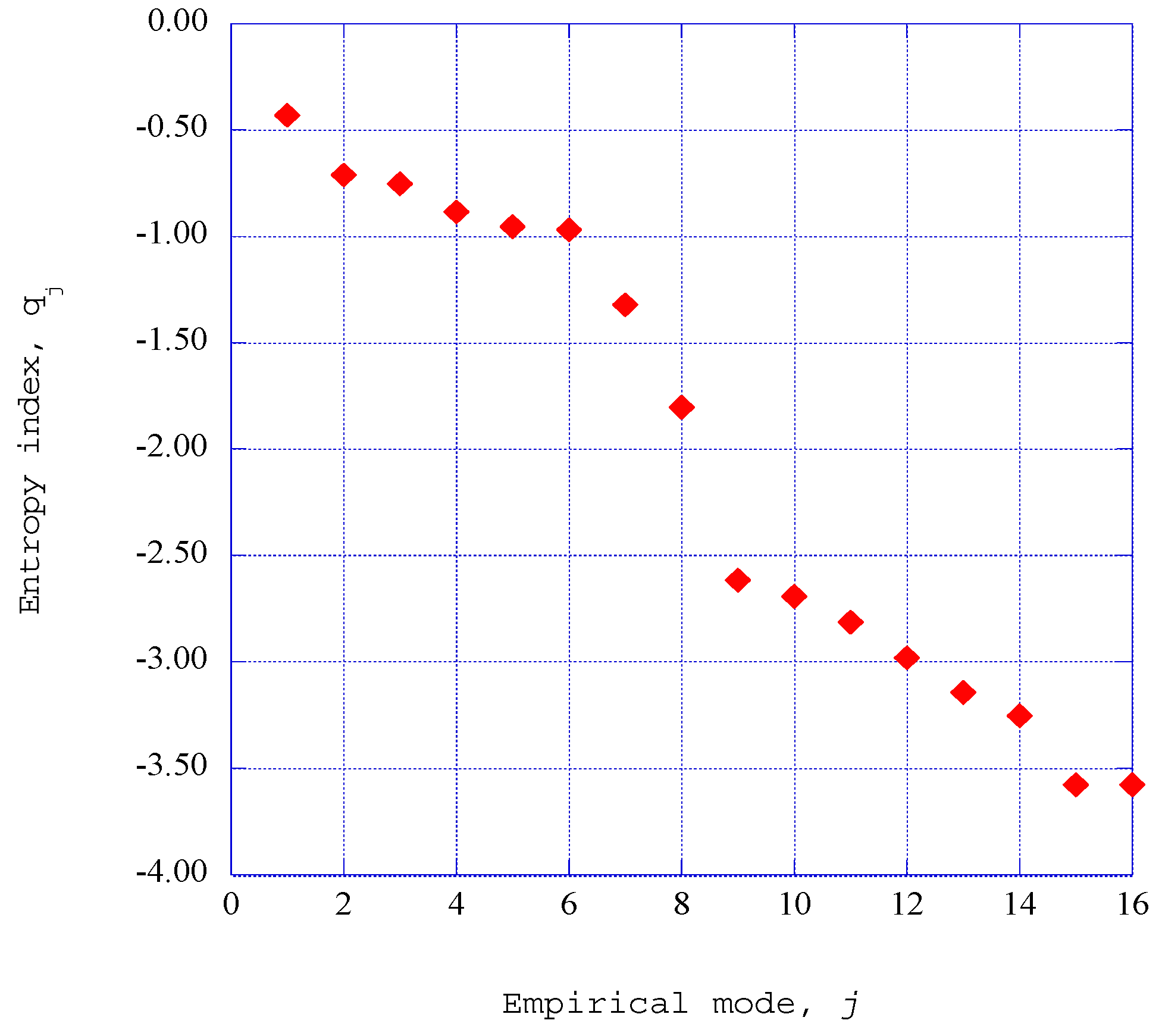
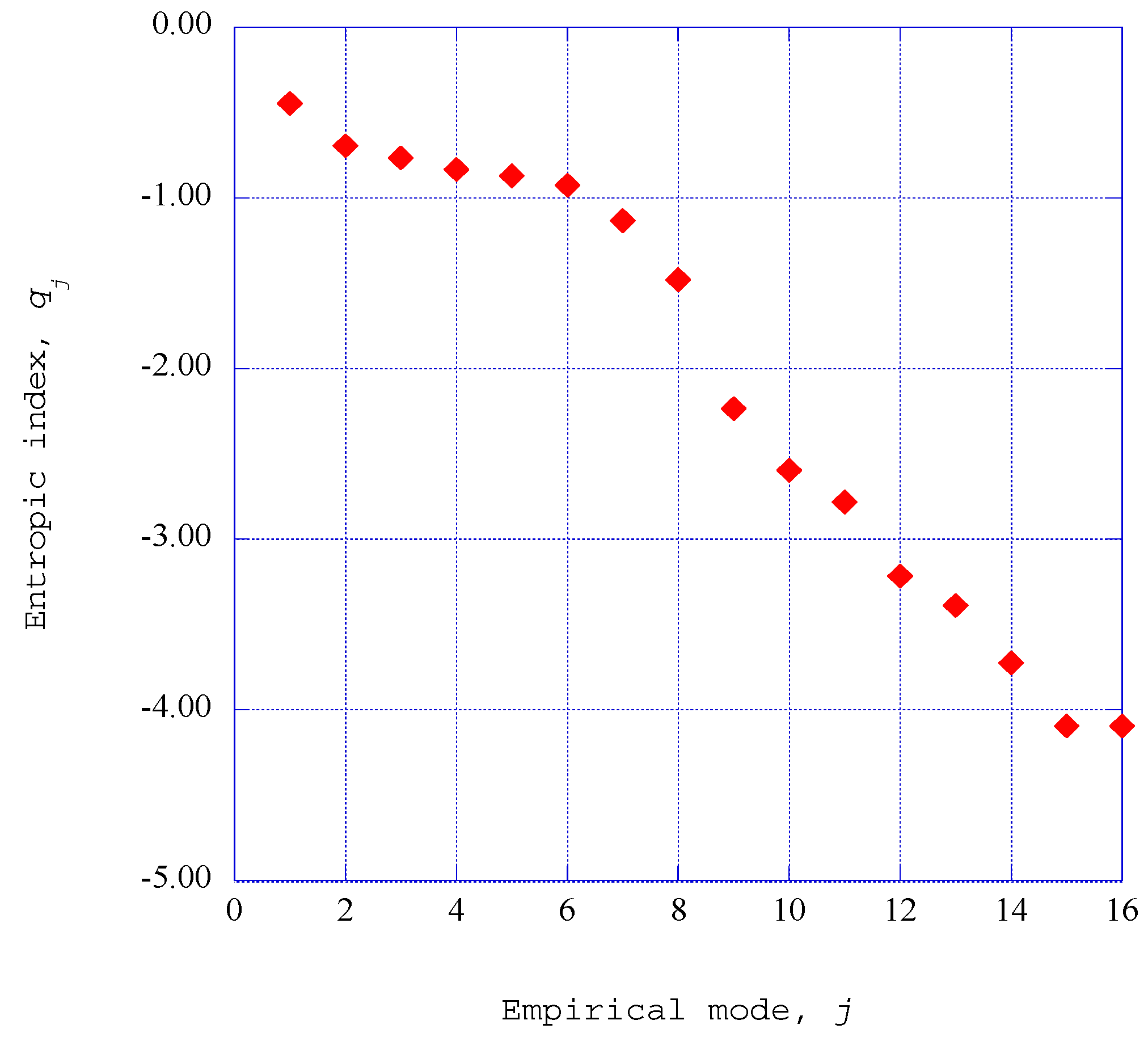
5.3. Empirical Entropic Indices for the Ordered Structures
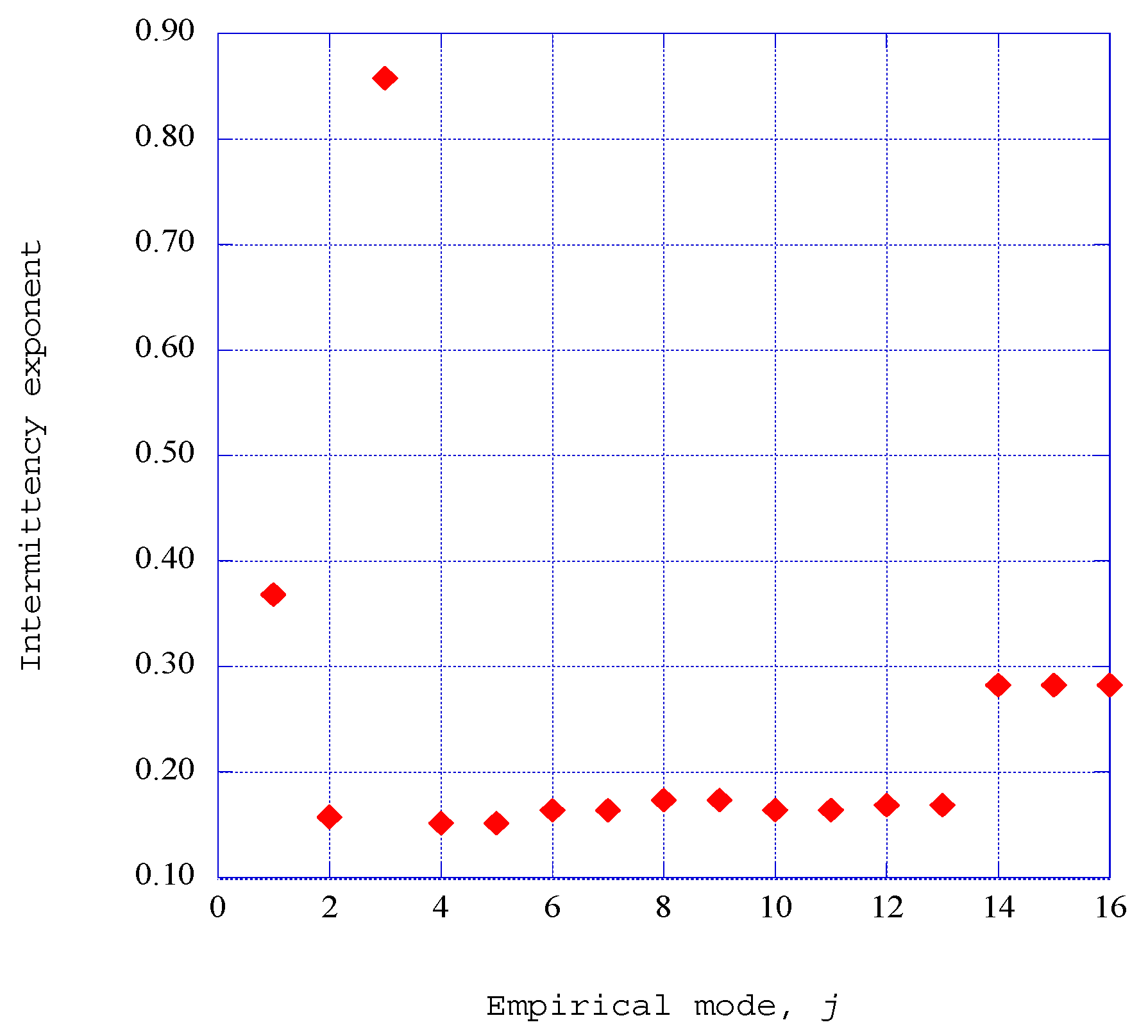
5.4. Empirical Intermittency Exponents for the Ordered Structures
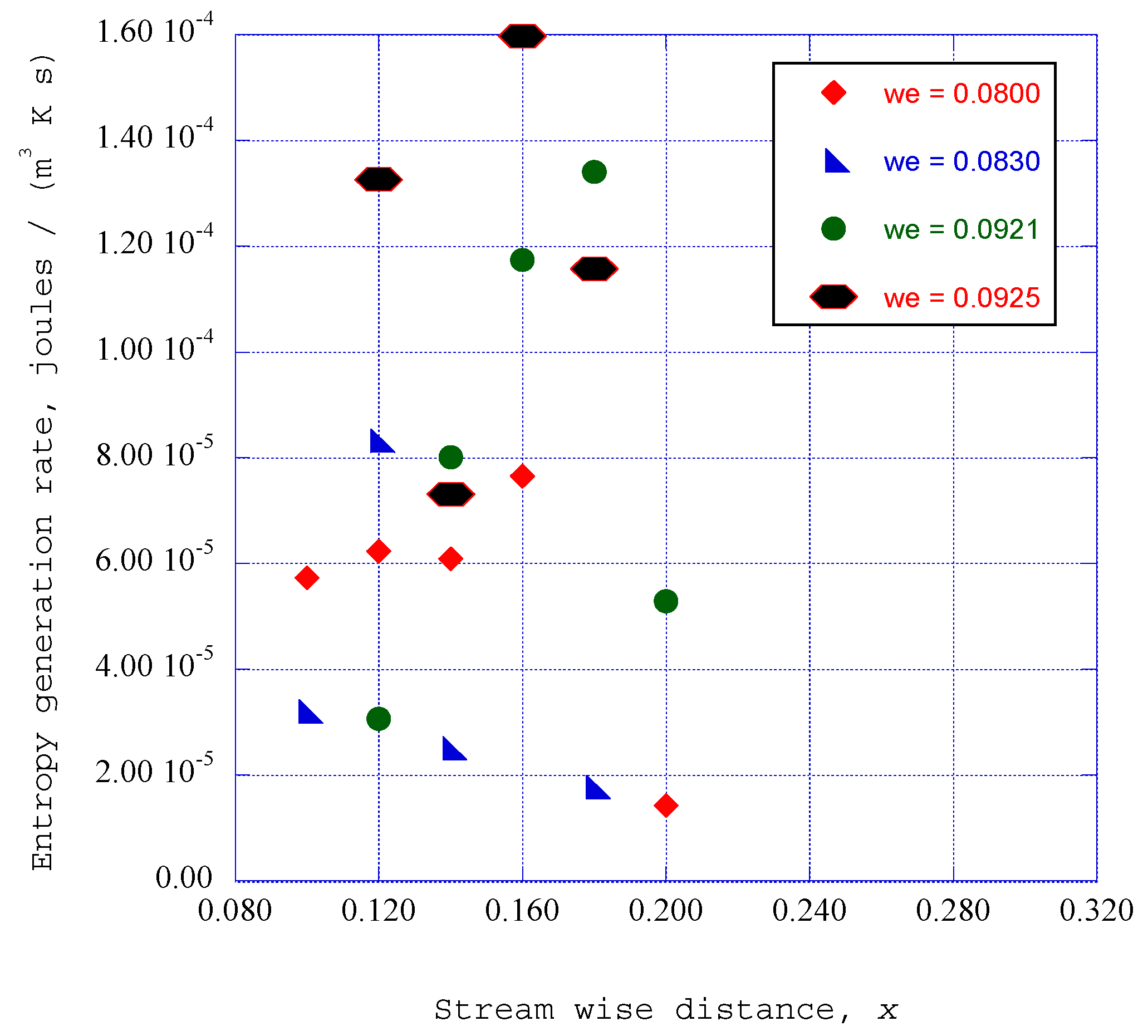
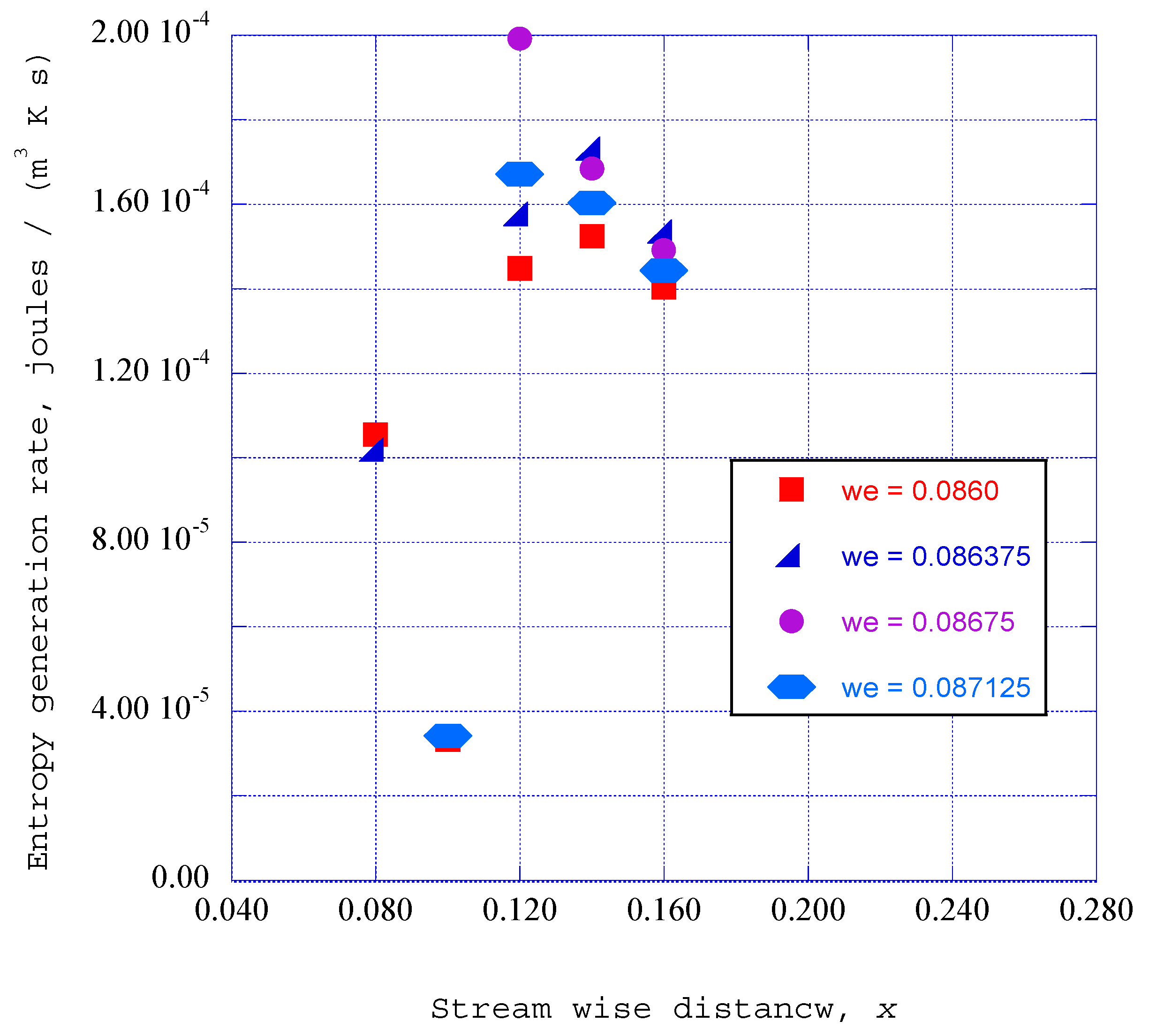
6. Entropy Generation Rates through the Ordered Structures
6.1. Kinetic Energy Available for Dissipation
6.2. Entropy Generation Rates for Relaxation Processes
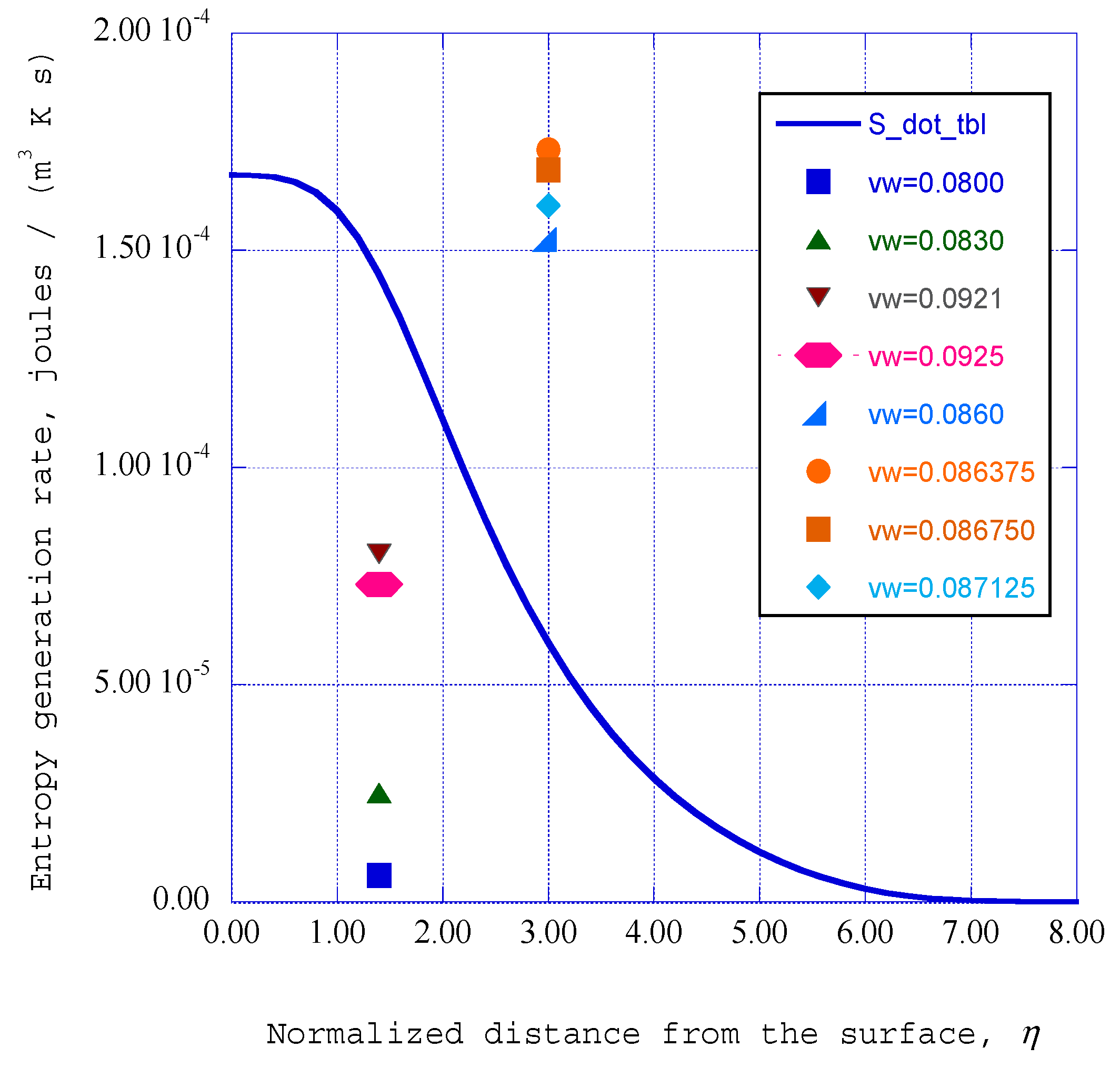
6.3. Entropy Generation Rates for a Turbulent Boundary Layer
7. Discussion
8. Conclusions
Acknowledgments
Conflicts of Interest
Nomenclature
| ai | Fluctuating i-th component of velocity wave vector |
| b | Coefficient in Equation (14) |
| b | Fluctuating Fourier component of the static pressure |
| b1 | Coefficient in modified Lorenz equations defined by Equation (35) |
| Cf | Skin-friction coefficient |
| F | Time-dependent feedback factor |
| j | Mode number empirical eigenvalue |
| J | Net source of kinetic energy dissipation rate, Equation (39) |
| k | Time-dependent wave number magnitude |
| k | Dimensional constant, Equation (27) |
| ki | Fluctuating i-th wave number of Fourier expansion |
| K | Adjustable weighting factor |
| m | Pressure gradient parameter, Equation (11) |
| p | Local static pressure |
| qj | Empirical entropic index for the empirical entropy of mode, j |
| r1 | Coefficient in modified Lorenz equations defined by Equation (33) |
| s | Entropy per unit mass |
| s1 | Coefficient in modified Lorenz equations defined by Equation (34) |
| Sempj | Empirical entropy for empirical mode, j |
Entropy generation rate through kinetic energy dissipation | |
Entropy generation rate in a turbulent boundary layer | |
| t | Time |
| u | Mean stream wise velocity in the x-direction in Equation (4) |
| u’ | Fluctuating stream wise velocity in Equation (4) |
| ue | Stream wise velocity at the outer edge of the x-y plane boundary layer |
| ui | The i-th component of the fluctuating velocity |
| Ui | Mean velocity in the i-th direction in the modified Lorenz equations |
| v | Mean normal velocity in Equation (4) |
| v’ | Fluctuating normal velocity in Equation (4) |
| we | Span wise velocity at the outer edge of the z-y plane boundary layer |
| x | Stream wise distance |
| xi | i-th direction |
| xj | j-th direction |
| y | Normal distance |
| z | Span wise distance |
Greek Letters
| δ | Boundary layer thickness |
| δlm | Kronecker delta |
| εm | Eddy viscosity |
Normalized eddy viscosity | |
| ζj | Intermittency exponent for the j-th mode in Equation (38) |
| η | Transformed normal distance parameter |
| λj | Eigenvalue for the empirical mode, j |
| μ | Mechanical potential in Equation (39) |
| ν | Kinematic viscosity of the gas mixture |
| ξj | Kinetic energy dissipation rate in the j-th empirical mode |
| ρ | Density |
| σy | Coefficient in modified Lorenz equations defined by Equation (31) |
| σx | Coefficient in modified Lorenz equations defined by Equation (32) |
| τw | Wall shear stress |
Subscripts
| E | Outer edge of the laminar boundary layer |
| i, j, l, m | Tensor indices |
| x | Component in the x-direction |
| y | Component in the y-direction |
| z | Component in the z-direction |
References
- Isaacson, L.K. Entropy Generation through Non-equilibrium Spiral Structures in Corner Flows with Sidewall Surface Mass Injection. Entropy 2016, 18, 47. [Google Scholar] [CrossRef]
- Cebeci, T.; Bradshaw, P. Momentum Transfer in Boundary Layers; Hemisphere: Washington, DC, USA, 1977; pp. 319–321. [Google Scholar]
- Cebeci, T.; Cousteix, J. Modeling and Computation of Boundary-Layer Flows; Horizons: Long Beach, CA, USA, 2005. [Google Scholar]
- Hansen, A.G. Similarity Analyses of Boundary Value Problems in Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964; pp. 86–92. [Google Scholar]
- Townsend, A.A. The Structure of Turbulent Shear Flow, 2nd ed.; Cambridge University Press: Cambridge, UK, 1976. [Google Scholar]
- Hellberg, C.S.; Orszag, S.A. Chaotic behavior of interacting elliptical instability modes. Phys. Fluids 1988, 31, 6–8. [Google Scholar] [CrossRef]
- Sparrow, C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors; Springer: New York, NY, USA, 1982. [Google Scholar]
- Attard, P. Non-Equilibrium Thermodynamics and Statistical Mechanics: Foundation and Applications; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Chen, C.H. Digital Waveform Processing and Recognition; CRC Press: Boca Raton, FL, USA, 1982; pp. 131–158. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Rissanen, J. Information and Complexity in Statistical Modeling; Springer: New York, NY, USA, 2007. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009; pp. 37–43. [Google Scholar]
- Arimitsu, T.; Arimitsu, N. Analysis of fully developed turbulence in terms of Tsallis statistics. Phys. Rev. E 2000, 61, 3237–3240. [Google Scholar] [CrossRef]
- Isaacson, L.K. Transitional Intermittency Exponents through Non-equilibrium Boundary-Layer Structures and Empirical Entropic Indices. Entropy 2014, 16, 2729–2755. [Google Scholar] [CrossRef]
- Mathieu, J.; Scott, J. An Introduction to Turbulent Flow; Cambridge University Press: Cambridge, UK, 2000; pp. 251–261. [Google Scholar]
- Manneville, P. Non-equilibrium Structures and Weak Turbulence; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. In Controlling Chaos: Theoretical and Practical Methods in Nonlinear Dynamics; Kapitaniak, T., Ed.; Academic Press: San Diego, CA, USA, 1996; pp. 142–145. [Google Scholar]
- Pérez, G.; Cerdeiral, H.A. Extracting messages masked by chaos. In Controlling Chaos: Theoretical and Practical Methods in Nonlinear Dynamics; Kapitaniak, T., Ed.; Academic Press: San Diego, CA, USA, 1996; pp. 157–160. [Google Scholar]
- Cuomo, K.M.; Oppenheim, A.V. Circuit implementation of synchronized chaos with applications to communications. In Controlling Chaos: Theoretical and Practical Methods in Nonlinear Dynamics; Kapitaniak, T., Ed.; Academic Press: San Diego, CA, USA, 1996; pp. 153–156. [Google Scholar]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; North-Holland: Amsterdam, Holland, 1962. [Google Scholar]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley: London, UK, 1971. [Google Scholar]
- Mariz, A.M. On the irreversible nature of the Tsallis and Renyi entropies. Phys. Lett. A 1992, 165, 409–411. [Google Scholar] [CrossRef]
- Moore, J.; Moore, J.G. Entropy Production Rates from Viscous Flow Calculations: Part I—A Turbulent Boundary Layer Flow. In Proceedings of the 28th ASME International Gas Turbine Conference and Exhibit, Phoenix, AZ, USA, 27–31 March 1983.
- White, F.M. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Bayley, F.J.; Turner, A.B. The Transpiration-Cooled Gas Turbine. J. Eng. Power 1970, 92, 351–358. [Google Scholar] [CrossRef]
- Cantwell, B.J. Organized Motion in Turbulent Flow. Ann. Rev. Fluid Mech. 1981, 13, 457–515. [Google Scholar] [CrossRef]
- Ersoy, S.; Walker, J.D.A. Viscous flow induced by counter-rotating vortices. Phys. Fluids 1985, 28, 2687–2698. [Google Scholar] [CrossRef]
- Boiko, A.V.; Grek, G.R.; Dovgal, A.V.; Kozlov, V.V. The Origin of Turbulence in Near-Wall Flows; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]

© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isaacson, L.K. Entropy Generation through Non-Equilibrium Ordered Structures in Corner Flows with Sidewall Mass Injection. Entropy 2016, 18, 279. https://doi.org/10.3390/e18080279
Isaacson LK. Entropy Generation through Non-Equilibrium Ordered Structures in Corner Flows with Sidewall Mass Injection. Entropy. 2016; 18(8):279. https://doi.org/10.3390/e18080279
Chicago/Turabian StyleIsaacson, LaVar King. 2016. "Entropy Generation through Non-Equilibrium Ordered Structures in Corner Flows with Sidewall Mass Injection" Entropy 18, no. 8: 279. https://doi.org/10.3390/e18080279
APA StyleIsaacson, L. K. (2016). Entropy Generation through Non-Equilibrium Ordered Structures in Corner Flows with Sidewall Mass Injection. Entropy, 18(8), 279. https://doi.org/10.3390/e18080279





