Thermal Characteristic Analysis and Experimental Study of a Spindle-Bearing System
Abstract
:1. Introduction
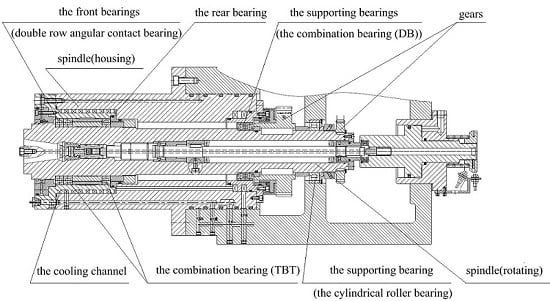
2. Thermo-Mechanical Coupling Model of the Spindle-Bearing System
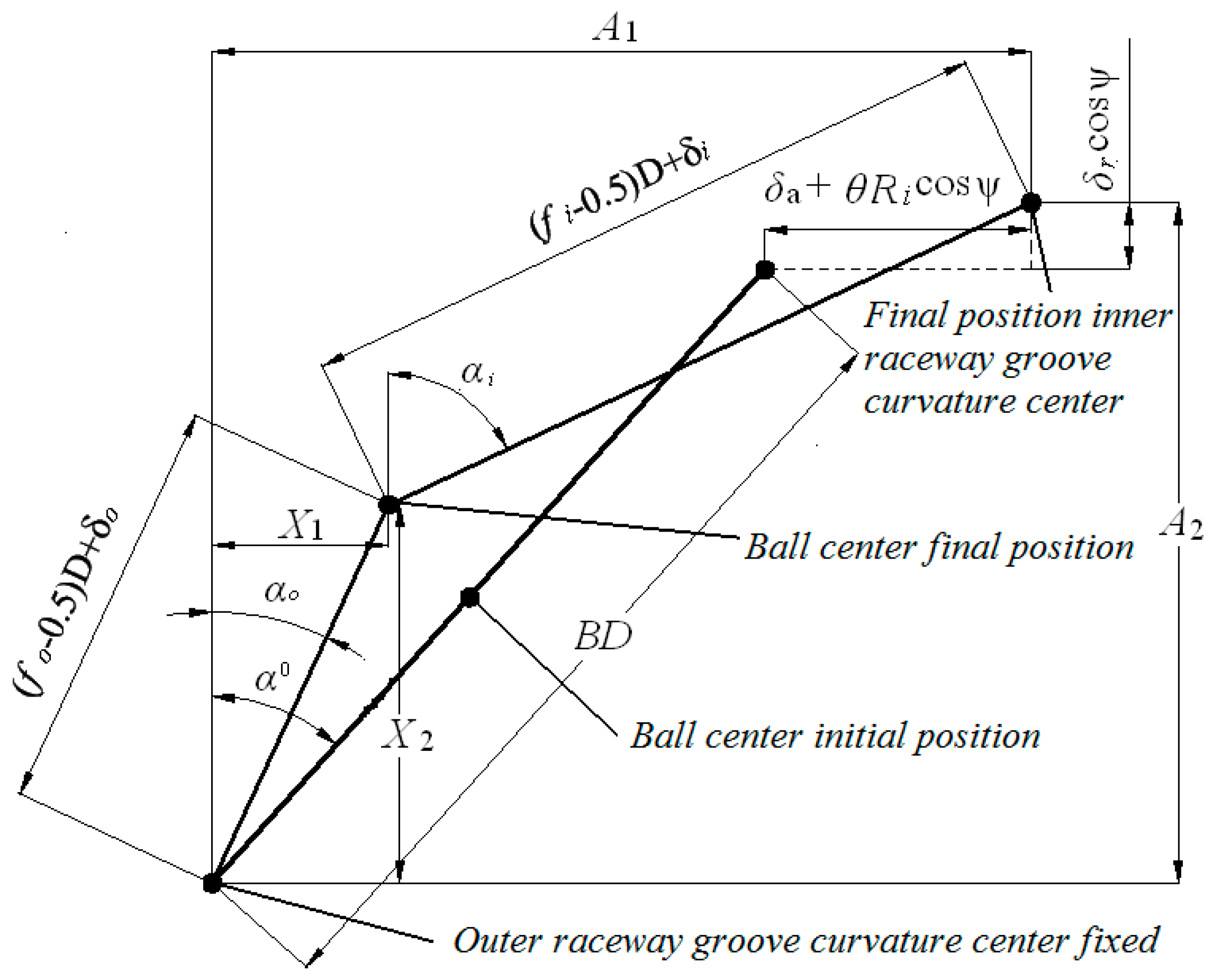
2.1. Deflection of High-Speed Ball Bearing under Applied Load
2.2. Frictional Heat Generation of High-Speed Ball Bearing
3. Heat Flow and Thermal Expansion Model
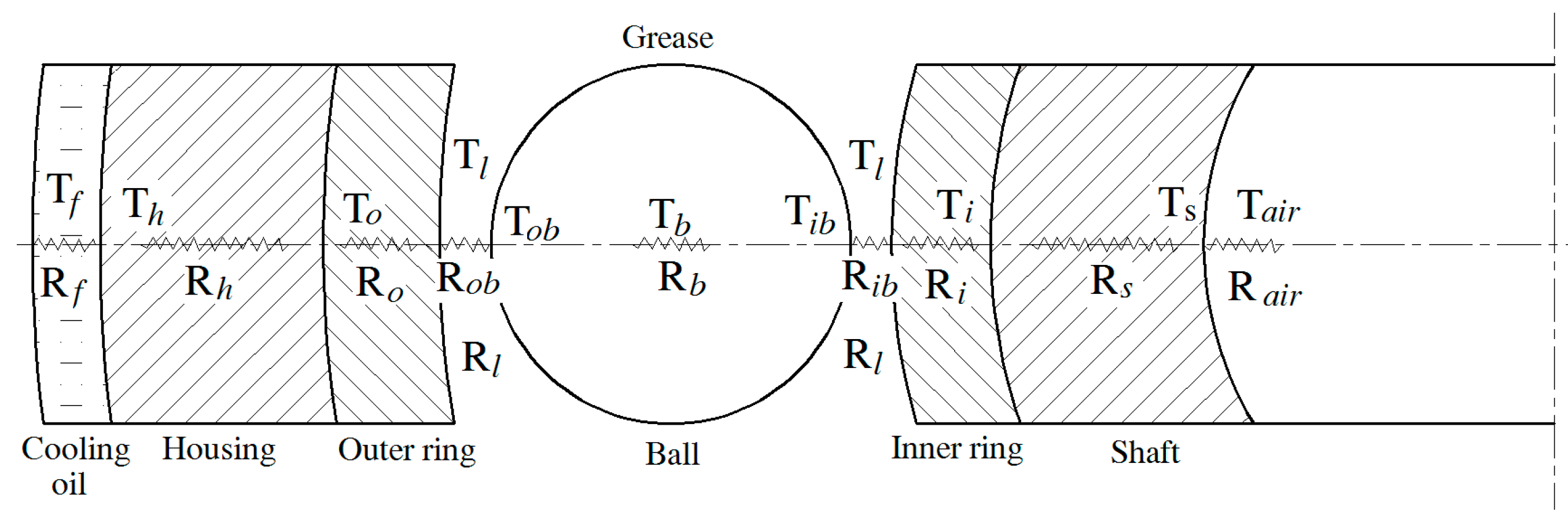
3.1. Heat Transfer Model
3.1.1. Thermal Contact Resistance between Rolling Element and Raceway Groove
3.1.2. Heat Transfer Coefficient of Lubricating Grease
3.1.3. Convective Heat Transfer Coefficient of Cooling Oil
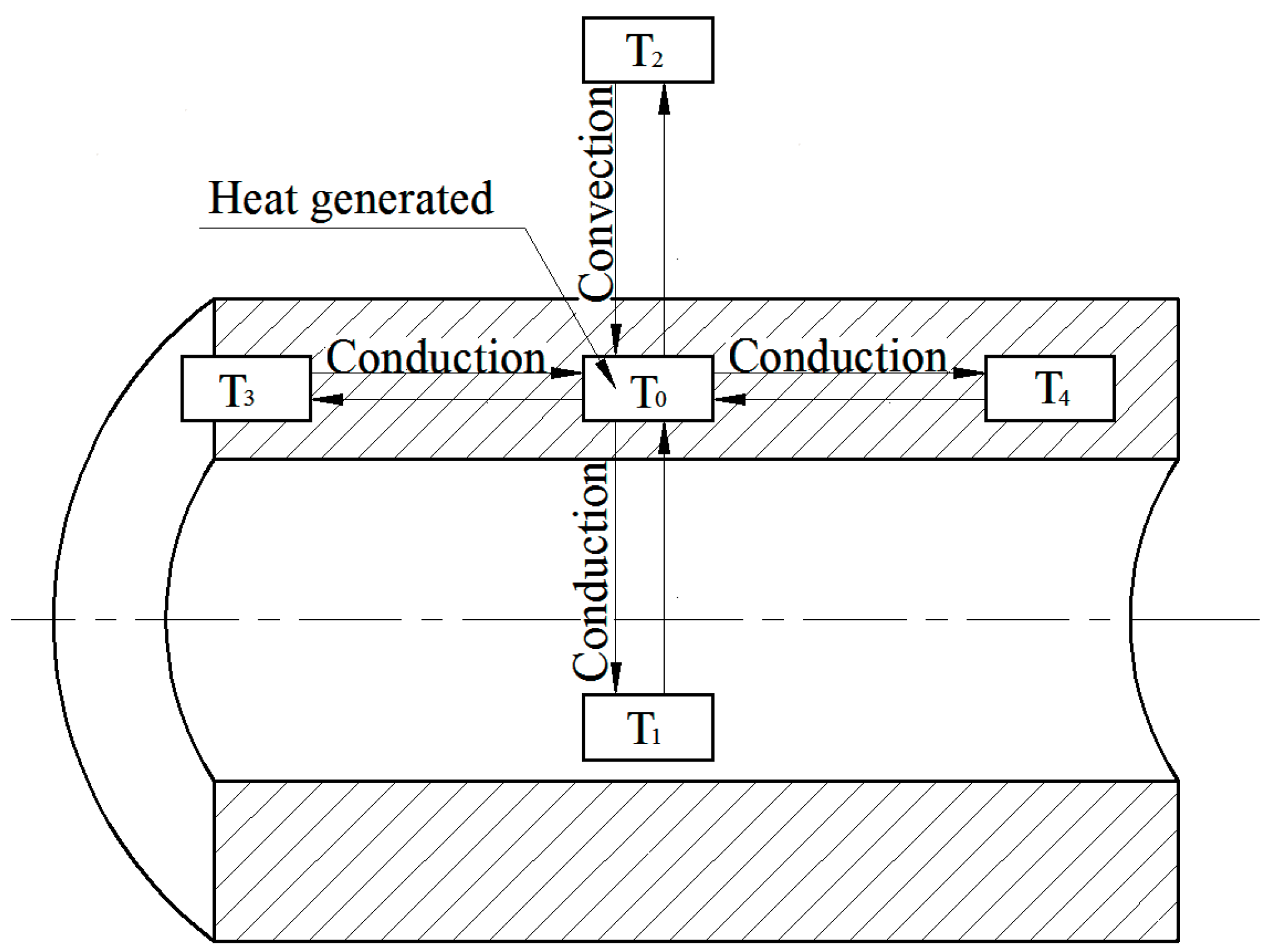
3.2. Temperature Distribution
3.3. Thermal Deformation
4. Result Analysis and Discussion
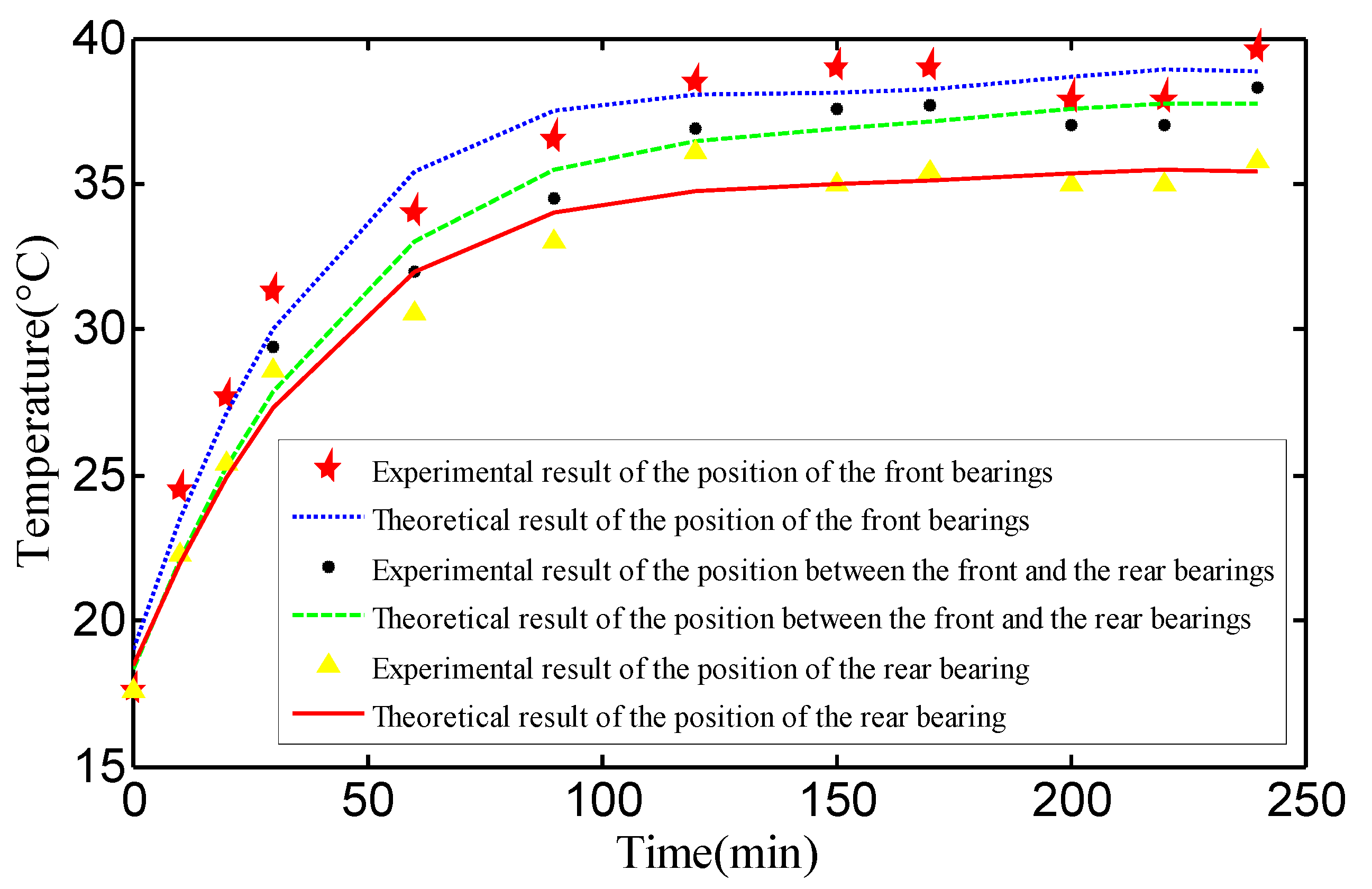
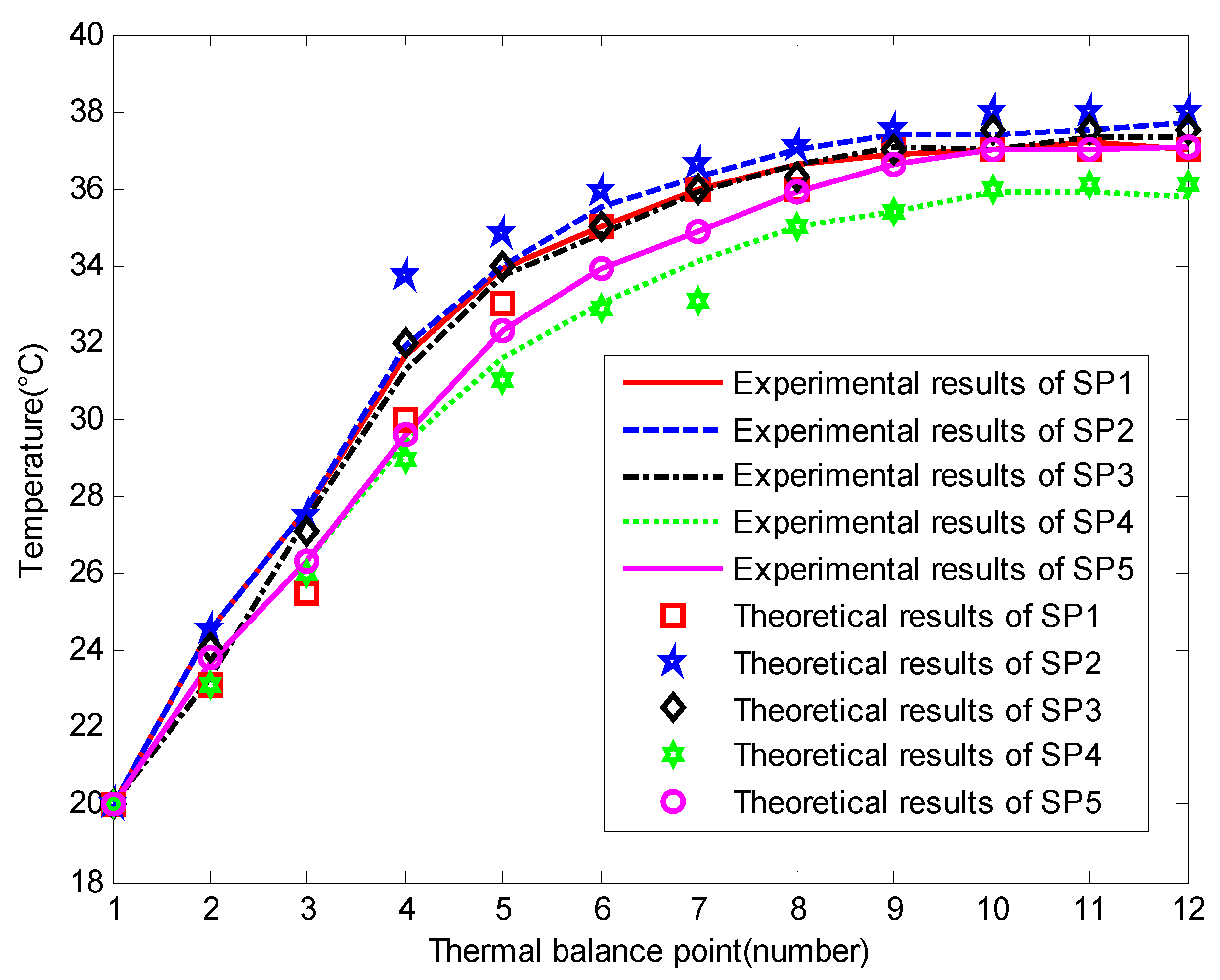
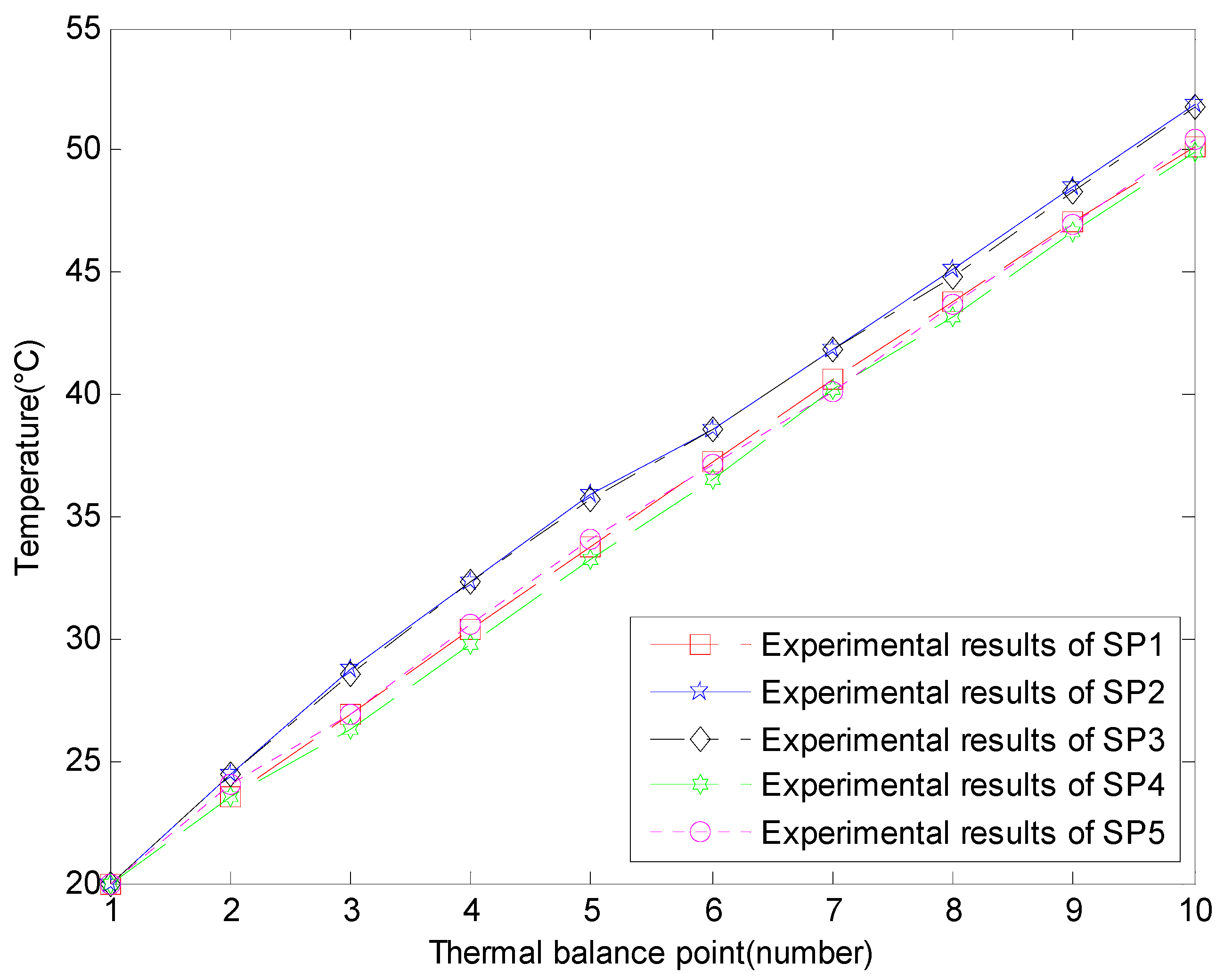
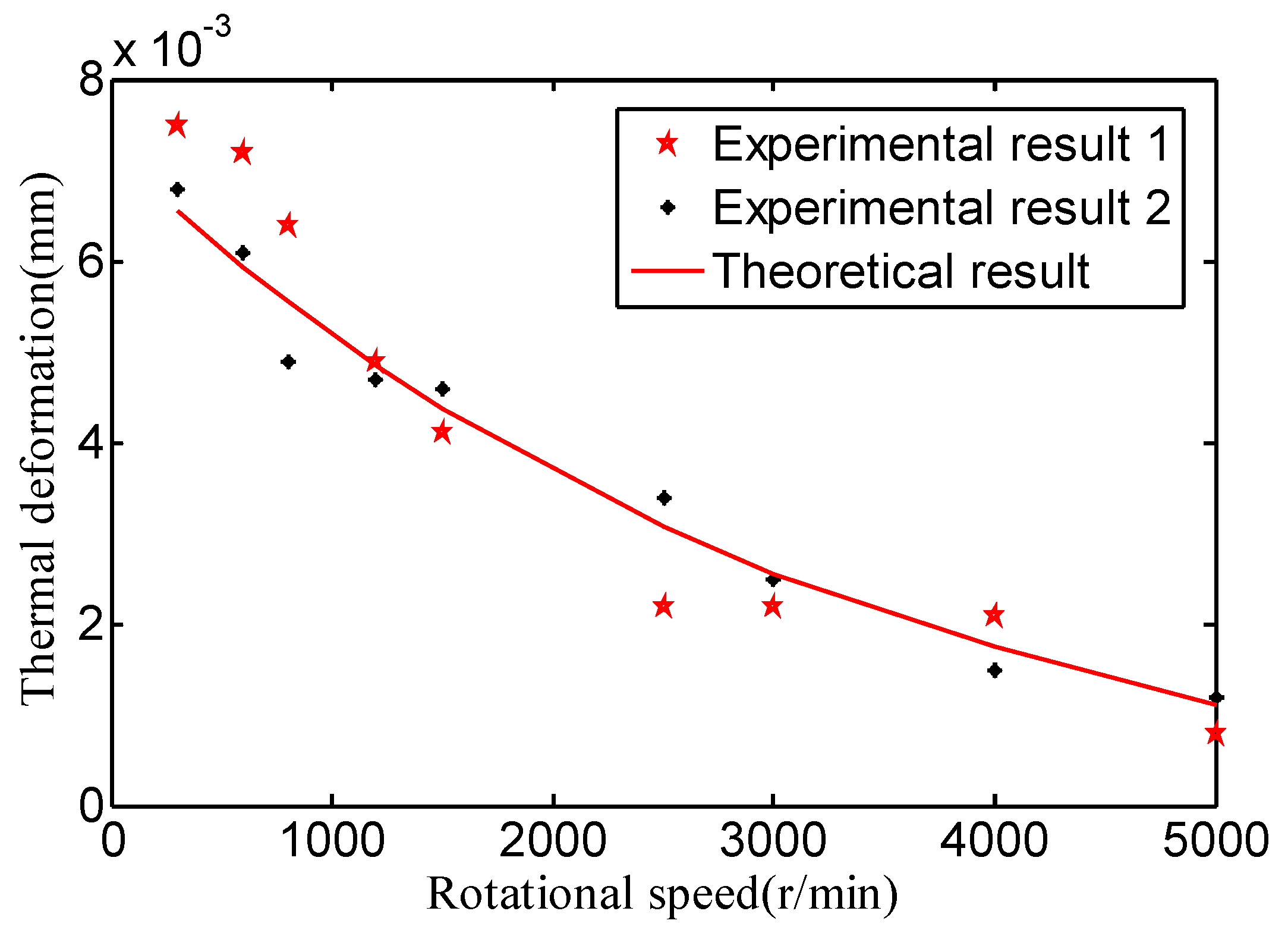
4.1. Experimental Verification
4.2. Numerical Analysis
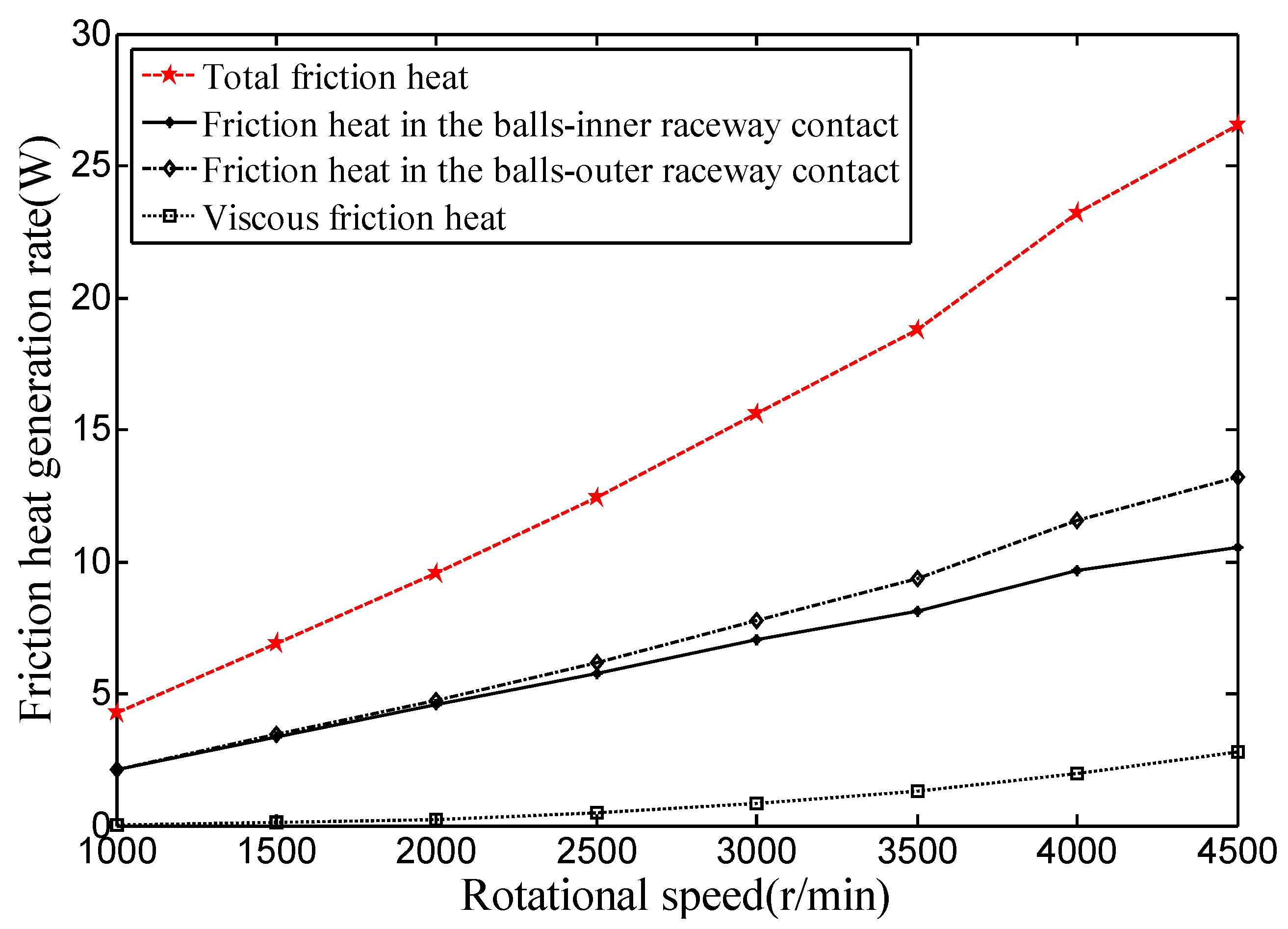
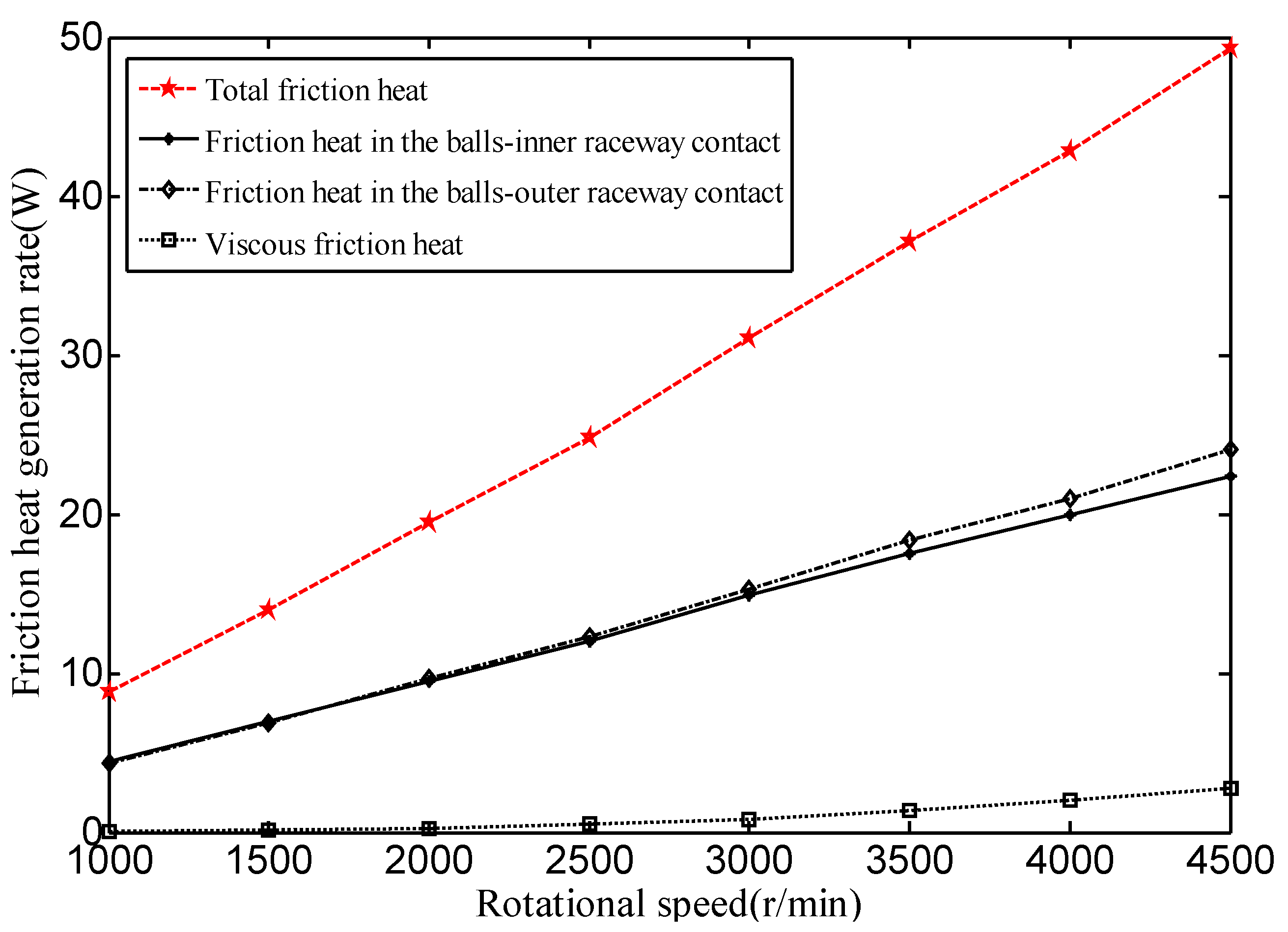
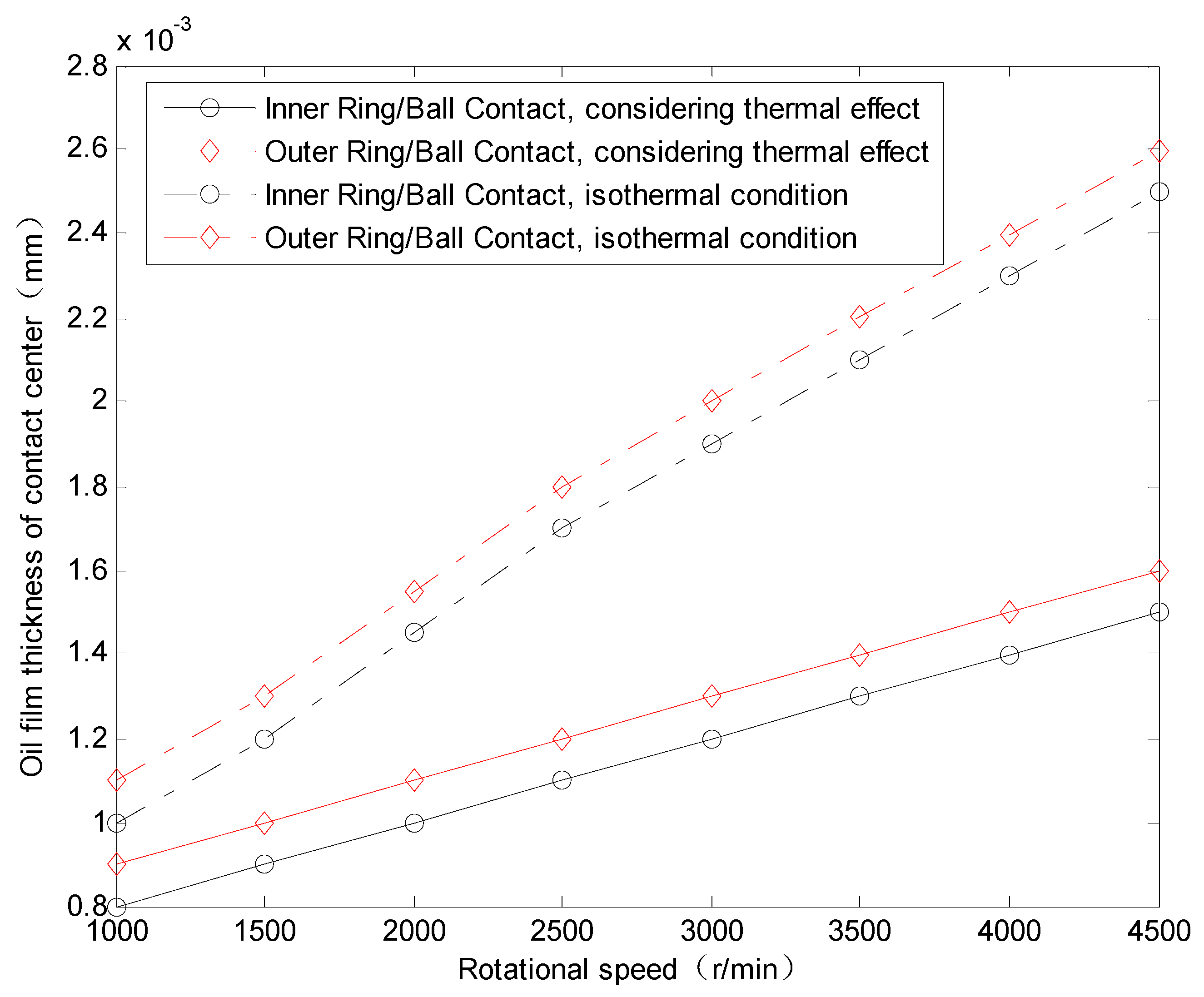
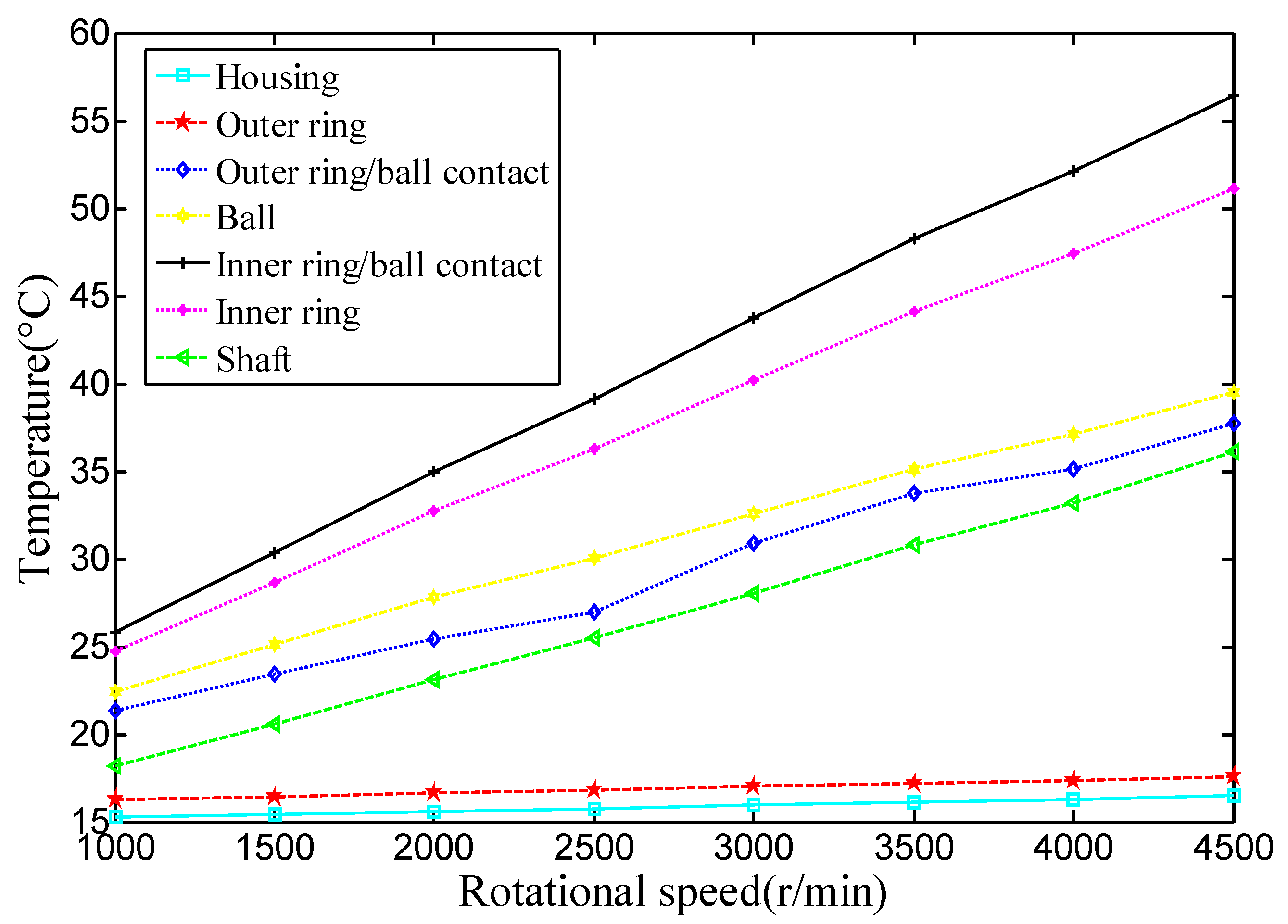
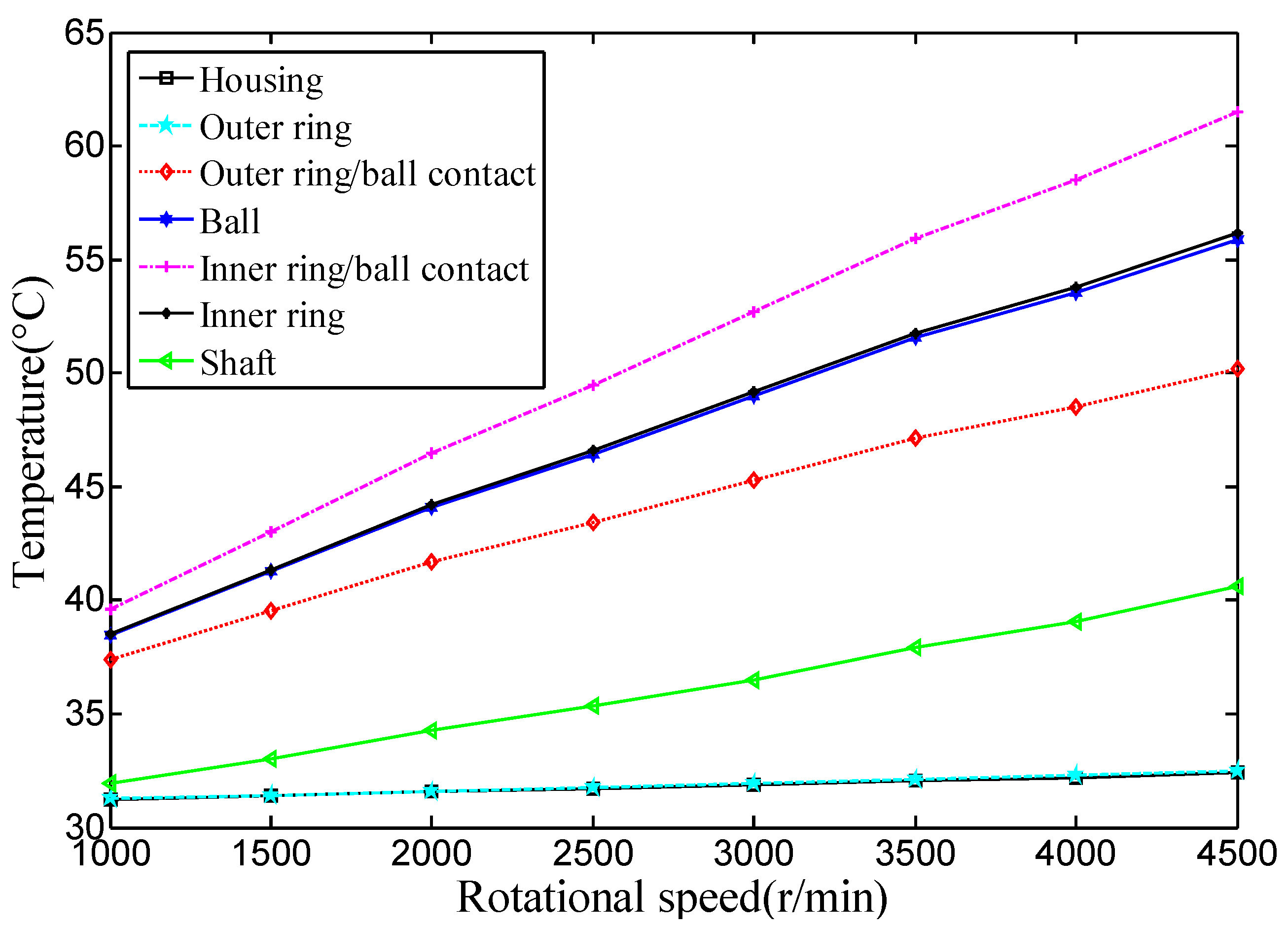
4.2.1. Effect of Rotational Speed and Preload
4.2.2. Effect of Lubricating Grease Temperature
4.2.3. Effect of Cooling System
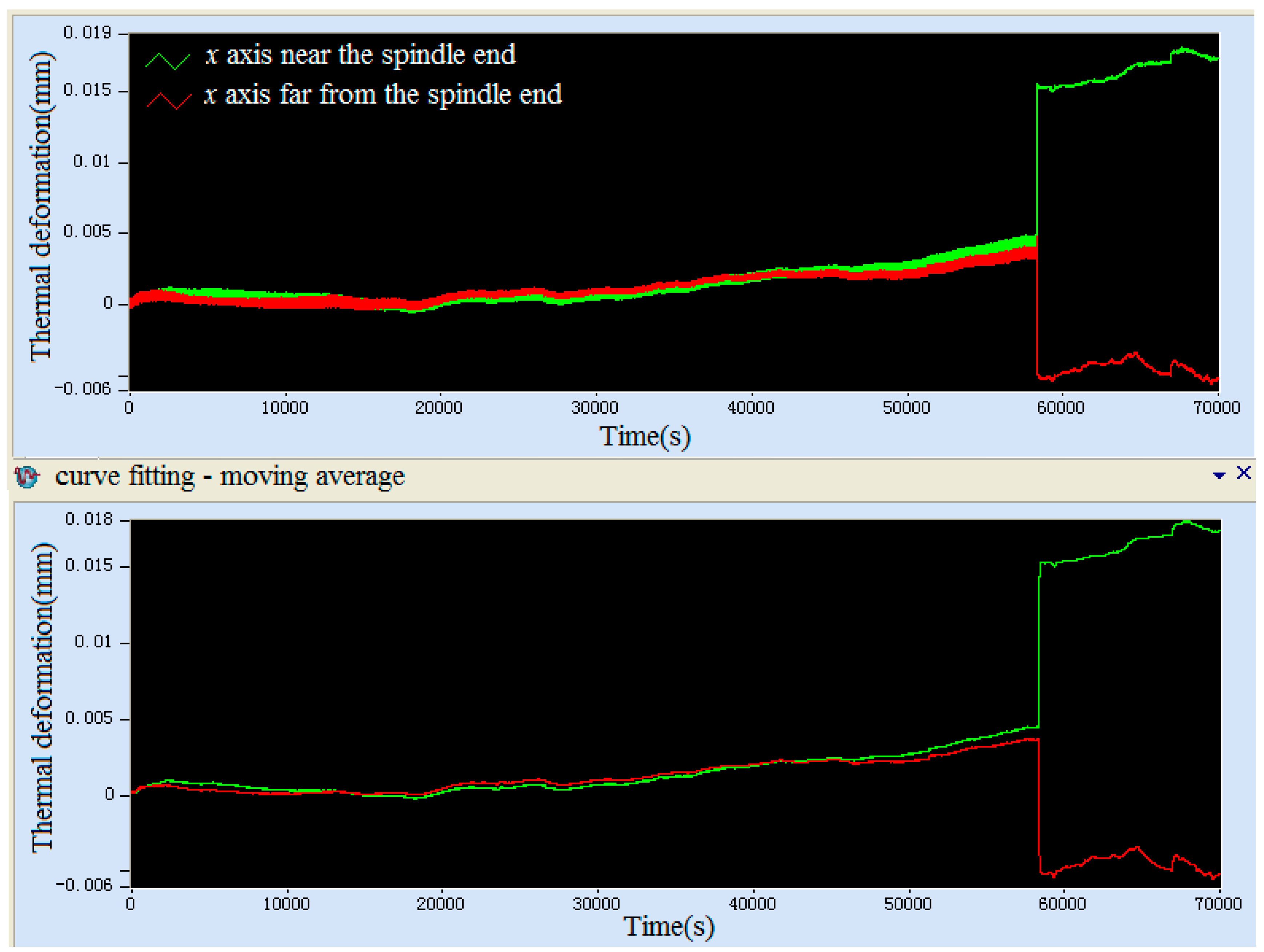
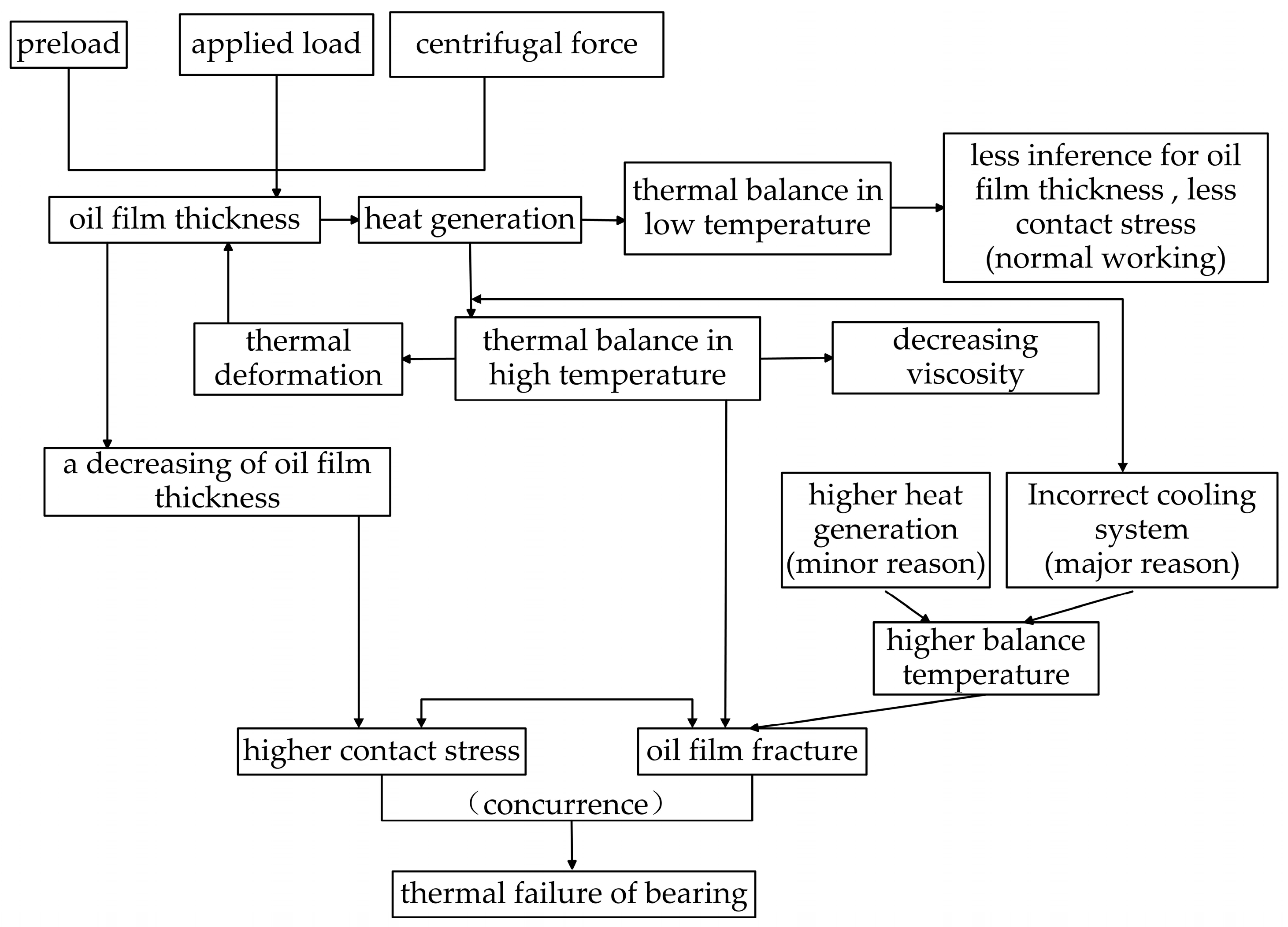
4.2.4. Analysis of Thermal Failure
5. Conclusions
- (1)
- The thermo-mechanical coupling model, the heat transfer model, and the numerical calculation of the temperature prediction model can be used to analyze the transient and steady state thermal characteristics of the spindle-bearing system owing to the lumped assumption of the spindle and the finite number of temperature nodes of the entire system. The main factors of models such as applied force, preload, lubricating state, surface morphology, and rotational speed are numerically analyzed.
- (2)
- A heat transfer model can be used to estimate critical parameters such as the thermal contact resistance between the rolling element and the raceway, the convective heat transfer coefficient of the cooling system, and the grease. The accuracy of the temperature distribution calculation depends on the selection of the boundary conditions and the initial temperature.
- (3)
- Various experimental schemes are designed and a number of experimental real-time measuring are conducted for comparative analysis. Not only are the effectiveness, accuracy, and practicability of the mathematical models verified, but also a comprehensive understanding about the thermal characteristic of the spindle system at the transient and steady state can be obtained. These experiments can make the spindle avoid the appearance of the instantaneous temperature peak and the unnecessary thermal failure in actual conditions.
- (4)
- Analysis of the spindle rotational speed, the preload of the spindle bearing, the grease temperature, and the cooling system are carried out. The significant effect of the high rotational speeds, preload oil viscosity, and heat transfer coefficients on the temperature or thermal failure of the bearing has been revealed, and schemes to improve the R&D of the spindle-bearing system are provided.
Author Contributions
Conflicts of Interest
Nomenclature
| A | distance between raceway groove curvature centers |
| f | r/D |
| B | fi + fo − 1, total curvature |
| dm | diameter of pitch circle |
| r | raceway groove curvature radius |
| D | ball diameter |
| a | semi-major axis of the contact area |
| b | semi-minor axis of the contact area |
| α0 | free contact angle |
| α | mounted contact angle |
| Fp | preload |
| E | Young’s modulus |
| ξ | Poisson’s ratio |
| δ | displacement of the bearing |
| θ | angular displacement of the bearing |
| Z | number of balls per bearing |
| ω | rotational speed |
| σ | normal contact stress |
| F(ρ) | curvature difference |
| Σ(ρ) | curvature sum |
| κ | eccentricity |
| β | ball pitch angle |
| β′ | ball yaw angle |
| Mgy′ | gyroscopic movement in y′ direction |
| Mgz′ | gyroscopic movement in z′ direction |
| Fc | centrifugal force |
| Fa | axial force |
| Ri(o) | the radius of the locus of the raceway groove curvature center |
| ψ | azimuth angle of the rolling element |
| τ | frictional shear stress |
| speed parameter | |
| load parameter | |
| G | material parameter |
| Q | ball-raceway normal load |
| F | frictional force |
| Fv | viscous friction force |
| H | heat generation rate |
Appendix A. Surface Friction Shear Stress between Rolling Element and Raceway Groove
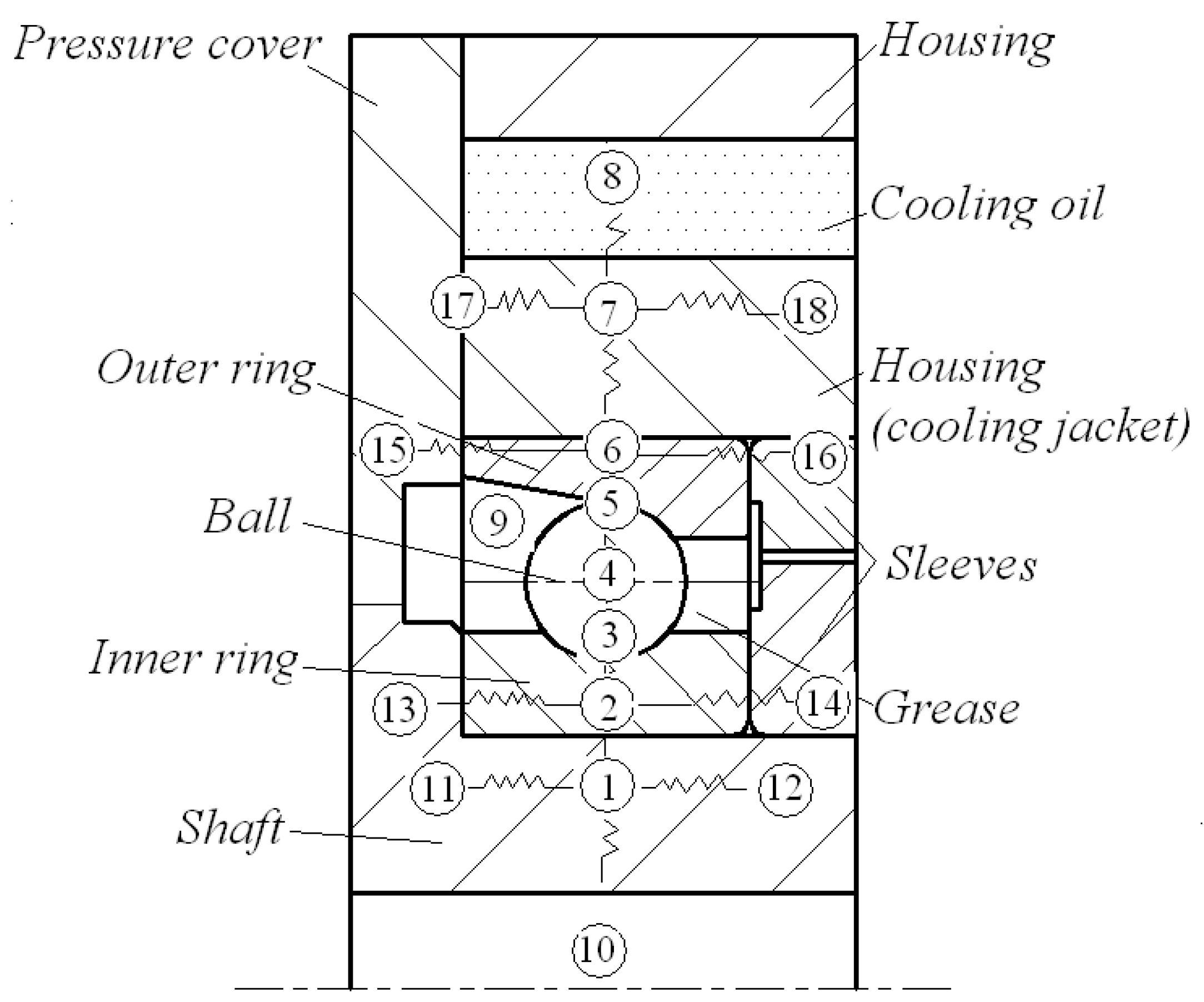
Appendix B. Heat Transfer System of the Temperature Nodes
| Node | A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | - | C | - | - | - | - | - | - | - | - | C | C | - | - | - | - | - | - | - |
| 2 | - | C | - | C | - | - | - | - | - | V | - | - | - | C | C | - | - | - | - | - |
| 3 | - | - | C | - | C | - | - | - | - | C | - | - | - | - | - | - | - | - | - | - |
| 4 | - | - | - | C | - | C | - | - | - | V | - | - | - | - | - | - | - | - | - | - |
| 5 | - | - | - | - | C | - | C | - | - | C | - | - | - | - | - | - | - | - | - | - |
| 6 | - | - | - | - | - | C | - | C | - | V | - | - | - | - | - | C | C | - | - | - |
| 7 | - | - | - | - | - | - | C | - | V | - | - | - | - | - | - | - | - | C | C | - |
| 8 | - | - | - | - | - | - | - | V | - | - | - | - | - | - | - | - | - | V | V | - |
| 9 | - | - | V | C | V | C | V | - | - | - | - | - | - | V | V | V | V | - | - | - |
| 10 | - | V | - | - | - | - | - | - | - | - | - | V | V | - | - | - | - | - | - | - |
| 11 | C | C | - | - | - | - | - | - | - | - | V | - | - | C | - | - | - | - | - | - |
| 12 | - | C | - | - | - | - | - | - | - | - | - | - | - | - | C | - | - | - | - | C |
| 13 | C | - | C | - | - | - | - | - | - | V | - | C | - | - | - | - | - | - | - | - |
| 14 | - | - | C | - | - | - | - | - | - | V | - | - | C | - | - | - | - | - | - | C |
| 15 | C | - | - | - | - | - | C | - | - | V | - | - | - | - | - | - | - | C | - | - |
| 16 | - | - | - | - | - | - | C | - | - | V | - | - | - | - | - | - | - | - | C | C |
| 17 | C | - | - | - | - | - | - | C | V | - | - | - | - | - | - | C | - | - | - | - |
| 18 | - | - | - | - | - | - | - | C | V | - | - | - | - | - | - | - | C | - | - | C |
References
- Tu, J.F.; Stein, J.L. On-line preload monitoring for anti-friction spindle bearings of high-speed machine tools. J. Dyn. Syst. Meas. Control Trans. ASME 1995, 117, 43–53. [Google Scholar] [CrossRef]
- Katter, J.G.; Tu, J.F. Bearing condition monitoring for preventive maintenance in a production environment. Tribol. Trans. 1996, 39, 936–942. [Google Scholar] [CrossRef]
- Choi, J.K.; Lee, D.G. Thermal characteristics of the spindle bearing system with a gear located on the bearing span. Int. J. Mach. Tools Manuf. 1998, 38, 1017–1030. [Google Scholar] [CrossRef]
- Lin, C.; Tu, J.F.; Kamman, J. An integrated thermo-mechanical-dynamic model to characterize motorized machine tool spindles during very high speed rotation. Int. J. Mach. Tools Manuf. 2003, 43, 1035–1050. [Google Scholar] [CrossRef]
- Nosonovsky, M. Entropy in Tribology: In the Search for Applications. Entropy 2010, 12, 1345–1390. [Google Scholar] [CrossRef]
- Lin, S.-K. Diversity and Entropy. Entropy 1999, 1, 1–3. [Google Scholar] [CrossRef]
- Min, X.; Shuyun, J.; Ying, C. An improved thermal model for machine tool bearings. Int. J. Mach. Tools Manuf. 2007, 47, 53–62. [Google Scholar] [CrossRef]
- Takabi, J.; Khonsari, M.M. Experimental testing and thermal analysis of ball bearings. Tribol. Int. 2013, 60, 93–103. [Google Scholar] [CrossRef]
- Bryant, M.D.; Khonsari, M.M. Application of Degradation-Entropy Generation Theorem to Dry Sliding Friction and Wear. In Proceedings of the STLE/ASME 2008 International Joint Tribology Conference, London, UK, 20–22 October 2008.
- Bryant, M.D. Entropy and dissipative processes of friction and wear. FME Trans. 2009, 37, 55–60. [Google Scholar]
- Amiri, M.; Khonsari, M.M.; Brahmeshwarkar, S. An Application of Dimensional Analysis to Entropy-Wear Relationship. J. Tribol. 2012, 134, 308–309. [Google Scholar] [CrossRef]
- Aghdam, A.B.; Khonsari, M.M. On the correlation between wear and entropy in dry sliding contact. Wear 2011, 270, 781–790. [Google Scholar] [CrossRef]
- Kagan, E. Turing Systems, Entropy, and Kinetic Models for Self-Healing Surfaces. Entropy 2010, 12, 554–569. [Google Scholar] [CrossRef]
- Aziz, A. Entropy Generation in Pressure Gradient Assisted Couette Flow with Different Thermal Boundary Conditions. Entropy 2006, 8, 50–62. [Google Scholar] [CrossRef]
- Prokopenko, M.; Gershenson, C. Entropy Methods in Guided Self-Organisation. Entropy 2014, 16, 5232–5241. [Google Scholar] [CrossRef]
- Bossmanns, B.; Tu, J.F. A thermal model for high speed motorized spindles. Int. J. Mach. Tools Manuf. 1999, 39, 1345–1366. [Google Scholar] [CrossRef]
- Holkup, T.; Cao, H.; Kolář, P.; Altintas, Y.; Zelený, J. Thermo-mechanical model of spindles. CIRP Ann. Manuf. Technol. 2010, 59, 365–368. [Google Scholar] [CrossRef]
- Mizuta, K.; Inoue, T.; Takahashi, Y.; Huang, S.; Ueda, K.; Omokawa, H. Heat transfer characteristics between inner and outer rings of an angular ball bearing. Heat Transf. Asian Res. 2003, 32, 42–57. [Google Scholar] [CrossRef]
- Chien, C.H.; Jang, J.Y. 3-D numerical and experimental analysis of a built-in motorized high-speed spindle with helical water cooling channel. Appl. Ther. Eng. 2008, 28, 2327–2336. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Advanced Concepts of Bearing Technology: Rolling Bearing Analysis, 5th ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Masjedi, M.; Khonsari, M.M. Theoretical and experimental investigation of traction coefficient in line-contact EHL of rough surface. Tribol. Int. 2014, 70, 179–189. [Google Scholar] [CrossRef]
- Takabi, J.; Khonsari, M.M. On the dynamic performance of roller bearings operating under low rotational speeds with consideration of surface roughness. Tribol. Int. 2015, 86, 62–71. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Ball Bearing Lubrication: The Elastohydrodynamics of Elliptical Contact; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Dowson, D. Elastohydrodynamic and micro-elastohydrodynamic lubrication. Wear 1995, 190, 125–138. [Google Scholar] [CrossRef]
- Nakajima, K. Thermal contact resistance between balls and rings of a bearing under axial, radial, and combined loads. J. Thermophys. Heat Transfer. 1995, 9, 88–95. [Google Scholar] [CrossRef]
- Hu, T.; Yin, G.; Deng, C. Approach to Study Bearing Thermal Preload Based on the Thermo-Mechanical Information Interaction Net. Int. J. Control Autom. 2014, 7, 299–312. [Google Scholar] [CrossRef]
- Tu, J.F.; Stein, J.L. Active thermal preload regulation for machine tool spindles with rolling element bearings. J. Manuf. Sci. Eng. Trans. ASME 1996, 118, 499–505. [Google Scholar] [CrossRef]
- Tu, J.F. Thermoelastic instability monitoring for preventing spindle bearing seizure. Tribol. Trans. 1995, 38, 11–18. [Google Scholar] [CrossRef]
- Stein, J.L.; Tu, J.F. A state-space model for monitoring thermally induced preload in anti-friction spindle bearings of high-speed machine tools. J. Dyn. Syst. Meas. Control Trans. ASME 1994, 116, 372–386. [Google Scholar] [CrossRef]
- Du, Z.C.; Yao, S.Y.; Yang, J.G. Thermal Behavior Analysis and Thermal Error Compensation for Motorized Spindle of Machine Tools. Int. J. Mach. Tools Manuf. 2015, 7, 1571–1581. [Google Scholar] [CrossRef]
- Kim, S.-M.; Lee, K.-J.; Lee, S.-K. Effect of bearing support structure on the high-speed spindle bearing compliance. Int. J. Mach. Tools Manuf. 2002, 42, 365–373. [Google Scholar] [CrossRef]
- Kim, S.-M.; Lee, K.-J. Prediction of thermo-elastic behavior in a spindle–bearing system considering bearing surroundings. Int. J. Mach. Tools Manuf. 2001, 41, 809–831. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, X.; Sun, H.; Wu, Q.; Liu, W. Experimental Study of Single Phase Flow in a Closed-Loop Cooling System with Integrated Mini-Channel Heat Sink. Entropy 2016, 18, 128–141. [Google Scholar] [CrossRef]
- Pang, L.; Wang, M. Optimal Thermal Design of a Stacked Mini-Channel Heat Sink Cooled by a Low Flow Rate Coolant. Entropy 2013, 15, 4716–4731. [Google Scholar] [CrossRef]
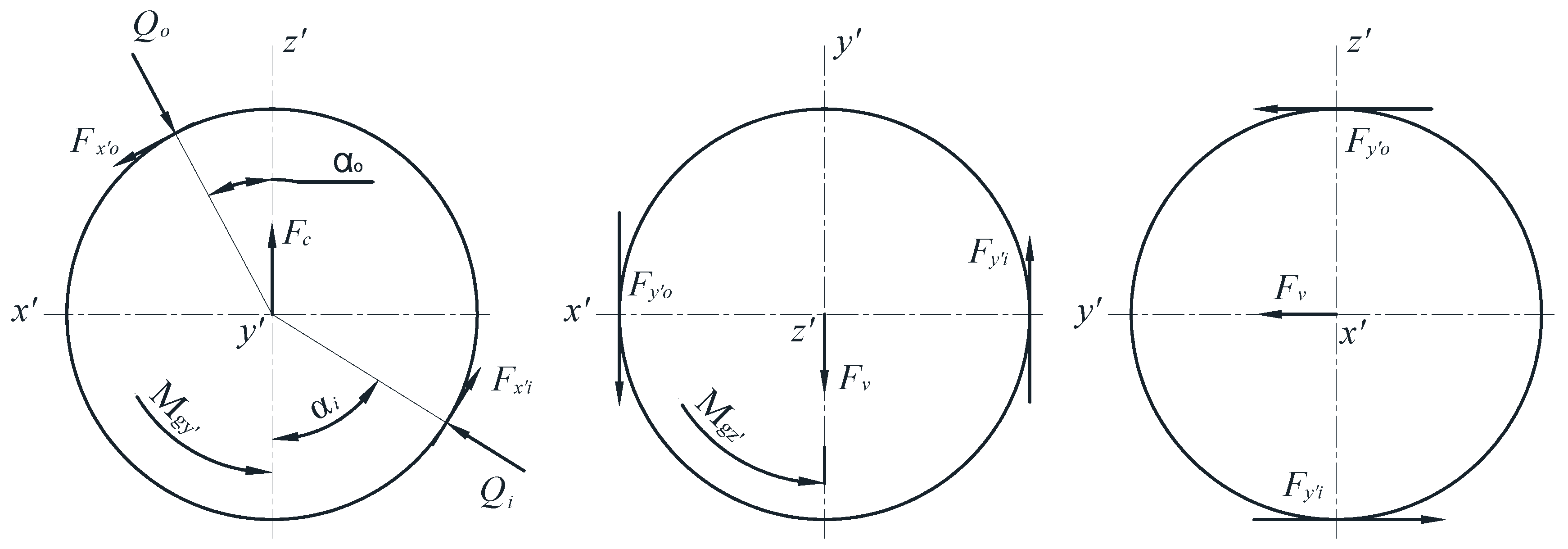



© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Tan, Q. Thermal Characteristic Analysis and Experimental Study of a Spindle-Bearing System. Entropy 2016, 18, 271. https://doi.org/10.3390/e18070271
Wu L, Tan Q. Thermal Characteristic Analysis and Experimental Study of a Spindle-Bearing System. Entropy. 2016; 18(7):271. https://doi.org/10.3390/e18070271
Chicago/Turabian StyleWu, Li, and Qingchang Tan. 2016. "Thermal Characteristic Analysis and Experimental Study of a Spindle-Bearing System" Entropy 18, no. 7: 271. https://doi.org/10.3390/e18070271
APA StyleWu, L., & Tan, Q. (2016). Thermal Characteristic Analysis and Experimental Study of a Spindle-Bearing System. Entropy, 18(7), 271. https://doi.org/10.3390/e18070271