Maximum Entropy Learning with Deep Belief Networks
Abstract
:1. Introduction
2. Preliminaries and Background
2.1. Restricted Boltzmann Machine
2.2. Gaussian Unit RBM for Continuous Data
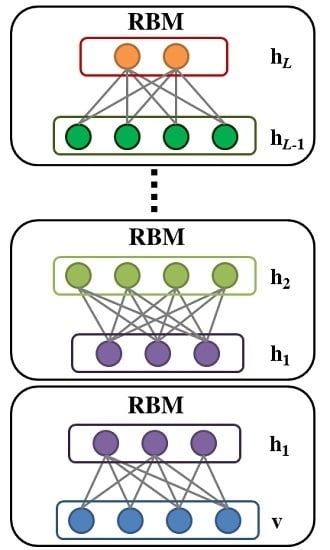
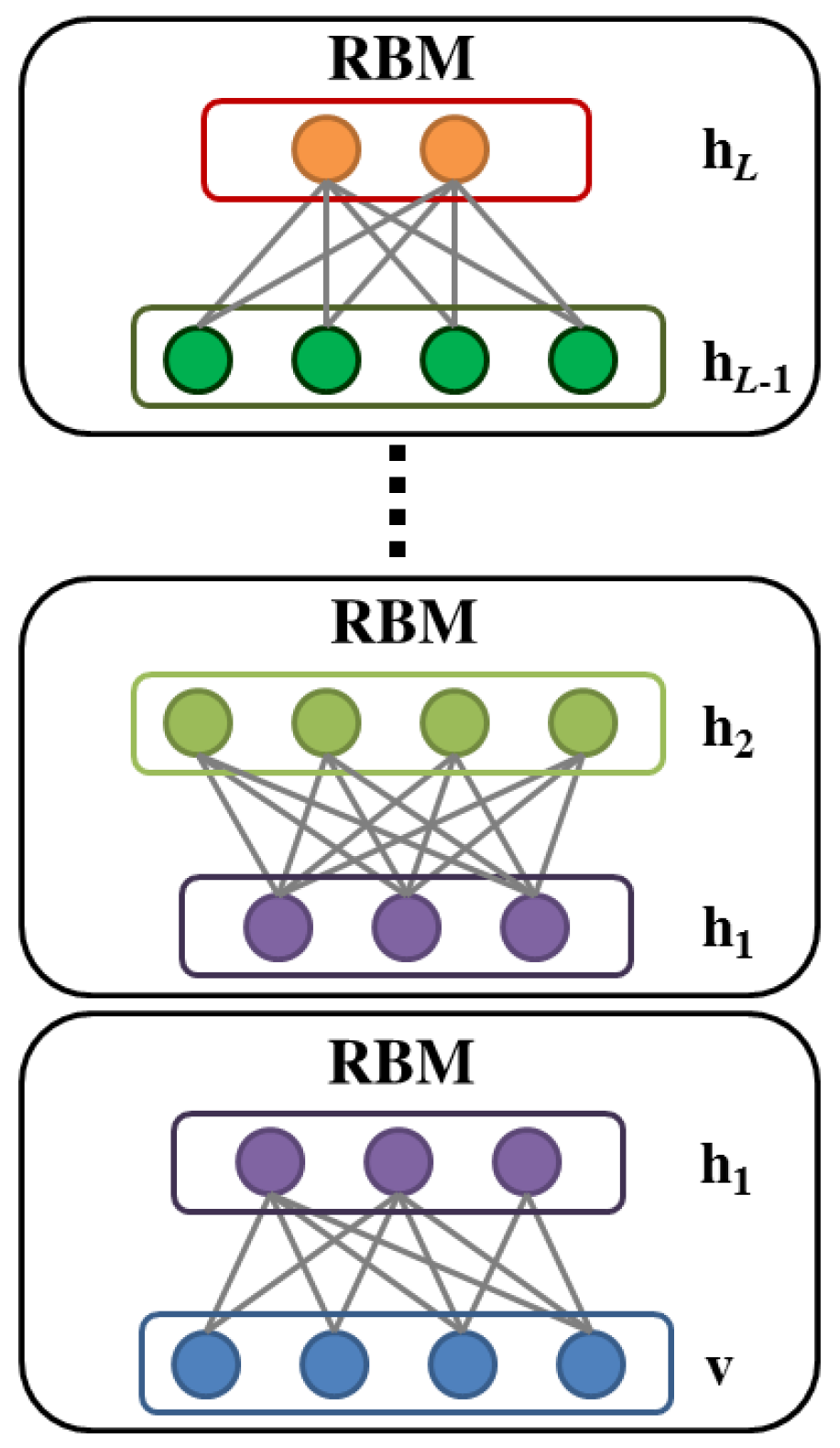
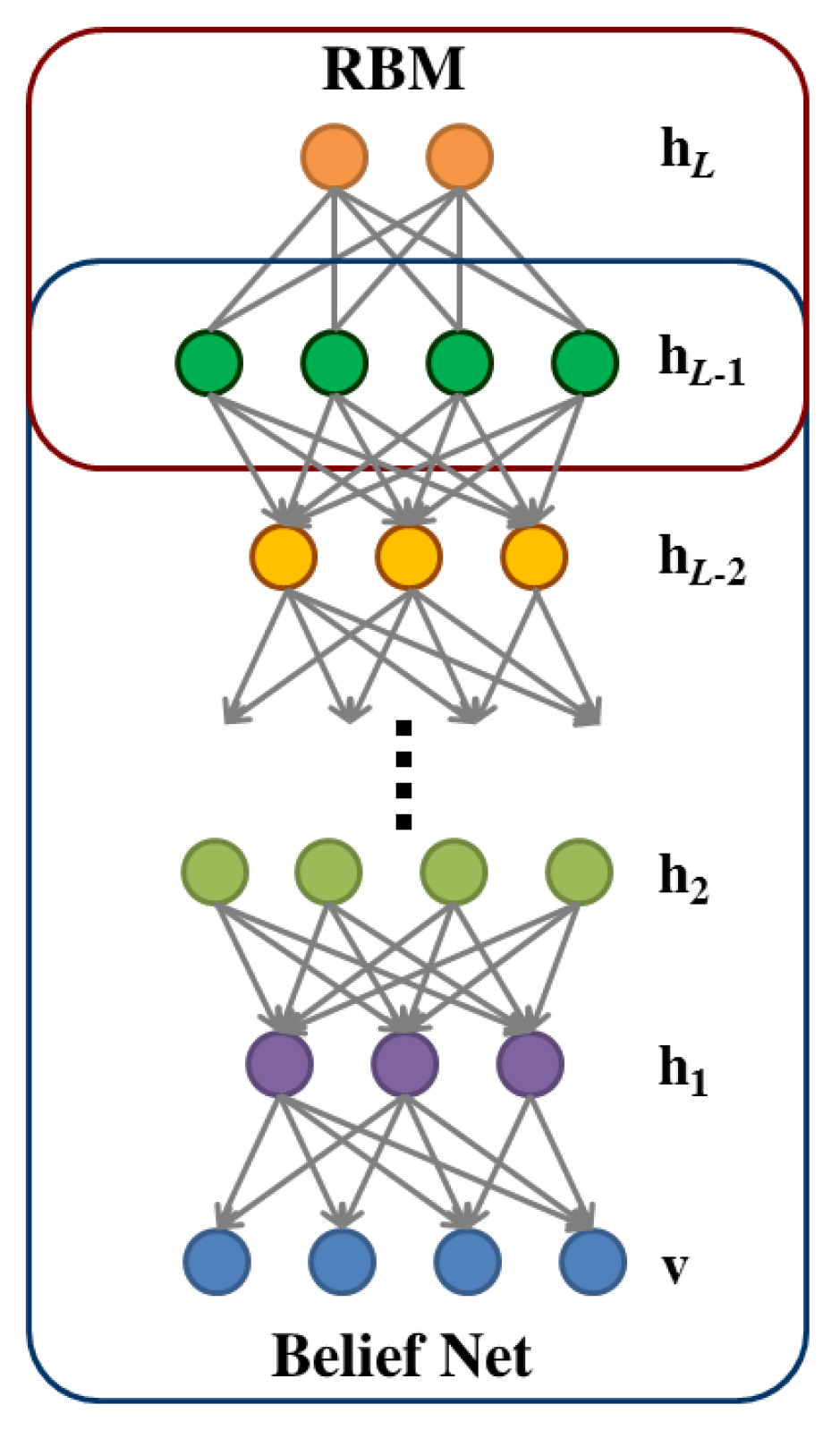
2.3. Deep Belief Network
2.4. Maximum Entropy Learning
3. Maximum Entropy Deep Belief Network
3.1. Maximum Entropy Restricted Boltzmann Machine
| Algorithm 1 Expectation Maximization–Contrastive Divergence Algorithm |
|
3.2. Greedy Layer-Wise Learning
3.3. Imposing Weight Decay and Sparsity Constraints
4. Experiment
4.1. Experiments on Object Recognition
4.1.1. Datasets and Protocol
4.1.2. Feature Learning
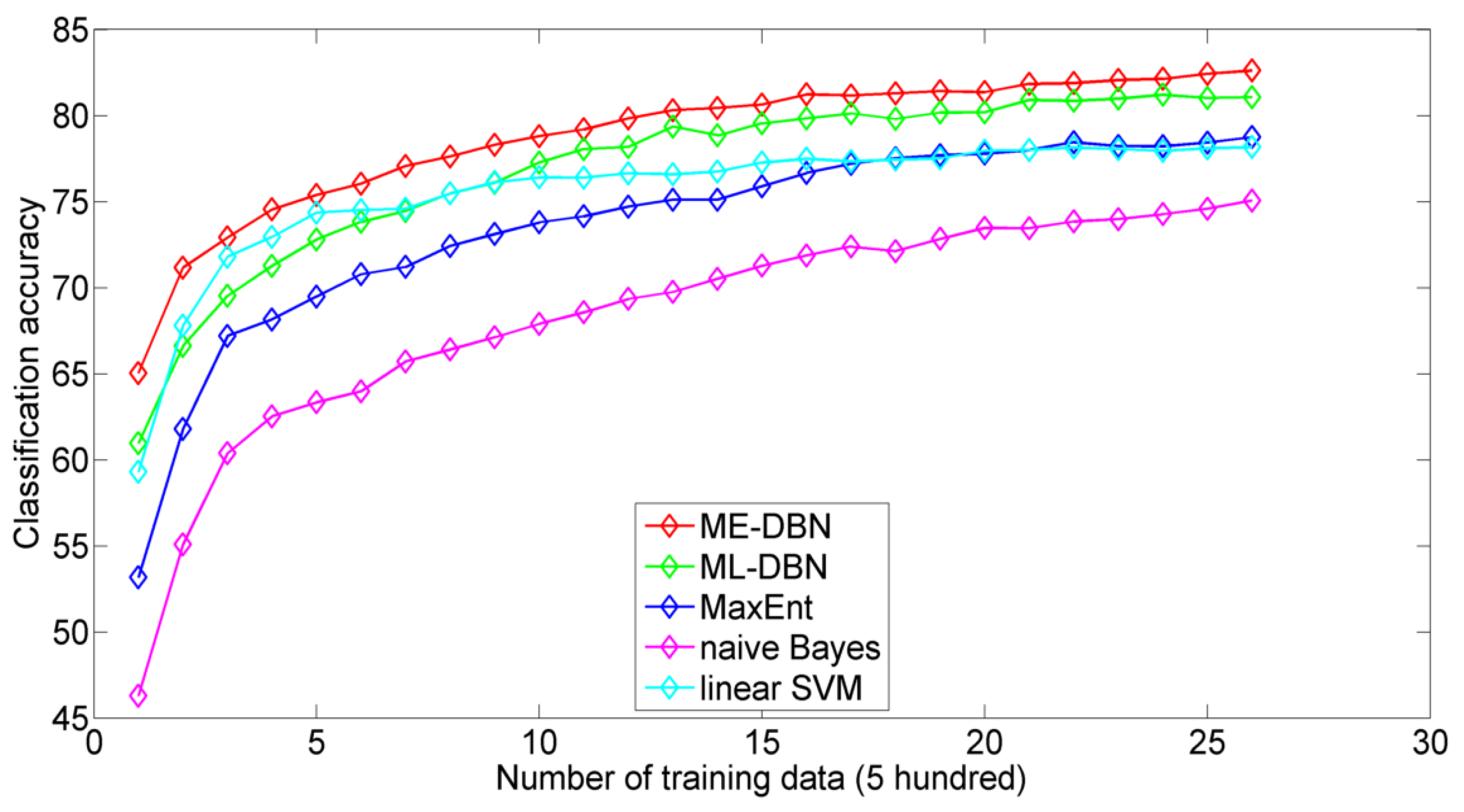
4.1.3. Classification Performance
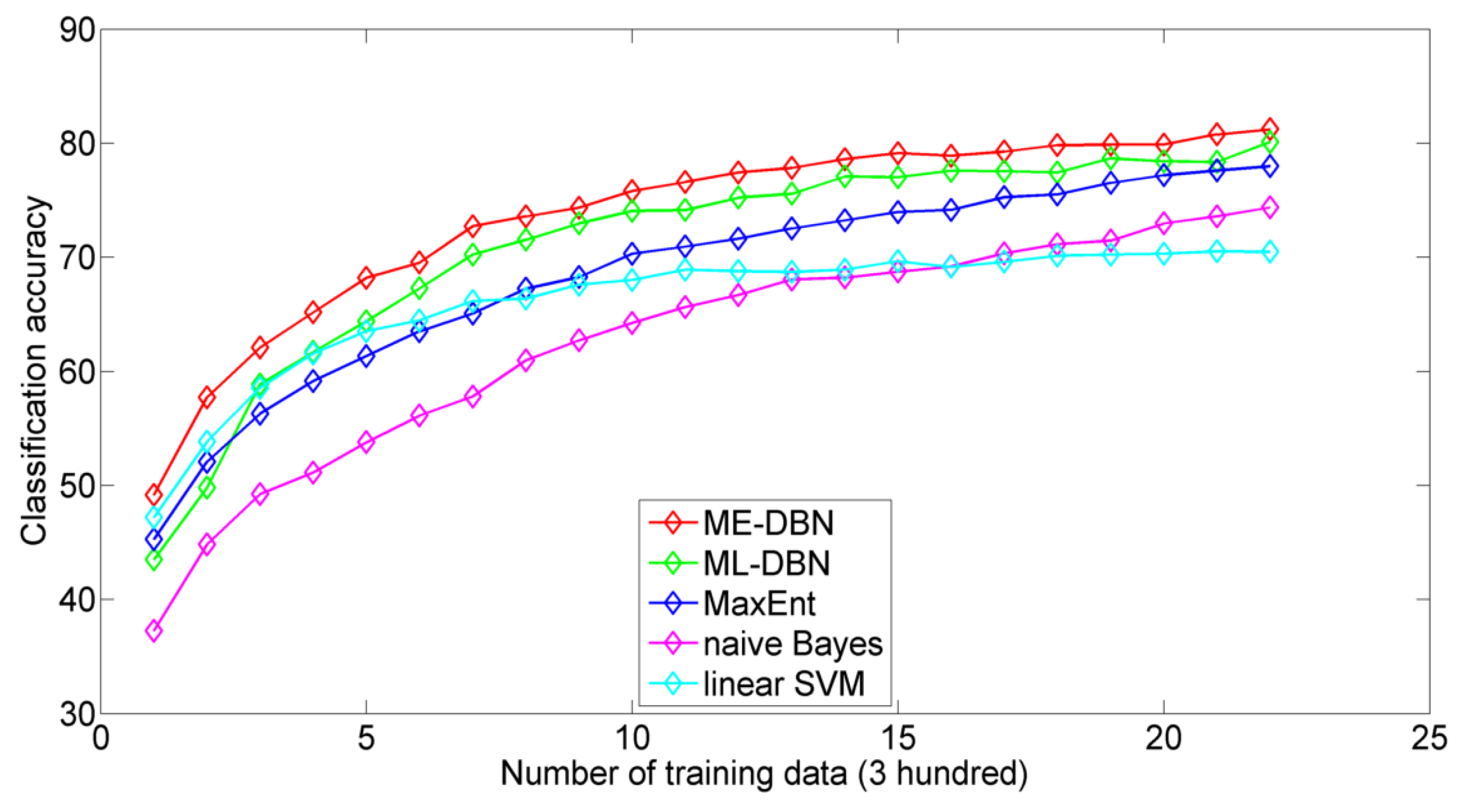
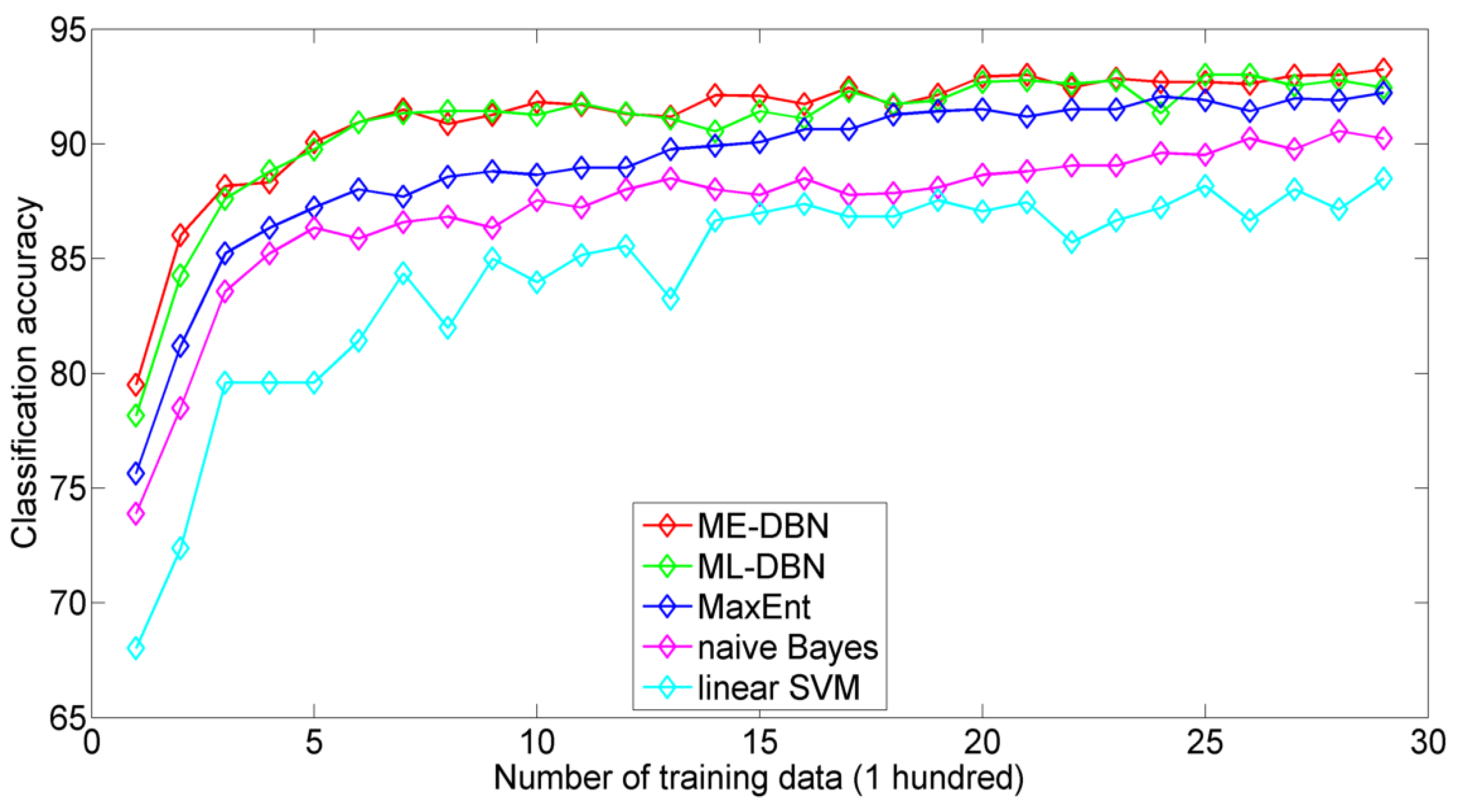
4.2. Experiments on Text Classification
4.2.1. Datasets and Protocol
4.2.2. Classification Performance
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hopfield, J.J.; Tank, D.W. Computing with neural circuits—A model. Science 1986, 233, 625–633. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- LeCun, Y.; Huang, F.J.; Bottou, L. Learning methods for generic object recognition with invariance to pose and lighting. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 2, pp. 97–104.
- Felleman, D.J.; van Essen, D.C. Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1991, 1, 1–47. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.S.; Mumford, D.; Romero, R.; Lamme, V.A. The role of the primary visual cortex in higher level vision. Vis. Res. 1998, 38, 2429–2454. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1988, 323, 533–536. [Google Scholar] [CrossRef]
- Hinton, G.E. Connectionist learning procedures. Artif. Intell. 1989, 40, 185–234. [Google Scholar] [CrossRef]
- Fu, L.; Hsu, H.H.; Principe, J.C. Incremental backpropagation learning networks. IEEE Trans. Neural Netw. 1996, 7, 757–761. [Google Scholar] [PubMed]
- Lake, B.M.; Salakhutdinov, R.; Tenenbaum, J.B. Human-level concept learning through probabilistic program induction. Science 2015, 350, 1332–1338. [Google Scholar] [CrossRef] [PubMed]
- Gopnik, A.; Glymour, C.; Sobel, D.M.; Schulz, L.E.; Kushnir, T.; Danks, D. A theory of causal learning in children: Causal maps and Bayes nets. Psychol. Rev. 2004, 111, 3–32. [Google Scholar] [CrossRef] [PubMed]
- Mumford, D. On the computational architecture of the neocortex. Biol. Cybern. 1992, 66, 241–251. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Smolensky, P. Information processing in dynamical systems: Foundations of harmony theory. In Parallel Distributed Processing; MIT Press: Cambridge, MA, USA, 1986; pp. 194–281. [Google Scholar]
- Bengio, Y.; LeCun, Y. Scaling Learning Algorithms towards AI; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Ackley, D.H.; Hinton, G.E.; Sejnowski, T.J. A learning algorithm for Boltzmann machines. Cogn. Sci. 1985, 9, 147–169. [Google Scholar] [CrossRef]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002, 14, 1771–1800. [Google Scholar] [CrossRef] [PubMed]
- Deng, L. Three classes of deep learning architectures and their applications: A tutorial survey. APSIPA Trans. Signal Inf. Process. Available online: https://www.microsoft.com/en-us/research/publication/three-classes-of-deep-learning-architectures-and-their-applications-a-tutorial-survey/ (accessed on 7 July 2016).
- Liu, F.; Liu, B.; Sun, C.; Liu, M.; Wang, X. Deep belief network-based approaches for link prediction in signed social networks. Entropy 2015, 17, 2140–2169. [Google Scholar] [CrossRef]
- Ma, X.; Wang, X. Average Contrastive Divergence for Training Restricted Boltzmann Machines. Entropy 2016, 18, 35. [Google Scholar] [CrossRef]
- Hinton, G.E. To recognize shapes, first learn to generate images. Prog. Brain Res. 2007, 165, 535–547. [Google Scholar] [PubMed]
- Erhan, D.; Manzagol, P.A.; Bengio, Y.; Bengio, S.; Vincent, P. The difficulty of training deep architectures and the effect of unsupervised pre-training. In Proceedings of the 12th International Conference on Artificial Intelligence and Statistics (AISTATS), Clearwater Beach, FL, USA, 16–18 April 2009; pp. 153–160.
- Larochelle, H.; Bengio, Y.; Louradour, J.; Lamblin, P. Exploring strategies for training deep neural networks. J. Mach. Learn. Res. 2009, 10, 1–40. [Google Scholar]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy layer-wise training of deep networks. In Proceedings of the Neural Information Processing Systems (NIPS’06), Vancouver, BC, Canada, 3–8 December 2007; Volume 19, pp. 153–160.
- Erhan, D.; Bengio, Y.; Courville, A.; Manzagol, P.A.; Vincent, P.; Bengio, S. Why does unsupervised pre-training help deep learning? J. Mach. Learn. Res. 2010, 11, 625–660. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Schneidman, E.; Berry, M.J.; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef] [PubMed]
- Yeh, F.C.; Tang, A.; Hobbs, J.P.; Hottowy, P.; Dabrowski, W.; Sher, A.; Litke, A.; Beggs, J.M. Maximum entropy approaches to living neural networks. Entropy 2010, 12, 89–106. [Google Scholar] [CrossRef]
- Haddad, W.M.; Hui, Q.; Bailey, J.M. Human brain networks: Spiking neuron models, multistability, synchronization, thermodynamics, maximum entropy production, and anesthetic cascade mechanisms. Entropy 2014, 16, 3939–4003. [Google Scholar] [CrossRef]
- Nasser, H.; Cessac, B. Parameter estimation for spatio-temporal maximum entropy distributions: Application to neural spike trains. Entropy 2014, 16, 2244–2277. [Google Scholar] [CrossRef]
- Ohiorhenuan, I.E.; Mechler, F.; Purpura, K.P.; Schmid, A.M.; Hu, Q.; Victor, J.D. Sparse coding and high-order correlations in fine-scale cortical networks. Nature 2010, 466, 617–621. [Google Scholar] [CrossRef] [PubMed]
- Bell, A.J.; Sejnowski, T.J. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef] [PubMed]
- MacKay, D. Maximum entropy connections: Neural networks. In Maximum Entropy and Bayesian Methods; Springer: Dordrecht, The Netherlands, 1991; pp. 237–244. [Google Scholar]
- Marrian, C.; Peckerar, M.; Mack, I.; Pati, Y. Electronic Neural Nets for Solving Ill-Posed Problems with an Entropy Regulariser. In Maximum Entropy and Bayesian Methods; Springer: Dordrecht, The Netherlands, 1989; pp. 371–376. [Google Scholar]
- Szu, H.; Kopriva, I. Unsupervised learning with stochastic gradient. Neurocomputing 2005, 68, 130–160. [Google Scholar] [CrossRef]
- Ingman, D.; Merlis, Y. Maximum entropy signal reconstruction with neural networks. IEEE Trans. Neural Netw. 1991, 3, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Choong, P.L.; Desilva, C.J.; Dawkins, H.J.; Sterrett, G.F. Entropy maximization networks: An application to breast cancer prognosis. IEEE Trans. Neural Netw. 1996, 7, 568–577. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Schwenk, H.; Senécal, J.S.; Morin, F.; Gauvain, J.L. Neural probabilistic language models. In Innovations in Machine Learning; Springer: Berlin, Germany, 2006; pp. 137–186. [Google Scholar]
- Sarikaya, R.; Hinton, G.E.; Deoras, A. Application of deep belief networks for natural language understanding. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 778–784. [Google Scholar] [CrossRef]
- Yu, D.; Seltzer, M.L.; Li, J.; Huang, J.T.; Seide, F. Feature learning in deep neural networks-studies on speech recognition tasks. In Proceedings of the International Conference on Learning Representations, Scottsdale, AZ, USA, 2–4 May 2013; pp. 1–9.
- Jing, H.; Tsao, Y. Sparse maximum entropy deep belief nets. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–6.
- Wang, S.; Schuurmans, D.; Peng, F.; Zhao, Y. Boltzmann machine learning with the latent maximum entropy principle. In Proceedings of the Nineteenth Conference on Uncertainty in Artificial Intelligence, Edmonton, AB, Canada, 1–4 August 2002; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2002; pp. 567–574. [Google Scholar]
- Mohamed, A.; Dahl, G.E.; Hinton, G. Acoustic modeling using deep belief networks. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 14–22. [Google Scholar]
- Hinton, G.E. A practical guide to training restricted boltzmann machines. In Neural Networks: Tricks of the Trade; Springer: Berlin, Germany, 2012; pp. 599–619. [Google Scholar]
- Fisher, R.A. On an absolute criterion for fitting frequency curves. Messenger Math. 1912, 41, 155–160. [Google Scholar]
- Chen, B.; Zhu, Y.; Hu, J.; Principe, J.C. System Parameter Identification: Information Criteria and Algorithms; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Chien, J.T.; Lu, T.W. Tikhonov regularization for deep neural network acoustic modeling. In Proceedings of the 2014 IEEE Spoken Language Technology Workshop (SLT), South Lake Tahoe, NV, USA, 7–10 December 2014; pp. 147–152.
- Larochelle, H.; Bengio, Y. Classification using discriminative restricted Boltzmann machines. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 536–543.
- Lewicki, M.S.; Sejnowski, T.J. Learning nonlinear overcomplete representations for efficient coding. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1998; pp. 556–562. [Google Scholar]
- Tomczak, J.M. Application of classification restricted Boltzmann machine to medical domains. World Appl. Sci. J. 2014, 31, 69–75. [Google Scholar]
- Salakhutdinov, R.; Hinton, G.E. Deep boltzmann machines. In Proceedings of the 12th International Confe-rence on Artificial Intelligence and Statistics (AISTATS), Clearwater Beach, FL, USA, 16–18 April 2009; Volume 5, pp. 448–455.
- Wang, S.; Greiner, R.; Wang, S. Consistency and generalization bounds for maximum entropy density estimation. Entropy 2013, 15, 5439–5463. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Lee, H.; Battle, A.; Raina, R.; Ng, A.Y. Efficient sparse coding algorithms. In Proceedings of the Neural Information Processing Systems (NIPS 2007), Vancouver, BC, Canada, 3–8 December 2007; Volume 20, pp. 801–808.
- Raina, R.; Battle, A.; Lee, H.; Packer, B.; Ng, A. Self-taught learning: transfer learning from unlabeled data. In Proceedings of the 24th Annual International Conference on Machine Learning, Corvallis, OR, USA, 20–24 June 2007; pp. 759–766.
- Tenenbaum, J.B.; Kemp, C.; Griffiths, T.L.; Goodman, N.D. How to grow a mind: Statistics, structure, and abstraction. Science 2011, 331, 1279–1285. [Google Scholar] [CrossRef] [PubMed]
- Berger, A.L.; Pietra, V.J.D.; Pietra, S.A.D. A maximum entropy approach to natural language processing. Comput. Linguist. 1996, 22, 39–71. [Google Scholar]
- Schneidman, E.; Still, S.; Berry, M.J.; Bialek, W. Network information and connected correlations. Phys. Rev. Lett. 2003, 91, 238701. [Google Scholar] [CrossRef] [PubMed]
- Atick, J.J. Could information theory provide an ecological theory of sensory processing? Netw. Comput. Neural Syst. 1992, 3, 213–251. [Google Scholar] [CrossRef]
- Lee, H.; Ekanadham, C.; Ng, A.Y. Sparse deep belief net model for visual area V2. In Proceedings of the Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 8–13 December 2008; pp. 873–880.
- Sutskever, I.; Tieleman, T. On the convergence properties of Contrastive Divergence. In Proceedings of the Thirteenth Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 789–795.
- Carreira-Perpinan, M.A.; Hinton, G.E. On Contrastive Divergence Learning. In Proceedings of the Tenth Workshop on Artificial Intelligence and Statistics, The Savannah Hotel, Barbados, 6–8 January 2005; pp. 59–66.
- Toutanova, K.; Manning, C.D. Enriching the Knowledge Sources Used in a Maximum Entropy Part-of-Speech Tagger. In Proceedings of the 2000 Joint SIGDAT Conference on Empirical Methods in Natural Language Processing and Very Large Corpora, Morristown, NJ, USA, 1–8 October 2000; pp. 63–70.
- Ratnaparkhi, A. A maximum entropy model for part-of-speech tagging. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP), Philadelphia, PA, USA, 17–18 May 1996; Volume 1, pp. 133–142.
- Nigam, K. Using maximum entropy for text classification. In Proceedings of the IJCAI’99 Workshop on Machine Learning for Information Filtering, Stockholm, Sweden, 31 July–6 August 1999; pp. 61–67.
- Wang, S.; Schuurmans, D.; Zhao, Y. The latent maximum entropy principle. ACM Trans. Knowl. Discov. Data 2012, 6, 8. [Google Scholar] [CrossRef]
- Wang, S.; Schuurmans, D.; Zhao, Y. The Latent Maximum Entropy Principle. In Proceedings of the IEEE International Symposium on Information Theory, Lausanne, Switzerland, 30 June–5 July 2002; p. 131.
- Berger, A. The Improved Iterative Scaling Algorithm: A Gentle Introduction. Carnegie Mellon University: Pittsburgh, PA, USA, Unpublished work. 1997. [Google Scholar]
- Darroch, J.N.; Ratcliff, D. Generalized Iterative Scaling for Log-Linear Models. Ann. Math. Stat. 1972, 43, 1470–1480. [Google Scholar] [CrossRef]
- Bilmes, J.A. A Gentle Tutorial on the EM Algorithm and Its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models; Technical Rerport TR-97-021; International Computer Science Institute (ICSI): Berkeley, CA, USA, 1997. [Google Scholar]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: Design of dictionaries for sparse representation. In Proceedings of the Signal Processing with Adaptative Sparse Structured Representations, Rennes, France, 16–18 November 2005; pp. 9–12.
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online Dictionary Learning for Sparse Coding. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 689–696.
- Gemmeke, J.F.; Virtanen, T.; Hurmalainen, A. Exemplar-Based Sparse Representations for Noise Robust Automatic Speech Recognition. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2067–2080. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Improving neural networks by preventing co-adaptation of feature detectors. 2012; arXiv:1207.0580. [Google Scholar]
- Decoste, D.; Schölkopf, B. Training Invariant Support Vector Machines. Mach. Learn. 2002, 46, 161–190. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. 3-D object recognition with deep belief nets. In Proceedings of the 23rd Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 1339–1347.
- Joachims, T. A Probabilistic Analysis of the Rocchio Algorithm with TFIDF for Text Categorization. In Proceedings of the Proceedings of the Fourteenth International Conference on Machine Learning, Nashville, TN, USA, 2–12 July 1997; pp. 143–151.
- McCallum, A.; Rosenfeld, R.; Mitchell, T.; Ng, A.Y. Improving Text Classification by Shrinkage in a Hierarchy of Classes. In Proceedings of the Fifteenth International Conference on Machine Learning, Madison, WI, USA, 24–27 July 1998; pp. 359–367.
- Cardoso-Cachopo, A.; Oliveira, A.L.; Redol, R.A. An empirical comparison of text categorization methods. In International Symposium, String Processing and Information Retrieval; Springer: Berlin, Germany, 2003; pp. 183–196. [Google Scholar]
- Zhai, C.; Lafferty, J. A study of smoothing methods for language models applied to information retrieval. ACM Trans. Inf. Syst. 2004, 22, 179–214. [Google Scholar] [CrossRef]
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. LIBLINEAR: A Library for Large Linear Classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]


| Dataset | Method | 5% | 10% | 15% | 20% |
|---|---|---|---|---|---|
| MNIST | ML-DBN | 4.90 | 3.39 | 2.75 | 2.45 |
| ME-DBN | 4.84 | 3.30 | 2.57 | 2.31 | |
| CME-DBN | 4.66 | 3.11 | 2.46 | 2.17 | |
| NORB | ML-DBN | 18.74 | 16.78 | 14.98 | 14.16 |
| ME-DBN | 17.69 | 14.58 | 13.86 | 13.17 | |
| CME-DBN | 16.36 | 13.53 | 13.37 | 12.71 |
| Dataset | SVM | ML-DBN | ME-DBN | CME-DBN |
|---|---|---|---|---|
| MNIST | 1.40% | 1.20% | 1.04% | 0.94% |
| NORB | 11.60% | 11.90% | 10.80% | 10.80% |
| Dataset | Method | 5% | 10% | 15% | 20% |
|---|---|---|---|---|---|
| Newsgroup | ML-DBN | 63.79 | 69.53 | 72.04 | 73.82 |
| ME-DBN | 68.11 | 72.92 | 74.97 | 76.05 | |
| CME-DBN | 68.57 | 74.72 | 76.43 | 78.78 | |
| Sector | ML-DBN | 46.64 | 58.85 | 63.05 | 67.29 |
| ME-DBN | 53.44 | 62.09 | 66.69 | 69.54 | |
| CME-DBN | 53.57 | 62.37 | 66.64 | 70.06 | |
| WebKB | ML-DBN | 81.22 | 87.61 | 89.28 | 90.95 |
| ME-DBN | 82.76 | 88.17 | 89.20 | 90.95 | |
| CME-DBN | 84.00 | 89.28 | 90.47 | 91.98 |
| Dataset | SVM | ML-DBN | ME-DBN | CME-DBN |
|---|---|---|---|---|
| Newsgroup | 75.07% | 81.07% | 82.62% | 84.99% |
| Sector | 74.36% | 80.11% | 81.23% | 81.56% |
| WebKB | 90.23% | 92.45% | 93.24% | 93.57% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, P.; Fu, S.-W.; Wang, S.-S.; Lai, Y.-H.; Tsao, Y. Maximum Entropy Learning with Deep Belief Networks. Entropy 2016, 18, 251. https://doi.org/10.3390/e18070251
Lin P, Fu S-W, Wang S-S, Lai Y-H, Tsao Y. Maximum Entropy Learning with Deep Belief Networks. Entropy. 2016; 18(7):251. https://doi.org/10.3390/e18070251
Chicago/Turabian StyleLin, Payton, Szu-Wei Fu, Syu-Siang Wang, Ying-Hui Lai, and Yu Tsao. 2016. "Maximum Entropy Learning with Deep Belief Networks" Entropy 18, no. 7: 251. https://doi.org/10.3390/e18070251
APA StyleLin, P., Fu, S.-W., Wang, S.-S., Lai, Y.-H., & Tsao, Y. (2016). Maximum Entropy Learning with Deep Belief Networks. Entropy, 18(7), 251. https://doi.org/10.3390/e18070251