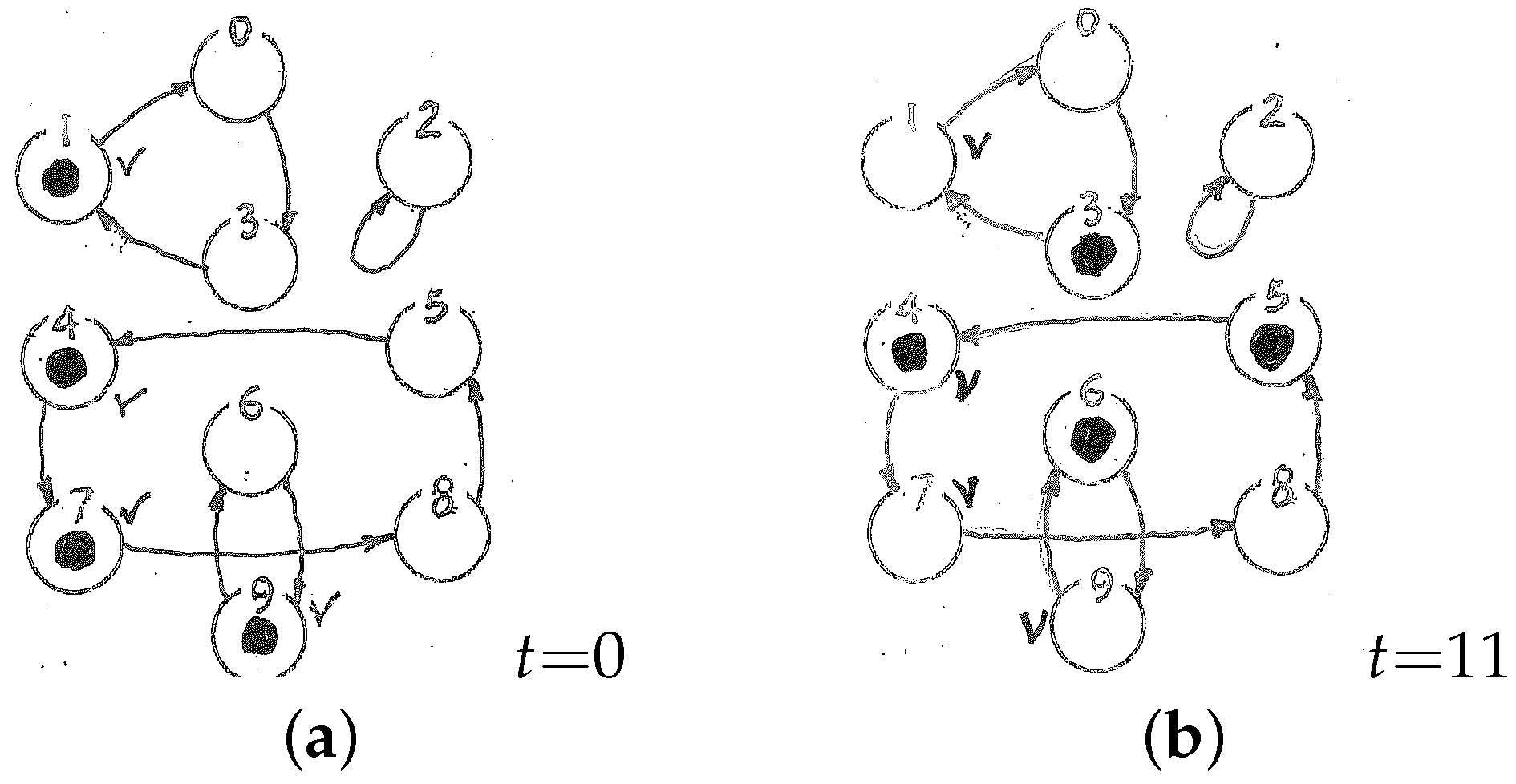Forgive them, for they mean not what they say.
—Paraphrase of Luke 23:34
1. Introduction
In recent decades, entropy has come to be applied very broadly. Moreover, like a few other scientific constructs which had “made the grade” in earlier decades—such as evolution, relativity, and quantum mechanics—entropy too has found favor with the general public and somehow managed to become a household word. It carries the right combination of glamor, tantalizing promise, and prurient mystery. It comes in handy in general conversation, without requiring of the parties much commitment or understanding. This of course abets vagueness, confusion, misuse, and abuse, and the propagation of “urban legends” about it that occasionally penetrate even responsible scientific quarters (see the
Shannon entry in
Section 4).
My primary purpose here is to review how and why the entropy “of a system” (the scare quotes, as we shall see, are deliberate) evolves in time as the system itself evolves; and to stress of what a radically different nature those two evolution processes are. To anticipate, the second process is in the nature of bookkeeping, which, to be useful, must first of all be honest.
As part of this endeavor, I will motivate and then introduce the concept of honest entropy. This fills, I believe, a gap in the literature of entropy and the second law of thermodynamics.
To help concentrate minds, my rhetorical (and pedagogical) device will take the form of a campaign to dispel a number of widespread
myths about entropy, such as:
- 1.
The belief that, in spite of having the same name and sporting the same formula, information-theoretical entropy (à la Shannon and Jaynes) is actually “something completely different” from physical entropy (à la Clausius, Boltzmann, and Gibbs).
- 2.
The myth—pace Clausius—that physical entropy is a property of a definite material body one can point to—such as the copper bar now lying on my lab bench—and is a physical property, like volume, temperature, composition, internal energy, etc., that anyone can objectively determine by physical means and track as it changes in time.
- 3.
The myth that the approach of an isolated system toward its maximum entropy, though generally
monotonic (i.e., without ever changing direction) as predicated by Clausius, is actually subject to
statistical fluctuations à la Ehrenfest (see
Section 7.5)—with entropy occasionally
decreasing rather than increasing.
- 4.
The myth that the (information-theoretical) entropy of the deck of cards now lying on my table is an intrinsic property of it, which anyone can determine by inspecting the deck itself.
- 5.
The belief that logarithms—as encountered in Boltzmann’s formula and Gibbs’s and Shannon’s are an essential feature of the entropy concept.
To add insult to injury, I will throw in two more old chestnuts:
- 6.
The myth that entropy, whether physical or information-theoretical, is something that you measure.
- 7.
The myth that the second law of thermodynamics is a law of
physics (please wait until
Section 5 before you cast your stone).
2. Myths: Pros and Cons
Relax now! I wholeheartedly grant that all good myths have at their core an element of truth, and that their telling and retelling may have pedagogical value. I myself can think of many circumstances where any one of the above myths may serve a useful purpose—as an aid to intuition, in popular science; as a stepping stone, in teaching; and in ordinary scientific discourse, as a convenient abbreviation when the underlying core truth is understood. Let us take the following dialogue as a case study.
- Teacher
Think of random number between 1 and 10.
- Pupil
Seven!
As an aside on the limitations of human psychology, let me remark that the empirical odds are about 1:1 in favor of this answer.
- Teacher
What? (sarcastically) What may make you think that seven, of all numbers, should be random? It’s an ordinary, perfectly definite number, like 1, 2, and 3—in fact, everyone knows it comes right after 6!
- Pupil
(blushes, embarrassed)
- Teacher
Class, Home assignment: list all numbers from 1 to 100 and put a mark next to those that are odd. On a separate column, mark all those that are prime. On a third column, mark all those that are random!
Of course, there is no such thing as a “random number”—that is a mythical beast. “Being random” is not the property of any particular number—this qualifier applies to a procedure that will generate a number. Thus, “Give me a random number” can only be understood as shorthand for “Use a random procedure to generate a number, and give me the result”.
To what extent a “random procedure” may itself be some sort of mythical beast, that’s another kettle of fish. Even though the art has made enormous strides since then, one should still keep in mind von Neumann’s quip, that “Anyone who attempts to generate random numbers by deterministic means is, of course, living in a state of sin” (but see end of
Section 8.5).
One may argue with John White [
1] that “Too much specific information presented
too soon may well be aesthetically undesirable” (the emphasis on “too soon” is suggested by the book’s author in a footnote). On the other hand, one may ask, with Gerald Dworkin [
2], “Are these ten lies justified?”
A compromise was acknowledged by the medieval Jewish philosopher Maimonides. Joseph Stern [
3] seems to conclude that the latter actually not only acknowleges but indeed endorses, and even
prescribes, the double standard of “[mythological] religion for the
masses and philosophy for the
elite.”
For my part, I prefer to ask, cui prodest? (“who has more to gain?”), the teacher or the pupil, and on what time scale? A short-term prop that is cheap for the teacher today may well leave a pupil happy now (less mental work), but with a model of the world that may have to be gutted and rebuilt later (if ever)—possibly at much greater cost. (The ten dollars’ worth of salt we spread on the driveway to save us the pain of snow shoveling will cost the community $200 for consequent damage to roads, bridges, cars, water supply, and wildlife.)n
What I recommend instead is to help build a world model that is honest from the start, while only making use—at least initially—of those constructs that are absolutely vital. The latter is a feature, not a regrettable concession!
3. Approach
It ain’t over till the fat lady sings!
—U.S. popular expression
In that spirit, I will start by introducing a very lean concept of entropy accompanied by a very lean concept of dynamical system, and in a few steps arrive at a very lean-and-mean second law of thermodynamics that does all the right things.
After that, beginning with the lean concept and making a single, modest generalization, I will arrive at a fully fleshed-out entropy—essentially the one you would be familiar with. This generalization—essentially, replacing a set by a
multiset—is pre-announced in a warning box at the beginning of
Section 5, but is actually carried out only in
Section 8.
I will finally argue that such generalization is not even strictly necessary (and possibly not even sufficient). It’s just a convenient shortcut, and besides it’s not universally applicable. One could get along just as well, if not better, by using a more sophisticated scenario as a “wrapper” for the lean entropy we had started with. This approach (
Section 8.5) may not be practical, since it doesn’t carry out any simplifications until the very last step (cf. the present section’s epigraph), and is thus exceedingly cumbersome—but it’s a good device for thought experiments.
All of the above is directly applicable not only to physics and communication channels, but also to scenarios of other sciences as well as to much of ordinary life.
On reading the above, many a one of you will respond with a dismissive sneer, “I already knew all of that!” and, pointing to a twelve-foot stack of books and papers on their office floor labeled Entropy and the Second Law, add “In fact, I have it all here!—ehem … someplace around here.”
Others, I hope, will go to their offices, and beaming with relief will throw out most of their twelve-foot stacks, keeping only a few trusted pieces—thus making room (in their brains as well as their offices) for the new, exciting stuff that I am sure will later show up in their lives. Pointing to the small stack left they will say with pride, after Hillel, “This is the entire thing—all the rest is commentary!” (When a potential convert approached Babylonian rabbi Hillel and asked whether he could be taught the entire Torah while standing on one foot—the 1st century BC equivalent of an “elevator speech”—Hillel summarized as follows, “That which is hateful to you do not do to others. All the rest is commentary. Now go and learn.”)
They will surely add with bated voice (as I imagine Hillel did too) “And, for that matter, mostly frivolous, repetitious, superfluous, of merely archival nature, or too technical—when not actually wrong!”
Familiarity with the concept of entropy is useful in all walks of life. Entropy rightly belongs to everybody—kind of a “Unesco World Heritage Concept”. But how many are in a position to step up and claim their inheritance? Not every Tom, Joan, and Harry can afford the space, in their brains as well as in their living rooms, for a twelve-foot stack of papers—or have the time, the preparation, and the discipline to wade through them!
Let us face it, outside of our specialty we are all Toms, Joans, and Harrises, and the baggage of our everyday interests and projects leaves little space in our lives for extra clutter. Pace Maimonides, I have attempted a drastic compression of the resources needed for everybody—not only the specialist—to understand “entropy and all that” and make an honest use of it. Compressing by popularizing, mythologizing, and patronizing is easy, but tends to throw out the baby with the bathwater; I wanted mine to be a lossless compression.
Working on this project was great fun, especially thinking of how much room it would make in my own life for new projects.
4. Entropy 000
Before attempting a reconstruction of entropy, let us see what kind of edifice we have to begin with, whose functionality we aim to duplicate by the most frugal means. Here is a brief historical sketch.
4.1. Clausius (1850)
For Clausius, entropy is a physical quantity pertaining to a body, like internal energy and mass. It has the physical dimension of heat capacity, denoted by , where E means a quantity “of the energy type” and , “of the temperature type”. Accordingly, it’s measured today in units of joules per kelvin (J/K).
Clausius wrote nine memoirs between 1850 and 1865, collected with an introduction and appendices in [
4]. The last few lines of the ninth memory (sporting a poetic concision comparable to the last few lines of Darwin’s
Origin of Species, 1859) are:
[Having introduced entropy beside energy,] we may express in the following manner the fundamental laws of the universe which correspond to the two fundamental theorems of the mechanics of heat.
Those are the famous two laws of thermodynamics. (For the casual reader, a popular but scientifically solid introduction may be found in [
5].)
The quantity that German physicist Rudolf Clausius thought up would tell under what conditions a thermodynamical “body” (or “system”, to use a more modern term) could progress from a given initial state to a desired final state
spontaneously—that is, without being pushed by an external agency. Clausius had initially called this quantity (for which he proposed the symbol
S) the “transformation content” of the body, but later himself coined for it the term “entropy”, in analogy with physical “energy” (having especially in mind the body’s internal energy
U, comprising both the mechanical and the thermal energy stored in the body itself). In his words,
We might call S the transformation content of the body, just as we termed the magnitude U its thermal and ergonal content. But as I hold it that terms for important magnitudes had better be made up from the ancient languages, so that they may be adopted unchanged in all modern languages, I propose to call the magnitude S the entropy of the body, from the Greek word tropē, transformation. I have intentionally formed the word entropy so as to be as similar as possible to the word energy, for the two magnitudes to be denoted by these words are so nearly allied in their physical meanings that a certain similarity in designation appears to be desirable.
The wordplay here is that in Greek tropē and érgon respectively mean “transformation” and “work” (as well as “activity”, “energy”, “force”), and en means “in”, so that “en-ergy” can be construed as “work-in-it” or “work contents” (note that the German for “contents” is In-halt or “in-held”); by the same token, “en-tropy” may well be taken to literally mean “transformation contents”.
4.2. Boltzmann (1877)
Boltzmann’s out-of-the-box intuition was that entropy is not a material quantity (“Five gallons of entropy—and check the tires!”), but just the logarithm of a
count. In his formula
S denotes entropy, ln is the natural logarithm (i.e., log in base
e), and
W the number of
complexions—as explained in a moment. The coefficient
k appends—to what is otherwise a
pure number—the physical dimensional unit required to remain consistent with Clausius’s usage.
Originally, those complexions were imagined to be the different ways that thermal energy can rearrange itself within a body of a certain description. These fine-grained internal arrangements roughly correspond to what today we call a body’s microstates (while a macrostate is the very description of the body in terms of the whole set of microstates it can possibly be found in). Note that Boltzmann’s “body” is already a more abstract entity than Clausius’s.
For Boltzmann, a “body” is no longer that one scrawny plucked chicken that you brought back from the farmer’s market, but an entry in the supermarket’s flyer—a type of product. That’s why when you meet your neighbor at the supermarket you can tell her, “I bought the same chicken as yours!” even though you two walk home with a pullet apiece.
Similarly, when the four customers from table 7 all ordered the same chicken dish they cannot complain if the four servings were not literally “the same”—there certainly were some small differences. In how many ways a serving can qualify as being a match for a given menu item, this may be just a philosophical question for a chef; but it may lead a physicist like Boltzmann to a revealing insight.
4.3. Gibbs (1902)
Gibbs’s idea of entropy is captured by the formula
in current use today.
Note that it is Gibbs that coined the name of the whole discipline,
statistical mechanics. Incidentally, Albert Einstein was unaware of Gibbs’s contributions in that field when, between 1902 and 1904, he wrote three papers on statistical mechanics. After reading Gibbs’s textbook, in the 1905 German translation by Ernst Zermelo, Einstein declared that Gibbs’s treatment was superior to his own and explained that he would not have written those papers if he had known Gibbs’s work [
6].
Gibbs’s formulation [
7] represents a modest generalization of Boltzmann’s approach—not a radical upheaval. Instead of individual microstates, the
i’s in the above formula represent
kinds of like microstates, and
denotes what
share of a certain population is represented by individuals of kind
i. In other words, instead of explicitly counting
individual microstates Gibbs counts
kinds of microstates, but weights them in terms of
what fraction of the total number of microstates each kind represents.
Note: This is the generalization mentioned at the beginning of
Section 3.
4.4. Von Neumann (1927)
In quantum mechanics, the concept of macroscopic state of a system is captured by a
density operator [
8,
9] (co-discovered by Lev Landau), a composite of an
empirical uncertainty already found in classical mechanics (“in principle we could always get a sharper picture of the state of a system through a more refined observation”) and an
irreducible uncertainty peculiar to quantum mechanics (“there are aspects of a system that we can know more about only at the cost of ending up knowing less about other aspects of the same system”).
Von Neumann’s entropy of a
density operator—which is a generalization of a probability distribution—is defined as
where the
’s are the
eigenvalues of the operator. Formally this is much like Gibbs’s expression.
According to standard quantum mechanics, there are concretely testable aspects of a physical system that cannot be accounted for by simply postulating a description of the whole universe in terms of a single
overarching probability distribution over it (this is an implication of
Bell’s inequality), but where, as far as physicists know, a density operator will do (cf.
Section 8.5).
4.5. Shannon (1948)
To answer questions of how much information could be “squeezed” through an information channel such as a telegraph line, Shannon came out in 1948 with a fully fleshed-out
Information Theory [
10,
11]. In this theory, the expression for entropy is
Note that this formula does away with Boltzmann’s and Gibbs’s “legacy” dimensional factor k (or von Neumann’s κ), so that here S remains a dimensionless quantity—a “pure number”.
In April 1961 Shannon was in residence at MIT for a week, and Prof Tribus, a pioneer at revealing the connections between information theory and thermodynamics and at adopting Jaynes’s
MaxEnt principle (see
Jaynes entry right below), had occasions to spend time with him. He asked Shannon whether he hadn’t been afraid, when he named his information-theoretic quantity “entropy”, that this would create confusion with the original use of the word in thermodynamics. According to Tribus’s recollection’s [
12], Shannon replied:
My greatest concern was what to call it. I thought of calling it “information”, but the word was overly used, so I decided to call it “uncertainty”. When I discussed it with John von Neumann, he had a better idea. Von Neumann told me, “You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name. In the second place, and more importantly, no one knows what entropy really is, so in a debate you will always have the advantage!”
The emphasis is mine. Note how, a good century after the invention of entropy, von Neumann—a polymath physicist—was well aware of how even professional physicists still stood somewhat confused as to what entropy really is.
Here I cannot resist a bit of gossip. In the same week, Tribus gave an MIT seminar on a new way, based on information theory, to derive thermodynamics. He states that a critical audience, comprised of students of American mechanical engineer Joseph Keenan (founder of the MIT school of thermodynamics) “tried to rip it apart”. Moreover, French mathematician Benoit Mandelbrot, who was in the audience, quickly attacked the MaxEnt interpretation, saying: “Everyone knows that Shannon’s derivation is in error” [
13].
That shows what strong feelings people may have about “mere matters of interpretation” of entropy and thermodynamics.
4.6. Jaynes (1952)
Edwin T. Jaynes was an ardent developer and preacher of the Bayesian interpretation of statistical mechanics. He “emphasized a natural correspondence between statistical mechanics and information theory. In particular, [he] offered a
new and very general rationale why the Gibbsian method of statistical mechanics works. He argued that the entropy of statistical mechanics and the information entropy of information theory are
principally the same thing. Consequently, statistical mechanics should be seen just as a particular application of a general tool of
logical inference” [
14] (emphasis mine).
He’s best known for the introduction of the
principle of maximum entropy (or
MaxEnt) [
15,
16,
17]. Adapting from [
18],
If, in a given context, you need to formulate a probability distribution on which to base your bets, choose, among all possible distributions that agree with what you know about the problem, the one having maximum entropy. Why? Is this guaranteed to be the “real” (whatever that may mean) probability distribution? Of course not! In fact you will most likely replace it with a new one as soon as you see the outcome of the next trial—because by then you will have one more piece of information. Why, then? Because any other choice—being tantamount to throwing away some of the information you have or assuming information you don’t have—would be indefensible.
This principle, then, introduces a criterion of honesty into the otherwise poorly constrained process of inference: ideal witnesses are expected not to just “tell the truth”, but tell the whole truth (as far as each can know it) and nothing but the truth.
The concept of “honest entropy” presented in this paper develops and refines the qualifiers “as far as” and “nothing but”.
4.7. Other Entrants (1945–)
A number of other concepts were developed in the past seventy years in attempts to quantify properties such as
variety,
diversity,
multiplicity,
richness, and
distinctiveness, making use of different kinds of
mean and of
scaling function. We will mention some of these in our deconstruction of Gibbs’s formula in
Section 8.
5. Entropy 001
If you can’t describe it, you can’t put it into your equations.
Indeed, the very hairs of your head are all numbered.
—Luke 12:7
In the mercantile world, there are obvious difficulties in determining a fair barter rate for goods of a different nature—“How much of my ‘land’ is your ‘oil’ worth?” Physics’ “merchants” have found it expedient to value certain of their wares in terms of a notional currency called
entropy. However, language and customs, as we know, vary from region to region and from time to time. Are we sure that Trader Gibbs’s entropy is the same thing as Master Boltzmann’s? How come Prof. Clausius’s entropy grows monotonically towards a maximum, while that used by Herr Ehrenfest may occasionally
dip? Which of these two merchants would you rather do business with? As we shall see (
Section 7.5), Herr Ehrenfest must have learned to play poker at a place where “peeking” was allowed!
Here we shall introduce a “primitive conceptual gage” for entropy, a reference benchmark against which more sophisticated entropy constructs can be tallied.
In biology, this role used to be played by the exemplar specimen of a species, kept in a museum. If there was a doubt about a naturalist’s correct identification of his specimen, in principle one could compare it to the exemplar and see whether (in spite of being hairier, larger, or of a slightly different color) it displayed certain essential characteristics of the latter (four legs, stubby tail, suckles offspring, yet lays eggs—remember the ornithorhyncus?).
As we shall see, a distinguishing trait of entropy is being of the nature of a count—the size (or cardinality) of a set. “If it ain’t a count, then it ain’t entropy!”
Those of you who are tempted to immediately cry “Foul! This is not the entropy we know!” should wait for
Section 8.1,
Section 8.3, and
Section 8.5, where probability distributions will be introduced and discussed. Similarly, those who expect to see logarithmic scaling should wait for
Section 8.2. The “lean” concept of entropy—that is, entropy as a count—announced in
Section 3, introduced in the present section, and used throughout for the first two-thirds of this paper—will be complemented in the last third (sections
Section 8 through
Section 10—by the “full-bodied” concept that you would be familiar with—namely, entropy as a
log of an
equivalent count).
What kind of bench should provide the benchmarks to tally entropy against? What makes a quantity “entropy-like” rather than, say, “velocity-like”? When we hear “the entropy of a body” (Clausius), or, in more modern terms, “of a system”, our first reflex should be “The entropy of precisely what? What kind of thing can entropy be a property of?” We already saw that in the phrase “prime number” the term “prime” is used to qualify a number as being prime, while in the locution “random number” what is really being qualified as random is not a number but a method for generating one.
Let us then announce, without further ado, that
Thus, entropy is a function that assigns a number to a description.
I have taken the liberty, for the sake of plainer English, to call “description” what is, more generally, a characterization, that is, something that can be used to narrow a choice, to tell by any means available whether or not an item belongs to a set. Take the phrase “Be considerate—of the prom photos in that box only pick one of which there are more than one copy left!” This doesn’t “describe” a photo in the narrow sense of “telling what it looks like”. Yet in the given circumstances, where I can see all the photos in the box at once, it surely characterizes a definite subset of them.
Having clarified the meaning of description, one may now ask, “Description of what?” Well, of practically anything of which many possibilities or variants are available, out of which the description itself will identify a subset. The ordering of a deck of cards; a card hand, such as “four-of-a-kind”; the set of possible microscopic inner arrangements of a human-scale object; a liter of gas described as “at standard conditions of pressure and temperature”, and thus entailing a certain (astronomical) number of possible complexions of position-and-velocity of its molecules; the state of a finite-state automaton; a generic “winning chess move”, as contrasted to a specific chess move which happens to be a winning one; or a computer procedure which you call on the basis of its API description. (An API, or Application Programming Interface, is a repertoire of accessible programming commands that hide low-level details not needed by the high-level programmer. In this way, application developers are free to change “under the hood” details of the technical implementation without disrupting the application’s behavior. Thus an API stands for a whole equivalence class of low-level programs yielding the same high-level behavior. One will trust that whatever code is underneath will do what the description seems to imply.) Other examples are an unread email message, and thus “whatever text the message consists of”; the vehicle that hit me; whatever parasite is responsible for my illness; an “alkaline metal”; a tic-tac-toe game; the next president of the United States; a plausible universe; even another description!
Here is an example of descriptions of an object. A policeman spots a man lying by the roadside. “Are you hurt? What’s the story?” “A glancing blow by a hit-and-run vehicle, officer.” “That’s not much help; there are perhaps a hundred thousand vehicles within fifty miles of here—I can’t stop everyone. But, let’s see, what kind of vehicle? A truck?” “No, it was a small car.” “That’s better—we’ve restricted the choice to about ten thousand cars. Did you notice the color?” “Yes, it was red!” “Splendid—we are down to a thousand. And when did this happen?” “Oh, no more than five minutes ago.” “Then they can only have gone a few miles. Within that reach, we are talking about a dozen cars. I will give it a try!” (speaking on his radio) “To all police cars: Hit-and-run accident near Springbrook’s North Exit. Stop all small red cars within five miles of there and report to me.”
Our target is undoubtedly one specific object—the car involved in the accident. It is generally believed, since the time of Laplace, that at a microscopic level of detail our physical world is strictly invertible. In principle, if at the present moment we took a sufficiently detailed snapshot of a large enough portion of the world around the site of the accident, and ran this system backwards in time by means of a sufficiently detailed simulation, in five minutes (of simulated time) a usable record of the accident—car, licence plate, driver, collision details—would materialize under our eyes.
But we can’t do that in practice—today at least! (Though we learn fast. Today we can routinely tell paternity, and have started deciphering affidavits written on gravitational waves a billion years ago and billions of billions of miles away.)
To try to bring the driver to justice, all we can use to identify the car by is whatever circumstantial evidence we can summon up—in plain words, a description of the car by witnesses (even inanimate ones, such as tire tracks). It will be up to courts and lawyers to pass in review all the conceivable objects that match that description, and see to what extent each of these objects fits in with other external factual data. For example, if it turns out that—at the time of the accident—a car otherwise matching the description had been captured by a videocamera filling up at a gas station, that particular car may be written off.
In the estimate of the officer, the first description (“a hit-and-run vehicle”) gave a hundred thousand matches. A more refined one (“a small car”) yielded one-tenth as many. The next refinement (“a red one”) further shrank the number of matches down to one thousand. Finally, taking into account also the timing (“less than five minutes ago”), the number of possible choices dwindled to a dozen.
So we have four different descriptions of the same target, and each comes with a number attached to it—the number of vehicles that match that description. This number is not, in any sense, an intrinsic property of the vehicle—it is a property of a description of it, including external details such as where and when.
I want to stress again that it is such a
number, associated with a
description and reflecting
how many items fit that description, that constitutes the essence of the
entropy concept. In
Section 8.3, after introducing the idea of
probability—again in a basic form (that is, without going into measure theory, whose whole worry is about problems caused by
infinities)—I will show that a very natural (and virtually inescapable) generalization of the concept of
description given here is that of a
probability distribution. In fact, it is on that generalization that the canonical definition of entropy rests—the entropy “of a probability distribution”. But to make sense of this we will have to clarify “probability” first.
Example 1. A colleague points at two identical-looking decks of cards on the table, both showing as top card an Ace of Spades. “These are ordinary 52-card decks. The first came directly from the factory—I just carefully removed the cellophane wrapper. As for the second, I shuffled it many times, and then continued shuffling until I got that ace back on top. Can you tell me the entropy of the two decks?” I reply, “The entropy of the first deck is 1, since only the default ordering—Ace of Spades, 2, 3, ..., Queen, King of Spades, and so forth for the other three suits—matches your description. The entropy of the second is of course 51 factorial. In fact, the top card clearly happens to be an Ace of Spades, and from what you told me any ordering of the remaining 51 card remains possible.”
“Excellent,” my friend replies, “while I make some tea, please go through the decks yourself to verify your answers.”
I diligently leaf through the two decks. Indeed, the first deck displays the standard ordering, while the second reveals, besides the top ace, a haphazard arrangement—but I note that the King of Hearts still immediately follows the Queen of Hearts.
“Was my description correct?” my colleague asks. “Yes,” I reply, “everything that I saw agrees with it.” “Then,” he asks, “can you tell me their entropies again?” “As far as I’m concerned,” I reply, “the entropy is 1 for the first deck and ... 1 for the second deck as well!” “Wait— you changed your mind about the second deck?” “Of course, my mind has literally changed—I definitely saw with my eyes—and even made a point of memorizing—what the specific ordering of the second deck was. Of course no other ordering would match it!”
We meet again a month later. He smiles and asks, “What did you say the entropy of the second deck was?” “It was 1,” I answer, “but as far as I am concerned, today its entropy is 50 factorial—or ” “And why so?” “In a month, I forgot all about it—except that it started with an Ace of Spades and that the King of Hearts followed his Queen.” (That leaves just 1 possibility for the first card; only 50 possible positions for the Queen out of the remaining 51, to make room for the King right after her; only 1 possible position for the King, that is, right after the Queen. As for the 49 cards that are left, they may come in any order.)
“You mean your entropy started with 51 factorial, then went down to 1, and now is up to 50 factorial—and all that while the deck itself was not changing a bit?” “Exactly—’my’ entropy, as you say. That is, the best description of the deck I could give myself, moment by moment, as I went through this comedy.”
The morale of this story is that the entropy “of a system”—that is, of a
description of it—maintained by me or any other agency—may evolve not only when the system itself evolves (say, somebody cut the deck) but also while the system itself
remains unchanged. It may
increase, if I lose or forget information about it. Even if I am very careful, it may increase if I know that the system itself is
nondeterministic (see
Section 8.4). It may
decrease, if I receive any information about the system that allows me to arrive at a more detailed picture of its makeup, or if I directly “peek” into it (see
Section 7.5 and [
20]). As we shall see, there are also systems whose entropy will honestly
decrease “all by itself”, even if the system is perfectly isolated and no one peeks! The second law of thermodynamics is valid for any
honest kind of description of certain
distinguished kinds of system (see
Section 7, and especially
Table 1, “invertible” column); as a special case, it
strictly applies to physics—as claimed by Clausius.
To help turn the above intuitive considerations and assurances into something more definite—stuff that you can trust because you created it yourself—in the next section we shall introduce dynamical systems, that is, systems whose state evolves in time by well-specified internal laws.
Using dynamical systems as a tool we shall fasten the patient to the operating table, as it were. By excising intervening layers of fat and connective tissue, we will lay bare with surgical precision the
contractual essence of the second law of thermodynamics (
Section 7).
6. Tracking Entropy
When I want to read a book, I write one!
—Benjamin Disraeli 1868
The best way to learn a subject is to write a book about it.
—Robert Baden–Powell, the founder of Boy Scouts, who morphed the previous quote in this way for pedagogical purposes
If I can’t picture it, I can’t understand it.
—Attributed to Albert Einstein by John Wheeler
What I cannot create, I do not understand.
—Richard Feynman 1998, scrawled on a blackboard shortly before his death
What I cannot build, I cannot understand.
—Craig Venter 2010, inscribed as a trademark on the first synthetic working genome—in the belief he was literally quoting Feynman
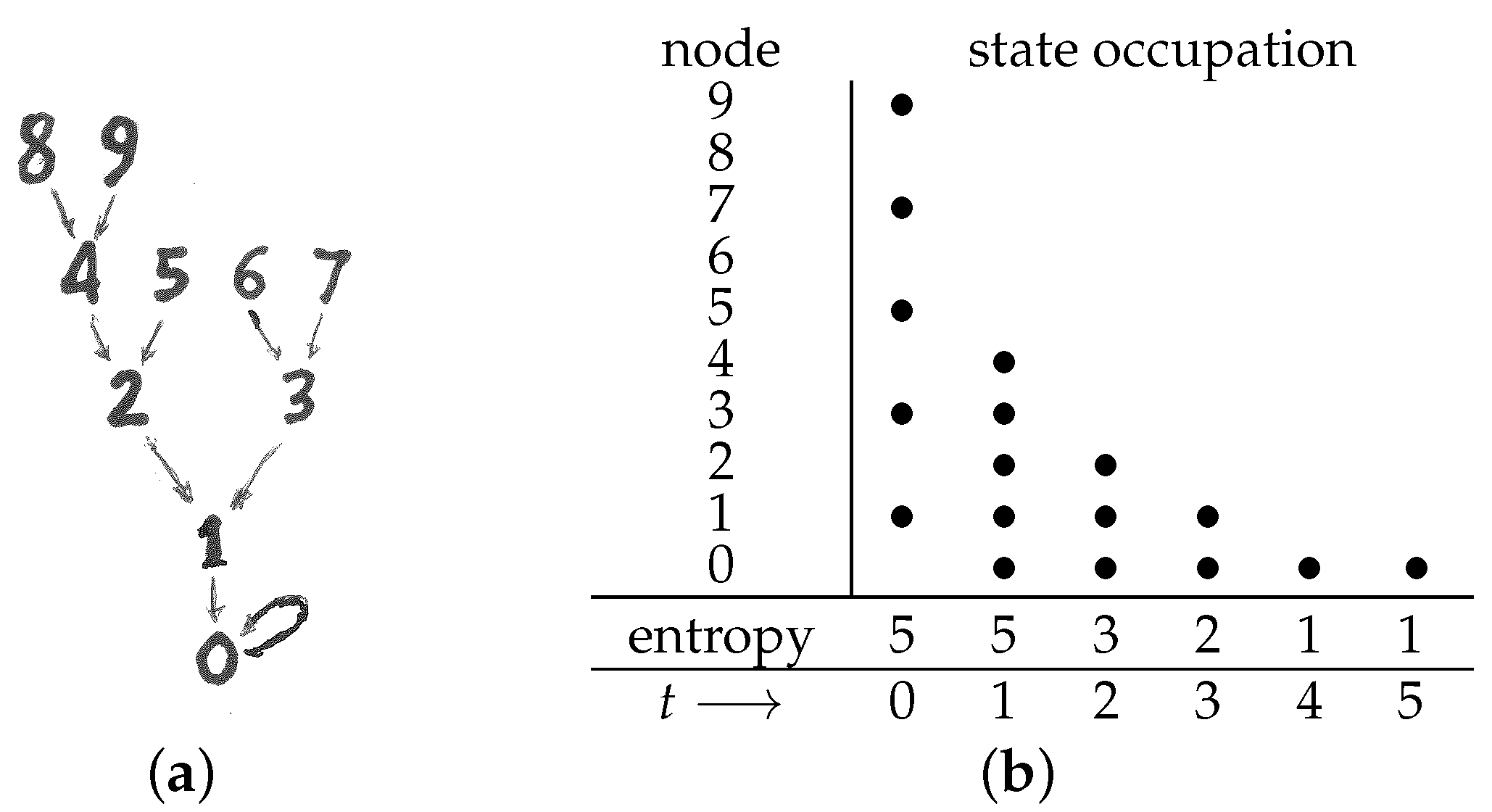
The above five quotations are a partial list of responses I got when I asked my brain “You know, that quote about how ‘one needs to touch it with hand to understand it’.” That provides a lower bound of 5 to the entropy (in the present sense) of my clue.
By the way, I realize that the best way to learn about entropy is to write a paper about it.
6.1. Dynamical Systems
A
dynamical system is an abstraction of a mechanical system that can be in any one of a set of internal
states, and is governed by an internal
rule given once and for all—external interventions or “miracles” are not allowed! Think of a music box or a planetary system (or, for that matter, a planetarium show or a billion-year computer simulation of the solar system—such as the one performed by Gerry Sussman and Jack Wisdom’s “digital orrery” [
21]).
If the rule makes the system “hop” directly from one state to the next, without going through a continuum of intermediate states (contrast a digital to an analog watch), the system is discrete. We shall set no upper limit to the number of states that a discrete system may have available. Moreover, though not essential for our arguments, it will help intuition and simplify the presentation to assume that the actual number of states, even though as large as desired, be finite.
A system is deterministic if its rule associates to each state a single successor state (that is, if the rule is a function from the state set to iself). For any chosen inital state, iteration of the rule produces, one after the other, a sequence of states called the trajectory from that initial state. In this sense, the rules embodies the dynamics—or the behavior—of the system for all possible initial conditions.
For the moment we shall restrict our attention to dynamical systems qualified by the above four properties, namely, (i) internal rules fixed once and for all, (ii) time-discrete, (iii) finite-state, and (iv) deterministic.
Thus, for us a
system will consist simply of a finite set of elements called
states and a
law or
rule that to each state assigns, as a
next state or
successor, an element from the same set. For example, the state set
S may consist of just the four states
(i.e.,
); and the rule
R, which must assign to each element of
S its successor, may be an arbitrary lookup table such as that on the left of (6), or its graphic equivalent—a
state-transition diagram—on the right.
This state-transition diagram is a directed graph where nodes denote states and whose outgoing arcs point to a node’s successor. As we have seen, in a deterministic system each node has a single successor; however, a node may well have more than one predecessor (like b, which has two), or even none (like a). A node may be its own successor, in which case the arc coming out of it loops back to it.
Since in ordinary scientific speech “state of a system” may often mean (especially in physics) a description of its makeup vague enough to leave room for several individual states, as in the “hit-and-run car” example of
Section 5, when necessary for clarity we may refer to the individual elements of the state set as
ur-states (“fundamental” or “atomic” states).
(What should be considered an ur-state is not a given, ultimate, intrinsic feature of a system. It is, at bottom, a
modeling decision—what in logic is called a
premise (
Section 8.3)—made for the purpose of evaluating its consequences. Thus, the entropy of a deck of cards discussed in the example of
Section 5 is based on the number of permutations of an ideal, indestructible deck consisisting of discrete symbols like “
K♠” and “
Q♣”, regardless of, say a card’s orientation or smell. After a zillion shuffles this ideal deck will be just as new, with its unblemished 52! ur-states, while a real deck will have been reduced to a pile of dust by continual wear and tear: billions of tiny specks susceptible to astronomically more permutations—and not even these are ultimate states of matter!)
In the rest of this section, where ur-states are represented by nodes of a graph, we shall call them simply nodes.
6.2. Day 1: Look! It’s Conserved!
Let us imagine that you keep a dynamical system well-guarded in your room. I am in a separate room, and we comunicate only by intercom.
- You
I have here a discrete dynamical system consisting of ten states labeled 0 through 9. I am going to select one of these as an initial node, and then I will make the system take a few steps—that is, successively move from one node to the next according to the system’s rule. Your task will be to identify the node in which the system is left at the end of this. Is that clear?
- Me
Yes! But aren’t you going to tell me what the actual system is—what rules it obeys?
- You
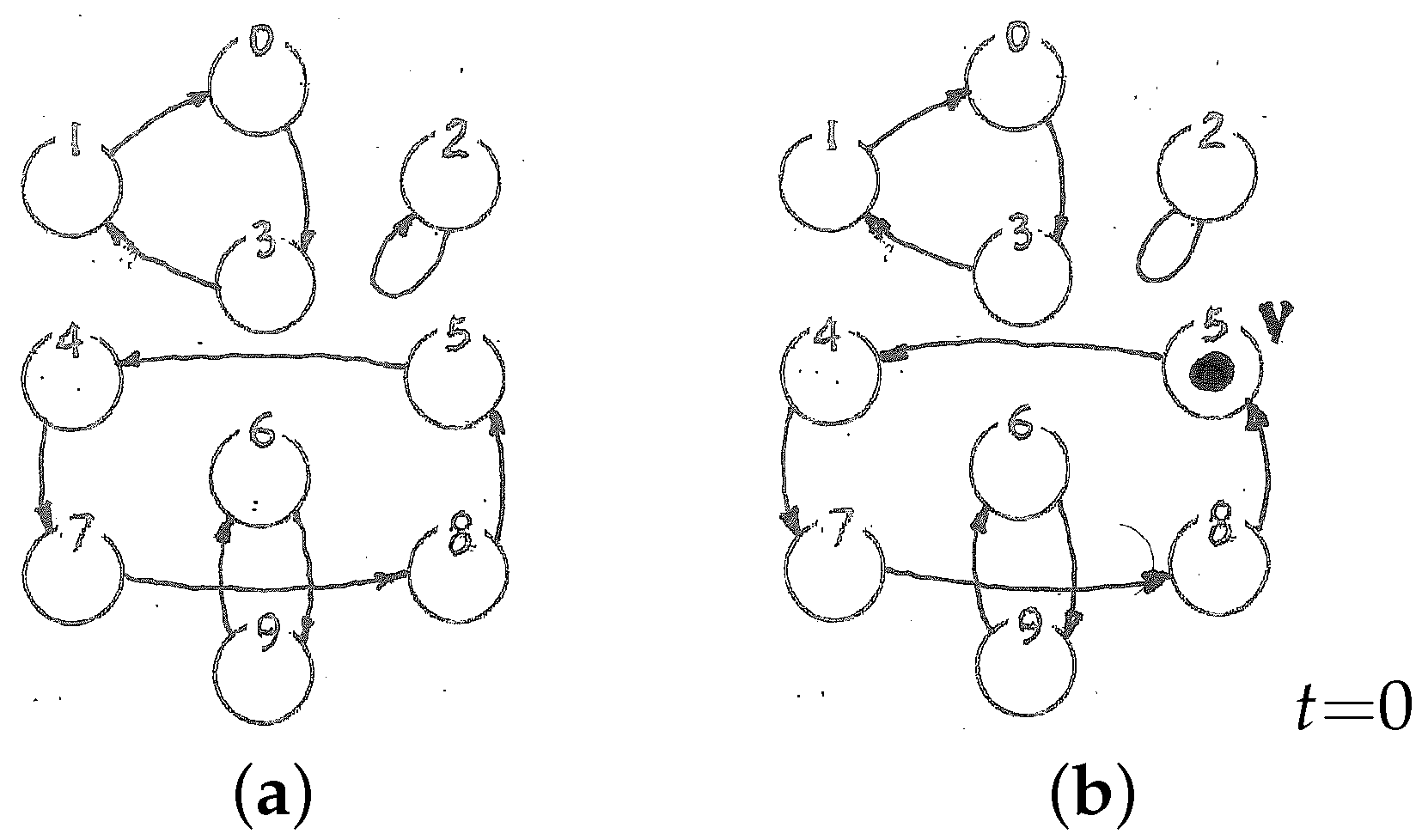
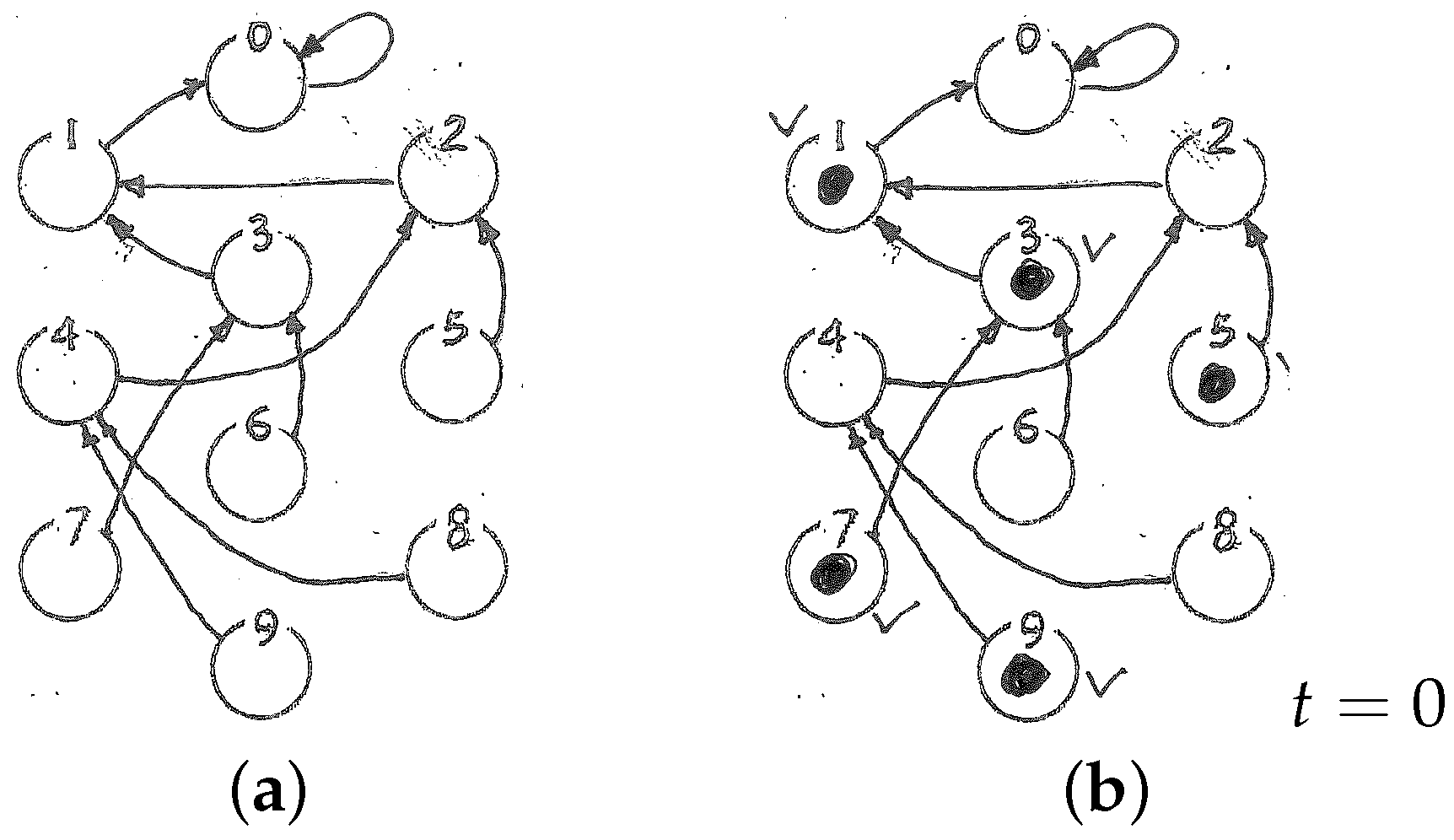
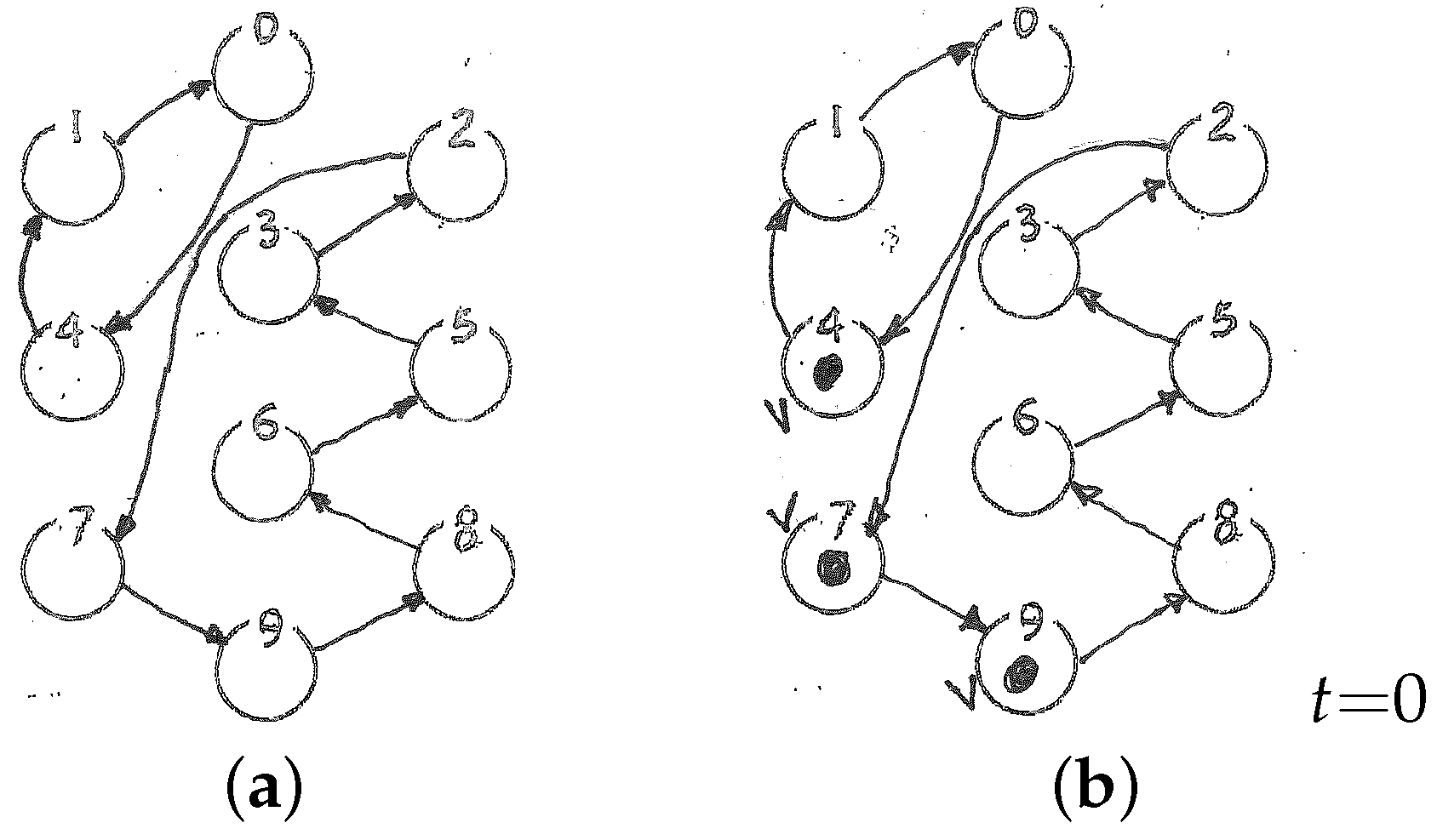
Oops! I’d forgotten. Let me fax you the entire transition diagram—it has nodes to represent states and arcs leading from each node to the next. (
faxes diagram of Figure 1a) Got it? OK! Now I’ve chosen an initial node and put a check mark next to it. Tell me what node it is.
- Me
How would I know? It could be any of the ten.
- You
Even though I know what node I have chosen for the initial node, and so the entropy of my description (how many nodes the system could possibly be in after I had made my choice) equals 1, nonetheless the entropy of your description—your “knowledge state” given what you’ve been told so far (and you can’t see my check mark)—is still “any of them ten”. Now I tell you what initial node I’ve chosen: it’s 5 (your entropy as to the initial state must surely be 1 now). My command “Step!” will mean I advance the system’s node by one step. Are you ready? Then let us start!
- Me
Just a moment! (
puts a checkmark next to initial node 5, for the record, and places a movable token on the node itself, as in Figure 1b) OK, shoot!
- You
Step!
- Me
(advances the token by one step; the token is now on node 4) OK!
- You
Step! Step! Got it?
- Me
Fine! (advances the token two more times)
- You
Take four steps this time! I’m done. What’s my final state?
- Me
(
takes four more steps on the graph and draws a dotted line on the diagram to trace the token’s entire trajectory, as in Figure 2; the token has landed on node 8) You must be now on node 8!
- You
Exactly! And I see that your entropy is still 1—no doubts about which state my system is in now, even if you don’t see it!
A little later—same setting.
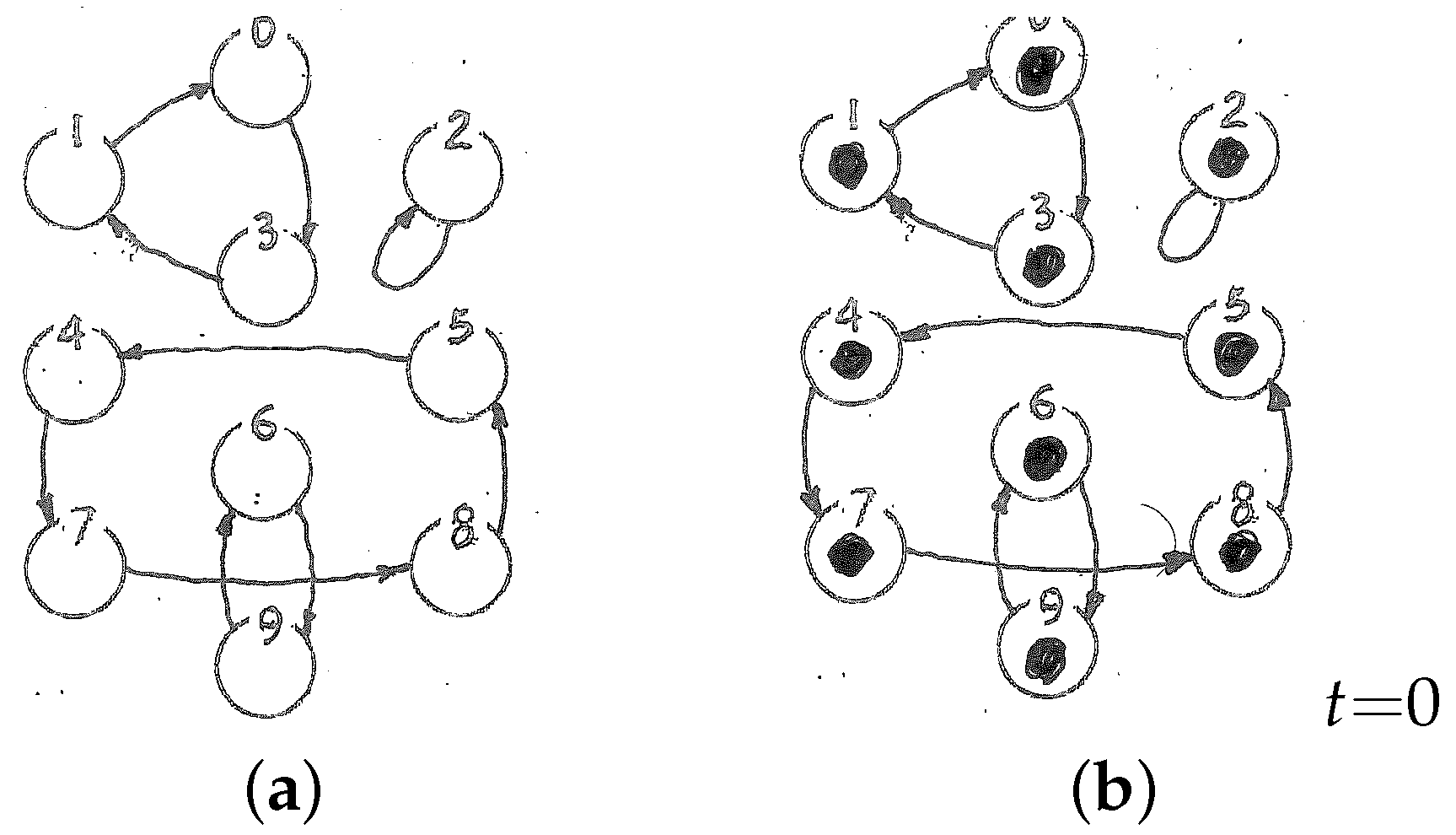
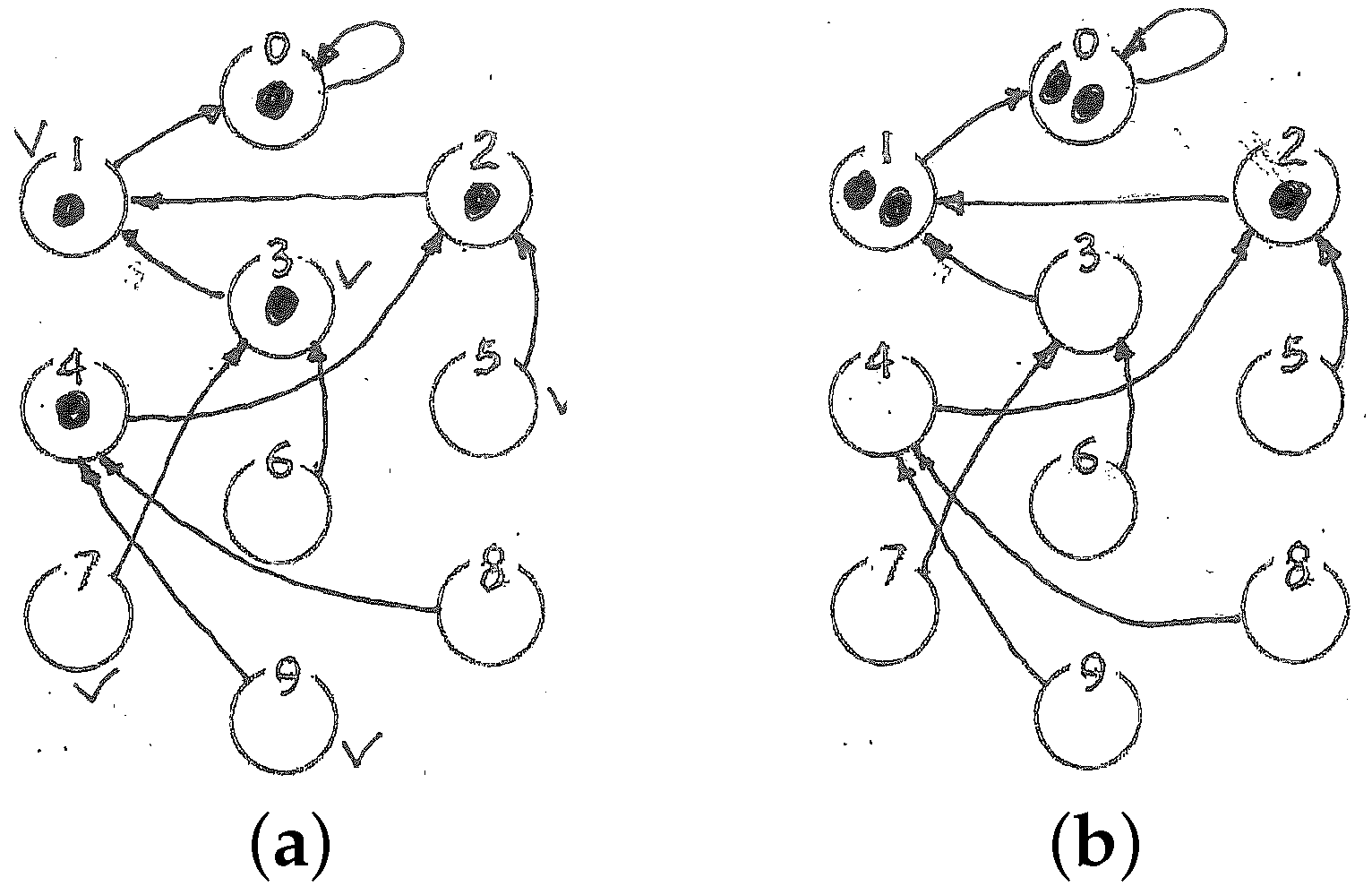
- You
This time I’m not going to tell you exactly which node I’ve chosen as the initial state—just that it is one of these: . Ready?
- Me
Just a moment! (
marks nodes 1, 4, 7, 9 on his diagram, for the record, and places a token on each, as in Figure 3a) Then my initial entropy is 4. I guess I will have to treat the four initial nodes as separate cases, and at every step advance the four tokens “in parallel”. Why not? it’s pretty much like if I were managing four game boards at once. Go ahead, shoot!
- You
Step! Step!
- Me
(carefully moves each of the four tokens two steps forward, all on the same diagram sheet) OK—but don’t go too fast!
- You
Now just do nine more steps—take your time! That will be all.
- Me
(
is done after a little while, and at the end also records the final
arrangement of tokens on his worksheet—as in Figure 3b) The final state may be any of these nodes:
.
You now invite me to your room to compare the outcome of my “duplicate play” with the final state of the “master play” in your room. The results agree, in the sense that (a) the final resting place of your (single) token matches one of the (four) places that are covered by a token in my board, and (b) there are no more tokens on my board than would be necessary to guarantee that result for any of the initial nodes you had stated as possible!
Also, I remark that in this case as well my entropy at the end of my “remote-control” performance is still equal to that of the initial state. (Of course it then collapsed from 4 to 1 as soon as I saw your actual final node.)
Still later—same setting.
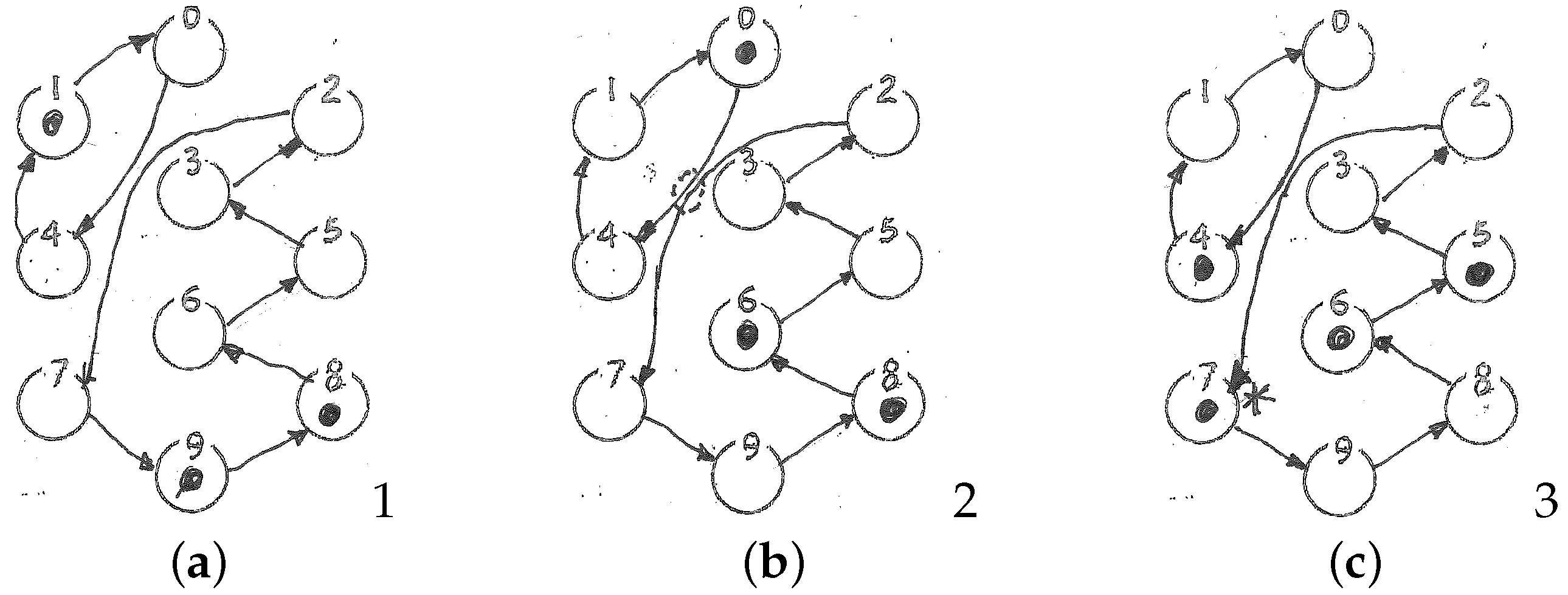
- You
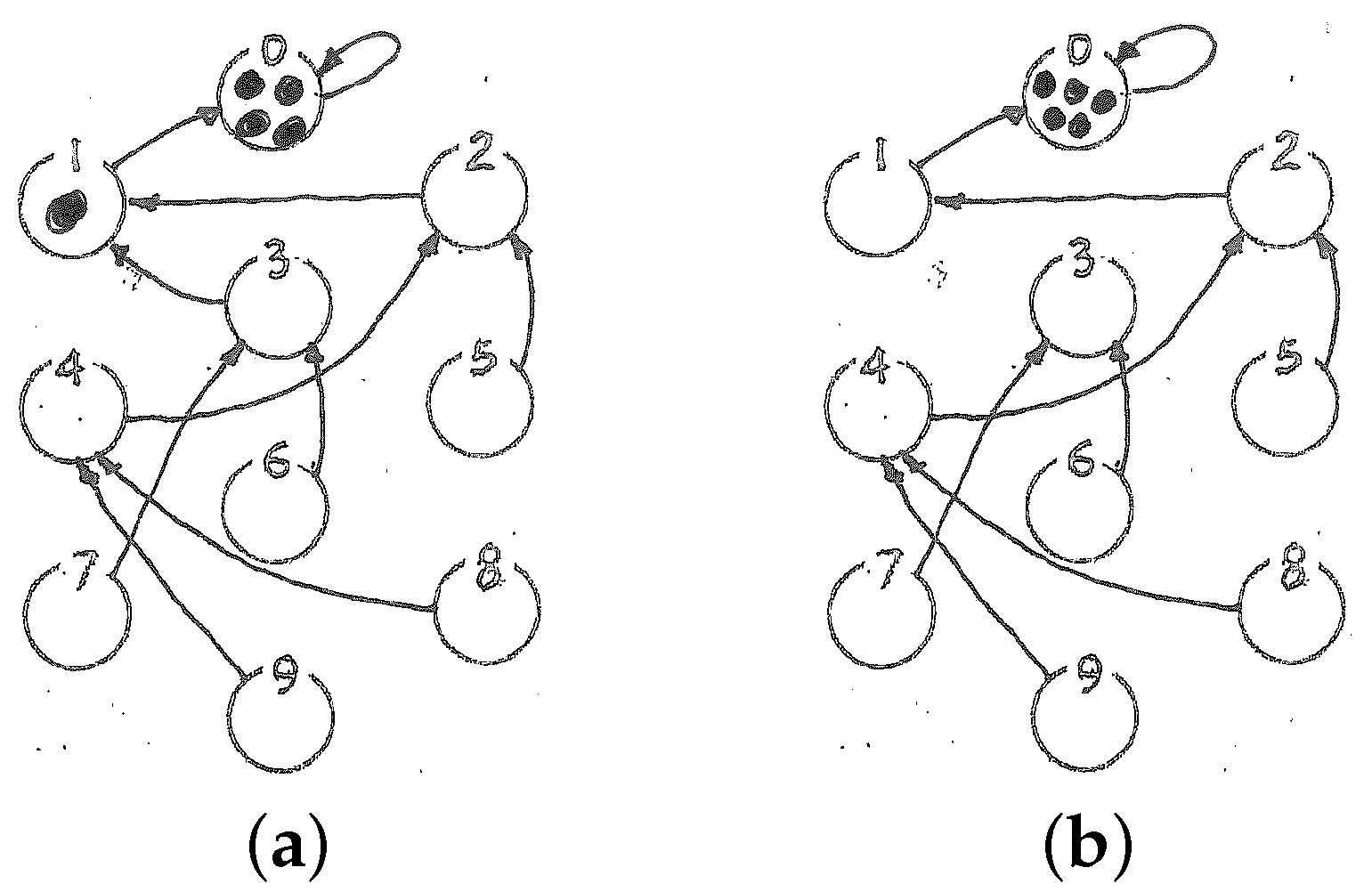
Look, I’m tired of choosing initial states. Let’s say that I may start from any node. Ready?
- me
(
dutifully marks all ten nodes as possible candidates for the initial state, and covers each with a token, for a total of ten tokens, as in Figure 4b) I’m ready!
- You
Then I’d like you to take eleven steps of it!
- me
I will—but with all these tokens it’s going to take a while! (moves each of the ten tokens one step forward) One! (a second step) Two! ... (notices that in spite of all that bustle nothing has changed as a result; looks again at the state diagram; then, in a flash of understanding) Done!
What has happened? By inspecting the state diagram of this particular dynamical system, I noticed that it consists of just loops, or closed trajectories. Not only does each node have exactly one successor, but also exactly one predecessor! Thus it never happens that two arcs flow into the same node, or that a node has no inlets at all. The dynamics (i.e., the system’s “next state” law!) is a one-to-one correspondence; in other words, it is invertible. That is, you could go backwards and unambiguously retrace your steps by following the arcs backwards. When stepping forward on this diagram, a “platoon” of n tokens occupying n distinct nodes will invariably land again on n distinct nodes—there are no “merges” of trajectories, no piling-ups of tokens onto the same node. The number of occupied nodes—the entropy of the platoon’s “footprint”—does not change as the platoon advances—no matter whether by one step or one billion, or whether you start with a single token (an ur-state), a small patrol of tokens, or a whole platoon! If we take “entropy” to mean “amount of information”, an invertible rule is (ach!) informationlossless—whether the system’s description is precise (it pinpoints a single ur-state) or vague (leaves one uncertain as to which of a set of many ur-states).
In the present case, since
all nodes were occupied by a token at the beginning of the evolution, as in
Figure 4, they will remain so after each step. Since my task is to record, on the basis of the initial description and the number of steps taken afterwards, the nodes possibly occupied
now, and
all nodes are “possibly occupied” at the start, the conclusion is that
all nodes are possibly occupied at
any time. In summary, even as the tokens advance, their occupation pattern does not change at all with time—and that’s why I can announce the final distribution instantly!
By the way, if in spite of the movement of tokens the overall token pattern is found to be the same at the end of each step, then this pattern is called an equilibrium state—another way of saying time-invariant or time-independent.
6.3. A “Poor Man’s” MaxEnt Principle?
Note that, in any of these duplicate plays, I strive to cover with tokens
every node for which I had some reason to think that they (but no others)
might be occupied in your master play—as remarked at the end of Day 1’s second dialogue (
Figure 3). What is the rationale for that?
In the Jaynes entry of
Section 4, we saw that the MaxEnt principle is but the implementation, in a statistical context, of a witness’s categorical imperative of
honesty (“the whole [ascertainable] truth and nothing but the truth”).
But in the present lean-entropy context, where no statistics has yet been introduced, the only tool that forecasters have at their disposal to implement that categorical imperative, in organizing and updating their evidence, is the blunter “all-or-nothing” of logic. Here, the “whole truth and nothing but the truth” clause is simply expressed by a sum of minterms, i.e., by the logic or-ing of and clauses; one may call this approach MaxMin. The result is a subset of the set of all conceivable ur-states (aka “outcomes”), or, equivalently, the characteristic function of that subset, which assigns to each outcome the stark choice between 1 and 0 (for “currently possible” and “currently not possible”). Contrast this with a probability distribution, which may assigns to each outcome a weight anywhere between 0 and 1: for the same honest intention, if you are given finer tools you may get sharper results.
What I want to stress is that the MaxEnt principle is not sacred: the ultimate criterion is that of honesty, of which MaxEnt is a derivative—the best implementation made possible by a certain kind of evidence and certain updating (or “evidence propagation”) tools. Even when the introduction of statistics will enable us to use MaxEnt instead of the present MaxMin, we may still not be doing the theoretical best in our inference task. That can only come by tracking the progress of ur-states by literally applying to the ur-state set the “ur-law” that maps ur-states to ur-states—no matter whether the state of a system is described as a single ur-state; by a subset of ur-states or a probability distribution over the set of ur-states; or other reasonable means. This concern is captured by the concept of internal entropy, defined in the next section.
6.4. Internal Entropy
The morale of Day 1’s dialogs is the theorem (the dialogs themselves are what one might call a “proof by example without loss of generality”) that
What is this “internal entropy” stuff? Just a physicist’s shorthand for what we have been practicing in the last three pages—that is, entropy as tracked by a certain kind of discipline. Namely, given a description (a collection of ur-states) of a system’s initial state, internal entropy is the entropy (the ur-state count) of this descriptions as it evolves strictly on the basis of a complete characterization of the subsequent transformations—how many steps and of which law.
At present, a state is described as a collection of ur-states, and, if the law is a many-to-one mapping (as in the dialog of
Section 6.5), when two or more trajectories
merge we shall apply the “MaxMin” honesty criterion (see
Section 6.3): the new occupation contents of a node is the
or (or
logic sum) of the contents of the predecessor nodes. But the above definition of
internal entropy applies just as well to probability-weighted ur-states, in which case a merging of trajectories gives as a resulting weight the
arithmetic sum of the predecessors’ weights.
What I termed “internal entropy” is often loosely called “microscopic” or “fine-grained” entropy. The latter terms are a historical legacy—they have nothing to do with very small systems per se. What can there be of microscopic about, say, a deck of cards? On the other hand, as this deck evolves according to the dynamics of, say, a zero-person solitary game, in which the player has no choice about how to move since all the moves are forced by the rule—and we are thus dealing with a dynamical system, its entropy (as a measure of my best achievable current description) evolves as well. This ideal process of accounting for entropy evolution is uniquely determined by the “internals” of the system (i.e., the objective rules of the solitary game), and not by any demands or happenings “external” to the system, like my (possibly non-ideal) accounting. (“If a tree falls in a forest and I was listening to my iPod full-blast, does the tree make a sound?” I may swear I heard no sound. However, in falling, the tree left marks that in principle any one can later investigate to determine what happened in the forest. If sufficient efforts are made, different investigators will come to the same conclusions, thus reconstructing an objective “internal” happening independent of my subjective, possibly faulty, “external” testimony.)
In brief, internal entropy is that whose changes are wholly determined by the ur-state transitions prescribed by a system’s rule. Note that from the present viewpoint, in agreement with Clausius’s intuition, internal-entropy
changes are to be associated with
transformations.
External-entropy changes (discussed in
Section 7 and beyond) are also associated with tranformations, but of a different kind.
The key feature of internal entropy is the assumption of complete knowledge of the rules—such as the transition diagram of the above dialogs—as they apply to the system’s ur-states. It doesn’t matter instead whether a description of the state of the system is fine or coarse—whether it pinpoints a ur-state (as in the first dialog), leaves open a number of possibilities (a “cloud” of ur-states, as in the second dialog), or is totally vacuous (as in the third).
Once we know the rule, we can in principle precisely apply it to any individual ur-state. The collective makeup of an ur-state cloud—which represents the ambiguity of our state of knowledge—is irrelevant; and so is (in principle) the amount of labor needed to apply the law to every ur-state.
Note that the token-pushing labor can be distributed among many workers and performed by them concurrently, independent of one another, since tokens do not interact. As a matter of fact, in certain situations the image of a
cloud of tokens crowded over a single state-diagram may not have adequate expressive power (see
Section 6.6). To play it safe, one should always imagine using as many instances of the game board—as many identical copies of the state diagram—as there are tokens, and have each token run
all by itself on its own board (see
Section 8.5).
6.5. Day 2: It Goes down!
- You
I just faxed you a new dynamical system—same ten states as the old, but the arcs are different (
see Figure 5a). Wanna play a game?
- Me
Sure! What’s up?
- You
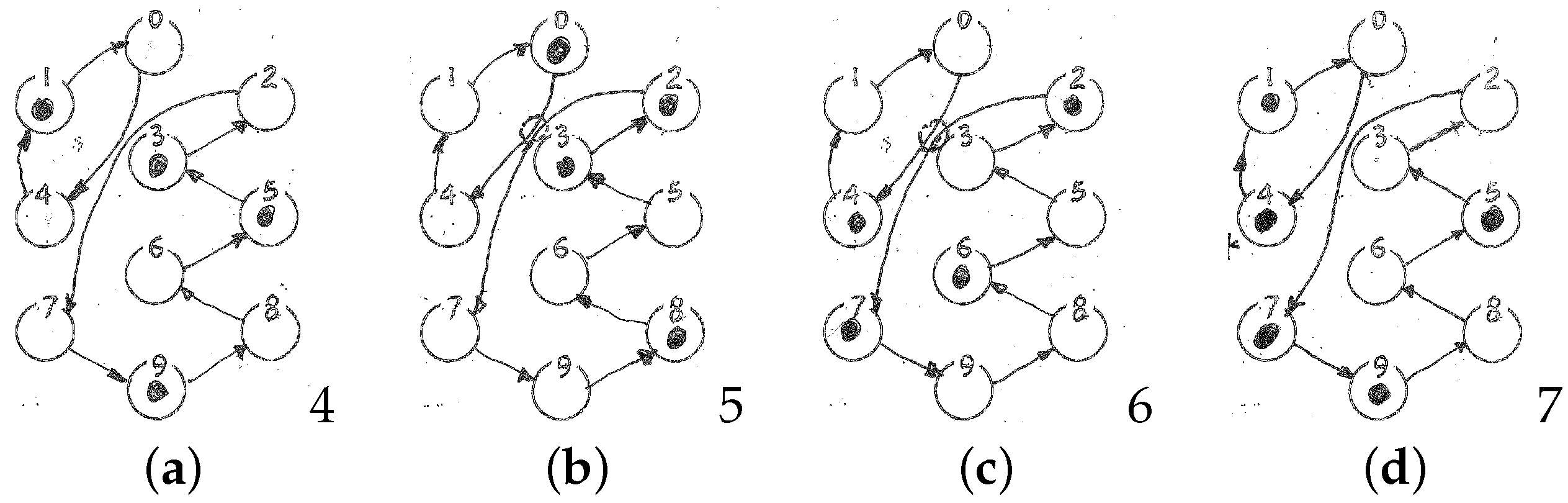
I’m asking you to tell me! I suspect there may be something different. Let me describe the initial state as “an odd number”.
- Me
You mean, any of
? I will have to use five tokens. (
see Figure 5b) Let me make your system go through a few steps and I will tell you what happens.
- You
Go ahead!
- Me
Well, on the first step the token moved forward like so: , , , , and . The occupancy is now ; the entropy level has remained at 5. Incidentally, the rule seems to be “divide by two and throw away the remainder”.
- You
Take one more step!
- Me
One moment! While the token on node 4 wants to go to node 2, both 3 and 2 want to go to 1 (
see Figure 6a), and both 1 and 0 to 0. What shall I do with this paired tokens?—allow a double occupancy and place them both on their destination node?
- you
The way we’ve been using tokens so far is to tell, “Given the system’s dynamics and the description of its initial state, there is a possibility that the system will be on this node.” With this interpretation at least, it doesn’t make a difference if you move both tokens to the node they want to occupy, or put only one token there and take the other off the board.
- Me
I’ll do the former—in all these “overbooking” cases, I’ll “put two or more passengers in the same seat!” (
see Figure 6b) Now there are tokens only at
; entropy has dropped from 5 to 3.
- you
Go on. Step! Step! Step!
- Me
Occupancy dwindled down first to nodes
(
see Figure 7a), then to just node
(
see Figure 7b)—and that’s where things will remain from now on. In fact, once a token has reached node 0, in one step it will cycle back to 0—and so on forever! It will never go off the board! Entropy went down to 2, then to 1, and now it is stuck there.
- you
So there were steps when the entropy didn’t change; and others when it went down; but none when it went up?
- Me
That’s right, the entropy of your system monotonically
decreases as time goes on, and I can prove it! In this diagram here (see
Figure 8a) I rearranged nodes and arcs to make explicit this inexorable march of events.
- you
That’s strange... physicists say that internal entropy can never decrease: if it did, one could exploit that to turn waste heat into useful mechanical work—to make a perpetual-motion machine! What is different with this system?
- Me
Well, physics is a special case, since its fundamental laws—whether in the classical or quantum-mechanical formulation—are believed to be strictly invertible. But the new system you gave me to play with is not invertible! (reassuringly) Don’t be embarrassed—I hear that the noninvertible ones are actually the majority!
- you
I’m satisfied with your explanation. But physicists also maintain that entropy keeps increasing all the time—only in ideal circumstances does it remain constant. Yet in invertible systems, as we saw in Day 1, internal entropy is strictly constant, and in noninvertible ones it sometimes goes down. Between invertible and noninvertible—that takes care of all systems, and so leaves no room for entropy ever to go up. It seems that the difficulty is how to make entropy go up rather than down! How do physical systems manage the trick of letting entropy increase in spite of their being governed, as you just said, by invertible laws?
6.6. Day 3: It Goes up!
Today you walk into my room with a glum face.
- you
My fax machine is broken. But I still don’t want you to peek into the system in my room—after all you are supposed to make forecasts, not reports. In lieu of faxing, I will chalk the transition table on a slate and give that to you.
- Me
Fine with me!
- you
(scribbles on the slate) Here is the system’s dynamics! Can you run seven steps of it? Start with as the initial state... Now—I’m sorry—I have to go see my doctor. I’ll be back after lunch.
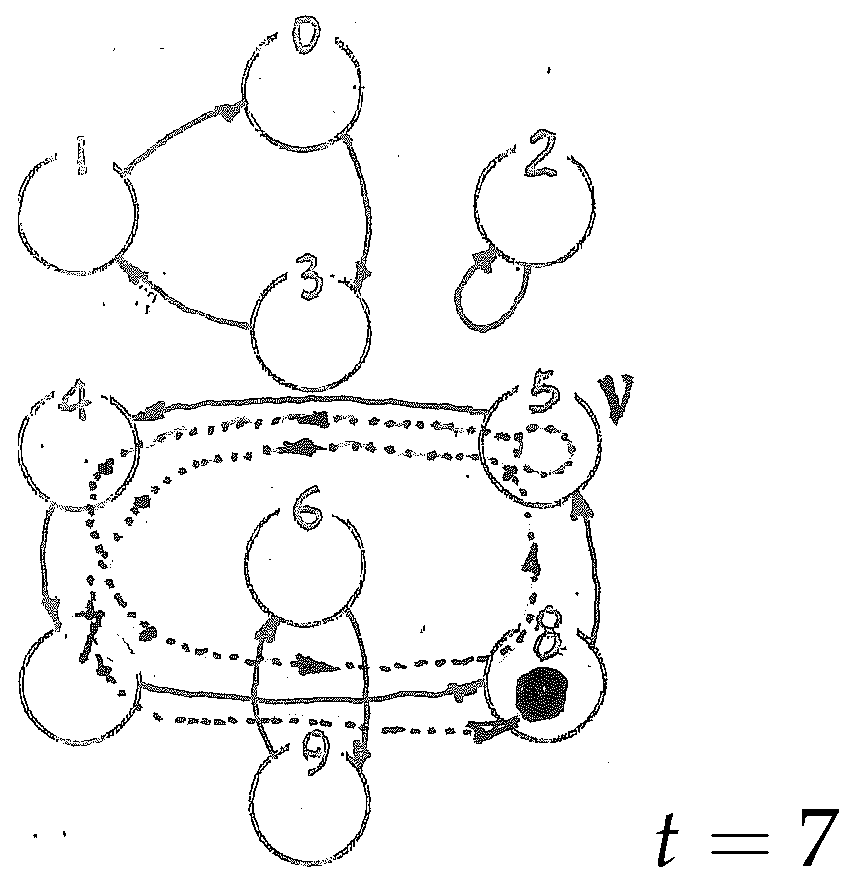
I pick up the slate. On it there is a graph with ten nodes and ten arcs (
Figure 9a)—as in the previous two days. I mark nodes
as the initial state and place one token on each (
Figure 9b). The inital entropy is clearly 3.
I observe that no two arcs converge onto the same node, so the system is invertible—as that of Day 1. I run two steps (
Figure 10) without any problems. However, on the third step I see a problem: When one of my tokens happens to be on node 0, as at time 2 (
Figure 10b), its outgoing arc at a certain point runs so close to that coming out of node 2 that’s hard for me (I left my reading glasses at home) to tell whether at that point the two arcs
run along each other or
cross. In my case, if the two arcs run parallel my token move should be
; if they cross,
. Note that the ambiguity in this scenario is not as to
which node, as when we gave a choice of several nodes for the initial state, but as to
which destination accroding to the rule—whether the transition table for node 0 says
or
.
Since my task is to determine, at every step, on what nodes there can be a token—that is, which system states are possible according to the information I have—the best I can do at the moment is entertain both possibilities at once for the token now leaving node 0, by placing tokens on both possible destinations—nodes 4 and 7.
My approach means, in substance, “when in doubt, track the consequences of all plausible alternative hypotheses.”
(When a “game” is played as a response to a real-life challenge, a token may mark, say, one of the places where a terrorist might be at the moment—remember the hit-and-run story? At the next step of the game that position is updated, say, according to the presumed speed of the vehicle and the nature of the terrain—and that is done “in parallel” for all alternative routes that terrorist may have taken. The rationale for choosing to act that way runs much like this. Suppose I forgot where I left my glasses and I have to instruct somebody to go get them for me. I am to give them a list of places where they should look. If one place which comes to my mind is not after all so likely, should I include it? If I do, the errand will take a little longer (or merely just as long, if they find my glasses before looking at that place). If I do not include it, and the glasses actually happen to be in that unlikely place, then my helper will come back after the longest possible time (having gone through all the places in the list) and still return empty-handed, adding, as it were, insult to injury! I would rather play it safe.)
I go all the way through the seven requested steps. At time 5 (
Figure 11b) I have a similar problem, but this time
both nodes at the head of the converging arcs have a token, so it does not matter whether the two arcs cross or go along. At time 6 (
Figure 11c), the token at node 2 encounters the same problem as node 0 at time 2, and so, “in doubt”, it takes both paths. I have now five tokens! (
Figure 11d)
You come back from the doctor.
- you
Well, how did it go? Where are your tokens now?
- me
At nodes ; the entropy is now 5.
- you
How can that be? I’m sure I had given you an invertible system, and thus the entropy should have remained constant. Or perhaps you believed I had given you five alternative nodes for the initial state?
- me
No, I know you only gave me three. But, owing to its poor readability, the graph you’d given me confronted me with two alternative routings. Effectively, instead of a single law I had two alternative laws to deal with. I did my best, and kept both alternative universes alive. My final number of tokens represents the logic or—the “merge”—of tokens from two parallel universes after seven steps of running.
- you
I guess you did your best—all this is very helpful. Thank you! In fact—please hang around—I have one more task in mind for you!
Note that the or operation (the “merge” of token patterns) is a hack—a simple but not necessarily the best way to extract a token count from the parallel evolution of a number of universes.
Here we have seen one way that entropy can go up. From Day 1 to Day 3 nothing has changed with the nature of the system’s law or of its initial state, but an accident of misplaced reading glasses prevented me from making out one bit of the law itself—“Do these two paths cross or run through side-by-side?” During the step where one token went through that juncture, the “internal law” that governed the movement of your tokens had not changed—specifically, it was still invertible—but because of some “external perturbation” my description of it went through a “forked path”. To represent the two alternative universes, my hack was to duplicate the token while remaining on a single game board. As a variant of that, I could instead have cut the token in half and let the two halves follow separate courses. The most conservative solution—I use that term literally—would have been to duplicate the whole setup, board and tokens, at the very beginning, when I realized I did not have my glasses; use the “across” variant of the law for one setup and the “along” variant for the other; and proceed with the simulation on both boards. Later, when I found my glasses, I would have resolved the doubt and accordingly simply discarded the wrong variant.
(You may argue, “What a waste of resources!” But this is exactly what is done today by employing speculative execution in microprocessors, where for the sake of reducing latency a computer system performs some task that may later turn out not to be needed. When the cpu encounters a conditional statement—“if 〈condition〉 then do 〈this〉 else 〈that〉”, and the value—true or false—of the condition is not yet known, it starts running through both “horns” of the dilemma—〈this〉 and 〈that〉—in parallel, using extra resources provided for the purpose. Some time later, when the condition’s value is known, one horn is lopped off and the resources already spent on it go down the drain. In this way we save time, since the “right” answer starts being computed (together with the “wrong” one) before the condition is known—but at the price of “haste makes waste”!)
No matter what hack I use,
my accounting of the process becomes in effect
nondeterministic (see
Section 8.4). Note I was careful not to say “stochastic” or “probabilistic”—that is, I did not give
weights to the two alternatives (that would be a higher-level hack, touched on briefly in
Section 8.3). Fact is, what kind of forensic analysis of the slate could have told me the odds of “across” vis-à-vis “along”? In all honesty, I could only say
Two roads diverged in a yellow wood,
And I traveled both,
And described to you both of them.
Now you choose—I was only a bookkeper!
A little later that afternoon.
- you
Sorry for that smudgy slate! To make up for it, as I was coming back from the doctor’s I typed on my laptop the rule for the system I gave you this morning—and a new set of initial conditions. The data are here on this USB memory stick. Can you please run the experiment again?
- me
Sure! But right now I have to pick up my daughter and stay with her through soccer practice. I’ll be back in three hours.
- you
Fine! I can wait—I got plenty of stuff to do myself.
After the embarrassment of missing my reading glasses, I feel a bit paranoid. So before leaving I put the memory stick inside a very-high-resolution particle detector—I have read that “electronic memory performance is highly affected by cosmic rays”.
When I come back, I analyze the content of the memory stick and see that the set of initial nodes reads . However, I discover that unfortunately one high-energy gamma-ray has hit the chip, passing through the least-significant bit of the memory word where that number 4 is stored. Typically, if anything happened at all, that bit would have been cleared—i.e., for this kind of memory, been forced to the value 0. So the least-significant bit of that 4 (0100 in binary), which now reads 0, may originally have been a 0 as now, or may have started out as a 1 and then been turned into a 0 by the cosmic ray. So, even if that bit had not been changed by the ray, I still do not know whether what now spells 4 was originally a 4 or a 5. In doubt, I will have to count both 4 and 5 among the possible initial nodes—in addition to the other three nodes in the given list. (Of course, if a 5 was already present in that list I would have concluded that the affected node must indeed have been a 4 to begin with, and not added a second 5 to the list.)
Well, you can guess the rest now. The description you wrote in the memory stick certainly had an initial entropy of 4, because there were only four entries in your initial-state set. The gamma-ray accident forced me to augment this set to —entropy 5. The law is clearly legible and the system is indeed invertible, so that—barring new accidents—the entropy will remain at 5 forever. However, at some time during my entire accounting process the entropy has increased from 3 to 4 in spite of the system’s being invertible.
7. The Second Law
The morale of Day 3’s dialogs (
Section 6.6) is that
What? What happened to the morale of Day 1? (top of
Section 6.4) Are we in Orwell’s
Animal Factory after the pigs’ takeover? There, the cherished slogan painted on the barn’s wall—which every barn animal remembered as
—was one day found augmented to
What has changed? Well, the new morale speaks of “honest” entropy, not of “internal” entropy. If we want to turn morale (
8) from a mere afterthought over the two isolated thought experiments of Day 3’s dialogs into a general
theorem, we will have to properly define “honest entropy”.
7.1. Honest Entropy as a Contract
Here we shall first motivate and then define
honest entropy. By proposing such a definition, my goal is to
capture the most natural (and plausibly a most generally useful) concept of entropy, if there were such a thing; if not, to help
shape one. As we shall see (
Section 8), our definition will naturally extend to the standard entropy context. Our definition applies not only to the updating of a description by a
deterministic law, but also to the case of a
nondeterministic law, regardless of whether the state of a system is given as a subset of ur-states or a probability distribution.
The nature of honest entropy reflects a contract much like that between an executive and a consultant. The executive has the power to decide how to use his institution’s resources for the institution’s greater good, but may not not be sure of the consequences of a given decision. So he decides to set aside some of those resources to hire a consultant to quickly estimate the actual consequences that a hypothetical decision taken now will have in two years.
The consultant will set up and run at 100× speed (two years to a week) a simplified version of the world which mimics essential aspects of the problem at hand. For the reason presented in
Section 8.3, this will typically be a
probabilistic model, consisting of (a) an initial probability distribution over a set of ur-states, and (b) a law describing its evolution in time. (A lean-entropy model, as indicated in
Section 6.3, will do as well).
This is fine conceptually, but in practice the ur-states are vastly too many to be treated one-by-one. In fact the number of ur-states grows exponentially with the system’s amount of detail—the number of its parts or features.
If my Social Security has “only” 9 pieces—its nine digits—that nonetheless means that the Social Security Administration must be ready to handle up to a billion files! The ur-state of even a simplified model of something like the weather or the market may easily run in the billions of digits, alphabetic characters, or pixels; a liter of gas may have parts—and the number of ur-states is an exponential of that! While it may still be practical to determine the successor of a single ur-state and iteratively follow it along its orbit, a fully general distribution consists of the weights of all the ur-states, and thus has as much bulk as the entire ur-state set. Only distributions that can be represented in a compact way owing to special properties can be handled, and only evolution rules that can themselves take advantage of those special properties can be applied; that is, the restrictions in the nature of a distribution also restrict what the dynamics itself can express. Thus, one should strive to retain a dynamics that can easily carry over across an evolution step at least those correlations (between parts of the model) that are of critical relevance.
In summary, the limited resources available force the consultant to drastically condense, and thus severely approximate, both the static description of the “state of the world” (as far as the executive’s query is concerned) and its dynamics. In light of the circumstances, this may still be an honest manner to proceed on the consultant’s part.
Within a week, the consultant delivers his forecast for the “state of the world” two years from now—and presents his invoice. How is our executive to determine if the contract was indeed fulfilled and that the product is worth its cost?
To be concrete, suppose that one element of the forecast were the market price of gold—as of two years from now. By its nature, the model will give for this price a probability distribution, typically approximating a normal distribution, with a certain mean (say, $1301/oz) and a certain standard deviation or spread, say, ±$700/oz. Now, such a spread is so large as to make the whole forecast business virtually worthless, because anyone could have told that “somewhere between $600/oz and $2000/oz” is practically a sure bet—no need to pay a consultant!
Would then our executive accept without a qualm a forecast of $1301±1/oz? With such an unbelievably narrow spread, he should sue the consultant for fraud and ask the court to immediately impound all his records: there are not enough resources on entire planet to grant such a sharp prediction!
From the above discussion one can begin to tease out rational terms of contract for engaging a forecasting consultant, along the following lines:
- 1.
The principal of the contract will have the option to engage an auditor to monitor the performance of the contract, from its onset (including setting up and running the model) up to one year after the forecast’s object date.
- 2.
No limits shall be set by the contractor to the amount of resources granted to the auditor for his task.
- 3.
All the data and procedures used by the contractor during the performance shall be made available to the auditor, and documented in such a way as to make the entire contract execution repeatable at will. Rationale and aims of unusual or ad hoc data-processing procedures should be clearly stated.
- 4.
The auditor shall not disclose any of the intellectual property originated by the contractor during the performance, except as evidence of breach of contract.
- 5.
The contractor may be fined for any breaches of bookkeeping and/or accounting rules, as indicated by the auditor, in the following matters.
- 6.
Random error. If, at any stage of the performance, simplifications or approximations of the model are introduced, or the model is affected by accidental disturbances, or just exposed to such disturbances, a detailed record of such events and exposures shall be kept. An upper bound to the entropy gain attendant to any such disturbance shall be provided independently for each event, and accumulated into an external entropy burden, which shall be added to the measurable (by inspection) “raw entropy” entropy of the final forecast.
At the same time as the auditor is charged with detecting violations to the above
random error clause, it might be expedient to additionally direct his attention to the following
systematic error clause:
- 7.
Systematic error. If, at any stage of the contract performance, transformations are applied to the model’s current state that, in light of the current state of the modeling art, grossly or unaccountably depart from the goal of converging toward the desired distribution mean, such deviations must be reported and accumulated in a qualitative way into an external center-of-mass burden.
However, rather than with honesty, the latter clause, about systematic error, has to do with competence—which is much harder to quantify. As Shannon discovered, among parameters that one could use to characterize a transformation, entropy change sticks out because any administrator with generic training can routinely determine it—much as he can determine the number of a candidate’s publications simply by counting them. More significant aspects of a transformation—or of a candidate—may require a great deal of specific expertise to evaluate. Desirable as it may be in a contract, we shall not include the last desideratum in the contract that defines honest entropy.
We have seen what the entropy of a description is. We have seen how this entropy changes as the description is updated by the literal application of a certain internal dynamics. We shall now define the honest entropy of a sequence of transformations.
Honest entropy. Given a “master” system that starting from a certain state has undergone a certain number of tranformations, an honest entropy change is defined as the computed entropy change of an independently simulated version of the system, started in an equivalent state and subjected to equivalent transformations. This equivalence shall be a mapping of states and transformations of the master system to those of the simulated system. For any point in which this mapping is not one-to-one, (it could be n-to-one, as in a homomorphism, or one-to-n, as in a Monte Carlo simulation, in both cases with a lean-entropy change of , but with different signs in the two cases), an upper bound to the attendant entropy change shall be assigned and the absolute value of it shall be added to an entropy burden accumulator. The final value of this entropy burden shall be added to the difference between final and initial entropies of the simulated system (which can be determined by inspection).
As for the procedural rules stipulated by the above definition, I did not pull them out of a hat. They essentially reflect the standard conventions for the
propagation of uncertainty (as in [
22], for one) in experimentation, simulation, and calculation.
I have tried to illustrate the rationale of the above procedural guidelines in the two dialogs of Day 3 (
Section 6.6), where external events superpose perturbations, or “noise”, on the internal evolution of a system: in one case on the system’s rule and in the other on the system’s state. Even though these events were
external to the system proper, honest dealing with them lead to a
smearing of our description of the system’s state, as compared to what it would have been by pure internal evolution.
For a familiar example of uncertainty propagation, suppose that in a numerical simulation one rounds off all numbers to three significant figures after each updating step. Then 3.14159 becomes 3.14, but the same value will have been arrived at from any number between and , with an uncertainty range of 0.01. Thus, even though roundoff is a many-to-one mapping, and so naively may seem to reduce uncertainty, in fact it will have destroyed part of the record, and thus leave us with an uncertainty range of 0.01 as to the original content of the record.
If the original number had been 3.14 to begin with, no uncertainty range—no entropy burden—need be attached to it because of the roundoff.
Finally, if the same number had been encoded onto an analog signal subject to a noise level of 0.1, and then turned back to digital form as—say, 3.22—by analog-to-digital conversion, we should associate with the latter an uncertainty range of 0.1.
Recall that in “internal entropy” the term “internal” does not refer to an entropy per se, but to a particular discipline through which an initial description is successively updated to reflect the effects that a certain sequence of transformations had on the state of a system. The object of the game was to give an accurate description of the system’s state at the end of these transformations.
In an analogous way, in “honest entropy” the term “honest” does not refer to an entropy value per se, but to a particular discipline used to arrive at it—usually when, as almost always the case—drastic simplifications are unavoidable.
Even within that discpline, an honest entropy is not unique; it depends on the specific simplification made. More drastic simplifications represent a coarser approximation of the system, and thus, when honestly acknowledged, yield a higher honest entropy. The latter only gives an upper bound to the entropy one could have arrived at by making a more accurate simulation of the master system. The best lower bound, of course, is the internal entropy.
Moreover, what is the auditor for? Clearly the uncertainty of a forecast—its entropy burden—decreases its value, and a consultant will be tempted not to report the full extent of it—as we all may be tempted with our tax burden. The likelihood of an audit should encourage our consultant to police himself and not push too hard the envelope (you may be amused to hear that this idiom comes from the mathematics of curves via the lingo of airplane performance limits—nothing to do with stationery) of the contract.
Any way of massaging or updating a description—even outright forgery—still leaves a description of sorts. For this reason, we shall still generally call simply “entropy” the count of all possible instantiations of that description—as questionable as the latter’s provenance may be.
Most forms of entropy that are not obtained via the
internal entropy discipline are traditionally called
macroscopic entropy (of which
coarse-grained entropy is a special case). Often a macroscopic entropy is arrived at by a
hybrid process. That is, the description is first updated by a
blind-reckoning procedure, that is, one
computes a few steps of the evolution of the system from given initial data and a given law,
without access to the system itself. Then one determines
by direct measurement some easily quantified parameter—usually a global macroscopic parameter such as mass, temperature, pressure, or the results of a poll; in other words, one “takes a peek” at the system. Finally, those two components are combined into a single description, and the entropy of
that description is reported. An example of this is given in
Section 7.5.
The concept of “macroscopic” in physics is actually a “kitchen sink” of more-or-less precise intuitions. In Gregg Jaeger’s words, “Macroscopicity turns out to be a rather vaguer and less consistently understood notion than typically assumed by physicists who have not explicitly explored the notion themselves” [
23]. Also, in [
24], “Long before the appearance of the term in quantum theory, consistent standard but different use of the notion of the macroscopic was made in thermal physics and statistical mechanics, in reference to the macroscopic variable and in connection with the relationship of the statistics of basic components to thermodynamical variables, e.g., temperature and pressure of collections.”
The concept of honest entropy may provide a quality-control reference point (“here we know what we are talking about”) in the commerce of macroscopic entropy.
What we shall do next, is present in a discursive way, always in the context of the present lean-entropy approach (“entropy-as-a-count”, as defined in
Section 5) an important conclusion of the present paper, concerning the relation between
honest entropy and the
second law of thermodynamics. We shall briefly revisit the second law after the deconstruction/reconstruction excursus of
Section 8.
Let us first recall that the
second law of thermodynamics, as formulated by Clausius on empirical grounds, can be paraphrased as
and that it is believed that
Further recall, from theorem (
7), that
(note that the object of internal-entropy bookkeping is always an
isolated system), while from the dialogs of
Section 6.5 we have (the dialog itself is what one might call a “proof by example without loss of generality”) the following theorem:
7.2. The Weak Second Law
Let us now run through a trivial exercise of logic. From theorems (
11) and (
12) we obtain a
weak second law, namely, that
From that law and assumption (
10) we get, as a corollary, that
We shall as well explicitly state the converse of theorem (
13), namely,
7.3. The Strong Second Law (Important!)
Using an argument formally similar to that used above for the weak law, but starting from a more practically interesting premise, I will arrive at a much stronger conclusion.
What I proclaim, and will just for the moment call the
strong second law of thermodynamics, is none but
The proof is straightforward; it follows directly from the definition of honest entropy in
Section 7.1 with the help of the following
Table 1:
As per this table, at any step the system’s honest entropy will
if the system is invertible: remain constant, or increase;
if the system is noninvertible: decrease, remain constant, or increase; moreover,
if for some appropriate current state description and low enough external noise a decrease can occur at all, then the system is noninvertible.
Note the asymmetry between the if and the only if. I can check that a system is invertible by its law, which is given to me, and from that I can make nonvacuous predictions about its entropy changes in different circumstances (noise vs no noise). Similarly, I can check that a system is noninvertible, by its law, and from that make some nonvacuous predictions about its entropy changes.
For the converse, however—that is, if I want to infer something about the invertibility of the system from the changes in entropy—the task is made more difficult by the presence of external noise. If I happen to hit a single state transition for which the entropy decreases, then, irrespective of external noise, I can conclude that the system is noninvertible. However, even if I manage to turn off all noise, to conclude that the system is invertible merely from its entropy changes I have to test all possible state transitions. In the limit as the system’s size goes to infinity, the experimental determination of invertibility vs noninvertibility on the basis of observed entropy changes (we are still speaking of entropy of a description) become de facto only semi-decidable.
Our strong second law has a nice feature. It reconciles Clausius’s sweeping statement, that “the entropy of the world increases”, based on empirical thermodynamics near equilibrium, with the statistical mechanical interpretation—which in certain “non-honest” conditions makes room for entropy fluctuations. We owe this reconciliation to the humble honest entropy.
A worked-out example of reconciliation of the paradox—up-and-down fluctuations
vs. monotonical increase of an expected value—is given in
Section 7.5. There, the score of a game is updated in real-time, while a forecaster updates, also in real-time, an
expected score based
only (a) on information available
at the beginning of the game and (b) just how many rounds of the game have been played so far—but none of the actual outcomes. In the actual game, the score may well go up and down; in these “blind-reckoning” forecasts, the expected score will monotonically increase
if and only if the system is
invertible!
On reflection, all this should not be surprising. Honest entropy is but an expression of the MaxEnt principle (see
Section 4, Jaynes entry) in the context of a
forecasting context (where by necessity one must perforce
anticipate the state of a system without seeing it, as the contractor of
Section 7.1), or whenever such “blind reckoning” is stipulated by the rules of engagement.
Moreover, this is the source of the generality of the strong second law of thermodynamics, and by implication, of Clausius’s second law!
7.4. Not a Physical Law?
In the title of this section (see Myth 7 in the Introduction), remark that what is emphasized is not “law” or “not”, but just the word “physical”. Now I shall explain what I mean; to the cognoscenti of you, this will not come as a surprise. The surprise, if any, may be that—as in Andersen’s “The Emperor’s Clothes”—somebody had the naiveté to say it aloud!
Every morning a shepherd would take his sheep out of the fold and every night he would put them back in. Sheep, like kindergarden children, have a way of getting out of line for any distraction. So the shepherd had to count and recount his sheep to make sure he got them all in. This shepherd had an inquisitive mind—and plenty of time to think. One day he observed, “Isn’t this an interesting coincidence? When I put seven sheep in the fold, and then three more, I end up with the same number of sheep as when I start with three and then add seven.” Our “protoscientist” experiments with different combinations of sheep numbers, and such a fact always holds true. “I have discovered a great physical law,” he concludes one day, “I’ll call it the Second Law of Sheepdynamics!”
I grant the shepherd the independent discovery of a law. However, to call it a physical law? I agree that this law is correct. Indeed, few things are truer than it—and that’s where the catch is! By the same token, the cheesemaker will (correctly) claim that cheese counting obeys a Second Law of Cheesemaking, and similarly the hot-chestnut seller, a law of Chestnutroasting. This is of course harmless, but a bit parochial: will you call those a dairy law and a roasting law? They are all already subsumed under a Commutative Law of Addition, and, to paraphrase Ockham, in science it is just not good manners to introduce more laws than necessary.
The second law of thermodynamics is at bottom a
counting inequality, valid, as we have seen in
Section 7.3, for all and only
invertible dynamical systems—be they physical as a gas or abstract as a Turing machine or a cellular automaton. It can be thought of as a law of
category theory.
As a corollary of that general law, the second law becomes a “physical law” on the mere premise that physics be at bottom an invertible dynamical system. In other words, as soon as one proposes for physics (say, on the basis of overwhelming experimental evidence) a model that is at bottom an invertible dynamics, physics automatically inherits the second law as an intrinsic property of that model.
In spite of my irreverence, I am emotionally very attached to the invertible dynamics model of our universe, and I’d place a large bet on it. However, just to play devil’s advocate, one may argue that the observed invertibility of microphysics might be just an emergent property of a noninvertible substrate. For example, in a finite (though no matter how large) deterministic dynamical system, any trajectory eventually falls into the attractor of (or “merges with”) a closed orbit. The collection of these closed orbits is of course an invertible system. So, after the system has run for a long time and most of the merges have occurred (to paraphrase Feyman’s, “When most fast things have happened”) and the remaining merges are ever rarer and farther between, the system will be de facto invertible and thus de facto obey the second law (eventually it will obey it strictly) in spite of its defining dynamics being noninvertible. I briefly discussed this devil’s advocate’s counterexample with Feynman in 1981, and he had no objections to the counterexample per se; the real question was of course whether such an “aged” system would still have enough stamina to support, on top and in spite of the aforementioned emergence of invertibility, complex emergent phenomena like life.
Physicists deserve praise for having been first at identifying and formulating the second law of thermodynamics. After Boltzmann, however, it must have been clear that this is a law of enormous generality, and thus belongs to everybody, not only physicists. It has become public domain!
Incidentally, this law should properly be called a law of thermostatics, since it does not prescribe a motion, but only forbids motion in certain directions. In physics, in a course of Statics, one studies when a scale is at equilibrium. However, the principles of statics have something to say even when a system is not at equilibrium. Namely, they will tell us to which side the scale will not tip—though not whether, when, or how fast it will tip to the other side.
Specifically, the second law of thermodynamics is valid for “any invertible dynamical system from which one is temporarily cut off”. In this sense, it is a law of logic in the form of information theory. Whenever you forget a bit about a system’s state, or a tooth slips in your mechanical simulation of it, you are in effect erasing one constraint from the state’s current description. By the MaxEnt principle, honesty or self-interest require that, every time you remove a constraint, you let the distribution that embodies that description spread out to “fill the slack” and thus remain MaxEnt.
It turns out that physics
does meet the above description. However,
a countless variety of other systems do too. On the other end, if the system is not as defined above—or it does, but at a certain point you restore your contact with it—-then this law no longer need apply (see
Section 7.5 for an example). It is in this sense that I argue that the second law is not a law of physics per se (such as instead, I suppose, is the first law—“conservation of energy”), much as the commutation property of sheep is not a law of shepherding per se.
The second law’s intuitive explanation is that we—a liter of gas, the weather, etc.,—are localized patches of a large, distributed (roughly, “spread out” rather than “lumped”), yet interconnected system. In this situation no agency can have total control of any portion of the universe—and fortunately so! Mice and men may claim a patch of this universe as exclusively their own, but their best-laid plans can never manage to unconditionally isolate and protect it from external influences. The latter may be felt by the claimants as “random disturbances” (that is, “hard to predict”), even when they may be a consequence (intended or unintended) of what other mice and men (or galactic agencies) are quite deliberately and cognizantly (thus nonrandomly from their viewpoint) doing with their patches. Or they may simply be a minor accidental side-effect of the explosion of a dumb supernova!
In the above paragraph we did not explicitly mention either physics or invertibility; we just envisioned any large distributed system with enough coupling (or “interaction between parts”) to keep it exciting—as long as that lasts. Politics, economics, and ecology are good examples.
You may object that at that level of aggregation the dynamics of a system may no longer be seen as invertible—even though that of the physical substrate were, and therefore there wouldn’t any longer be a guarantee that the second principle strictly held. That is true, but if you look at the right column (
noninvertible) of
Table 1, you will see that the net entropy change would remain
as long as the “forking of paths” (
Section 6.6) contributed by the
external noise—the crowds jostling about you—overwhelmed the the “merging of paths” (
Section 6.5)—dictated by a noninvertible internal dynamics. The above state of affairs is a very likely one in almost any conceivable universe, invertible or not, considering that, if the “noninvertibility” of a system were too drastic, everything would soon “freeze” and there wouldn’t be any one left to ask questions. According to Norman Margolus (personal communication), an
invertibile pinball machine was the Creator’s obvious choice, for it yields “the most playing time for your quarter”!
7.5. Fluctuations Paradoxes; Macroscopic Entropy
Since its introduction, the second law has been (and still is) plagued by objections and paradoxes—chief representatives of which are the Loschmidt (or reversal) paradox (Kelvin 1874, Loschmidt 1876), the recurrence paradox (Zermelo 1896), and the well known Maxwell’s demon paradox (Maxwell 1866).
In short, these paradoxes present theoretical or empirical examples where in the course of time physical entropy would spontaneously
decrease, in violation of the second law. At the core of these paradoxes there usually is some version of the
mind projection fallacy (see
Section 8.3) where one starts with a mental construct such as “witchness”, and incorrectly assumes that if there is a “property of being a witch” there must exist an object with that property—and happily goes on a witch hunt.
We have already given two toy examples of this—the witch hunt for
random numbers in a list of integers (
Section 2), and the “concrete example” in
Section 5. In the latter, the high entropy of a shuffled deck miraculously collapses—by just looking at the deck—to the the minimal entropy of a virgin deck (1 in our count scale, 0 in the conventional log-count scale). No amount of torture will extract from that deck a confession of
its current entropy, since there is no such thing
in the deck itself.
Here we shall give, as a more detailed example—a streamlined version of that proposed by Paul and Tatiana Ehrenfest as representative of the
fluctuations paradox [
25].
Consider a row of 100 checker pieces, or tokens, but white on one face and black on the other, and a bingo machine from which at every shot one will obtain one at random of 100 balls numbered 1–100, to be announced and immediately placed back in the basket. An ur-state of the row is any specific configuration of face colors (black and white) for the tokens; there are thus different ur-states.
Initially, all 100 tokens show white faces. This information uniquely characterizes the system’s state, and so this state’s entropy is 1. Balls are drawn sequentially, and, every time ball n is drawn, token n is turned over (or “flipped”). The row will display an increasing number of black tokens, and soon some black tokens will start to turn white again. When black and white tokens are close to an equal number, the frequency of black→white transitions will approximately match that of white→black ones, and the white:black ratio will be dynamically maintained at approximately 50:50, where the entropy is maximal. While, as we have seen, there is only one configurations showing no black tokens, there are configurations with a 50:50 population! Small population fluctuations about the 50:50 ratio are common, and thus corresponding departures of entropy from that ceiling value of , or “entropy fluctuations”, are common.
However, on what conditions? Suppose that instead of 100 tokens in a row we had a square of one-million by one-million tokens (a trillion in all) displayed on a screen. For comparison, an ordinary TV screen has only about 1000×1000 pixels; this number is chosen to be large enough that one can barely make out the individual pixels. Then in practice, when viewing our entire 1,000,000×1,000,000 screenful of tokens, we won’t be able to distinguish configurations that differ just by the color of a few individual tokens, since from that distance we will have a slightly blurred picture! And the value—in terms of information conveyed—of a blurred picture is inversely proportional to the amount of blurring—that is, the
number of different fine-grained pictures that in effect have been confused with one another by the blurring. This is indeed the
entropy—or, with Clausius original term (cf.
Section 4), the “transformation contents” of the blurring transformation.
In spite of the blurring, all is not lost. The overall intensity of black on white scattered over a surface is additive. In half-screen printing—that fine mesh of variable-size dots barely perceptible in the texture of a newspaper picture—a number of black dots of a certain size over an otherwise white area, collectively give the visual impression of a certain level of grey. Moreover, that level is something we can easily perceive, or measure with a photocell; this will provide an indirect way to estimate at least the number, if not the precise position, of black tokens present in a certain area.
As a result, we do receive some information, and the entropy of the picture we see is less than that of knowing that “it could be just any picture”. In effect we are allowed to peek—though through blurred glasses.
Returning to our row of tokens, let us suppose that the whole updating process is taking place in a separate room, out of my sight and hearing. There tokens are flipped according to “bingo calls” like “Flip token 7!”, “Flip token 75!”, etc., regularly spaced one second apart. Suppose further that after a while I am invited to bet a dollar on the current token configuration, with odds 1:n—that is, I get n dollars if I have hit on the right configuration. What value of n should I insist on for the game to be fair?
With this picture in mind, let us consider the following three scenarios:
- (i)
Internal entropy. (a) I am given the initial token configuration, (b) I can hear the bingo calls through an intercom, and (c) I am willing and capable to update my mental model of the process according to the information given to me.
Then anything above one dollar will be reward enough, since I will be able to track the process in full detail and on my own. That will make mine a sure bet! No needs to bother entropy.
Remark that the law of this dynamical system—the entire sequence of flips announced to me—is deterministic and invertible. To see this, suppose that my friend Elsie wants to “predict” the whole sequence of token configuration backwards, starting from the last configuration, using only the laws of the dynamics that had been applied to go forward. To this purpose I give her the sequence of bingo calls as it had been given to me; this sequence, together with the provision that each called token is to be flipped, represent the entire law. Starting with the last configuration as an initial state, she applies that sequence of instructions, but using the inverse operations in the reverse order. Now, the inverse of “flip” happens to be again “flip”, so Elsie will progressively unflip each token that had been flipped, finally holding in her hand the initial configuration as reconstructed from the last and the law.
- (ii)
Honest entropy with an external component. In this scenario, I cannot hear the contents of the bingo calls—but I can still infer when each is made by looking at my watch.
In this case, after one step the choice of possible configurations jumps from 1 to 100; in fact, I know that one token has flipped, but I don’t know which. Note that the law is deterministic for the guy who flips the tokens in the other room—it is being “dictated” to him by the bingo caller and thus he has no choice. However it is nondeterministic for me, as I don’t hear the numbers called.
On the second step, in one case out of 100 (but I do not know which) the caller will draw the same number as on the first step, in which case that token will get unflipped and we go back to the original configuration—a single ur-state. In the other 99 out of 100 cases a new token will be hit, so the result will be two black-faced token—and of distinct configurations like that there are 100×99/2. By taking the geometric mean of the two situations, weighted respectively 1 and 99, we get an equivalent ur-state count of , and so forth, step after step of blind reckoning with more and more complicated expressions for the expected equivalent count, converging to an asymptotic value of for , corresponding to an expected number of 50 black tokens.
Note that even though the actual number of black tokens may go up and down, the above sequence of entropy values, relating to my state of knowledge, is strictly monotonically increasing, with no fluctuations whatsoever.
- (iii)
Partial peeking. In this last scenario, I do not want to do all those tedious computations to determine the extent of my uncertainty. Fortunately I discover that in the wall between the two rooms there is a groundglass window. The blurry view through it does not let me distinguish the individual tokens, but it lets me estimate the number of black tokens by the level of gray of the row as a whole seen as a blurry patch. Then, by monitoring this number in real time (as “parasite” of the actual game being played in the next room, I can enjoy some of it without having to perform a simulation of it myself), I can infer the number of token configurations corresponding to the current estimated number of black tokens. Depending on the specific tokens affected step by step, this number is quite likely to display fluctuations about the general trend, in violation of the strong second law!
The entropy obtained in the third scenario is not, of course, a form of what we called “honest entropy”; here I peeked! It is an example of what is commonly called
coarse-grained entropy to distinguish it from
microscopic entropy (which, as already mentioned, roughly corresponds to what we called
internal entropy). Also see the end of
Section 7.1.
8. Shannon’s Formula Deconstructed
Had we but world enough, and time, This coyness, Lady, were no crime
—Andrew Marvell (“To his coy mistress”, ca. 1650)
Here we shall start with the standard entropy formula in Shannon’s form (
4),
which, as we have seen, drops the “physical legacy” dimensional coefficient
k of Equation (
2), and will deconstruct it in a number of steps in order to subject it to “structural analysis”.
Though nice and compact, the Shannon formula for entropy is not very transparent to the uninitiated.
- 1.
Why the leading minus sign, since probabilities are positive?
- 2.
Where does the logarithm come from?
- 3.
How come the quantity appears two times in the formula? Does it play different roles in the two places?
- 4.
What is all this probability stuff?
Finally,
- 5.
What does the whole thing mean?
Among other things, we will argue that, after peeling off the convenient but inessential logarithmic wrapping, this formula is a generalization of a count, and as such is drop-in ready, as it were, for replacement of the entropy-as-a-count used in the arguments of the preceding sections.
At the end of the day, we will conclude that the structure of that formula was sound—though a bit baroque—and that most of the pieces that we had taken out to examine can go right back in.
As a first thing, the naive may wonder where that minus sign might have come from, since one is dealing with positive quantities throughout. Let us acknowledge that this is a purely
graphical convenience. After passing through the logarithmic filter, division become
subtraction and inverse become
opposite (or the “negative” in casual talk). When
is written in display style it appears as
, and thus is ugly and wastes vertical space—even more when we substitute for
p a taller expression. Thus the minus sign does not indicate something conceptual that you may have missed, but is merely a spacesaving device. If we waive this “convenience”, Equation (
17) becomes
with no minus sign! At this point, one is immediately reminded that, if
is a probability distribution and
a random variable over
i (a more modern term is “random
function”) then
is the
expectation (or
expected value) of
x, denoted
. In our case, Equation (
18) can be rewritten as
The argument of the expectation is, as expected (no pun intended), a random variable, spelled in a customary shorthand; the full spelling is the expression in curly braces. The value of the expectation is the arithmetic average of (the values of) the random variable in the argument. Next, we will discuss the meaning of that random variable.
8.1. Equivalent Count
We have seen in that in Equation (
19), while
p is a
probability distribution,
is instead a
random variable over the same set of outcomes (the latter labeled
). With the same shorthand,
is also a random variable; the fact that its
value for outcome
i happens to equal the
inverse of the
value of the
probability weight of the same outcome, is not a mathematical tautology (like “
is course the inverse of
x—
by definition”) but a
coincidence—an artifact arising
by construction in making up that particular random variable.
Imagine an urn containing n marbles which may have different colors, red, green, blue, etc., and count the number of marbles of each color, Not being interested in the total number n but only in the fraction of marbles of each color, we rewrite that fraction as a probability distribution , where . The value n is thereby lost.
At this point we assign to the marbles a posteriori a new property—let us call it equivalent count—besides their color. Remark that this property will not depend on the physical features of a marble per se—color, radius, mass, or even where it is in the urn—but only on how many marbles of the same color there are in the urn relative to the total number. As a property “of a marble” it has a peculiar behavior. For example, it will change by the simple fact of adding a new marble, of any color, to the urn, without touching the original one. Even if, as part of a nationwide lottery game, the “urn” consisted of the joint contents of two widely separate containers, yet making a minimal change to the contents of one container will affect the equivalent count of a marble in the other container, even though no physical interaction between the two containers has taken place.
In our case, that “spooky action at a distance”, as Einstein might have called it (cf. [
26]), has to do with the
self-referential nature of the construction of the “equivalent count” random function. In effect, the latter is a “property” of the physical marble only insofar as it is a property of the
entire distribution, which in turn is an expresson of the joint makeup of the two containers. (We had the same issue with the prom photo example of
Section 5.) This “entanglement”, as it were, takes place not in the concrete world, but only within the abstract construct of a distribution—which
by definition changes
as a whole whenever the makeup of the urn is altered.
If the ’s happen to be all equal, then , where n is the number of outcomes in the distribution of which the are the weights. Intuitively, if the size of a pizza slice is one-third of the whole pizza and the pizza has been cut into equal parts, then the number of slices must be three. We can think of the equivalent count of a single slice of any size (independent of the sizes of the other slices) as the number of slices of that size which could be cut out of the whole pizza, counting in that number also the fraction of a slice that might be left as a “remainder. Thus if we have just two slices, of sizes respectively 1/3 and 2/3, the equivalent count of the first slice will be 3 and that of the second 1.5 (that is, we can only get one-and-a-half slice of that size from the whole pizza).
It is clear that
p and
, while numerically just the inverse of one another, stand for quantities that are of a rather different nature. To highlight that, it will be helpful to give the random variable
equivalent count, born
, its own symbol
v; that is,
.
I’ve come to believe that much of the confusion, uneasiness, and controversy surrounding entropy hinges on that disturbing self-referential nature of “equivalent count”.
The magic allure of self-reference has been extensively and gloriously illuminated by logician and magician Raymond Sullyvan (my vote for a “Unesco World Heritage Unique Human Resource”) in his popular books—for one,
Forever Undecided: A puzzle guide to Gödel [
27].
8.2. Why Logarithms?
From the viewpont of the above subsection, the entropy S of the urn is the log of the mean equivalent count of a certain kind of outcome—in our case, marble color (the mean being taken over all individual marbles).
What happens if we strip the log from
S by taking the exponential of the whole expression—thus obtaining the quantity
? Use of the logarithm is very convenient in practice (and, as we stress below, also has an important conceptual role in the physics of information), but is mathematically irrelevant. It just lowers by 1 the rank of arithmetical operations: a product turns into a sum, a quotient into a difference, a power into a multiple, and, as we have seen, an inverse into an opposite. What is important now is that a
geometric mean turns into an
arithmetic mean. If we “undo” the log in
S we get back the geometric mean. Thus
V can be rewritten as follows (where we use the variable
v for the equivalent count
as introduced at the end of
Section 8.1):
where the pre-subscript G reminds one that what we intend is the
geometric mean.
We shall call
variety the quantity
V introduced above. Then Equation (
20) reads as “The variety of a distribution is the (geometric) mean of its equivalent count”. If we went whole hog and used
self-variety as a term for the equivalent count
v, then we would notice the tautological equivalence of the above sentence with a better known sentence, namely, “The information (or entropy) of a distribution is the (arithmetic) mean of its self-information
”.
The term “variety” in this general context was introduced by Ross Ashby in 1956 [
28]. Even though his use of the term with the meaning of “simple count” rather than “equivalent count” is today deprecated (see
Section 8.3), he clearly makes the point that reporting a count as such or through a log of it is a practical rather than conceptual issue: “Variety can be stated as an integer, ... or as the
logarithm to the base 2 of the number, i.e., in bits.”
More recently, and by wide consensus,
variety has been reintroduced—with the present meaning of “mean equivalent count”—as one of the most useful indices of diversity [
16,
29]. This mostly in biology, taxonomy, paleontology, ecology, economics, cataloging and inventorying,
etc. To quote from Straathof’s abstract [
30]:
The antilog of Shannon’s entropy is a suitable index of product variety for three reasons. First, for symmetric product types it is equal to the number of product types. Second, disaggregation of the underlying product set always leads to an increase in measured product variety. Third, the introduction or disappearance of a marginal type does not cause a discrete change in the variety index. These properties hold for a class of weights that includes, but is not limited to, frequencies.
The preference in those areas for this “antilog of Shannon’s entropy” rather than Shannon’s entropy itself—in other words, for dealing with an equivalent count rather than the log of this count—seems obvious to me. In those applications, one has to materially go through those things that are counted (the items of an inventory, the species of a certain genus, etc.), and the resulting number is on a human (or computer) scale, because one is counting tangible objects—whether “bodies”, pieces of a data structure, or computational events.
In physics and in information science, on the other hand, one is often counting states of a system, rather than pieces of it, and that grows exponentially with the number of pieces. For a mole of gas, with molecules, in ordinary conditions one can have some states! Physicists can touch with hand a specific ur-state—and, even that, as a norm, for just a fleeting moment: water molecules collide a trillion times per second! As the Greek philosopher Heraclitus ( BC) put it, “You cannot step twice into the same river”. One can deal with the entire collection of ur-states through a symbolic object—a formula or a numeral. For example, the above number’s decimal representation, which is already a logarithmic compression of a tally count (the scrawled daily marks on the wall of a prisoner’s cell) is “only” a trillion trillion digits, thus large but not astronomical. However, one can never see in one’s laboratory or explicitly represent in one’s computer all those states, simultaneously or even just sequentially. This number is hyper-astronomical: for comparison the total number of elementary particles in the universe is estimated to be a “puny” .
To paraphrase the quote at the beginning of this section, the physicist could well tell the catalog librarian: “Had we but world enough, and time, your spurning of logarithms, Lady, were no crime!”
Beside the practicality of Marvel’s entreats to his coy mistress (the poem’s point is that when he was finished counting her beauties they would both be too old to be able to enjoy them), there is a strong physical reason for using a logarithm when counting states of a distributed system. This log essentially counts the number of material parts of the system—which are all physically present at once. It measures the amount of the physical resource available to generate states with—the quantity of state-making stuff. On the other hand, the state set—the collection of all possible states of an extended systems is clearly only a potentiality—a mental fiction. As we have seen, not even a microgram of matter will be able to go through all its possible quantum states during the age of the universe, and at any moment will be in only one of them.
We have seen that, in its standard form, entropy uses a logarithmic scale just as a convenient wrapper for the more intuitive variety (our “mean equivalent count”), and that the leading minus sign in its formula is graphical space-saving device made available by the presence of the log.
Moreover, in any large multicomponent system—be it a computer or a microgram of matter—even a tiny part of it won’t be able to go through even a tiny fraction of its state set before the least interaction with the rest of the world makes its current state, its state set, and its very dynamics obsolete.
That is illustrated by Borel’s memorable example [
31], of how a tiny displacement of a tiny mass on Sirius will totally disrupt, in a few collisions’ time, the trajectories of gas molecules in a sample on Earth.
We have also seen that, when we partition a collection of marbles by, say, color, and look at the resulting color classes, a more informative measure of the collection’s variety than merely counting the classes is indeed their mean equivalent count. Giving weight to classes is generalization that one “cannot refuse”!
In the next subsection we briefly deconstruct probability.
8.3. What is Probability?
In Gibbs’s and Shannon’s formulas above, the letter p, which we used for a generic “share” or “weight,” actually stands for probability, and a collection of ’s with and is accordingly called a probability distribution.
But what is probability? A serious problem was raised by Bruno de Finetti—economist, mathematician, and a pioneer of neo-Bayesianism. We shall see that in phrases like “this face of the die has probability 1/6”—as well as “this brick has entropy 18” or “7 is a random number”—do not literally mean that “having probability 1/6”, “entropy 18”, or “being random” are intrinsic properties of the named objects. They are at best shorthands (and as such often useful) for properties of certain viewpoints or decisions of an
external nature. It is in this vein that on the first day of his probability lectures Prof. de Finetti would shock his students with the wake-up call: “PROBABILITY DOES NOT EXIST!” And he would go on:
The abandonment of superstitious beliefs about the existence of Phlogiston, the Cosmic Ether, Absolute Space and Time, ..., or Fairies and Witches, was an essential step along the road to scientific thinking. Probability, too, if regarded as something endowed with some kind of objective existence, is no less a misleading misconception, an illusory attempt to exteriorize or materialize our true probabilistic beliefs.
However, if entropy is supposed to be a numerical weight of a probability distribution, and
probability does
not exist, then entropy is indeed in big trouble! A contemporary apologist [
32] tries to make de Finetti’s slogan more palatable by explaining: “[What he means is] that probability does not exist in an
objective sense. Rather, probability exists only
subjectively within the minds of individuals.”
Good try! (I am not being sarcastic.) The issue is, were we just looking for probability in the wrong material object—say, this six-faced ivory die instead of the gambler’s brain? No! The problem is not where we were looking, but what we were looking for.
Probability is not a fact, but a working hypothesis—the major premise in a syllogism.
Plato having said “If (major premise) all men are immortal—and (minor premise) Socrates is a man—then (conclusion) Socrates is immortal”, on Socrates’ death his wife Xantippe can tell Plato, “I know for a fact that Socrates was a man—your minor premise was right. But Socrates is dead now—your major premise must have been wrong!”
In other words, Plato did not dictate “All men are immortal (full stop) and therefore Socrates (who’s a man) is immortal (full stop)”, but just proffered a noncommittal “If ...then.”
Jaynes paid a tribute to physics when he called his lifetime project [
33]
Probability Theory: The Logic of Science. He had previously written a paper that carries a more
general title, “Probability theory as logic” [
34]. However, within this more ecumenic framework, what distinguishes probability from ordinary logic? I would have added “Probability theory as logic
in parallel”.
The idea is that the “probability of an event” is a specialized kind (not just a vague analog) of a syllogism machine—let us call it ParSyll—which takes as arguments a probability distribution P for the major premise and an event x for the minor premise, and returns as a conclusion a number . Thus, .
The internals of this machine work as follows. The major premise P is a lookup table—a list of primitive objects called outcomes each accompanied by a numerical weight. The minor premise x—an event—is any collection of outcomes—typically specified by some criterion related to the problem at hand. Given the set x, ParSyll breaks it up into its elements and looks up in P each of these elements separately and independently, adding up the resulting weights as they come. Since the order of the addends is irrelevant, the lookups (each of which is in essence a “microsyllogisms”) can be performed in any order or concurrently, and thus “in parallel”. The total accumulated weight is output as a conclusion—the probability of that event.
A nurse is filling out a form for a patient who happens to be an event: “Eye color?” “Brown!” “Height?” “Five foot nine!” “Probability?” “How would I know?” “You’re right, I have to look it up in my database. One moment ... today your probability is 1/4!” Note the different direction of information flow for eye color and probability.
Jaynes calls “mind projection fallacy” the “confusion between reality and a state of knowledge about reality” [
33,
34]. “The belief that probabilities are realities existing in Nature is pure mind projection fallacy”, since a probability “is something that we
assign, in order to represent a state of knowledge”, while counts and frequencies are “factual properties of the real world that we
measure or
estimate” (emphasis mine).
This confusion is certainly facilitated when a verbal shortcut—such as using “my” in different senses (cf. the climax “my nose, my dog, my son, my wife, my job, my country, my God”)—crystallizes into a mental groove.
The “ambition prize” for mental projection fallacy (the philosophical term for this is reification, that is, “turning a mental construct into a thing”) must be given to Anselm of Canterbury’s ontological proof of God’s existence (1078): (major premise) God is a being than which nothing greater can be conceived; (minor premise) One can conceive of a God A existing in one’s mind, even if one denies the existence of this God A in reality; (reduction ad absurdum) Then one can conceive of a being B just like God A but having the additional property of existing in reality; but (in contradiction to the minor premise) that being B would be even greater than God A, (conclusion) Therefore, God exists!
a colleague: And, if I may ask, where did get your major premise?
The answer to the above question, or the equivalent “And where did you get your probability distribution?” can only be “I made it up, to put into tentative use and see how well it works.” “What do you mean, ‘you made it up’; didn’t you use the best of your knowledge to fabricate it?” “Not the best of my knowledge—that might be the case, but is irrelevant. I put into it some specially crafted, pointed working hypotheses, to see where they would lead. Or maybe I put into it a colleague and competitor’s presented data (about which I am suspicious), to see whether they would lead to unbelievable conclusions.” “If my probability distribution works well, whether to make earnest predictions or to expose a colleague’s fraud, I may encourage others to use it.” This is the gist, and the gift, of MaxEnt.
It is well known that the exercise of logic never adds to our knowledge: its role is to make a certain aspect of that knowledge clearer or more explicit, while keeping all the rest conveniently out of our sight.
If the machinery of probability is just “logic in parallel”, then using it will never give us more than is contained in the probability distribution we started with. So the question arises, “When (in order to use the convenience of that machinery) we turned our initial description in terms of more-or-less vague constrains into a probability distribution—something more handy to circulate and to play with—are we sure that we didn’t throw out at least some of the baby with the bathwater?”
To skirt that dilemma, would it be possible, at least in principle, to skip the probability stage? To directly go from a description to a recommendation for action (say, to bet on a certain event), or to directly compute from a description of the initial state our best description of the final state? (Note that I leave open the possibility that such descriptions might not even be expressible as probability distributions.)
8.4. Nondeterministic Systems
With a
one-to-many (or
nondeterministic) law, a trajectory may fork out into many branches. We have explicitly dealt with many-to-one laws, as in the Day 2 dialog and in
Section 7, but not with
one-to-many laws. In the two dialogs of Day 3 (
Section 6.6), we ascribed the de facto nondeterminism to external “perturbations”, not to the internal law.
One-to-many laws of a genuine internal nature are encountered, for instance, in automata theory. In physics and many other fields, on the other hand, one-to-many laws usually arise from an attempt to incorporate (for theoretical or practical convenience) into the internal laws of a nominally self-contained system the effects of small pertubations of an external nature, especially when the latter are statistically predictable—as in Boltzmann’s well-known gas transport equation.
We could have easily added a third column to
Table 1 to account for formally
nondeterministic dynamical systems. However, while its contribution to the top row (internal entropy budget) would have been “
”, and thus different from the “
” of the second column (invertible), the
total would have been the
same for both columns. Thus a third column for one-to-many laws wouldn’t have introduced a very informative distinction: internal nondeterminism and external noise are hard to tease apart in theory as well as in practice.
In physics, this ambiguous aspect of nondeterminism is always lurking in the background, when it is not stomping in the foregroud. All this, while exciting in itself, is only marginally relevant to the present exploration of the “core meaning” of entropy, and we shall not delve into it here.
8.5. The “Many-scenarios Interpretation” of Probability
A the end of
Section 8.3 we actually raised two questions, namely,
Let us go (say, via MaxEnt) from a description—in terms of facts stated or constraints given—to a probability distribution. Is such a conversion information lossless?
Does a description in terms of facts stated or constraints given not constitute by itself a bona fide major premise? Moreover, does the passage of time for a dynamical system, together with a list of the random disturbances affecting its internal dynamics as well as the degradations externally introduced by our abridged bookkeeping—does all of this not constitute by itself a minor premise? If so, can a plain—though possibly gigantic—syllogism not derive the desired conclusion from those major and minor premises?
Before tackling the above two questions, let us dwell first on a difficulty that affects both. Namely, many descriptions are too vague to be usable
by themselves as a major premise or as a recipe for a probability distribution. For example, if you intend to use the MaxEnt principle, what range of probability distributions may satisfy a constraint such as “Tomorrow is going to be much warmer?” Approaches like Zadeh’s
fuzzy logic [
35], that quantize warmness as, say, lukewarm, warmish, warm, very warm, and hot, haven’t made inroads in spite of their superficial appeal—and not much else seems to be on the horizon.
I will dispose summarily of Question 1, unfortunately because at the moment I am not quite sure of the answer. What first comes to my mind is, “Can one go back from a probability distribution to the set of constraints that generated it via MaxEnt? (Or at least to an acceptable equivalence class of constraints?)” If one could do that in a systematic way, then the two formulations would be equivalent, and the transformation from one and the other (and vice versa) would be invertible and thus information-lossless.
In this repect, let me quote Jaynes [
36] (the emphasis is mine):
Fuzzy Sets are (quite obviously, to anyone trained in Bayesian inference) crude approximations to Bayesian prior probabilities. They were created only because their practitioners persisted in thinking of probability in terms of a “randomness” supposed to exist in Nature but never well defined; and so concluded that probability theory is not applicable to such problems. As soon as one recognizes probability as the general way to specify incomplete information, the reason for introducing Fuzzy Sets disappears.
The ambiguity here is in that “specify incomplete information” clause. Does it mean, as Jaynes seems to indicate, “completely capture” the incomplete information, or simply “do the best we can with the given information, even though we have no way to use all of it?” In the “much warmer” example given above, it seems to me that all that one can consistently use is the constraint “greater than”, while the “much” qualifier, without further qualification or some usage statistics, must unfortunately be discarded. This is the case even though we feel that “much warmer” somehow conveys more information than just “warmer”.
Coming to Question 2, just as we started—à la Boltzmann—with entropy as a count, now let us start—à la Laplace—with probability as a ratio of counts, i.e., favorable over total. Here there is no need to externally assign different weights to different outcomes via a probability distribution, since the weight of an outcome is a naturally defined internal quantity—simply the number of representative points—the “favorable count”—of that outcome. The outcomes thus make up a multiset, and the events are all the possible subsets of outcomes.
A multiset is like an ordinary set, except that any element may appear in it in multiple instances (rather than a single one). Let X be the collection of all these “sets of clones” or outcomes. If is the total number of elements in the multiset (counting each outcome x with its multiplicity ), then the collection is evidently a probability distribution.
In the simplest case, with just two outcomes, 0 (for “heads”) and 1 (for “tails”), the four possible events , , , and —representing respectively “neither heads nor tails”, “heads”, “tails”, and “heads or tails”—have counts of 0, 1, 1, and 2, which, divided by the number 2 of outcomes, yield “probabilities” 0, , , and 1. However, this model of an abstract ideal coin becomes instantly useless as soon as we want to use it for a real coin—no matter how ever-so-slight its bias may be. As they say, the model does not “degrade gracefully”.
Let us take a more flexible approach. Consider the collection
P of all Python programs consisting of no more than two hundred characters and such that at each press of a button each of these program will output (say, within a thousand machine cycles) a single binary digit. Let the programs in this well-defined collection be sequentially numbered
, where of course
N is a hyper-astronomical number. Let us run all these programs in parallel, and collect into one set the
N binary digits generated by one button press, each digit tagged by the number
n of the program it came from. Approximately half of those digits will be 0’s and the other half 1’s. Now just ignore the tags, and you will have a
multiset with just two outcomes, 0 and 1, one being present in
(
) copies and the other in
(
) copies. We offer this deterministic piece of machinery as a model of a (non-deterministic)
coin-tossing machine. To model coins with different biases, just tinker with this collection
P of program by throwing out of it a number of its elements.
Unless you know well what you are doing, you will have a hard time getting out of the decimated collection an expected value other than one close to some special value such as 0, 1/2, or 1—just as with an
ordinary coin (have you
tried to machine a coin that will reliably give heads 3.14% of the time?). Of course, by running this astronomical number of programs
one-by-one and selectively discarding a fraction of them according to whether their output is 0 or 1, you can “easily” make this coin tosser come up with any probability in between—or behave deterministically for you while still remaining random for the noninitiated. Physical situations of this kind are wonderfully discussed in Jaynes’s book [
33].
Going back to the statement of Question 2, that gigantic syllogism’s conclusion may well turn out to be a gigantic table with 0 and 1 values attached without apparent rhyme or reason to the zillion individual outcomes or ur-states that make up the event of concern—no probability distribution was involved! Then it is up to us to take the responsibility—as a single optional final step—to summarize that table by counting the 1’s for each event and using those numbers as the weights of the respective events.
That is no worse, and possibly better, than going through the probability-distribution bottleneck, since in that way we keep all of the information we have till the end (that is why this approach is so cumbersome) and then only at the last step throw away what we sensibly can. In the traditional approach, we jettison most of what seems irrelevant (or just too unwieldly) before take-off; that makes for a lighter flight, but will it take us to the same destination?
If you are worried that this “many-worlds” approach may still not yield enough randomness for the coin, I can throw in more layers of “super-worlds” (this is a mental experiment, after all) each having different rules for generating its own lower-level many worlds, and so forth ad infinitum. I suspect that the limit of this process, which still uses purely deterministic resources at every level is the only definition of randomness that a Laplace would have been happy with.
9. The Dynamics of Entropy
When we say “the entropy of a black hole” or “entropy of the market” we must mean something like “the entropy of (a probability distribution of (quantum states of (...of (...of (...of (a certain kind of (black hole))...))))). All of the “of’s” in this hierarchy are like different levels of civil servants with technical roles that are useful but not necessarily very transparent. Moreover entropy, as a function that maps a descritpion to a count, has no initiative—it “just obeys orders!” A policy-maker must do a bit of homework up and down the hierarchy to figure out the precise effect of an order given from the top of the hierarchical chain.
(Chains of command of this kind beginning with “entropy” are employed in all sorts of disciplines. Some are short and widely used, and have developed standards of usage and an agreed upon lingo. So, when we say “The entropy of a Valentine message is less than a bit per typed character” (think of the endless repetition of “love” and “dove” and “blue” and “you”), everyone in the data transmission business will understand that this entropy is not about a single character, word, or message, but, skipping several levels of the hierarchy, is about the language—the vocabulary, the style, the mannerism—used by Valentine chatter as a whole.)
Chains headed by “entropy” are less transparent in other situations. In addition, there may be many chains of the form “entropy of ...〈 something〉” where the last link, “〈something〉”, is the same for both, but the internal makeup of the chain is different. So asking “Mack, what’s the entropy of that brick?” may get you surprisingly different responses even though they all have “Mack” and “brick” as first and last link.
The problem all started with Clausius, who, as we have seen in
Section 4, was careful to coin for the quantity he had discovered a new-greek neologism that could hardly be used for anything else. When he spoke of the “entropy of a transformation” he had in mind not a function but some sort of fluid that had coursed in or out of a certain object subjected to a certain treatment or “transformation”—or even had been
generated within it in the course of the treatment. In that context, there was only one thing that could be meant by “a certain amount of entropy”.
Luckily for Clausius’s fame, entropy was eventually found to be not a physical substance but an abstract concept of
enormous generality—a
counting concept (cf. the
Boltzmann entry in
Section 4 and the Shepherd’s Parable in
Section 7.4). Consequently, today the kinds of things that have a meaningful entropy associated with them are legion, and a
single thing may have associated with it
several entropies—which quantify different aspects of it or different levels of description.
Certain of these new uses of entropy operate at a more abstract level than Clausius’s original construct. However, they still play essentially the very function which Clausius originally envisaged for his entropy, which is as fundamentally important today as it was then. Namely, to determine whether there are states of a dynamical system that are so easy to reach from a given state that the transition from the latter to one of them can occur just about spontaneously, and whether there are states that are instead virtually unreachable. Similarly, to determine under what conditions a chemical reaction will run in one direction rather than the other, and what can be done to make this reaction faster and more efficient, or, on the contrary, to inhibit it. All that is of ultimate importance in chemistry, biology, materials science, energy conversion, and so forth. Expectedly—but regrettably—it is in this area that much confusion arises.
While the objective in those areas is to determine, at least in a qualitative way, the dynamics of a system by discovering which state transitions are more likely, the strategy to calculate this has some affinity with a static variational method. That is, (a) imagine a number of possible states and the transitions between any two of these states, (b) compute the entropy difference attached to each of these transitions, and then (c) consider most likely those transition that are accompanied by the largest entropy increases. All of this may sound like wordplay unless one understands the underlying linguistic ambiguity. When people speak of a certain system state here, they actually mean a broad description, and a system is (tautologically) more likely to be in an ur-state matching a certain description if this description is broader, that is, encompasses a larger number of ur-states.
Naively, one may imagine that a transition from one description to another reflects in some way an actual transition of the system from an
ur-state to another according to the system’s internal dynamics—but this need not be the case! We have hinted at this at the end of
Section 5. Here, we shall illustrate this in more detail by a parable:
A precious gold coin has been stolen from me; through an anonymous phone call I learn that the coin may have been hidden in one of numerous sacs of base-metal coins stored in a customs warehouse. I go there and ask to go through the contents of the sacs to retrieve my gold coin. Given the vagueness of the hint and the scale of the requested operation, to the customs officer this seems a frivolous request, but he eventually allows me to go through one single sac of my choice. I should mark that sac now, but come back in the morning for the actual search, since he wants to have with him a witness to the operation. The sacs come in all different sizes. Not having any idea of which sac my coin might be in, I of course choose the largest.
To better hide the coin, unbeknownst to me and the officer, the thief, who has reasons to fear curious eyes, had been randomly moving it every night from one sac to another. I come in in the morning; officer and witness are already there. Before I open the marked sac—call it sac A—a warehouse employee remarks that a pile of several more sacs of coins had been found in a corner. One of them—call it sac B—is much larger than sac A; I ask—and am allowed—to switch my choice to sac B. I riffle through the sac. Unsurprisingly, given the number of sacs, the coin is not there. End of the story.
Now, I shall call “ur-state” of a coin (“microscopic” state) the exact physical spot where the coin finds itself, and “state” of the coin (“macroscopic” state) the sac in which the coin is contained (as far as I am concerned, that level of detail is all that that matters). Based on the information I had at the moment, the most likely state for the coin to be in, the evening before, was sac A; by midmorning, it had moved to B; and by the end of the morning, it had moved back to A or to some other sac in the newly dicovered pile (why?). As for the coin’s ur-state, it had been shifted during the night from a position inside some sac C to a position inside a sac other than B (how do we know?). That’s it!
There was indeed a correlation (an implication, in our case) between the coin’s internal dynamics—that of its ur-state—and that of its state: the coin’s microlocation implies what sac it is in, while the converse is not true—being in a certain sac says nothing about where in the sac. On the other hand, in our scenario the correlation between the internal dynamics and that of my “best-choice” sac (based merely on sac size) is very shallow: when this choice moved from sac X to sac Y, that didn’t mean that the coin itself had moved from a position inside X to one inside Y. In our contrived scenario, my best-choice sac changed quite independently of the movements of the coin itself!
In the combinatorics of large systems, there is often a much better correlation than this between microscopic and macroscopic dynamics. (More honestly said, we don’t even take into consideration a proposed macroscopic dynamics unless it is strongly implied by the microscopics—When it is dark, we look for the key only near a lampost; where else?)
Thus, in 100 coin tosses, the expected number of heads is 50, and even though it is in priciple possible to get as a result the ur-state “0 heads”, a state with heads is indeed overwhelmingly more likely. In the above gold coin example, if one sac was way larger than the aggregate of all the others, for that very “reason”(?) the coin would be virtually certain to contain it. You will agree that this “reason”—the argumentation used by entropy—is of a very different kind than “the coin is likely to be there because I put it there”.
You might conclude from all this that thermodynamics is but a collection of trivial tautologies—and you would of course be right. However, precisely that is what makes the laws of thermodynamics so universal and so useful.
10. Conclusions
Returning to the definition of
honest entropy in
Section 7.1 and its illustration by an executive/consultant/auditor contract, we have seen that the entropy “of a system” is that of this continually adjusted probability distribution representing the state
of a model. Every act of approximation, truncation, compression, erasure,
etc., that entails loss or discarding of information gives a
positive contribution to the system’s
honest entropy.
Negative contributions could only come from
peeking (which we have ruled out by contract; see
Section 7.5), or from losses of
internal entropy, which, as we have seen, can only arise from the possible
noninvertibility of the internal dynamics.
In a nutshell, if the consultant’s deliverable is thought of as the expected value of a system variable, then this deliverable will be deemed useless if not accompanied by a standard deviation honestly calculated according to an accepted discipline of propagation of uncertainty. With an appropriate scaling, the latter is what we call honest entropy.
A consultant need to be kept honest in spite of the obvious lure of claiming for his forecasts a smaller entropy burden than they actually bear. To this purpose the executive may occasionally use a more expensive auditor (peer review?) to go through the consultant’s books and verify that the latter’s entropy was appropriately adjusted upwards every time he took a shortcut.
If entropy is a way to quantify the “known unknowns” of a system’s state, usually representing the diffusive spread, the blurring, the unavoidable random error attendant to the use of a low-resolution model, what can one say about estimating “unknown unknowns”, that is, the unintentional systematic errors that a model may introduce? Entropy is silent on this. One may reasonably demand honest accountants, but for the latter estimate one would need imaginative, out-of-the-box, “creative”—as it were—accountants; and that is an oxymoronic job description that brings in drawbacks of its own! So we will leave that job to the most competent specialists of each discipline—peer review, again?
In Shakespeare’s memorable words,
- Glendower
I can call spirits from the vasty deep.
- Hotspur
Why, so can I, or so can any man; but will they come when you do call for them?
- Glendower
Why, I can teach you, cousin, to command the devil.
- Hotspur
And I can teach thee, cousin, to shame the devil by telling the truth. Tell truth and shame the devil.
—Shakespeare (“Henry The Fourth, Part I”, Act 3, scene 1, 52–58)
With the concept of honest entropy I tried to capture a physicist’s—but not only a physicist’s—idealization of something like a “best accounting practice” when making predictions. If you can, measure; if you can’t measure, peek. If you can’t either, all you can do is imagine and compute—but, if you care about your reputation, attach to your predictions their “honest entropy” margin of error.
If I had to explain entropy standing on one leg instead of writing a thirty-page article, I would ask, “Why is parking into a tight spot harder than coming out of it? Note that the process is mechanically invertible—for every path going in there is a well-defined time-reverse path coming out.”
answer: (I am dead serious) Because of the second law of thermodynamics—There are many more ways (greater entropy) for my car to be in the middle of the street than in a tight parking spot!
If then I had to explain honest entropy standing on one big toe, I would answer, with Joseph Stalin, “It’s not the votes that count, but who counts the votes!”