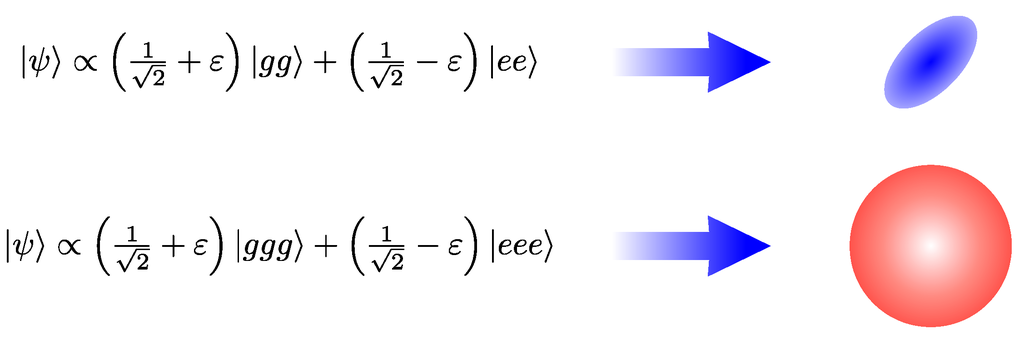Abstract
In this paper, we address the question: To what extent is the quantum state preparation of multiatom clusters (before they are injected into the microwave cavity) instrumental for determining not only the kind of machine we may operate, but also the quantitative bounds of its performance? Figuratively speaking, if the multiatom cluster is the “crude oil”, the question is: Which preparation of the cluster is the refining process that can deliver a “gasoline” with a “specific octane”? We classify coherences or quantum correlations among the atoms according to their ability to serve as: (i) fuel for nonthermal machines corresponding to atomic states whose coherences displace or squeeze the cavity field, as well as cause its heating; and (ii) fuel that is purely “combustible”, i.e., corresponds to atomic states that only allow for heat and entropy exchange with the field and can energize a proper heat engine. We identify highly promising multiatom states for each kind of fuel and propose viable experimental schemes for their implementation.
1. Introduction
The maser (microwave amplification by stimulated emission of radiation) was conceived of based on thermodynamic considerations [1,2]. In its micromaser implementation, coherent radiation is generated by inverted two-level (Rydberg) atoms that are randomly injected into a microwave cavity one by one [3,4,5]. For years, the focus of micromaser studies had been on its quantum-electrodynamics features [4,5,6,7,8,9,10,11,12,13,14,15,16], including its extensions to the cooperative regime of multiatom clusters that are simultaneously present in the cavity [11,12], until Scully et al. [17,18] revived the interest in the thermodynamics of such devices. They treated the atomic beam as a thermodynamic resource, since randomly-injected atoms, which are discarded (traced out) after they exit the cavity, constitute an effective reservoir (bath) for the cavity field mode (in the Markovian approximation).
The surprising finding of Scully et al. [17,18] was that a beam of three-level atoms with coherence between two of its levels may be viewed as a nonthermal, quantum-coherent (“phaseonium”) bath that, given an appropriate phase of the inter-level coherence, can thermalize the cavity field to a temperature , where T is the atoms’ temperature without coherence. The dramatic consequence of the higher temperature attainable by the cavity field owing to the phaseonium coherence is a transgression of the nominal Carnot efficiency bound in a heat engine, with the cavity field in the role of a working fluid (WF): if the WF undergoes a cycle where it is coupled to the phaseonium bath in one stroke and to a cold bath at temperature in another, then the efficiency bound of the engine satisfies , instead of . This landmark proposal has triggered a variety of proposals for engine schemes based on nonthermal baths that are capable of “super-Carnot” operation [19,20,21,22,23,24,25,26,27,28], among them engines fueled by a squeezed nonthermal bath [26].
Some of us have recently asserted [29] that machines fueled by nonthermal baths may be divided into two categories according to their operation paradigm:
- Machines of the first kind are those fueled by a nonthermal bath, such as a squeezed-thermal or coherently-displaced thermal bath, that render the WF steady-state non-passive [30,31,32,33,34,35,36]. Such baths change the machine into a thermo-mechanical engine that, unlike a heat engine, is fueled by both mechanical work and heat imparted by the bath to the WF. The Carnot bound may be transgressed in such machines at the expense of work supplied by the bath. However, their efficiency bound cannot be properly compared to the Carnot bound, since the latter is a restriction imposed by the second law on heat [37], but not on work imparted by the bath.
- Machines of the second kind are those where the WF is thermalized by the nonthermal bath, as is the case of an engine fueled by a phaseonium bath. Such a machine is a proper heat engine, but the ability of the phaseonium bath to thermalize the WF to a temperature elevates its Carnot bound above that associated with an incoherent bath at temperature T.
Intriguingly, in micromaser setups, a beam of multiatom clusters has been shown to thermalize the cavity-field WF in some cases [19,20], but also coherently displaces [21,27] or squeezes it [38]. This implies that the WF may receive both work (and thus, become non-passive) and heat from the bath. The cavity field may thus be the key ingredient in machines of the two kinds surveyed above. However, the criteria whereby atoms in a micromaser can fuel machines of either the first or the second kind are generally unknown, notwithstanding several recent results obtained along this line [19,20].
Here, we pose the question: To what extent is the quantum state preparation of multiatom clusters (before they are injected into the cavity) instrumental for determining not only the kind of machine we may operate, but also the quantitative bounds of its performance? Figuratively speaking, if the multiatom cluster is the “crude oil”, the question is: Which preparation of the cluster is the refining process that can deliver a “gasoline” with a “specific octane”?
To answer this question, we first derive (in Section 2) a master equation that governs the cavity field under the standard assumption of a short interaction of each atom with the cavity field, , where g is the atom-field coupling strength and τ is the interaction time. In this regime, the steady-state density matrix of the cavity field may only be a Gaussian state: thermal, coherently-displaced or squeezed [39,40]. This restriction is shown to imply (Section 3) that two- or three-atom clusters suffice for the preparation of all Gaussian states of the field, thus making larger clusters qualitatively redundant. Section 4.1 and Section 4.2 are devoted, respectively, to the classification of coherences or quantum correlations among the atoms that may be associated with: (i) fuel for machines of the first kind that correspond to states whose coherences displace or squeeze the cavity field, as well as cause its heating; and (ii) fuel for machines of the second kind that is purely “combustible”, i.e., corresponds to atomic states that only allow for heat and entropy exchange with the field. In both Section 4.1 and Section 4.2, we identify highly promising multiatom states for each kind of fuel and infer the best parameters relevant to the machine operation. In Section 5, we discuss the results and propose viable experimental protocols for their implementation.
2. Model and Effective Master Equation
We consider a micromaser-type setup wherein the cavity-field mode is the working fluid (WF) that is energized (fueled) by a beam of two-level atoms, which are injected into the cavity at random, Poisson-distributed, times [4,15]. In contrast to the standard micromaser scenario [5,41], the atomic beam is here assumed to be composed of N-atom clusters that are prepared in a controlled quantum-correlated (entangled) state prior to their injection into the cavity, where they interact with the cavity field simultaneously (see Figure 1). Yet, the replacement of single atoms by N-atom clusters does not change the basic premise of micromaser theory, whereby their random injections allow one to treat the atom clusters as an ergodic “bath” that is continuously coupled to the cavity mode, so that the latter is governed by a master equation (upon tracing out this “bath”) [5,15,41]. Nevertheless, we will show that quantum coherence or interatomic quantum correlations (entanglement) in the cluster may crucially influence the dynamics of the cavity field. Experimentally feasible schemes for the present scenario will be discussed in Section 5.
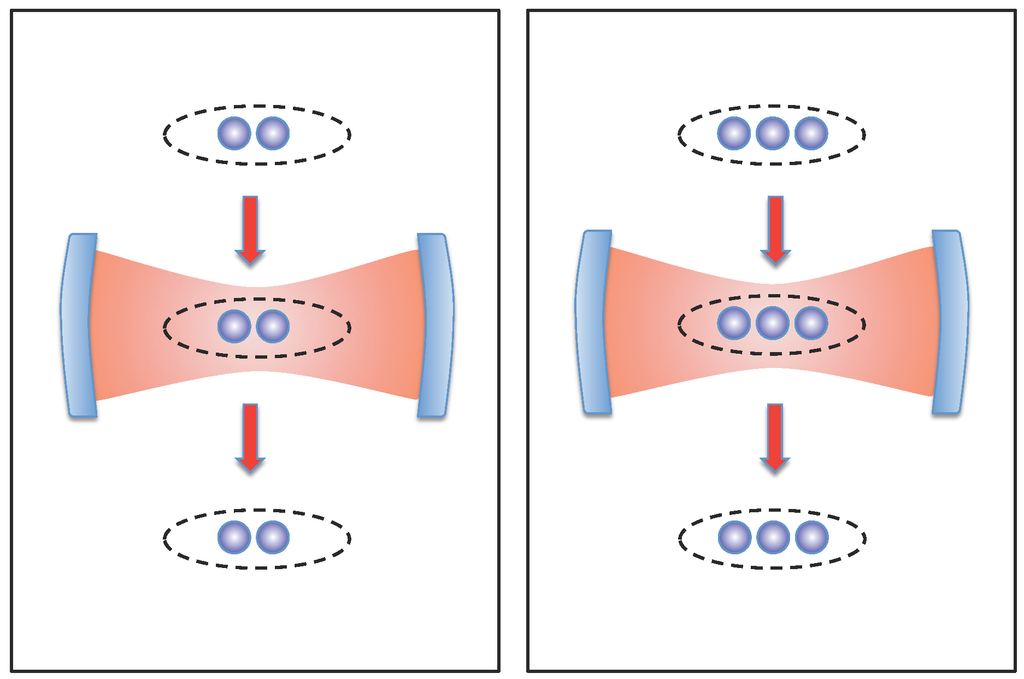
Figure 1.
A schematic of the two- and three-atom micromaser model, where clusters of two-level atoms are injected into a single-mode cavity repeatedly in a Poissonian random sequence. The transition time of the atoms through the cavity is much shorter than the cavity lifetime, atomic relaxation and dephasing times or the mean free-time between the interactions, so that there can be at most one cluster present in the cavity at a time. The cavity-mode steady-state crucially depends on the state of the cluster, as shown here.
In keeping with the standard assumptions of micromaser theory [16,41], we take the transition time of the atoms through the cavity to be short enough to neglect atomic relaxation and dephasing, as well as cavity loss, and to assume that there can be at most one cluster present in the cavity at a given time. Under these standard assumptions, we may derive a master equation for the dynamics of the cavity field.
The interaction of the atomic cluster with the cavity is described by the Tavis–Cummings model [42]:
where the atom, cavity and interaction Hamiltonians are respectively given by:
Here, are the annihilation and creation operators for the cavity field and are the z, raising and lowering Pauli operators for the k-th atom with . The atomic transition frequency is resonant with the cavity frequency . The interaction between the atoms and the cavity is assumed to be spatially homogeneous with strength g.
Under the foregoing assumptions, the combined system of the atomic cluster and the cavity field evolves unitarily during the short interaction time τ. The unitary propagator in the interaction picture can be analytically computed to second order in (see Appendix A, Appendix B, and Appendix C). Denoting the injection time of the j-th cluster into the cavity by , the evolution of the reduced density operator of the field mode, which is obtained upon tracing out the atoms, reads [43,44]:
Here, is the initial density operator of the atomic cluster, and is a superoperator that propagates the cavity state to . The atomic clusters arrive randomly at a rate p and pass through the cavity within a time interval of with a probability of . The field changes according to when a cluster is present and otherwise does not change at all, so that the overall change of the field state is:
For , we obtain the master equation:
which describes the Markovian dynamics of the single-mode cavity [5,20,21,22]. Here, we do not include the usual cavity decay term, in order to clearly identify the role of coherences for the field evolution, particularly whether it thermalizes or not, but it is straightforward to do so.
The master Equation (5) can be rewritten as:
where denote the matrix elements of . In the standard basis of energy-state products, the diagonal elements are the populations and the off-diagonal elements with the coherences or quantum correlations, respectively. This standard basis is for one atom and shown in Figure 2 for two () and three atoms, respectively.
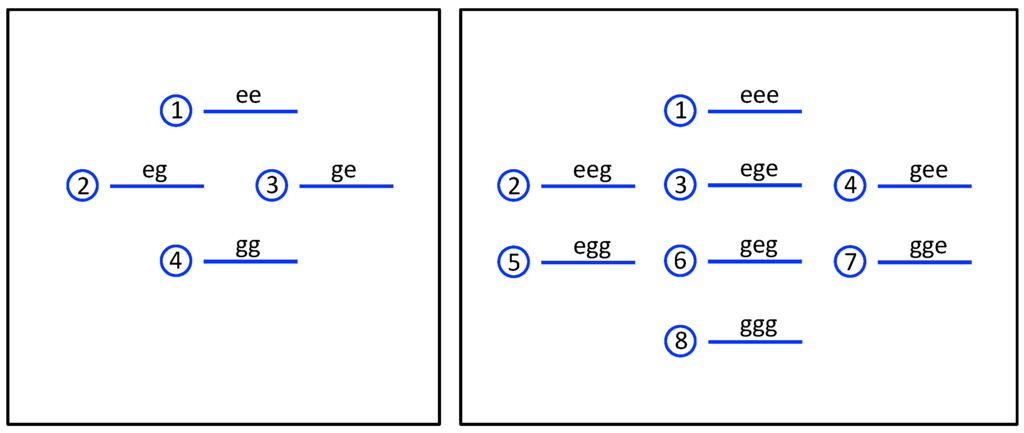
Figure 2.
Energy levels of clusters of two- and three two-level atoms. The numbers next to the levels correspond to the indices used in the text to denote their corresponding position in the natural basis.
Using the explicit forms of the respective propagators for one-, two- and three-atom clusters (Equations (A2), (B9) and (C6) in the Appendix), the master Equation (6) can be expressed in the illuminating form:
Here, the first term corresponds to the effect of a coherent drive applied to the cavity, which is described by the effective Hamiltonian:
The Lindbladian in Equation (7) describes a squeezing process and is given by:
where is an effective coupling rate. The squeezing excitation and de-excitation Lindbladians are:
respectively [39]. The Lindbladian is given by:
where:
which are the Lindbladians for incoherent de-excitation and excitation, respectively. The coefficients for different cluster sizes are shown in Table 1.

Table 1.
Coefficients of the master Equation (7) for different cluster sizes. For later convenience, we have defined for three-atom clusters the abbreviations , , and .
The master Equation (7) is a central result of our work. It describes the dynamics of the cavity field mode that is induced by the passage of the atomic clusters. It allows for the generation of arbitrary (Gaussian) field states, i.e., thermal, displaced and squeezed states. Higher-order (i.e., non-Gaussian) processes cannot be induced by a second-order master equation. The case is the minimal cluster generating these processes: adding another particle () does not make a qualitative difference compared to Equation (7).
3. Classification of Coherences as Different Types of Fuel
The key observation we infer from Equation (7) is that coherences or correlations in the multiatom cluster may be classified according to the disjoint blocks in the density matrix that are associated with qualitatively different terms in the master equation, each term giving rise to a different kind of field dynamics. Figuratively, the different coherences are different types of fuel for the cavity-field WF (Figure 3):
- The blocks adjacent to the main diagonal of the matrix in the standard basis of Figure 2 contain coherences that can only induce absorption and emission processes in the field (WF), as they are associated with in the master Equation (7). We shall refer to these elements as heat-exchange coherences. They have a caloric (“flammable”) value, i.e., they may contribute to the thermalization of the cavity field. Heat-exchange coherences do not arise in the single-atom case, as they correlate states of the same energy, e.g., in two-atom clusters and in three-atom clusters.
- Displacement coherences associated with the term in the master Equation (7) arise for all cluster sizes as they correlate states differing by one excitation, i.e., and in single atoms, and its Hermitian conjugate in two-atom clusters and, say, in three-atom clusters.
- Squeezing coherences correspond to an exchange of two excitations and may exist in two-atom clusters in the form of and its Hermitian conjugate or in three-atom clusters in, say, the form .
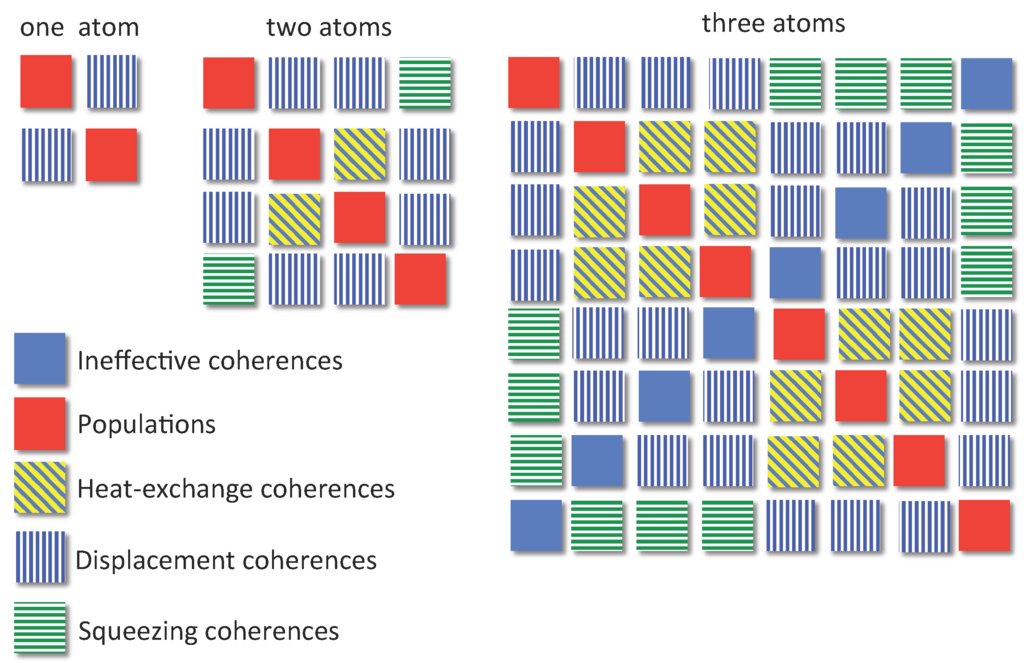
Figure 3.
Density matrix of the atomic cluster for one (left), two (middle) and three (right) atoms, respectively, with color- and pattern-filled squares representing the different roles of the coherences with respect to the cavity-field evolution described by the master Equation (7). Red plain dark squares are populations, and light blue squares are ineffective coherences. Yellow diagonal striped squares are zeroth order coherences that can contribute to thermalization. Dark blue vertical striped squares are first order coherences that can contribute to the coherent displacement of the cavity field. Green horizontal striped squares are second order coherences contributing to the squeezing of the cavity field.
Those matrix elements of that do not contribute to the field evolution shall be called ineffective coherences.
Larger cluster sizes will not change the qualitative features of the master Equation (7), which holds to second order in and, thus, may only induce the same second-order (Gaussian) processes as listed above. The different types of coherences and their relation to the number of excitations are illustrated in the tree diagram of Figure 4 (which should not be confused with the same term in graph theory).
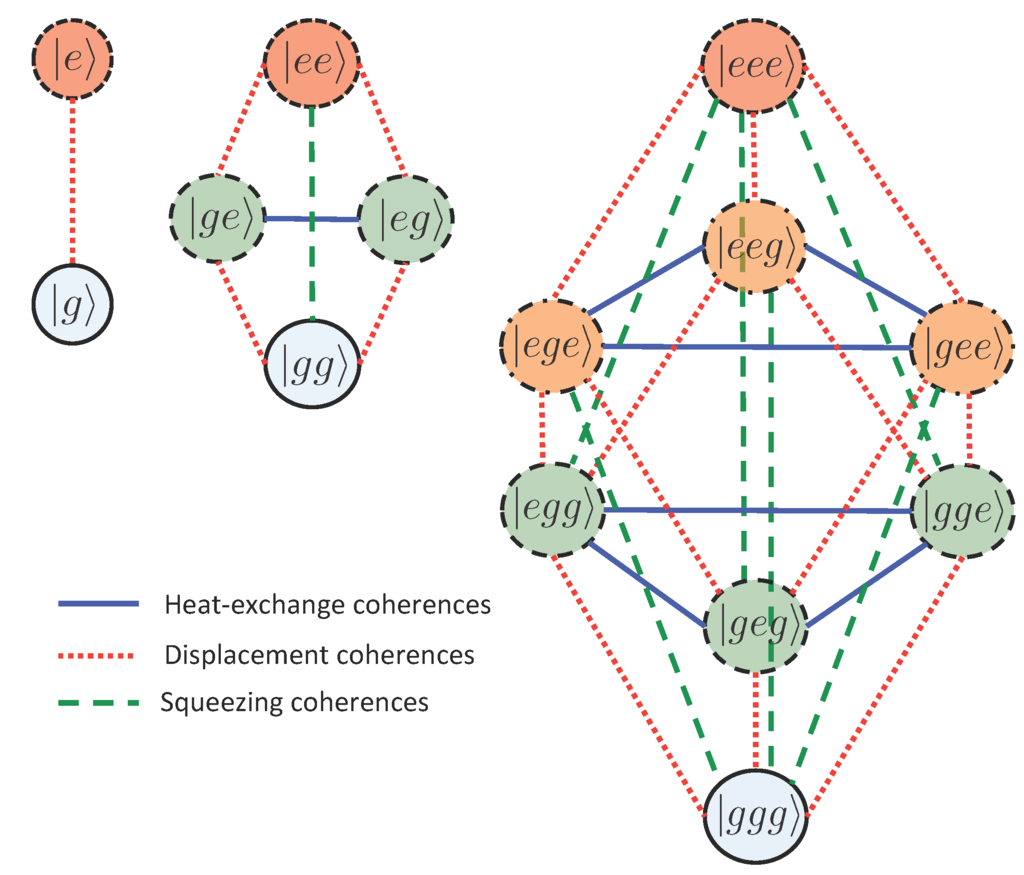
Figure 4.
Trees of coherence for one- (left), two- (middle) and three- (right) atom clusters, respectively. The circles are the basis states, where the same color indicates the same number of excitations. Blue solid lines indicate heat-exchange coherences that may contribute to thermalization of the cavity field. These coherences between states with the same number of excitations only appear in the multipartite case. Displacement coherences (red dotted lines) between states differing by one excitation arise for all particle numbers. Squeezing coherences (green dashed lines) are between states differing by two excitations.
5. Discussion
We have studied the thermodynamic implications of a generalized micromaser model wherein the cavity mode interacts with a beam of quantum-coherent or quantum-correlated multiatom clusters. Our central goal has been to classify the states of such clusters prior to their injection into the cavity according to their ability to fuel the cavity field as “working fluid” in a machine of either the first kind (thermo-mechanical engine) or the second kind (heat engine). To this end, we have derived a Lindblad master equation for the cavity field mode that describes absorption and emission of the field, its coherent displacement and squeezing caused by the atoms that may act, respectively, as a thermal, displaced-thermal or squeezed-thermal bath. These distinct Gaussian processes that the field may undergo are determined by the prefactors of the respective terms in the master equation that are, in turn, determined by disjoint blocks (coherences) of the multiatom density matrix.
The main results of our analysis are as follows:
- An important insight that we have obtained is that two- and three-atom clusters are capable of acting as fuel for both kinds of machines in a highly effective fashion, so that there is no need to involve larger clusters. Still, a larger number of coherences as the cluster grows in size may further enhance the work output.
- For machines of the first kind, our analysis has revealed a particularly promising, simple, fuel in the form of two-atom clusters whose state is a nearly equal superposition of doubly-excited and doubly-ground states. Such a state is expected to give rise to very large squeezing of the cavity field. It may thus present a far superior alternative to existing squeezing schemes of cavity fields [46,47,48]. Such a strong squeezing may have fascinating applications [48] also outside of quantum thermodynamics. Our interest here is that this strong squeezing source may fuel a cavity field in a hybrid thermo-mechanical machine [29] with nearly 100% efficiency, at the expense of mechanical work supplied by the two-atom clusters.
- For machines of the second kind, we have found W-states of three-atom clusters to act as conventional heat-bath fuel at a positive finite temperature that is controllable by the W-state. By contrast, three-atom GHZ- and E-states have been found to correspond to effective baths at infinite or negative temperatures, respectively, that do not allow for a thermal steady-state solution for the cavity field. On the other hand, nearly-equal mixtures of W- and E-states have been identified as fuel capable of thermalizing the cavity field to an ultrahigh temperature.
To conclude, our results are potentially useful for the design of thermal and nonthermal machines based on micromaser setups. The availability of all Gaussian processes via the preparation of two- and three-atom clusters allows one to implement heat engines (wherein the cavity field is thermalized), but also thermo-mechanical engines (wherein the cavity mode is coherently displaced or squeezed).
We wish to stress the feasibility of the diverse forms of the state preparation of multiatom clusters (prior to their injection into the cavity) that we have employed in our analysis:
- The arsenal of quantum gate operations [51] can in principle prepare two or three trapped atoms in an entangled state on demand, but such a preparation may require single-atom addressability.
- Alternatively, W-states can be generated via quantum feedback control [55] or at fusion-based light-matter interfaces [56]. Multipartite entangled states may also be generated via photon-mediated interactions, as recently discussed in [57].
- Another alternative is an optimized probabilistic scheme for multiatom entangled-state preparation in a cavity [58].
- For two-atom entangled-state preparation, we may resort to controlled diatomic dissociation [59], collisions in a cavity [60] or long-range dipole-dipole interactions [61].
On the fundamental side, our results provide clues to the thermalization or non-thermalization of a system (here, the cavity field) via its contact with quantum-correlated multipartite clusters that act as nonthermal baths. Such processes reflect the subtle rapport between quantum correlations in the bath and thermalization [20].
Acknowledgments
Ceren B. Dağ is thankful for intuitive discussions with A. Levent Subası and A. Ümit Hardal. Özgür E. Müstecaplıoğlu acknowledges support from Koç University and Lockheed Martin Corporation University Research Agreement. Gershon Kurizki acknowledges the ISF and BSF for support.
Author Contributions
The ideas of classification of quantum coherences and classification of quantum machines were conceived by Özgür E. Müstecaplıoğlu and Gershon Kurizki, respectively. Ceren B. Dağ, Özgür E. Müstecaplıoğlu and Wolfgang Niedenzu equally contributed to the analytical and numerical calculations. All authors revised and wrote the paper in collaboration. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Time-Evolution Operator for a One-Atom Micromaser
For one atom the time-evolution operator
to second order in readily evaluates to
Appendix B. Time-Evolution Operator for a Two-Atom Micromaser
The time-evolution operator
of the joint cavity–atoms system can be computed to second order in using the collective angular-momentum operators such that
The latter can be decomposed into irreducible subspaces by changing from the computational basis (spanned by products of single-atom and states, cf. Figure 2) to the basis of Dicke states [53] by means of the transformation matrix
The addition of two spin- gives rise to a triplet and a singlet, . As a consequence,
and the propagator is given by the direct sum
where to second order in
Here denotes the unit matrix of the same dimensionality as . Explicitly, we find
and
Transforming back to the computational basis yields
Appendix C. Time-Evolution Operator for a Three-Atom Micromaser
For three particles one proceeds exactly like in the preceding section. The transformation matrix now reads [53]
The addition of three spin- gives rise to a quadruplet and two doublets, . As a consequence,
and the propagator is given by the direct sum
where
and
Transforming back to the computational basis (cf. Figure 2) yields the matrix elements
of the time-evolution operator. The remaining elements evaluate to zero.
Appendix D. Maser Threshold
It is illuminating to derive the threshold condition from the mean photon number, following Reference [20]. We first take and thereby eliminate the coherent-displacement and squeezing terms. According to Equation (3), the cavity density matrix will change to
after the passage of the j-th atom during the short interaction time τ. The mean photon number can be calculated to be
The change of the mean photon number between consecutive injections of two atom clusters is determined by the increment ratio k, which is given by
Assuming that the cavity is initially in the vacuum state, the last term in Equation (D2) yields the mean number of photons after the first-cluster passage, . After the j-th cluster passage the mean photon number rises to
The summation in Equation (D4) is convergent if , which is equivalent to the threshold condition . As , the summation converges to Equation (14c).
References
- Lamb, W.E.; Schleich, W.P.; Scully, M.O.; Townes, C.H. Laser physics: Quantum controversy in action. Rev. Mod. Phys. 1999, 71, S263–S273. [Google Scholar] [CrossRef]
- Schawlow, A.L.; Townes, C.H. Infrared and Optical Masers. Phys. Rev. 1958, 112, 1940–1949. [Google Scholar] [CrossRef]
- Walther, H. One-atom maser and other experiments on cavity quantum electrodynamics. Phys. Uspekhi 1996, 39, 727. [Google Scholar] [CrossRef]
- Meschede, D.; Walther, H.; Müller, G. One-Atom Maser. Phys. Rev. Lett. 1985, 54, 551–554. [Google Scholar] [CrossRef] [PubMed]
- Filipowicz, P.; Javanainen, J.; Meystre, P. Theory of a microscopic maser. Phys. Rev. A 1986, 34, 3077–3087. [Google Scholar] [CrossRef]
- Varcoe, B.T.H.; Brattke, S.; Weidinger, M.; Walther, H. Preparing pure photon number states of the radiation field. Nature 2000, 403, 743–746. [Google Scholar] [PubMed]
- Rempe, G.; Walther, H.; Klein, N. Observation of quantum collapse and revival in a one-atom maser. Phys. Rev. Lett. 1987, 58, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Weidinger, M.; Varcoe, B.T.H.; Heerlein, R.; Walther, H. Trapping States in the Micromaser. Phys. Rev. Lett. 1999, 82, 3795–3798. [Google Scholar] [CrossRef]
- Temnov, V.V. Superradiance and subradiance in the overdamped many-atom micromaser. Phys. Rev. A 2005, 71, 053818. [Google Scholar] [CrossRef]
- Brune, M.; Raimond, J.M.; Goy, P.; Davidovich, L.; Haroche, S. Realization of a two-photon maser oscillator. Phys. Rev. Lett. 1987, 59, 1899–1902. [Google Scholar] [CrossRef] [PubMed]
- Orszag, M.; Ramírez, R.; Retamal, J.C.; Saavedra, C. Quantum cooperative effects in a micromaser. Phys. Rev. A 1994, 49, 2933–2937. [Google Scholar]
- D’Ariano, G.M.; Sterpi, N.; Zucchetti, A. Fine Structure of Thresholds in a Micromaser Pumped with Atom Clusters. Phys. Rev. Lett. 1995, 74, 900–903. [Google Scholar] [CrossRef] [PubMed]
- Krause, J.; Scully, M.O.; Walther, H. Quantum theory of the micromaser: Symmetry breaking via off-diagonal atomic injection. Phys. Rev. A 1986, 34, 2032–2037. [Google Scholar] [CrossRef]
- Casagrande, F.; Lulli, A.; Santagostino, V. Coherently driven and coherently pumped micromaser. Phys. Rev. A 2002, 65, 023809. [Google Scholar] [CrossRef]
- Cresser, J.D. Quantum-field model of the injected atomic beam in the micromaser. Phys. Rev. A 1992, 46, 5913–5931. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Scully, M.O. Extracting Work from a Single Heat Bath via Vanishing Quantum Coherence II: Microscopic Model. AIP Conf. Proc. 2002, 643, 83–91. [Google Scholar]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting Work from a Single Heat Bath via Vanishing Quantum Coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Dillenschneider, R.; Lutz, E. Energetics of quantum correlations. Europhys. Lett. 2009, 88, 50003. [Google Scholar] [CrossRef]
- Li, H.; Zou, J.; Yu, W.L.; Xu, B.M.; Li, J.G.; Shao, B. Quantum coherence rather than quantum correlations reflect the effects of a reservoir on a system’s work capability. Phys. Rev. E 2014, 89, 052132. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.Q.; Dong, H.; Sun, C.P. Single-particle machine for quantum thermalization. Phys. Rev. A 2010, 81, 052121. [Google Scholar] [CrossRef]
- Quan, H.T.; Zhang, P.; Sun, C.P. Quantum-classical transition of photon-Carnot engine induced by quantum decoherence. Phys. Rev. E 2006, 73, 036122. [Google Scholar] [CrossRef] [PubMed]
- De Liberato, S.; Ueda, M. Carnot’s theorem for nonthermal stationary reservoirs. Phys. Rev. E 2011, 84, 051122. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.L.; Wang, T.; Yi, X.X. Effects of reservoir squeezing on quantum systems and work extraction. Phys. Rev. E 2012, 86, 051105. [Google Scholar] [CrossRef] [PubMed]
- Abah, O.; Lutz, E. Efficiency of heat engines coupled to nonequilibrium reservoirs. EPL Europhys. Lett. 2014, 106, 20001. [Google Scholar] [CrossRef]
- Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Nanoscale Heat Engine Beyond the Carnot Limit. Phys. Rev. Lett. 2014, 112, 030602. [Google Scholar] [CrossRef] [PubMed]
- Hardal, A.Ü.C.; Müstecaplıoğlu, Ö.E. Superradiant Quantum Heat Engine. Sci. Rep. 2015, 5, 12953. [Google Scholar] [CrossRef] [PubMed]
- Türkpençe, D.; Müstecaplıoğlu, O.E. Quantum fuel with multilevel atomic coherence for ultrahigh specific work in a photonic Carnot engine. Phys. Rev. E 2016, 93, 012145. [Google Scholar] [CrossRef] [PubMed]
- Niedenzu, W.; Gelbwaser-Klimovsky, D.; Kofman, A.G.; Kurizki, G. Efficiency bounds for quantum engines powered by non-thermal baths. 2015. [Google Scholar]
- Pusz, W.; Woronowicz, S.L. Passive states and KMS states for general quantum systems. Commun. Math. Phys. 1978, 58, 273–290. [Google Scholar] [CrossRef]
- Lenard, A. Thermodynamical proof of the Gibbs formula for elementary quantum systems. J. Stat. Phys. 1978, 19, 575–586. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Balian, R.; Nieuwenhuizen, T.M. Maximal work extraction from finite quantum systems. EPL Europhys. Lett. 2004, 67, 565. [Google Scholar] [CrossRef]
- Binder, F.; Vinjanampathy, S.; Modi, K.; Goold, J. Quantum thermodynamics of general quantum processes. Phys. Rev. E 2015, 91, 032119. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Alicki, R.; Kurizki, G. Work and energy gain of heat-pumped quantized amplifiers. Europhys. Lett. 2013, 103, 60005. [Google Scholar] [CrossRef]
- Gelbwaser-Klimovsky, D.; Kurizki, G. Heat-machine control by quantum-state preparation: From quantum engines to refrigerators. Phys. Rev. E 2014, 90, 022102. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Niedenzu, W.; Kurizki, G. Thermodynamics of Quantum Systems Under Dynamical Control. Adv. At. Mol. Opt. Phys. 2015, 64, 329–407. [Google Scholar]
- Schwabl, F. Statistical Mechanics, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Qamar, S.; Zaheer, K.; Zubairy, M. Generation of steady state squeezing in micromaser. Opt. Commun. 1990, 78, 341–345. [Google Scholar] [CrossRef]
- Walls, D.F.; Milburn, G.J. Quantum Optics, 2nd ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Adesso, G.; Illuminati, F. Entanglement in continuous-variable systems: Recent advances and current perspectives. J. Phys. A Math. Theor. 2007, 40, 7821–7880. [Google Scholar] [CrossRef]
- Meystre, P.; Sargent, M. Elements of Quantum Optics; Springer: Berlin, Germany, 2007. [Google Scholar]
- Tavis, M.; Cummings, F.W. Exact Solution for an N-Molecule—Radiation-Field Hamiltonian. Phys. Rev. 1968, 170, 379–384. [Google Scholar] [CrossRef]
- Schaller, G. Open Quantum Systems Far from Equilibrium; Springer: Basel, Switzerland, 2014. [Google Scholar]
- Gardiner, C.W. Quantum Noise, a Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics; Springer: Berlin, Germany, 2000. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Wenger, J.; Tualle-Brouri, R.; Grangier, P. Non-Gaussian Statistics from Individual Pulses of Squeezed Light. Phys. Rev. Lett. 2004, 92, 153601. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Tan, A.; Jia, X.; Zhang, J.; Xie, C.; Peng, K. Experimental Preparation of Quadripartite Cluster and Greenberger-Horne-Zeilinger Entangled States for Continuous Variables. Phys. Rev. Lett. 2007, 98, 070502. [Google Scholar] [CrossRef] [PubMed]
- Eberle, T.; Steinlechner, S.; Bauchrowitz, J.; Händchen, V.; Vahlbruch, H.; Mehmet, M.; Müller-Ebhardt, H.; Schnabel, R. Quantum Enhancement of the Zero-Area Sagnac Interferometer Topology for Gravitational Wave Detection. Phys. Rev. Lett. 2010, 104, 251102. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Lamb, W.E. Quantum Theory of an Optical Maser. I. General Theory. Phys. Rev. 1967, 159, 208–226. [Google Scholar] [CrossRef]
- Davidovich, L. Sub-Poissonian processes in quantum optics. Rev. Mod. Phys. 1996, 68, 127–173. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical cOherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Agarwal, G.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Huang, S.Y.; Goan, H.S.; Li, X.Q.; Milburn, G.J. Generation and stabilization of a three-qubit entangled W state in circuit QED via quantum feedback control. Phys. Rev. A 2013, 88, 062311. [Google Scholar] [CrossRef]
- Zang, X.P.; Yang, M.; Ozaydin, F.; Song, W.; Cao, Z.L. Generating multi-atom entangled W states via light-matter interface based fusion mechanism. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Aron, C.; Kulkarni, M.; Türeci, H.E. Photon-Mediated Interactions: A Scalable Tool to Create and Sustain Entangled States of N Atoms. Phys. Rev. X 2016, 6, 011032. [Google Scholar] [CrossRef]
- Mandilara, A.; Akulin, V.M.; Kolar, M.; Kurizki, G. Control of multiatom entanglement in a cavity. Phys. Rev. A 2007, 75, 022327. [Google Scholar] [CrossRef]
- Kurizki, G.; Ben-Reuven, A. Theory of cooperative fluorescence from products of reactions or collisions: Identical neutral atomic fragments. Phys. Rev. A 1987, 36, 90–104. [Google Scholar] [CrossRef]
- Deb, B.; Kurizki, G. Formation of Giant Quasibound Cold Diatoms by Strong Atom-Cavity Coupling. Phys. Rev. Lett. 1999, 83, 714–717. [Google Scholar] [CrossRef]
- Shahmoon, E.; Kurizki, G. Nonradiative interaction and entanglement between distant atoms. Phys. Rev. A 2013, 87, 033831. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).