Abstract
In this paper we consider quantum walks whose evolution converges to the Dirac equation in the limit of small wave-vectors. We show exact Fast Fourier implementation of the Dirac quantum walks in one, two, and three space dimensions. The behaviour of particle states—defined as states smoothly peaked in some wave-vector eigenstate of the walk—is described by an approximated dispersive differential equation that for small wave-vectors gives the usual Dirac particle and antiparticle kinematics. The accuracy of the approximation is provided in terms of a lower bound on the fidelity between the exactly evolved state and the approximated one. The jittering of the position operator expectation value for states having both a particle and an antiparticle component is analytically derived and observed in the numerical implementations.
PACS:
03.67.Ac; 03.67.-a
1. Introduction
Thinking about the discrete evolution of physical systems, the most natural example is certainly a particle moving on a lattice. A (classical) random walk is exactly the description of a particle which moves in discrete time steps and with certain probabilities from one lattice position to the neighboring lattice positions. These models have gained increasing attention, showing several applications in the fields of mathematics, physics, chemistry, computer science, natural sciences, and economics [,,]. A quantum version of such a random walk—denoted quantum walk (QW)—was first introduced in [], where the motion (right or left) of a spin- particle is decided by a measurement of the z-component of its spin. Subsequently, the measurement was replaced by a unitary operator on the internal space, also known as coin space [,], determining the evolution of the internal degree of freedom of the system. This model, known as coined quantum walk, has been proven to provide a computational speedup over classical random walks for a class of problems—such as some oracular problems, element distinctness problem, and the triangle finding problem. The Grover’s search algorithm can also be implemented as a QW [,,,,,,]. The rigorous definition of QW can be found in Refs. [,] for the one-dimensional case, and in [] for QW s on graphs of any dimension (see also [] for a complete review including walks with continuous time evolution not considered in the present context).
Aside from the interest in quantum algorithms, QW s provide a fully quantum model of evolution for a system with an internal degree of freedom. As such, QW s have been considered as discrete quantum simulators for particle-physics. Interestingly, it has been proven that QW s have the capability of simulating free relativistic particle dynamics [,,,,,,,,,,,,,], providing—in contrast with other discretisation schemes based on finite-differences and which in general do not preserve the norm—a local unitary model underlying relativistic dynamics.
In the light of this success, in Ref. [] the authors propose a discrete theory for quantum field dynamics based on finite dimensional quantum systems in interaction. Assuming the locality, homogeneity, and unitarity of the interaction, it follows that the systems must evolve according to a QW. Moreover, the above assumptions are very restrictive and the only QW s admissible on the cubic lattice in one, two, and three dimensions are proved to recover the usual relativistic Weyl equation in the limit of small wave-vectors. The massive case is obtained coupling two massless QW s, and in other works also the Maxwell equation [] for Bosonic fields is proved to be compatible with an elementary QW model. Finally, the Lorentz covariance, which is broken by the discreteness of the walk, can be recovered as an approximated symmetry [] in the relativistic limit. These results show how QW s not only provide a useful way of simulating relativistic free evolution ,but also can be considered as a fundamental approach to quantum field theory (see Refs. [,] for a review).
Here we consider the Dirac QW s derived in Ref. [] and present both an analytical and a numerical study of their kinematics, recovering the characteristic traits of the usual Dirac equation.
We show “smooth-states” peaked around some wave-vector eigenstate of the QW can be considered as particle states. We present an analytical approximation of particle states evolution deriving a wave-vector-dependent differential equation for the walk evolution. Then we analyse in detail dynamical quantities such as the walk position and velocity operators and study their evolution. An intrinsic relativistic quantum processes of the Dirac field, denoted Zitterbewegung, first considered by Schrödinger [] and corresponding to a jittering of the mean position for a relativistic particle, is recovered from the QW evolution. The theoretical existence of the quivering motion has been evidenced by numerical simulations of the Dirac equation and of quantum field theory. While Zitterbewegung oscillations cannot be directly observed by current experimental techniques for a Dirac electron since the amplitude should by very small (equal to the Compton wavelength with m the rest mass of the relativistic particle, namely m for an electron), solid state and atomic physics provide physical hardware to simulate the phenomenon [,,,,,,,,,,,,,,,,], and they have recently boosted a renewed interest in the Dirac equation features.
2. Quantum Walks
A quantum walk is a local unitary evolution of a quantum system with Hilbert space , where V is a countable set and is called coin space—namely, the internal degree of freedom of the walker, integer.
A QW on is defined by assigning a mapping , such that , which associates to each pair of vertices a matrix, called transition matrix, acting on the coin space. Then is a solution of the QW if it satisfies the following update rule for a given initial condition :
where is the QW wave-function. Since the QW evolution is unitary, the transition matrices should satisfy the following conditions for all :
where is the identity on the coin space . Such a QW carries an associated graph defined by the set of non-null transition matrices as the directed graph with vertex set V and edge set . The locality condition amounts to requiring that for every vertex , the cardinality of its out-neighbourhood , and in-neighbourhood , is uniformly bounded over V—namely for every .
In Ref. [] it has been shown that assuming the QW homogeneous (the vertices of the graph cannot be distinguished by the walk dynamics) the graph Γ is actually a Cayley graph of a group G. Given a group G and taking , the Cayley graph of G with connection set S is defined as the coloured directed graph with vertex set G, edge set and colouring given by . We will assume hereafter that the connection set S is a generating set for G—which entails that the Cayley graph is unilaterally connected—and it is symmetric. Namely, . The walk unitary operator corresponding to the update rule of Equation (1) can be expressed in terms of the right-regular representation of G on defined as the map such that . Assuming, by homogeneity, that we can choose the transition matrices independently of the vertex so that for every and , we can write the walk operator as
Now the unitarity conditions on U translate into the following conditions of the transition matrices :
Fourier Representation of Abelian QW s
As pointed out by Ambainis et al. [], there are two general ways to study the evolution of a QW. On the one hand, one can exploit the algebraic properties of the walk transition matrixes to obtain a path-sum solution, where the QW transition amplitude to a given site is expressed as a combinatorial sum over all the paths leading to that site. Regarding this approach, in Ref. [] the authors provided a solution for the Hadamard Walk, whereas Konno derived the solution for an arbitrary coined QW []. Considering the application of QW s to the description of relativistic particles, also the Dirac QW in -dimensions and the massless Dirac QW in -dimensions have been analytically solved in position space [,]. On the other hand, when a QW is defined on the Cayley graph of an Abelian group, the walk dynamics can be studied in its Fourier representation, providing analytical solutions and also approximate asymptotic solutions in the long-time limit.
Let us now consider QW s defined on Cayley graphs of free Abelian groups. That is, with generating set S. Adopting the usual additive notation for the group operation on , the right-regular representation of is expressed as
Moreover it decomposes in one-dimensional irreducible representations, as can be easily seen from the fact that the translations are diagonal on the plane waves
where denotes the first Brillouin zone, which depends on the specific Cayley graph we are considering.
Therefore, we can write the walk operator of Equation (3) in the direct integral decomposition
For each we can diagonalise the matrix obtaining
where is the dispersion relation of the walk and is the eigenvector of corresponding to the eigenvalue , with . We notice that we have considered the representation given by the factorized orthonormal basis for the walk Hilbert space , with the canonical basis in .
3. The Dirac QW in One, Two, and Three Space Dimensions
In This Section, we present the Dirac QW s in one, two, and three space dimensions derived in Ref. []. We will see that in the limit of small wave-vectors, the Dirac walks simulate the usual Dirac equation evolution. We start from the simplest case of massless Dirac QW, also denoted Weyl QW. The massive walk will be given by coupling two Weyl QW s with the coupling parameter interpreted a posteriori as the mass of the Dirac field.
3.1. The Weyl Quantum Walk
In Ref. [], the authors derive the unique QW s on Cayley graphs of for satisfying—besides locality and unitarity—the assumptions of homogeneity and discrete isotropy, and with minimal dimension s of the coin space to have non-identical evolution. As first noticed by Meyer [], the only solution for scalar QW s on Cayley graphs of free-Abelian groups is the identical QW; in order to have non-trivial dynamics, one has to take at least .
Let us start from Cayley graphs of , the most relevant from the physical perspective. It can be proved (see []) that only the body-centred cubic lattice (BCC) allows one to define a QW satisfying the above assumptions. The BCC lattice is the Cayley graph where is the set of generators of the group and is the corresponding set of their inverses; a convenient choice for the generators is the following:
The first Brillouin zone of the BCC lattice is defined in Cartesian coordinates as and it is depicted in Figure 1.
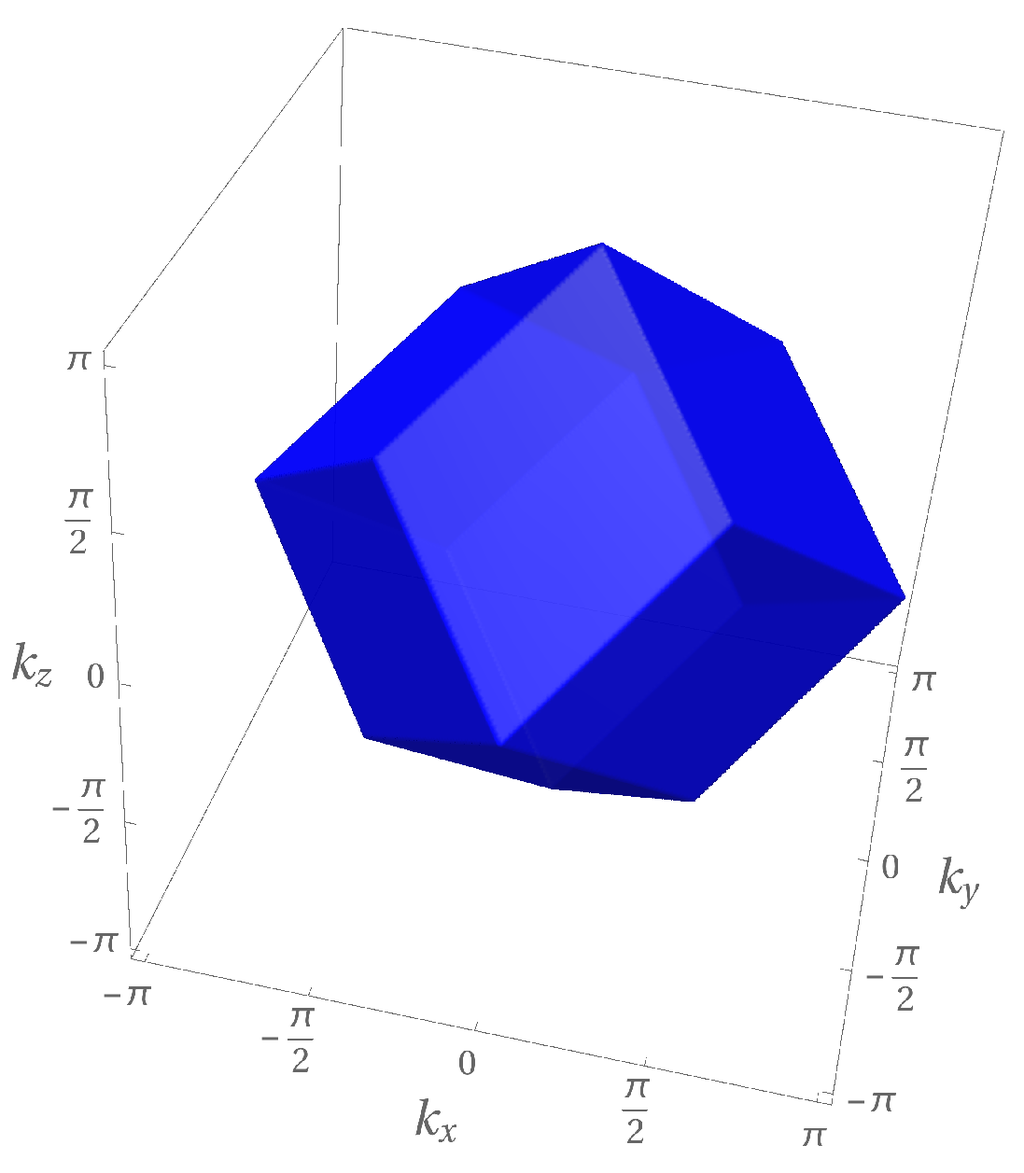
Figure 1.
First Brillouin zone of the BCC lattice (rhombic dodecahedron).
The unique solutions on the BCC lattice can be summarised as:
where σ is the vector with components given by the Pauli matrices , and . The walk matrix has spectrum with dispersion relation and group velocity , representing the speed of a wave-packet peaked around the central wave-vector .
Let us consider now ; also in this case our assumptions single out only one Cayley graph of , the square lattice, involving two generators , with and ; the first Brillouin zone in this case is given by , where and . The unitary matrix of the walk in Fourier representation is given by:
with dispersion relation .
Finally, for , the unique Cayley graph satisfying our requirements for is the lattice itself, considered as the free Abelian group on one generator . From the unitarity conditions one gets the unique solution
with dispersion relation .
From Equations (10) to (12), we see that the Weyl QW in dimension is of the form
for certain and with dispersion relation
Now it is easy to show that the evolution of the walks Equations (10) to (12) obeys Weyl’s equation in the limit of small wave-vectors, and thus we call them Weyl QW s. Let us introduce the interpolating Hamiltonian defined in the wave-vector space as the matrix such that and governing the continuous-time evolution, interpolating exactly the discrete dynamics of the walk. As one can check, the interpolating Hamiltonian is
and by power expanding at the first order in , one has
whose first order term coincides with the usual Weyl Hamiltonian in d dimensions, with , once the wave-vector is interpreted as the momentum.
It will be useful for the considerations of the following sections to consider the eigenvectors of the QW. Since the structure of the matrix is independent of the dimension, we will give here the general expression of the eigenvectors. Let us now rewrite the unitary matrix as:
where and are related to the functions in Equation (13) by the equations and . We can then solve the eigenvalue problem
obtaining the following expression for the eigenvectors , with ,
where .
3.2. The Massive Case
Now we present QW s which manifest Dirac dynamics. We consider a walk resulting from the local coupling of two Weyl QW s. One can show [] that there is only one possible local coupling of two Weyl QW s, and that in the small wave-vector limit the resulting walks approximate the Dirac’s equation. The unique local coupling of Weyl’s QW s, modulo unitary conjugation, is of the form
We can provide a convenient expression of the walk in terms of the gamma matrices in spinorial representation:
where and are those given previously for the Weyl’s QW s. From Equation (21) we can see that the dispersion relation in this case is simply given by
In this case, the interpolating Hamiltonian has the form
and to the first order in and m one obtains the usual Dirac’s Hamiltonian
We notice that the Dirac QW walk not only provides the usual Dirac dispersion relation in the limit small wave-vectors, but also the correct spinorial dynamics of the Dirac equation.
It is worth noticing that in dimension , the Dirac QW decouples into two identical massive QW s [,], written explicitly as
where , . In one space dimensions, similar QW have been studied in the literature. For example in Refs. [,], the authors consider the relation between arbitrary coined QWs and relativistic dynamics.
For the massive QW s, the eigenvalue equation takes the form:
and the four eigenvectors , with can be written as
with φ, , and defined for the corresponding massless QW of Equations (18) and (19).
4. Numerical Simulation of the Weyl and Dirac QW s
In order to evaluate numerically the evolution of QW s, one can adopt two different approaches. On the one hand, one can exploit the update rule in position space given by Equation (1), which is straightforward to implement numerically. This approach, however, is not very efficient if we only want to know the evolved state at some specific time t, since it would require t successive updates of the state. On the other hand, the Fourier representation of the walk allows one to directly compute the evolution at a specific time—the complexity of the computation being that of the Fourier Transform, which can be efficiently implemented via a Fast Fourier Transform (FFT) algorithm such as the Cooley–Tukey FFT algorithm [].
Recalling the general expressions in Equations (7) and (8), the evolution of a state is given by the subsequent application of the walk unitary . Therefore, the state at time t can be expressed in terms of its representation in Fourier space as the Fourier Transform
where is the r-component in the eigenbasis of the walk of the discrete-time Fourier transform of . The notation of the eigenbasis refers here to that of Equation (8), where r runs over and s is the dimension of the coin. Now, the numerical data used to represent the state in Fourier space constitute a discrete sampling of it, say at frequencies with and the total number of samples in dimension i. Implementing periodic boundary conditions, this amounts to taking samples in direct space over a finite region, extending the data periodically to the whole lattice.
Let us consider now the simple cubic lattice of . Let us consider a restriction of to a finite region , with , such that . Then, is periodically extended to ; namely , with periodicity matrix given by . The Fourier Transform of the sequence coincides with the Discrete Fourier Transform (DFT) defined as
where and . The inversion formula is then given by:
Here we have chosen the set of Fourier indices so that the frequencies actually computed lie in the interval .
For the Dirac QW in -dimensions, we have to consider instead the BCC lattice. One can show [] that it is possible to reduce the DFT on the BCC lattice to two rectangular DFT s, allowing implementation of the DFT via usual rectangular FFT algorithms. We can describe the BCC lattice choosing as vertex set , where . A suitable truncation of a sequence , to a function defined on a finite set can be obtained choosing the fundamental region and periodically extending it to G. The original sequence can be further split into two subsequences on the even and odd indices and , for all . As a consequence, these two sequences and are periodic with periodicity matrix : for all and in and . The Fourier Transform of is defined as usual as
where the set of Fourier indices can be chosen as . As shown in Ref. [], one can exploit the geometry of the BCC lattice to reduce the DFT with to two functions and with restricted now to . This allows for the computation of the DFT in terms of the usual rectangular DFT s:
with and . Finally, from the two sequences and , we can write the inversion formulae for and as:
5. Kinematics of the Dirac QW
Here we study the kinematics of the Dirac QW presented in Section 3. We show that there exists a class of states whose evolution resembles the evolution of a particle with a given wave-vector. Their evolution can be described by an approximated differential equation with coefficients depending on the particle wave-vector. We observe that the positive and negative frequency eigenstates of the walk correspond to Dirac particle and antiparticle states.
Finally, we consider the position operator for the Dirac QW and find that the mean position of states having both positive and negative frequency components present the typical jittering phenomenon—denoted Zitterbewegung—of relativistic particles. The Zitterbewegung was first discovered by Schrödinger in 1930 [], who pointed out that in the Dirac equation for free relativistic electrons, the velocity operator does not commute with the Dirac Hamiltonian. As a consequence, the evolution of the position operator shows—in addition to the classical motion proportional to the group velocity—a fast periodic oscillation with frequency and amplitude equal to the Compton wavelength , with m the rest mass of the relativistic particle. This oscillating motion is due [] to the interference of states corresponding to the positive and negative energies firstly appeared as solutions to the Dirac equation. The trembling is also shown to disappear with time [] for a wave-packet particle state. The same phenomenology is recovered in the Dirac QW scenario that also presents solutions having positive and negative frequency eigenvalues.
5.1. Approximated Dispersive Differential Equation
We denote a quantum state of the walker a particle state if it is localized in a region of the lattice at a given instant of time and if the walk evolution preserves its localization. Accordingly, we take the following of particle state as a state that is narrow-banded in the wave-vector space.
Definition 1 (Particle-state).
A particle-state for the Dirac QW is a wave-packet smoothly peaked around some eigenvector of the walk. Namely, for a given
where is a smooth function satisfying the bound
In the next Proposition, we derive a dispersive differential equation governing the evolution for particle-states and which makes clear their particle behaviour. It will be convenient to work with the continuous time t, interpolating exactly the discrete walk evolution . Accordingly, we consider , t to be real-valued continuous variable by extending the Fourier transform
to real , t. Since the walk is band-limited in momenta , then the continuous function is completely defined by its value on the discrete points of the walk causal network (the sampling of a band-limited function is stated in the Nyquist-Shannon Sampling Theorem). However, all numerical results will be given only for the discrete t, namely for repeated applications of the walk unitary operator and for discrete lattice sites .
Proposition 1 (Dispersive differential equation).
Consider the evolution of the Dirac QW of Section 3 on a particle-state as in Definition 1. Then for any positive integer n, the state at time t is given by
where is solution of the following differential equation
and
Proof.
First we notice that at time t the particle-state in the momentum representation is simply , while in the position representation it is
Now we take the time derivative of and expand Ω vs. in . The coefficients of the expansion can be regarded as derivatives with respect to the space coordinates and taken out of the integral (dominated derivative theorem), leading to the following dispersive differential equation:
where is a multiindex and . If we truncate the above expansion at the nth order and denote by the solution of the corresponding truncated differential equation, with the identification of the initial condition , we get the approximate state Equation (43) at time t
Using the definition of particle-state in Definition 1, one can compute the accuracy of the approximation Equation (46) in terms of the parameters , and ε, evaluating the overlap between the states Equations (43) and (46). That is,
where
Therefore, the exact state at time t can be approximated by Equation (46) with the accuracy given by the overlap in Equation (47). ☐
This approximation fails to be accurate for a sufficiently large value of t. More precisely, if we require the overlap to satisfy , for some , then for the approximated solution can deviate significantly from that of the QW. A typical application of the above proposition is the second order approximation of the state evolution. In that case, Equation (40) gives
where and are respectively to drift vector and to the diffusion tensor for the particle state. Accordingly, the state will translate with group velocity given by the drift vector and its distribution in space will spread as described by the diffusion tensor.
In Figure 2, we show the numerical evolution (see Section 4) of a Gaussian particle-state in dimensions.
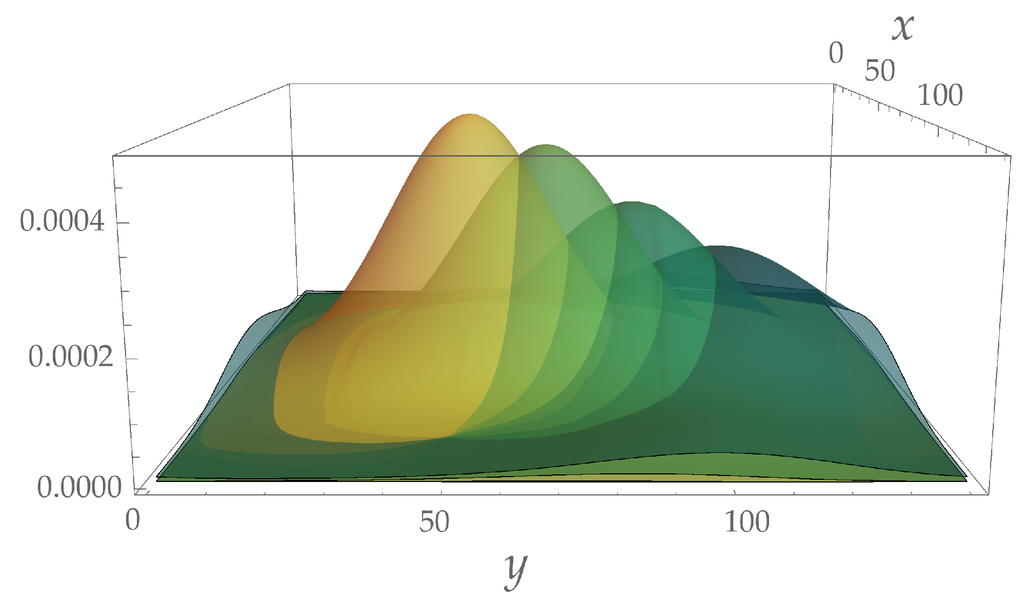
Figure 2.
Evolution for time-steps of a particle state as in Definition 1 for the Dirac QW in dimensions with only positive energy components (the marginal along the z axis is represented). Here the state is Gaussian with parameters: mass , mean wave-vector , width for . Evolution in time is shown as a colour gradient from light to dark; one can notice the spreading of the wave-packet as time increases. Probability distribution shown at times .
5.2. The Evolution of the QW Position Operator
Up to now we have considered only smooth-states (see Definition 1) whose walk evolution is well described by the approximate differential equation derived in Proposition 1. On the other hand, in the QW framework we are allowed to consider states very far apart from the smooth ones, and in the limit one can also consider perfectly localized states as with and , , where denotes the basis corresponding to the Dirac field representation in Equation (21). Since these states involve large momentum components, their evolution according to the QW dynamics will be very different from the one given by the Dirac equation. We can say that the QW determines different regimes with respect to a given reference scale at which the evolution deviates from the relativistic regime given by the Dirac equation [,]. However, in a QW context, the study of such states can give essential information regarding the dynamical properties of these models [,,,]. One can see in Figure 3 and Figure 4 the numerical evolution (see Section 4) of a perfectly localised state, according to the Dirac QW in -dimensions.
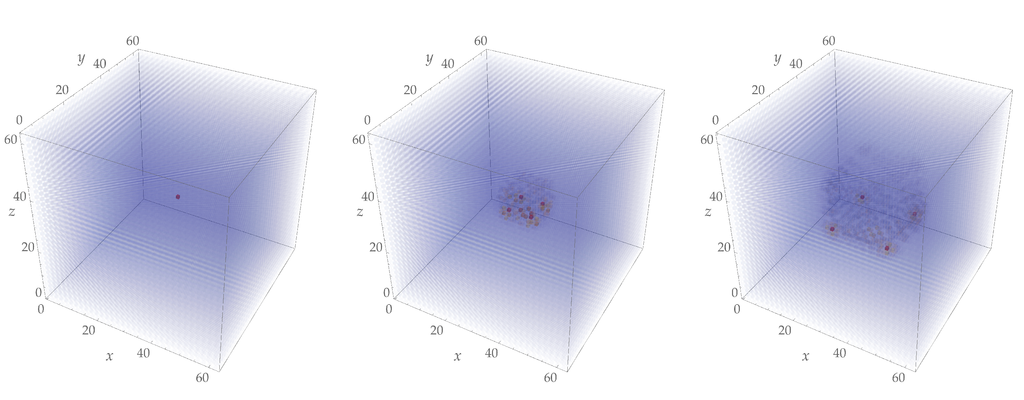
Figure 3.
Evolution of a perfectly localised state for the Dirac QW in -dimensions. The figures show the probability distribution at times , from left to right. In this case, the mass parameter is and the spinor in the canonical basis is .
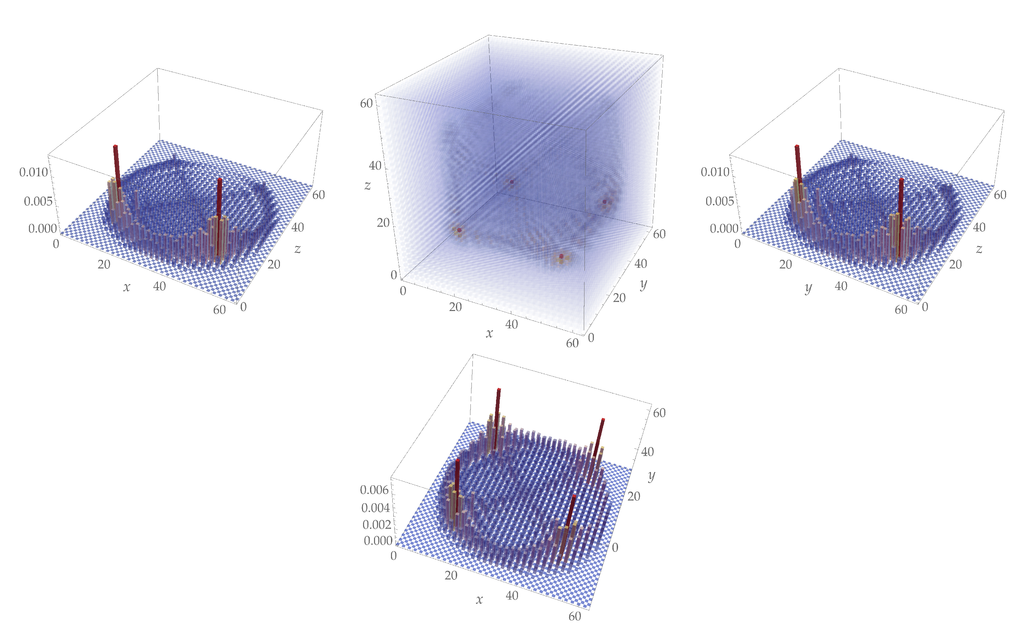
Figure 4.
Evolution of a perfectly localised state for the Dirac QW in -dimensions. Top-centre: final probability distribution of the same initial state of Figure 3, after time-steps. Top-left: projection of the state along the y-axis; top-right: projection along the x-axis; bottom: projection on the -plane.
The position operator X providing the representation —namely, the operator such that — is . Accordingly, the average position for an arbitrary one-particle state is given by .
The definition of the mechanical momentum would need an interacting theory allowing momentum exchange between different particles. However, in Section 3, we have seen that for small and m, the wave-vector (namely the conjugated variable of via the Fourier transform) corresponds to the Dirac particle momentum. Moreover, the momentum operator should correspond to the generator of translations over the lattice. Therefore, as conjugated momentum we take the following operator . We can now compute the commutator between and , . That is,
where in the second equality it was possible to interchange the sum and the integral according to the Fubini Theorem. Integrating by parts we get
where is a generic state and the discrete Fourier transform of . We notice that Equation (50) differs from the usual canonical commutation relation by a boundary term, in agreement with the existence of perfectly localized states for the walk , , for which the expectation value in Equation (50) vanishes. In the following evolution of the position expectation value, we will consider states having negligible boundary term in Equation (50).
The evolution of the position operator can be computed via the velocity and the acceleration operators derived by the commutator with the walk Hamiltonian
From direct computation (and neglecting the boundary terms of the commutators), it follows
and
Now we can derive the analytical expression of by doubly integrating the acceleration operator , with . A lengthy but simple computation (notice that ) shows that , which gives
Therefore, integrating the first time we get
with , and integrating again one has
where
The operator in Equations (56) and (57) is the classical component of the velocity operator which, in the Hamiltonian diagonal basis Equation (64), is proportional to the group velocity . In addition to the classical contribution , we see that the position operator Equation (57) presents, as in the usual Dirac theory, a time-dependent component and a constant shift term . Since have
the position operator Equation (57) mean value for the generic state having both particle and positive and negative frequency components can always be written as
with Re denoting the real part. The first two terms simply correspond to the “classical” evolution of the particle and antiparticle components of the initial state , which evolve independently according to the classical component of the velocity operator. The interference between positive and negative frequencies is responsible for the term in Equation (62). Obviously, in case of having only positive or negative component, the interference disappears. The additional term consists of two contributions: a constant shift and a time dependent term.
Taking for example a superposition of particle and antiparticle states (see Definition 1),
where are the Dirac walk eigenvectors of Equation (27). One can show that the time dependent contribution is an oscillating term that for goes to 0 as , and whose amplitude is bounded by —say by the Compton wavelength in the usual dimensional units (see Ref [] for the proof in one space dimension). Accordingly, can be considered as the QW analogue of the so-called Zitterbewegung.
In Figure 5 and Figure 6, we show two numerical examples (see Section 4) of mean position evolution for the Dirac QW in one and three space dimensions, respectively. In the first case, one can also notice the time-damping of the jittering amplitudes.
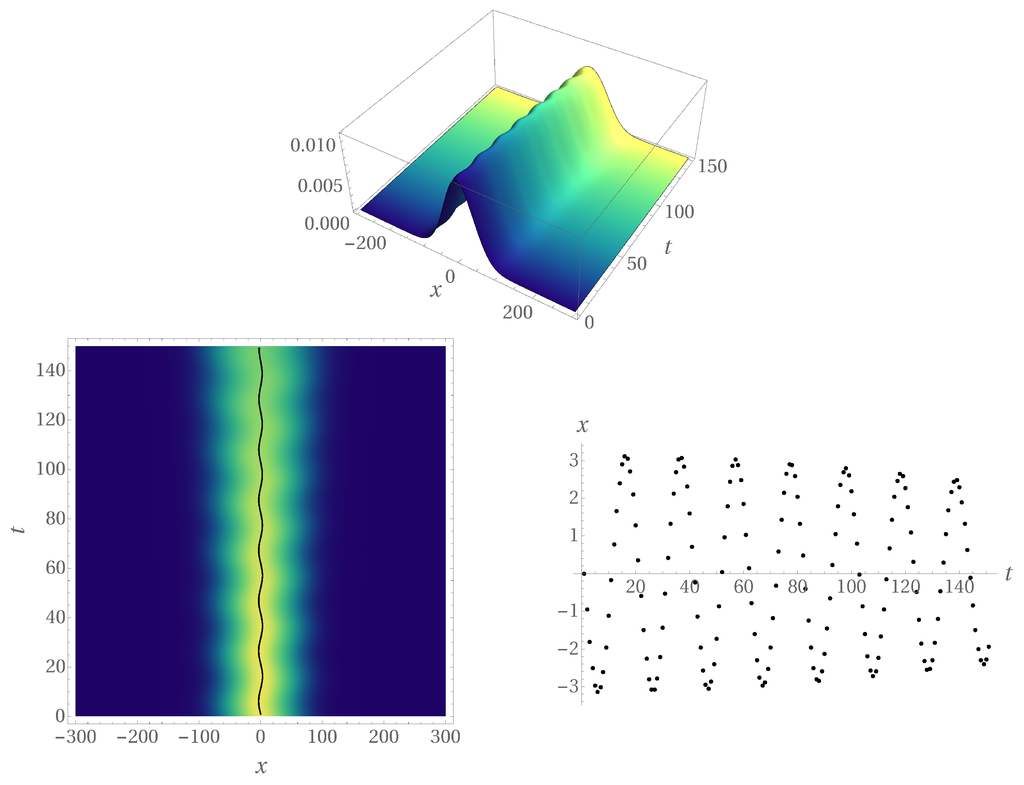
Figure 5.
Evolution according to the Dirac QW in dimensions for time-steps of particle states having both a particle and an antiparticle component, as defined in Equation (63). Here the states are Gaussian with parameters: mass , width , mean wave-vector , . Top and bottom-left: probability distribution of the position. Bottom-right: evolution of position mean value.
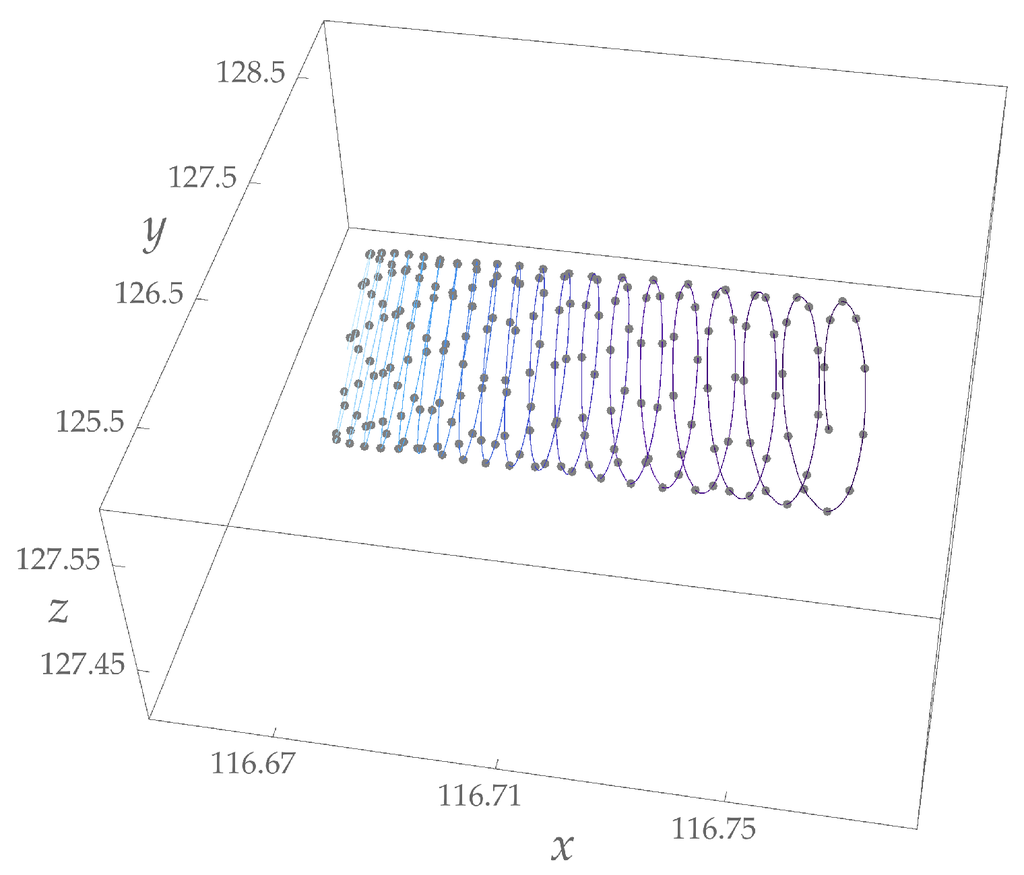
Figure 6.
Evolution for the mean position according to the Dirac QW in dimensions for time-steps of particle states having both a particle and an antiparticle component, as defined in Equation (63). Here the states are Gaussian with parameters: mass , mean wave-vector , width for ; the spinor components in the walk eigenbasis are , with the first two components corresponding to the positive energy part and the second two to the negative one; time evolution from left to right.
Remark 1 (Newton–Wigner position operator evolution).
As in QFT, one can define the Newton–Wigner position operator which does not mix states with positive and negative eigenvalues. Given the operator providing the Foldy–Wouthuysen representation of the Dirac walk, namely the representation in which the Hamiltonian is diagonal
the Newton–Wigner rotated position operator is defined as
As in the usual QFT, the Newton–Wigner position operator Equation (66) does not suffer the jittering of the mean position even for states having both a particle and an antiparticle component. Indeed, in this case, the velocity operator
corresponds to the classical component of the velocity operator in Equation (56) and leads to a null acceleration . By integrating Equation (67), we see that the time evolution of the Newton–Wigner position operator is simply
6. Conclusions
The QW framework, say a lattice of quantum systems in local unitary interaction, appears to be very promising both from the information-theoretical perspective, in that QWs can be exploited to solve efficiently some search problems, and for the connection existing between the a discrete time quantum walk evolution and the relativistic equations of motion. In this paper, we analyse both numerically and analytically the properties of QWs on Abelian lattices up to dimensions. The Weyl QWs considered here are the only isotropic (all the directions on the lattice are equivalent) QWs admissible on Abelian lattices and with two-dimensional coin system. The QWs in one and two space dimensions are defined on the simple cubic lattice while the QW in dimensions is defined on the body-centered cubic lattice. As shown in Ref. [], any other topology fails to accommodate a non-trivial QW (by trivial QW we mean a walk corresponding to the identical evolution or to a shift in a fixed direction). The only coupling of two Weyl QWs that preserves locality is then defined Dirac QW. Remarkably, the selected walks are compatible with a “large scale” relativistic dynamics.
The analytical results of this paper show that for particle states as defined in Definition 1, the Weyl and Dirac QW dynamics is well approximated by a dispersive differential equation whose drift and diffusion coefficients reduce to the usual Weyl and Dirac ones in the limit of small wave-vectors. The numerical results are the first simulations of QWs in dimensions and on the BCC lattice. The numerical results are given for the Dirac QW in and dimensions for different types of initial states. In dimensions we show the evolution of both particle states and perfectly localised states. In dimensions, the evolution of the superposition of positive and negative energy states for the Dirac QW produces (as depicted in Figure 5) the well-known Zitterbewegung effect of the relativistic electron. The appearance of this oscillating phenomenon is also shown for the Dirac QW in dimensions (see Figure 6).
As already mentioned, the QW framework can accommodate from a theoretical viewpoint a local discrete time unitary evolution as the microscopic description of relativistic particle dynamics. The last one is obtained as an approximation of the QW evolution for a specific class of quantum states; namely, states narrow-banded in small wave-vectors (see Definition 1). The same QW on arbitrary states (for example, localized states) shows a very different dynamical behaviour that cannot be interpreted as a particle evolution. While the approximation of Proposition 1 only works for narrow-banded states, the numerical analysis presented in the manuscript applies to arbitrary states.
Our results agree with other works (see for example Ref. []) in one space dimensions that studied the continuum limit of QWs, namely the lattice spacings and the time steps are sent to 0, in comparison with the Dirac or the Klein–Gordon equations. Here we do not take the same continuum limit but show that for specific input states the QW evolution recovers the relativistic one. Moreover, we do not consider only one space dimension, but also the two and three space dimensional case where the notion of spin becomes relevant.
Discrete time QWs provide a local and unitary evolution underlying the relativistic dynamics and do not start from a finite difference counterpart of the relativistic differential equations (or Hamiltonians). The main difference is in the notion of locality, since the locality of the Hamiltonian does not correspond to the locality of the unitary operator and vice versa. As a consequence the “effective” Hamiltonian corresponding to the Weyl (Dirac) QW differs from the usual Weyl (Dirac) finite difference Hamiltonian (see the function that appears in Equations (15) and (23)). In the limit of small wave-vectors, the two Hamiltonians coincide, and both give the usual relativistic dynamics. However, for large wave-vectors they differ significantly.
The Weyl and Dirac QWs presented in this paper also provide an alternative way to discretize the usual Weyl and Dirac dynamics. The numerical results of this manuscript can be compared with other numerical approaches in the literature; see for example Ref. [,,,,], where the authors adopt split-operator schemes to approximate the solutions of the Weyl and Dirac differential equations and recover the usual relativistic dynamics in the continuum limit.
Acknowledgments
This work has been supported in part by the Templeton Foundation under the project ID# 43796 A Quantum-Digital Universe.
Author Contributions
Giacomo Mauro D’Ariano conceived the project. Nicola Mosco implemented all the numerical simulations writing original codes in C++ and in Wolfram Mathematica. Paolo Perinotti and Alessandro Tosini provided the analytical analysis. Correspondence and requests for materials should be addressed to all the authors. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1. [Google Scholar]
- Weiss, G. Aspects and Applications of the Random Walk (Random Materials & Processes S.); North-Holland: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Cox, D.R. Renewal Theory; Methuen: London, UK, 1962; Volume 1. [Google Scholar]
- Aharonov, Y.; Davidovich, L.; Zagury, N. Quantum random walks. Phys. Rev. A 1993, 48, 1687–1690. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, D.; Ambainis, A.; Kempe, J.; Vazirani, U. Quantum walks on graphs. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing—STOC ’01, Heraklion, Greece, 6–8 July 2001; pp. 50–59.
- Ambainis, A.; Bach, E.; Nayak, A.; Vishwanath, A.; Watrous, J. One-dimensional quantum walks. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing—STOC ’01, Heraklion, Greece, 6–8 July 2001; pp. 37–49.
- Childs, A.M.; Cleve, R.; Deotto, E.; Farhi, E.; Gutmann, S.; Spielman, D.A. Exponential algorithmic speedup by a quantum walk. In Proceedings of the Thirty-Fifth ACM Symposium on Theory of Computing—STOC ’03, San Diego, CA, USA, 9–11 June 2003; p. 59.
- Ambainis, A. Quantum walk algorithm for element distinctness. SIAM J. Comput. 2007, 37, 210–239. [Google Scholar] [CrossRef]
- Magniez, F.; Santha, M.; Szegedy, M. Quantum algorithms for the triangle problem. SIAM J. Comput. 2007, 37, 413–424. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A quantum algorithm for the Hamiltonian NAND tree. 2007. arXiv:quant-ph/0702144. [Google Scholar]
- Santha, M. Quantum walk based search algorithms. In Proceedings of the 5th International Conference Theory and Applications of Models of Computation: (TAMC 2008), Xi’an, China, 25–29 April 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 31–46. [Google Scholar]
- Portugal, R. Quantum Walks and Search Algorithms; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wong, T.G. Grover search with lackadaisical quantum walks. J. Phys. A Math. Theor. 2015, 48, 435304. [Google Scholar] [CrossRef]
- Nayak, A.; Vishwanath, A. Quantum Walk on the Line. 2000. arXiv:quant-ph/0010117. [Google Scholar]
- Kempe, J. Quantum random walks: An introductory overview. Contemp. Phys. 2003, 44, 307–327. [Google Scholar] [CrossRef]
- Succi, S.; Benzi, R. Lattice Boltzmann equation for quantum mechanics. Phys. D Nonlinear Phenom. 1993, 69, 327–332. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I. Weyl, Dirac, and Maxwell equations on a lattice as unitary cellular automata. Phys. Rev. D 1994, 49, 6920–6927. [Google Scholar] [CrossRef]
- Meyer, D.A. From quantum cellular automata to quantum lattice gases. J. Stat. Phys. 1996, 85, 551–574. [Google Scholar] [CrossRef]
- Strauch, F. Relativistic quantum walks. Phys. Rev. A 2006, 73, 054302. [Google Scholar] [CrossRef]
- Yepez, J. Quantum lattice-gas model for computational fluid dynamics. Phys. Rev. E 2001, 63, 046702. [Google Scholar] [CrossRef] [PubMed]
- D’Ariano, G.M. The quantum field as a quantum computer. Phys. Lett. A 2012, 376, 697–702. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Tosini, A. Quantum field as a quantum cellular automaton: The Dirac free evolution in one dimension. Ann. Phys. 2015, 354, 244–264. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Tosini, A. Dirac quantum cellular automaton in one dimension: Zitterbewegung and scattering from potential. Phys. Rev. A 2013, 88, 032301. [Google Scholar] [CrossRef]
- Arrighi, P.; Nesme, V.; Forets, M. The Dirac equation as a quantum walk: Higher dimensions, observational convergence. J. Phys. A Math. Theor. 2014, 47, 465302. [Google Scholar] [CrossRef]
- Arrighi, P.; Facchini, S. Decoupled quantum walks, models of the Klein-Gordon and wave equations. Europhys. Lett. 2013, 104, 60004. [Google Scholar] [CrossRef]
- Farrelly, T.C.; Short, A.J. Discrete spacetime and relativistic quantum particles. Phys. Rev. A 2014, 89, 062109. [Google Scholar] [CrossRef]
- Farrelly, T.C.; Short, A.J. Causal fermions in discrete space-time. Phys. Rev. A 2014, 89, 012302. [Google Scholar] [CrossRef]
- Katori, M.; Fujino, S.; Konno, N. Quantum walks and orbital states of a Weyl particle. Phys. Rev. A 2005, 72, 012316. [Google Scholar] [CrossRef]
- Bracken, A.J.; Ellinas, D.; Smyrnakis, I. Free-Dirac-particle evolution as a quantum random walk. Phys. Rev. A 2007, 75, 022322. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Perinotti, P. Derivation of the Dirac equation from principles of information processing. Phys. Rev. A 2014, 90, 062106. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Perinotti, P. Quantum cellular automaton theory of light. Ann. Phys. 2016, 368, 177–190. [Google Scholar] [CrossRef]
- Bibeau-Delisle, A.; Bisio, A.; D’Ariano, G.M.; Perinotti, P.; Tosini, A. Doubly special relativity from quantum cellular automata. Europhys. Lett. 2015, 109, 50003. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Perinotti, P.; Tosini, A. Weyl, Dirac and Maxwell Quantum Cellular Automata. Found. Phys. 2015, 45, 1203–1221. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Perinotti, P.; Tosini, A. Free Quantum Field Theory from Quantum Cellular Automata. Found. Phys. 2015, 45, 1137–1152. [Google Scholar] [CrossRef]
- Schrödinger, E. Über die kräftefreie Bewegung in der relativistischen Quantenmechanik; Akademie der wissenschaften in kommission bei W. de Gruyter u. Company: Berlin, Germany, 1930. (In German) [Google Scholar]
- Cannata, F.; Ferrari, L. Effects of the nonrelativistic Zitterbewegung on the electron-phonon interaction in two-band systems. Phys. Rev. B 1991, 44, 8599. [Google Scholar] [CrossRef]
- Ferrari, L.; Russo, G. Nonrelativistic zitterbewegung in two-band systems. Phys. Rev. B 1990, 42, 7454. [Google Scholar] [CrossRef]
- Cannata, F.; Ferrari, L.; Russo, G. Dirac-like behaviour of a non-relativistic tight binding Hamiltonian in one dimension. Solid State Commun. 1990, 74, 309–312. [Google Scholar] [CrossRef]
- Lurié, D.; Cremer, S. Zitterbewegung of quasiparticles in superconductors. Physica 1970, 50, 224–240. [Google Scholar] [CrossRef]
- Shen, S.Q. Spin Transverse Force on Spin Current in an Electric Field. Phys. Rev. Lett. 2005, 95, 187203. [Google Scholar] [CrossRef] [PubMed]
- Bernardes, E.; Schliemann, J.; Lee, M.; Egues, J.C.; Loss, D. Spin-Orbit Interaction in Symmetric Wells with Two Subbands. Phys. Rev. Lett. 2007, 99, 076603. [Google Scholar] [CrossRef] [PubMed]
- Lamata, L.; León, J.; Schätz, T.; Solano, E. Dirac equation and quantum relativistic effects in a single trapped ion. Phys. Rev. Lett. 2007, 98, 253005. [Google Scholar] [CrossRef] [PubMed]
- Gerritsma, R.; Kirchmair, G.; Zähringer, F.; Solano, E.; Blatt, R.; Roos, C. Quantum simulation of the Dirac equation. Nature 2010, 463, 68–71. [Google Scholar] [CrossRef] [PubMed]
- Cserti, J.; Dávid, G. Unified description of Zitterbewegung for spintronic, graphene, and superconducting systems. Phys. Rev. B 2006, 74, 172305. [Google Scholar] [CrossRef]
- Rusin, T.M.; Zawadzki, W. Transient Zitterbewegung of charge carriers in mono-and bilayer graphene, and carbon nanotubes. Phys. Rev. B 2007, 76, 195439. [Google Scholar] [CrossRef]
- Schliemann, J.; Loss, D.; Westervelt, R.M. Zitterbewegung of electronic wave packets in III-V zinc-blende semiconductor quantum wells. Phys. Rev. Lett. 2005, 94, 206801. [Google Scholar] [CrossRef] [PubMed]
- Zawadzki, W. Zitterbewegung and its effects on electrons in semiconductors. Phys. Rev. B 2005, 72, 085217. [Google Scholar] [CrossRef]
- Zawadzki, W.; Rusin, T. Nature of electron Zitterbewegung in crystalline solids. Phys. Lett. A 2010, 374, 3533–3537. [Google Scholar] [CrossRef]
- Geim, A.; Novoselov, K. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Zawadzki, W.; Rusin, T. Zitterbewegung (trembling motion) of electrons in semiconductors: A review. J. Phys. Condens. Matter 2011, 23, 143201. [Google Scholar] [CrossRef] [PubMed]
- Vaishnav, J.Y.; Clark, C.W. Observing zitterbewegung with ultracold atoms. Phys. Rev. Lett. 2008, 100, 153002. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X. Observing Zitterbewegung for Photons near the Dirac Point of a Two-Dimensional Photonic Crystal. Phys. Rev. Lett. 2008, 100, 113903. [Google Scholar] [CrossRef] [PubMed]
- Konno, N. Quantum Random Walks in One Dimension. Quantum Inf. Process. 2002, 1, 345–354. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Mosco, N.; Perinotti, P.; Tosini, A. Path-integral solution of the one-dimensional Dirac quantum cellular automaton. Phys. Lett. A 2014, 378, 3165–3168. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Mosco, N.; Perinotti, P.; Tosini, A. Discrete Feynman propagator for the Weyl quantum walk in 2 + 1 dimensions. Europhys. Lett. 2015, 109, 40012. [Google Scholar] [CrossRef]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Alim, U.; Möller, T. A Fast Fourier Transform with Rectangular Output on the BCC and FCC Lattices. In Proceedings of the International Conference on Sampling Theory and Applications (SampTA), Marseille, France, 18–22 May 2009.
- Huang, K. On the zitterbewegung of the Dirac electron. Am. J. Phys. 1952, 20, 479–484. [Google Scholar] [CrossRef]
- Lock, J.A. The Zitterbewegung of a free localized Dirac particle. Am. J. Phys 1979, 47, 797–802. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Perinotti, P. Lorentz symmetry for 3d Quantum Cellular Automata. 2015. arXiv:1503.01017. [Google Scholar]
- Thaller, B. Visualizing the kinematics of relativistic wave packets. 2004. arXiv:quant-ph/0409079. [Google Scholar]
- Braun, J.W.; Su, Q.; Grobe, R. Numerical approach to solve the time-dependent Dirac equation. Phys. Rev. A 1999, 59, 604–612. [Google Scholar] [CrossRef]
- Mocken, G.R.; Keitel, C.H. FFT-split-operator code for solving the Dirac equation in 2+1 dimensions. Comput. Phys. Commun. 2008, 178, 868–882. [Google Scholar] [CrossRef]
- Fillion-Gourdeau, F.; Lorin, E.; Bandrauk, A.D. Numerical solution of the time-dependent Dirac equation in coordinate space without fermion-doubling. Comput. Phys. Commun. 2012, 183, 1403–1415. [Google Scholar] [CrossRef]
- Bauke, H.; Keitel, C.H. Accelerating the Fourier split operator method via graphics processing units. Comput. Phys. Commun. 2011, 182, 2454–2463. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).