Numerical Investigation of Thermal Radiation and Viscous Effects on Entropy Generation in Forced Convection Blood Flow over an Axisymmetric Stretching Sheet

Abstract

Numerical and analytical investigation of the effects of thermal radiation and viscous heating on a convective flow of a non-Newtonian, incompressible fluid in an axisymmetric stretching sheet with constant temperature wall is performed. The power law model of the blood is used for the non-Newtonian model of the fluid and the Rosseland model for the thermal radiative heat transfer in an absorbing medium and viscous heating are considered as the heat sources. The non-dimensional governing equations are transformed to similarity form and solved numerically. A parameter study on entropy generation in medium is presented based on the Second Law of Thermodynamics by considering various parameters such as the thermal radiation parameter, the Brinkman number, Prandtl number, Eckert number.

1. Introduction

Heat transfer in forced convection in axisymmetric flow of a power-law fluid past a stretching sheet occurs in numerous applications such as the polymer industry [1], cooling of metallic plates [2], drawing of plastic sheets [3], fiber and wire drawing [4], hot rolling [5], paper fabrication [6], aerodynamics [7], etc. The heat transfer phenomenon is a serious criterion in such applications as the nature of the final product is dependent on the heat transfer rate [8,9,10]. There are some studies that take care of the calculation of the temperature and velocity fields for the axisymmetric flow of a power-law fluid past a stretching sheet without considering the effect of thermal radiation [11,12], but heat transfer by simultaneous radiation and convection is important in various cases [13,14].

Based on these applications, Crane [15] initiated the study on boundary layer flow induced in cylindrical coordinate due to a stretching cylinder. Crane’s work was developed in heat transfer by Wang [16], viscous effects by Burde [17] and Ishak [18,19], stagnation point effects by Weidman and Ali [20], slip effects by Wang and Ng [21], oscillation by Munawar et al. [22], hydromagnetic effects by Vajravelu et al. [23], permeable wall by Vajravelu et al. [24], etc.

The blood flow inside the sample body is used for an anthropometric test device by Joodaki et al. [25]. They simulated obese post-mortem human surrogate (PMHS) occupants’ kinematics in simulated frontal crashes where blood is screened for HIV and hepatitis A, B and C. In their simulations cardiovascular systems were pressurized to a nominal in vivo level (approximately 10 kPa for both) via tracheostomy and Hetastarch blood plasma replacement solution immediately prior to testing. Including cardiovascular systems leads to new results in comparison with the tests that were previously published [26,27]. In their experiments the vascular boundaries were exposed to a high rate of surface stretching while containing the blood [25]. The wall motion also can be induced by the tissue surface. Another application of vascular stretching is contractile function studies of permeabilized small mesenteric arteries. Small mesenteric artery rings were stretched to an optimum length by the normalization procedure described in contractile function studies of intact small mesenteric arteries [28]. In addition, the importance of wall stretching in vascular development has been comprehensively reviewed by Jones [29] and wall-blood interactions by Das et al. [30]. While blood exhibits viscoelastic behavior which may be attributed to the viscoelastic properties of the individual red cells and the internal structures formed by cellular interactions, it cannot be modeled as a non-Newtonian fluid.

Entropy generation effects due to flow and heat transfer over stretching flat plates in Cartesian coordinates have been investigated by numerous researchers [31,32,33,34,35,36,37,38]. On the other hand, a smaller number of investigations are considered in collected works concerning the study of entropy generation effects in flow over stretching surfaces in cylindrical coordinates [39,40] in comparison with Cartesian coordinate studies. Considering all the above, the goal of the present article was to investigate entropy production in the steady state fully developed forced convection incompressible flow over an axisymmetric stretching sheet such that the stretching wall is subjected to different wall temperatures and the Rosseland approximation model. The effects of thermal radiation coefficient, Prantdl number, and Brinkmann number on entropy generation are investigated analytically. The equations are solved numerically and the results are interpreted using graphs and tables.

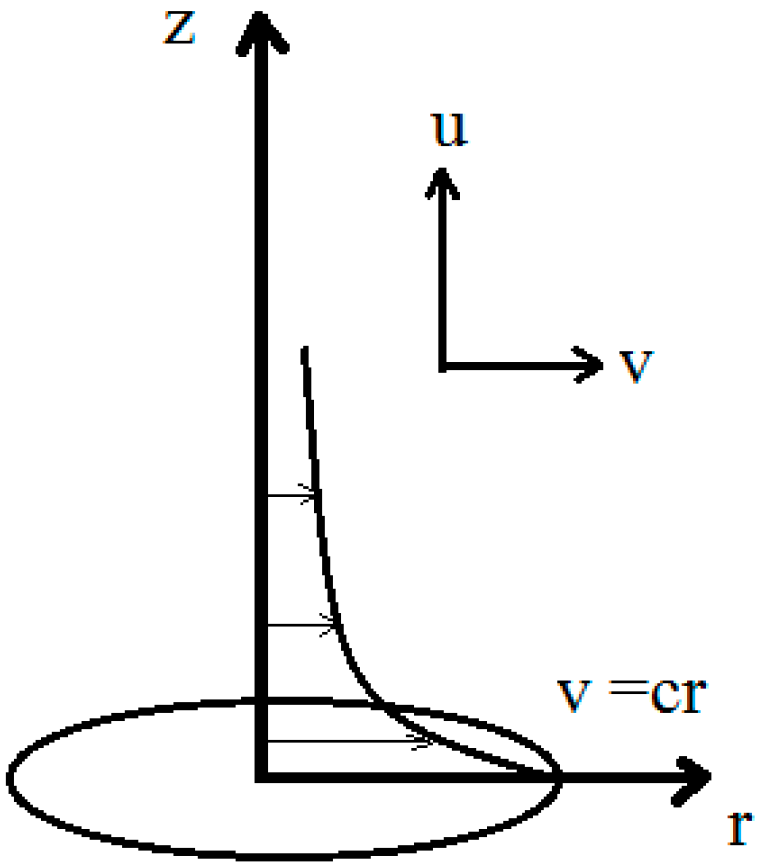
2. Governing Equations

With the purpose of comprehending the essential basics of laminar blood flow over an infinitely stretching sheet, a two-dimensional outline as exposed in Figure 1 is considered. The blood is considered non-Newtonian and incompressible. As illustrated, the fluid in contact with the surface of the non-permeable sheet will travel along with the sheet without any slippage. In this problem, an optically thick (highly absorbing medium) incompressible power law fluid passed a radially stretching sheet. The r- and z-components of the velocity at any point are denoted by v and u; while the stretching sheet (z = 0) is maintained at the uniform temperatures T_w, respectively. The temperature difference between the medium temperature, T_∞, and the stretching sheet, T_w, is also assumed to be high enough to induce heat transfer due to radiation. Since an infinitely large medium is assumed, the flow velocity at far distances from the plate is assumed to be zero.

In cylindrical coordinates the continuity ($v_{\varphi }$ = 0) and momentum (v_zz ≫ v_rr) equations are:

$$\frac{\partial v}{\partial r}+\frac{v}{r}+\frac{\partial u}{\partial z}=0$$

(1)

$$\rho \left(v\frac{\partial v}{\partial r}+u\frac{\partial v}{\partial z}\right)=\frac{\partial }{\partial z}\left(K{\left|\frac{\partial v}{\partial z}\right|}^{n-1}\frac{\partial v}{\partial z}\right)$$

(2)

where (u,v) are the velocity components in the (z,r) directions, ρ is the fluid density, the flow consistency index of blood is K = 0.017 Pa·sⁿ and the power law index for blood is n = 0.708. For n = 1 the fluid is Newtonian, with a dynamic coefficient of viscosity k. For n > 1 the behavior of the fluid is dilatant or shear-thickening and for 0 < n < 1 the behavior is shear-thinning. In this work we shall restrict our study to the blood flow and the values of the power law around n = 0.708 which can represent the effect of perturbations near this point an variation of steady state value exposed to impact [25,26,27]. The energy equation for thermal radiative absorbance of thermal radiation in a semi-transparent gray medium is considered here that as ruled by the Rosseland approximation [41] for conductive radiative heat flux. The diffusion approximation is extremely convenient to use. The equation of energy is:

$$\rho C_p\left(v\frac{\partial T}{\partial r}+u\frac{\partial T}{\partial z}\right)=\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}-\frac{\partial q_r}{\partial y}\right)+K{\left|\frac{\partial v}{\partial z}\right|}^{n+1}$$

(3)

Following the Rosseland approximation (for the case of an optically thin grey medium) with radiative heat flux q_r in Equation (3) is modeled as:

$$q_r=-\frac{4\sigma *}{3k*}\frac{\partial T^4}{\partial y}$$

(4)

where σ* and $k*$ are the Stephan-Boltzman constant and the mean absorption coefficient, respectively. As the differences within the flow are such that T⁴ can be expressed as a linear function of temperature, $T^4=T_{\infty }^4+4T_{\infty }^3\left(T-T_{\infty }^{}\right)+\mathrm{...}$, expanding T⁴ in a Taylor series about T_∞ and neglecting higher order terms thus:

$$T^4\approx 4T_{\infty }^{3}T-3T_{\infty }^4$$

(5)

One may define a radiative conductivity. This model is more valuable for the optically thick medium with optical thickness (k*r) greater than 3 and the boundary layer equations that govern the heat transfer phenomenon is written as [38]:

$$\rho C_p\left(v\frac{\partial T}{\partial r}+u\frac{\partial T}{\partial z}\right)=\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}+\frac{4\sigma }{3\chi }\frac{\partial \left(n^2{T}^4\right)}{\partial z}\right)+K{\left|\frac{\partial v}{\partial z}\right|}^{n+1}$$

(6)

where T is the medium temperature, k is the thermal conductivity of the fluid, μ is the viscosity of the fluid, σ is the Stefan-Boltzmann constant, n is the refractive index, and χ is the Rosseland-mean absorption coefficient (for absorption, scattering, and/or extinction) of the optically thick medium. The associated boundary conditions at the solid walls and infinity are:

$$v\left(z=0\right)=cr$$

(7)

$$v\left(z=\infty \right)=0$$

(8)

$$u\left(z=0\right)=0$$

(9)

$$T\left(z=0\right)=T_w$$

(10)

$$T\left(z=\infty \right)=T_{\infty }$$

(11)

The system of Equations (1), (2) and (6)–(11) can be solved numerically or analytically. Similar equations are solved in other studies by numerical methods [42,43,44] or analytical series solution methods [45]. In thermodynamics, entropy is a measure of disorder and defined as a degree of the number of specific means where a thermodynamic system could be settled. The entropy is a state function and its alteration associated to the initial and final state. In keeping with the Second Law of Thermodynamics, the entropy of an insulated system on no condition decreases; such a system will automatically change in the direction of thermodynamic equilibrium, the arrangement with maximum entropy. The present system which is not isolated and has the irreversible processes decrease in entropy provided them increase the entropy of its surroundings by at least that same quantity (increase the combined entropy of the system and its environment).

The irreversibility in the boundary layer flow of a blood fluid has two components of energy and momentum. Consequently, local volumetric entropy production may occur as a result of fluid friction and heat transfer in the direction of finite temperature gradients. Following Jamalabadi [45], the volumetric rate of entropy generation is given by:

$${\dot{S^{‴}}}_g=\frac{1}{T_{\infty }^2}\left(k\frac{\partial T}{\partial z}+\frac{16T_{\infty }^3{n}^2\sigma }{3\chi }\frac{\partial T}{\partial z}\right)\left(\frac{\partial T}{\partial z}\right)+\frac{K}{T_{\infty }}{\left|\frac{\partial v}{\partial z}\right|}^{n+1}$$

(12)

The first term in Equation (8) refers to the heat transfer irreversibility and the second term symbolizes the local entropy generation rate due to fluid friction, correspondingly.

The equivalent stream formulations of momentum and energy equations are:

$$\frac{1}{r^2}\frac{{\partial }^2\psi }{\partial r\partial z}\frac{\partial \psi }{\partial z}-\frac{1}{r^3}{\left(\frac{\partial \psi }{\partial z}\right)}^2-\frac{1}{r^2}\frac{\partial \psi }{\partial r}\frac{{\partial }^2\psi }{\partial z^2}=\frac{K}{\rho }{\left(-\frac{1}{r}\right)}^n\frac{\partial }{\partial z}\left({\left|\frac{{\partial }^2\psi }{\partial z^2}\right|}^{n-1}\frac{{\partial }^2\psi }{\partial z^2}\right)$$

(13)

$$\frac{1}{r}\frac{\partial \psi }{\partial r}\frac{\partial \theta }{\partial z}-\frac{1}{r}\frac{\partial \psi }{\partial z}\frac{\partial \theta }{\partial r}=\alpha \frac{{\partial }^2\theta }{\partial z^2}\left(1+N_R\right)+\frac{K}{\rho C_p\left(T_w-T_{\infty }\right)}{\left|-\frac{1}{r}\frac{{\partial }^2\psi }{\partial z^2}\right|}^{n+1}$$

(14)

where ψ denotes the stream function and is defined as:

$$v=-\frac{1}{r}\frac{\partial \psi }{\partial z}$$

(15)

$$u=\frac{1}{r}\frac{\partial \psi }{\partial r}$$

(16)

where θ denotes the dimensionless temperature and is defined as:

$$\theta =\frac{T-T_{\infty }}{T_w-T_{\infty }}$$

(17)

and N_R is 16k_R where k_R is the radiation conductivity:

$$k_R=\frac{\sigma n^2{\left(T_w-T_{\infty }\right)}_{}^3}{3k\chi }$$

(18)

Since the Equation (13) is a parabolic partial differential equation and since there is no geometric length scale in the problem, a similarity type of solution will be sought. The r component of velocity will have the following functional form:

$$v=cr{f}^{\prime }(\eta )$$

(19)

where η is the similarity variable, f is the dimensionless stream function , and the prime denotes differentiation with respect to η. But when η is constant, v should be constant. Since the similarity variable is:

$$\eta ={\left(\frac{\rho c^{2-n}(3n+1)}{Kn(n+1)}\right)}^{\frac{1}{n+1}}{r}^{\frac{1-n}{1+n}}z$$

(20)

Although the similarity parameter η, is independent of radial coordinate when describes the motion of a Newtonian fluid (in the case n = 1), but the velocity is linearly dependent on the radial coordinates as stated by Equation (19). To explore the physical meaning of the results of the similarity solution in a Newtonian case with variable viscosity see the Makinde et al. [43].

As well, for values of n < 1, the similarity variable is an increasing function of both variables “r” and “z”. This fact seems to be in contrast to the similarity variable in Cartesian coordinate which is a ratio between the variables “y” and “x” (Blasius boundary layer). Again, those figures with n < 1 are physically inadmisible. This difference between the cylindrical coordinates and Cartesian coordinates is not essential as in a similarity solution we look for a solution which at least one co-ordinate lack a distinguished origin; more physically, it describes a flow which “looks the same” either at all times, or at all length scales.

In order to elucidate the physical principle, in this paper the non-dimensionalized variables are presented. The non-dimensional parameters which arise are:

$$Pr=\frac{C_{p}K{\left(cr\right)}^{n-1}}{k}$$

(21)

$$Br=\frac{K{\left(cr\right)}^{n+1}}{k\left(T_w-T_{\infty }\right)}$$

(22)

$$Be=\frac{\left(k+\frac{16T_{\infty }^3{n}^2\sigma }{3\chi }\right){\left(\frac{\partial T}{\partial z}\right)}^2}{\left(k+\frac{16T_{\infty }^3{n}^2\sigma }{3\chi }\right){\left(\frac{\partial T}{\partial z}\right)}^2+K{T}_{\infty }^{}{\left|\frac{\partial v}{\partial z}\right|}^{n+1}}$$

(23)

$$N_s=\frac{T_{\infty }{\dot{S^{‴}}}_g}{K{c}^{n+1}}={\dot{S^{‴}}}_g=\frac{1}{K{c}^{n+1}{T}_{\infty }^{}}\left(k+\frac{16T_{\infty }^3{n}^2\sigma }{3\chi }\right){\left(\frac{\partial T}{\partial z}\right)}^2+{\left|\frac{1}{c}\frac{\partial v}{\partial z}\right|}^{n+1}$$

(24)

where the Pr is the Prantdl number, Be is the Bejan number (in the context of thermodynamics, the ratio of heat transfer irreversibility to total irreversibility due to heat transfer and fluid friction; in the context of fluid mechanics, the dimensionless pressure drop along a channel), Br is the ratio between heat produced by viscous dissipation and heat conduction (the ratio of viscous heat generation to external heating), and N_s is the dimensionless form of local entropy generation rate in Equation (12). From Equation (23), it is obvious that the Bejan number ranges from 0 < Be < 1. While Be = 0 represents the limit case of fluid friction dominated irreversibility, Be = 1 corresponds to the limit case of heat transfer dominated irreversibility. The contribution of both heat transfer and fluid friction to entropy production in the flow system is the same when Be = 0.5. These expressions may be evaluated as follows:

Substituting various derivatives that appear in the boundary-layer Equations (9) and (10), and considering dimensionless parameters in Equations (13), (14) and (21)–(24), the non-dimensional momentum and energy equations as a system of ordinary coupled differential equations can be rewritten as:

$${\left|f^{″}(\eta )\right|}^{n-1}{f}^{‴}(\eta )+f(\eta )f^{″}(\eta )-\frac{n+1}{3n+1}{\left(f^{\prime }(\eta )\right)}^2=0$$

(25)

$$(1+N_R){\theta }^{″}+\frac{2n\mathrm{Pr}}{n+1}f{\theta }^{\prime }+Br{f^{″}}^2=0,$$

(26)

In addition, the non-dimensional form of the boundary conditions in the equations from Equations (3) to Equations (6) can be rewritten as:

$$f(0)=0$$

(27)

$$f^{\prime }(0)=1$$

(28)

$$\underset{\eta \to \infty }{\lim }{f}^{\prime }(\eta )=0$$

(29)

$$\theta \left(z=0\right)=1$$

(30)

$$\underset{\eta \to \infty }{\lim }\theta (\eta )=0$$

(31)

The components of dimensionless entropy generation are:

$$S_U={\left|f^{″}\right|}^{n+1}\left(\frac{\rho c^{2-n}(3n+1)}{Kn(n+1)}\right)$$

(32)

$$S_{\theta }=\frac{{\left(\frac{\rho (3n+1)}{n(n+1)}\right)}^{\frac{2}{n+1}}\left(k+\frac{16T_{\infty }^3{n}^2\sigma }{3\chi }\right)}{K^{\frac{n+3}{n+1}}{c}^{\frac{3-4n-n^2}{n+1}}{T}_{\infty }^{}}{\left({\theta }^{\prime }\right)}^2$$

(33)

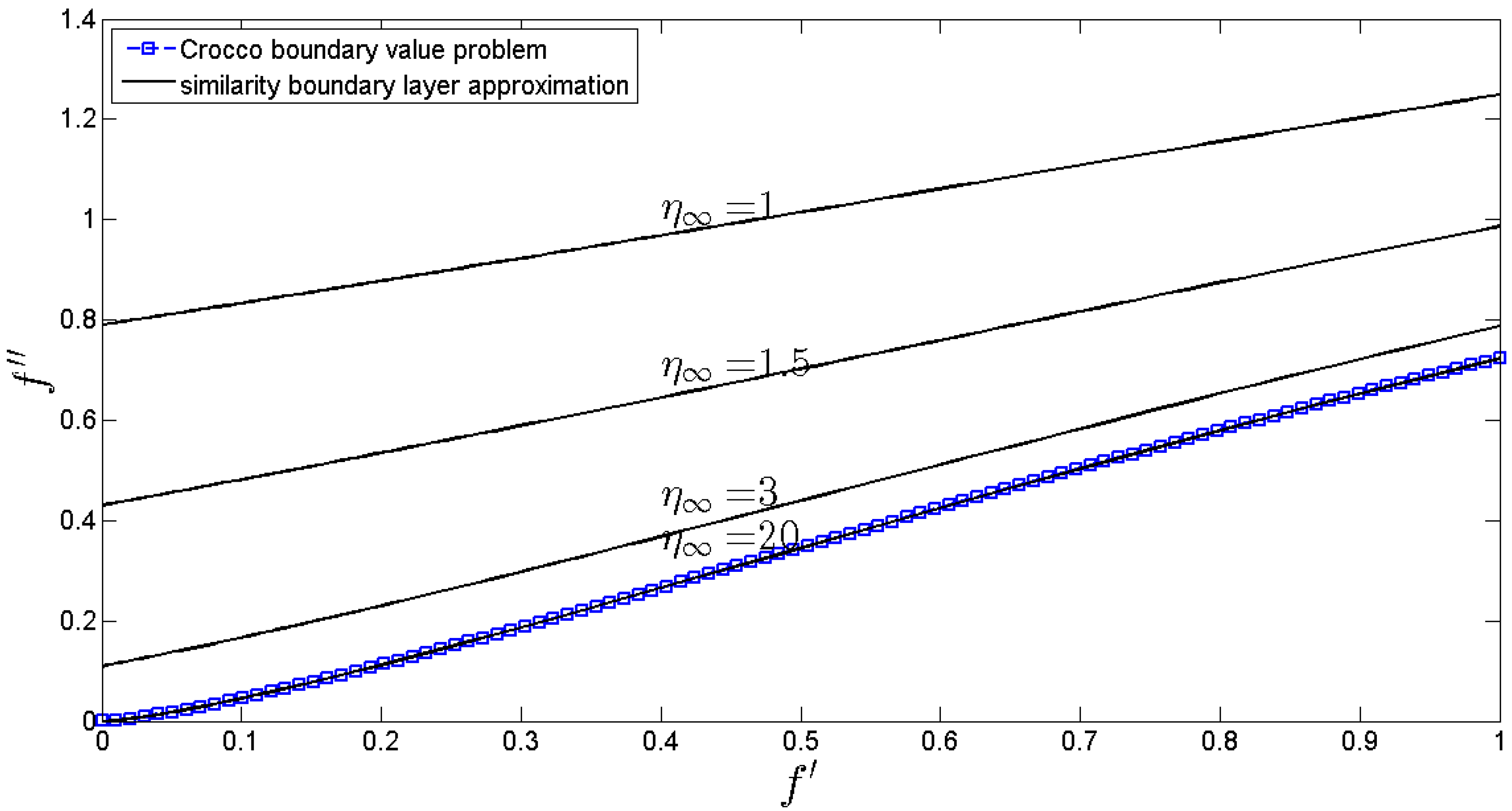
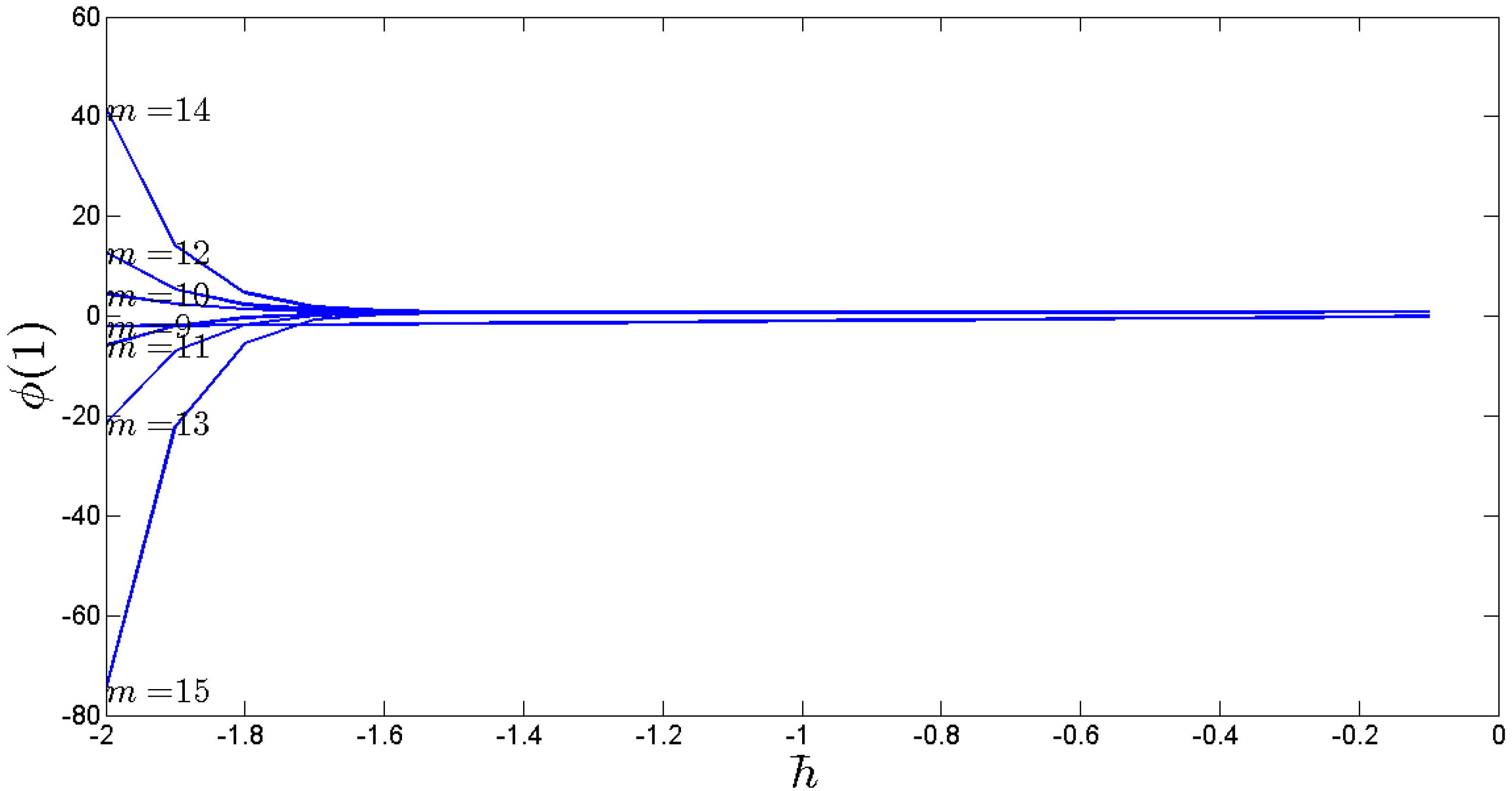
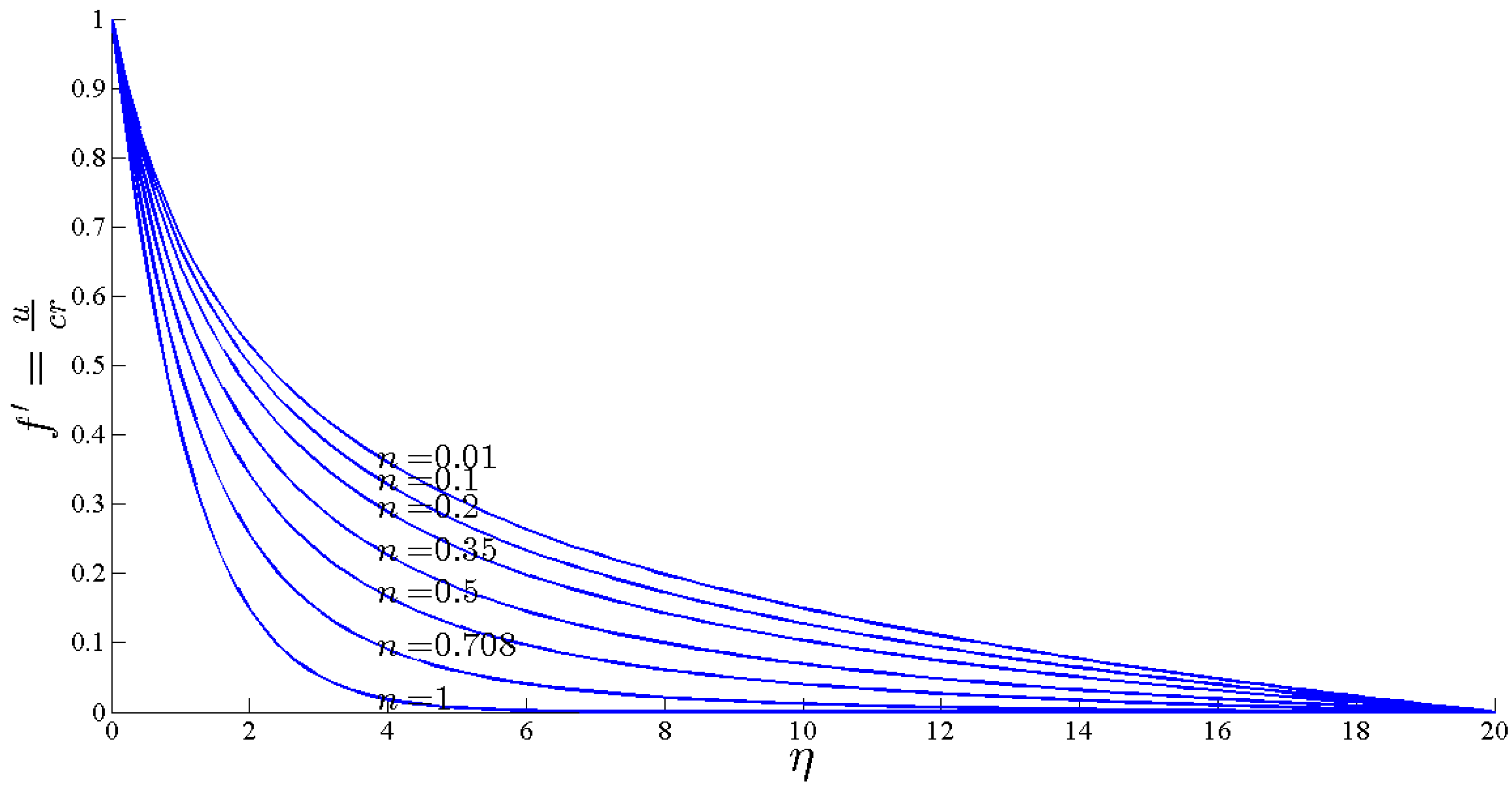
3. Results and Discussions

Solving the Equations (25) and (26) with the boundary conditions of Equations (27)–(31) is presented in this section. That system of ordinary differential equations are the governing equations of steady state blood forced convection flow in thermal radiative absorbing medium with viscous effects over an axisymmetric stretching sheet under the no-slip conditions. After solving that problem the entropy generation in the blood flow is discussed.

To avoid the error caused by replacing finite length as the boundary layer thickness instead of infinity length the Crocco variables are introduced to transform the system of equations into a finite boundary problem. The Crocco transform which uses the derivative of the main function (f′) as the independent variable (instead of η) is:

$$\lambda =f^{\prime }(\eta )$$

(34)

$$\varphi (\lambda )=\frac{3n+1}{{\left(n+1\right)}^2}{\left|f^{″}(\eta )\right|}^{n+1}$$

(35)

which convert Equations (25) into:

$$\varphi {\varphi }^{″}+\frac{\left(n-1\right)\lambda \varphi +{\lambda }^2{\varphi }^{\prime }-{{\varphi }^{\prime }}^2}{n+1}=0$$

(36)

and transform Equations (27)–(29) into:

$$\varphi (0)=0$$

(37)

$${\varphi }^{\prime }(1)=1$$

(38)

This has the advantage that the integration region is then finite. The non-dimensional first order differential governing Equation (25) is solved numerically by using Runge‒Kutta‒Fehlberg method with shooting technique [34] for various finite boundary layer lengths. The results are compared with the solution of Crocco-transformed Equation (36) and plotted in Figure 2. The solution of 1D governing Equations (25) and (26), which can be solved using HAM (Homotopy Analysis Method) analytical techniques, is classified as the parabolic partial differential equations and cannot be considered as a computational fluid dynamics. The deduction of the boundary layer equations, by use of the order of magnitude analysis on governing Navier‒Stokes equations of viscous fluid flow leads to a parabolic partial differential equations, rather than the elliptical form of the full Navier‒Stokes equations.

The governing equation of momentum for the continuous stretching sheet immersed in blood can be solved analytically by use of the Homotopy Analysis Method (HAM). To solve the non-linear equation expressed by Equation (36) and subject to the boundary conditions of Equations (37) and (38). The non-linear operator is defined as follows:

$$N_f[\varphi (\lambda :q)]=\varphi (\lambda :q){\varphi }^{″}(\lambda :q)-\frac{{{\varphi }^{\prime }}^2(\lambda :q)}{n+1}+\frac{{\lambda }^2}{n+1}{\varphi }^{\prime }(\lambda :q)+\frac{n-1}{n+1}\lambda \varphi (\lambda :q)$$

(39)

where $q\in [0,1]$ is the embedding parameter. As the embedding parameter increases from 0 to 1, the parameters expressed by $\varphi$ (η; q) vary from the initial guess (q = 0), $\varphi$ (η) to the exact solution, $\varphi$ (η), which expanding in a power series of q in by Taylor’s theorem; Similar to the Blasius which provided a solution in power series, using Taylor series with respect to q results in:

$$L[{\varphi }_m(\lambda )-{\varphi }_{m-1}(\lambda )]/\hslash ={\displaystyle \sum _{r=0}^{m-1}\left({\varphi }_m{{\varphi }^{″}}_{m-r-1}-\frac{{\varphi }_m{{\varphi }^{\prime }}_{m-r-1}}{n+1}\right)}+\frac{{\lambda }^2}{n+1}{{\varphi }^{\prime }}_{m-1}+\frac{n-1}{n+1}\lambda {\varphi }_{m-1}$$

(40)

where $\hslash$ is an auxiliary parameter, ${\varphi }_{m-1}$ is an initial approximation to the solution that satisfies the given boundary conditions, the initial approximation and linear operator defined by linear function (${\varphi }_0$ = λ). The linear operator L should normally be of the same order as the non-linear operator. Homotopy analysis method can be expressed by many different base functions (Liao [46]), according to the governing equations. It is straightforward to use a base function in the form of polynomials:

$$\varphi (\eta ;q)={\varphi }_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{\varphi }_m(\eta )q^m}$$

(41)

where:

$${\varphi }_m(\eta )=\frac{1}{m!}{\frac{{\partial }^m\varphi (\eta ;q)}{\partial q^m}|}_{q=0}$$

(42)

where the corresponding high-order terms have solutions with a functional form similar to the base functions. Note that the zero-order deformation Equation (42) contains the auxiliary parameter and the auxiliary function. Assuming that both auxiliary parameter and the auxiliary function are properly chosen so that the series is convergent at q = 1, the second approximation is:

$${\varphi }_1(\eta )=\frac{3n+3+\hslash (3-n)}{3n+3}\lambda -\frac{\hslash }{2n+2}{\lambda }^2+\frac{\hslash n}{12n+12}{\lambda }^4$$

(43)

Figure 3 presents the effect of varying the number of terms in polynomial approximation to the $\varphi$ (1) versus auxiliary parameter ($\varphi$ (1)_exact = 0.6888095535). As shown the HAM has the acceptable results for the series with more than 10 terms. Figure 4 illustrates the effect of the power-law index on the non-dimensional velocity profile. For all of the curves, the η_∞ is considered as 20 which Figure 2 proves has enough accuracy for numerical computations. As noted before the current research is focused on blood flow for which the flow consistency index and power law index is given (n = 0.708). Although the flow consistency index appears in the similarity variable the final solution is independent of the flow consistency index and is just a function of the power law index. As shown, by increasing the power-law index the boundary layer thickness is smaller and the effect of the moving surface is just sensed at near distances.

The second derivativee of the dimensionless stream function versus power-law index is shown in Figure 5. As presented, with an increase of the power-law index the second derivative of the dimensionless stream function is greater. As the second derivative of the dimensionless stream function is a measure of the skin friction coefficient, a higher friction at the surface based on the increase of the power-law index is reasonable. Figure 6 illustrates the non-dimensional temperature profile for various power-law indexes. Similar to Figure 4 for all curves the η_∞ is considered as 20 and by increasing the power-law index the thermal boundary layer thickness is smaller and the effect of the moving surface just sensed at near distances. The corresponding derivative of the dimensionless temperature which is a measure of the Nusselt number for the power-law indexes of 0.01, 0.1, and 0.708 is illustrated in Figure 7. As shown by increasing the power-law index the thinner thermal boundary layer leads to a higher rate of heat exchange. In Figure 8 the dimensionless thermal entropy generated versus similarity variable for various power-law indexes is presented. As shown most of the thermal entropy generation occurs near the stretching wall and it increases with the increase of power law index.

Figure 9 illustrates the non-dimensional temperature profile for various Prantdl numbers. As demonstrated by increasing the Prantdl number the thermal boundary layer depth is reduced and the effect of the stretching sheet surface is felt in the fluid near it. The corresponding derivative of dimensionless temperature which is a measure of Nusselt number for Prantdl numbers in the range of 0.01 through 7 is exemplified in Figure 10. As revealed by the growth of the Prantdl number the skinny thermal boundary layer causes a greater heat transfer rate. In Figure 11 the dimensionless thermal entropy generated versus similarity variable for various Prantdl numbers is presented. As shown most of the thermal entropy generation occurs near the stretching wall and it decrease rapidly as the Prantdl number increases.

Figure 12 illustrates the effect of thermal radiation parameter on various thermal and entropy generation aspects of the system. An accurate investigation of the non-dimensional temperature profile for various thermal radiation parameter near the wall (like the other figures the results of Figure 2 is used here and all profiles have η_∞ equal to 20) the thermal boundary layer depth is increased by increasing the thermal radiation parameter (in η_∞ < 1) and the effect of a stretching sheet surface affects the temperature in the adjacent fluid. The matching derivative of the dimensionless temperature is proportional to Nusselt number for the thermal radiation parameters in range of 0.01 through 10 in logarithmic scale as exemplified in Figure 13. As discovered by intensification of the thermal radiation parameter the lean thermal boundary layer causes a better convective heat transfer. In Figure 14 the dimensionless thermal entropy produced versus similarity variable for numerous thermal radiation parameters is revealed. As shown most of the thermal entropy generation occurs near the stretching sheet and it decreases quickly as the thermal radiation parameter increases.

The effect of the Brinkman parameter as a measure of viscous dissipation is demonstrated in Figure 15. As seen in Figure 15, by increasing the Br from 0.01 to 10 the dimensionless temperature increased. For low values of Br the dimensionless temperature is not changed. As shown the θ′ is increased dramatically by increasing Br even while at low Br it changes smoothly as presented in Figure 16. Figure 17 exemplifies the effect of the Brinkman number on the dimensionless temperature component of the entropy profiles. As seen by increasing Br the temperature component of the entropy increases, especially near the wall. The maximum again appears at the walls. By increasing of distance from the stretching wall, the dimensionless temperature profile decreases and this loss is more for lower Brinkman numbers. As illustrated in Figure 18 the Br has less effect on total S_u than S_θ, but similarly it is increased by increases of Br.

4. Conclusions

In this study, the investigation of steady state flow near an axisymmetric stretching sheet with thermal radiation and viscous heating has been thoroughly performed. The results can be summarized as follows:

(1)

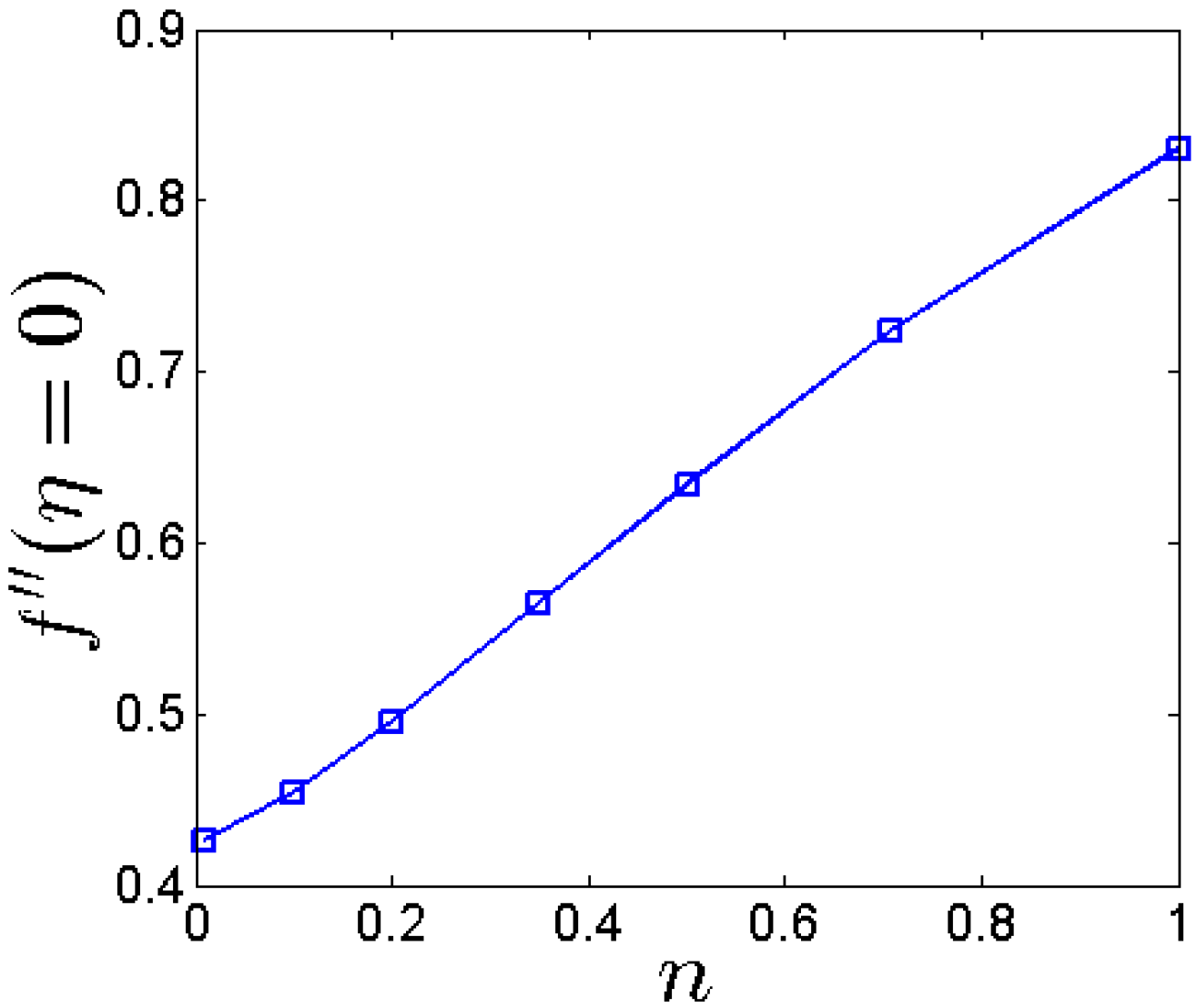
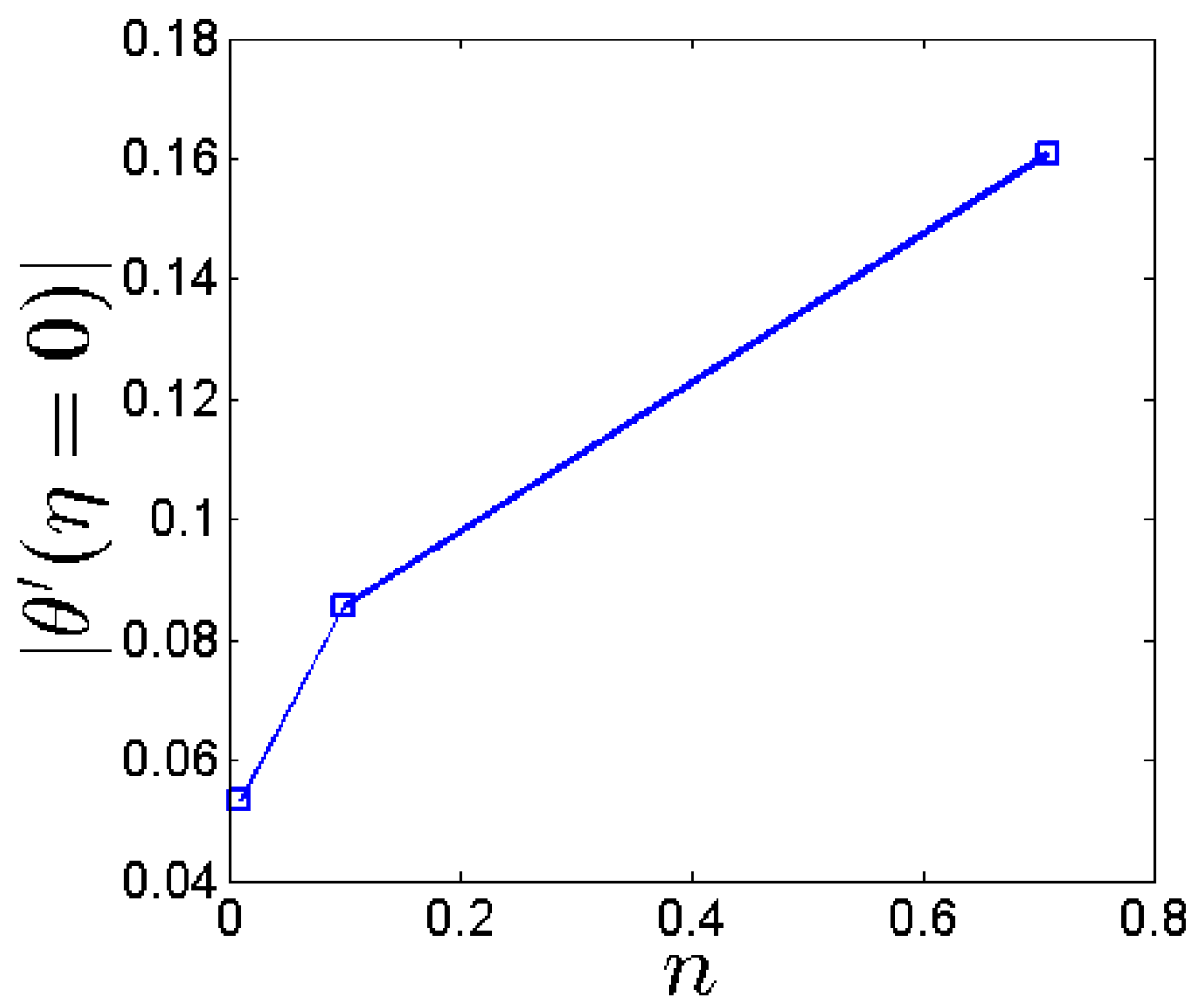
By increasing n, the boundary layer of fluid flow and heat flow is decreased and the heat transfer rate and fluid friction on the stretching sheet is increased.

(2)

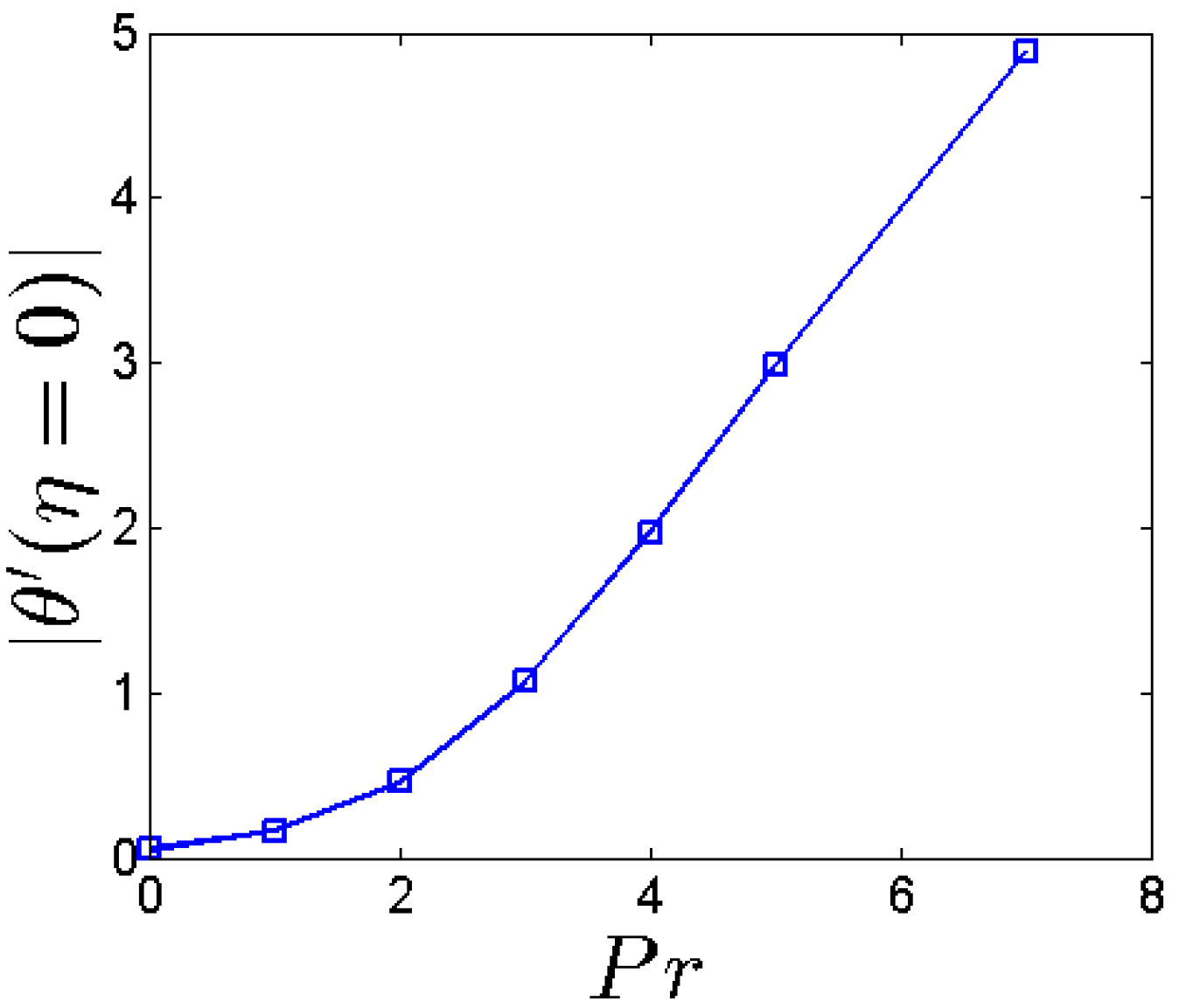
By increasing Pr, the boundary layer of fluid flow is decreased and the heat transfer rate on the stretching sheet is increased.

(3)

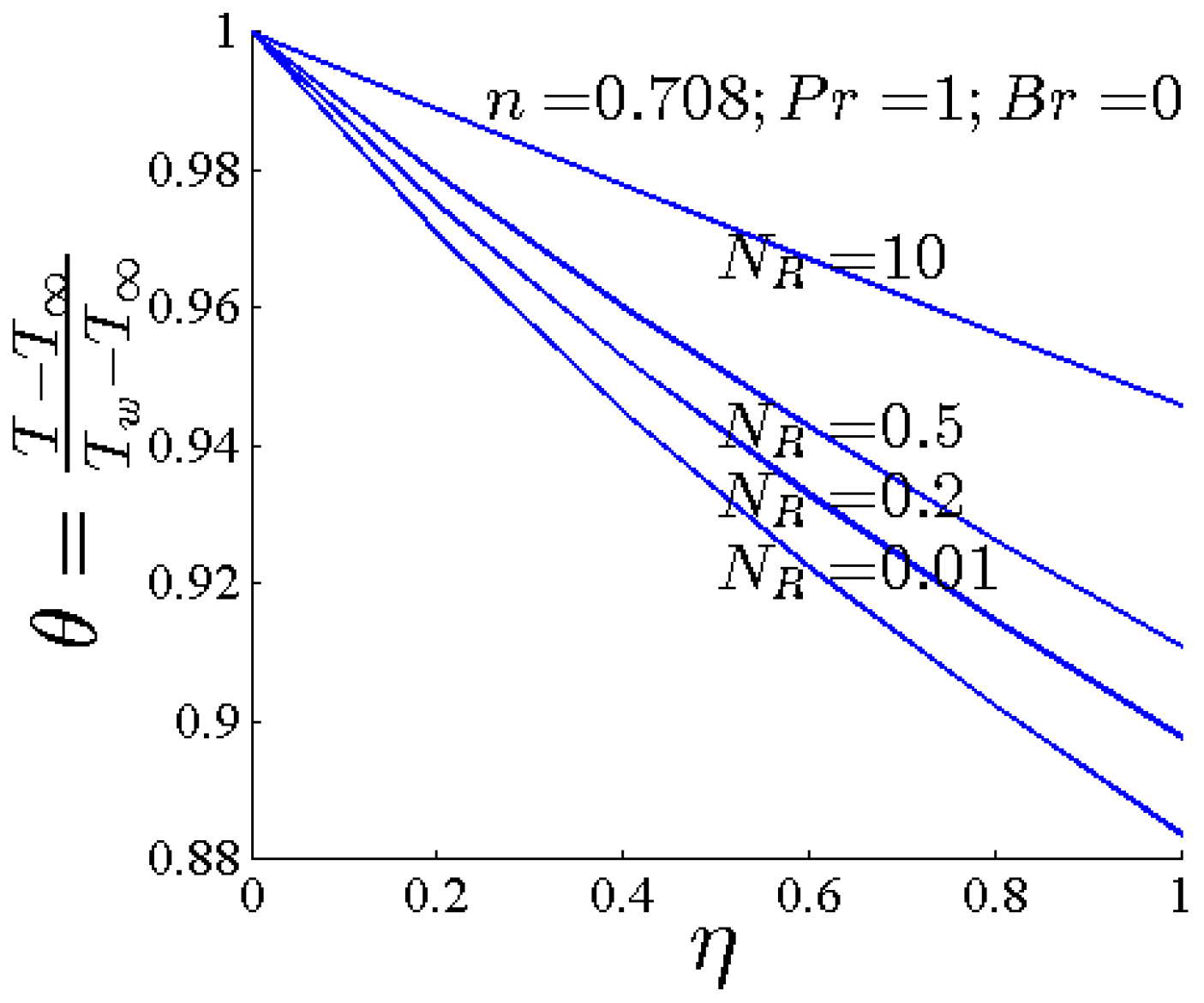
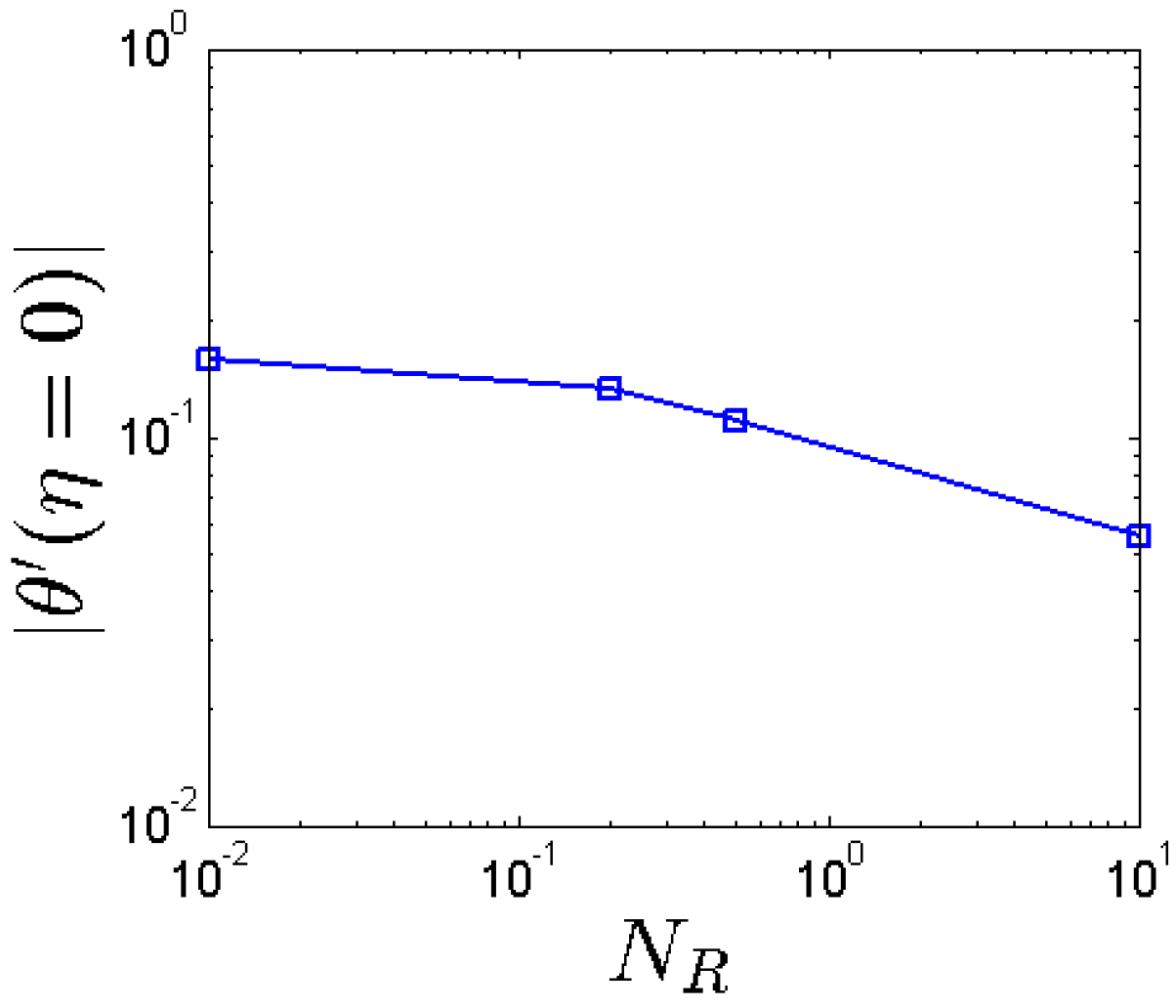
By increasing N_R, the boundary layer of fluid flow is increased and the convective heat transfer rate on the stretching sheet is decreased.

(4)

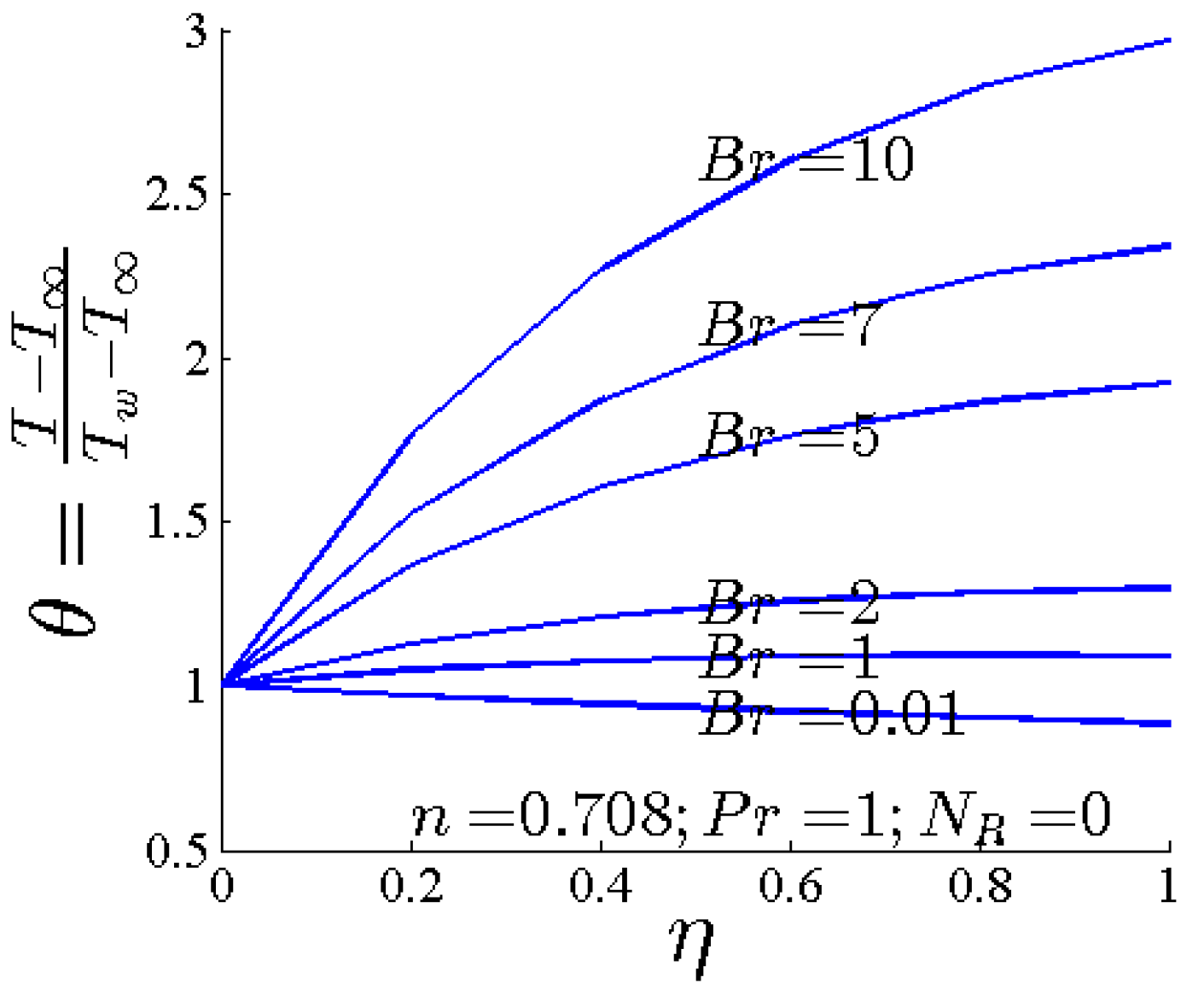
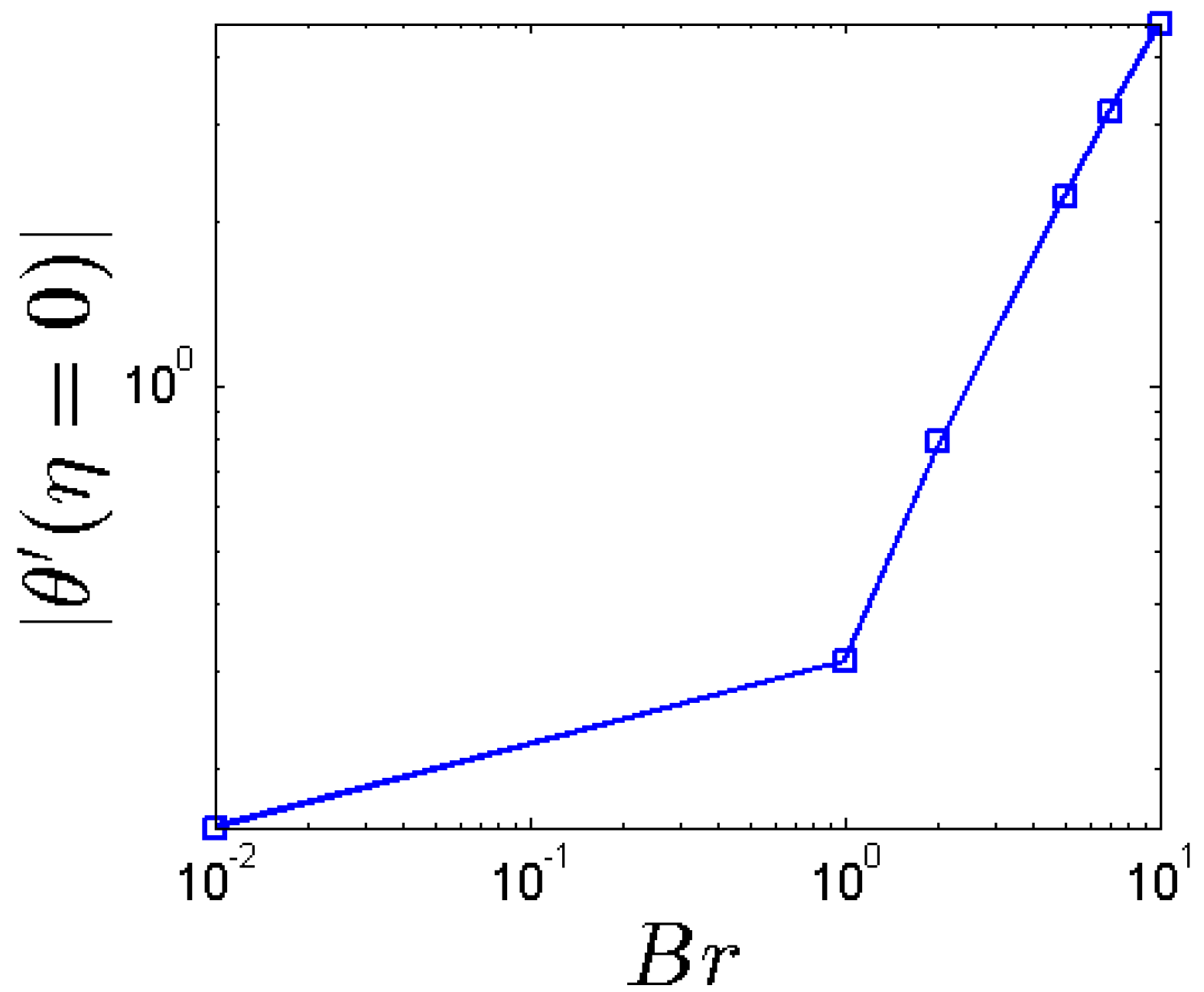
By increasing Br, the boundary layer of fluid flow and the convective heat transfer rate on the stretching sheet are increased.

(5)

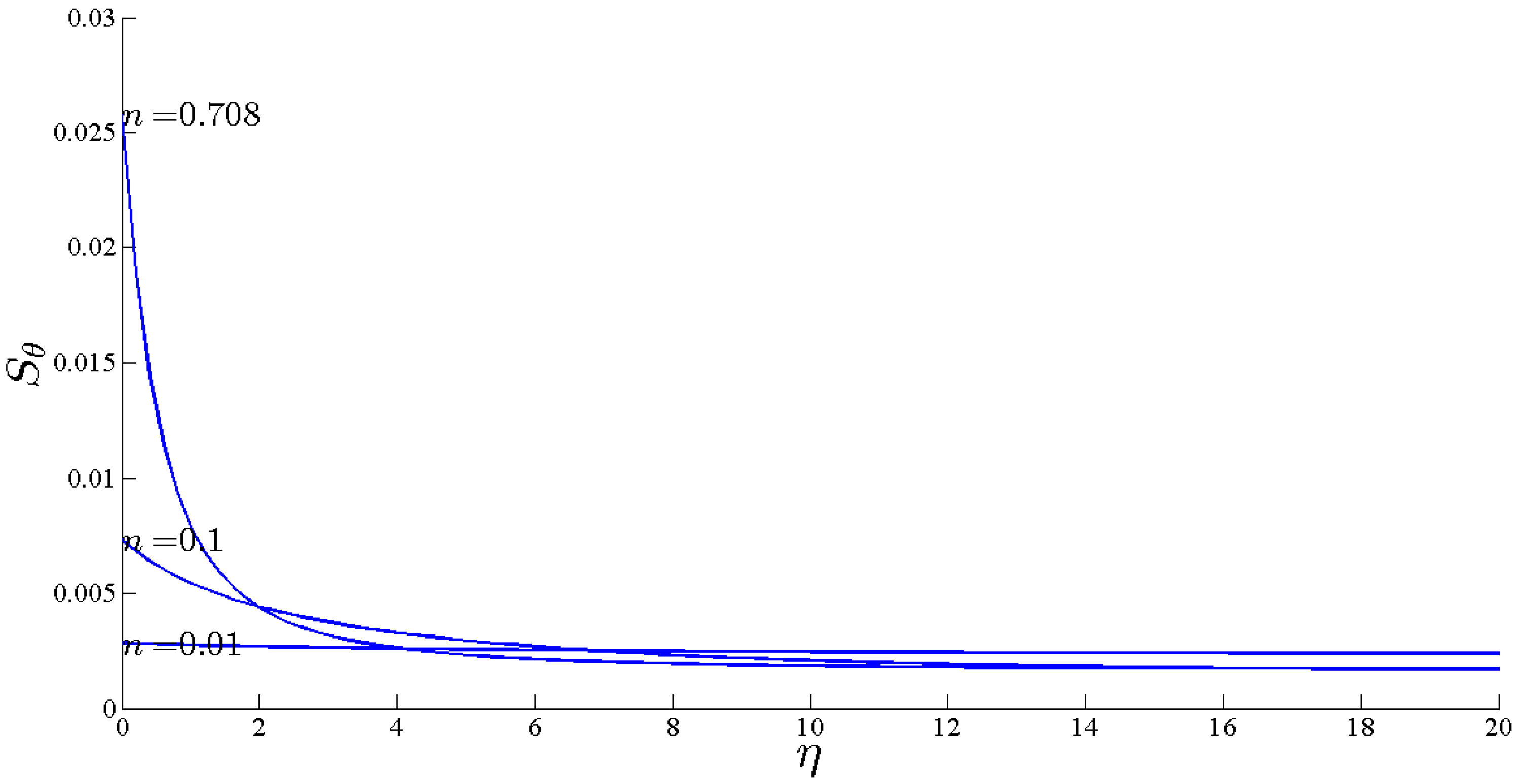
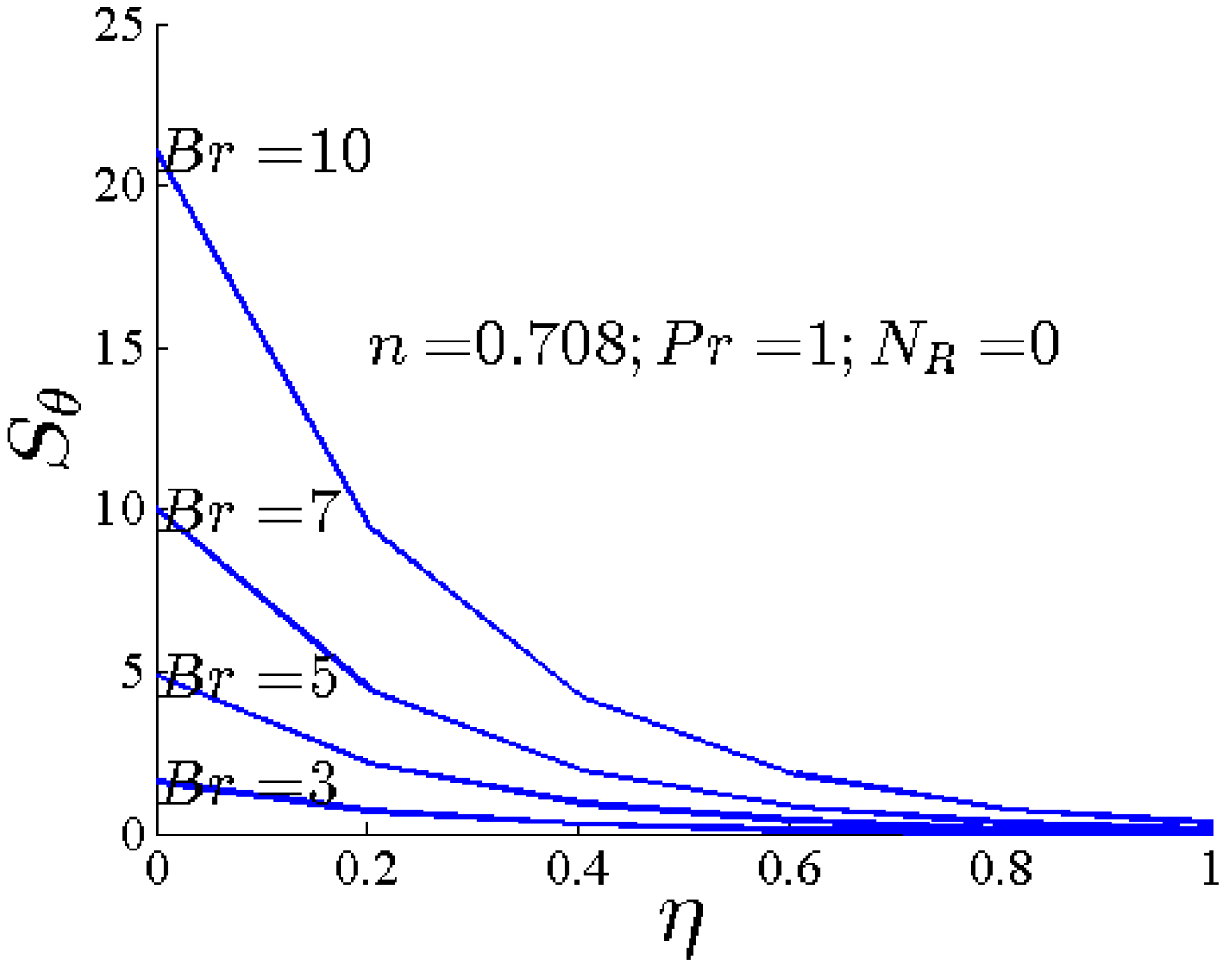
By increasing n, Pr the heat transfer part of the entropy increases dramatically while the viscous part of the entropy is not changed.

(6)

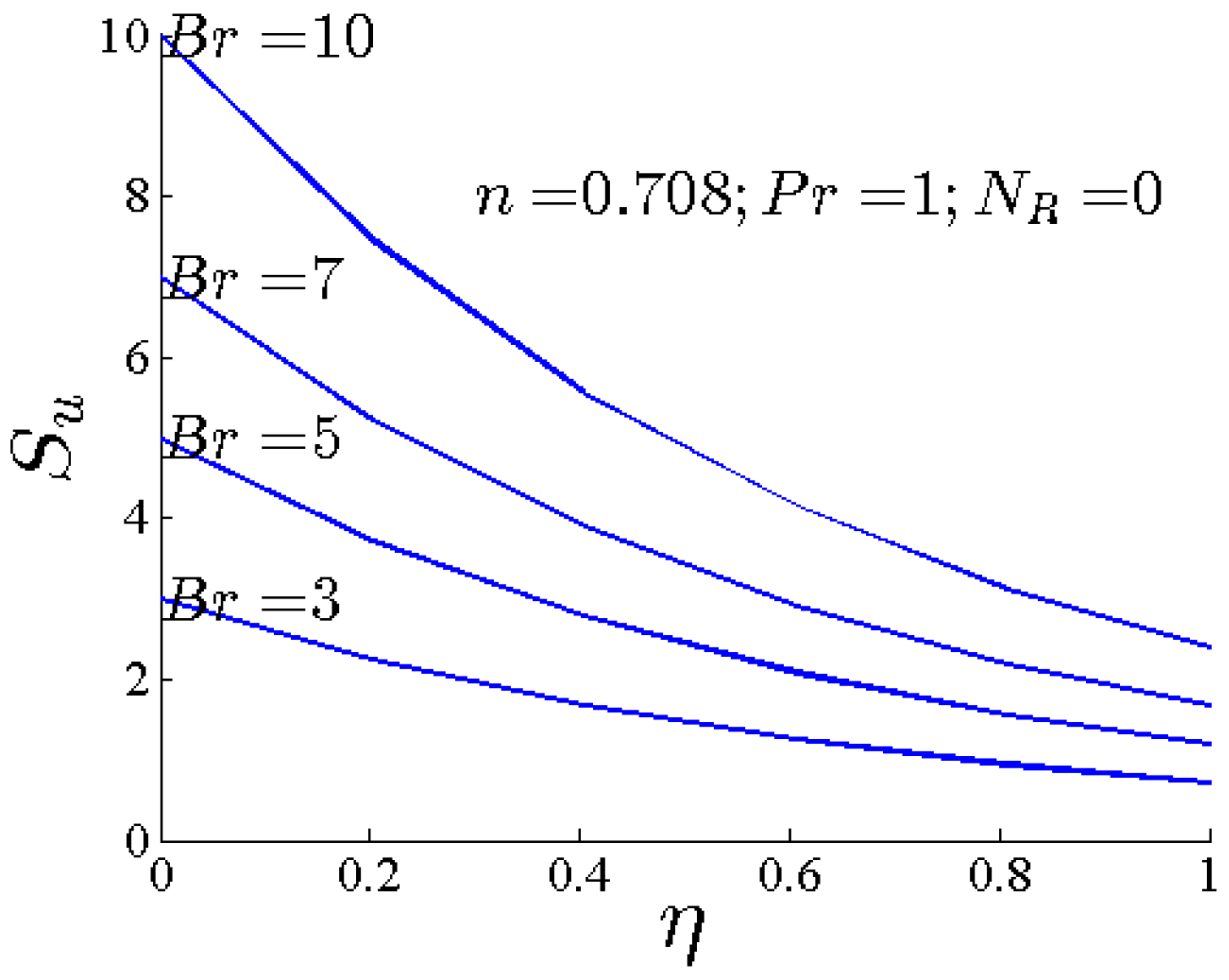
By increasing Br, the total heat transfer entropy generation and its component increase.

(7)

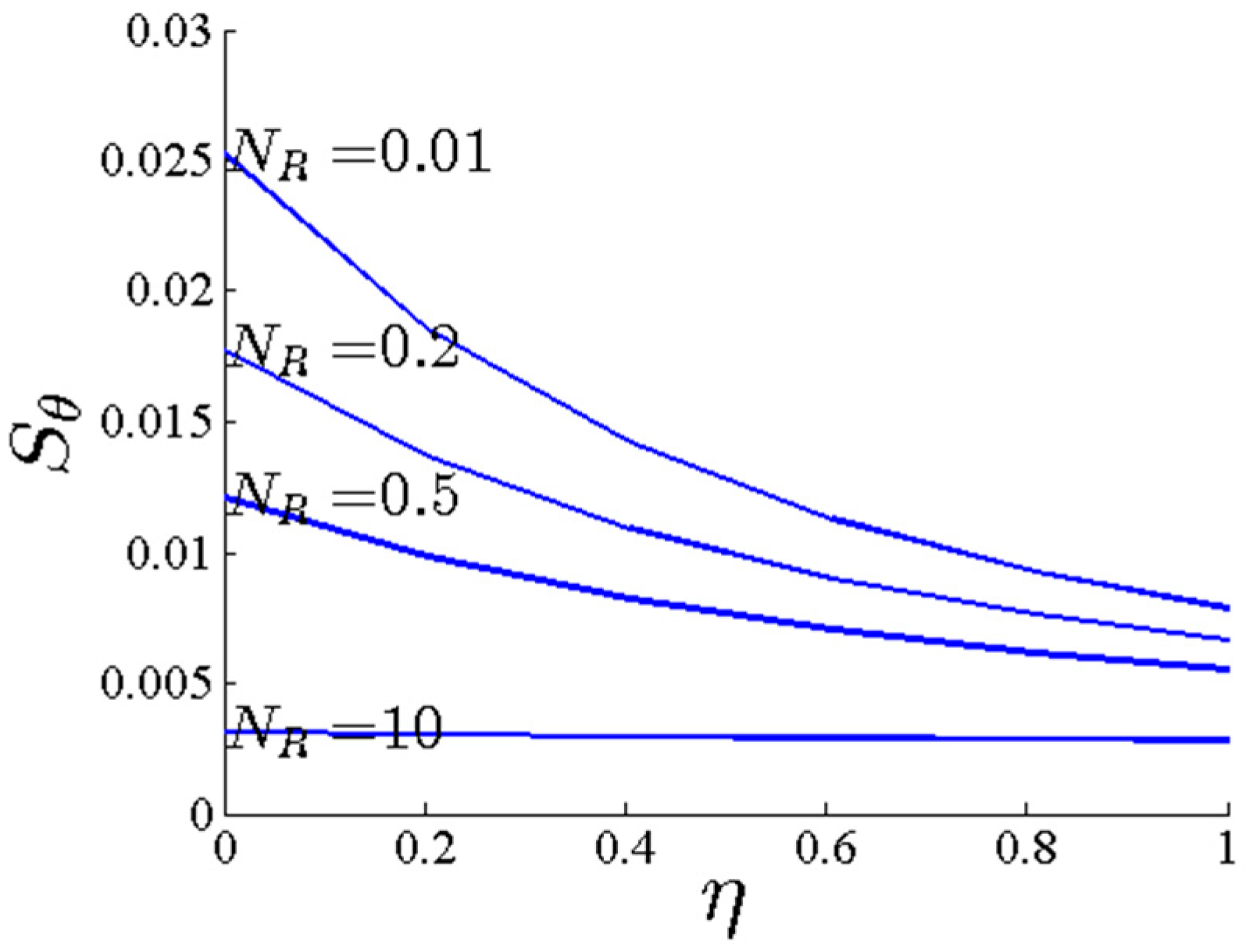
By increasing N_R, the thermal heat transfer entropy generation decreases.