An Intelligent and Fast Chaotic Encryption Using Digital Logic Circuits for Ad-Hoc and Ubiquitous Computing

Abstract

Delays added by the encryption process represent an overhead for smart computing devices in ad-hoc and ubiquitous computing intelligent systems. Digital Logic Circuits are faster than other computing techniques, so these can be used for fast encryption to minimize processing delays. Chaotic Encryption is more attack-resilient than other encryption techniques. One of the most attractive properties of cryptography is known as an avalanche effect, in which two different keys produce distinct cipher text for the same information. Important properties of chaotic systems are sensitivity to initial conditions and nonlinearity, which makes two similar keys that generate different cipher text a source of confusion. In this paper a novel fast and secure Chaotic Map-based encryption technique using 2’s Compliment (CET-2C) has been proposed, which uses a logistic map which implies that a negligible difference in parameters of the map generates different cipher text. Cryptanalysis of the proposed algorithm shows the strength and security of algorithm and keys. Performance of the proposed algorithm has been analyzed in terms of running time, throughput and power consumption. It is to be shown in comparison graphs that the proposed algorithm gave better results compare to different algorithms like AES and some others.

1. Introduction

As a ubiquitous trend in the environment, chaos is a type of deterministic random process provided by nonlinear dynamical systems. The main characteristics of chaotic systems are sensitive to initial conditions, randomness, diffusion, confusion and ergodicity. Chaotic systems have become an important topic of research because of these properties and are widely used in cryptography [1,2]. The existing-related research about chaos-based cryptography includes symmetric encryptions; security protocols and algorithms, asymmetric encryption and hash functions [3,4,5].

In recent years, the one way hash functions based on chaotic logistic maps, including 1D & 2D piecewise linear/nonlinear logistical map, high dimensional chaotic map, chaotic neural networks, hyper chaos and chaos S-Box have been modified [6,7,8]. Chaos map-based different algorithms, techniques and methods are constructed using hash functions, so high dimensionality dynamic systems have become an important and interesting research area in several scientific fields in the areas of computer science and secure communications [9,10,11]. Chaotic functions are sensitive to initial conditions—any negligible difference in the initial value generates a completely different cipher text. This means the cryptosystem using chaos theory will be strong against brute force attacks [12,13,14,15]. These properties of chaos have high potential for several applications in cryptosystems provided long term predictions on chaotic systems [16,17].

A novel chaos-based cryptographic technique using digital logic circuits is proposed in this paper for fast and secure encryption and decryption of information for several real time applications [18,19]. A chaotic logistic map provides a high degree of randomness and ergodicity to resist the linear and differential attacks and also enhances the security by providing confusion and diffusion to the system [20,21,22,23,24].

These previous techniques have solved many problems of cryptography and enhanced security and performance, but these techniques have some major drawbacks. The existing algorithms and methods are not easily understandable for users because they employ many mathematical functions. Symmetric key cryptosystems use the same single key every time for encryption and decryption. If the key is known by an intruder then the message is easily deduced. In a symmetric key cryptosystem, if an intruder knows the chaos function and the initial value of the chaos function, then the intruder can easily deduce the message. The encryption speed of chaotic cryptography is much slower than traditional cryptography, so a symmetric key cryptography technique is proposed, which uses more than one key for encryption and decryption. These keys are the same for encryption and decryption at one time but different keys are used for distinct messages. Security has been enhanced by using multiple keys and the randomness of keys is also enhanced by using digital concepts like 2’s complement. Even if an intruder knows the keys used one time, then the keys are changed the next time for the same message. The speed of encryption has been also increased by using digital concepts like XORing gate rather than difficult mathematical functions.

The rest of the paper is organized into several sections. Related works and a literature survey are briefly described in Section 2. In Section 3 the proposed cryptosystem and algorithms are described. In Section 4, an example of the proposed crypto systemis explained. Then the security of keys is analyzed in Section 5 with the help of key parameters. In Section 6, the proposed technique is analyzed against all four cryptanalysis attacks. Its performance is evaluated in terms of encryption time, throughput and power consumption in Section 7. In Section 8, the performance of the algorithm is compared with some algorithms like AES and others, which are described in different papers. In Section 9, the paper is concluded.

2. Related Work

Industrial and communication systems largely use unpredictable and practical cryp to systems for highly secure and fast transmission of information with little memory capacity [10,18], so they can satisfy the requirements of industrial control and military used in WiFi and ZigBee networks [6,14]. These proposed methods are analyzed in the UACI, NPCR and NIST environment.

An electrocardiogram (ECG) encryption system for biometric recognition collects ECG signals from an encrypted person using a portable instrument [18]. Simulation results show that the secrecy and security are enhanced by using an efficient large key size and complex algorithms widely used in multimedia applications [25].

Some mathematical properties have also determined the security and performance of distinct algorithms and systems using dynamic, chaotic cryptography [11,26]. Periodic switching of cryptographic keys is a different concept to boost the security of cryptographic systems in which chaotic behavior is combined with the periodic switching of keys [8]. It is represented that the running time complexity of the chosen plaintext, and a cipher text attack can be reduced to yield a simple set of linear equations [27,28]. The performance of the algorithm is measured in terms of cost, time and speed. Several one-dimension chaotic maps have been used to generate independent and approximately uniform pseudo-dynamic sequences for faster and time efficient encryption on blocks of data. Simulation results analyzed the efficiency and resistance against difference and linear cryptanalysis attacks and showed the high performance of the algorithm [5,29]. Fast encryption provides reliability and high security slightly, but at the same time highly reduces the running time [21,30,31]. Table 1 summarizes all the author’s works on chaotic based encryption scheme on the basis of some characteristics.

Table 1. Comparison table (Authors’ names and performance comparison of their research papers).

Features	Alem Haddush Fitwi et al. [3]	Amir Akhavan1 et al. [12]	Amit Pande et al. [20]	Ashraf Zaher et al. [1]	Ayman Mousa et al. [4]	Bassem Bakhache et al. [6]	Bhavana Agrawal et al. [9]
Security	Secure enough	High	Comparatively high	Secure Enough	High	High	Medium
Cryptanalysis Attack Prevention	Brute Force	Forgery and Birthday Attack	Except Known plaintext	-	-	Linear and Differential	All Four
Cipher type	Stream	Stream	Stream	Stream	Block	Stream	Stream
Application Area	Multimedia System	Real Time Applications	Real Time Embedded Systems	Communication System	-	Industrial Control	Communication System
Space Complexity	High	Medium	High	Medium	Enough High	Low	High
Implementation of algorithm	Complex	Complex	Hard	Hard	Complex Enough	Highly Complex	Complex
Used technique	Hysteresis Switched System	High Dimensional Chaotic Map	MLM based PRNG	Chaos Shift Keying	-	PWLCM	Chaos based RSA and AES
Efficiency/Reliability	Medium	High	Medium	Medium	Medium	High	High
Methodology/Environment	NIST and Monte Carlo Test	SP800-22 and DIEHARD Test Suits	XilinxVirtex-6 FPGA	Duffing Oscillator	Microsoft SQL	NIST Environment	-
Speed (Processing)	Low	High	Enough	Medium	High	High	Medium
Prediction Possibility	No	No	No	Yes	No	Slightly	Yes
Feasible	At Some Condition	Yes	No	Yes	Yes	No	Yes
Accuracy	Medium	High	Medium	High	Medium	Medium	Medium
Key length	Large	Large Enough	High	Large Enough	Large	Slightly Large	Large
Cost	High	High	High	Medium	Medium	Low	High
Quality Assurance	High	High	Applicable	High	Reasonable	Resemblance	Applicable

3. Proposed Methodology/Scheme

A novel, fast and secure “Chaotic Map based Encryption Technique using 2’s Compliment (CET-2C)” has been proposed using one or more than one keys for the encryption and decryption process but at any time instant the encryption and decryption keys are similar. It means different messages are encrypted via different multiple keys to increase the security against known cryptanalysis attacks. Firstly, the number of keys has been generated with the help of chaos logistic function (logistic map) providing only the initial condition.

These keys have been prohibited from providing some proper condition, so all the characters of the information are encrypted and decrypted with these difference and multiple keys. Multiple keys have been used to increase the randomness as well as security, and it is not necessary that any repeated characters in the information be encrypted and decrypted with a similar key.

The complexity of keys has been increased by using some digital logic like 2’s compliment code so the randomness of keys is enhanced with better security. These complex random keys have provided fast, feasible and efficient encryption in secure communication so the intruder is not sure about the generation of keys.

The necessary notations which are used for the key generation, encryption and decryption scheme are the following: $P_i$ = Plain text; C_i = Cipher text; $E(P_i)$ = Encryption of the plain text $P_i$; $D(C_i)$ = Decryption of the cipher text $C_i$.

For n = 1 to j:

$$X_{n+1}=\{A\times X_n(X_n-1)\}MOD256$$

A = any integer (1, 2, 3, ...); $X_n$ = initial value of chaotic function which is 2, 3, 4,……, j = Number of keys; $X_{n+1}$ = keys $K_1,K_2,K_3,..............K_j$ (after applying gray code on $X_{n+1}$).

3.1. Scheme for Key Generation

(1) Initially the pseudo random numbers are generated by using the chaotic map function at both ends (sender and receiver).

For n = 1 to j:

$$X_{n+1}=\{A\times X_n(X_n-1)\}MOD256$$

(2) The multiple different keys are generated by applying 2’s compliment on different values of $X_{n+1}$ and the number of keys is fixed by providing some suitable condition j.

(3) Complexity and security of keys are enhanced by applying 2’s compliment code on X_n+1 so keys are random and independent with each other.

(4) These keys are converted into 8-bit binary form.

3.2. Scheme for Encryption Process

Each character is represented in ASCII character format which are converted into 8-bit binary numbers with respect to their decimal numbers. These characters are encrypted by using a digital logic bitwise XNOR gate function. This XNOR operation is performed on each character by a single binary coded key. Keys are also repeated for encrypting and decrypting the whole information.

$P_1$ = ASCII (Character 1); $P_1$ is represented in 8-bit binary numbers:

$$E_{k_1}(P_1)=C_1$$

$P_2$ = ASCII (Character 2); $P_2$ is represented in 8-bit binary numbers:

$$E_{k_2}(P_2)=C_2$$

…,

$P_i$ = ASCII (Character i); $P_i$ is represented in 8-bit binary numbers:

$$E_{k_m}(P_i)=C_i$$

where m = 1 to j.

3.3. Scheme for Decryption Process

The cipher texts have been decrypted (converted into plain text) by using the reverse process of the encryption technique:

$$P_1=D_{k_1}(C_1)$$

$P_1$ is represented into ASCII ($P_1$) with respect to its decimal value. Character 1 = ASCII ($P_1$):

$$P_2=D_{k_2}(C_2)$$

$P_2$ is represented into ASCII ($P_2$) with respect to its decimal value. Character 2 = ASCII ($P_2$):

…,

$$P_i=D_{k_m}(C_i)$$

where m = 1 to j; $P_i$ is represented in ASCII ($P_i$) with respect to its decimal value; Character i = ASCII ($P_i$)

3.4. Key Generation Algorithm

(1) Select the values of parameter (M, A, $X_n$).

(2) Generate the pseudo random numbers from the logistic map equation.

For n = 1 to j:

$$X_{n+1}=\{A\times X_n(X_n-1)\}MOD256$$

(3) Apply 2’s compliment code on these pseudo random numbers which are generated from $X_{n+1}$ to generate the keys $K_1,K_2,K_3,..............K_j$.

(4) Keys are converted into 8-bit binary form.

3.5. Encryption Algorithm

(1) Each character is converted into an ASCII character,$P_i$ = ASCII (Character i).

ASCII character $P_i$ is represented into 8-bit binary form.

$E_{k_m}(P_i)=C_i$ for all i > 0, and m = 1 to j, using this equation for encrypting the message. Where $E_{k_m}(P_i)$ is bit wise XNOR perform on plaintext $P_i$ with a single key $K_m$.

3.6. Decryption Algorithm

(1) $P_i=D_{k_m}(C_i)$ for all i > 0 and m = 1 to j, using this equation for decrypting the cipher text. where $D_{k_m}(C_i)$ is bit wise XNOR perform on cipher text $C_i$ with a single key $K_m$.

(2) Plain text $P_i$ is represented into ASCII ($P_i$) with respect to its decimal value.

(3) So Character i = ASCII ($P_i$).

4. Example

Given plain text–PIYUSHS

Letter	ASCII	Binary Number
P	80	01010000
I	73	01001001
Y	89	01011001
U	85	01010101
S	83	01010011
H	72	01001000
S	83	01010011

4.1. Key Generation

$$X_{n+1}=\{A\times X_n(X_n-1)\}MOD256$$

Let A = 6, $X_n$ = 4, Number of Keys j = 5

For j = 1

• $X_{n+1}$ = {6 × 4 × (4 − 1)} MOD 256
• $X_{n+1}$ = 72

For j = 2

• $X_{n+1}$ = {6 × 72 × (72 − 1)} MOD 256
• $X_{n+1}$ = 208

For j = 3

• $X_{n+1}$ = {6 × 208 × (208 − 1)} MOD 256
• $X_{n+1}$ = 32

For j = 4

• $X_{n+1}$ = {6 × 32 × (32 − 1)} MOD 256
• $X_{n+1}$ = 64

For j = 5

• $X_{n+1}$ = {6 × 64 × (64 − 1)} MOD 256
• $X_{n+1}$ = 128
• $X_{n+1}$ = 72, 208, 32, 64, 128.

The keys are established by applying 2’s compliment code on pseudo random numbers $X_{n+1}$. 1’s compliment is generated by converting 0 to 1 and 1 to 0 then 2’s compliment is generated by adding 1 in 1’s compliment of numbers:

  $X_{n+1}$ = 72 = 01001000

1’s compliment 10110111

          + 1

2’s compliment 10111000 = 184

72 = 01001000	2’s compliment	=	10111000	=	184
208 = 11010000	2’s compliment	=	00110000	=	48
32 = 00100000	2’s compliment	=	11100000	=	224
64 = 01000000	2’s compliment	=	11000000	=	192
128 = 10000000	2’s compliment	=	10000000	=	128

Keys (K₁ = 184, K₂ = 48, K₃ = 224, K₄ = 192, K₅ = 128).

4.2. Encryption Algorithm

Encryption scheme converts the plain text into unreadable cipher text by using different multiple keys (Table 2).

Table 2. Cipher text for plain text.

Plain Text (ASCII)	XNOR	Key ${\mathit{K}}_{\mathit{j}}$	Cipher Text
P		184	00010111
80			23
01010000	XNOR	10111000	↨
I		48	10000110
73			134
01001001	XNOR	00110000	Å
Y		224	01000110
89			70
01011001	XNOR	11100000	F
U		192	01101010
85			106
01010101	XNOR	11000000	j
S		128	00101100
83			44
01010011	XNOR	10000000	,
H		184	00001111
72			15
01001000	XNOR	10111000	☼
S		48	10011100
83			156
01010011	XNOR	00110000	£

Cipher text—↨ÅFj,☼£

Given Text: -PIYUSHS

P

ASCII–80

01010000

Key ($K_1$) = 184 (10111000)

Cipher Text–
Plaintext	XNOR	Key
P	XNOR	184
80	XNOR	184
01010000	XNOR	10111000

0	XNOR	1	=	0
1	XNOR	0	=	0
0	XNOR	1	=	0
1	XNOR	1	=	1
0	XNOR	1	=	0
0	XNOR	0	=	1
0	XNOR	0	=	1
0	XNOR	0	=	1
Cipher Text–00010111 = 23 = ↨

4.3. Decryption Algorithm

Decryption scheme converts the unreadable cipher text into readable plain text by using the similar keys (Table 3).

Table 3. Plain text for cipher text.

Cipher Text	XNOR	Key ${\mathit{K}}_{\mathit{j}}$	Plain Text (ASCII)
↨		184	01010000
23			80
00010111	XNOR	10111000	P
Å		48	01001001
134			73
10000110	XNOR	00110000	I
F		224	01011001
70			89
01000110	XNOR	11100000	Y
j		192	01010101
106			85
01101010	XNOR	11000000	U
,		128	01010011
44			83
00101100	XNOR	10000000	S
☼		184	01001000
15			72
00001111	XNOR	10111000	H
£		48	01010011
156			83
10011100	XNOR	00110000	S

Plain text–PIYUSHS.

Cipher text–↨ÅFj,☼£

↨

ASCII–23

00010111

Key ($K_1$) = 184 (10111000)

Plain Text:
Cipher Text	XNOR	Key
↨	XNOR	184
23	XNOR	184
00010111	XNOR	10111000

0	XNOR	1	=	0
0	XNOR	0	=	1
0	XNOR	1	=	0
1	XNOR	1	=	1
0	XNOR	1	=	0
1	XNOR	0	=	0
1	XNOR	0	=	0
1	XNOR	0	=	0
Plain Text–01010000 = 80 = P

5. Analysis of Key Security

To find and compute all the values (J, A, $X_n$) is difficult. In this section the sensitivity of the secret key has been represented with negligible difference in the key parameters:

$$X_{n+1}=\{A\times X_n(X_n-1)\}MOD256$$

Plain text–PIYUSHS; Parameter (J, A, $X_n$); Keys ($K_1,K_2,K_3,..............K_j$).

5.1. Sensitivity of Number of Keys J

It has been described that if a number of keys are changed, then the cipher texts are also fully changed from one another for the same plain text. In Table 4 negligible dissimilarity in the j (number of keys) generates different cipher text.

Table 4. Sensitivity of Number of Keys j.

j	A	${\mathit{X}}_{\mathit{n}}$	${\mathit{X}}_{\mathit{n}+\mathbf{1}}$	Keys (${\mathit{K}}_{\mathit{j}}$)	Cipher Text
2	6	4	72,208	184,48,184,48,184,48,184	↨Å▲Üç
3	6	4	72,208,32	184,48,224,184,48,224,184	↨ÅF↕£W
4	6	4	72,208,32,64	184,48,224,192,184,48,224	↨ÅFjçL
5	6	4	72,208,32,64,128	184,48,224,192,128,184,48	↨ÅFj,☼£

5.2. Sensitivity of Constant A

It has been described that negligible changes in constant A produce fully different keys so cipher texts are also different from each other. In Table 5 it has been shown that little difference in the values of constant A produced different cipher text.

Table 5. Sensitivity of Constant A.

j	A	${\mathit{X}}_{\mathit{n}}$	${\mathit{X}}_{\mathit{n}+\mathbf{1}}$	Keys (${\mathit{K}}_{\mathit{j}}$)	Cipher Text
5	2	4	24,80,96,64,128	232,176,160,192,128,232,176	G♠♠j,_∟
5	3	4	36,196,228,132,164	220,60,28,124,92,220,60	sè║╓≡kÉ
5	5	4	60,80,192,0,0	196,176,64,1,1,196,176	k♠µ½¡s∟
5	6	4	72,208,32,64,128	184,48,224,192,128,184,48	↨ÅFj,☼£

5.3. Sensitivity of Initial Condition X_n

It has been described that little changes in the initial condition X_n produces fully different keys, so cipher texts are completely different. This is known as confusion. In Table 6 it has been shown that little difference in values of initial variable $X_n$ produced fully different cipher text.

Table 6. Sensitivity of initial condition $X_n$.

j	A	${\mathit{X}}_{\mathit{n}}$	${\mathit{X}}_{\mathit{n}+\mathbf{1}}$	Keys (${\mathit{K}}_{\mathit{j}}$)	Cipher Text
5	6	2	12,24,240,96,192	244,232,16,160,64,244,232	[^╢LF∞CD
5	6	3	36,136,80,32,64	220,120,176,224,192,220,120	s╬▬Jlk╘
5	6	4	72,208,32,64,128	184,48,224,192,128,184,48	↨ÅFj,☼£
5	6	5	120,176,224,192,128	136,80,32,64,128,136,80	'µÅΩ,?ⁿ

6. Cryptanalysis

Cryptanalysis is a method which is used to verify the security of an algorithm by breaking the codes of the algorithm and getting the possible encryption keys and plain text as well.

6.1. Cipher Text Only Attacks

Parameter (j = 5, A = 6, $X_n$ = 4)

Keys (184,48,224,192,128)

Given: $C_1=E_{k_1}(P_1),C_2=E_{k_2}(P_2),................,C_i=E_{k_m}(P_i)$ where m = 1 to j.

Deduce: -Either $P_1,P_2,P_3,.....................P_i$;

$K_1,K_2,K_3,K_4,K_5;$

Or an algorithm to deduce $P_{i+1}$

From $C_{i+1}=E_{k_m}(P_{i+1})$

Keys (184,48,224,192,128)

Example:

$P_1$ = Q then	$C_1=E_{k_1}(P_1)=E_{184}$	(Q) = ▬
$P_2$ = QQ then	$C_2=E_{k_{1,2}}(P_2)=E_{184,48}$	(QQ) = ▬₧
$P_3$ = QQQ then	$C_3=E_{k_{1,2,3}}(P_3)=E_{184,48,224}$	(QQQ) = ▬₧N
$P_4$ = QQQQ then	$C_4=E_{k_{1,2,3,4}}(P_4)=E_{184,48,224,192}$	(QQQQ) = ▬₧Nn
$P_5$ = QQQQQ then	$C_5=E_{k_{1,2,3,4,5}}(P_5)=E_{184,48,224,192,128}$	(QQQQQ) = ▬₧Nn.
$P_6$ = QQQQQQ then	$C_6=E_{k_{1,2,3,4,5,1}}(P_6)=E_{184,48,224,192,128,184}$	(QQQQQQ) = ▬₧Nn.▬

From the above example, it is to be said that if any character is repeated many times in the text, the cipher text is completely different for same letter Q. The Cipher text of Character Q finding as the first letter is dissimilar from Q finding as nth character in plaintext.

6.2. Known Plain Text Attack

Parameter (j = 5, A = 6, $X_n$ = 4)

Keys (184,48,224,192,128)

Given: $P_1,C_1=E_{k_1}(P_1),P_2,C_2=E_{k_2}(P_2),..............P_i,C_i=E_{k_m}(P_i)$ where m = 1 to j

Deduce: -Either $K_1,K_2,K_3,K_4,K_5;$

Or an algorithm to deduce $P_{i+1}$

From $C_{i+1}=E_{k_m}(P_{i+1})$

Keys (184,48,224,192,128)

Example:

$P_1$ = R then	$C_1=E_{k_1}(P_1)=E_{184}$	(R) = §
$P_2$ = RR then	$C_2=E_{k_{1,2}}(P_2)=E_{184,48}$	(RR)= §¥
$P_3$ = RRR then	$C_3=E_{k_{1,2,3}}(P_3)=E_{184,48,224}$	(RRR) = §¥M
$P_4$ = RRRR then	$C_4=E_{k_{1,2,3,4}}(P_4)=E_{184,48,224,192}$	(RRRR) = §¥Mm
$P_5$ = RRRRR then	$C_5=E_{k_{1,2,3,4,5}}(P_5)=E_{184,48,224,192,128}$	(RRRRR) = §¥Mm-
$P_6$ = RRRRRR then	$C_6=E_{k_{1,2,3,4,5,1}}(P_6)=E_{184,48,224,192,128,184}$	(RRRRRR) = §¥Mm-§

From the example, it can be said that there are several plain texts with their corresponding cipher text. It is hard to compute the key or the algorithm which is used for encryption of plain texts for decrypting them. Keys are generated by very restricted and sensitive parameters. The cipher text of the Character R found as the first letter is different as that of the letter R found as the nth character in the plaintext.

6.3. Chosen Plaintext Attacks

Parameter (j = 5, A = 6, $X_n$ = 4)

Keys (184,48,224,192,128)

Given: $P_1,C_1=E_{k_1}(P_1),P_2,C_2=E_{k_2}(P_2),..............P_i,C_i=E_{k_m}(P_i)$ Where the cryptanalysis gets to decide $P_1,P_2,P_3,.....................P_i$ and m = 1 to j.

Deduce: -Either $P_1,P_2,P_3,.....................P_i$;

Or an algorithm to deduce $P_{i+1}$

From $C_{i+1}=E_{k_m}(P_{i+1})$

Keys (184,48,224,192,128)

Example:

• $P_1$ = DE then cipher text $C_1=E_{k_{1,2}}(P_1)=E_{184,48}$ (DE) = ♥è
• $P_2$ = ED then cipher text $C_2=E_{k_{1,2}}(P_2)=E_{184,48}$ (ED) = ☻ï

It is not easy to find out the key or the algorithm to decrypt the cipher text which is to be encrypted with the same keys.

6.4. Chosen Cipher Text Attack

Parameter (j = 5, A = 6, $X_n$ = 4)

Keys (184,48,224,192,128)

Given: $C_1,P_1=D_{k_1}(C_1),C_2,P_2=D_{k_2}(C_2),..........,C_i,P_i=D_{k_m}(C_i)$ where m = 1 to j

Deduce: -$K_1,K_2,K_3,K_4,K_5;$

Example:

• $C_1$ = ♥è then plaintext $P_1=D_{k_{1,2}}(C_1)=D_{184,48}$ (♥è) = DE
• $C_2$ = ☻ï then plain text $P_2=D_{k_{1,2}}(C_2)=D_{184,48}$ (☻ï) = ED

Keys are produced by two different parameters $X_n$ and A which are very sensitive and independent, so it is not easy to deduce the keys by knowing the cipher text and its decrypted plaintext.

7. Performance Analysis

In this paper, pertinent metrics are recognized. Performance of the proposed chaotic algorithm(CET-2C) is measured, and finally compared with the existing one secret key, AES, encryption algorithm and also compared with different algorithms using same data size published in Springer [12], Hindawi [17] and EEA [3] publications. It is to be shown that CET-2C is not affected by the data set, and only depends upon the data size.

Metrics and Performance

In this paper, five significant metrics is described to estimate the performance of the proposed algorithm (CET-2C). The metrics include: encryption/decryption time, CPU time, cipher size, power consumption, and encryption throughput. Then the experiment is performed, and performance results are measured using a laptop having a Intel (R) Core (TM) i3-3110M processor CPU @ 2.40GHz, and a RAM of 2GB. The results are also calculated using a laptop having an Intel Pentium Dual-Core CPU @ 2.60 GHz processor and 2 GB RAM and a laptop having an Intel (R) Pentium (R) Dual CPU T2370 @ 1.73 GHz processor and 1 GB RAM for comparison with other algorithms.

Encryption Time

The encryption time is based on the running time complexity of the algorithm, length of the key, and the plaintext size to be encrypted with various encryption algorithms. Hence, in this paper, a number of encryption times for different plaintext sizes and key length are selected and analyzed by using CPU clock time [3]. A variety of data sizes ranging from 0 MB to 80 MB are encrypted and their corresponding encryption times are collected. It is shown by a graph that the encryption time increases with increasing the data size. The encryption time and data size are linearly increased in Figure 1.

Figure 1. Message size versus encryption time.

Encryption Throughput, X_e

It is defined as the number of bytes of plaintext encrypted (cipher text completed) during an observation period (encryption time) [3]. Mathematically:

$$X_e=\frac{\text{Number of Completions in Bytes}}{\text{Encryption Time (}s)}$$

In the proposed algorithm, Throughput linearity is enhanced as the data size is increased in Figure 2.

Figure 2. Message size versus throughput.

Power Consumption

Power is needed for running fast CPUs and memory based on the usability of devices and algorithms. The energy cost of the encryption process is defined as the product of the total number of clock cycles required by the encryption process and average current drawn by each CPU clock cycle in the ampere cycle. The total energy cost is calculated in ampere seconds by dividing the ampere cycles by the clock frequency in cycles/second of a processor [3]. Then results are multiplied with the processor’s operating voltage to obtain the energy cost in joule. The CET-2C consumed the amount of energy for encryption or decryption is given by:

$$E=V_{cc}\times I\times TJ$$

where $V_{cc}$ = Processor’s operating voltage; T = Encryption time; I = Average current per CPU cycle.

In this paper, the experiments were performed and results were collected using a laptop equipped with an Intel (R) Core (TM) i3-3110M processor CPU. The approximate average current consumed is 100 mA and the CPU voltage is $V_{cc}$ = 1.25 V (both obtained from the Intel Manual).

The variations of energy consumption with different data sizes are shown in the graph which is represented that the energy consumed during an encrypting process is directly proportional to the encryption time in Figure 3.

Figure 3. Message size versus energy consumption.

CPU Time

The CPU process time is defined as the time when the CPU is busy in the calculation of a particular process. When the load of CPU is increased then CPU time is also enhanced linearly [3]. In this paper, the CPU time is given by:

$$\text{CPU busytime},T_{CPU}=\frac{\text{CPU utilization}}{\text{Observation period}}$$

where CPU utilization = Obtained from the task manager; Observation period = Encryption Time in Figure 4.

Figure 4. Message size versus CPU time.

Cipher Size

Shannon’s Characteristics of “Good” Ciphers states that the size of the encrypted text should be no larger than the plaintext of the original message. In this work, the size of plaintext and cipher text are shown to be the same, thus satisfying Shannon’s size Characteristics of “Good” Ciphers rule.

8. Comparison with AES and Chaotic Algorithms [3]

The performance of the proposed algorithm (CET-2C) is compared with a popular secret key encryption algorithm, AES, and with Chaotic Algorithms [3,12] using the data size same as provided in [3,12,17]. The plaintexts used in the proposed algorithm, are encrypted using AES, and a Chaotic Algorithm [3,12] and their performance is evaluated and analyzed using the same metrics as above.

8.1. Encryption Time

Encryption times for the same set of several data sizes (200 KB to 450 KB) are collected using a laptop equipped with an Intel (R) Pentium (R) Dual CPU T2370 @ 1.73 GHz processor, and 1 GB RAM and used to analyze the performance of the CET-2C, and the results put into graphic form and tabular form (Table 7).

Table 7. Encryption times of Chaotic Algorithm [3], AES [3] and CET-2C.

Message Sizes in KB	Encryption Time in Seconds
	Chaotic Algorithm [3]	AES [3]	CET-2C
200	1.65	1	0.0698
250	2.05	1	0.076
300	2.48	1	0.082
350	2.83	1	0.0891
400	3.35	1	0.0976
450	3.75	1	0.1054

Figure 5 shows the proposed algorithm CET-2C is much faster compared to AES [3] and the Chaotic Algorithm for multiple message sizes from 200 KB to 450 KB [3]. CET-2C is also applied for large data sizes with lower encryption time. The results illustrate that the encryption time increases linearly when it is compared with other algorithms.

Figure 5. Encryption times of Chaotic Algorithm [3], AES [3] and CET-2C.

Overall % Gain of CET-2C over Chaotic Algorithm [3] for Encryption Time with increasing the message size:

$$G_{p}of\text{ CET-2C over }CA=\frac{E{T}_{CET-2C}(\text{at Different Message Sizes})-E{T}_{CA}(\text{at Different MessageSizes})}{E{T}_{CA}(\text{at Different Message Sizes})}$$

Here $G_p$ = Overall % Gain at Different Message Sizes; ET = Encryption Time; CA = Chaotic Algorithm; CET-2C = Chaotic Map based Encryption Technique using 2’s Compliment.

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 200 KB

$$\text{\% Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{0.0698-1.65}{1.65}\right|\times 100=95.77$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 250 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{0.076-2.05}{2.05}\right|\times 100=96.29$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 300 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{0.082-2.48}{2.48}\right|\times 100=96.69$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 350 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{0.0891-2.83}{2.83}\right|\times 100=96.85$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 400 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{0.0976-3.35}{3.35}\right|\times 100=97.09$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 450 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{0.1054-3.75}{3.75}\right|\times 100=97.19$$

Overall % Gain of CET-2C over AES [3] for Encryption Time with increasing the message size

$$G_p\text{of CET-2C over AES}=\frac{E{T}_{CET-2C}(\text{at Different Message Sizes})-E{T}_{AES}(\text{at Different Message Sizes})}{E{T}_{AES}(\text{at Different Message Sizes})}$$

where, AES = Advance Encryption Standard.

% Gain of CET-2C over AES [3] when message size is 200 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{AES}}{E{T}_{AES}}\times 100=\left|\frac{0.0698-1}{1}\right|\times 100=93.02$$

% Gain of CET-2C over AES [3] when message size is 250 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{AES}}{E{T}_{AES}}\times 100=\left|\frac{0.076-1}{1}\right|\times 100=92.4$$

% Gain of CET-2C over AES [3] when message size is 300 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{AES}}{E{T}_{AES}}\times 100=\left|\frac{0.082-1}{1}\right|\times 100=91.8$$

% Gain of CET-2C over AES [3] when message size is 350 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{AES}}{E{T}_{AES}}\times 100=\left|\frac{0.0891-1}{1}\right|\times 100=91.09$$

% Gain of CET-2C over AES [3] when message size is 400 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{AES}}{E{T}_{AES}}\times 100=\left|\frac{0.0976-1}{1}\right|\times 100=90.24$$

% Gain of CET-2C over AES [3] when message size is 450 KB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{AES}}{E{T}_{AES}}\times 100=\left|\frac{0.1054-1}{1}\right|\times 100=89.46$$

Table 8 illustrates that overall gain % of CET-2C for encryption time is higher as compared with the Chaotic Algorithm [3] and AES [3]. For the 350 KB message size the overall % gain of CET-2C is 96.85% and 91.09% when it is compared with the Chaotic Algorithm [3] and AES [3]. It shows that the performance of CET-2C is increased with multiple message sizes. 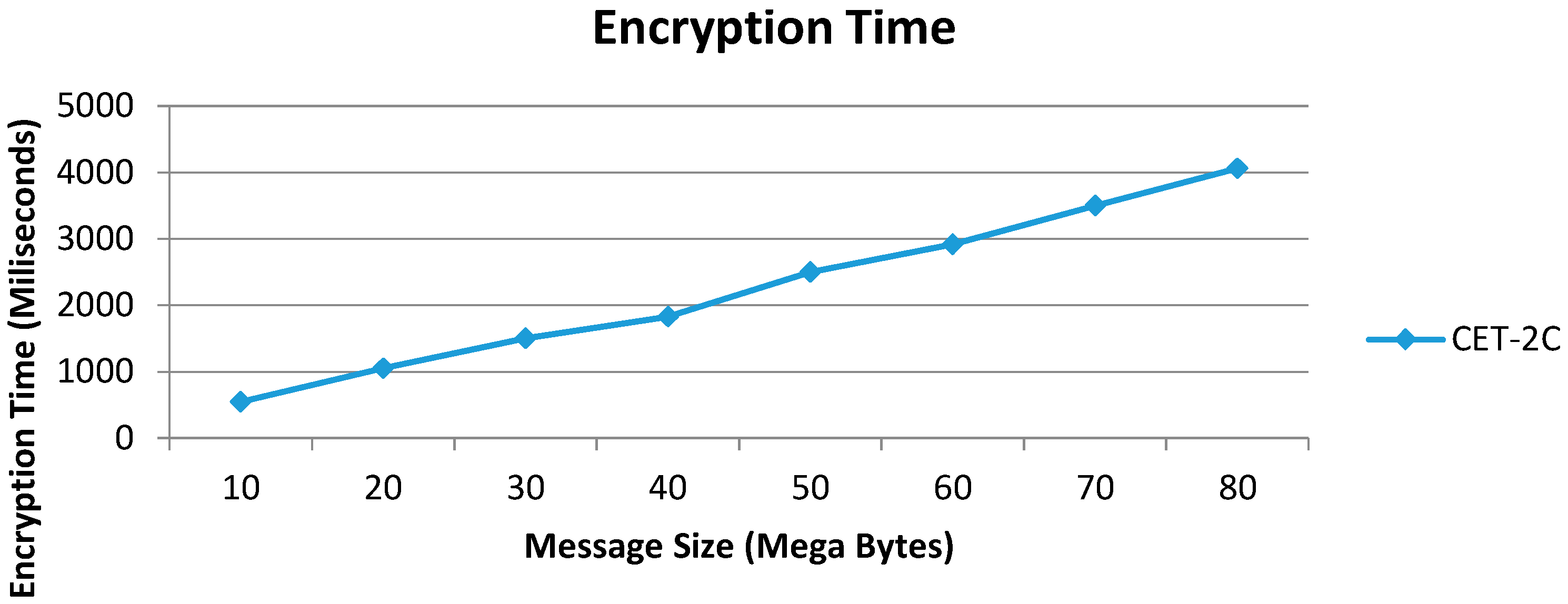The encryption time is also calculated for large data sizes in MB (10 MB to 80 MB) using a laptop with an Intel (R) Pentium (R) Dual CPU T2370 processor of @ 1.73 GHz, and 1 GB RAM (Table 9).

Table 8. Overall % Gain of CET-2C over Chaotic Algorithm [3] and AES [3] for encryption time.

Message Sizes in KB	Overall % Gain for Encryption Time of CET-2C
	CET-2C over Chaotic Algorithm [3]	CET-2C over AES [3]
200	95.77	93.02
250	96.29	92.4
300	96.69	91.8
350	96.85	91.09
400	97.09	90.24
450	97.19	89.46

Table 9. Encryption time of compared Algorithm [12] and CET-2C.

Message Sizes in MB	Encryption Time in Milliseconds
	Compared Algorithm [12]	CET-2C
10	1500	1250
20	3500	2400
30	5300	4876
40	6800	6050
50	8500	8000
60	10,300	9700
70	12,100	10,800
80	13,800	12,000

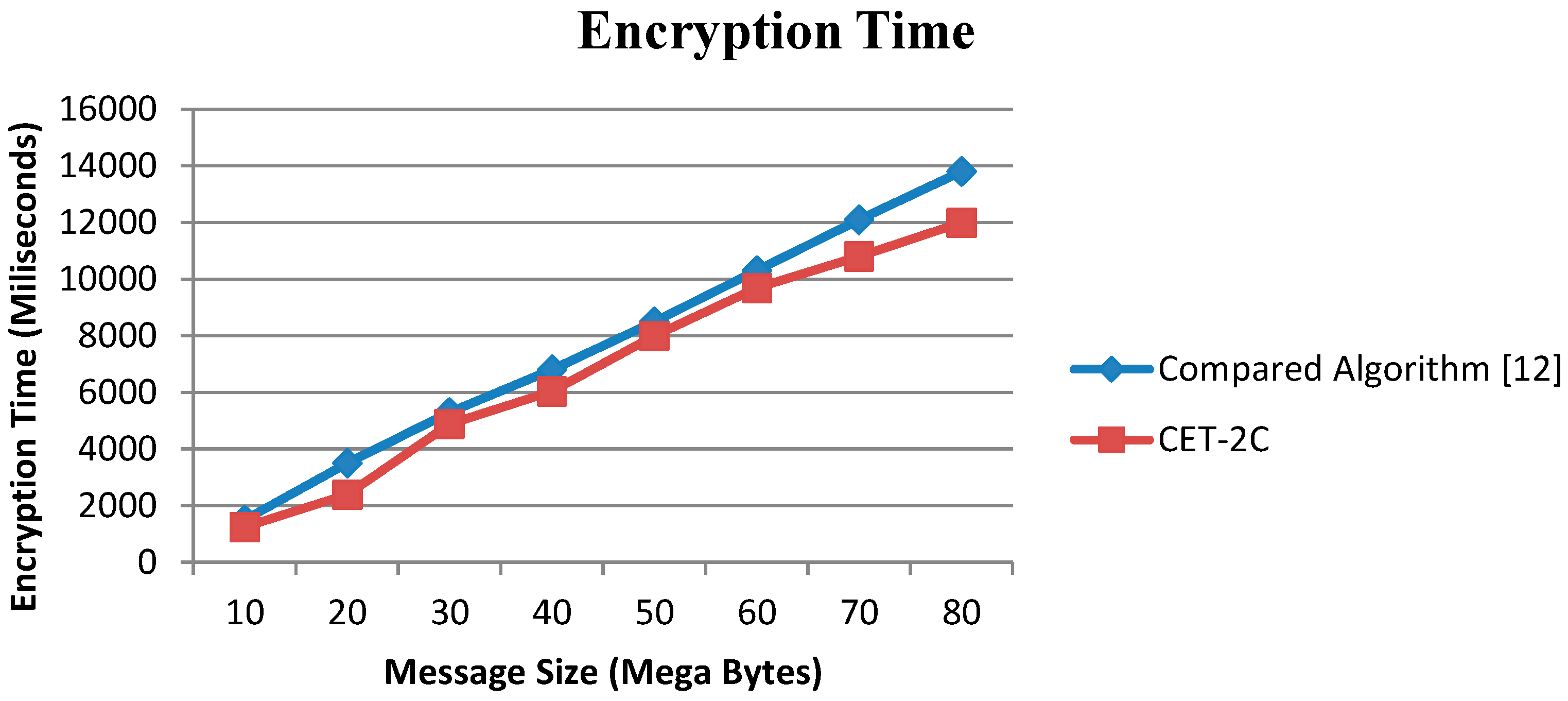
Figure 6 shows that the time required for encryption in the proposed CET-2C algorithm is lower compared to the algorithm [12] for different message sizes in MB. For 80 MB message the encryption time of CET-2C is 12 sand for the comparison algorithm [12] it is 13.8 s. This shows that CET-2C is much faster than the comparable algorithm [12].

Figure 6. Encryption time of compared Algorithm [12] and CET-2C.

Overall % Gain of CET-2C over Compared Algorithm [12] for Encryption Time with increasing message size.

$$G_{p}o\text{f CET-2C over CA}=\frac{E{T}_{CET-2C}(\text{at Different Message Sizes})-E{T}_{CA}(\text{at Different Message Sizes})}{E{T}_{CA}(\text{at Different Message Sizes})}$$

Here $G_p$ = Overall % Gain at Different Message Sizes; ET = Encryption Time; CA = Compared Algorithm; CET-2C = Chaotic Map based Encryption Technique using 2’s Compliment

% Gain of CET-2C over Compared Algorithm [12] when message size is 10 MB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{1250-1500}{1500}\right|\times 100=16.67$$

% Gain of CET-2C over Compared Algorithm [12] when message size is 20 MB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{2400-3500}{3500}\right|\times 100=31.43$$

% Gain of CET-2C over Compared Algorithm [12] when message size is 30 MB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{4876-5300}{5300}\right|\times 100=8.00$$

% Gain of CET-2C over Compared Algorithm [12] when message size is 40 MB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{6050-6800}{6800}\right|\times 100=11.03$$

% Gain of CET-2C over Compared Algorithm [12] when message size is 50 MB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{8000-8500}{8500}\right|\times 100=5.88$$

% Gain of CET-2C over Compared Algorithm [12] when message size is 60 MB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{9700-10300}{10300}\right|\times 100=5.83$$

% Gain of CET-2C over Compared Algorithm [12] when message size is 70 MB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{10800-12100}{12100}\right|\times 100=10.74$$

% Gain of CET-2C over Compared Algorithm [12] when message size is 80 MB

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA}}{E{T}_{CA}}\times 100=\left|\frac{12000-13800}{13800}\right|\times 100=13.04$$

Table 10 illustrates that the overall encryption time gain % of CET-2C is higher as compared with the compared algorithm [12]. At the message size 20 MB the overall % gain of CET-2C is 31.43% when compared with the compared algorithm [12]. This shows that the performance of CET-2C is increased with multiple message sizes.

Table 10. Overall %Gain of CET-2C over the compared Algorithm [12] for encryption time.

Message Sizes in MB	Overall % Gain for Encryption Time of CET-2C
	CET-2C over Compared Algorithm [12]
10	16.67
20	31.43
30	8.00
40	11.03
50	5.88
60	5.83
70	10.74
80	13.04

The data sizes was also taken in bytes and experiments performed to calculate the encryption time using a laptop with an Intel (R) Core (TM) i3-3110M processor @ 2.40GHzCPU, and a RAM of 2GB (Table 11).

Table 11. Encryption time of compared Algorithms 1 and 2 [17] and CET-2C.

Message Sizes in Bytes	Encryption Time in Milliseconds
	Compared Algorithm1 [17]	Compared Algorithm2 [17]	CET-2C
100,000	1	3	54
500,000	4	5	75
600,000	204	620	82
700,000	410	1230	97
800,000	640	1930	120

Figure 7 shows that for small dataset sizes (100 KB and 500 KB) the comparison algorithms [17] performed the encryption with slightly higher speed, but for large data sizes (larger than 500 KB) the encryption time is instantly increased. The graph of our proposed algorithm CET-2C increased linearly for small to large data sizes.

Figure 7. Encryption times of compared Algorithms 1 and 2 [17] and CET-2C.

Overall % Gain of CET-2C over compared Algorithm 1 [17] for encryption time with increasing the message size:

$$G_p\text{of CET-2C over CA1}=\frac{E{T}_{CET-2C}(\text{at Different Message Sizes})-E{T}_{CA1}(\text{at Different Message Sizes})}{E{T}_{CA1}(\text{at Different Message Sizes})}$$

Here $G_p$ = Overall % Gain at Different Message Sizes; ET = Encryption Time; CA1 = Compared Algorithm 1; CET-2C = Chaotic Map based Encryption Technique using 2’s Compliment.

% Gain of CET-2C over Compared Algorithm 1 [17] when message size is 100,000 Bytes

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA1}}{E{T}_{CA1}}\times 100=\left|\frac{54-1}{54}\right|\times 100=98.15$$

% Gain of CET-2C over compared Algorithm 1 [17] when message size is 500,000 Bytes

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA1}}{E{T}_{CA1}}\times 100=\left|\frac{75-4}{75}\right|\times 100=94.67$$

% Gain of CET-2C over compared Algorithm 1 [17] when message size is 600,000 Bytes

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA1}}{E{T}_{CA1}}\times 100=\left|\frac{82-204}{204}\right|\times 100=59.08$$

% Gain of CET-2C over compared Algorithm 1 [17] when message size is 700,000 Bytes

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA1}}{E{T}_{CA1}}\times 100=\left|\frac{97-410}{410}\right|\times 100=76.34$$

% Gain of CET-2C over Compared Algorithm 1 [17] when message size is 800,000 Bytes

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA1}}{E{T}_{CA1}}\times 100=\left|\frac{120-640}{640}\right|\times 100=81.25$$

Overall % Gain of CET-2C over Compared Algorithm 2 [17] for Encryption Time with increasing the message size

$$G_{p}o\text{f CET-2C over CA2}=\frac{E{T}_{CET-2C}(\text{at Different Message Sizes})-E{T}_{CA2}(\text{at Different Message Sizes})}{E{T}_{CA2}(\text{at Different Message Sizes})}$$

Here $G_p$ = Overall % Gain at Different Message Sizes; ET = Encryption Time; CA2 = Compared Algorithm 2; CET-2C = Chaotic Map based Encryption Technique using 2’s Compliment.

% Gain of CET-2C over compared Algorithm 1 [17] when message size is 100,000 Bytes

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA2}}{E{T}_{CA2}}\times 100=\left|\frac{54-3}{54}\right|\times 100=94.44$$

% Gain of CET-2C over compared Algorithm 1 [17] when message size is 500,000 Bytes

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA2}}{E{T}_{CA2}}\times 100=\left|\frac{75-5}{75}\right|\times 100=93.33$$

% Gain of CET-2C over compared Algorithm 1 [17] when message size is 600,000 Bytes

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA2}}{E{T}_{CA2}}\times 100=\left|\frac{82-620}{620}\right|\times 100=86.77$$

% Gain of CET-2C over compared Algorithm 1 [17] when message size is 700,000 Bytes

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA2}}{E{T}_{CA2}}\times 100=\left|\frac{97-1230}{1230}\right|\times 100=92.11$$

% Gain of CET-2C over compared Algorithm1 [17] when message size is 800,000 Bytes

$$\%\text{ Gain of CET-2C }=\frac{E{T}_{CET-2C}-E{T}_{CA2}}{E{T}_{CA2}}\times 100=\left|\frac{120-1930}{1930}\right|\times 100=93.78$$

Table 12 illustrates that the overall gain % of CET-2C for encryption time is negative as compared with the compared Algorithms 1 and 2 [17] for small data sizes (up to 500 KB), meaning that CET-2C takes a longer time for encryption. After 500 KB the encryption time is lower than for comparable Algorithms 1 and 2 [17] so the overall performance of CET-2C is enhanced for larger data sizes. At the message size of 700 KB the overall % gain of CET-2C is 76.34% and 92.11% when it is compared with compared Algorithm 1 and 2, respectively [17].This shows that the performance of CET-2C is increased with increased message size.

Table 12. Overall %Gain of CET-2C over compared Algorithms 1 and 2 [17] for encryption time.

Message Sizes in Bytes	Overall % Gain for Encryption Time of CET-2C
	CET-2C over Compared Algorithm 1 [17]	CET-2C over Compared Algorithm 2 [17]
100,000	−98.15	−94.44
500,000	−94.67	−93.33
600,000	59.80	86.77
700,000	76.34	92.11
800,000	81.25	93.78

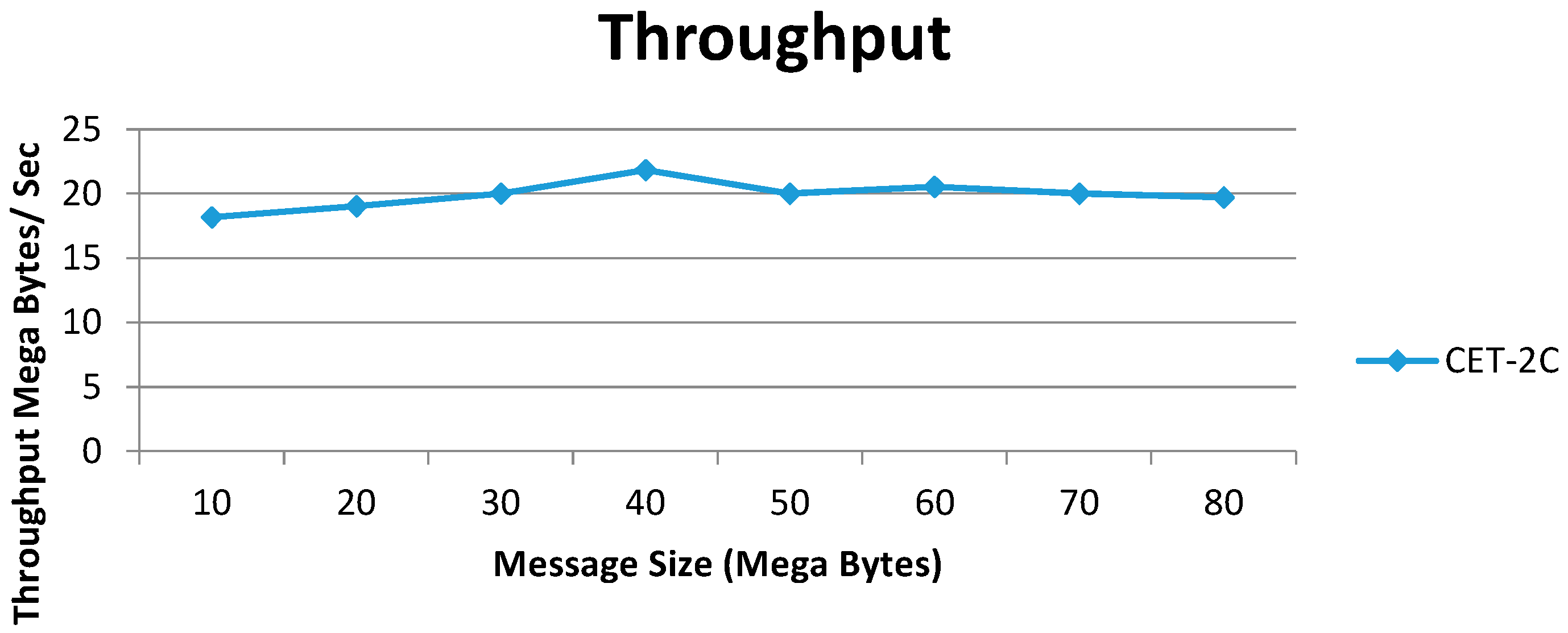
8.2. Encryption Throughput

The graph representing the throughput performance of the proposed algorithm CET-2C is much higher for any data size compared to the AES and Chaotic Algorithm [3]. It was analyzed using a laptop having an Intel (R) Pentium (R) Dual T2370 @ 1.73 GHz processor CPU, and 1 GB RAM (Table 13).

Table 13. Encryption throughput of Chaotic Algorithm [3], AES [3] and CET-2C.

Message Sizes in Bytes	Encryption Throughput in Bytes/Second
	Chaotic Algorithm [3]	AES [3]	CET-2C
10,000	20,000	2000	50,000
20,000	17,000	2000	44,847
30,000	16,700	2000	49,342
40,000	16,500	2000	57,405
50,000	16,400	2000	64,049

Figure 8 shows that the throughput of the proposed algorithm CET-2C is much higher compared to the chaotic algorithm [3] and AES [3] for different message sizes in bytes. For a 50,000 byte message the throughput of CET-2C is 64,049 bytes/s and the Chaotic Algorithm [3] and AES [3] have throughputs of 16,400 and 2000 bytes/s, respectively. This shows that CET-2C is much faster than the comparable algorithm [3].

Figure 8. Encryption throughput of Chaotic Algorithm [3], AES [3] and CET-2C.

Overall % Gain of CET-2C over Chaotic Algorithm [3] for Encryption Throughput with increasing the message size

$$G_p\text{of CET-2C over CA}=\frac{ET{h}_{CET-2C}(\text{at Different Message Sizes})-ET{h}_{CA}(\text{at Different Message Sizes})}{ET{h}_{CA}(\text{at Different Message Sizes})}$$

Here $G_p$= Overall % Gain at Different Message Sizes; ETh = Encryption Throughput; CA = Chaotic Algorithm.

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 10,000 bytes

$$\%\text{ Gain of CET-2C }=\frac{ET{h}_{CET-2C}-ET{h}_{CA}}{ET{h}_{CA}}\times 100=\left|\frac{50000-20000}{20000}\right|\times 100=150$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 20,000 bytes

$$\%\text{ Gain of CET-2C }=\frac{ET{h}_{CET-2C}-ET{h}_{CA}}{ET{h}_{CA}}\times 100=\left|\frac{44847-17000}{17000}\right|\times 100=164$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 30,000 bytes

$$\%\text{ Gain of CET-2C }=\frac{ET{h}_{CET-2C}-ET{h}_{CA}}{ET{h}_{CA}}\times 100=\left|\frac{49342-16700}{16700}\right|\times 100=195$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 40,000 bytes

$$\%\text{ Gain of CET-2C }=\frac{ET{h}_{CET-2C}-ET{h}_{CA}}{ET{h}_{CA}}\times 100=\left|\frac{57405-16500}{16500}\right|\times 100=248$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 50,000 bytes

$$\%\text{ Gain of CET-2C }=\frac{ET{h}_{CET-2C}-ET{h}_{CA}}{ET{h}_{CA}}\times 100=\left|\frac{64049-16400}{16400}\right|\times 100=490$$

Overall % Gain of CET-2C over AES [3] for Encryption Throughput with increasing the message size

$$G_p\text{of CET-2C over CA}=\frac{ET{h}_{CET-2C}(\text{at Different Message Sizes})-ET{h}_{AES}(\text{at Different Message Sizes})}{ET{h}_{AES}(\text{at Different Message Sizes})}$$

where AES = Advance Encryption Standard.

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 10,000 bytes

$$\%\text{ Gain of CET-2C }=\frac{ET{h}_{CET-2C}-ET{h}_{AES}}{ET{h}_{AES}}\times 100=\left|\frac{50000-2000}{2000}\right|\times 100=2400$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 20,000 bytes

$$\%\text{ Gain of CET-2C }=\frac{ET{h}_{CET-2C}-ET{h}_{AES}}{ET{h}_{AES}}\times 100=\left|\frac{44847-2000}{2000}\right|\times 100=2142$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 30,000 bytes

$$\%\text{ Gain of CET-2C }=\frac{ET{h}_{CET-2C}-ET{h}_{AES}}{ET{h}_{AES}}\times 100=\left|\frac{49342-2000}{2000}\right|\times 100=2367$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 40,000 bytes

$$\%\text{ Gain of CET-2C }=\frac{ET{h}_{CET-2C}-ET{h}_{AES}}{ET{h}_{AES}}\times 100=\left|\frac{57405-2000}{2000}\right|\times 100=2770$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 50,000 bytes

$$\%\text{ Gain of CET-2C }=\frac{ET{h}_{CET-2C}-ET{h}_{AES}}{ET{h}_{AES}}\times 100=\left|\frac{64049-2000}{2000}\right|\times 100=3102$$

Table 14 illustrates that overall gain % of CET-2C for encryption throughput is much higher as compared with the chaotic algorithm [3] and AES [3]. For the message size of 30,000 bytes the overall % gain of CET-2C is 195% and 2367% when it is compared with the Chaotic Algorithm [3] and AES [3]. This shows that the performance of CET-2C is increased with increasing message size. AES provides sconstant encryption time, so the throughput of AES is also constant. This indicates that CET-2Cprovidesmuchhigher encryption throughput than AES [3].

Table 14. Overall %Gain of CET-2C over Chaotic Algorithm [3] and AES [3] for encryption throughput.

Message Sizes in Bytes	Overall % Gain for Encryption Throughput of CET-2C
	CET-2C over Chaotic Algorithm [3]	CET-2C over AES [3]
10,000	150	2400
20,000	164	2142
30,000	195	2367
40,000	248	2770
50,000	490	3102

8.3. Encryption Power Consumption

The graph demonstrates that the proposed algorithm has lesser power consumption than AES and the Chaotic Algorithm [3] for any data size. This was analyzed using a laptop having an Intel (R) Pentium (R) Dual processor T2370 @ 1.73 GHzCPU, and 1 GB RAM (Table 15).

Table 15. Energy consumption of AES [3], Chaotic Algorithm [3] and CET-2C.

Message Sizes in Kb	Energy Consumption in J
	Chaotic Algorithm [3]	AES [3]	CET-2C
200	0.20625	0.125	0.008725
250	0.25625	0.125	0.0095
300	0.31	0.125	0.01025
350	0.35375	0.125	0.011138
400	0.41875	0.125	0.0122
450	0.46875	0.125	0.0225

Figure 9 shows the proposed algorithm CET-2C has less power consumption compared to AES [3] and the chaotic algorithm for multiple message sizes ranging from 200 KB to 450 KB [3]. The results illustrate that the energy consumptionincreases linearly like the encryption time when it is compared with other algorithms.

Figure 9. Energy consumption of AES [3], Chaotic Algorithm [3] and CET-2C.

Overall % Gain of CET-2C over Chaotic Algorithm [3] for Energy Consumption with increasing the message size.

$$G_p\text{of CET-2C over CA}=\frac{E{C}_{CET-2C}(\text{at Different Message Sizes})-E{C}_{CA}(\text{at Different Message Sizes})}{E{C}_{CA}(\text{at Different Message Sizes})}$$

Here $G_p$ = Overall % Gain at Different Message Sizes; EC = Energy Consumption; CA = Chaotic Algorithm.

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 200 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.008725-0.20625}{0.20625}\right|\times 100=95.77$$

% Gain of CET-2 Cover Chaotic Algorithm [3] when message size is 250 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.0095-0.25625}{0.25625}\right|\times 100=96.29$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 300 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.01025-0.31}{0.31}\right|\times 100=96.69$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 350 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.011138-0.35375}{0.35375}\right|\times 100=96.85$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 400 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.0122-0.41875}{0.41875}\right|\times 100=97.09$$

% Gain of CET-2C over Chaotic Algorithm [3] when message size is 450 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.013175-0.46875}{0.46875}\right|\times 100=97.19$$

Overall % Gain of CET-2C over AES [3] for Encryption Time with increasing the message size

$$G_p\text{of CET-2C over AES}=\frac{E{C}_{CET-2C}(\text{at Different Message Sizes})-E{C}_{AES}(\text{at Different Message Sizes})}{E{C}_{AES}(\text{at Different Message Sizes})}$$

where AES = Advance Encryption Standard.

% Gain of CET-2C over AES [3] when message size is 200 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.008725-0.125}{0.125}\right|\times 100=93.02$$

% Gain of CET-2C over AES [3] when message size is 250 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.0095-0.125}{0.125}\right|\times 100=92.4$$

% Gain of CET-2C over AES [3] when message size is 300 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.01025-0.125}{0.125}\right|\times 100=91.8$$

% Gain of CET-2C over AES [3] when message size is 350 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.011138-0.125}{0.125}\right|\times 100=91.09$$

% Gain of CET-2C over AES [3] when message size is 400 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.0122-0.125}{0.125}\right|\times 100=90.24$$

% Gain of CET-2C over AES [3] when message size is 450 KB

$$\%\text{ Gain of CET-2C }=\frac{E{C}_{CET-2C}-E{C}_{AES}}{E{C}_{AES}}\times 100=\left|\frac{0.013175-0.125}{0.125}\right|\times 100=89.46$$

Table 16 illustrates that the overall gain % of CET-2C of energy consumption is lower as compared with the chaotic algorithm [3] and AES [3]. At the message size of 450 Kb the overall % gain of CET-2C is 97.19% and 89.46% when it is compared with the chaotic algorithm [3] and AES [3]. This shows that the performance of CET-2C is increased with increasing message size.

Table 16. Overall % Gain of CET-2C over Chaotic Algorithm [3] and AES [3] for energy consumption.

Message Sizes in Kb	Overall % Gain for Energy Consumption of CET-2C
	CET-2C over Chaotic Algorithm [3]	CET-2C over AES [3]
200	95.77	93.02
250	96.29	92.4
300	96.69	91.8
350	96.85	91.09
400	97.09	90.24
450	97.19	89.46

9. Conclusions

Chaotic functions have been widely used in different applications to generate pseudo-random numbers to produce random values in short times, which may be used for various real time applications. In this paper a novel digital logic-based, chaotic encryption technique has been developed, which works based on chaos theory, using the sensitivity of parameters like a constant A and initial condition Xn with the properties of chaotic systems for ubiquitous and ad-hoc computing. The efficiency of the encryption technique also depends on the number of keys, which are generated by the use of the chaotic function. It has been also shown that keys are completely different when the parameters are changed slightly. This demonstrates the security of the keys. Cryptanalysis of the proposed algorithm shows the strength and security of the algorithm and keys. The performance of a proposed algorithm has been analyzed in terms of running time, throughput and power consumption. It is to be shown in comparison graphs that the proposed algorithm gave better results compared to different algorithms like AES and some others. The graphs show that the CET-2C gives 97% better encryption time, 95% better throughput and 98% better power consumption as compared to the other algorithms. This could be used for providing a better trade-off between security and computational complexity. In the future chaos theory could be used in highly secure and fast encryption systems, capable of processing very large dataset sizes on the order of GB with low space complexity. Digital circuits are very useful for fast encryption, as they are easily understandable and maintainable for processing messages compared to mathematical models. The private networks have security concerns and they need several techniques for hiding and encoding the messages moving between their private systems. This could be achieved by using chaos-based cryptography in the future.