Quantum Heat Machines Equivalence, Work Extraction beyond Markovianity, and Strong Coupling via Heat Exchangers
Abstract
:1. Introduction
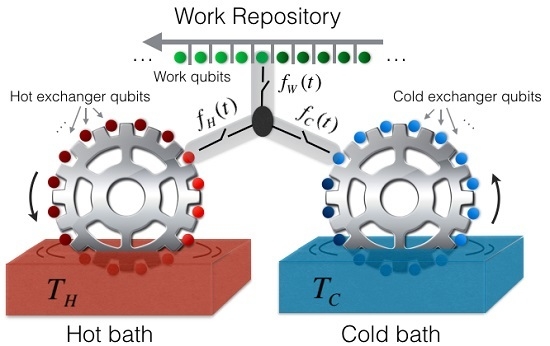
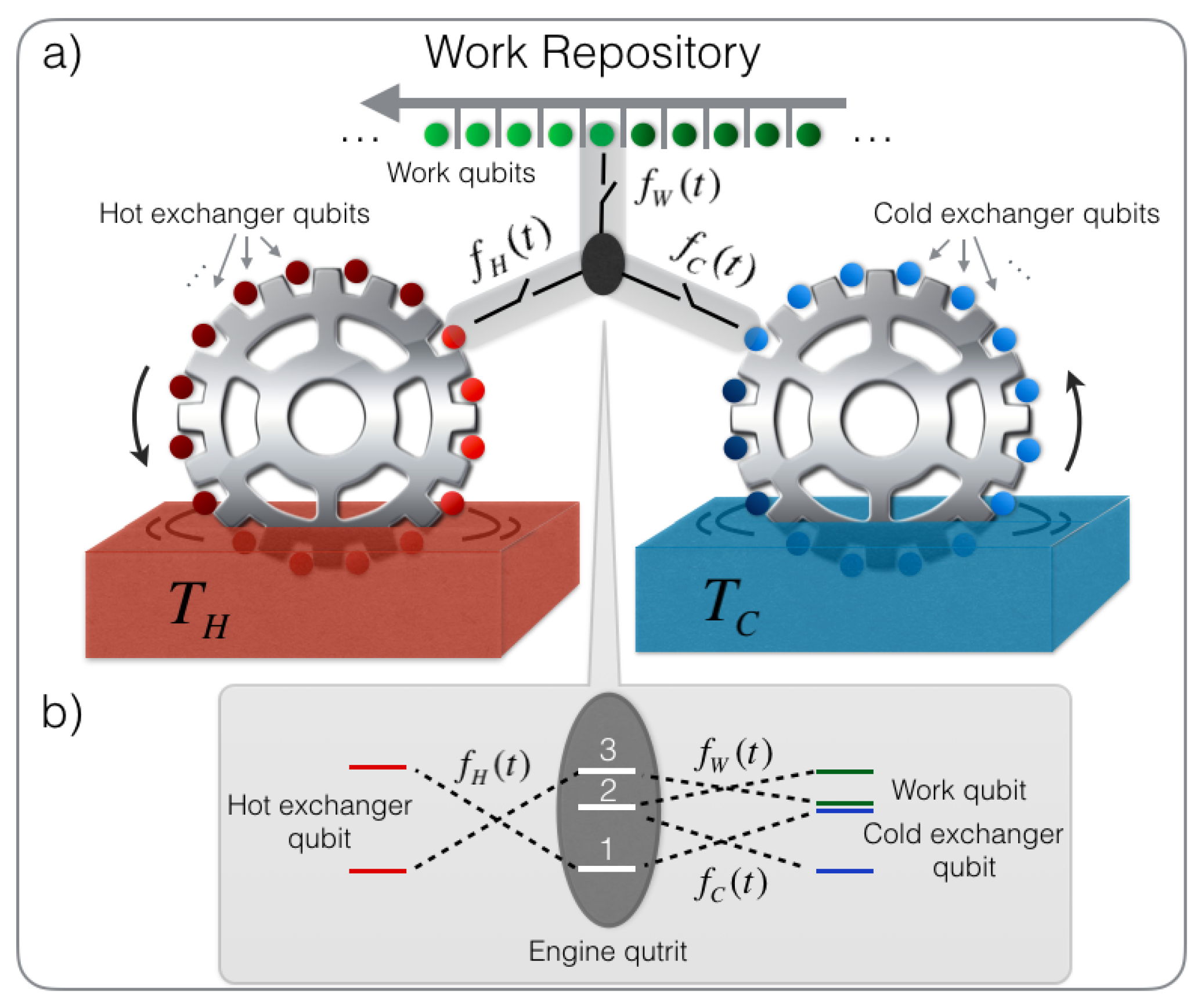
2. The Setup
2.1. The Heat Exchanger and the Baths
2.2. The Engine
2.3. The Coupling of the Engine to the Heat Exchangers and to the Work Repository
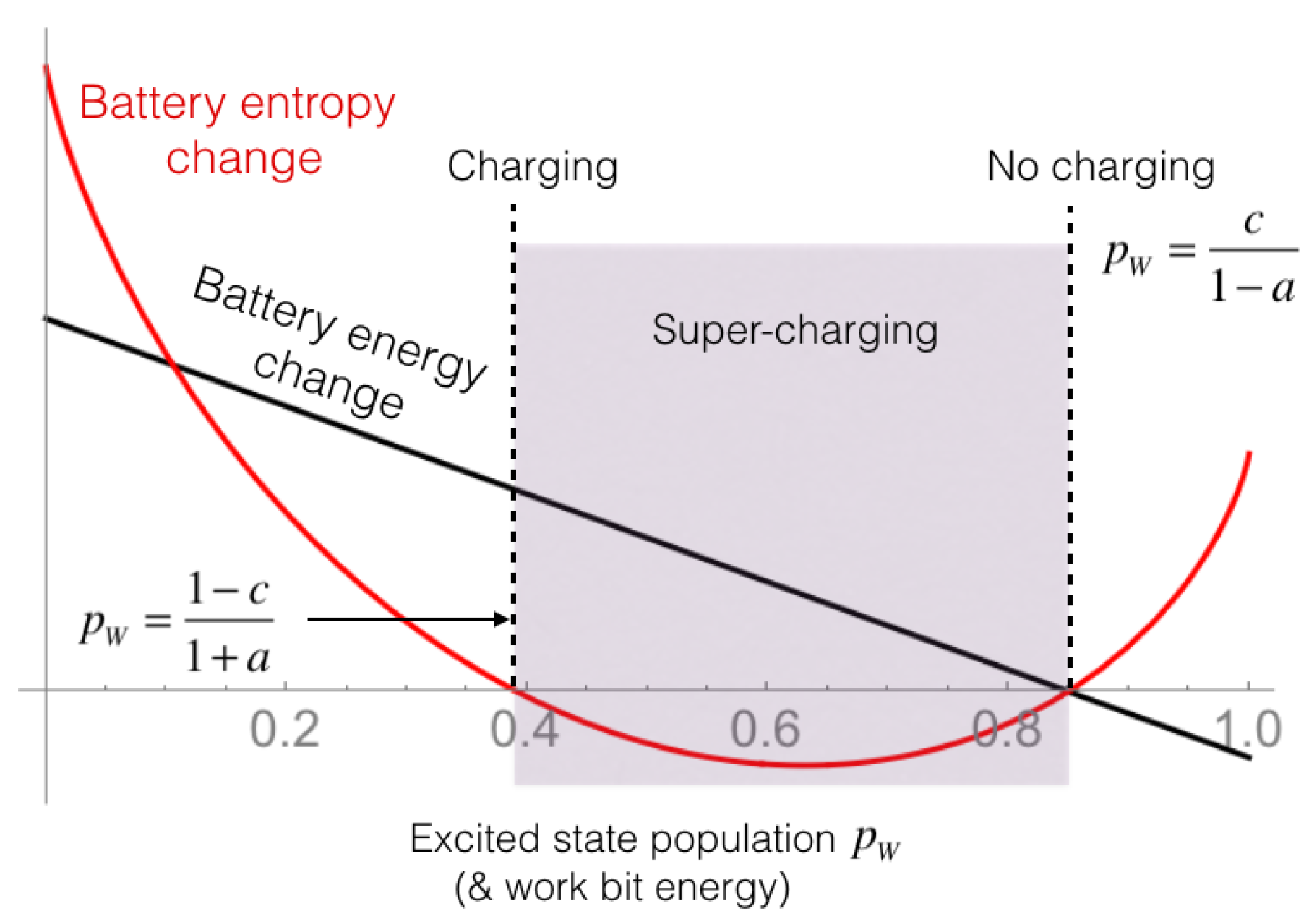
2.4. The Work Repository
2.5. Heat and Work
3. Results
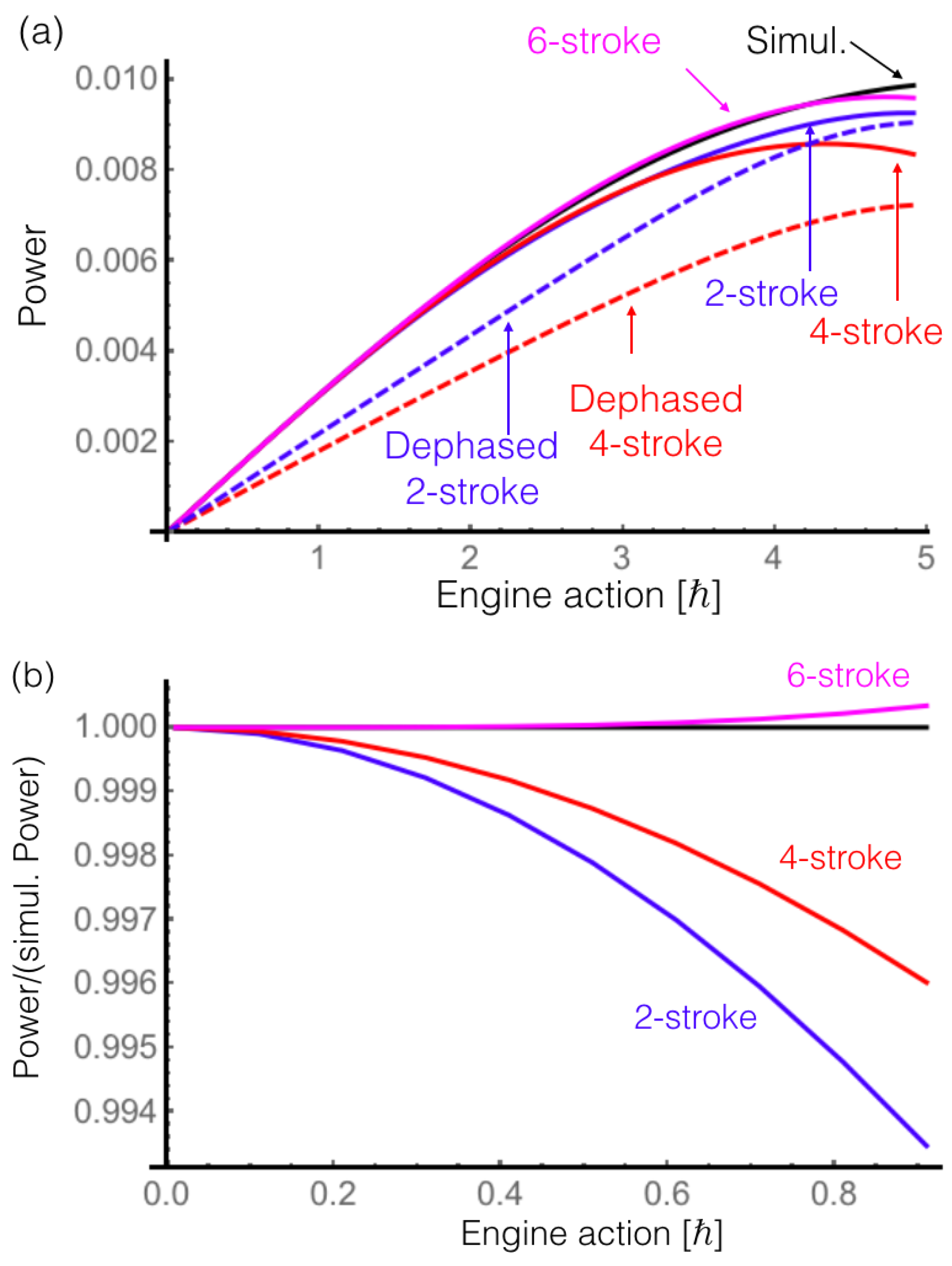
3.1. The Equivalence of Heat Machines in the Non-Markovian Regime
3.2. Work Extraction
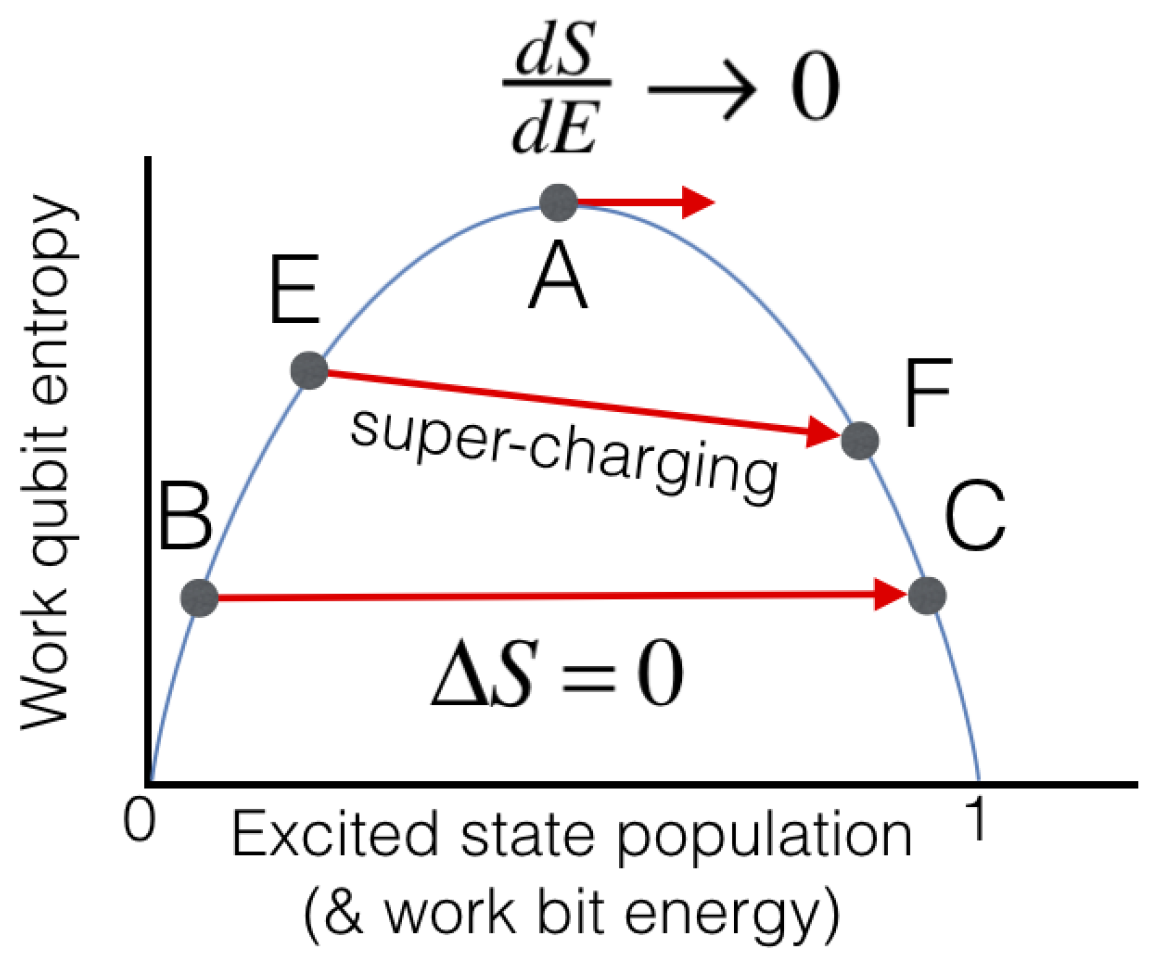
3.2.1. The Initial State of the Battery in Strong and Weak Coupling
3.2.2. Beyond the Semi-Classical Limit of the Driving Field
3.3. Higher Order Splittings
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Uzdin, R.; Levy, A.; Kosloff, R. Equivalence of Quantum Heat Machines, and Quantum-Thermodynamic Signatures. Phys. Rev. X 2015, 5, 031044. [Google Scholar] [CrossRef]
- Mitchison, M.T.; Woods, M.P.; Prior, J.; Huber, M. Coherence-assisted single-shot cooling by quantum absorption refrigerators. New J. Phys. 2015, 17, 115013. [Google Scholar] [CrossRef]
- Goold, J.; Huber, M.; Riera, A.; del Rio, L.; Skrzypczyk, P. The role of quantum information in thermodynamics—A topical review. J. Phys. A Math. Theor. 2016, 49, 143001. [Google Scholar] [CrossRef]
- Vinjanampathy, S.; Anders, J. Quantum Thermodynamics. 2013. [Google Scholar] [CrossRef]
- Millen, J.; Xuereb, A. Perspective on quantum thermodynamics. New J. Phys. 2016, 18, 011002. [Google Scholar] [CrossRef]
- Scovil, H.E.D.; Schulz-DuBois, E.O. Three-Level Masers as Heat Engines. Phys. Rev. Lett. 1959, 2, 262–263. [Google Scholar] [CrossRef]
- Geva, E.; Kosloff, R. The Three-Level Quantum Amplifier as a Heat Engine: A Study in Finite-Time Thermodynamics. Phys. Rev. E 1994, 49, 3903–3918. [Google Scholar] [CrossRef]
- Geva, E.; Kosloff, R. The Quantum Heat Engine and Heat Pump: An Irreversible Thermodynamic Analysis of the Three-Level Amplifier. J. Chem. Phys. 1996, 104, 7681–7698. [Google Scholar] [CrossRef]
- Alicki, R. The quantum open system as a model of the heat engine. J. Phys A Math. Gen. 1979, 12, L103. [Google Scholar] [CrossRef]
- Kosloff, R. A Quantum Mechanical Open System as a Model of a Heat Engine. J. Chem. Phys. 1984, 80, 1625–1631. [Google Scholar] [CrossRef]
- Feldmann, T.; Kosloff, R. Performance of Discrete Heat Engines and Heat Pumps in Finite Time. Phys. Rev. E 2000, 61, 4774–4790. [Google Scholar] [CrossRef]
- Rezek, Y.; Kosloff, R. Irreversible performance of a quantum harmonic heat engine. New J. Phys. 2006, 8, 83. [Google Scholar] [CrossRef]
- Kosloff, R.; Levy, A. Quantum Heat Engines and Refrigerators: Continuous Devices. Annu. Rev. Phys. Chem. 2014, 65, 365–393. [Google Scholar] [CrossRef] [PubMed]
- Harbola, U.; Rahav, S.; Mukamel, S. Quantum heat engines: A thermodynamic analysis of power and efficiency. Euro. Phys. Lett. 2012, 99, 50005. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Hovhannisyan, K.; Mahler, G. Optimal refrigerator. Phys. Rev. E 2010, 81, 051129. [Google Scholar] [CrossRef] [PubMed]
- Linden, N.; Popescu, S.; Skrzypczyk, P. How Small Can Thermal Machines Be? The Smallest Possible Refrigerator. Phys. Rev. Lett. 2010, 105, 130401. [Google Scholar] [CrossRef] [PubMed]
- Henrich, M.J.; Rempp, F.; Mahler, G. Quantum thermodynamic Otto machines: A spin-system approach. Eur. Phys. J. 2005, 151, 157–165. [Google Scholar] [CrossRef]
- Skrzypczyk, P.; Short, A.J.; Popescu, S. Work extraction and thermodynamics for individual quantum systems. Nat. Commun. 2014, 5, 4185. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Alicki, R.; Kurizki, G. Work and energy gain of heat-pumped quantized amplifiers. Europhys. Lett. 2013, 103, 60005. [Google Scholar] [CrossRef]
- Kolář, M.; Gelbwaser-Klimovsky, D.; Alicki, R.; Kurizki, G. Quantum Bath Refrigeration towards Absolute Zero: Challenging the Unattainability Principle. Phys. Rev. Lett. 2012, 109, 090601. [Google Scholar] [CrossRef] [PubMed]
- Alicki, R. Quantum Thermodynamics: An Example of Two-Level Quantum Machine. Open Syst. Inf. Dyn. 2014, 21, 1440002. [Google Scholar] [CrossRef]
- Quan, H.; Liu, Y.X.; Sun, C.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef] [PubMed]
- Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Nanoscale Heat Engine Beyond the Carnot Limit. Phys. Rev. Lett. 2014, 112, 030602. [Google Scholar] [CrossRef] [PubMed]
- Binder, F.; Vinjanampathy, S.; Modi, K.; Goold, J. Quantum thermodynamics of general quantum processes. Phys. Rev. E 2015, 91, 032119. [Google Scholar] [CrossRef] [PubMed]
- Correa, L.A.; Palao, J.P.; Alonso, D.; Adesso, G. Quantum-enhanced absorption refrigerators. Sci. Rep. 2014, 4, 3949. [Google Scholar] [CrossRef] [PubMed]
- Dorner, R.; Clark, S.; Heaney, L.; Fazio, R.; Goold, J.; Vedral, V. Extracting quantum work statistics and fluctuation theorems by single-qubit interferometry. Phys. Rev. Lett. 2013, 110, 230601. [Google Scholar] [CrossRef] [PubMed]
- Correa, L.A.; Palao, J.P.; Adesso, G.; Alonso, D. Performance bound for quantum absorption refrigerators. Phys. Rev. E 2013, 87, 042131. [Google Scholar] [CrossRef] [PubMed]
- Dorner, R.; Goold, J.; Cormick, C.; Paternostro, M.; Vedral, V. Emergent thermodynamics in a quenched quantum many-body system. Phys. Rev. Lett. 2012, 109, 160601. [Google Scholar] [CrossRef] [PubMed]
- Del Campo, A.; Goold, J.; Paternostro, M. More bang for your buck: Super-adiabatic quantum engines. Sci. Rep. 2014, 4, 6208. [Google Scholar] [CrossRef] [PubMed]
- Malabarba, A.S.; Short, A.J.; Kammerlander, P. Clock-Driven Quantum Thermal Engines. New J. Phys. 2015, 17, 045027. [Google Scholar] [CrossRef]
- Gelbwaser-Klimovsky, D.; Niedenzu, W.; Kurizki, G. Chapter Twelve—Thermodynamics of Quantum Systems Under Dynamical Control. In Advances In Atomic, Molecular, and Optical Physics; Academic Press: Salt Lake City, UT, USA, 2015; Volume 64, pp. 329–407. [Google Scholar]
- Whitney, R.S. Most efficient quantum thermoelectric at finite power output. Phys. Rev. Lett. 2014, 112, 130601. [Google Scholar] [CrossRef] [PubMed]
- Allahverdyan, A.E.; Hovhannisyan, K.; Mahler, G. Optimal refrigerator. Phys. Rev. E 2010, 81, 051129. [Google Scholar] [CrossRef] [PubMed]
- Mari, A.; Eisert, J. Cooling by Heating: Very Hot Thermal Light Can Significantly Cool Quantum Systems. Phys. Rev. Lett. 2012, 108, 120602. [Google Scholar] [CrossRef] [PubMed]
- Bakr, W.S.; Preiss, P.M.; Tai, M.E.; Ma, R.; Simon, J.; Greiner, M. Orbital excitation blockade and algorithmic cooling in quantum gases. Nature 2011, 480, 500–503. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Baugh, J.; Moussa, O.; Ryan, C.A.; Nayak, A.; Laflamme, R. Experimental implementation of heat-bath algorithmic cooling using solid-state nuclear magnetic resonance. Nature 2005, 438, 470–473. [Google Scholar] [CrossRef] [PubMed]
- Boykin, P.O.; Mor, T.; Roychowdhury, V.; Vatan, F.; Vrijen, R. Algorithmic cooling and scalable NMR quantum computers. Proc. Natl. Acad. Sci. USA 2002, 99, 3388–3393. [Google Scholar] [CrossRef] [PubMed]
- Rempp, F.; Michel, M.; Mahler, G. Cyclic Cooling Algorithm. Phys. Rev. A 2007, 76, 032325. [Google Scholar] [CrossRef]
- Segal, D.; Nitzan, A. Molecular heat pump. Phys. Rev. E 2006, 73, 026109. [Google Scholar] [CrossRef] [PubMed]
- Schulman, L.J.; Mor, T.; Weinstein, Y. Physical limits of heat-bath algorithmic cooling. Phys. Rev. Lett. 2005, 94, 120501. [Google Scholar] [CrossRef] [PubMed]
- Oscar Boykin, P.; Mor, T.; Roychowdhury, V.; Vatan, F.; Vrijen, R. Algorithmic cooling and scalable NMR quantum computer. Proc. Nat. Acad. Sci. 2002, 99, 3388–3393. [Google Scholar] [CrossRef] [PubMed]
- Skrzypczyk, P.; Brunner, N.; Linden, N.; Popescu, S. The smallest refrigerators can reach maximal efficiency. J. Phys. A Math. Theor. 2011, 44, 492002. [Google Scholar] [CrossRef]
- Brandner, K.; Bauer, M.; Schmid, M.T.; Seifert, U. Coherence-enhanced efficiency of feedback-driven quantum engines. New J. Phys. 2015, 17, 065006. [Google Scholar] [CrossRef]
- Bulnes Cuetara, G.; Engels, A.; Esposito, M. Stochastic thermodynamics of rapidly driven quantum systems. New J. Phys. 2015, 17, 055002. [Google Scholar] [CrossRef]
- Perarnau-Llobet, M.; Hovhannisyan, K.V.; Huber, M.; Skrzypczyk, P.; Brunner, N.; Acín, A. Extractable Work from Correlations. Phys. Rev. X 2015, 5, 041011. [Google Scholar] [CrossRef]
- Roßnagel, J.; Dawkins, S.T.; Tolazzi, K.N.; Abah, O.; Lutz, E.; Schmidt-Kaler, F.; Singer, K. A single-atom heat engine. Available online: http://arxiv.org/abs/1510.03681 (accessed on 23 March 2016).
- Venturelli, D.; Fazio, R.; Giovannetti, V. Minimal self-contained quantum refrigeration machine based on four quantum dots. Phys. Rev. Lett. 2013, 110, 256801. [Google Scholar] [CrossRef] [PubMed]
- Bergenfeldt, C.; Samuelsson, P.; Sothmann, B.; Flindt, C.; Büttiker, M. Hybrid microwave-cavity heat engine. Phys. Rev. Lett. 2014, 112, 076803. [Google Scholar] [CrossRef] [PubMed]
- Niskanen, A.; Nakamura, Y.; Pekola, J. Information entropic superconducting microcooler. Phys. Rev. B 2007, 76, 174523. [Google Scholar] [CrossRef]
- Brask, J.B.; Haack, G.; Brunner, N.; Huber, M. Autonomous quantum thermal machine for generating steady-state entanglement. New J. Phys. 2015, 17, 113029. [Google Scholar] [CrossRef]
- Campisi, M.; Pekola, J.; Fazio, R. Nonequilibrium fluctuations in quantum heat engines: Theory, example, and possible solid state experiments. New J. Phys. 2015, 17, 035012. [Google Scholar] [CrossRef]
- Pekola, J.P. Towards quantum thermodynamics in electronic circuits. Nat. Phys. 2015, 11, 118–123. [Google Scholar] [CrossRef]
- Fialko, O.; Hallwood, D. Isolated quantum heat engine. Phys. Rev. Lett. 2012, 108, 085303. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Bariani, F.; Meystre, P. Quantum optomechanical heat engine. Phys. Rev. Lett. 2014, 112, 150602. [Google Scholar] [CrossRef] [PubMed]
- Dechant, A.; Kiesel, N.; Lutz, E. All-Optical Nanomechanical Heat Engine. Phys. Rev. Lett. 2015, 114, 183602. [Google Scholar] [CrossRef] [PubMed]
- Thierschmann, H.; Sánchez, R.; Sothmann, B.; Arnold, F.; Heyn, C.; Hansen, W.; Buhmann, H.; Molenkamp, L.W. Three-terminal energy harvester with coupled quantum dots. Nat. Nanotechnol. 2015, 10, 854–858. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, R.; Büttiker, M. Optimal energy quanta to current conversion. Phys. Rev. B 2011, 83, 085428. [Google Scholar] [CrossRef]
- Roche, B.; Roulleau, P.; Jullien, T.; Jompol, Y.; Farrer, I.; Ritchie, D.; Glattli, D. Harvesting dissipated energy with a mesoscopic ratchet. Nat. Commun. 2015, 6, 6383. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, F.; Pfeffer, P.; Höfling, S.; Kamp, M.; Worschech, L. Voltage fluctuation to current converter with coulomb-coupled quantum dots. Phys. Rev. Lett. 2015, 114, 146805. [Google Scholar] [CrossRef] [PubMed]
- Sothmann, B.; Sánchez, R.; Jordan, A.N.; Büttiker, M. Rectification of thermal fluctuations in a chaotic cavity heat engine. Phys. Rev. B 2012, 85, 205301. [Google Scholar] [CrossRef]
- Sagawa, T. Second law-like inequalities with quantum relative entropy: An introduction. Lect. Quantum Comput. Thermodyn. Stat. Phys. 2012, 8, 127. Available online: http://arxiv.org/abs/1202.0983 (accessed on 2 April 2016). [Google Scholar]
- Kammerlander, P.; Anders, J. Quantum measurement and its role in thermodynamics. Available online: http://arxiv.org/abs/1502.02673 (accessed on 29 March 2016).
- Jaramillo, J.; Beau, M.; del Campo, A. Quantum Supremacy of Many-Particle Thermal Machines. Available online: http://arxiv.org/abs/1510.04633 (accessed on 3 April 2016).
- Lostaglio, M.; Jennings, D.; Rudolph, T. Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 2015, 6, 6383. [Google Scholar] [CrossRef] [PubMed]
- Ćwikliński, P.; Studziński, M.; Horodecki, M.; Oppenheim, J. Limitations on the Evolution of Quantum Coherences: Towards Fully Quantum Second Laws of Thermodynamics. Phys. Rev. Lett. 2015, 115, 210403. [Google Scholar] [CrossRef] [PubMed]
- Korzekwa, K.; Lostaglio, M.; Oppenheim, J.; Jennings, D. The extraction of work from quantum coherence. Available online: http://arxiv.org/abs/1506.07875 (accessed on 22 February 2016).
- Åberg, J. Catalytic coherence. Phys. Rev. Lett. 2014, 113, 150402. [Google Scholar] [CrossRef] [PubMed]
- Levy, A.; Kosloff, R. Quantum absorption refrigerator. Phys. Rev. Lett. 2012, 108, 070604. [Google Scholar] [CrossRef] [PubMed]
- Breuer, H.-P.; Petruccione, F. Open Quantum Systems; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- Gallego, R.; Riera, A.; Eisert, J. Thermal machines beyond the weak coupling regime. New J. Phys. 2014, 16, 125009. [Google Scholar] [CrossRef]
- Esposito, M.; Ochoa, M.A.; Galperin, M. Quantum Thermodynamics: A Nonequilibrium Green’s Function Approach. Phys. Rev. Lett. 2015, 114, 080602. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Aspuru-Guzik, A. Strongly coupled quantum heat machines. J. Phys. Chem. Lett. 2015, 6, 3477–3482. [Google Scholar] [CrossRef] [PubMed]
- Uzdin, R.; Kosloff, R. The multilevel four-stroke swap engine and its environment. New J. Phys. 2014, 16, 095003. [Google Scholar] [CrossRef]
- Rybár, T.; Filippov, S.N.; Ziman, M.; Bužek, V. Simulation of indivisible qubit channels in collision models. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 154006. [Google Scholar] [CrossRef]
- Ziman, M.; Štelmachovič, P.; Bužek, V. Description of quantum dynamics of open systems based on collision-like models. Open Syst. Inf. Dyn. 2005, 12, 81–91. [Google Scholar] [CrossRef]
- Gennaro, G.; Benenti, G.; Palma, G.M. Relaxation due to random collisions with a many-qudit environment. Phys. Rev. A 2009, 79, 022105. [Google Scholar] [CrossRef]
- Gennaro, G.; Benenti, G.; Palma, G.M. Entanglement dynamics and relaxation in a few-qubit system interacting with random collisions. Europhys. Lett. 2008, 82, 20006. [Google Scholar] [CrossRef]
- Woods, M.P.; Ng, N.; Wehner, S. The maximum efficiency of nano heat engines depends on more than temperature. Available online: http://arxiv.org/abs/1506.02322 (accessed on 1 April 2016).
- Uzdin, R. Coherence recycling, collective operation, and coherence induced reversibility in quantum heat engines. Available online: http://arxiv.org/abs/1509.06289 (accessed on 1 April 2016).
- De Raedt, H. Product formula algorithms for solving the time dependent Schrödinger equation. Comput. Phys. Rep. 1987, 7, 1–72. [Google Scholar] [CrossRef]
- Feit, M.; Fleck, J.; Steiger, A. Solution of the Schrödinger equation by a spectral method. J. Comput. Phys. 1982, 47, 412–433. [Google Scholar] [CrossRef]
- Jahnke, T.; Lubich, C. Error bounds for exponential operator splittings. BIT Numer. Math. 2000, 40, 735–744. [Google Scholar] [CrossRef]
- Levy, A.; Alicki, R.; Kosloff, R. Quantum refrigerators and the third law of thermodynamics. Phys. Rev. E 2012, 85, 061126. [Google Scholar] [CrossRef] [PubMed]
- Levy, A.; Diósi, L.; Kosloff, R. Quantum Flywheel. Available online: http://arxiv.org/abs/1602.04322 (accessed on 21 March 2016).
- Blanes, S.; Casas, F. On the necessity of negative coefficients for operator splitting schemes of order higher than two. Appl. Numer. Math. 2005, 54, 23–37. [Google Scholar] [CrossRef]
- Yoshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzdin, R.; Levy, A.; Kosloff, R. Quantum Heat Machines Equivalence, Work Extraction beyond Markovianity, and Strong Coupling via Heat Exchangers. Entropy 2016, 18, 124. https://doi.org/10.3390/e18040124
Uzdin R, Levy A, Kosloff R. Quantum Heat Machines Equivalence, Work Extraction beyond Markovianity, and Strong Coupling via Heat Exchangers. Entropy. 2016; 18(4):124. https://doi.org/10.3390/e18040124
Chicago/Turabian StyleUzdin, Raam, Amikam Levy, and Ronnie Kosloff. 2016. "Quantum Heat Machines Equivalence, Work Extraction beyond Markovianity, and Strong Coupling via Heat Exchangers" Entropy 18, no. 4: 124. https://doi.org/10.3390/e18040124
APA StyleUzdin, R., Levy, A., & Kosloff, R. (2016). Quantum Heat Machines Equivalence, Work Extraction beyond Markovianity, and Strong Coupling via Heat Exchangers. Entropy, 18(4), 124. https://doi.org/10.3390/e18040124