The Effect of Spin Squeezing on the Entanglement Entropy of Kicked Tops
Abstract
:1. Introduction
2. Two-Coupled Quantum Kicked Tops
2.1. Kicked Tops
2.2. Initial States
2.3. Quantum Kicked Top Evolution
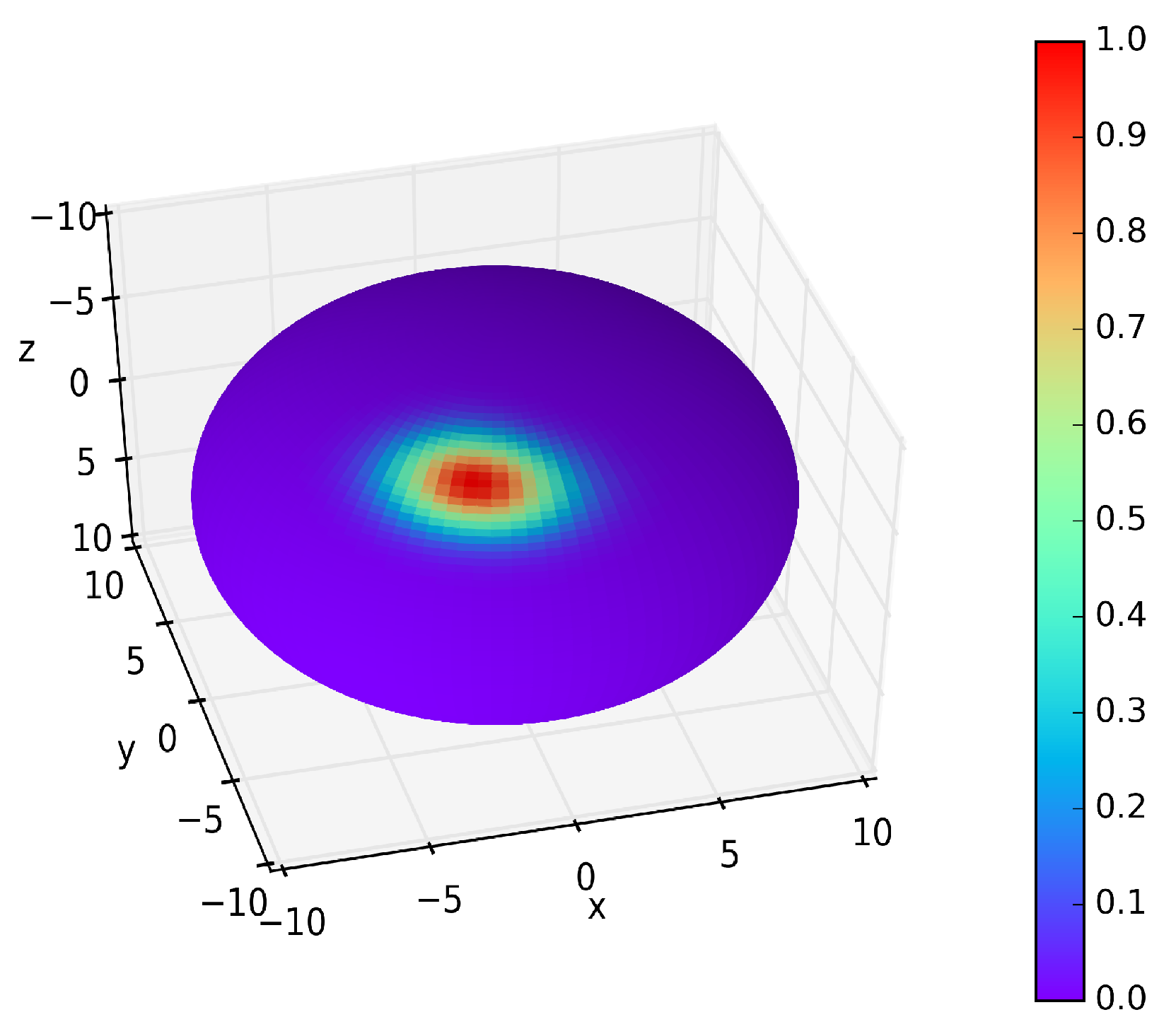
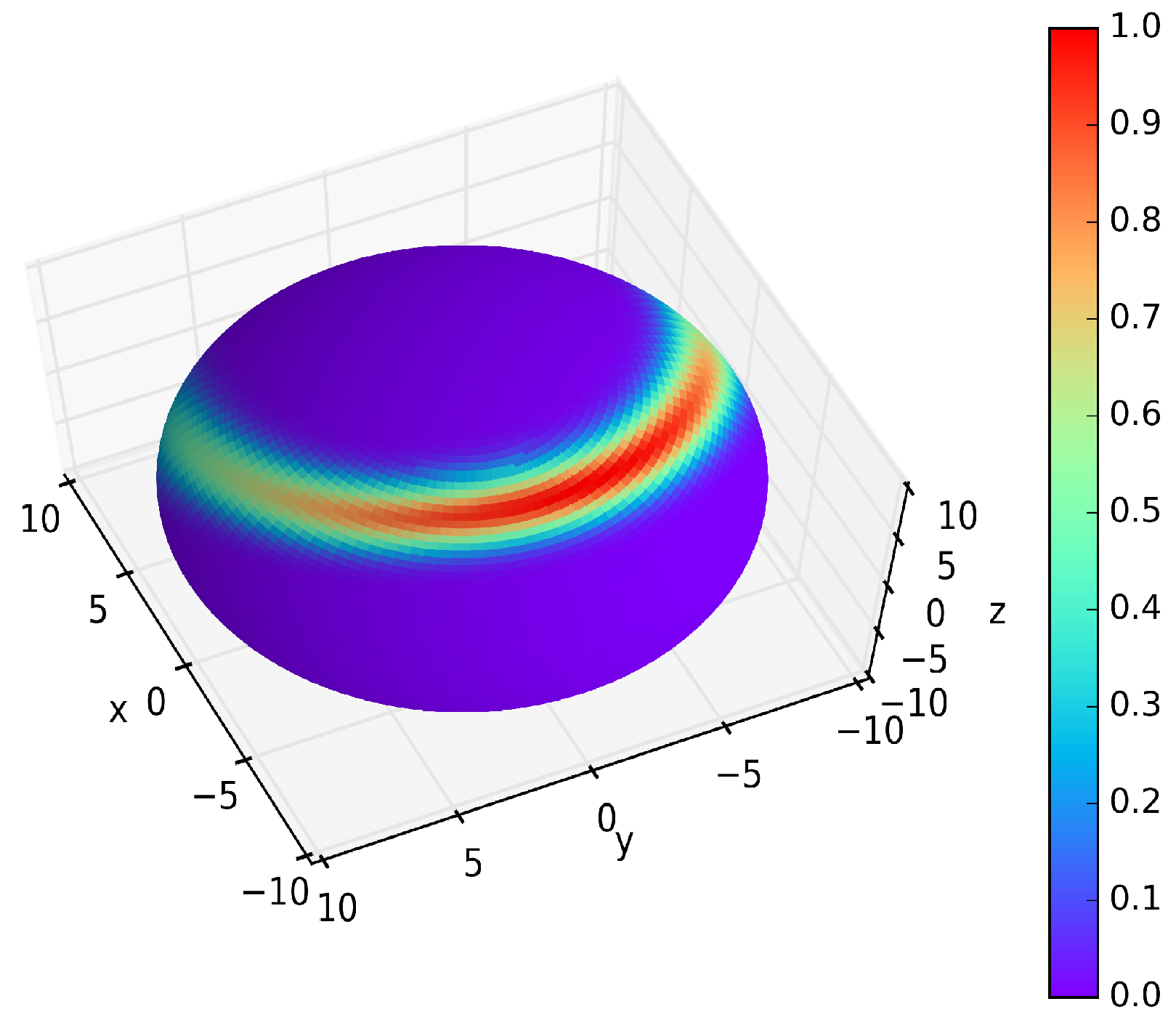
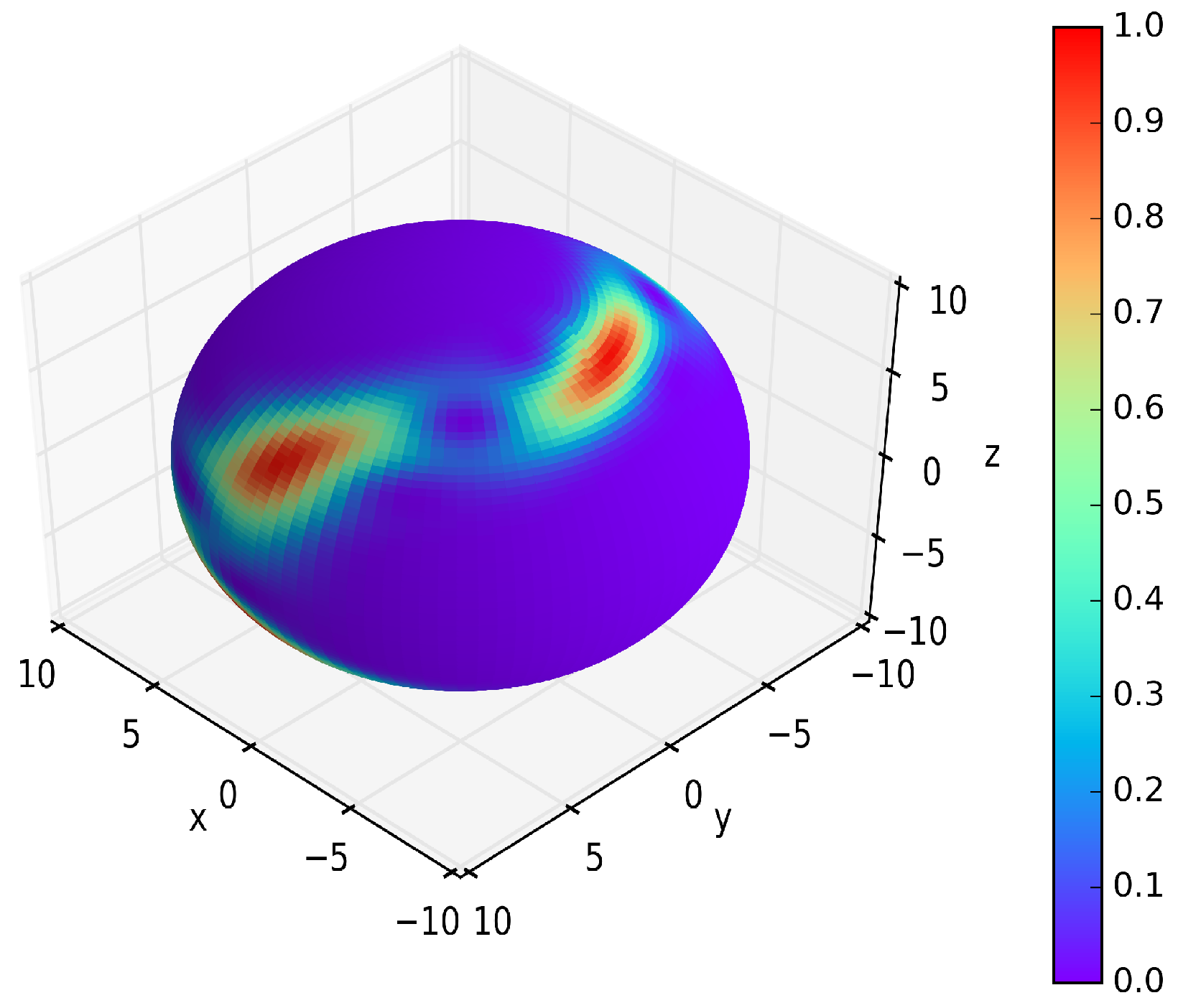
2.4. Spin Squeezing
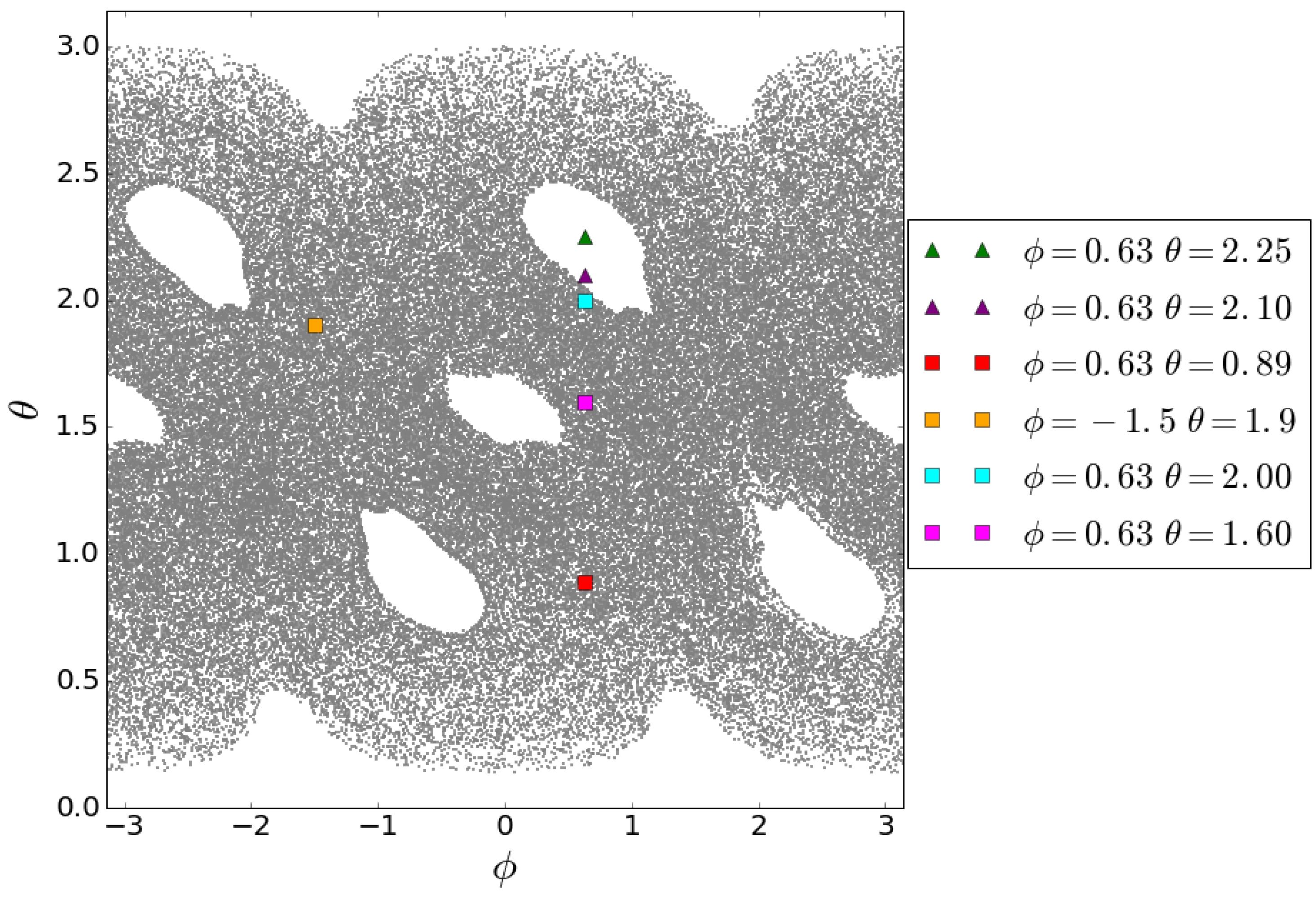
3. Quantum-Classical Correspondence
4. Quantification of Entanglement
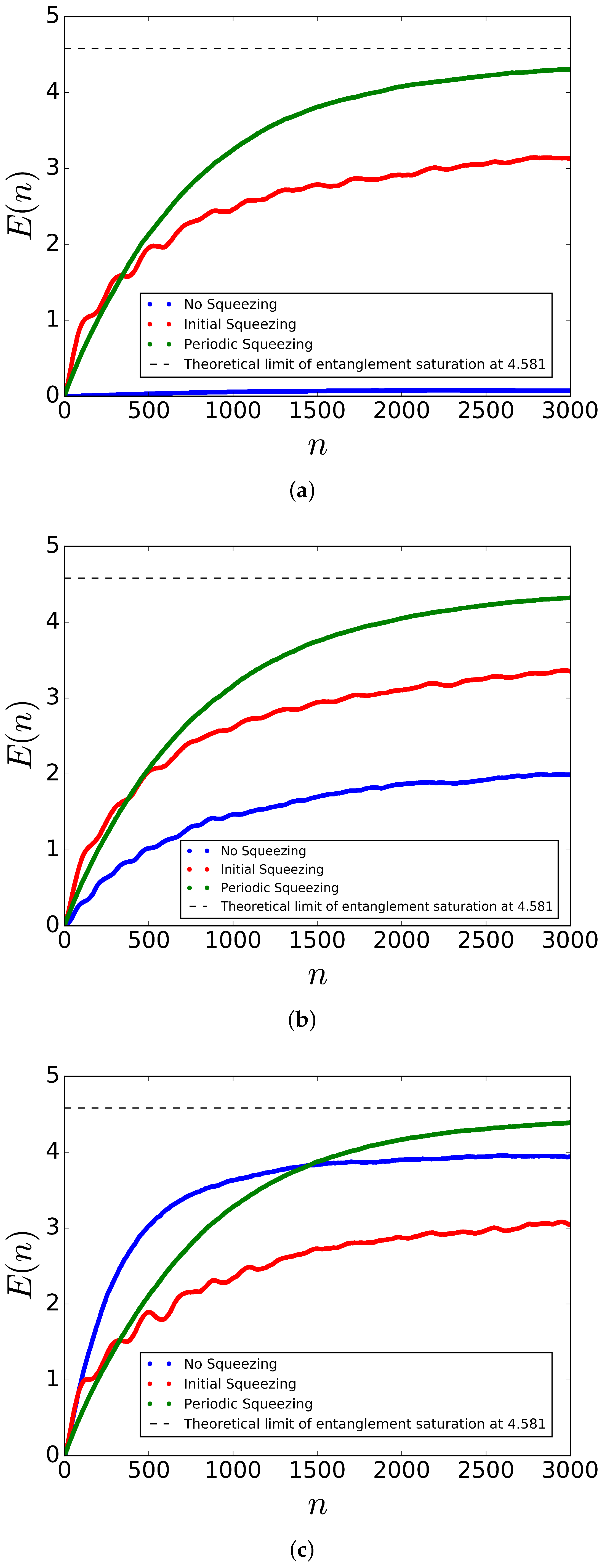
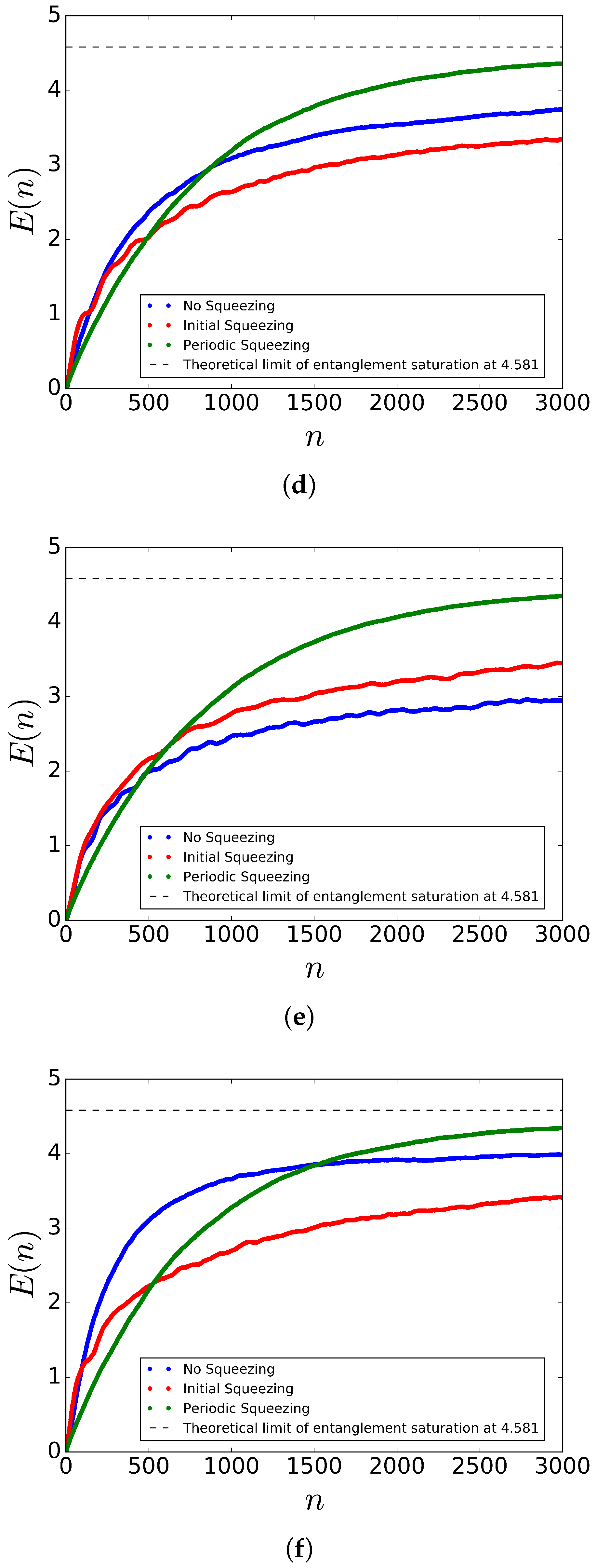
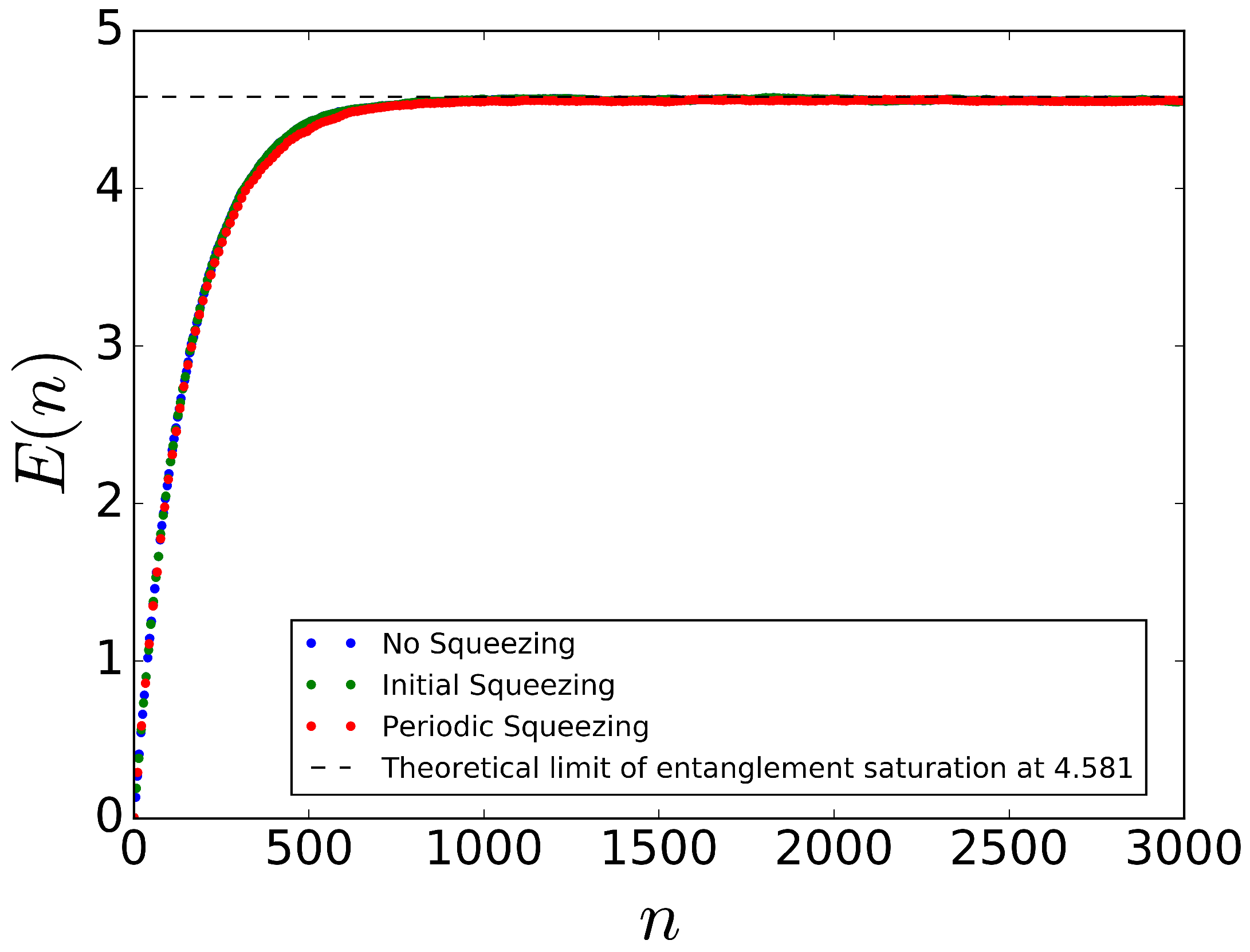
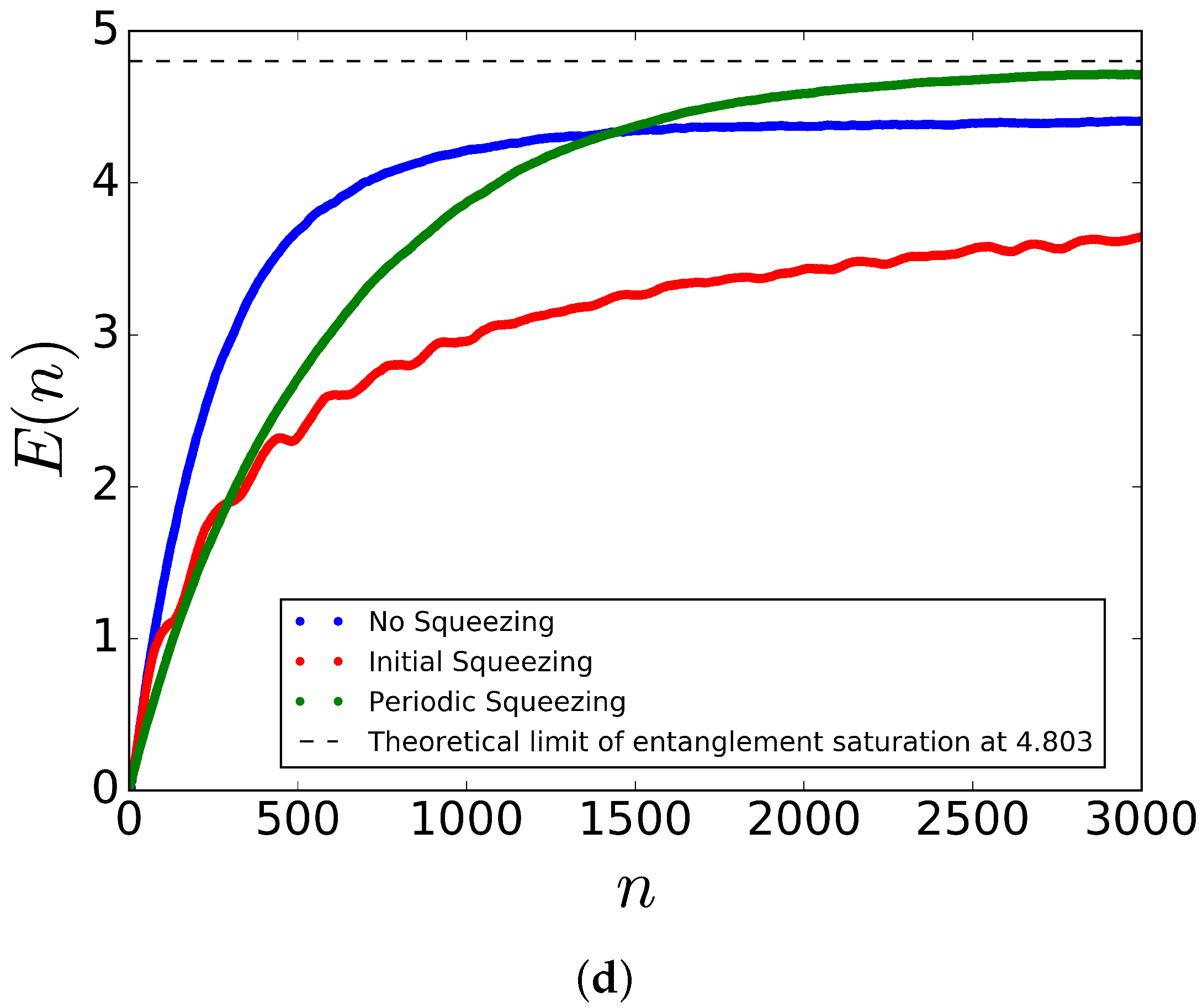
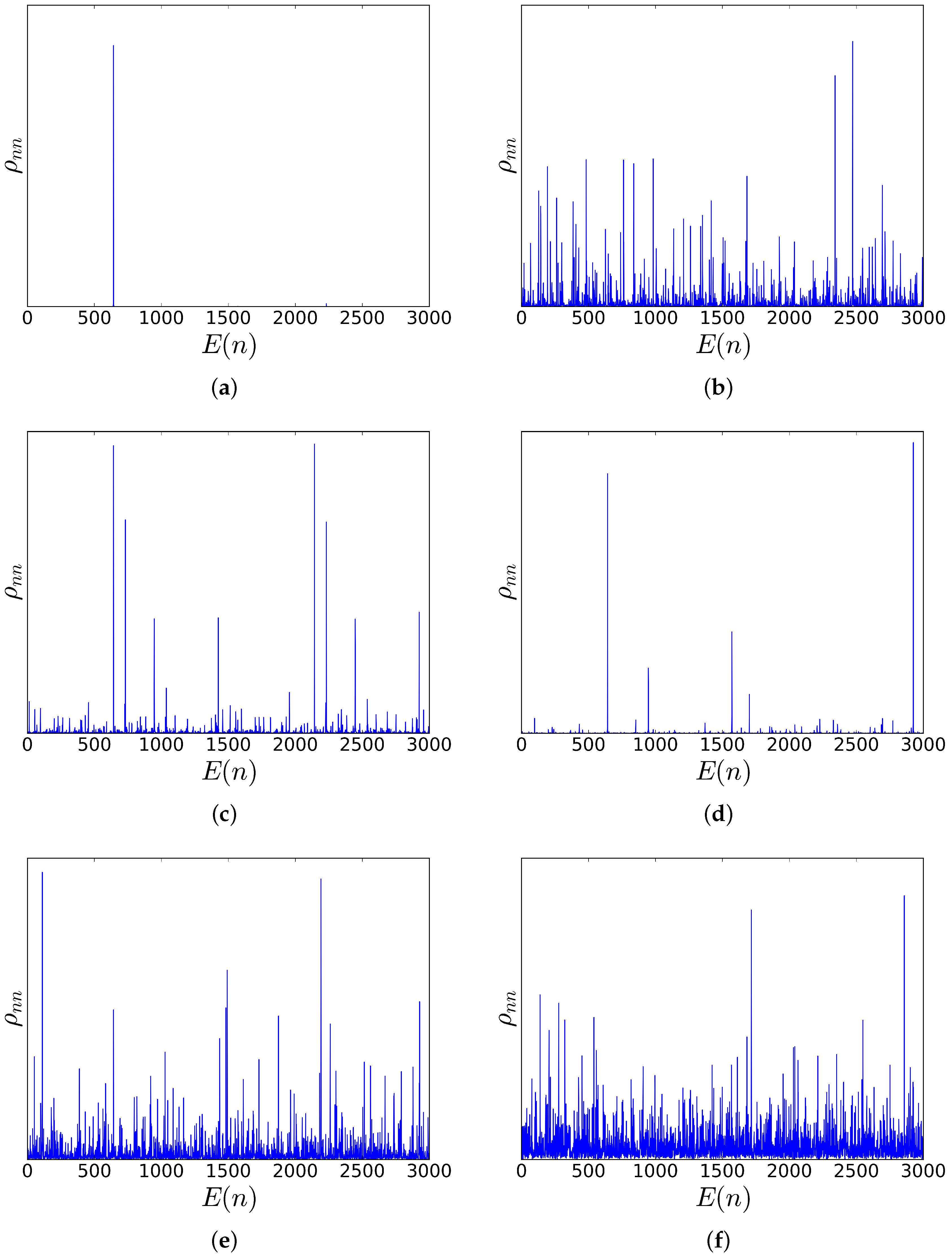
5. Results and Discussion
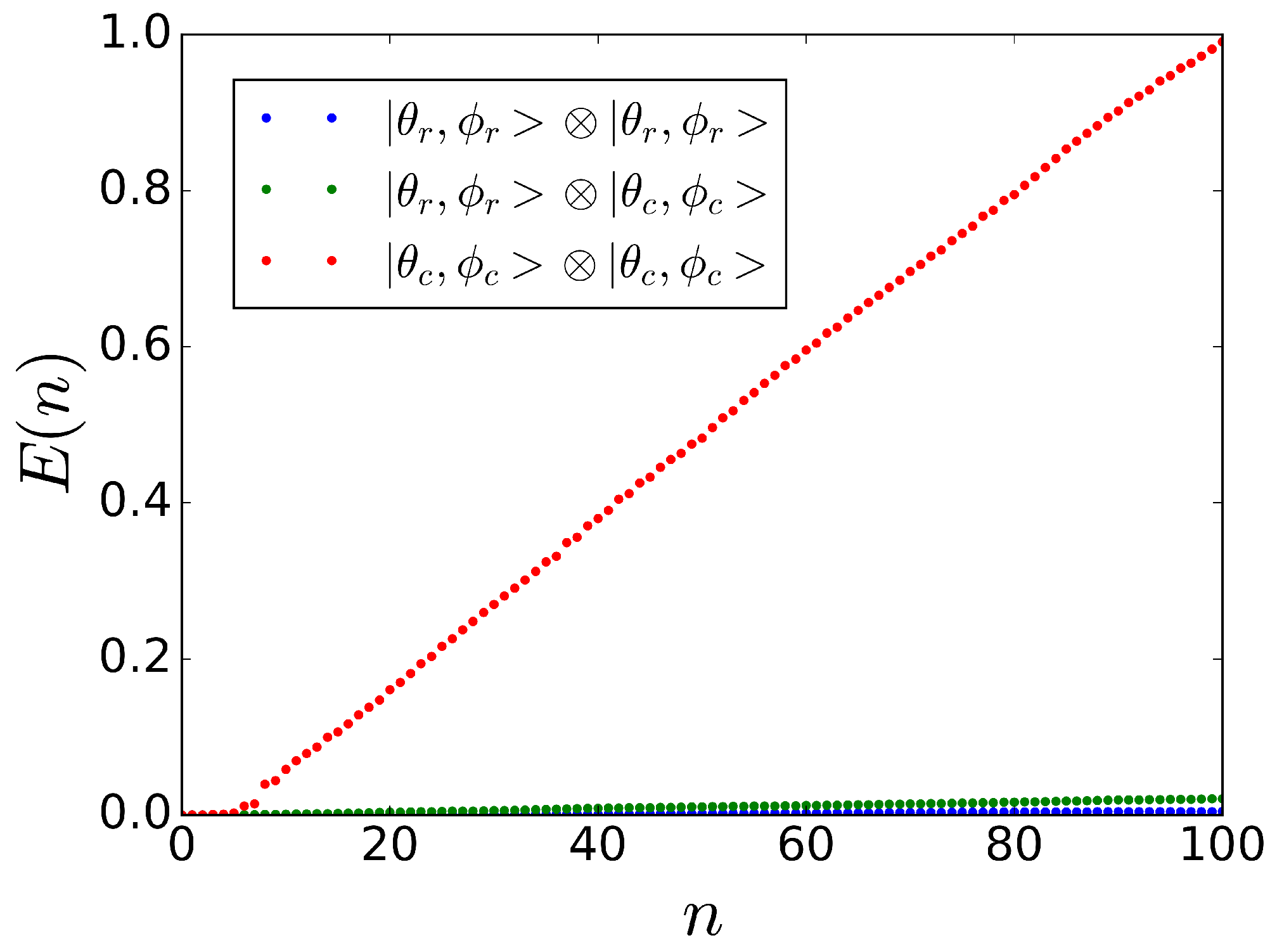
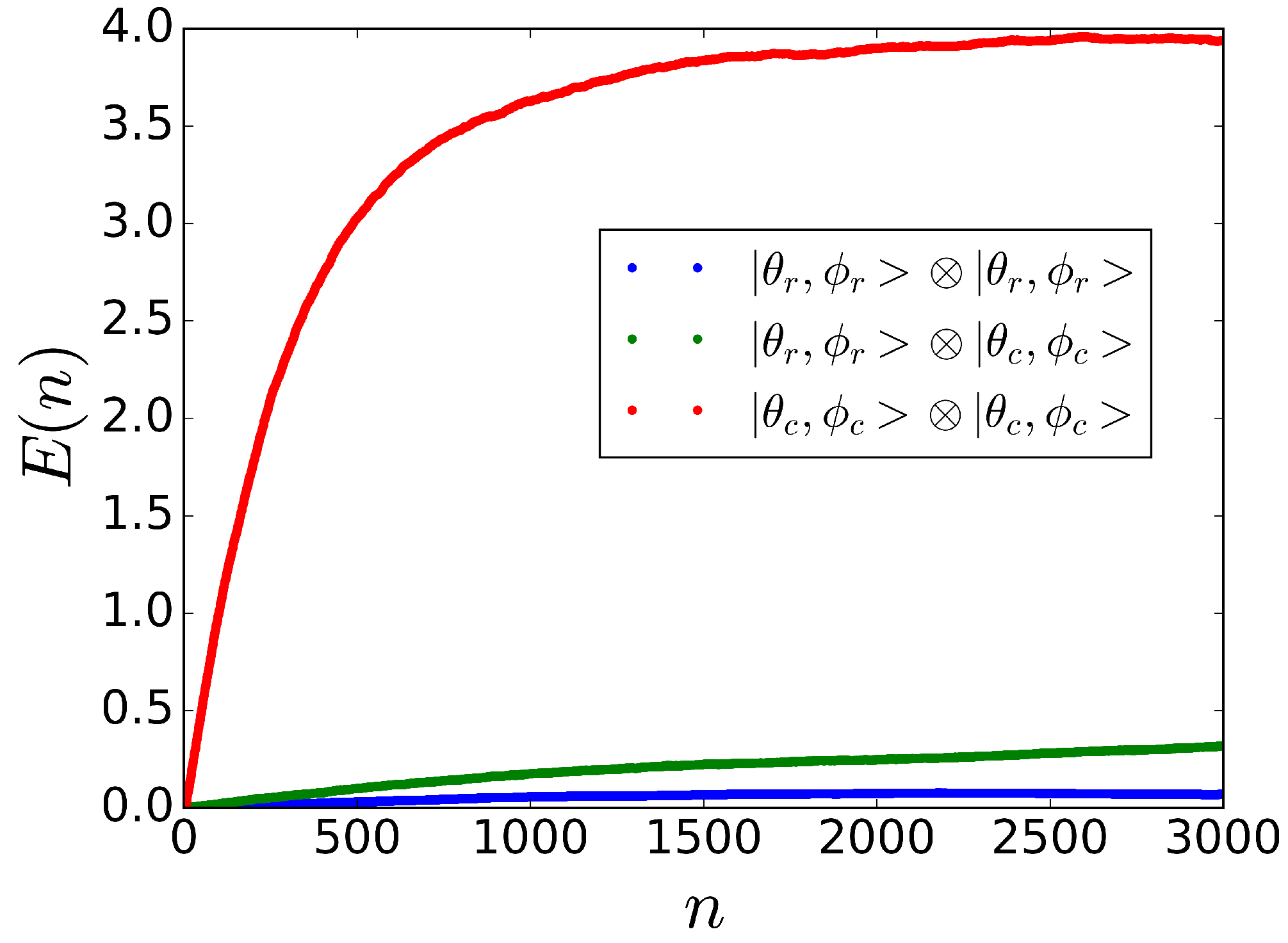
5.1. Entanglement without Spin Squeezing
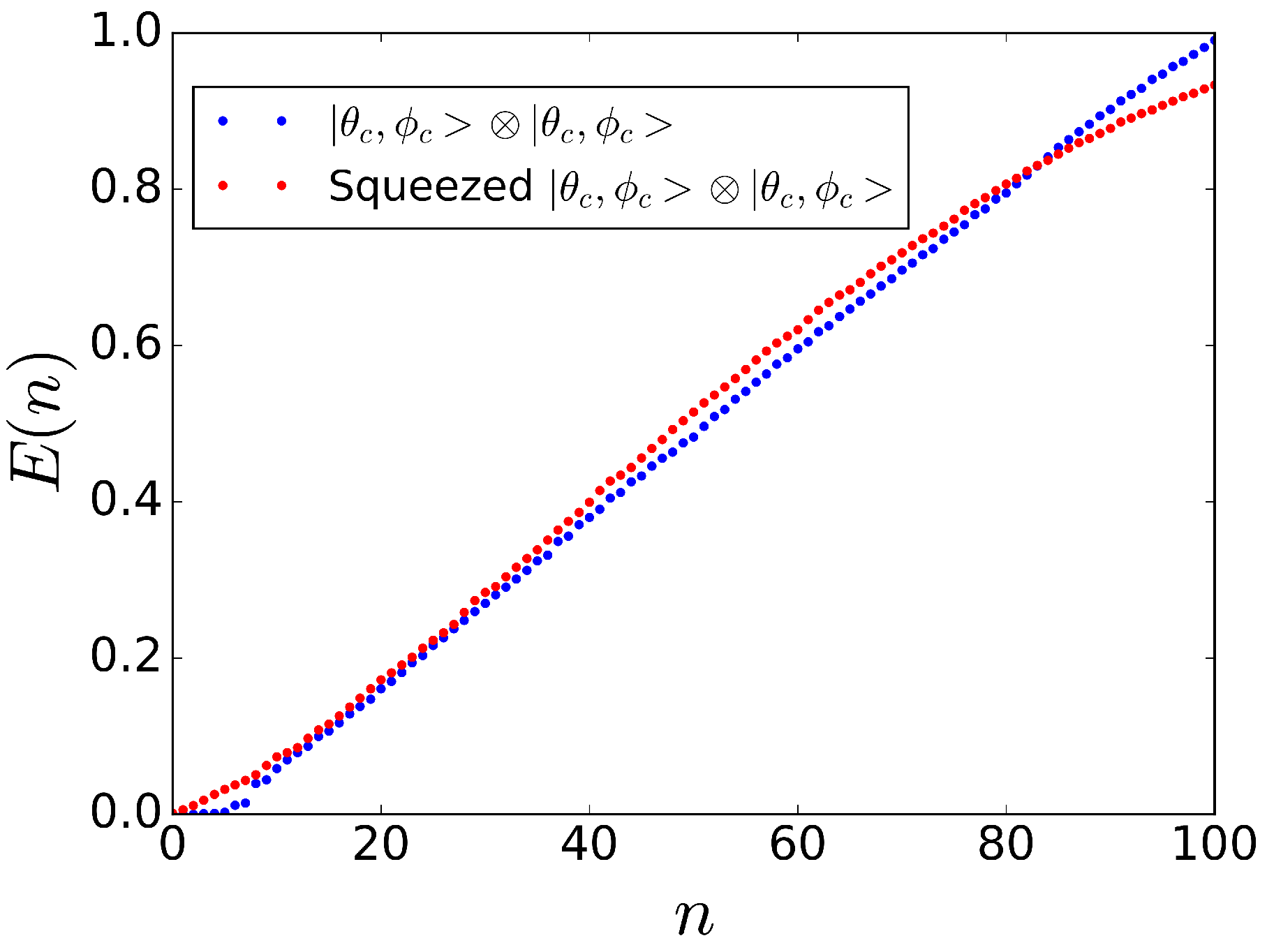
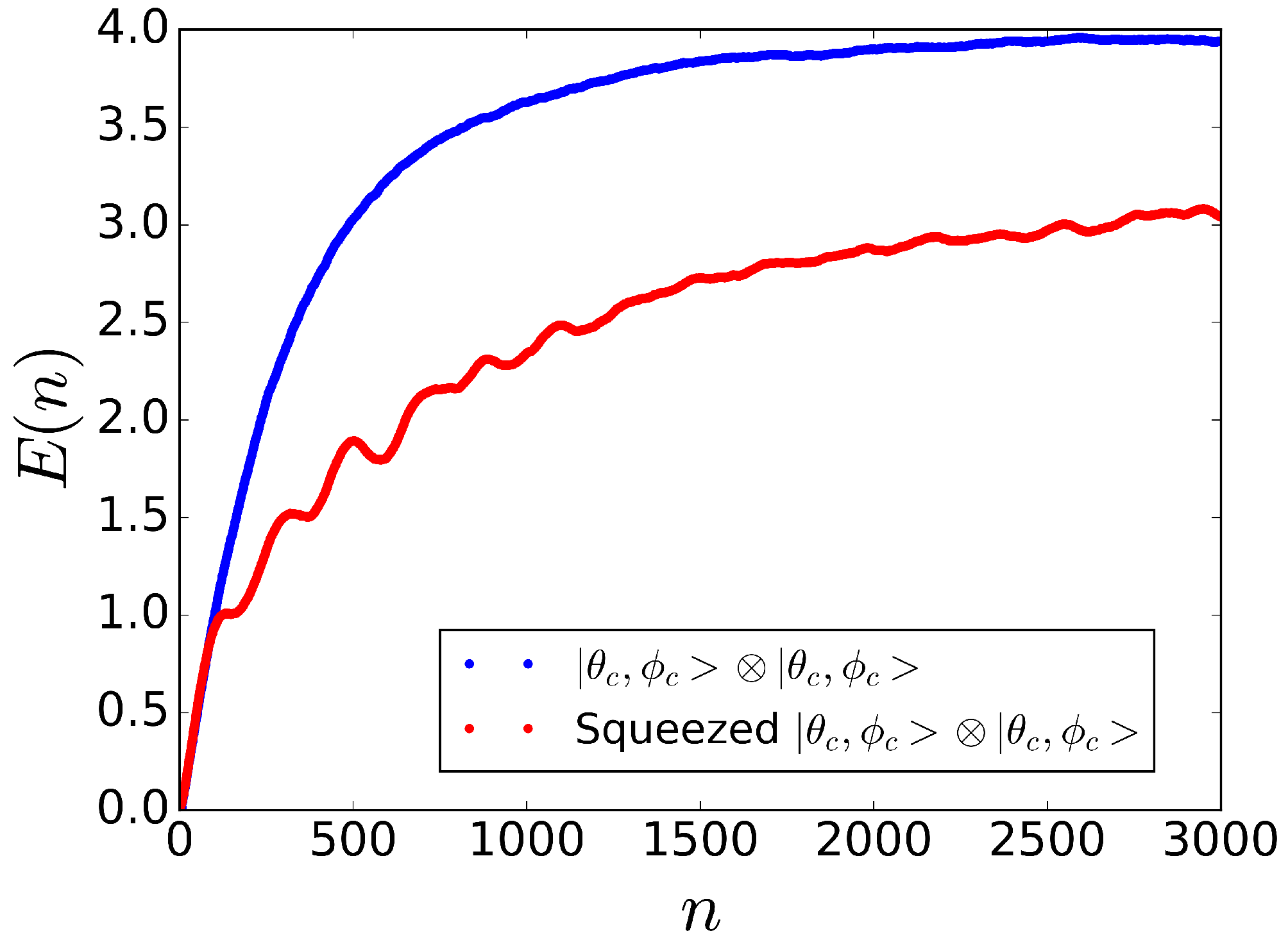
5.2. Initial Spin Squeezing and Periodic Spin Squeezing
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Haake, F.; Shepelyansky, D. The kicked rotator as a limit of the kicked top. Europhys. Lett. 1988, 5, 671–676. [Google Scholar] [CrossRef]
- Schack, R.; D’Ariano, G.M.; Caves, C.M. Hypersensitivity to perturbation in the quantum kicked top. Phys. Rev. E 1994, 50, 972–987. [Google Scholar] [CrossRef]
- Chaudhury, S.; Smith, A.; Anderson, B.E.; Ghose, S.; Jessen, P.S. Quantum signatures of chaos in a kicked top. Nature 2009, 461, 768–771. [Google Scholar] [CrossRef] [PubMed]
- Ghose, S.; Stock, R.; Jessen, P.; Lal, R.; Silberfarb, A. Chaos, entanglement, and decoherence in the quantum kicked top. Phys. Rev. A 2008, 78, 042318. [Google Scholar] [CrossRef]
- Berry, M.V. The Bakerian lecture, 1987: Quantum chaology. Proc. R. Soc. Lond. A 1987, 413, 183–198. [Google Scholar] [CrossRef]
- Berry, M. Quantum chaology, not quantum chaos. Physica Scripta 1989, 40, 335–336. [Google Scholar] [CrossRef]
- Haake, F. Quantum Signatures of Chaos; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Peres, A. Stability of quantum motion in chaotic and regular systems. Phys. Rev. A 1984, 30, 1610–1615. [Google Scholar] [CrossRef]
- Emerson, J.; Weinstein, Y.S.; Lloyd, S.; Cory, D. Fidelity decay as an efficient indicator of quantum chaos. Phys. Rev. Lett. 2002, 89, 284102. [Google Scholar] [CrossRef] [PubMed]
- Heller, E.J. Bound-state eigenfunctions of classically chaotic Hamiltonian systems: Scars of periodic orbits. Phys. Rev. Lett. 1984, 53, 1515–1518. [Google Scholar] [CrossRef]
- Wang, X.; Ghose, S.; Sanders, B.C.; Hu, B. Entanglement as a signature of quantum chaos. Phys. Rev. E 2004, 70, 016217. [Google Scholar] [CrossRef] [PubMed]
- Miller, P.A.; Sarkar, S. Signatures of chaos in the entanglement of two coupled quantum kicked tops. Phys. Rev. E 1999, 60, 1542–1550. [Google Scholar] [CrossRef]
- Er, C.; Chung, N.N.; Chew, L.Y. Threshold effect and entanglement enhancement through local squeezing of initial separable states in continuous-variable systems. Physica Scripta 2013, 87, 025001. [Google Scholar] [CrossRef]
- Joseph, S.K.; Chew, L.Y.; Sanjuan, M.A.F. Effect of squeezing and Planck constant dependence in short time semiclassical entanglement. Eur. Phys. J. D 2014, 68, 1–11. [Google Scholar] [CrossRef]
- Joseph, S.K.; Chew, L.Y.; Sanjuán, M.A. Impact of quantum–classical correspondence on entanglement enhancement by single-mode squeezing. Phys. Lett. A 2014, 378, 2603–2610. [Google Scholar] [CrossRef]
- Demkowicz-Dobrzański, R.; Kuś, M. Global entangling properties of the coupled kicked tops. Phys. Rev. E 2004, 70, 066216. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, J.N.; Lakshminarayan, A. Entanglement production in coupled chaotic systems: Case of the kicked tops. Phys. Rev. E 2004, 69, 016201. [Google Scholar] [CrossRef] [PubMed]
- Steane, A. Quantum computing. Rep. Prog. Phys. 1998, 61, 117. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Wineland, D.J.; Bollinger, J.J.; Itano, W.M.; Moore, F.L.; Heinzen, D.J. Spin squeezing and reduced quantum noise in spectroscopy. Phys. Rev. A 1992, 46, R6797–R6800. [Google Scholar] [CrossRef] [PubMed]
- Leroux, I.D.; Schleier-Smith, M.H.; Vuletić, V. Orientation-dependent entanglement lifetime in a squeezed atomic clock. Phys. Rev. Lett. 2010, 104, 250801. [Google Scholar] [CrossRef] [PubMed]
- Louchet-Chauvet, A.; Appel, J.; Renema, J.J.; Oblak, D.; Kjaergaard, N.; Polzik, E.S. Entanglement-assisted atomic clock beyond the projection noise limit. New J. Phys. 2010, 12, 065032. [Google Scholar] [CrossRef]
- André, A.; Sørensen, A.S.; Lukin, M.D. Stability of atomic clocks based on entangled atoms. Phys. Rev. Lett. 2004, 92, 230801. [Google Scholar] [CrossRef] [PubMed]
- Goda, K.; Miyakawa, O.; Mikhailov, E.E.; Saraf, S.; Adhikari, R.; McKenzie, K.; Ward, R.; Vass, S.; Weinstein, A.J.; Mavalvala, N. A quantum-enhanced prototype gravitational-wave detector. Nat. Phys. 2008, 4, 472–476. [Google Scholar] [CrossRef]
- Gühne, O.; Tóth, G. Entanglement detection. Phys. Rep. 2009, 474, 1–75. [Google Scholar] [CrossRef]
- Tóth, G.; Knapp, C.; Gühne, O.; Briegel, H.J. Spin squeezing and entanglement. Phys. Rev. A 2009, 79, 042334. [Google Scholar] [CrossRef]
- Kitagawa, M.; Ueda, M. Squeezed spin states. Phys. Rev. A 1993, 47, 5138–5143. [Google Scholar] [CrossRef] [PubMed]
- Haake, F.; Kuś, M.; Scharf, R. Classical and quantum chaos for a kicked top. Zeitschrift für Physik B Condensed Matter 1987, 65, 381–395. [Google Scholar] [CrossRef]
- D’Ariano, G.; Evangelista, L.; Saraceno, M. Classical and quantum structures in the kicked-top model. Phys. Rev. A 1992, 45, 3646–3658. [Google Scholar] [CrossRef] [PubMed]
- Glauber, R.J.; Haake, F. Superradiant pulses and directed angular momentum states. Phys. Rev. A 1976, 13, 357–366. [Google Scholar] [CrossRef]
- Tinkham, M. Group Theory and Quantum Mechanics; Dover Publications: Mineola, NY, USA, 2003. [Google Scholar]
- Wigner, E.P. Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra; Elsevier: Philadelphia, PA, USA, 2012. [Google Scholar]
- Wodkiewicz, K.; Eberly, J.H. Coherent states, squeezed fluctuations, and the SU(2) am SU(1, 1) groups in quantum-optics applications. J. Opt. Soc. Am. B 1985, 2, 458–466. [Google Scholar] [CrossRef]
- Johansson, J.R.; Nation, P.D.; Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2013, 184, 1234–1240. [Google Scholar] [CrossRef]
- Johansson, J.R.; Nation, P.D.; Nori, F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2012, 183, 1760–1772. [Google Scholar] [CrossRef]
- Wang, X.; Zanardi, P. Quantum entanglement and Bell inequalities in Heisenberg spin chains. Phys. Lett. A 2002, 301, 1–6. [Google Scholar] [CrossRef]
- Bandyopadhyay, J.N.; Lakshminarayan, A. Testing statistical bounds on entanglement using quantum chaos. Phys. Rev. Lett. 2002, 89, 060402. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Wang, X.; Yan, D.; Zong, Z. Spin squeezing properties in the quantum kicked top model. J. Phys. B 2006, 39, 559–568. [Google Scholar] [CrossRef]
- Ghose, S.; Sanders, B.C. Entanglement dynamics in chaotic systems. Phys. Rev. A 2004, 70, 062315. [Google Scholar] [CrossRef]
- Zhang, S.-H.; Jie, Q.-L. Quantum-classical correspondence in entanglement production: Entropy and classical tori. Phys. Rev. A 2008, 77, 012312. [Google Scholar] [CrossRef]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ong, E.T.S.; Chew, L.Y. The Effect of Spin Squeezing on the Entanglement Entropy of Kicked Tops. Entropy 2016, 18, 116. https://doi.org/10.3390/e18040116
Ong ETS, Chew LY. The Effect of Spin Squeezing on the Entanglement Entropy of Kicked Tops. Entropy. 2016; 18(4):116. https://doi.org/10.3390/e18040116
Chicago/Turabian StyleOng, Ernest Teng Siang, and Lock Yue Chew. 2016. "The Effect of Spin Squeezing on the Entanglement Entropy of Kicked Tops" Entropy 18, no. 4: 116. https://doi.org/10.3390/e18040116
APA StyleOng, E. T. S., & Chew, L. Y. (2016). The Effect of Spin Squeezing on the Entanglement Entropy of Kicked Tops. Entropy, 18(4), 116. https://doi.org/10.3390/e18040116






