Entropy Generation on MHD Casson Nanofluid Flow over a Porous Stretching/Shrinking Surface
Abstract
:1. Introduction
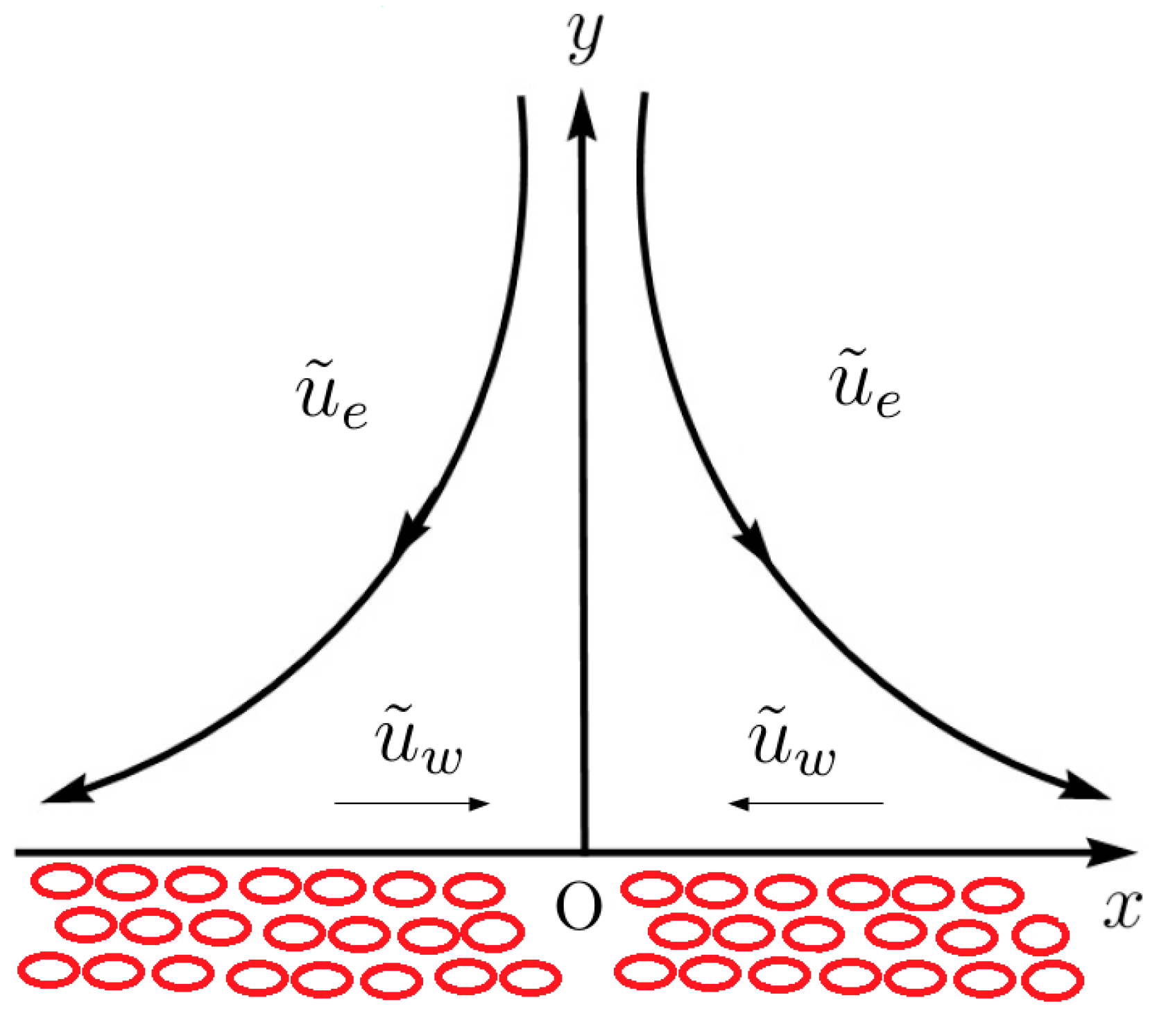
2. Mathematical Formulation
3. Physical Quantities of Interest
4. Numerical Method
5. Entropy Generation Analysis
6. Results and Discussion
7. Conclusions
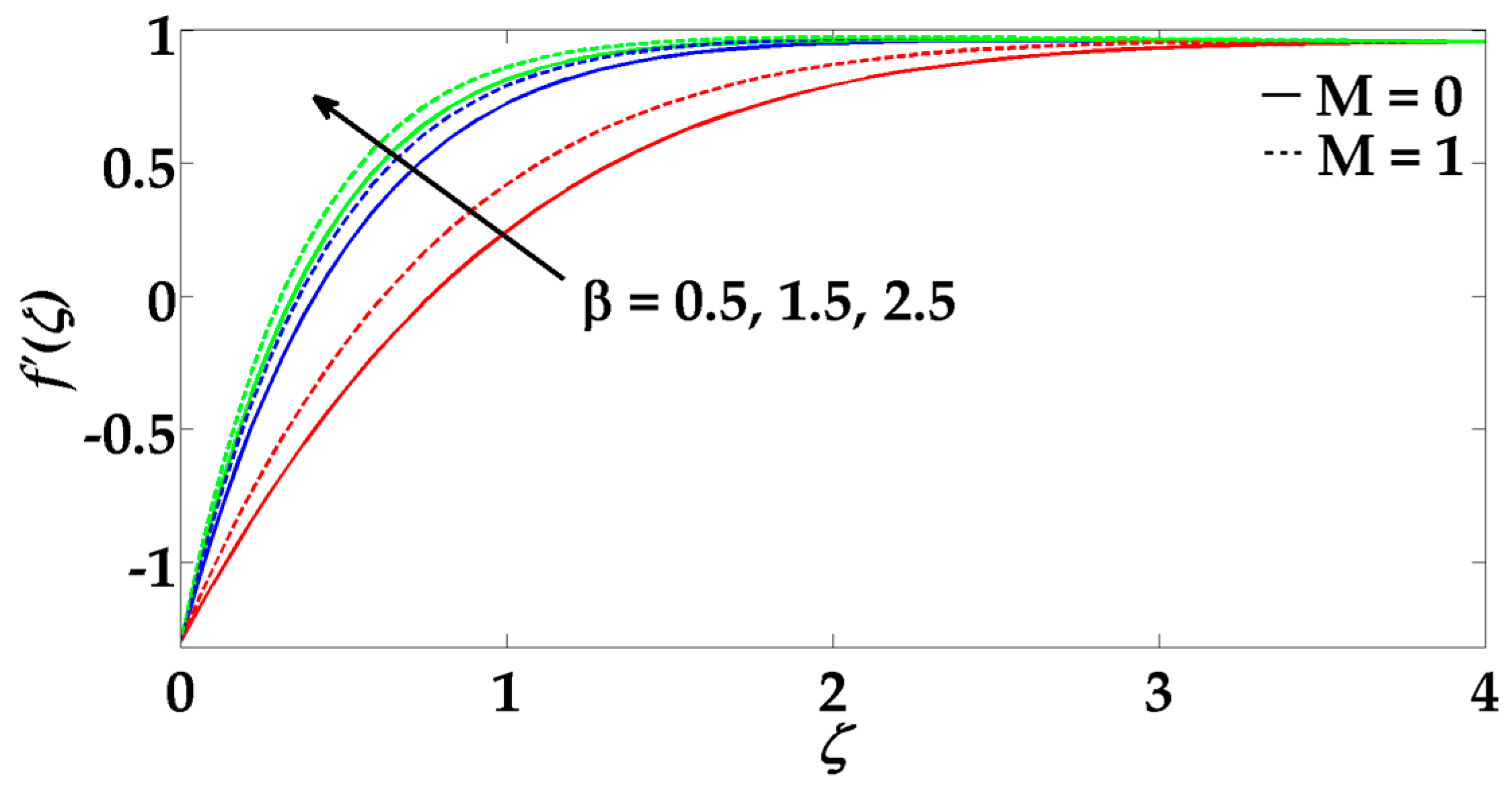
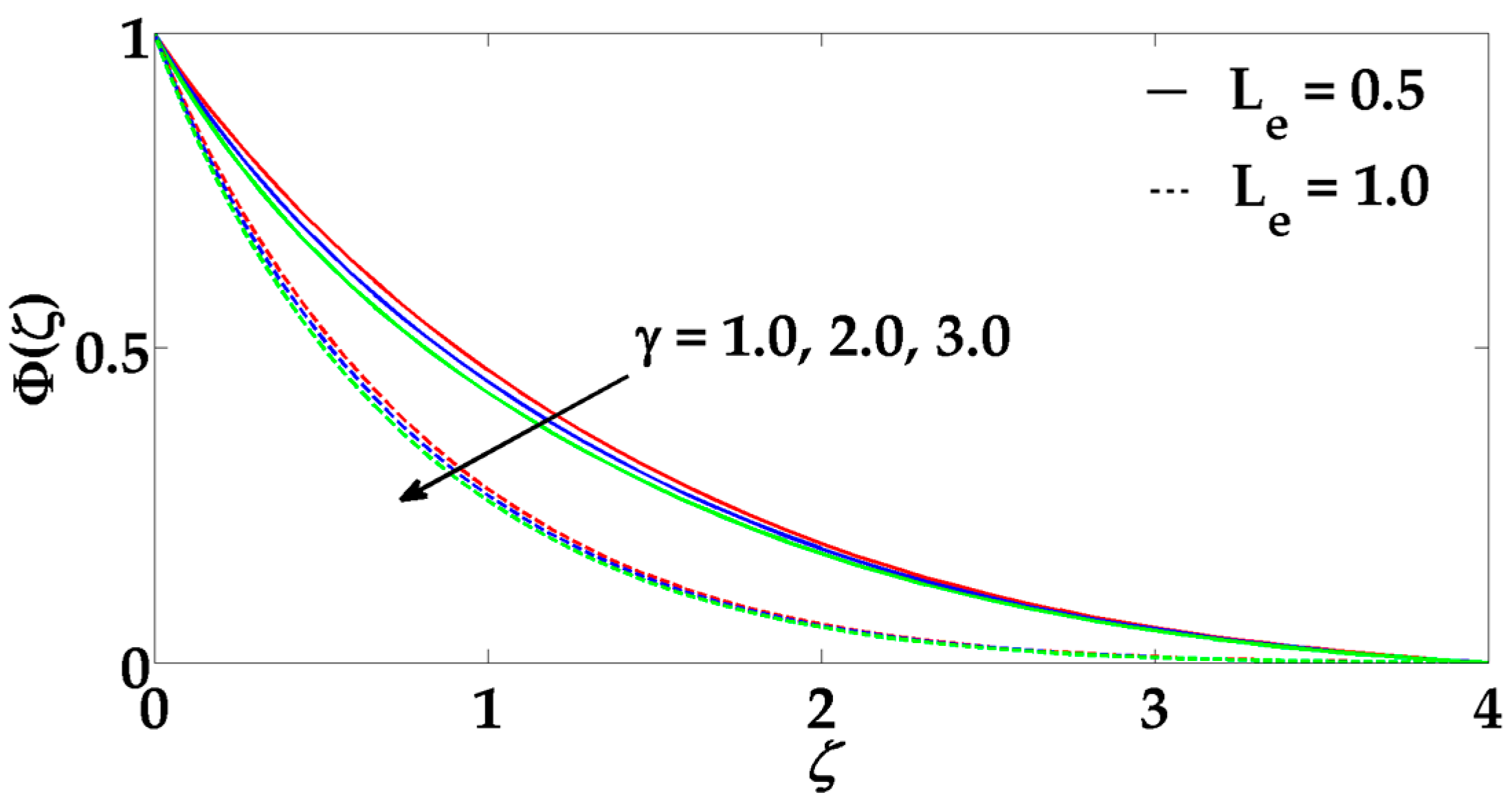
- Velocity profile decreases for magnetic parameter and porosity parameter but increases with the enhancement in Casson nanofluid parameter.
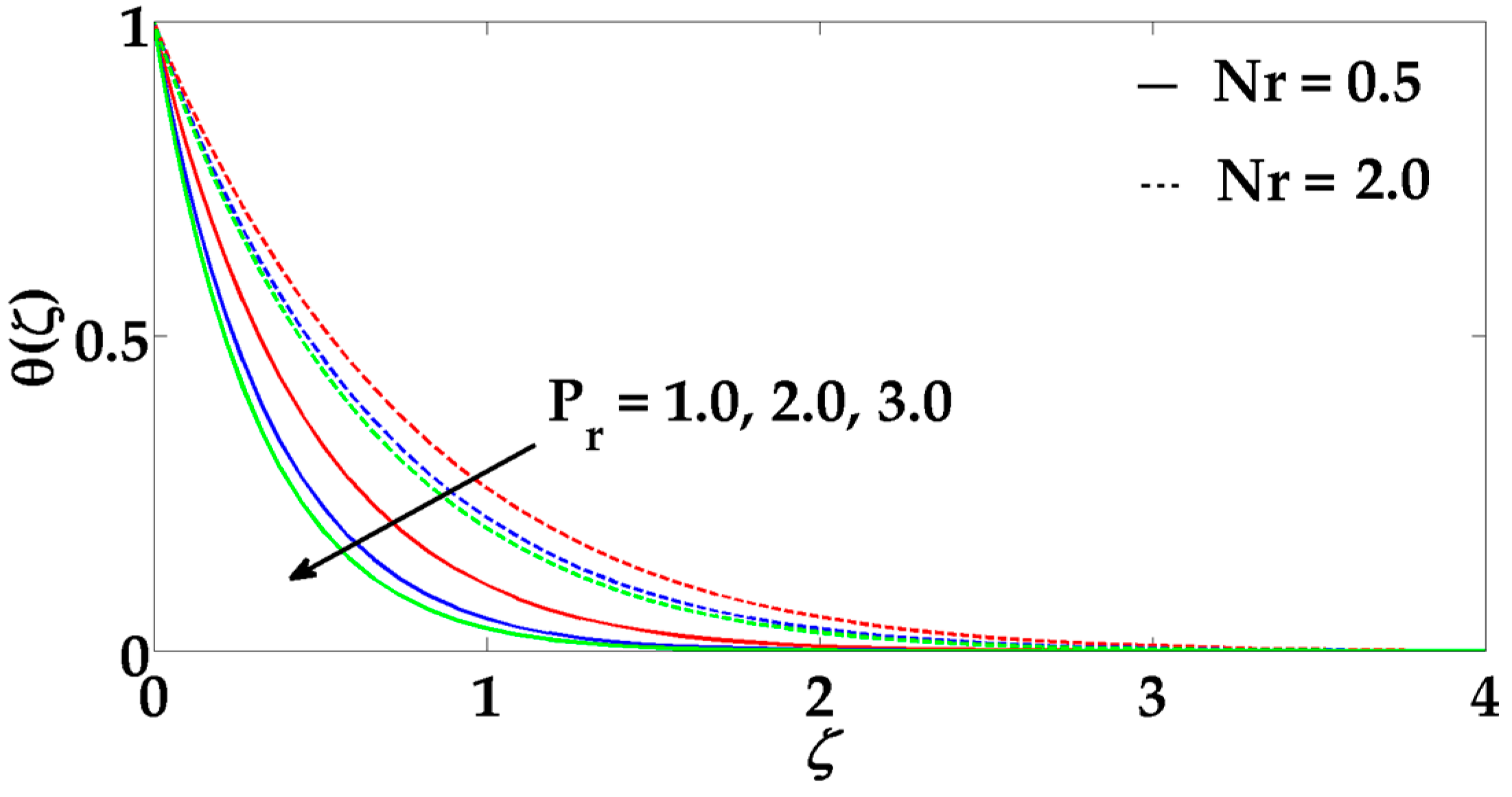
- When the Prandtl number increases, it tends to decrease the thermal boundary layer.
- Due to an influence of Lewis number, the concentration profile gets steeper.
- For larger values of radiation parameter, temperature profile rises.
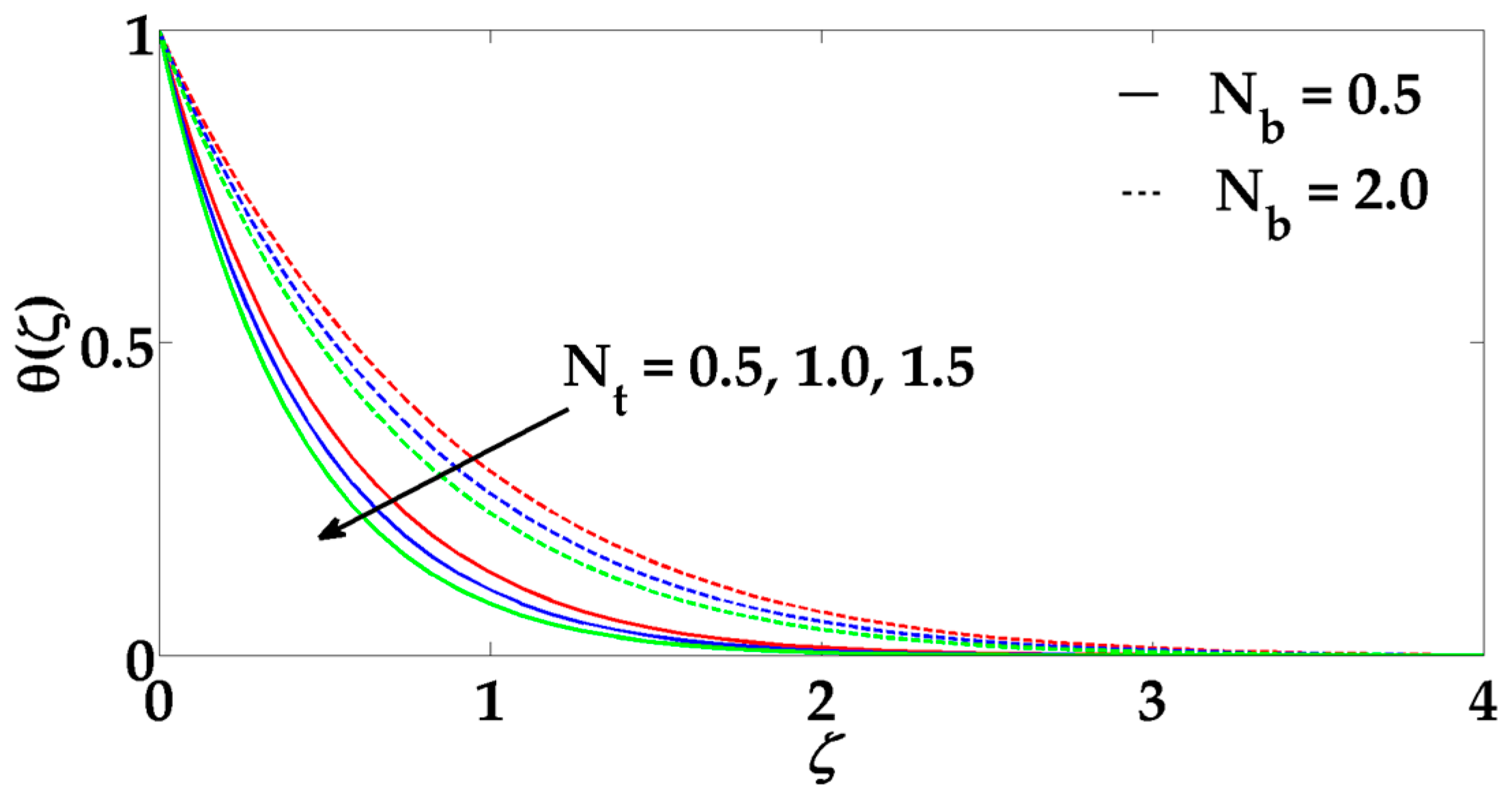
- Concentration profile decreases for higher values ofchemical reaction parameter and Brownian motion parameter but its behaviors seem to be opposite for thermophoresis parameter increases.
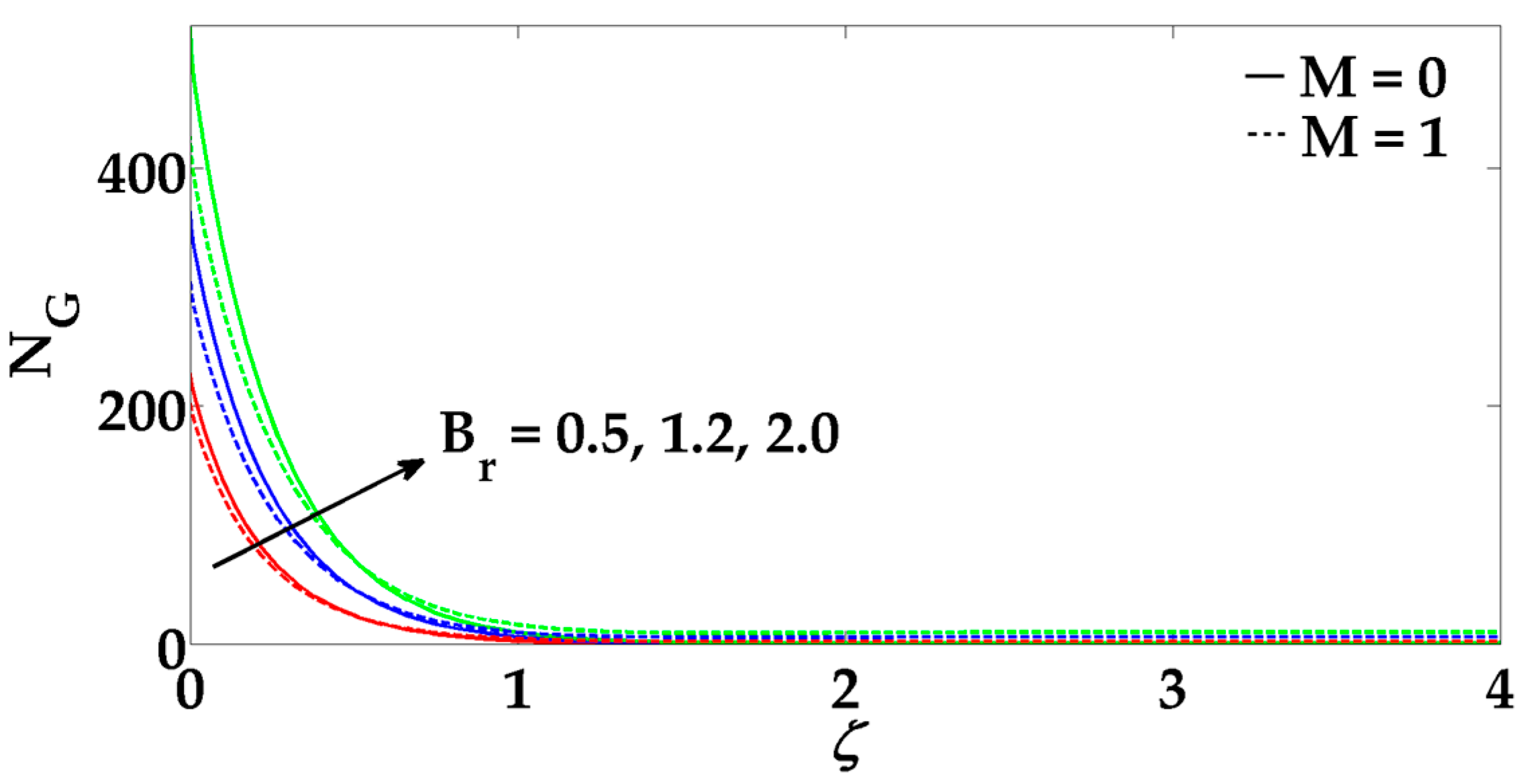
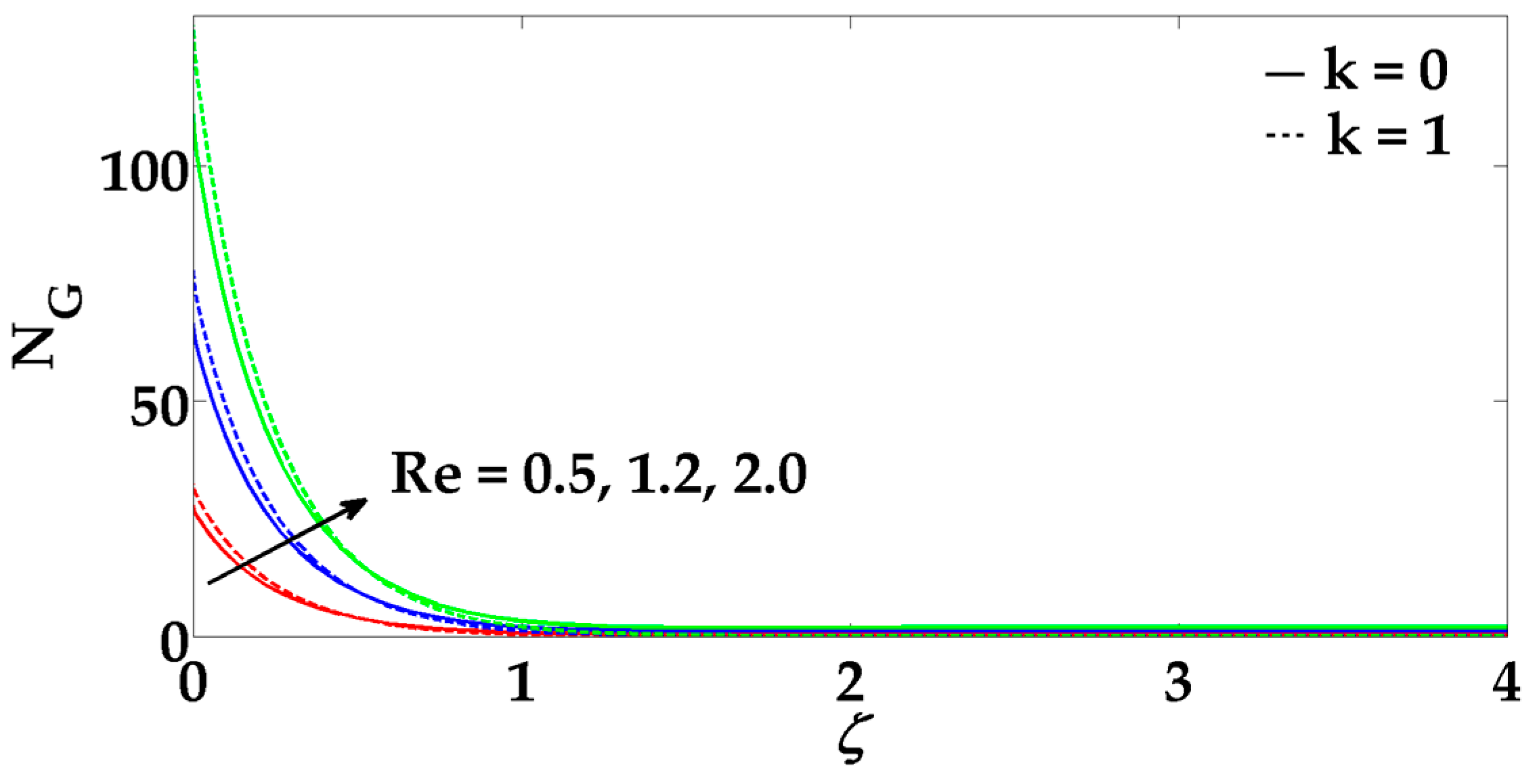
- Increasing in Brinkman number, Reynolds number, Hartmann number and porosity parameter cause an increment in the entropy generation.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–106. [Google Scholar]
- Xuan, Y.; Li, Q. Investigation on convective heat transfer and flow features of nanofluids. J. Heat Transf. 2003, 125, 151–155. [Google Scholar] [CrossRef]
- Khalili, S.; Tamim, H.; Khalili, A.; Rashidi, M.M. Unsteady convective heat and mass transfer in pseudoplastic nanofluid over a stretching wall. Adv. Powder Technol. 2015, 26, 1319–1326. [Google Scholar] [CrossRef]
- Xiao, B.; Yang, Y.; Chen, L. Developing a novel form of thermal conductivity of nanofluids with Brownian motion effect by means of fractal geometry. Powder Technol. 2013, 239, 409–414. [Google Scholar] [CrossRef]
- Xiao, B.; Yu, B.; Wang, Z.; Chen, L. A fractal model for heat transfer of nanofluids by convection in a pool. Phys. Lett. A 2009, 373, 4178–4181. [Google Scholar] [CrossRef]
- Ali, M.; Zeitoun, O.; Almotairi, S. Natural convection heat transfer inside vertical circular enclosure filled with water-based Al2O3 nanofluids. Int. J. Therm. Sci. 2013, 63, 115–124. [Google Scholar] [CrossRef]
- Ali, M.; Zeitoun, O.; Almotairi, S.; Al-Ansary, H. The effect of Alumina-water nanofluid on natural convection heat transfer inside vertical circular enclosure heated from above. Heat Transf. Eng. 2013, 34, 1289–1299. [Google Scholar] [CrossRef]
- Zeitoun, O.; Ali, M. Nanofluid impingement jet heat transfer. Nanoscale Res. Lett. 2012, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Zeitoun, O.; Ali, M.; Al-Ansary, H. The effect of particle concentration on cooling of a circular horizontal surface using nanofluid jets. Nanosc. Microsc. Therm. 2013, 17, 154–171. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rashidi, M.M.; Ganji, D.D. Effect of non-uniform magnetic field on forced convection heat transfer Fe3O4 water nanofluid. Comput. Method. Appl. M 2015, 294, 299–312. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.; Bhatti, M. Application of drug delivery in magnetohydrodynamics peristaltic blood flow of nano fluid in a nan-uniform channel. J. Mech. Med. Biol. 2015, 1650052. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D.D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J. Mol. Liq. 2014, 190, 112–120. [Google Scholar] [CrossRef]
- Malvandi, A.; Hedayati, F.; Ganji, D.D. Slip effects on unsteady stagnation point flow of a nanofluid over a stretching sheet. Powder Technol. 2014, 253, 377–384. [Google Scholar] [CrossRef]
- Abbas, Z.; Sheikh, M.; Motsa, S.S. Numerical solution of binary chemical reaction on stagnation point flow of Casson fluid over a stretching/shrinking sheet with thermal radiation. Energy 2016, 95, 12–20. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ali, M.; Freidoonimehr, N.; Rostami, B.; Hossain, M.A. Mixed convective heat transfer for MHD viscoelastic fluid flow over a porous wedge with thermal radiation. Adv. Mech. Eng. 2014, 6, 735939. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S. MHD three-dimensional boundary layer flow of casson nanofluid past a linearly stretching sheet with convective boundary condition. IEEE Trans. Nanotechnol. 2014, 13, 109–115. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hayat, T.; Alsaedi, A. MHD free convection of Al2O3–water nanofluid considering thermal radiation: A numerical study. Int. J. Heat Mass Transf. 2016, 96, 513–524. [Google Scholar] [CrossRef]
- Hamad, M.A.A.; Ferdows, M. Similarity solution of boundary layer stagnation-point flow towards a heated porous stretching sheet saturated with a nanofluid with heat absorption/generation and suction/blowing: A lie group analysis. Commun. Nonlinear Sci. 2012, 17, 132–140. [Google Scholar] [CrossRef]
- Kameshwaran, P.K.; Shaw, S.; Sibanda, P.; Murthy, P.V.S.N. Homogeneous–heterogeneous reactions in a nanofluid flow due to a porous stretching sheet. Int. J. Heat Mass Trans. 2013, 57, 465–472. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ganesh, N.V.; Hakeem, A.K.A.; Ganga, B. Buoyancy effect on MHD flow of nanofluid over a stretching sheet in the presence of thermal radiation. J. Mol. Liq. 2014, 198, 234–238. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Rashidi, M.M. Ferrofluid flow and heat transfer in a semi annulus enclosure in the presence of magnetic source considering thermal radiation. J. Taiwan Inst. Chem. Eng. 2015, 47, 6–17. [Google Scholar] [CrossRef]
- Chamkha, J. A MHD flow of a uniformly stretched vertical permeable surface in the presence of heat generation/absorption and a chemical reaction. Int. Commun. Heat Mass Trans. 2003, 30, 413–422. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv. Powder Technol. 2015, 26, 542–552. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M.; Ellahi, R. Peristaltic flow with thermal conductivity of H2O + Cu nanofluid and entropy generation. Results Phys. 2015, 5, 115–124. [Google Scholar] [CrossRef]
- Akbar, N.S. Entropy Generation Analysis for a CNT Suspension Nanofluid in Plumb Ducts with Peristalsis. Entropy 2015, 17, 1411–1424. [Google Scholar] [CrossRef]
- Oztop, H.F.; Al-Salem, K. A review on entropy generation in natural and mixed convection heat transfer for energy systems, Renew. Sust. Energy Rev. 2012, 16, 911–920. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Trans. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Freidoonimehr, N.; Rahimi, A.B. Comment on effects of thermophoresis and Brownian motion on nanofluid heat transfer and entropy generation by M. Mahmoodi, Sh. Kandelousi. J. Mol. Liq. 2016, 216, 99–102. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Shahid, A.; Rashidi, M.M. Numerical simulation of fluid flow over a shrinking porous sheet by successive linearization method. Alex. Eng. J. 2016, 55, 51–56. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Ishak, A.; Pop, I. MHD Stagnation-Point Flow and Heat Transfer with Effects of Viscous Dissipation, Joule Heating and Partial Velocity Slip. Sci. Rep. 2015, 5, 1–8. [Google Scholar] [CrossRef]
- Aman, F.; Ishak, A.; Pop, I. Magnetohydrodynamic stagnation-point flow towards a stretching/shrinking sheet with slip effects. Int. Commun. Heat Mass Trans. 2013, 47, 68–72. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non-Linear. Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]


| Symbol | Names |
|---|---|
| Velocity components | |
| Cartesian coordinate | |
| Pressure | |
| Porosity parameter | |
| Dimensionless entropy number | |
| Reynolds number | |
| Time | |
| Mean absorption coefficient | |
| Suction/injection parameter | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Heat flux | |
| Mass flux | |
| Brinkman number | |
| Environmental temperature (K) | |
| Hartman number | |
| Magnetic field | |
| Radiation parameter | |
| Temperature and Concentration | |
| Acceleration due to gravity | |
| Brownian diffusion coefficient | |
| Thermophoretic diffusion coefficient | |
| Chemical reaction parameter |
| Symbol | Names |
|---|---|
| Thermal conductivity of the nano particles | |
| Casson fluid parameter | |
| Stefan-Boltzmann constant | |
| Viscosity of the fluid | |
| , | Dimensionless constant parameter |
| Dimensionless temperature difference | |
| Nano particle volume fraction | |
| Temperature profile | |
| Electrical conductivity | |
| Stream function | |
| Effective heat capacity of nano particle | |
| Nano fluid kinematic viscosity | |
| Dimensionless chemical reaction parameter | |
| Yield stress | |
| Plastic viscosity |
| 2.4214 | ||||||
| 2.7039 | ||||||
| 2.6669 | ||||||
| 2.6496 | ||||||
| 0.5 | ||||||
| 1.0 | 2.6213 | |||||
| 1.5 | 2.6395 | |||||
| 0.4 | 2.7434 | |||||
| 1.0 | ||||||
| 1.5 | 1.9490 | |||||
| 0.5 | 1.6378 | |||||
| 1.0 | ||||||
| 1.5 |
| 1.5233 | ||||||
| 1.4914 | ||||||
| 1.5315 | ||||||
| 1.5142 | ||||||
| 2 | ||||||
| 1.8734 | ||||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 0.4 | ||||||
| 1.0 | 2.5908 | |||||
| 1.5 | ||||||
| 0.5 | 3.6647 | |||||
| 1.1 | 2.9208 | |||||
| 1.5 | 2.5908 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qing, J.; Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M.; Ali, M.E.-S. Entropy Generation on MHD Casson Nanofluid Flow over a Porous Stretching/Shrinking Surface. Entropy 2016, 18, 123. https://doi.org/10.3390/e18040123
Qing J, Bhatti MM, Abbas MA, Rashidi MM, Ali ME-S. Entropy Generation on MHD Casson Nanofluid Flow over a Porous Stretching/Shrinking Surface. Entropy. 2016; 18(4):123. https://doi.org/10.3390/e18040123
Chicago/Turabian StyleQing, Jia, Muhammad Mubashir Bhatti, Munawwar Ali Abbas, Mohammad Mehdi Rashidi, and Mohamed El-Sayed Ali. 2016. "Entropy Generation on MHD Casson Nanofluid Flow over a Porous Stretching/Shrinking Surface" Entropy 18, no. 4: 123. https://doi.org/10.3390/e18040123
APA StyleQing, J., Bhatti, M. M., Abbas, M. A., Rashidi, M. M., & Ali, M. E.-S. (2016). Entropy Generation on MHD Casson Nanofluid Flow over a Porous Stretching/Shrinking Surface. Entropy, 18(4), 123. https://doi.org/10.3390/e18040123







