Entropy Generation and Natural Convection of CuO-Water Nanofluid in C-Shaped Cavity under Magnetic Field
Abstract
:1. Introduction
2. Problem Description and Mathematical Modeling
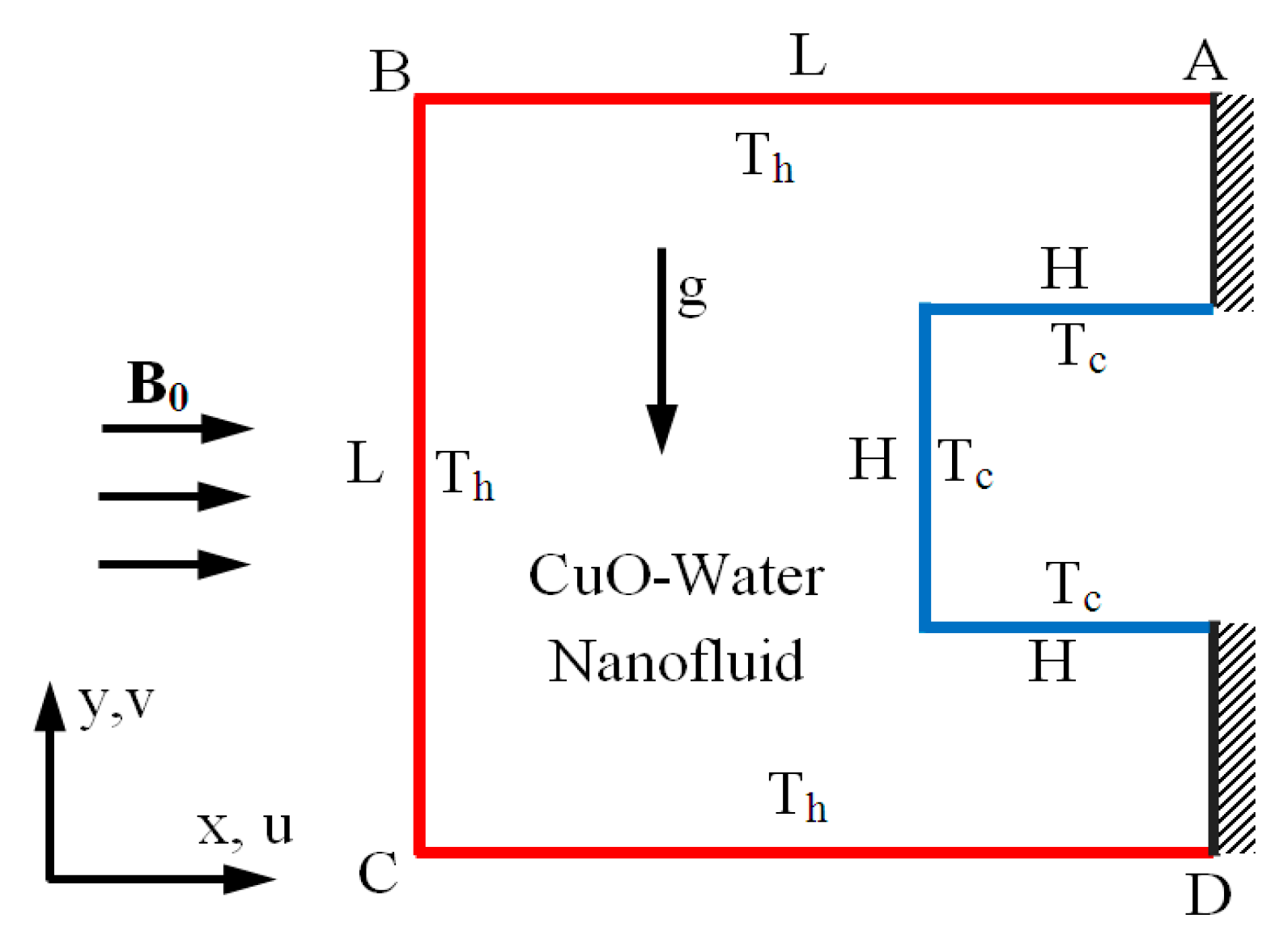
| Physical properties | Fluid phase | CuO |
|---|---|---|
| Cp (j/kg·K) | 4179 | 540 |
| ρ (kg/m3) | 997.1 | 6500 |
| Pr | 6.2 | – |
| 0.613 | 18 | |
| () | 0.05 |
3. Numerical Solution and Grid Dependency Test
| Grid points | ||||||
|---|---|---|---|---|---|---|
| AR = 0.1 | Ra = 1000 | 0.6884 | 0.6771 | 0.6333 | 0.6328 | 0.6328 |
| Ra = 15,000 | 0.6851 | 0.6674 | 0.6617 | 0.6605 | 0.6604 | |
| AR = 0.7 | Ra = 1000 | 5.2215 | 5.2069 | 5.2018 | 5.2008 | 5.2007 |
| Ra = 15,000 | 5.2433 | 5.2163 | 5.2052 | 5.2026 | 5.2024 |

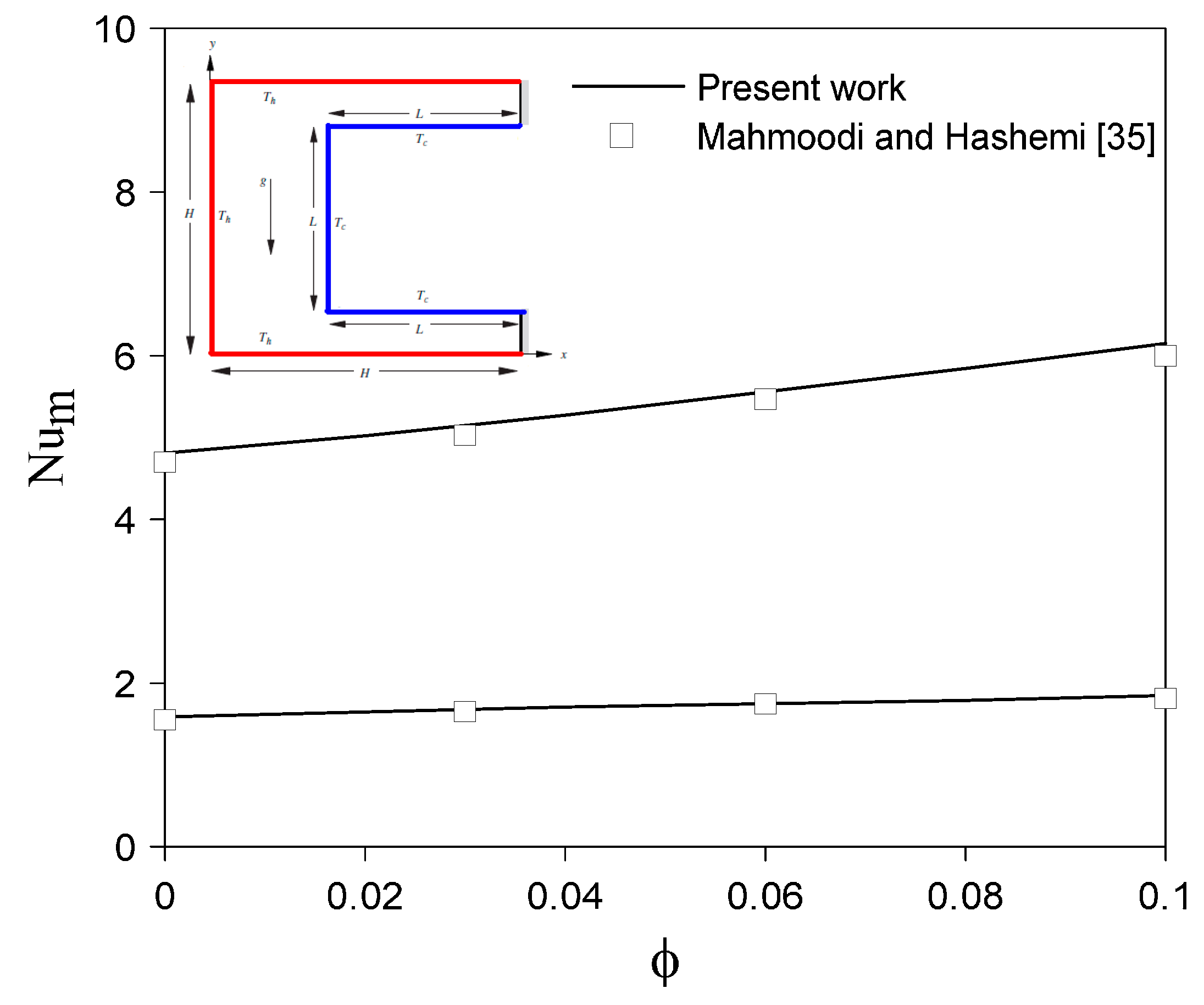
4. Results and Discussion
4.1. Effect of Raylirgh Number
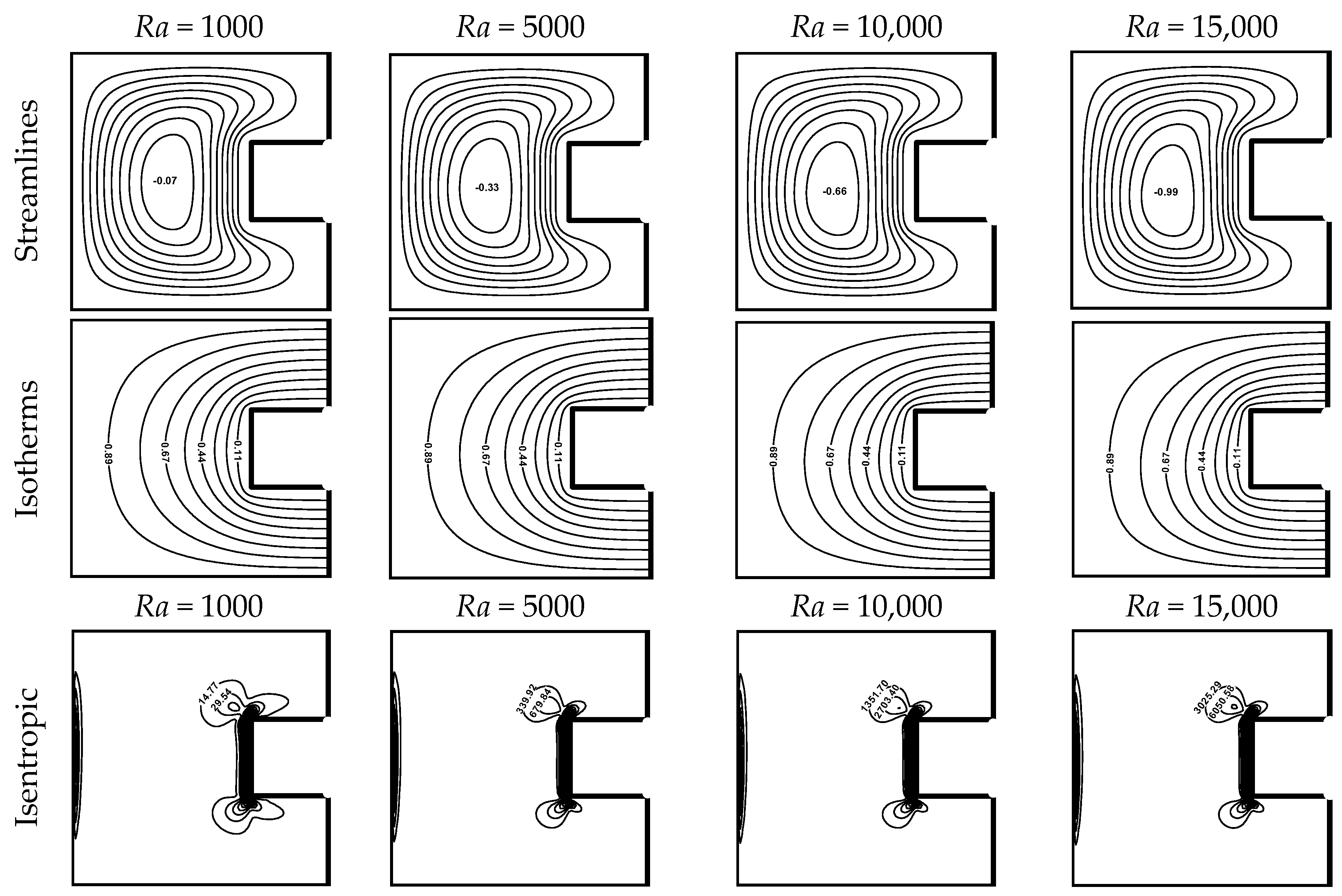
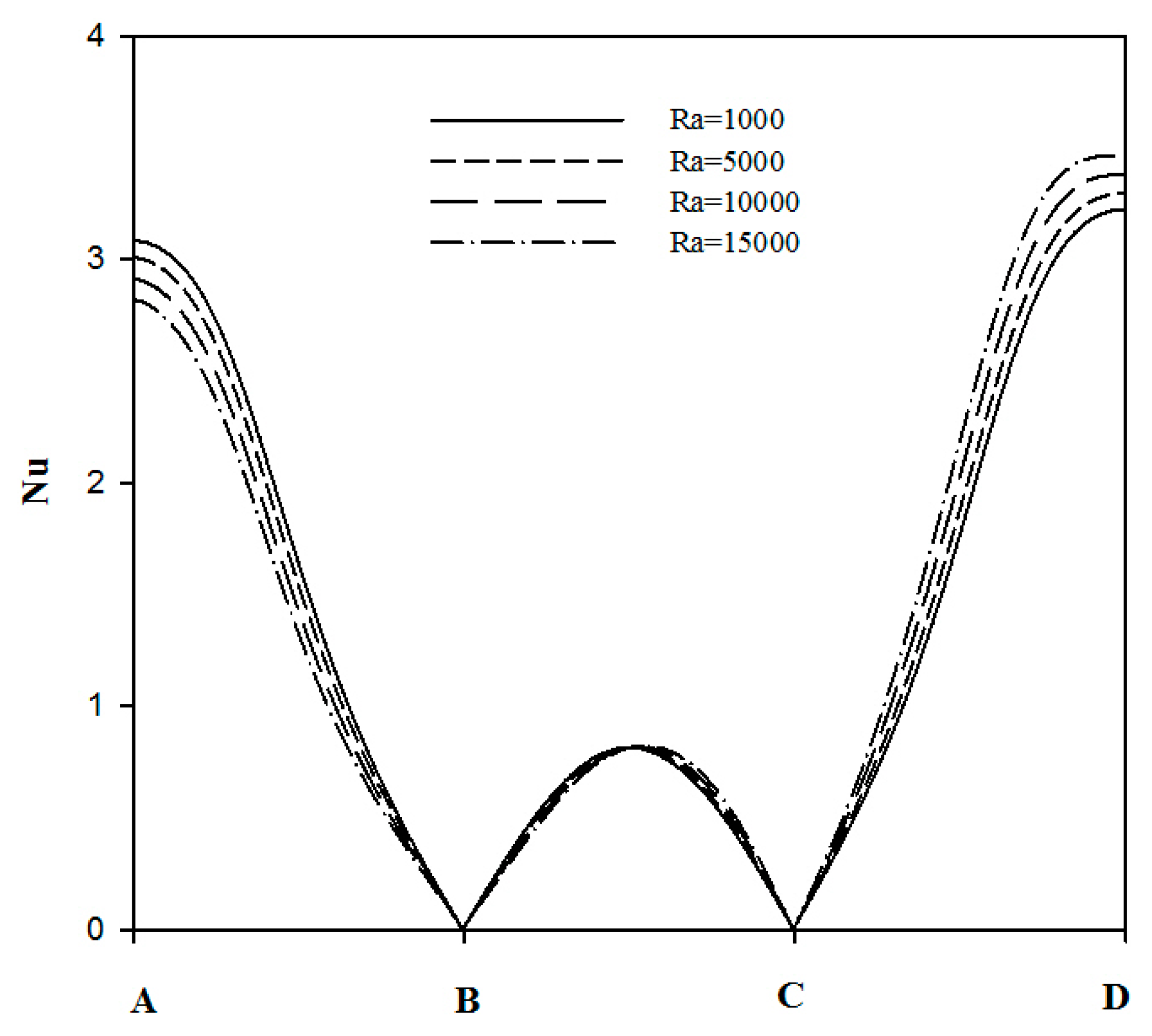
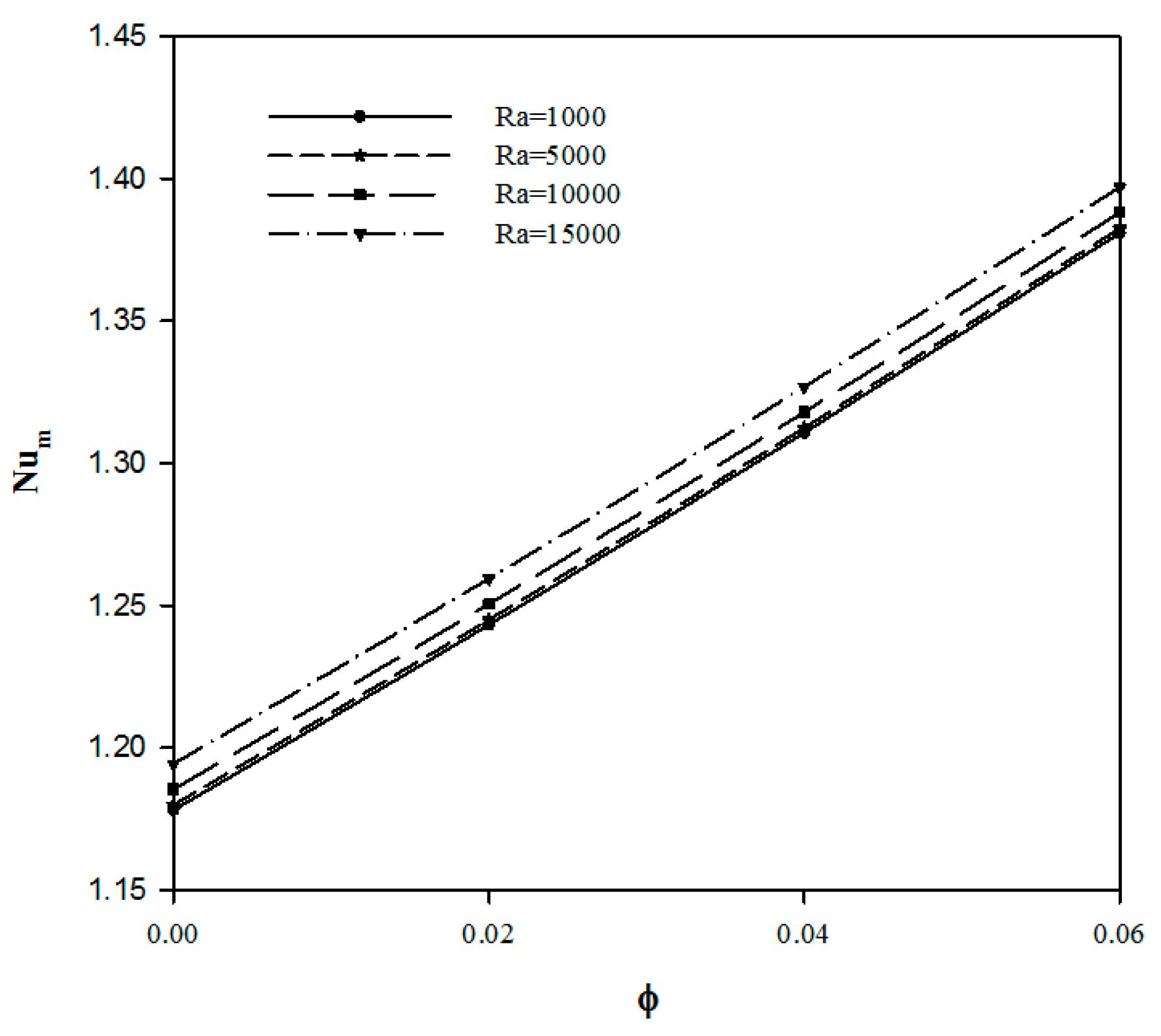
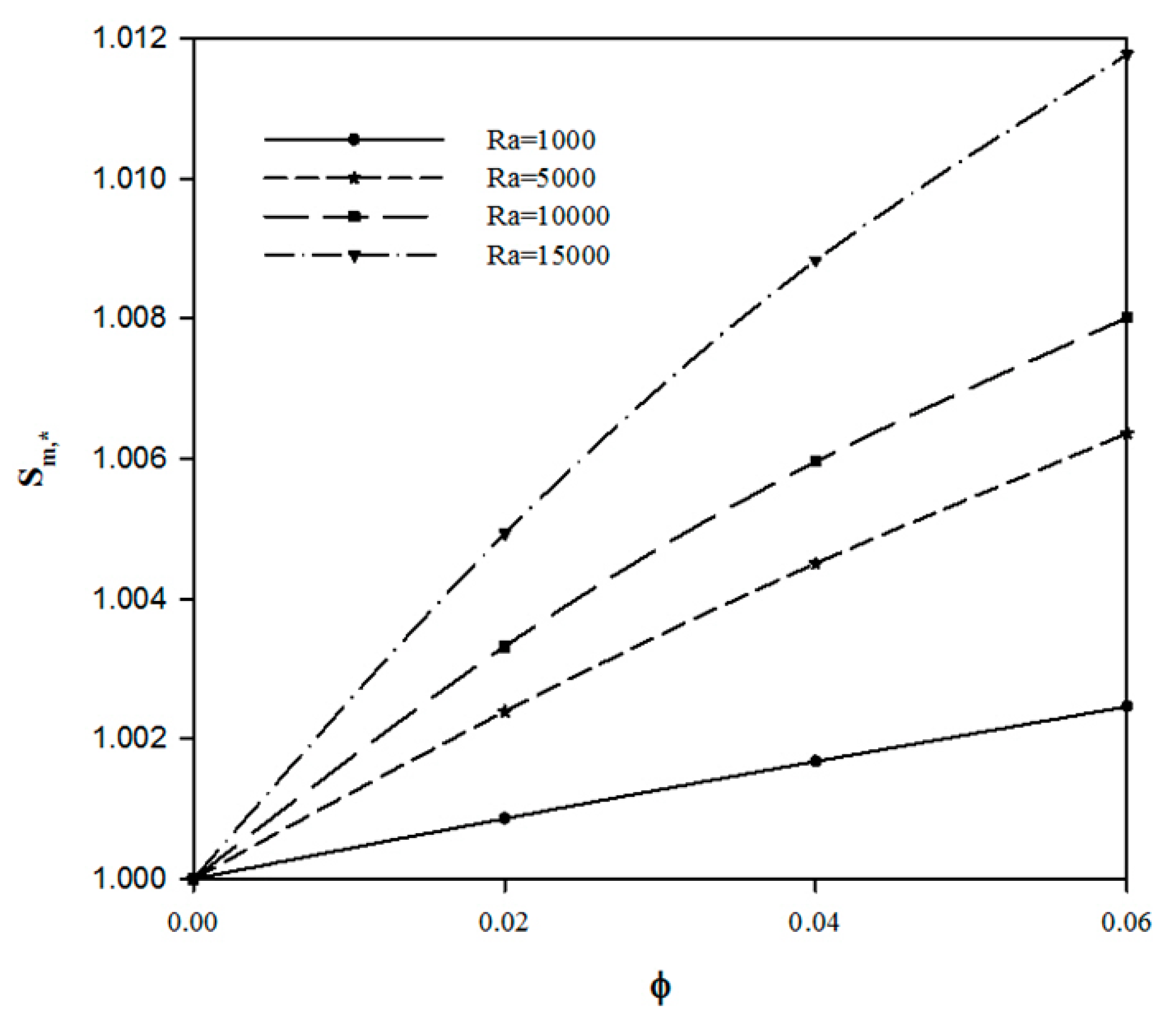
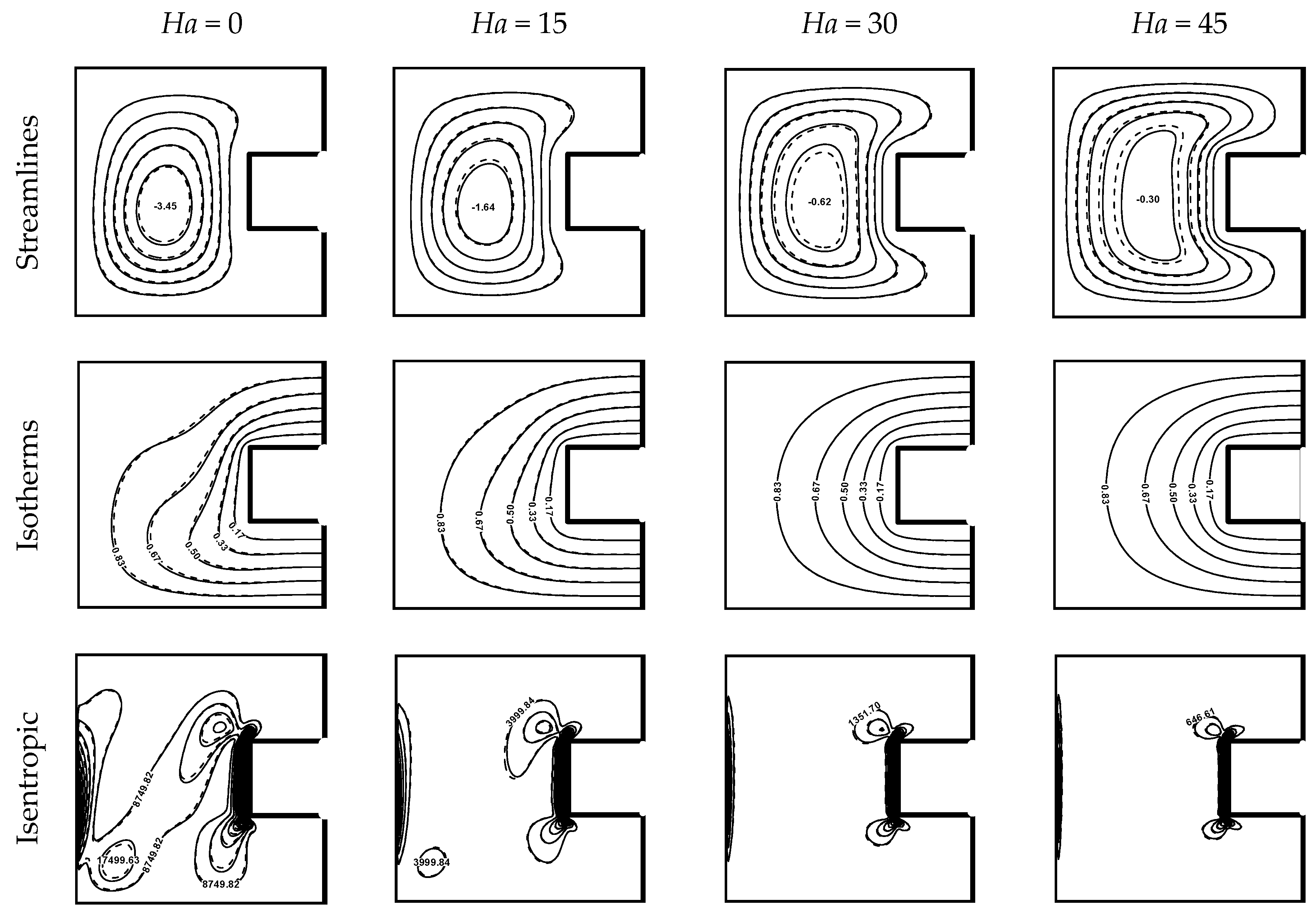
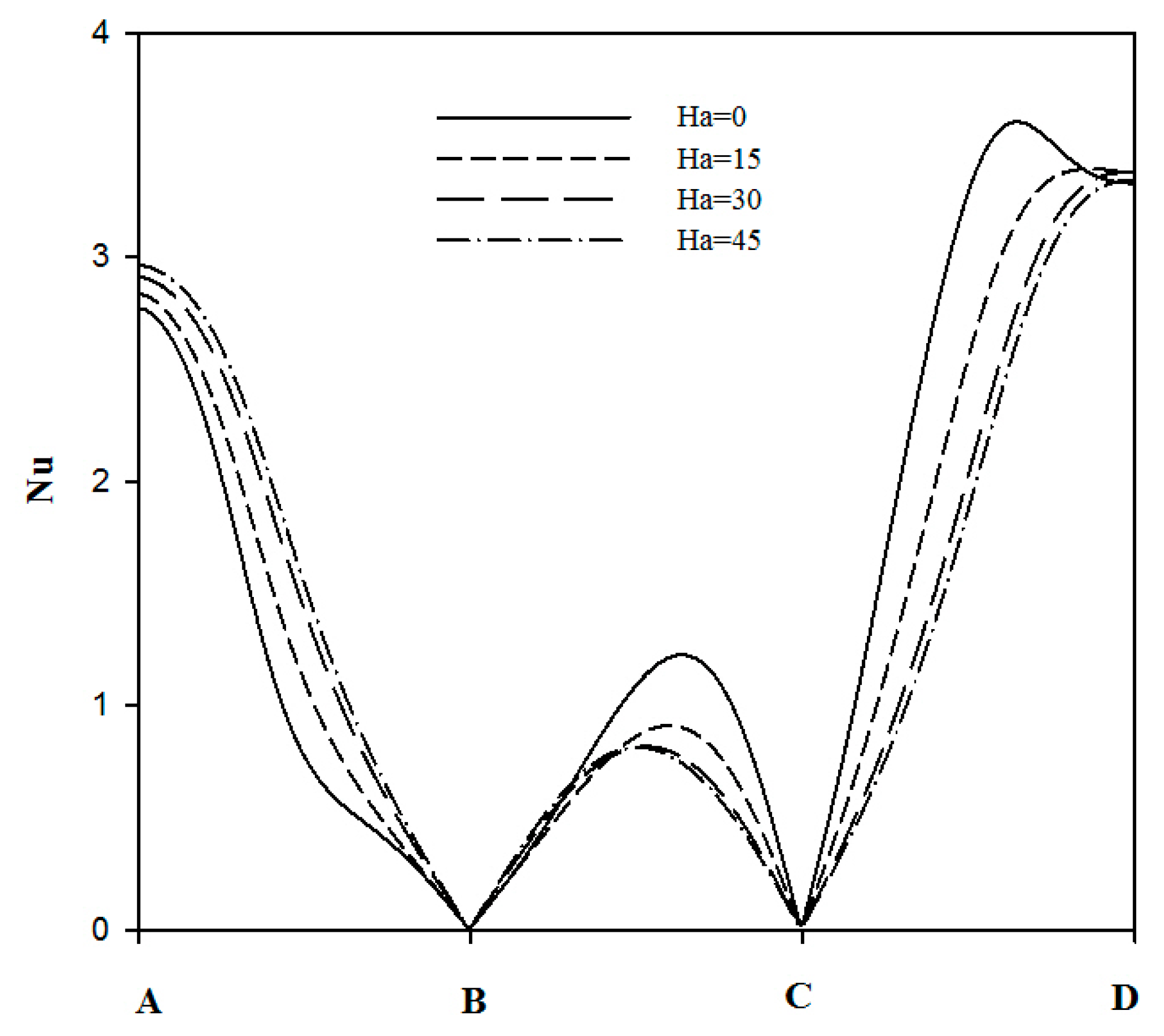
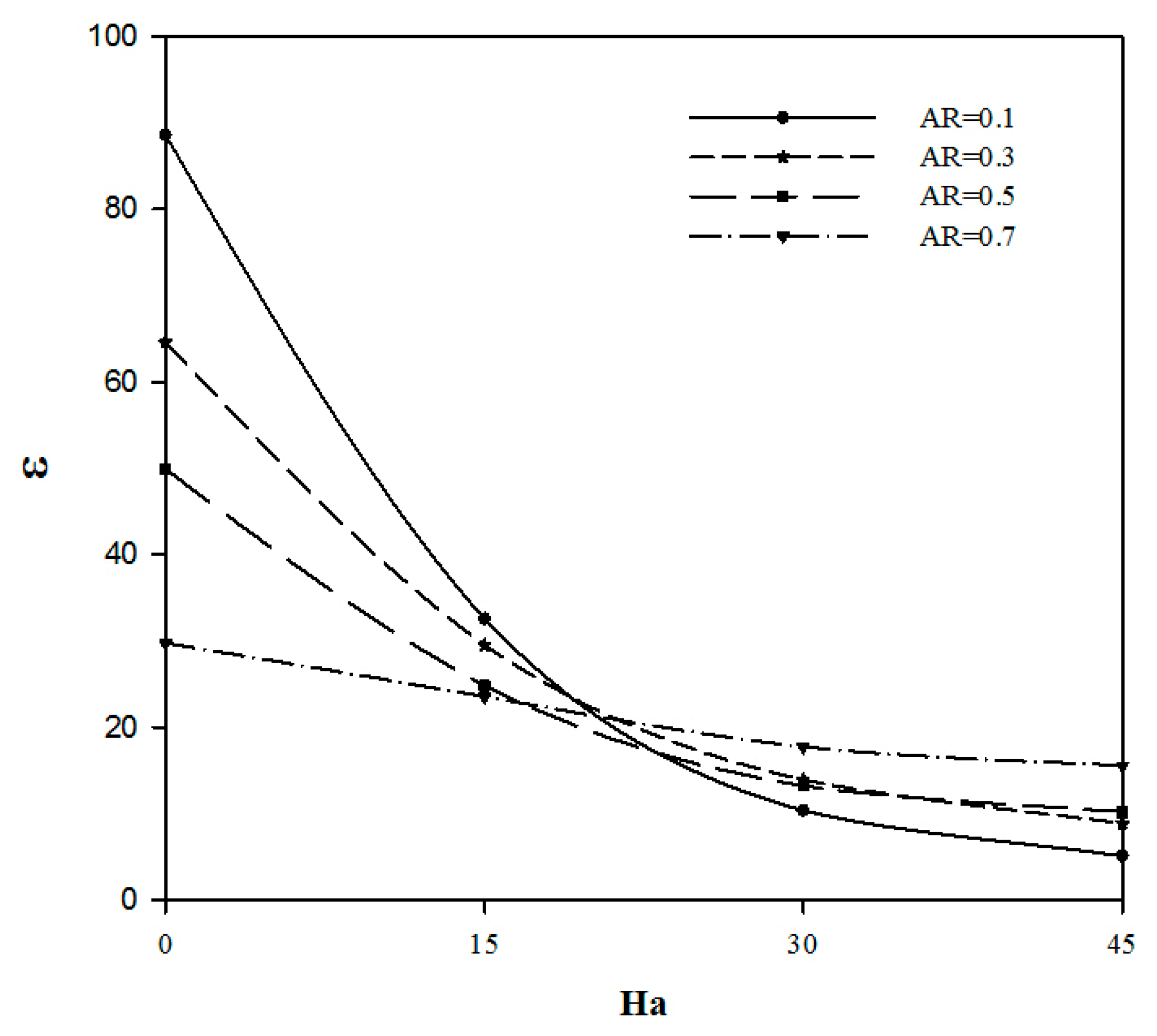
4.2. Effect of Hartman Number
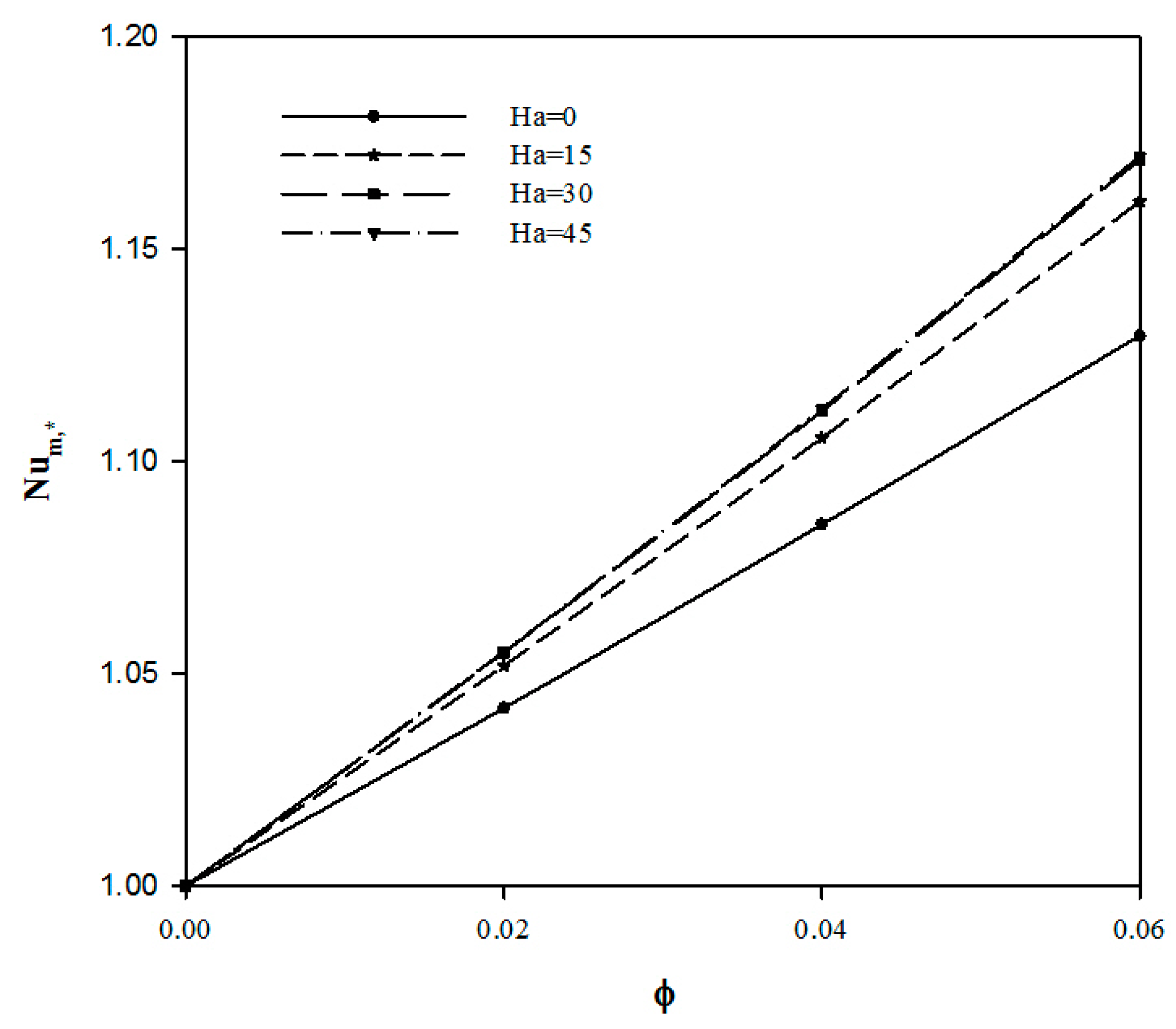
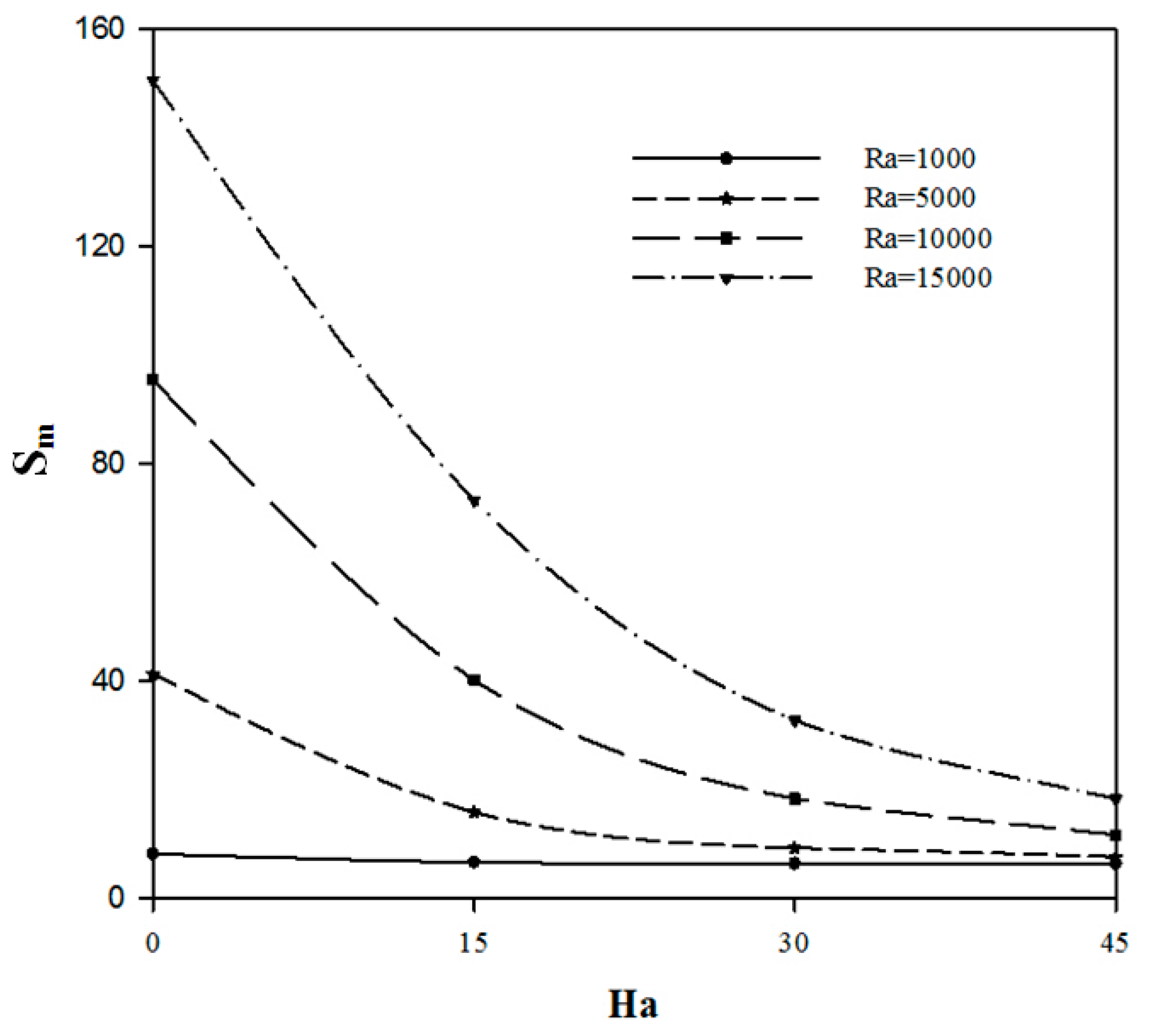

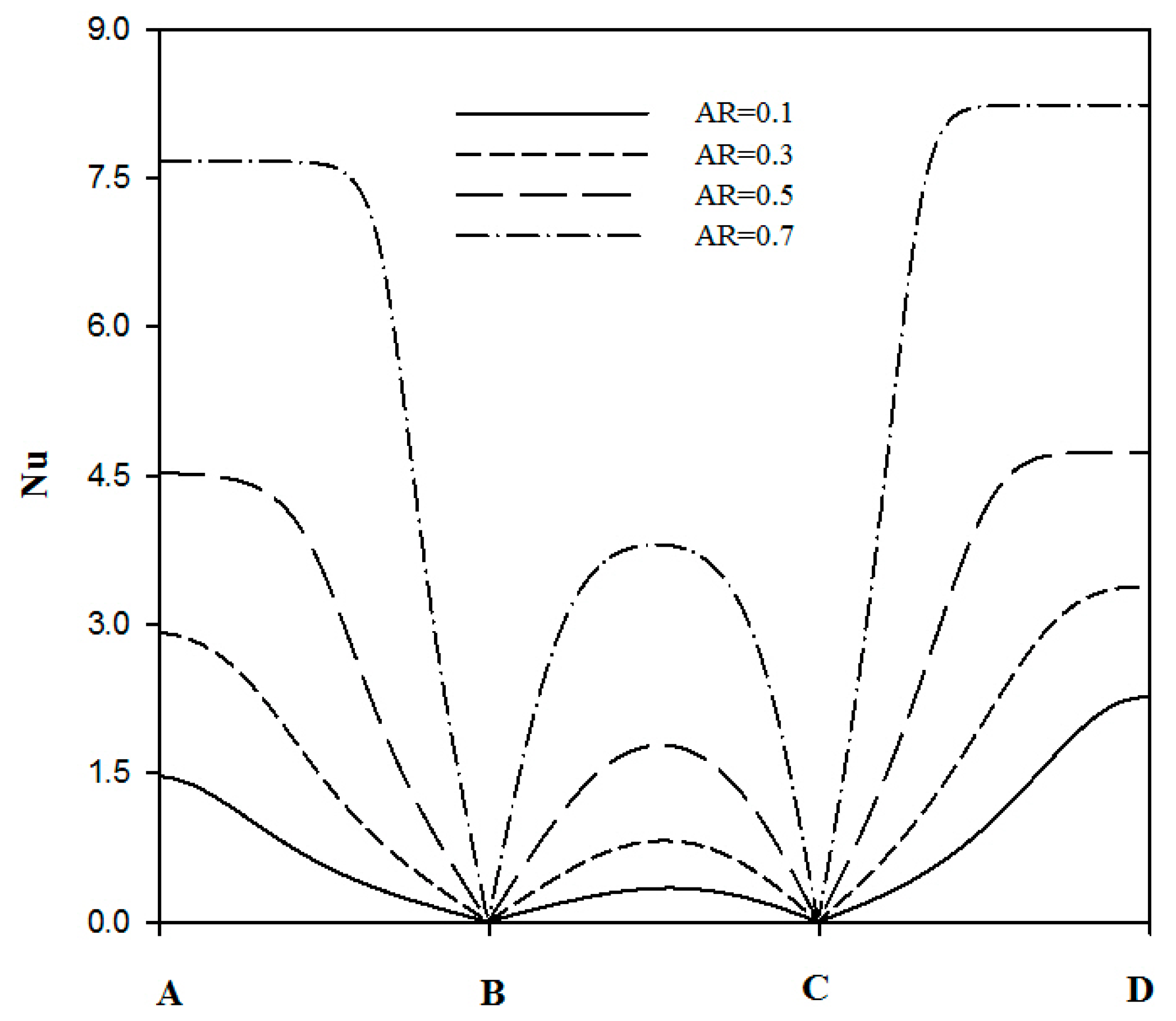
4.3. Effect of the Aspect Ratio
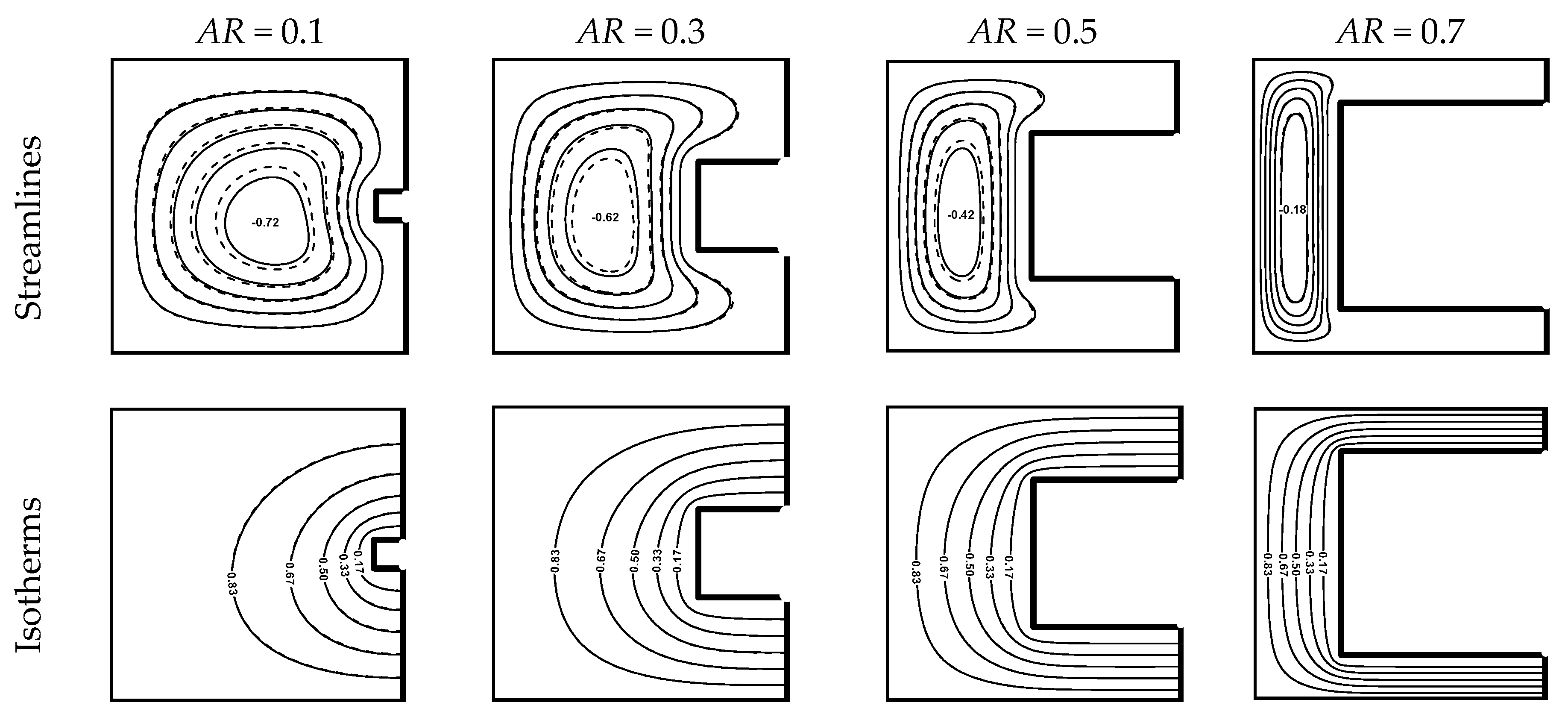
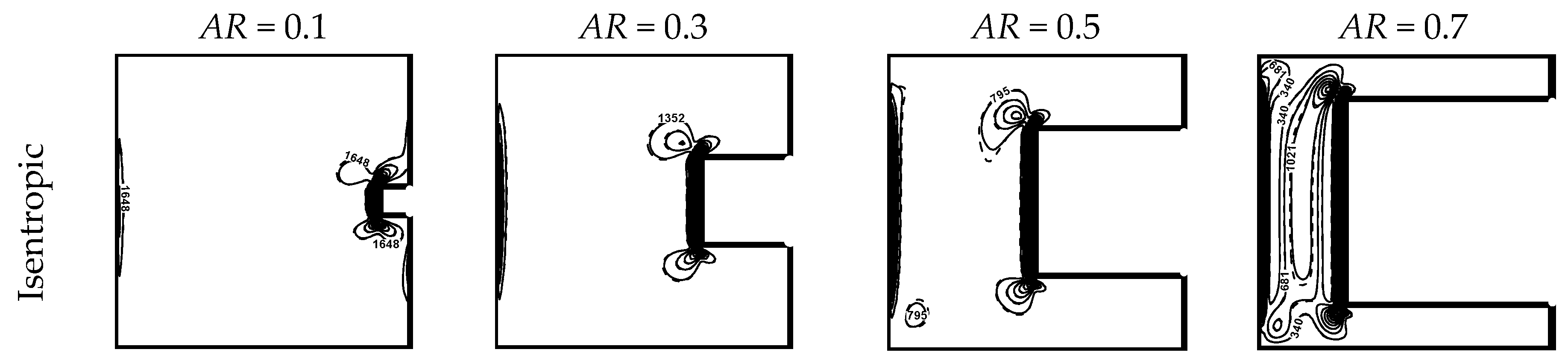

5. Conclusions
- (1)
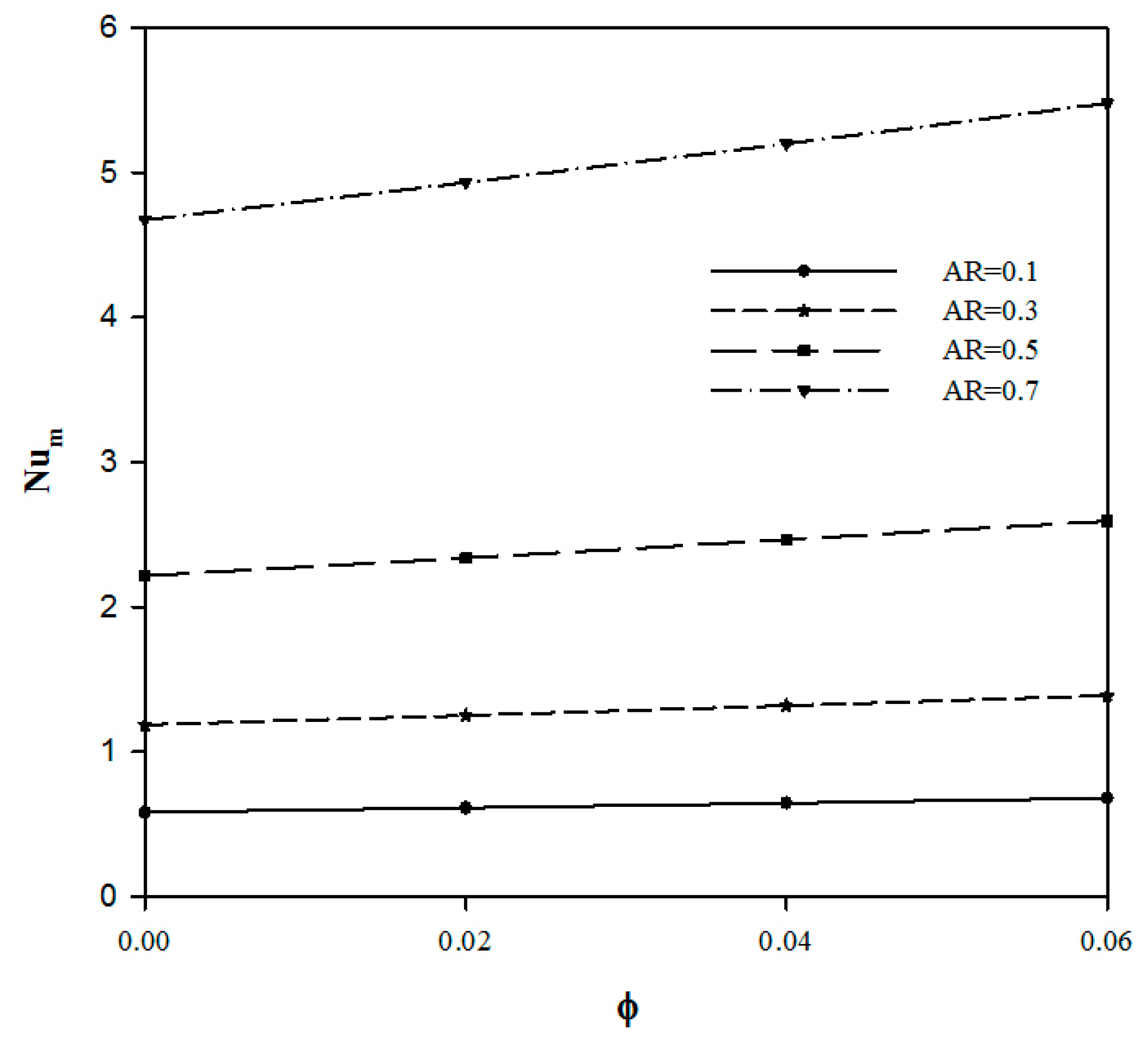
- The addition of nanoparticles enhances the convective heat transfer inside the C-shaped cavity at all Rayleigh numbers, whereas the entropy generation increases with increasing the volume fraction of the nanoparticles. This increase becomes fast at higher Rayleigh number.
- (2)
- The average Nusselt number increases considerably when the hot and cold walls become narrower, i.e., at higher aspect ratio.
- (3)
- The nanofluid utilization becomes more pronounced at lower aspect ratio.
- (4)
- The applied magnetic field is an inactive process at lower Rayleigh number.
- (5)
- The entropy generation rate decreases rapidly with the applied magnetic field.
- (6)
- A threshold value of Hartman number equal to 30 can give the best thermal performance in the C-shaped cavity.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| B0 | Magnetic field strength, T | Greek symbols | |
| Specific heat, J·kg−1·K−1 | Thermal diffusivity, m2·s−1 | ||
| Gravitational acceleration, m·s2 | Thermal expansion coefficient, K−1 | ||
| Length of heat source, m | ε | performance criterion () | |
| Hartmann number, | Solid volume fraction | ||
| k | Thermal conductivity, W·m−1·K−1 | Effective electrical conductivity, μ·S/cm | |
| Length of cavity, m | Boltzmann constant, J·K−1 | ||
| Local Nusselt number | Dimensionless temperature, | ||
| Num | Average Nusselt number of heat source | Dynamic viscosity, N·S·m−2 | |
| Fluid pressure, Pa | Kinematic viscosity, m2·s−1 | ||
| Dimensionless pressure, | Density, kg·m3 | ||
| Prandtl number, νf/αf | Subscripts | ||
| Temperature, K | Cold | ||
| Tc | Cold wall temperature, K | Pure fluid | |
| Hot wall temperature, K | hot wall | ||
| Velocity components in x, y directions, m·s−1 | Average | ||
| Dimensionless Velocity components, | Nanofluid | ||
| Cartesian coordinates, m | Nanoparticle | ||
| X,Y | Dimensionless coordinates, (x,y)/L | ||
References
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A. Second-law analysis in heat transfer and thermal design. Adv. Heat Transf. 1982, 15, 1–58. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Mahmud, S.; Fraser, R.A. Second law analysis of heat transfer and fluid flow inside a cylindrical annular space. Exergy Int. J. 2002, 2, 322–329. [Google Scholar] [CrossRef]
- Mahmud, S.; Islam, A.K.M.S. Laminar free convection and entropy generation inside an inclined wavy enclosure. Int. J. Therm. Sci. 2003, 42, 1003–1012. [Google Scholar] [CrossRef]
- Bouabid, M.; Magherbi, M.; Hidouri, N.; Ben Brahim, A. Entropy generation at natural convection in an inclined rectangular cavity. Entropy 2011, 13, 1020–1033. [Google Scholar] [CrossRef]
- Cheng, X.; Liang, X. Discussion on the applicability of entropy generation minimization to the analyses and optimizations of thermodynamic processes. Energy Convers. Manag. 2013, 73, 121–127. [Google Scholar] [CrossRef]
- Baytas, A.C. Entropy generation for natural convection in an inclined porous cavity. Int. J. Heat Mass Transf. 2000, 43, 2089–2099. [Google Scholar] [CrossRef]
- Al-Hadhrami, A.K.; Elliott, L.; Ingham, D.B. A New model for viscous dissipation in porous media across a range of permeability values. Transp. Porous Media 2003, 53, 117–122. [Google Scholar] [CrossRef]
- Mahmud, S.; Fraser, R.A. Magneto-hydrodynamic free convection and entropy generation in a square porous cavity. Int. J. Heat Mass Transf. 2004, 47, 3245–3256. [Google Scholar] [CrossRef]
- Hooman, K.; Ejlali, A. Entropy generation for forced convection in a porous saturated circular tube with uniform wall temperature. Int. Commun. Heat Mass Transf. 2007, 34, 408–419. [Google Scholar] [CrossRef]
- Zahmatkesh, I. On the importance of thermal boundary conditions in heat transfer and entropy generation for natural convection inside a porous enclosure. Int. J. Therm. Sci. 2008, 47, 339–346. [Google Scholar] [CrossRef]
- Varol, Y.; Oztop, H.F.; Pop, I. Entropy generation due to natural convection in non-uniformly heated porous isosceles triangular enclosures at different positions. Int. J. Heat Mass Transf. 2009, 52, 1193–1205. [Google Scholar] [CrossRef]
- Basak, T.; Kaluri, R.S.; Balakrishnan, A.R. Entropy generation during natural convection in a porous cavity: Effect of thermal boundary conditions. Numer. Heat Transf. 2012, 62, 336–364. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluid with Nanoparticles. In Proceedings of 1995 ASME International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995.
- Aminossadati, S.M.; Ghasemi, B. The effects of orientation of an inclined enclosure on laminar natural convection. Int. J. Heat Technol. 2005, 23, 43–49. [Google Scholar]
- Ghasemi, B.; Aminossadati, S.M. Brownian motion of nanoparticles in a triangular enclosure with natural convection. Int. J. Therm. Sci. 2010, 49, 931–940. [Google Scholar] [CrossRef]
- Abu-Nada, E.; Chamkha, A.J. Effect of nanofluid variable properties on natural convection in enclosures filled with a CuO–EG–water nanofluid. Int. J. Therm. Sci. 2010, 49, 2339–2352. [Google Scholar] [CrossRef]
- Nemati, H.; Frhadi, M.; Sedighi, K.; Ashorynejad, H.R.; Fattahi, E. Magnetic field effects on natural convection flow of nanofluid in a rectangular cavity using the Lattice Boltzmann model. Sci. Iran. 2012, 19, 303–310. [Google Scholar] [CrossRef]
- Mahmoudi, A.H.; Pop, I.; Shahi, M. Effect of magnetic field on natural convection in a triangular enclosure filled with nanofluid. Int. J. Therm. Sci. 2012, 59, 126–140. [Google Scholar] [CrossRef]
- Habibi, M.M.; Pop, I. Natural convection flow and heat transfer in an eccentric annulus filled by Copper nanofluid. Int. J. Heat Mass Transf. 2013, 61, 353–364. [Google Scholar] [CrossRef]
- Sheikhzadeh, G.A.; Dastmalchi, M.; Khorasanizadeh, H. Effects of nanoparticles transport mechanisms on Al2O3-water nanofluid natural convection in a square enclosure. Int. J. Therm. Sci. 2013, 66, 51–62. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Seyyedi, S.M.; Ganji, D.D.; Rokni, H.B.; Soleimani, S. Application of LBM in simulation of natural convection in a nanofluid filled square cavity with curve boundaries. Powder Technol. 2013, 247, 87–94. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ellahi, R.; Zeeshan, A. Simulation of MHD CuO-water nanofluid flow and convective heat transfer considering Lorentz forces. J. Magn. Magn. Mater. 2014, 369, 69–80. [Google Scholar] [CrossRef]
- Kashani, S.; Ranjbar, A.A.; Mastiani, M.; Mirzaei, H. Entropy generation and natural convection of nanoparticle-water mixture (nanofluid) near water density inversion in an enclosure with various patterns of vertical wavy walls. Appl. Math. Comput. 2014, 226, 180–193. [Google Scholar] [CrossRef]
- Cho, C.-C.; Yau, H.-T.; Chiu, C.-H.; Chiu, K.-C. Numerical investigation into natural convection and entropy generation in a nanofluid-filled U-shaped cavity. Entropy 2015, 17, 5980–5994. [Google Scholar] [CrossRef]
- Ting, T.W.; Hung, Y.M.; Guo, N. Entropy generation of viscous dissipative nanofluid flow in thermal non-equilibrium porous media embedded in microchannels. Int. J. Heat Mass Transf. 2015, 81, 862–877. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Mejri, I.; Abbassi, M.A.; Omri, A. Analysis of the entropy generation in a nanofluid-filled cavity in the presence of magnetic field and uniform heat generation/absorption. J. Mol. Liq. 2014, 198, 63–77. [Google Scholar] [CrossRef]
- Aghaei, A.; Khorasanizadeh, H.; Sheikhzadeh, G.; Abbaszadeh, M. Numerical study of magnetic field on mixed convection and entropy generation of nanofluid in a trapezoidal enclosure. J. Magn. Magn. Mater. 2016, 403, 133–145. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Simulation of heat transfer and entropy generation of MHD natural convection of non-Newtonian nanofluid in an enclosure. Int. J. Heat Mass Transf. 2016, 92, 1066–1089. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu-H2O nanofluid on entropy generation. Int. J. Heat Mass Transf. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Ismael, M.A.; Armaghani, T.; Chamkha, A.J. Conjugate heat transfer and entropy generation in a cavity filled with a nanofluid-saturated porous media and heated by a triangular solid. J. Taiwan Inst. Chem. Eng. 2015, in press. [Google Scholar] [CrossRef]
- Biserni, C.; Rocha, L.A.O.; Stanescu, G.; Lorenzini, E. Constructal H-shaped cavities according to Bejan’s theory. Int. J. Heat Mass Transf. 2007, 50, 2132–2138. [Google Scholar] [CrossRef]
- Mahmoodi, M. Numerical simulation of free convection of a nanofluid in L-shaped cavities. Int. J. Therm. Sci. 2011, 50, 1731–1740. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Hashemi, S.M. Numerical study of natural convection of a nanofluid in C-shaped enclosures. Int. J. Therm. Sci. 2012, 55, 76–89. [Google Scholar] [CrossRef]
- Cho, C.-C.; Yau, H.-T.; Chen, C.-K. Enhancement of natural convection heat transfer in a U-shaped cavity filled with Al2O3-water nanofluid. Therm. Sci. 2012, 16, 1317–1323. [Google Scholar] [CrossRef]
- Mansour, M.A.; Bakeir, M.A.; Chamkha, A. Natural convection inside a C-shaped nanofluid-filled enclosure with localized heat sources. Int. J. Numer. Method Heat Fluid Flow 2014, 24, 1954–1978. [Google Scholar] [CrossRef]
- Mojumder, S.; Saha, S.; Saha, S.; Mamun, M.A.H. Effect of magnetic field on natural convection in a C-shaped cavity filled with ferrofluid. Procedia Eng. 2015, 105, 96–104. [Google Scholar] [CrossRef]
- Kasaeipoor, A.; Ghasemi, B.; Aminossadati, S.M. Convection of Cu-water nanofluid in a vented T-shaped cavity in the presence of magnetic field. Int. J. Therm. Sci. 2015, 94, 50–60. [Google Scholar] [CrossRef]
- Al-Zamily, A.M.J. Effect of magnetic field on natural convection in a nanofluid-filled semi-circular enclosure with heat flux source. Comput. Fluids 2014, 103, 71–85. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Gorji-Bandpy, M.; Soleimani, S. Magnetic field effect on nanofluid flow and heat transfer using KKL model. J. Taiwan Inst. Chem. Eng. 2014, 45, 795–807. [Google Scholar] [CrossRef]
- Öğüt, E.B. Natural convection of water-based nanofluids in an inclined enclosure with a heat source. Int. J. Therm. Sci. 2009, 48, 2063–2073. [Google Scholar] [CrossRef]
- Masoumi, N.; Sohrabi, N.; Behzadmehr, A. A new model for calculating the effective viscosity of nanofluids. J. Phys. D 2009, 42, 055501. [Google Scholar] [CrossRef]
- Chon, C.H.; Kihm, K.D.; Lee, S.P.; Choi, S.U.S. Empirical correlation finding the role of temperature and particle size for nanofluid (Al2O3) thermal conductivity enhancement. Appl. Phys. Lett. 2005, 87, 153107. [Google Scholar] [CrossRef]
- Mintsa, H.A.; Roy, G.; Nguyen, C.T.; Doucet, D. New temperature dependent thermal conductivity data for water-based nanofluids. Int. J. Therm. Sci. 2009, 48, 363–371. [Google Scholar] [CrossRef]
- Popa, C.V.; Kasaeian, A.B.; Nasiri, S.; Korichi, A.; Polidori, G. Natural convection heat and mass transfer modeling for Cu/water and CuO/water nanofluids. Adv. Mech. Eng. 2013. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 2nd ed.; Oxford University Press: Cambridge, UK, 1904. [Google Scholar]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Pirmohammadi, M.; Ghassemi, M. Effect of magnetic field on convection heat transfer inside a tilted square enclosure. Int. Commun. Heat Mass Transf. 2009, 36, 776–780. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chamkha, A.; Ismael, M.; Kasaeipoor, A.; Armaghani, T. Entropy Generation and Natural Convection of CuO-Water Nanofluid in C-Shaped Cavity under Magnetic Field. Entropy 2016, 18, 50. https://doi.org/10.3390/e18020050
Chamkha A, Ismael M, Kasaeipoor A, Armaghani T. Entropy Generation and Natural Convection of CuO-Water Nanofluid in C-Shaped Cavity under Magnetic Field. Entropy. 2016; 18(2):50. https://doi.org/10.3390/e18020050
Chicago/Turabian StyleChamkha, Ali, Muneer Ismael, Abbas Kasaeipoor, and Taher Armaghani. 2016. "Entropy Generation and Natural Convection of CuO-Water Nanofluid in C-Shaped Cavity under Magnetic Field" Entropy 18, no. 2: 50. https://doi.org/10.3390/e18020050
APA StyleChamkha, A., Ismael, M., Kasaeipoor, A., & Armaghani, T. (2016). Entropy Generation and Natural Convection of CuO-Water Nanofluid in C-Shaped Cavity under Magnetic Field. Entropy, 18(2), 50. https://doi.org/10.3390/e18020050







