Abstract
In this article, entropy generation due to natural convection in entrapped trapezoidal cavities filled with nanofluid under the influence of magnetic field was numerically investigated. The upper (lower) enclosure is filled with CuO-water (AlO-water) nanofluid. The top and bottom horizontal walls of the trapezoidal enclosures are maintained at constant hot temperature while other inclined walls of the enclosures are at constant cold temperature. Different combinations of Hartmann numbers are imposed on the upper and lower trapezoidal cavities. Numerical simulations are conducted for different values of Rayleigh numbers, Hartmann number and solid volume fraction of the nanofluid by using the finite element method. In the upper and lower trapezoidal cavities magnetic fields with different combinations of Hartmann numbers are imposed. It is observed that the averaged heat transfer reduction with magnetic field is more pronounced at the highest value of the Rayleigh number. When there is no magnetic field in the lower cavity, the averaged Nusselt number enhances as the value of the Hartmann number of the upper cavity increases. The heat transfer enhancement rates with nanofluids which are in the range of 10% and 12% are not affected by the presence of the magnetic field. Second law analysis of the system for various values of Hartmann number and nanoparticle volume fractions of upper and lower trapezoidal domains is performed.
1. Introduction
Natural convection in cavities is encountered in various applications including chemical reactors, heat exchangers, cooling of electronic devices, room ventilation and solar collectors due to its simplicity and low cost. A comprehensive review was made by Ostrach [1]. Natural convection in trapezoidal cavities has been studied extensively [2,3,4,5,6,7]. Silva et al. [8] numerically investigated the natural convection in trapezoidal cavities with two internal baffles. They studied the effects of inclination angles of the upper surface as well as the effect of the Rayleigh number, the Prandtl number, and the baffle height on the fluid flow and heat transfer. Varol [9] performed a numerical study of natural convection in divided trapezoidal enclosures filled with fluid saturated porous media. He has noted that that the conduction mode of heat transfer became dominant for higher thickness of the partition, low thermal conductivity ratio and low Rayleigh numbers. Natarajan et al. [10] numerically studied the natural convection in a trapezoidal cavity with uniform and non-uniform heating of bottom wall for a range of Rayleigh and Prandtl numbers using finite element method. They showed that non-uniform heating of the bottom wall produces greater heat transfer rate at the center of the bottom wall than uniform heating. Eyden et al. [11] numerically and experimentally studied the turbulent double diffusive natural convection in a trapezoidal enclosure which mimics an idealized situation in underground coal gasification. They reported that the numerical model can reproduce the essential features of the process.
The magnetic field effect on convective heat transfer were studied extensively recently since it may found imporatnst applciation areas such as coolers of nuclear reactors, purification of molten metals, MEMs and many others [12,13]. To control the convective heat transfer characteristics in various systems external magnetic field may be imposed in various systems[14,15,16,17,18]. Öztop et al. [19] studied the effect of magnetic field in a top sided lid-driven enclosure with a corner heater. They observed that Nusset number deteriorates as the strength of the magnetic field increases and magnetic field can be utilized to control the convection inside the enclosure. Hasanuzzaman et al. [20] studied the influence of magnetic field on free convection for a trapezoidal cavity with finite element method and showed that the Nusselt number deteriorates with magnetic field strength. Hossain and Alim [21] performed two dimensional MHD natural convection within trapezoidal cavity with non-uniformly heated bottom wall by using the finite element method. They showed that the average Nusselt number at the non-uniform heating of bottom wall of the cavity depends on the dimensionless parameters and also tilts angles.
Nanofluids are used in various heat transfer applications. Different nano sized particles such as , Cu, CuO, , are added in the base fluid to enhance the thermal characteristics of the base flow [22,23,24,25,26,27,28,29]. Magnetohydrodynamics studies with added nanoparticles to the base fluids were received attention during recent years in various heat transfer applications [30,31,32,33,34]. Ghasemi et al. [31] investigated the MHD free convection in a cavity filled with - nanofluid. They observed that the Nusselt number enhances or deteriorates as the nanoparticle volume fraction increases depending on the value of Ha and Ra numbers. Mahmoudi et al. [35] numerically studied the magnetohydrodynamics free convection in a triangular cavity filled with nanofluid.
Second law analysis with entropy generation concept can be utilized to evaluate the system performance under various operating conditions [36,37,38,39,40]. The available energy destruction can be quantified by the measurement of irreversibility during a process which is called entropy generation rate. The fundamentals of entropy generation minimization was presented by Bejan [41]. Öztop and Al-Salem [42] made a review of entropy generation in natural and mixed convection for energy systems. MHD convection with nanofluids related to entropy generation and second law analysis were studied by several researchers [43,44,45,46]. Thermal management of free convection within trapezoidal cavities with distributions of heatlines and entropy generation by using the Galerkin finite element method was investigated in reference [47]. Optimal tilt angles of the square cavity were found in a tilted porous cavity with natural convection effect based on minimum entropy generation.
In this study, heat transfer and fluid flow inside two trapezoidal cavities were numerically investigated. This configuration may be encountered in heat exchanger for the purpose of heat recovery from hot fluids passing through a bundle of tubes. Varol [48] numerically studied the heat transfer and fluid flow within two entrapped porous trapezoidal cavities using finite difference method. The effects of Darcy-modified Rayleigh number, aspect ratio of trapezoidal cavities and thermal conductivity ratio were studied. It was observed that local Nusselt number exhibits wavy distribution for the lower trapezoidal cavity. Basak et al. [49] studied the fluid flow and heat transfer in entrapped porous triangular cavities for a range of Darcy number, Prandtl number, Rayleigh number using finite element method. Heatline approach was used to visualize the heat flow. They observed that averaged heat transfer is higher for upper triangular cavity compared to the lower cavity. Oscillatory behavior of the local Nusselt number was observed for the upper triangular cavity at low Pr and high Da number.
Natural convection and entropy generation in entrapped trapezoidal cavities filled with nanofluids under the influence of magnetic field has never been studied despite its importance in heat recovery heat exchanger systems. The present numerical investigation aims at studying the effects of Rayleigh number, Hartmann number, solid volume fraction of the nanofluid on the fluid flow and heat transfer characteristics in entrapped trapezoidal cavities. Second law analysis for various system parameters of the upper and lower trapezoidal domains is also performed which can be used for thermal management and system performance evaluation of the trapezoidal cavity.
2. Physical Model and Mathematical Formulation
The entrapped trapezoidal cavities are shown schematically in Figure 1. The fluid is entrapped in the trapezoidal enclosures. The top and bottom wall of the cavities are kept at constant temperature of while the inclined side walls are at constant temperature of with . All the walls of the cavities have no-slip boundary conditions. The upper cavity is filled with CuO-water nanofluid while AlO-water nanofluid is used in the lower trapezoidal cavity. Magnetic fields B0 and B1 with inclination angle of and are imposed for the lower and upper trapezoidal domains. Thermo-physical properties of water, CuO and AlO at the reference temperature are presented in Table 1. Joule heating, displacement currents and induced magnetic field effects are assumed to be negligible. The flow is assumed to be 2D, laminar and the density in the buoyancy force is approximated according to Boussinesq approximation.

Table 1.
Thermophysical properties [24,32,35].
| Property | Water | CuO | AlO |
|---|---|---|---|
| ρ (kg/m) | 997.1 | 6500 | 3970 |
| (J/kg·K) | 4179 | 540 | 765 |
| (W·m·K) | 0.6 | 18 | 25 |
| β (1/K) | |||
| (Ω·m) |
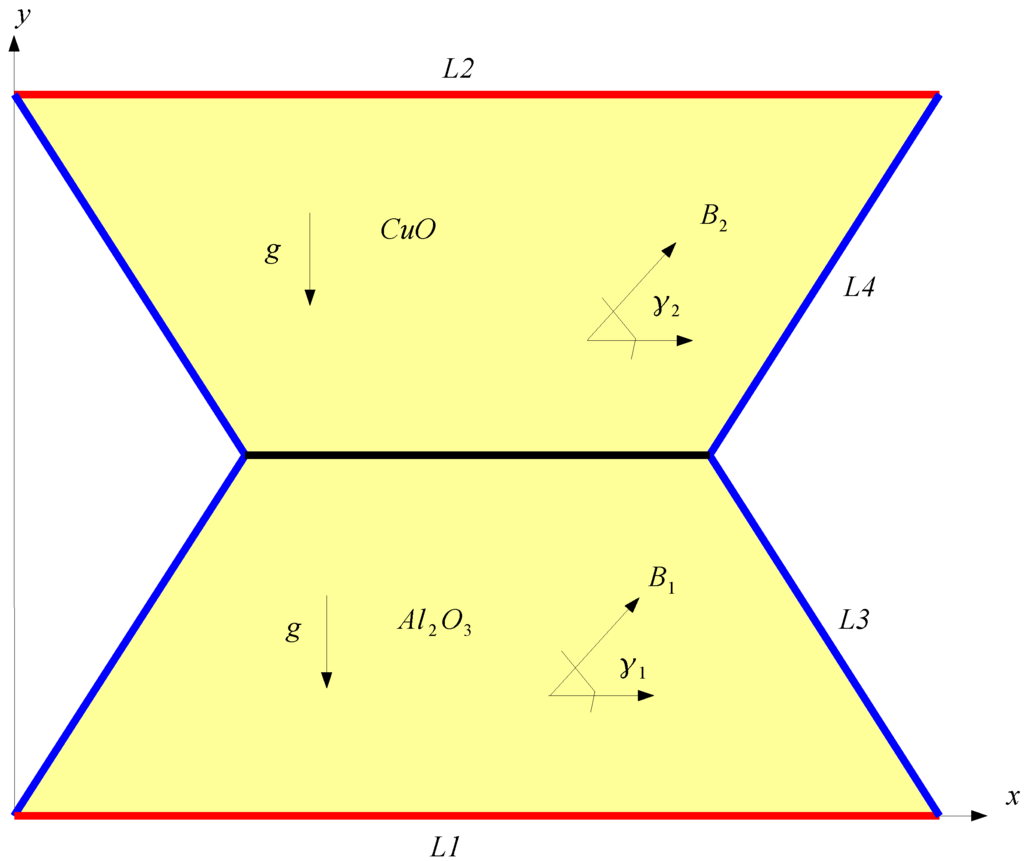
Figure 1.
Schematic description of the physical model.
For each of the subdomains, conservation equations and entropy generation equation in a 2D Cartesian coordinate system can be written as:
where is the thermal diffusivity of the nanofluid.
Entropy generation due to heat transfer, viscous dissipation and MHD flow are represented by the first, second and third terms on the right hand side of the above equation.
The effective thermo-physical properties of nanofluids in the numerical simulation were defined by using the following formulas [32,33]:
where the subscripts and p denote the base fluid, nanofluid and solid particle, respectively.
The effective thermal conductivity of the nanofluid includes the effect of Brownian motion. In this model, the effects of particle size, particle volume fraction and temperature dependence are taken into account and it is given by the following formula ([50]):
where is the static thermal conductivity as given by [51]:
The interaction between the nanoparticles and the effect of temperature are included in the models as:
where the function for Cu-water nanofluid is given in [50].
The effective viscosity of the nanofluid due to micro mixing in the suspension was given by [50].
where the first terms on the right hand side of equation is the viscosity of the nanofluid given in ([52]).
By using the following dimensionless parameters:
The non-dimensional form of the Equations (1)–(4) can be written as:
The appropriate forms of the non-dimensional boundary conditions are:
- For the inclined walls of the trapezoidal enclosures:
- For the top and bottom horizontal walls:
- Along the interface of the trapezoidal domains (continuity condition):a-b-
Local Nusselt number on the walls of the trapezoidal enclosures is calculated as:
Averaged heat transfer is obtained after integrating the local Nusselt number along the walls:
3. Solution Method and Validation of Code
Galerkin weighted residual finite element method was utilized to solve the governing equations. The Galerkin procedure was used to establish the weak form the governing equations. Velocity components, pressure and temperature are approximated using Lagrange finite elements of different orders. Residuals for each of the conservation equation is obtained by substituting the approximations into the governing equations. To simplify the nonlinear terms in the momentum equations, Newton-Raphson iteration algorithm was utilized. The convergence of the solution is assumed when the relative for each of the variables satisfy the following convergence criteria:
Grid independence of the solution was assured. Table 2 shows the averaged Nusselt numbers along the top and bottom walls of the trapezoidal enclosure for various grid sizes (). The validation of the study is made against the results of Basak et al. [49]. Streamline and isotherm comparisons are shown in Figure 2 for ). Local Nusselt numbers along the top and bottom horizontal walls of the cavities computed in Basak et al. [49] and computed with present solver are demonstrated in Figure 3. The results depicted in Figure 2 and Figure 3 provide sufficient confidence for the accuracy of the present solver.

Table 2.
Grid independence test.
| Grid Name | Grid Size | Nu (L1) | Nu (L2) |
|---|---|---|---|
| G1 | 938 | 11.92 | 7.67 |
| G2 | 2684 | 12.08 | 8.63 |
| G3 | 33182 | 14.13 | 11.33 |
| G4 | 48772 | 14.56 | 11.77 |
| G5 | 64672 | 14.89 | 11.82 |
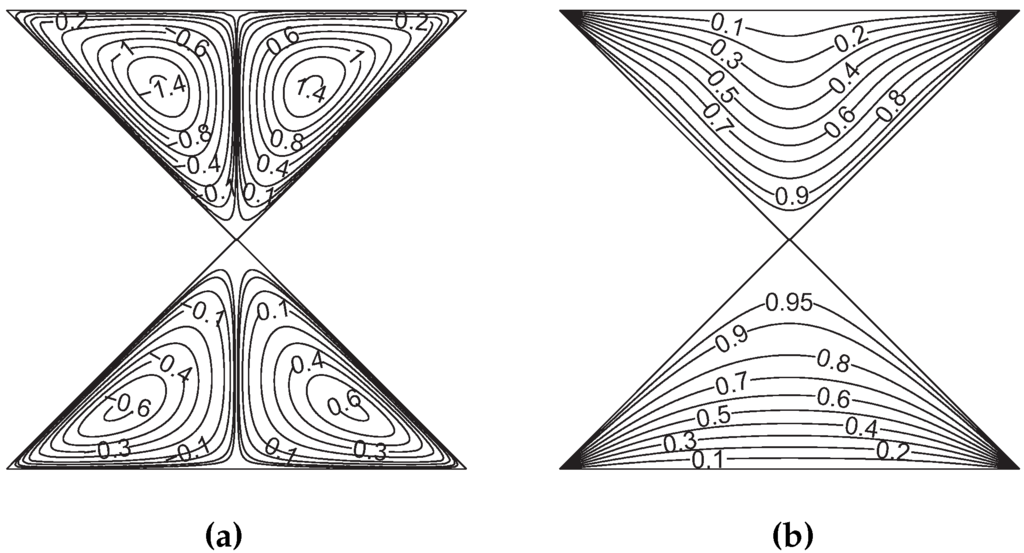

Figure 2.
Code validation study, comparison of streamlines and isotherms with Basak et al. [49], . (a) streamline, Basak et al. [49]; (b) isotherm, Basak et al. [49]; (c) streamline, present solver; (d) isotherm, present solver.
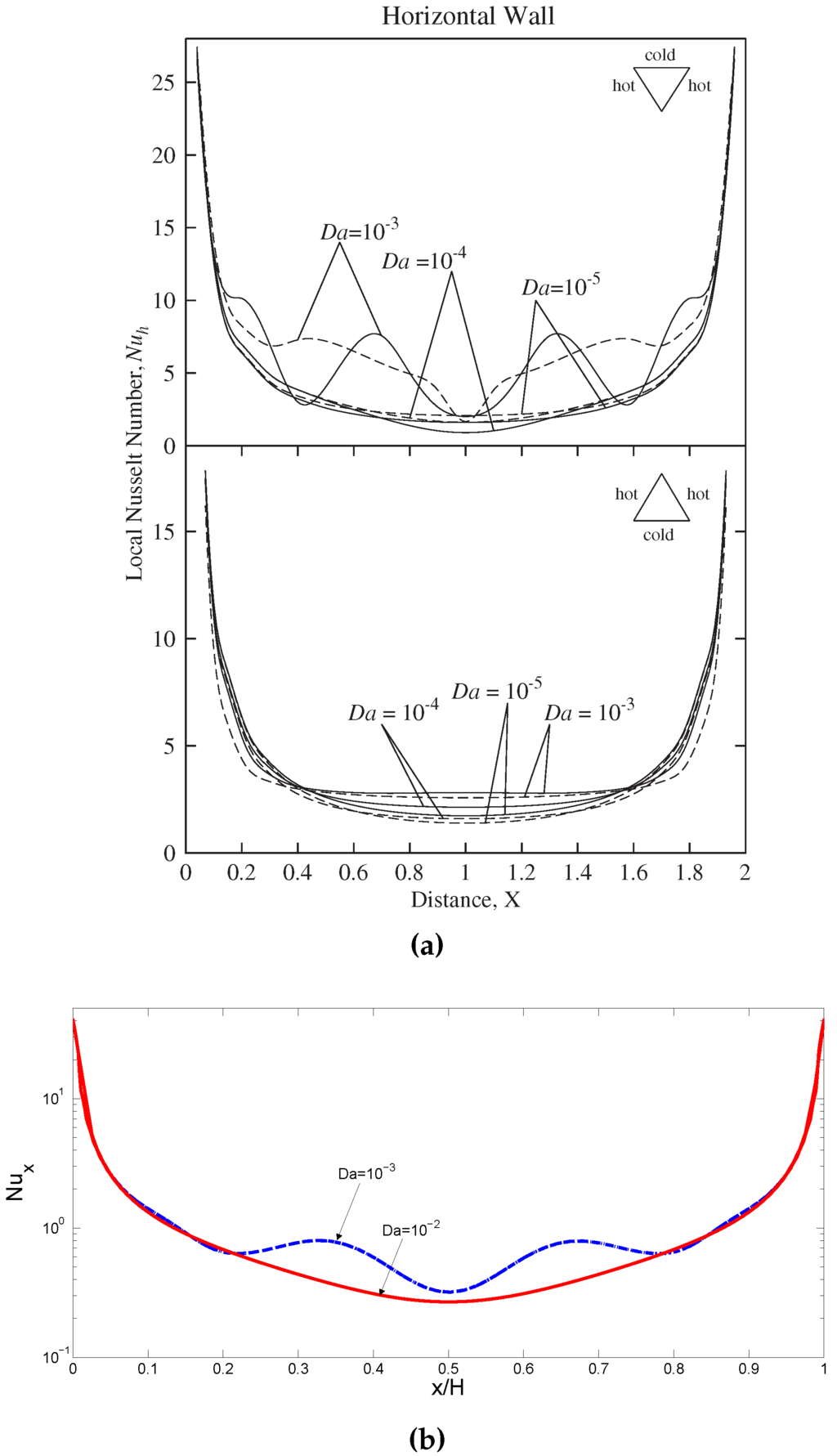
Figure 3.
Code validation study, comparison of local Nusselt numbers along the top and bottom wall with Basak et al. [49], , (a) local Nusselt numbers, Basak et al. [49]; (b) top wall, present solver; (c) bottom wall, present solver.
4. Results and Discussion
The numerical investigation was performed for various values of Rayleigh numbers (between and ), Hartmann number (between 0 and 50) and solid volume fraction of the nanofluid (between 0 and 0.04). Different combinations of Hartmann numbers were imposed in the upper (D2) and lower (D1) trapezoidal cavities. The upper and lower enclosures were filled with CuO-water and AlO-water nanofluid under the influence of horizontally aligned magnetic fields (). Entropy generation due to natural convection for various values of Hartmann number and nanoparticle volume fractions of upper and lower trapezoidal domains is investigated.
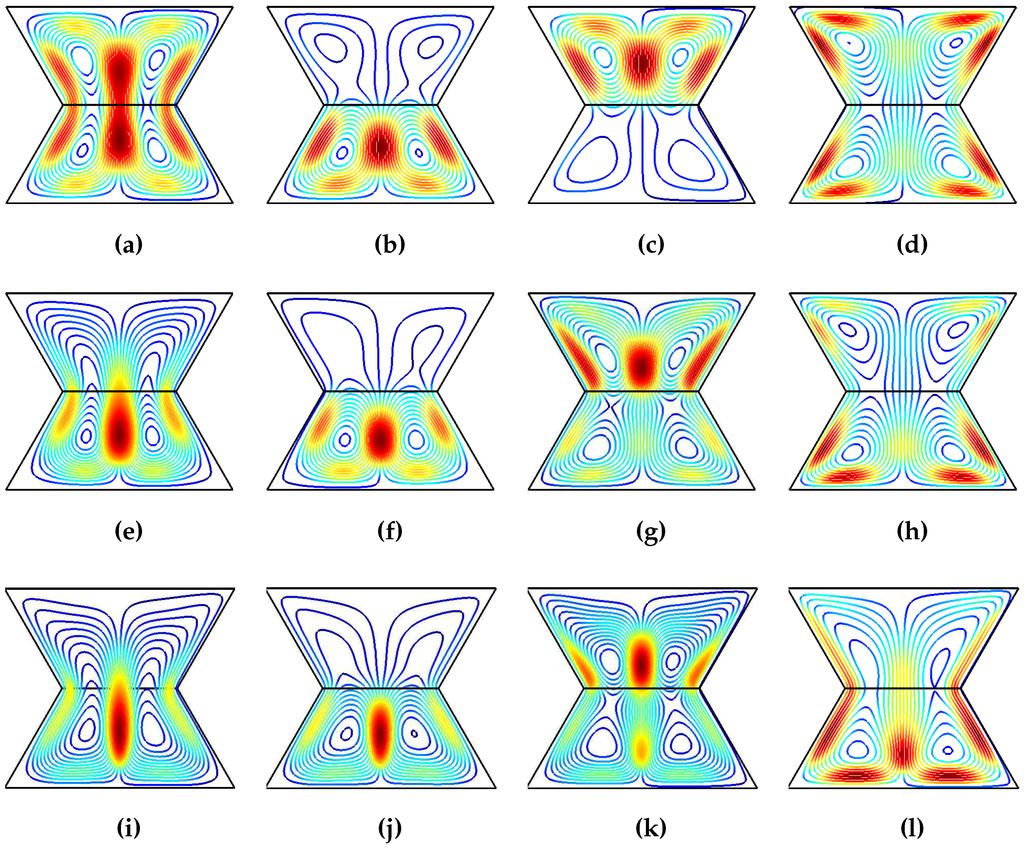
Figure 4.
Effects of varying Rayleigh number on the streamlines for various Hartmann number combinations (), , (a) ; (b) ; (c) ; (d) ; (e) ; (f) ; (g) ; (h) ; (i) ; (j) ; (k) ; (l) .
The influence of varying Rayleigh number on the flow patterns and temperature distribution are demonstrated in Figure 4 and Figure 5 for various Hartmann number combinations of the lower and upper domains (). The upper and lower trapezoidal cavities are occupied by two counter rotating vortcies in the absence of the magnetic field. As the value of the Rayleigh number enhances, the vortex in the upper domain gets distorted and flow motion increases in the lower domain. The flow motion is dampened and the strength of the convection decreases with increasing Hartmann number of the upper domain in the absence of the magnetic field in the lower cavity (Figure 4b–j). When the magnetic field is imposed only in the lower cavity as in Figure 4c,g,k, the flow motion enhances and strength of the convection increases for the lower cavity with higher values of Rayleigh numbers. When imposing magnetic field for the upper trapezoidal domains, the velocity gradient of the upper cavity is much lower than that of the bottom cavity (Figure 4b,f,j) in all Rayleigh number condition. While, when imposing magnetic filed for the lower trapezoidal domains, although the velocity gradient of the bottom cavity is much lower than that of the upper cavity (Figure 4c), the velocity gradient differences between the two cavities in Figure 4g,k are small due to the natual convection effect is more pronounced in the lower trapezoidal cavity compared to upper one. The thermal patterns show the increased effect of natural convection in the absence of magnetic field with increasing Rayleigh numbers as the isotherms show plume like distributions in the interior cavity and steep temperate gradients are seen along the walls of the upper and lower cavities. As the magnetic field is imposed only in the lower (upper) trapezoidal cavity, the isotherm distribution in the upper (lower) cavity slightly effected. The convection is decreased and isotherms become less clustered along the walls of the cavities due to the dampening of the flow motion when the magnetic field is imposed on both domains (Figure 5h,l).
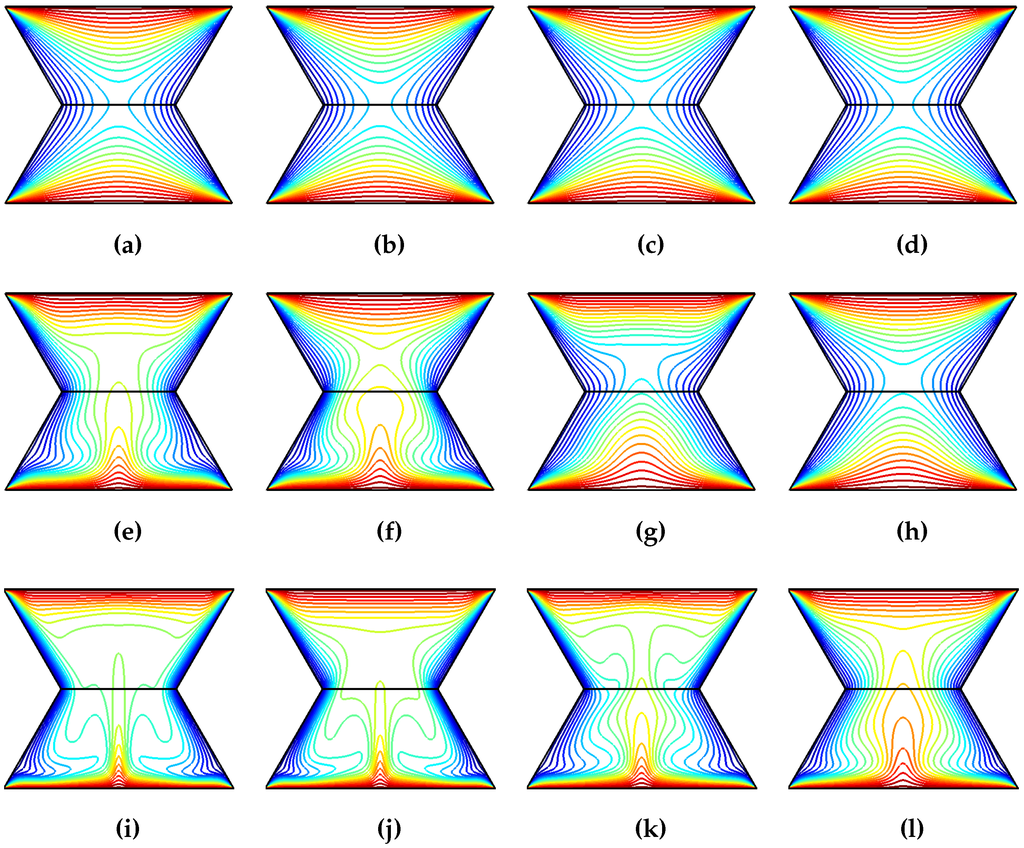
Figure 5.
Isotherms for various Rayleigh numbers and different Hartmann number combinations (), . (a) ; (b) ; (c) ; (d) ; (e) ; (f) ; (g) ; (h) ; (i) ; (j) ; (k) ; (l) .
The local Nusselt number distributions along the bottom (top) and side wall of the lower (upper) cavity are demonstrated in Figure 6 (Figure 7) for various Rayleigh numbers (Ha = 30, Ha = 30, ). Local heat transfer is locally enhanced with Rayleigh number along the bottom wall and the increase is significant from Rayleigh number to . Along the side wall of the lower trapezoidal cavity, at the highest Rayleigh number, the local heat transfer is first increased along the first half of the lower part of the side wall then deteriorates. Along the top wall of the upper domain, heat transfer is enhanced in the parts of the wall at and . Along the side wall of the upper domain, the enhancement in the Nusselt number is noticeable only for Rayleigh number of . The averaged Nusselt number along the top and bottom wall of the trapezoidal cavities are shown in Table 3 for various Rayleigh number and Hartmann number combinations of the domains. The effect of the magnetic field on the reduction of the natural convection of the upper and lower cavities is effective for the highest value of the Rayleigh numbers. Averaged heat transfer decreases by and for the lower and upper cavities at (Ha = 30, Ha = 30) compared to case in the absence of the magnetic field at Rayleigh number of .

Table 3.
Averaged Nusselt number along the bottom and top wall of the domains for various Rayleigh numbers and different Hartmann number combinations ().
| Ra | Ha | Ha | Nu (L1) | Nu (L2) |
|---|---|---|---|---|
| 10 | 0 | 0 | 10.638 | 10.602 |
| 10 | 0 | 20 | 10.635 | 10.604 |
| 10 | 20 | 0 | 10.634 | 10.605 |
| 10 | 30 | 30 | 10.632 | 10.607 |
| 10 | 0 | 0 | 10.737 | 10.553 |
| 10 | 0 | 20 | 10.717 | 10.564 |
| 10 | 20 | 0 | 10.659 | 10.599 |
| 10 | 30 | 30 | 10.639 | 10.601 |
| 10 | 0 | 0 | 13.238 | 9.999 |
| 10 | 0 | 20 | 12.942 | 10.143 |
| 10 | 20 | 0 | 11.177 | 10.603 |
| 10 | 30 | 30 | 10.793 | 10.554 |
| 10 | 0 | 0 | 18.061 | 10.172 |
| 10 | 0 | 20 | 17.753 | 9.671 |
| 10 | 20 | 0 | 16.315 | 10.188 |
| 10 | 30 | 30 | 14.995 | 9.521 |
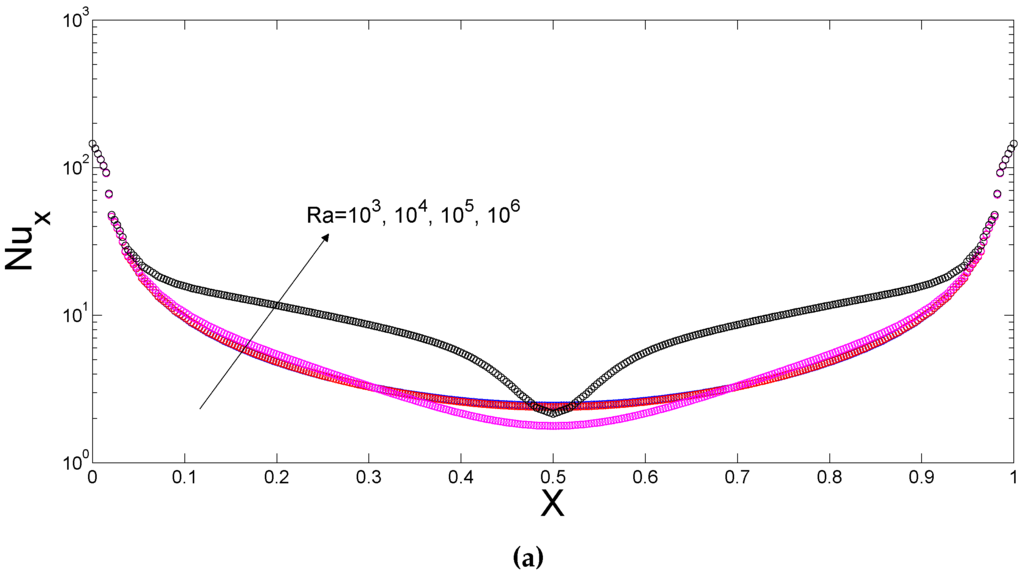
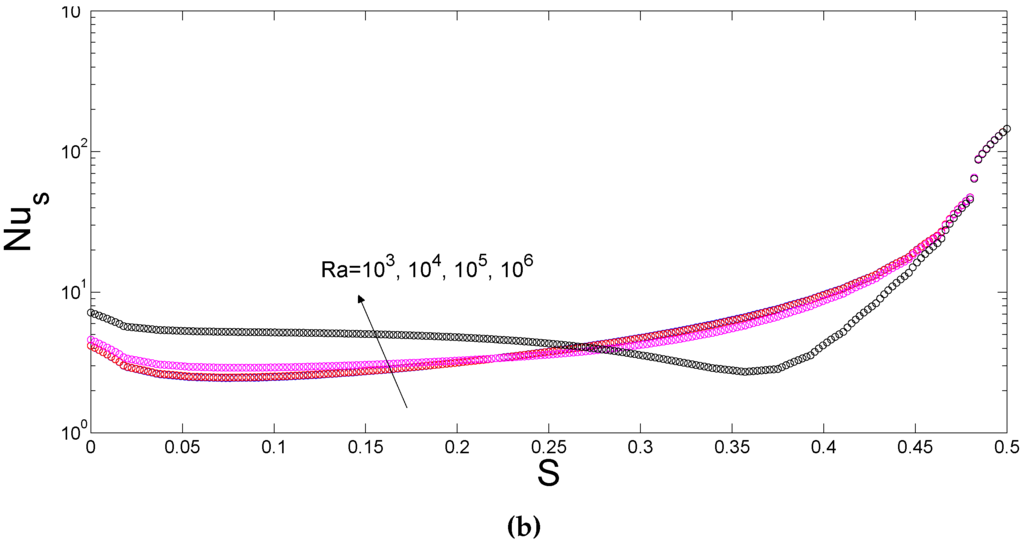
Figure 6.
Local Nusselt number distributions along the bottom and lower side wall for various Rayleigh numbers (). (a) L1; (b) L3.
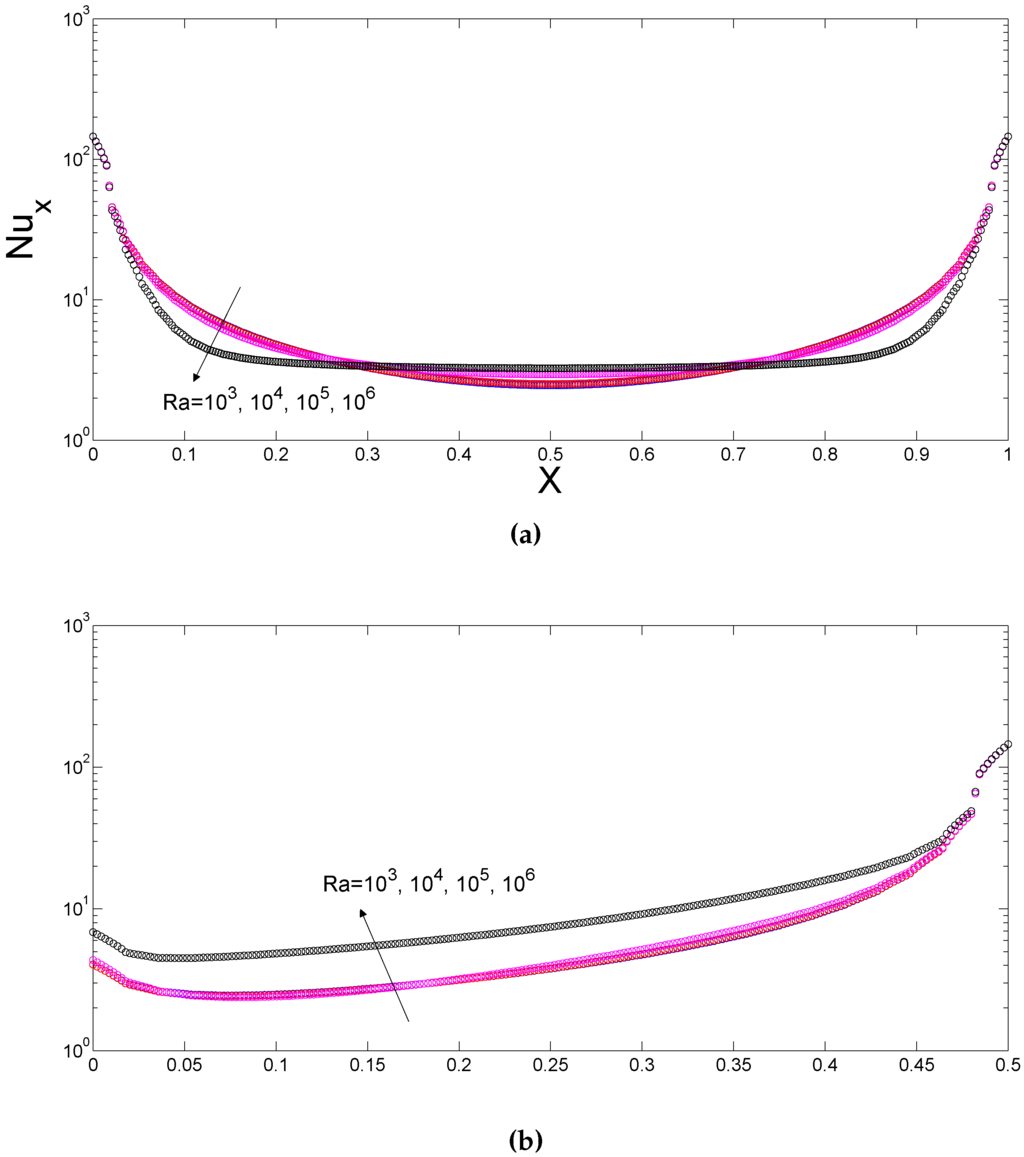
Figure 7.
Local Nusselt number distributions along the top and upper side wall for various Rayleigh numbers (). (a) L2; (b) L4.
The effects of the varying Hartmann number combinations of the upper and lower domains on the flow and thermal patterns are demonstrated in Figure 8 and Figure 9 at fixed values of (Ra = , ). The first row (column) of Figure 8 shows the effect of Hartmann number in the upper (lower) cavity on the flow patterns. In the absence of magnetic field for the lower domain, the flow motion is decreased and convection is strongly dampened in the upper trapezoidal cavity with increasing Hartmann number (Figure 8b,c) whereas the size and the extent of the two counter rotating vortices on the lower cavity are slightly effected. When the magnetic field is imposed only in the lower domain (Figure 8a,d,g), the convection in the lower domain is strongly decreased at the highest value of Hartmann number and the flow motion accelerates and the strength of convection increases in the upper domain. Another interesting result is seen in when Figure 8f is compared with Figure 8i. As the Hartmann number of the first domain is increased from 20 to 50, the upper trapezoidal cavity is occupied with two counter rotating vortices and the maximum value of the streamfuction is decreased in the lower cavity. Isotherms show the reduction of the convection inside the cavities with increasing the magnetic field strength and isotherms are bless clustered along the mid of the bottom wall of the lower and top wall of the upper cavities. The heat transfer process in the lower cavity is effective when the magnetic strength of the upper cavity enhances as seen in Figure 9a,b,c. Temperate gradients become steeper along the top wall of the upper cavity when the Hartmann number of the lower cavity increases as seen in Figure 9a,d,g. The local Nusselt number plots along the bottom (top) and side walls of the lower (upper) cavity are demonstrated in Figure 10 (Figure 11). Increasing the magnetic field strength of the lower cavity deteriorates the local heat transfer along the bottom wall and enhances it partly for locations at and along the top wall of the upper cavity. As the value of the Hartmann number enhances, the local heat transfer along the side wall of the lower trapezoidal cavity generally decreases. The averaged Nusselt numbers along the bottom and top walls of the lower and upper cavities are shown in Table 4. As the value of the magnetic strength of the lower domains decreases, the average heat transfer in that domain is reduced. In the absence of magnetic field in the lower cavity, the averaged Nusselt number enhances with increasing magnetic field strength of the upper cavity. The trend of decreasing heat transfer with magnetic field is seen for the Hartmann number of the first domain which is greater than 10. The averaged Nusselt number is reduced by for the lower domain and enhanced by for the upper domain at Hartmann number pairs of (Ha = 50, Ha = 0) compared to case in the absence of magnetic field.

Table 4.
Averaged Nusselt number distributions along the bottom and top walls of the trapezoidal domains for various Hartmann numbers of the domains ().
| Ha | Ha | Nu (L1) | Nu (L2) |
|---|---|---|---|
| 0 | 0 | 13.245 | 9.996 |
| 0 | 10 | 13.112 | 9.976 |
| 0 | 20 | 12.949 | 10.137 |
| 0 | 30 | 12.877 | 10.242 |
| 0 | 50 | 12.819 | 10.329 |
| 10 | 0 | 12.370 | 10.172 |
| 10 | 10 | 12.300 | 10.124 |
| 10 | 20 | 12.208 | 10.217 |
| 10 | 30 | 12.165 | 10.292 |
| 10 | 50 | 12.130 | 10.363 |
| 20 | 0 | 11.180 | 10.606 |
| 20 | 10 | 11.174 | 10.521 |
| 20 | 20 | 11.163 | 10.464 |
| 20 | 30 | 11.156 | 10.457 |
| 20 | 50 | 11.149 | 10.471 |
| 30 | 0 | 10.816 | 10.748 |
| 30 | 10 | 10.810 | 10.667 |
| 30 | 20 | 10.801 | 10.585 |
| 30 | 30 | 10.794 | 10.555 |
| 30 | 50 | 10.787 | 10.546 |
| 50 | 0 | 10.716 | 10.796 |
| 50 | 10 | 10.708 | 10.720 |
| 50 | 20 | 10.696 | 10.635 |
| 50 | 30 | 10.686 | 10.599 |
| 50 | 50 | 10.675 | 10.583 |
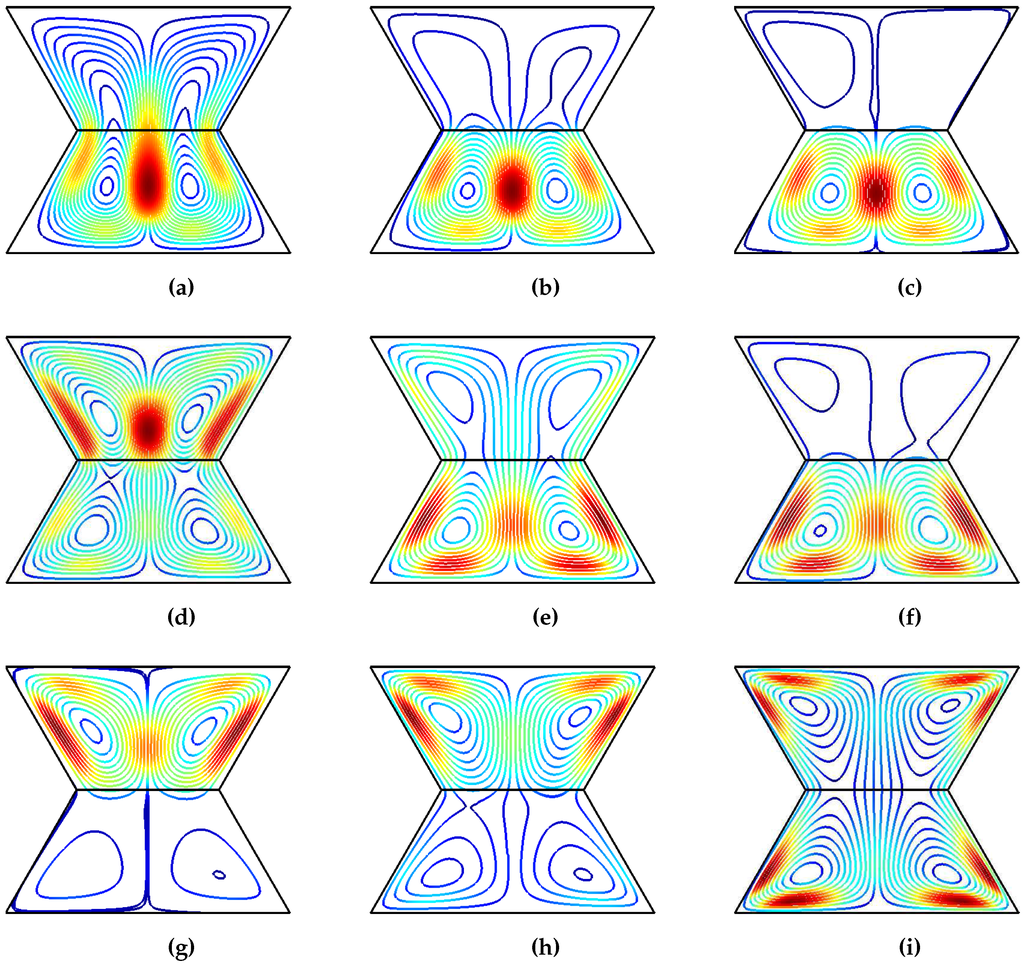
Figure 8.
Effects of varying Hartmann numbers of the upper and lower domains on the streamline distributions (), (a) ; (b) ; (c) ; (d) ; (e) ; (f) ; (g) ; (h) ; (i) .
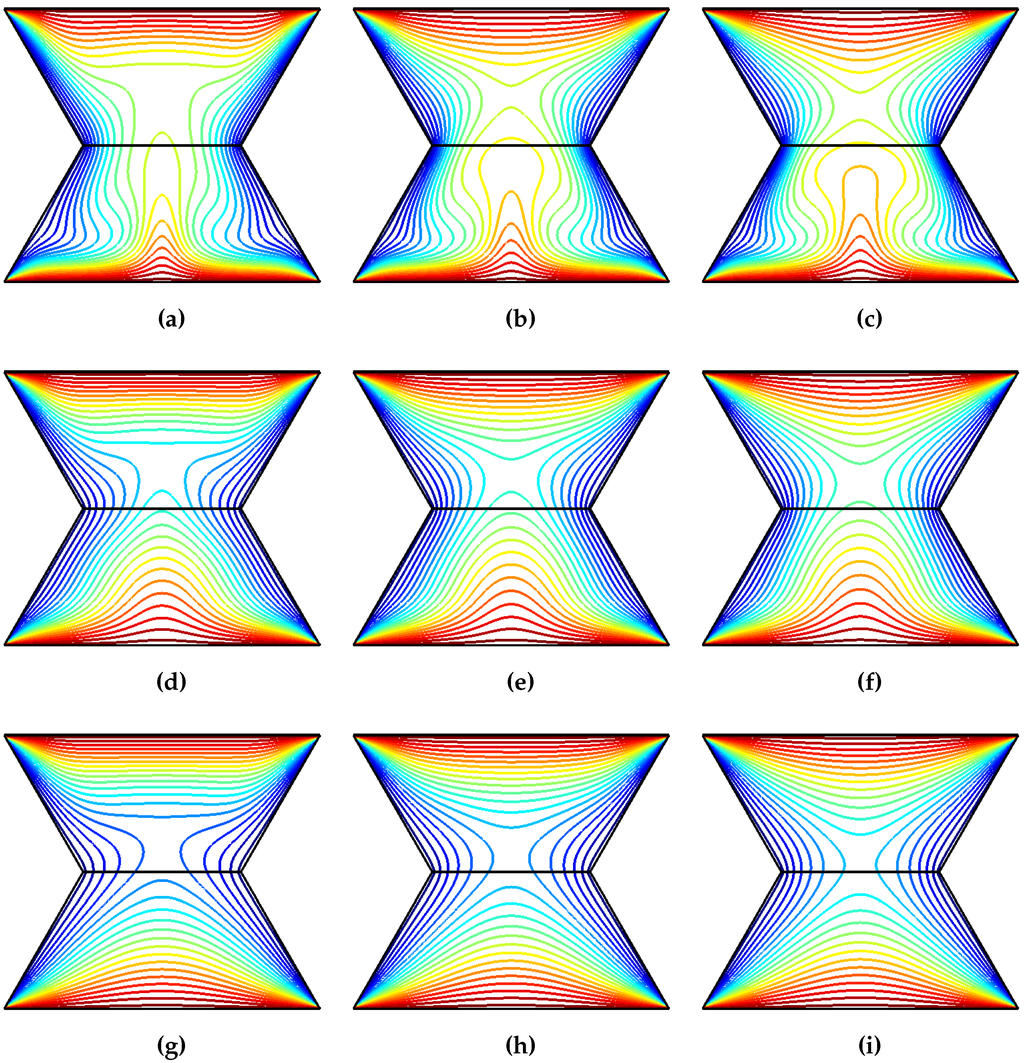
Figure 9.
Effects of varying Hartmann numbers of the upper and lower domains on the isotherm distributions (), (a) ; (b) ; (c) ; (d) ; (e) ; (f) ; (g) ; (h) ; (i) .
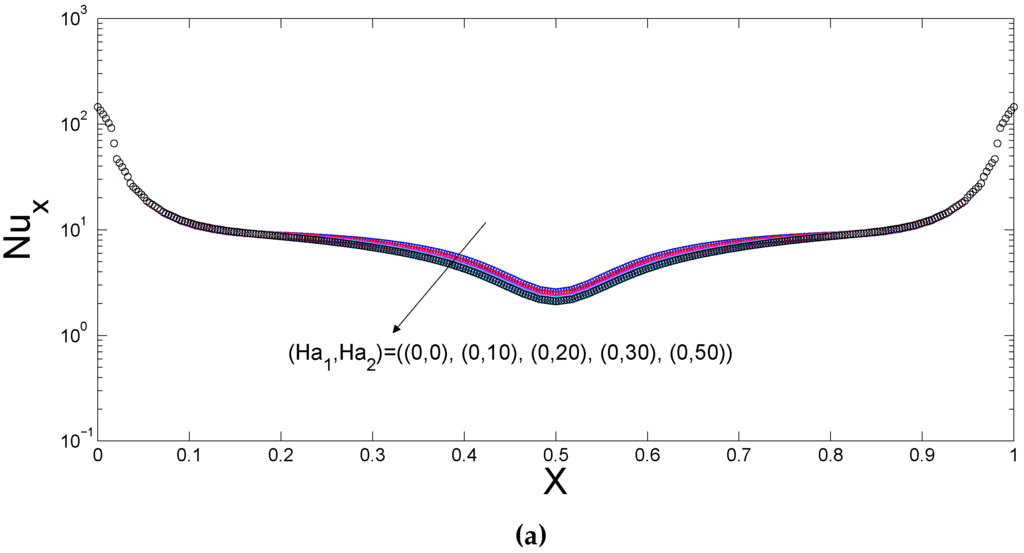
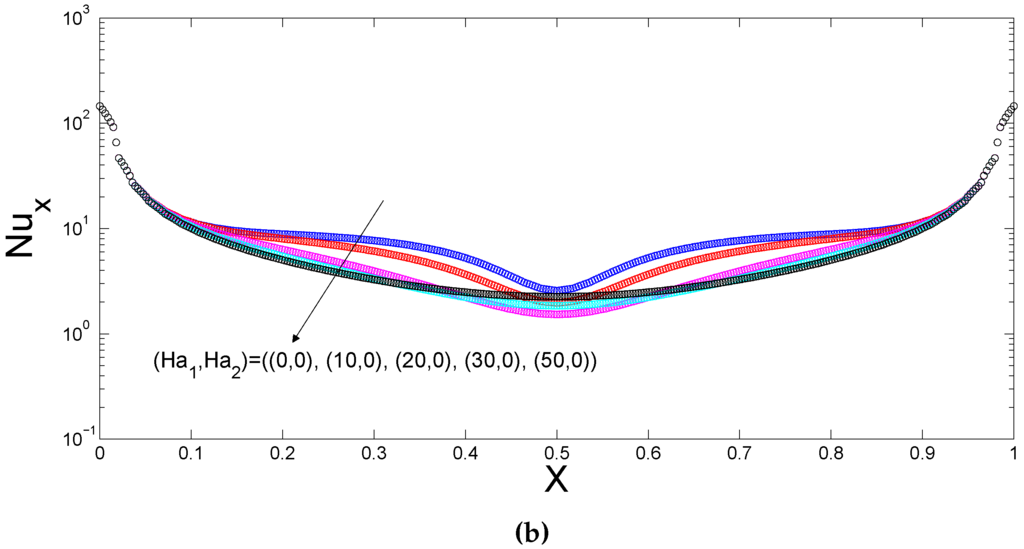
Figure 10.
Local Nusselt number distributions along the bottom and lower side wall for various Hartmann numbers of the upper and lower domains (), (a) L1; (b) L3.
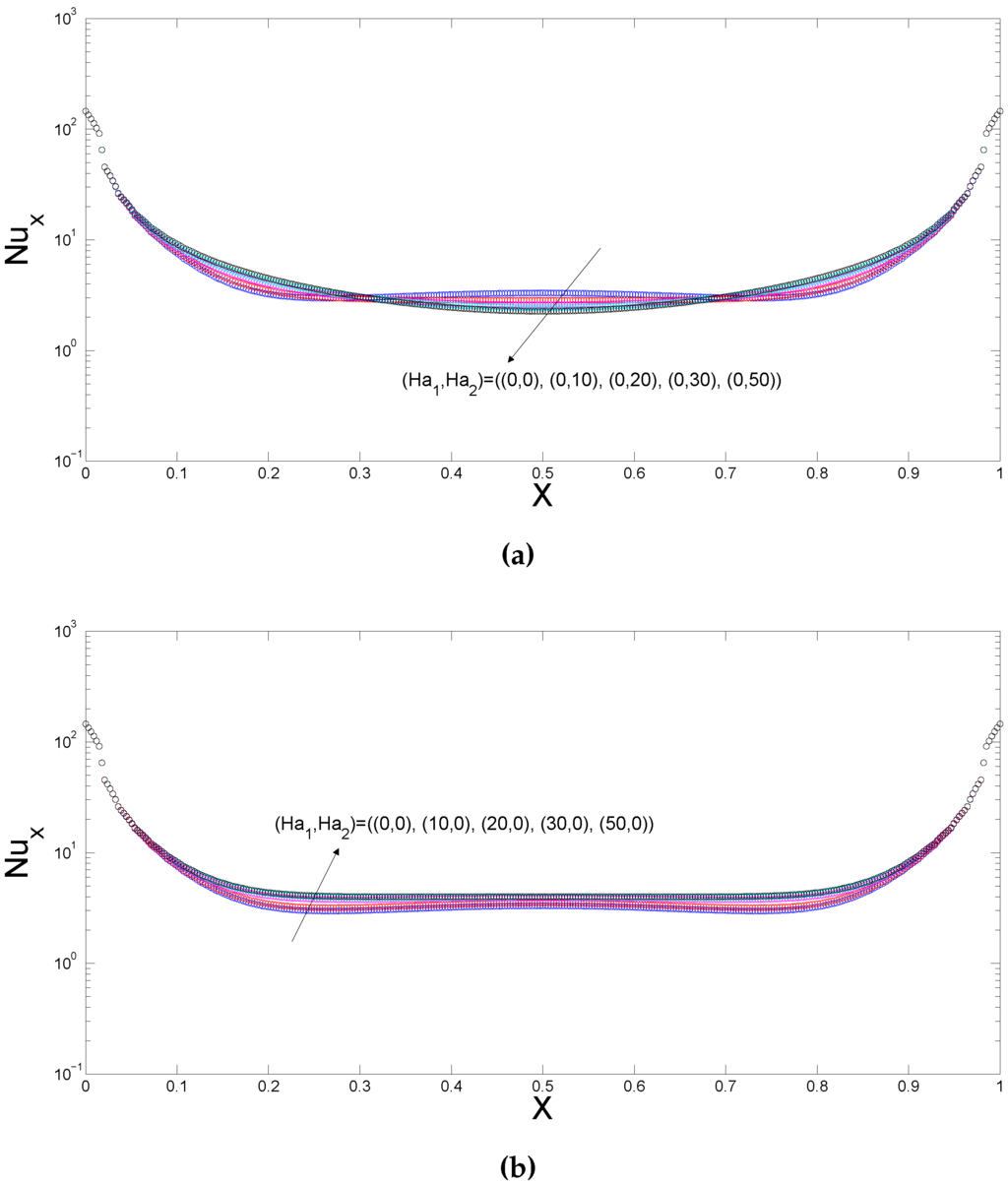
Figure 11.
Local Nusselt number distributions along the top and upper side wall for various Hartmann numbers of the upper and lower domains (), (a) L2; (b) L4.
AlO and CuO nanoparticles of different solid volume fractions are added to the base fluids in the lower and upper cavities by the same amount which is denoted by ϕ. Nanoparticles enhance the thermal conductivity of the base fluid which results in better convection characteristics inside the cavities. Table 5 and Table 6 represent the average Nusselt number distributions along the bottom and top wall of the triangular cavities for various nanoparticle volume fraction and Hartmann numbers for fixed value of and , respectively. The averaged heat transfer enhancements are in the range of 10% and 12% for the highest nanoparticle volume fraction compared to base fluid at . The enhancements in the heat transfer are higher for the bottom wall of the lower cavity as compared to top wall of the upper cavity where heat transfer process is less effective. Heat transfer enhancement rate with nanofluids is not affected with the presence of the magnetic field.

Table 5.
Effects of nanoparticle volume fraction on the average Nusselt number for various Hartmann numbers of the upper and lower trapezoidal domains ().
| φ | Ha | Ha | Nu (L1) | Nu (L2) |
|---|---|---|---|---|
| 0 | 0 | 0 | 10.993 | 9.954 |
| 0.01 | 0 | 0 | 11.316 | 10.213 |
| 0.02 | 0 | 0 | 11.644 | 10.478 |
| 0.03 | 0 | 0 | 11.977 | 10.749 |
| 0.04 | 0 | 0 | 12.315 | 11.025 |
| 0 | 0 | 20 | 10.921 | 10.00 |
| 0.01 | 0 | 20 | 11.241 | 10.263 |
| 0.02 | 0 | 20 | 11.565 | 10.531 |
| 0.03 | 0 | 20 | 11.893 | 10.804 |
| 0.04 | 0 | 20 | 12.227 | 11.082 |
| 0 | 20 | 0 | 10.478 | 10.163 |
| 0.01 | 20 | 0 | 10.776 | 10.438 |
| 0.02 | 20 | 0 | 11.079 | 10.717 |
| 0.03 | 20 | 0 | 11.388 | 11.001 |
| 0.04 | 20 | 0 | 11.702 | 11.292 |
| 0 | 30 | 30 | 10.438 | 10.139 |
| 0.01 | 30 | 30 | 10.734 | 10.409 |
| 0.02 | 30 | 30 | 11.035 | 10.685 |
| 0.03 | 30 | 30 | 11.342 | 10.965 |
| 0.04 | 30 | 30 | 11.655 | 11.251 |

Table 6.
Effects of nanoparticle volume fraction on the average Nusselt number for various Hartmann numbers of the upper and lower trapezoidal domains ().
| φ | Ha | Ha | Nu (L1) | Nu (L2) |
|---|---|---|---|---|
| 0 | 0 | 0 | 16.283 | 10.043 |
| 0.01 | 0 | 16.758 | 16.299 | 10.318 |
| 0.02 | 0 | 0 | 17.240 | 10.599 |
| 0.03 | 0 | 0 | 17.728 | 10.885 |
| 0.04 | 0 | 0 | 18.222 | 11.176 |
| 0 | 0 | 20 | 15.918 | 9.739 |
| 0.01 | 0 | 20 | 16.394 | 9.990 |
| 0.02 | 0 | 20 | 16.876 | 10.247 |
| 0.03 | 0 | 20 | 17.364 | 10.510 |
| 0.04 | 0 | 20 | 17.857 | 10.779 |
| 0 | 20 | 0 | 14.438 | 10.180 |
| 0.01 | 20 | 0 | 14.863 | 10.461 |
| 0.02 | 20 | 0 | 15.293 | 10.747 |
| 0.03 | 20 | 0 | 15.727 | 11.038 |
| 0.04 | 20 | 0 | 16.166 | 11.336 |
| 0 | 30 | 30 | 13.022 | 9.992 |
| 0.01 | 30 | 30 | 13.411 | 10.248 |
| 0.02 | 30 | 30 | 13.803 | 10.509 |
| 0.03 | 30 | 30 | 14.199 | 10.777 |
| 0.04 | 30 | 30 | 14.599 | 11.052 |
The total entropy generation of the upper and lower trapezoidal domains are normalized with the configurations when there is no magnetic field at Ha = 0 () or when there is only base fluid at (). Figure 12a,b demonstrates the influence of varying Hartmann number and nanoparticle volume fraction on the variation of the normalized entropy generation of the upper and lower domains. Fluid motion is dampened and strength of the convection is reduced with the increase of the magnetic field strength for both domains. There is slightly change in the entropy generation for Hartmann number higher than 30 in the lower domain and for Hartmann number higher than 20 in the upper domain. This is due to the fact that conduction is the dominant heat transfer mechanism in the cavities for those cases and there is slightly change of convection in the cavities and there si slightly change of gradients of the velocities and temperature. The normalized entropy generation enhances as the solid volume fraction of the nanoparticles increases. Steep temperature gradients are seen adjacent to the hot and cold walls of the cavities as the solid volume fraction increases. The increment of the effective thermal conductivity and viscosity of the nanofluid results in heat transfer enhancement and fluid friction irreversibility and therefore the total entropy generation of the domains increases with ϕ.
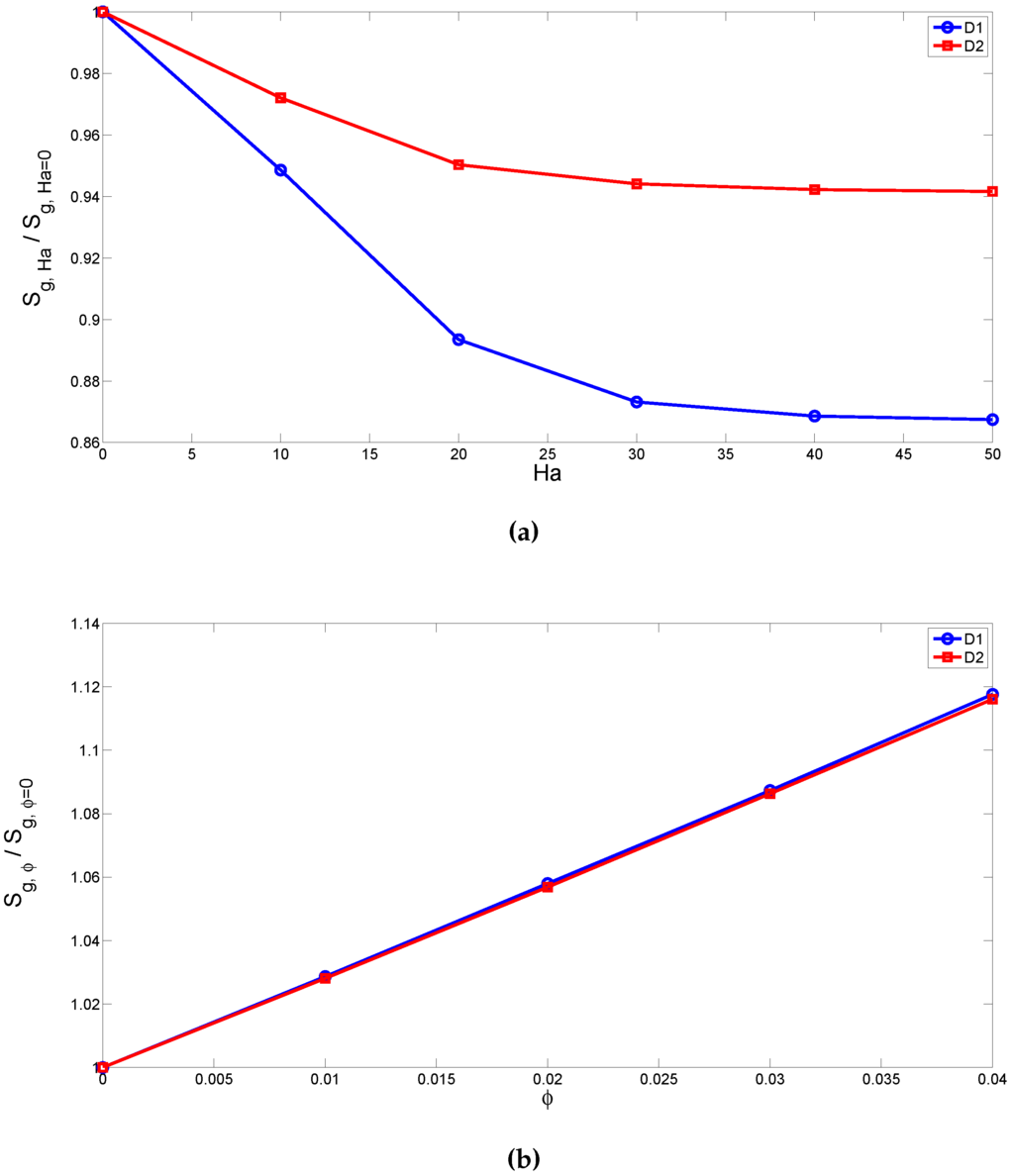
Figure 12.
Normalized entropy generation for the upper and lower trapezoidal domains, (a) for and various Hartmann numbers; (b) for , Ha = Ha = 10 and various nanoparticle volume fractions.
Table 7 shows the normalized entropy generation for various Hartmann number combinations of the upper and lower domains. The entropy generation ratio decreases with Hartmann number and this is more pronounced for the lower domain. At the higher values of the Hartmann numbers, the entropy generation ratio remains relatively constant for both domains.

Table 7.
Normalized entropy generation for lower and upper trapezoidal domains for various Hartmann numbers of the domains ().
| Ha | Ha | S* (D1) | S* (D2) |
|---|---|---|---|
| 0 | 0 | 1.0000 | 1.0000 |
| 0 | 10 | 1.0029 | 0.9811 |
| 0 | 20 | 1.0087 | 0.9716 |
| 0 | 30 | 1.0145 | 0.9703 |
| 0 | 50 | 1.0174 | 0.9685 |
| 10 | 0 | 0.9449 | 0.9905 |
| 10 | 10 | 0.9478 | 0.9716 |
| 10 | 20 | 0.9536 | 0.9653 |
| 10 | 30 | 0.9594 | 0.9621 |
| 10 | 50 | 0.9652 | 0.9590 |
| 20 | 0 | 0.8922 | 0.9685 |
| 20 | 10 | 0.8928 | 0.9621 |
| 20 | 20 | 0.8942 | 0.9527 |
| 20 | 30 | 0.8957 | 0.9495 |
| 20 | 50 | 0.8971 | 0.9464 |
| 30 | 0 | 0.8725 | 0.9685 |
| 30 | 10 | 0.8725 | 0.9590 |
| 30 | 20 | 0.8725 | 0.9502 |
| 30 | 30 | 0.8739 | 0.9464 |
| 30 | 50 | 0.8754 | 0.9432 |
| 50 | 0 | 0.8693 | 0.9685 |
| 50 | 10 | 0.8690 | 0.9590 |
| 50 | 20 | 0.8684 | 0.9495 |
| 50 | 30 | 0.8681 | 0.9461 |
| 50 | 50 | 0.8681 | 0.9435 |

Table 8.
Effects of nanoparticle volume fraction on the entropy generation ratio for various Hartmann numbers of the upper and lower trapezoidal domains ().
| φ | Ha | Ha | S* (D1) | S* (D2) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1.0000 | 1.0000 |
| 0.01 | 0 | 0 | 1.0292 | 1.0277 |
| 0.02 | 0 | 0 | 1.0584 | 1.0563 |
| 0.03 | 0 | 0 | 1.0882 | 1.0856 |
| 0.04 | 0 | 0 | 1.1185 | 1.1154 |
| 0 | 0 | 20 | 1.0022 | 0.9961 |
| 0.01 | 0 | 20 | 1.0308 | 1.0236 |
| 0.02 | 0 | 20 | 1.0639 | 1.0514 |
| 0.03 | 0 | 20 | 1.0904 | 1.0802 |
| 0.04 | 0 | 20 | 1.1185 | 1.1088 |
| 0 | 20 | 0 | 0.9713 | 0.9956 |
| 0.01 | 20 | 0 | 0.9989 | 1.0235 |
| 0.02 | 20 | 0 | 1.0271 | 1.0518 |
| 0.03 | 20 | 0 | 1.0552 | 1.0806 |
| 0.04 | 20 | 0 | 1.0844 | 1.1099 |
| 0 | 30 | 30 | 0.9708 | 0.9901 |
| 0.01 | 30 | 30 | 0.9978 | 1.0172 |
| 0.02 | 30 | 30 | 1.0260 | 1.0448 |
| 0.03 | 30 | 30 | 1.0541 | 1.0729 |
| 0.04 | 30 | 30 | 1.0833 | 1.1016 |
The influence of varying nanoparticle volume fractions on the variation of the normalized entropy generation for various Hartmann number combinations of both domains is show in Table 8. The entropy generation ratio increases more in the absence of the magnetic field as the solid nanoparticle volume fraction increases even though the contribution of the entropy generation due to the magnetic field decreases. This is due to the contribution of entropy generation due to the heat transfer is higher compared to other terms in the entropy generation equation (Equation (5)).
5. Conclusions
In this study, MHD natural convection and entropy generation in entrapped trapezoidal cavities filled with different nanofluids is numerically investigated. Some important conclusions from the numerical simulation results can be drawn as:
- At the highest value of the Rayleigh number, the magnetic field is more effective on the reduction of the natural convection of the upper and lower cavities.
- When the Hartmann number of the lower cavity incraeses, the local heat transfer along the bottom wall is deteriorated and it is enhanced partly for locations at and along the top wall of the upper cavity.
- In the absence of magnetic field in the lower cavity, the averaged heat transfer increases with increasing values of the Hartmann number of the upper cavity. When the Hatmann number of the lower cavity is greater than 10, convection is reduced for the upper domain.
- The averaged Nusselt number increments are in the range of 10% and 12% for the highest solid volume fraction of the nanoparticle compared to base fluid. The heat transfer enhancement rates with nanofluids are not influenced by the presence of the magnetic field.
- The normalized entropy generation increases with increasing values of solid volume fraction of the nanoparticles and decreasing values of magnetic field strength for both domains. The entropy generation ratio decreases for the lower trapezoidal domain is more pronounced compared to upper one with increasing Hartmann number.
Author Contributions
Fatih Selimefendigil performed the numerical simulations and wrote some sections of the manuscript. Hakan F. Öztop and Nidal Abu-Hamdeh prepared some other sections of the paper and analyzed the numerical experiments. All of the authors contributed equally for reviewing and revising the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| B magnetic field strength |
| Gr Grashof number, |
| h local heat transfer coefficient, (W/mK) |
| Ha Hartmann number, |
| k thermal conductivity, (W/m·K) |
| H length of the enclosure, (m) |
| n unit normal vector |
| Nu local Nusselt number |
| p pressure, (Pa) |
| P non-dimensional pressure |
| Pr Prandtl number, |
| T temperature, (K) |
| u, v x-y velocity components, (m/s) |
| x, y Cartesian coordinates, (m) |
| X, Y dimensionless coordinates |
| Greek Characters |
| α thermal diffusivity, (m/s) |
| β expansion coefficient, (1/K) |
| ϕ nanoparticle volume fraction |
| θ non-dimensional temperature, |
| ν kinematic viscosity, (m/s) |
| ρ density of the fluid, (kg/m) |
| γ strength of the dipole |
| σ electrical conductivity, (S/m) |
| Subscripts |
| c cold wall |
| m average |
| h hot wall |
References
- Ostrach, S. Natural convection in enclosures. J. Heat Transf. 1988, 110, 1175–1190. [Google Scholar] [CrossRef]
- Natarajan, E.; Roy, S.; Basak, T. Effect of Various Thermal Boundary Conditions on Natural Convection in a Trapezoidal Cavity with Linearly Heated Side Wall(s). Numer. Heat Transf. Part B 2007, 52, 551–568. [Google Scholar] [CrossRef]
- Fontana, É.; da Silva, A.; Mariani, V.C.; Marcondes, F. The Influence of Baffles on the Natural Convection in Trapezoidal Cavities. Numer. Heat Transf. Part A 2010, 58, 125–145. [Google Scholar] [CrossRef]
- Moukalled, F.; Darwish, M. Natural Convection in a Partitioned Trapezoidal Cavity Heated from the Side. Numer. Heat Transf. Part A 2003, 43, 543–563. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Basak, T.; Öztop, H.F.; Varol, Y. Mixed convection and role of multiple solutions in lid-driven trapezoidal enclosures. Int. J. Heat Mass Transf. 2013, 63, 366–388. [Google Scholar] [CrossRef]
- Basak, T.; Roy, S.; Pop, I. Heat flow analysis for natural convection within trapezoidal enclosures based on heatline concept. Int. J. Heat Mass Transf. 2009, 52, 2471–2483. [Google Scholar] [CrossRef]
- Basak, T.; Roy, S.; Singh, S.K.; Pop, I. Finite element simulation of natural convection within porous trapezoidal enclosures for various inclination angles: Effect of various wall heating. Int. J. Heat Mass Transf. 2009, 52, 4135–4150. [Google Scholar] [CrossRef]
- Da Silva, A.; Fontana, É.; Mariani, V.C.; Marcondes, F. Numerical investigation of several physical and geometric parameters in the natural convection into trapezoidal cavities. Int. J. Heat Mass Transf. 2012, 55, 6808–6818. [Google Scholar] [CrossRef]
- Varol, Y. Natural convection in divided trapezoidal cavities filled with fluid saturated porous media. Int. Commun. Heat Mass Transf. 2010, 37, 1350–1358. [Google Scholar] [CrossRef]
- Natarajan, E.; Basak, T.; Roy, S. Natural convection flows in a trapezoidal enclosure with uniform and non-uniform heating of bottom wall. Int. J. Heat Mass Transf. 2008, 51, 747–756. [Google Scholar] [CrossRef]
- Van der Eyden, J.T.; van der Meer, T.H.; Hanjalić, K. Double-diffusive natural convection in trapezoidal enclosures. Inf. J. Heat Mass Transf. 1998, 41, 1885–1898. [Google Scholar] [CrossRef]
- Sathiyamoorthy, M.; Chamkha, A. Effect of magnetic field on natural convection flow in a liquid gallium filled square cavity for linearly heated side walls. Int. J. Therm. Sci. 2010, 49, 1856–1865. [Google Scholar] [CrossRef]
- Chamkha, A.J. Unsteady MHD convective heat and mass transfer past a semi-infinite vertical permeable moving plate with heat absorption. Int. J. Eng. Sci. 2004, 42, 217–230. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Forced convection of ferrofluids in a vented cavity with a rotating cylinder. Int. J. Therm. Sci. 2014, 86, 258–275. [Google Scholar] [CrossRef]
- Rahman, M.; Alim, M.; Sarker, M. Numerical study on the conjugate effect of joule heating and magnato-hydrodynamics mixed convection in an obstructed lid-driven square cavity. Int. Commun. Heat Mass Transf. 2010, 37, 524–534. [Google Scholar] [CrossRef]
- Yu, P.; Qiu, J.; Qin, Q.; Tian, Z. Numerical investigation of natural convection in a rectangular cavity under different directions of uniform magnetic field. Int. J. Heat Mass Transf. 2013, 67, 1131–1144. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.; Soleimani, S.; Seyyedi, S.M. Natural convection of nanofluids in an enclosure between a circular and a sinusoidal cylinder in the presence of magnetic field. Int. Commun. Heat Mass Transf. 2012, 39, 1435–1443. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Effect of a rotating cylinder in forced convection of ferrofluid over a backward facing step. Int. J. Heat Mass Transf. 2014, 71, 142–148. [Google Scholar] [CrossRef]
- Öztop, H.F.; Al-Salem, K.; Pop, I. MHD mixed convection in a lid-driven cavity with corner heater. Int. J. Heat Mass Transf. 2011, 54, 3494–3504. [Google Scholar] [CrossRef]
- Hasanuzzaman, M.; Öztop, H.F.; Rahman, M.; Rahim, N.; Saidur, R.; Varol, Y. Magnetohydrodynamic natural convection in trapezoidal cavities. Int. Commun. Heat Mass Transf. 2012, 39, 1384–1394. [Google Scholar] [CrossRef]
- Hossain, M.S.; Alim, M.A. MHD free convection within trapezoidal cavity with non-uniformly heated bottom wall. Int. J. Heat Mass Transf. 2014, 69, 327–336. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Mixed convection in a two-sided elastic walled and SiO2 nanofluid filled cavity with internal heat generation: Effects of inner rotating cylinder and nanoparticle’s shape. J. Mol. Liq. 2015, 212, 509–516. [Google Scholar] [CrossRef]
- Li, G.; Aktas, M.; Bayazitoglu, Y. A Review on the Discrete Boltzmann Model for Nanofluid Heat Transfer in Enclosures and Channels. Numer. Heat Transf. Part B 2015, 67, 463–488. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Identification of forced convection in pulsating flow at a backward facing step with a stationary cylinder subjected to nanofluid. Int. Commun. Heat Mass Transf. 2013, 45, 111–121. [Google Scholar] [CrossRef]
- Rahman, M.M.; Saha, S.; Mojumder, S.; Naim, A.G.; Saidur, R.; Ibrahim, T.A. Effect of Sine-Squared Thermal Boundary Condition on Augmentation of Heat Transfer in a Triangular Solar Collector Filled with Different Nanofluids. Numer. Heat Transf. Part B 2015, 68, 53–74. [Google Scholar] [CrossRef]
- Wang, P.; Bai, M.; Lv, J.; Zhang, L.; Cui, W.; Li, G. Comparison of Multidimensional Simulation Models for Nanofluids Flow Characteristics. Numer. Heat Transf. Part B 2013, 63, 62–83. [Google Scholar]
- Selimefendigil, F.; Öztop, H.F. Pulsating nanofluids jet impingement cooling of a heated horizontal surface. Int. J. Heat Mass Transf. 2014, 69, 54–65. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Gros, T.; Pop, I. Steady-state free convection in right-angle porous trapezoidal cavity filled by a nanofluid: Buongiorno’s mathematical model. Eur. J. Mech. B-Fluid. 2015, 53, 241–250. [Google Scholar] [CrossRef]
- Sheremet, M.; Pop, I.; Rahman, M. Three-dimensional natural convection in a porous enclosure filled with a nanofluid using Buongiorno’s mathematical model. Int. J. Heat Mass Transf. 2015, 82, 396–405. [Google Scholar] [CrossRef]
- Kefayati, G.R. Simulation of Ferrofluid Heat Dissipation Effect on Natural Convection at an Inclined Cavity Filled with Kerosene/Cobalt Utilizing the Lattice Boltzmann Method. Numer. Heat Transf. Part A 2014, 65, 509–530. [Google Scholar] [CrossRef]
- Ghasemi, B.; Aminossadati, S.M.; Raisi, A. Magnetic field effect on natural convection in a nanofluid-filled square enclosure. Int. J. Therm. Sci. 2011, 50, 1748–1756. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.D. Numerical investigation of MHD effects on Al2O3-water nanofluid flow and heat transfer in a semi-annulus enclosure using LBM. Energy 2013, 60, 501–510. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Numerical study of MHD mixed convection in a nanofluid filled lid driven square enclosure with a rotating cylinder. Int. J. Heat Mass Transf. 2014, 78, 741–754. [Google Scholar] [CrossRef]
- Sarkar, S.; Ganguly, S.; Biswas, G. Buoyancy Driven Convection of Nanofluids in an Infinitely Long Channel under the Effect of a Magnetic Field. Int. J. Heat Mass Transf. 2014, 71, 328–340. [Google Scholar] [CrossRef]
- Mahmoudi, A.H.; Pop, I.; Shahi, M. Effect of magnetic field on natural convection in a triangular enclosure filled with nanofluid. Int. J. Therm. Sci. 2012, 59, 126–140. [Google Scholar] [CrossRef]
- Basak, T.; Gunda, P.; Anandalakshmi, R. Analysis of entropy generation during natural convection in porous right-angled triangular cavities with various thermal boundary conditions. Int. J. Heat Mass Transf. 2012, 55, 4521–4535. [Google Scholar] [CrossRef]
- Basak, T.; Anandalakshmi, R.; Gunda, P. Role of entropy generation during convective thermal processing in right-angled triangular enclosures with various wall heatings. Chem. Eng. Res. Des. 2012, 90, 1779–1799. [Google Scholar] [CrossRef]
- Varol, Y.; Öztop, H.F.; Pop, I. Entropy generation due to natural convection in non-uniformly heated porous isosceles triangular enclosures at different positions. Int. J. Heat Mass Transf. 2009, 52, 1193–1205. [Google Scholar] [CrossRef]
- Bhardwaj, S.; Dalal, A. Analysis of natural convection heat transfer and entropy generation inside porous right-angled triangular enclosure. Int. J. Heat Mass Transf. 2013, 65, 500–513. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Natural convection and entropy generation of nanofluid filled cavity having different shaped obstacles under the influence of magnetic field and internal heat generation. J. Taiwan Inst. Chem. Eng. 2015, 56, 42–56. [Google Scholar] [CrossRef]
- Bejan, A. Second law analysis in heat transfer. Energy 1980, 5, 720–732. [Google Scholar] [CrossRef]
- Öztop, H.F.; Al-Salem, K. A review on entropy generation in natural and mixed convection heat transfer for energy systems. Renew. Sustain. Energy Rev. 2012, 16, 911–920. [Google Scholar] [CrossRef]
- Mahian, O.; Öztop, H.; Pop, I.; Mahmud, S.; Wongwises, S. Entropy generation between two vertical cylinders in the presence of MHD flow subjected to constant wall temperature. Int. Commun. Heat Mass Transf. 2013, 44, 87–92. [Google Scholar] [CrossRef]
- Esmaeilpour, M.; Abdollahzadeh, M. Free convection and entropy generation of nanofluid inside an enclosure with different patterns of vertical wavy walls. Int. J. Therm. Sci. 2012, 52, 127–136. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kleinstreuer, C.; Al-Nimr, M.A.; Pop, I.; Sahin, A.Z.; Wongwises, S. A review of entropy generation in nanofluid flow. Int. J. Heat Mass Transf. 2013, 65, 514–532. [Google Scholar] [CrossRef]
- Hajialigol, N.; Fattahi, A.; Ahmadi, M.H.; Qomi, M.E.; Kakoli, E. MHD mixed convection and entropy generation in a 3-D microchannel using Al2O3-water nanofluid. J. Taiwan Inst. Chem. Eng. 2015, 46, 30–42. [Google Scholar] [CrossRef]
- Ramakrishna, D.; Basak, T.; Roy, S.; Momoniat, E. Analysis of thermal efficiency via analysis of heat flow and entropy generation during natural convection within porous trapezoidal cavities. Int. J. Heat Mass Transf. 2014, 77, 98–113. [Google Scholar] [CrossRef]
- Varol, Y. Natural convection for hot materials confined within two entrapped porous trapezoidal cavities. Int. Commun. Heat Mass Transf. 2012, 39, 282–290. [Google Scholar] [CrossRef]
- Basak, T.; Roy, S.; Ramakrishna, D.; Pandey, B.D. Analysis of heat recovery and heat transfer within entrapped porous triangular cavities via heatline approach. Int. J. Heat Mass Transf. 2010, 53, 3655–3669. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Laminar nanofluid flow in microheat-sinks. Int. J. Heat Mass Transf. 2005, 48, 2652–2661. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Oxford University Press: Oxford, UK, 1873. [Google Scholar]
- Brinkman, H.C. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571–581. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).