In order to test the performance of the NBAME model, after collecting and preprocessing the games’ statistics, we turn to the problem of predicting the outcomes of NBA playoff games for each season individually from the 2007–08 season to the 2014–15 season. We made experiments with the dataset using the NBAME model and some other machine learning algorithms.
4.1. Data Collection and Preprocessing
We created a crawler program to extract the 14 basic technical features of both teams and the home team’s win or loss from
http://www.stat-nba.com/, collected a total of 10,271 records for all games for seasons ranging from the 2007–08 season to the 2014–15 season, and stored them into a MySQL database.
After the original data set was obtained, we cleaned it using Java 1.7. First, we combined the two teams’ 14 basic technical features of the same game into a single record for the game. The features of a game therefore contained 28 basic technical features and a label indicating a win or loss for the home team. Secondly, we calculated the mean of each basic technical feature from the most recent six games prior to the candidate game being predicted. If teams didn’t have at least six games before the game started, we took the mean of the basic technical feature for any games prior to the candidate game. We cannot predict the outcome of the first game of each season because of the absence of prior data.
Table 2 shows the home team’s most recent six games’ basic technical features obtained from the website and their mean values that we used for predicting the upcoming game.
Table 3 shows sample records of the mean values of features computed as demonstrated in
Table 2 for games on 31 December 2014. Subscripts
h and
a in Table 3 indicate the home team and away team respectively, for example
means Field Goal Made by the home team; the abbreviations are derived from Table 1. As shown in
Table 3, each training example is of the form
, which corresponds to the statistics and outcome of a game.
is a 28-dimensional vector that contains the input variables, and
indicates whether the home team won
or lost
in that game. The first 28 columns indicate the basic technical features for each team as obtained by computing an average of the previous six games played by the corresponding team. The 29-th column is the actual outcome of the game, corresponding to the predicted game labeled as “Home team win”, takes on only two values: 1 or 0; Here, the number 1 indicates that the home team won and 0 indicates otherwise. We used this basic technical features dataset to train the NBAME model by the principle of Maximum Entropy and predict the result of the coming game during the NBA playoffs for each season.
According to the Maximum Entropy principle, the NBAME model needs to be trained on a sufficient amount of training data. However, training data in each season is limited, and thus there is a possible threat of over-fitting; if there are too many feature functions such that the number of training samples is lower than the number of feature functions, the probability distribution model will over-fit, resulting in high variance. Consequently, we get a better performance with the training data but low accuracy with testing data.
We used
k-means clustering for data discretization with the R version 3.2.2. We applied the clustering software package [
44] using the Partitioning Around Medoids (PAM) function to cluster the data of each feature. The number of clusters are the input parameters, and their values often involve clustering effects. A crucial choice to make was the number of clusters to be used; the Silhouette Coefficient (SC) [
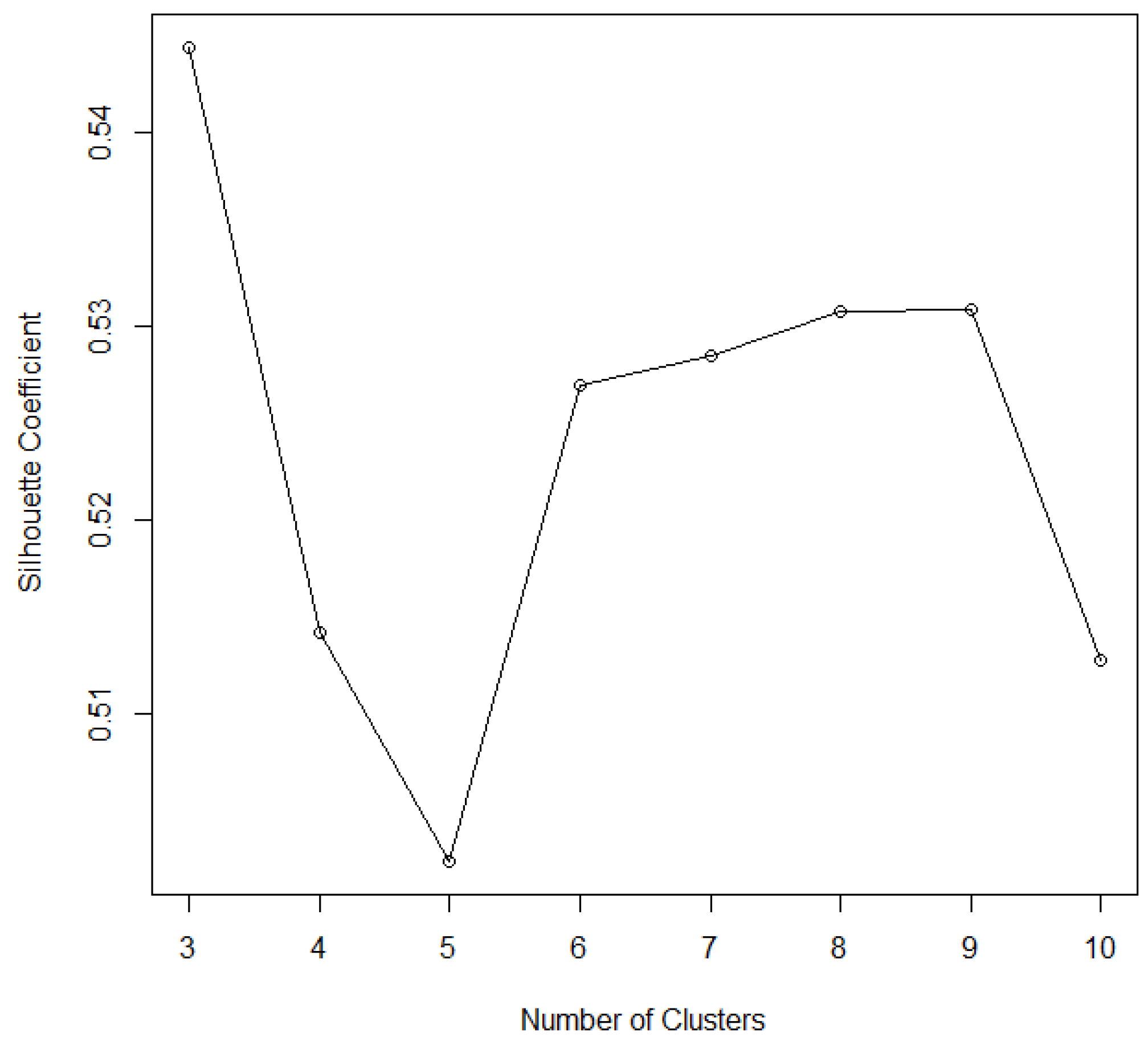
45] can be used to solve this problem, which combines condensation degree and degree of separation. It indicated the effectiveness of clustering with an SC value between −1 and +1—the greater the value, the better result of clustering. According to this principle, we could try to use some parameters of numbers of clustering, calculating the SC repeatedly under the condition of different cluster numbers, and then we can choose the one with the highest SC, which corresponds to the number of best clusters.
We calculate the SC of the away teams’ score when
k ranges from 3 to 10 (two clusters are not enough to obviously distinguish a lot of data).
Figure 1 shows the relationship between the
k value and SC by
k-means clustering to discretize the away teams’ score, where there is haphazard change in the SC value of the away teams’ score as the number of clusters increases from 3 to 10 in the 2014–15 season. We note that when
k is 3, SC is at a maximum with a value of 0.545. Thus, the cluster number of the away teams’ score is assumed to be 3.
Figure 2 shows discrete values of the away teams’ score after
k-means clustering when the SC is 0.545 and the distribution in each cluster is also indicated by different colors. The top blue cluster contains games whose away team scores range between 104 and 125. Ranges for the green (middle) and red (bottom) clusters are 97 to 103 and 80 to 96 respectively. We use
k-means clustering to discretize home teams’ score values and other basic technical features for each game in the same way. Some samples of the experimental data set can be seen in the
Table 4.
Subscripts
h and
a in
Table 4 indicate the home team and away team respectively, for example
means Field Goal Made by the home team; the abbreviations are derived from
Table 1. In
Table 4, the first 14 columns represent the home teams’ basic technical feature values after
k-means clustering discretization. The last column is the home teams’ actual wins or losses of the game. Others represent the away home teams’ basic technical feature values after
k-means clustering discretization. It is also the final dataset that is applied to train the NBAME model and make predictions for the NBA playoffs. We sort them by the date, separate them by season, save the data for each season to a file, and then use data in each file to train and test the NBAME model repeatedly.
4.2. The Results of the NBAME Model for Predicting the NBA Playoffs
We used the feature vectors to construct the NBAME model with the Maximum Entropy principle and trained the parameter
with the GIS algorithm. Then, we applied 28 basic technical features of the coming game to the NBAME model and calculated the probability of the home team’s victory in the game,
. Since
is a continuous value, the model makes a prediction based on a defined threshold: with a threshold of 0.5, it makes a prediction based on the conditions set in Equation (
11) (meaning that if our model outputs a probability greater than or equal to 0.5, we decide that the home team wins, else we decide that the home team loses)
Finally, we compared the decision of our model to the true outcome of the game. If it was the same, then we said the prediction of the NBAME model was right, and we added 1 to the count of the correct prediction. Eventually, we would get the total number of predictions correctly, and we divided it by the number instances from the data set that we used to test it, which is our model’s forecast accuracy. Accuracy was used as performance measure, and it was calculated by the following formula:
The NBAME model outputs the probability of the home team’s win in the upcoming game given the coming game’s features. The home team would be more likely to win if the model output a probability greater than the threshold value. At this point, it is important to note that setting a high confidence improves the accuracy of our model predictions with a drawback of predicting fewer games. For example, if we set a threshold of 0.6, it makes predictions based on conditions defined in Equation (
13), implying that the model will not take a prediction decision for all games with output probabilities between 0.4 and 0.6:
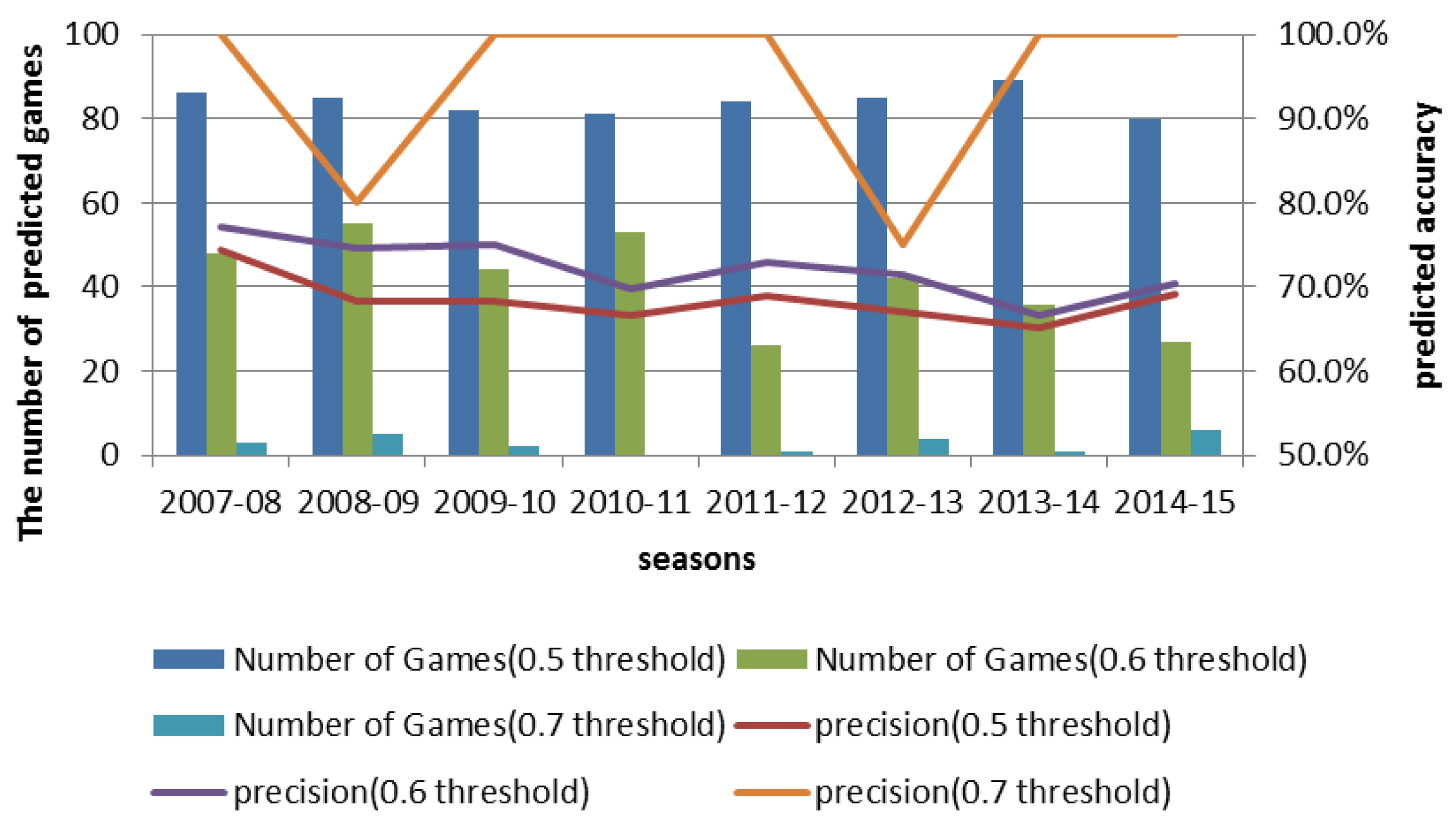
Table 5 and
Table 6 show the prediction results and the number of predicted games for each season using the defined thresholds of 0.5, 0.6, and 0.7.
From
Table 5, the first row shows the prediction results for eight seasons of NBA playoff games by the NBAME model using a threshold of 0.5 (with a 0.5 threshold, the model makes predictions for all the playoffs). We notice that at 0.5 threshold, prediction accuracy of the model reaches as high as 74.4% in the 2007–08 season. If we increase the threshold, the number of games for which we could make a decision for all of the seasons reduces. For example, the number of predicted games decreased from 86 to 48 when we increased the threshold from 0.5 to 0.6 in the 2007–08 season; however, prediction accuracy improved from 74.4% to 77.1%. Similarly, when we increased the threshold from 0.6 to 0.7 in the 2007–08 season, the number of predicted games reduced from 48 to six with a 22.9% increase in prediction accuracy. This shows that we can trade the number of games for which we can make a prediction for an improved prediction accuracy, which can be of great commercial value. The results show that the proposed model is suitable to forecast the outcome of NBA playoffs while achieving high prediction accuracy.
Figure 3 shows the effect of varying thresholds on the number of predicted games and prediction accuracy for playoffs during the 2007–08 season and the 2014–15 season.
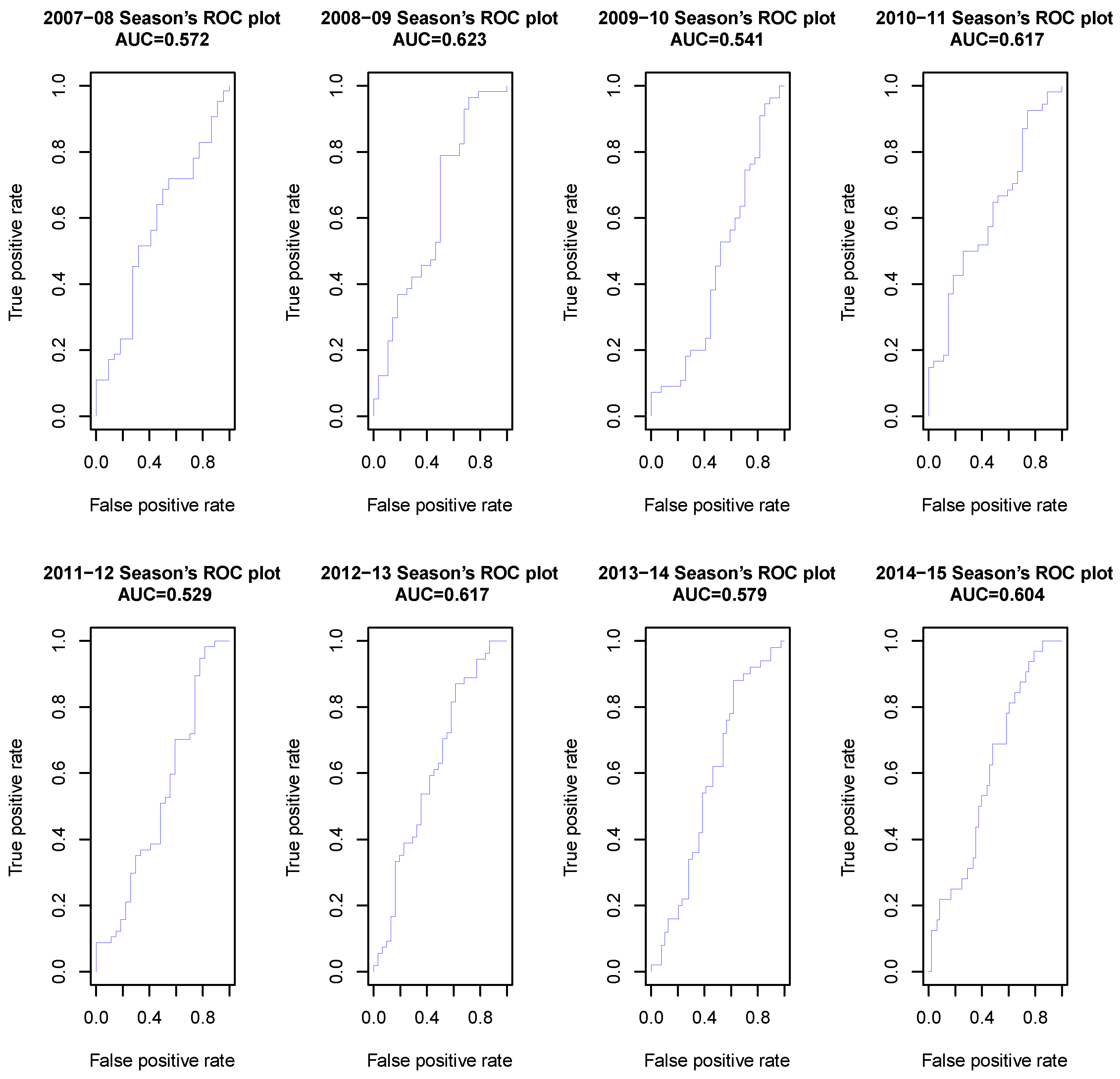
We also used Receiver Operating Characteristics (ROCs) [
46,
47] and the Area Under Curve (AUC) [
48,
49] to evaluate the quality of our NBAME model. We imported the probability of the home team’s winning and the true outcome of the game into R, and used prediction and performance function within the RROC package 1.0-7 [
50] to plot the ROC curve and calculated AUC values for the eight seasons, and the results are presented in
Figure 4.
4.3. Comparison of NBAME Model with Some Selected Existing Machine Learning Algorithms
To evaluate the NBAME model, we compared its performance with selected other machine learning algorithms (Naive Bayes, Logistic Regression, Back Propagation (BP) Neural Networks, Random Forest) in the Waikato Environment for Knowledge Analysis (WEKA 3.6) [
51].
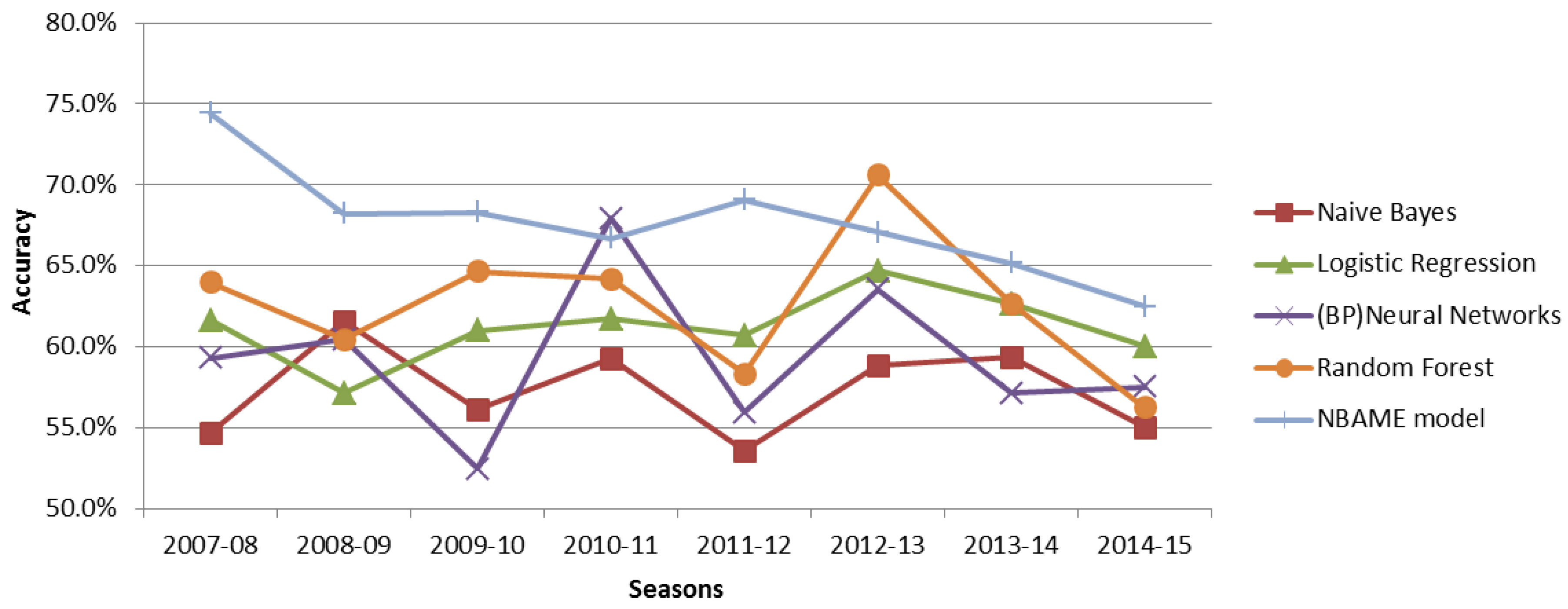
Table 7 shows the results obtained when the features in Table 1 were used together with these algorithms to predict the outcome of NBA playoffs between 2007 and 2015 in
Table 7, and
Figure 5 presents a graphical representation of the results.
From
Table 7 and
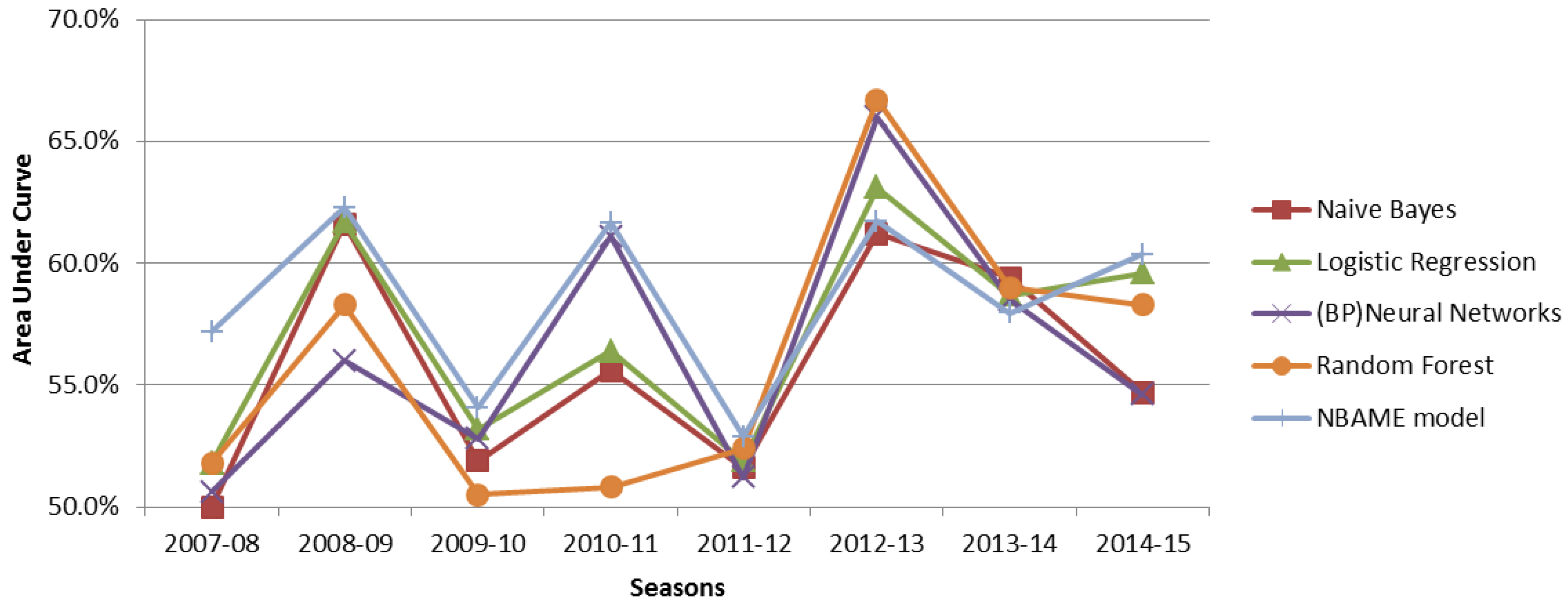
Figure 5, we realize that our model outperformed all of the other classifiers for all seasons under consideration except for the 2010–11 season and the 2012–13 season, where our model was outperformed by Neural Networks and Random Forest, respectively. The Random Forest algorithm follows closely in the second position. The Naive Bayes had the lowest prediction accuracy with an average of about 60%, and this may have been caused by its assumption that all the features were independent, which was not the case. Accuracy results from the Neural Networks suffer adverse variations between seasons. For example, in the 2010–11 season, the Neural Networks registered impressive prediction accuracy at 67.9% but drastically reduced to 52.4% in the 2009–10 season. These variations could be explained by insufficiently small size of the training dataset that may have caused the model to overfit the data. Standard Logistic Regression, also a log-linear algorithm, had a relatively stable prediction accuracy for all seasons, similar to the NBAME. The NBAME outperformed the standard logistic regression because the former avoids overfitting by using regularisation techniques.
We give the AUC values in
Table 8, which make us view our NBAME model performance from another perspective, and
Figure 5 shows a graphical representation of the same values.
Figure 6 shows that each algorithm’s AUC value is not very high due to a high number of features, yet working with only a small size of the training dataset [
52]. The NBAME model is almost the top performing model in all seasons except 2012–13 and 2013–14. All algorithms show similar trends for all seasons. For example, they all performed very well in the 2012–13 season while experiencing the worst performance in the 2011–12 season. This indicates that some seasons are more difficult to predict than others. The difficulty in accurately forecasting results of a particular season is certainly triggered by unanticipated natural factors in the season; for example, the low performance in the 2011–12 season can be explained by the lockout that reduced the number of games from 82 to 66, thus reducing the training dataset size; in the same season, Derrick Rose, Joakim Noah, and David West were injured, leading to their failure to participate in the playoffs. Similarly, the controversy regarding Clippers’ owner Donald Sterling’s racist comments that arose in the 2013–14 season playoffs, and attracted protests from the Clippers and all NBA teams’ players, could have reduced the players’ morale, resulting in a very unpredictable season.