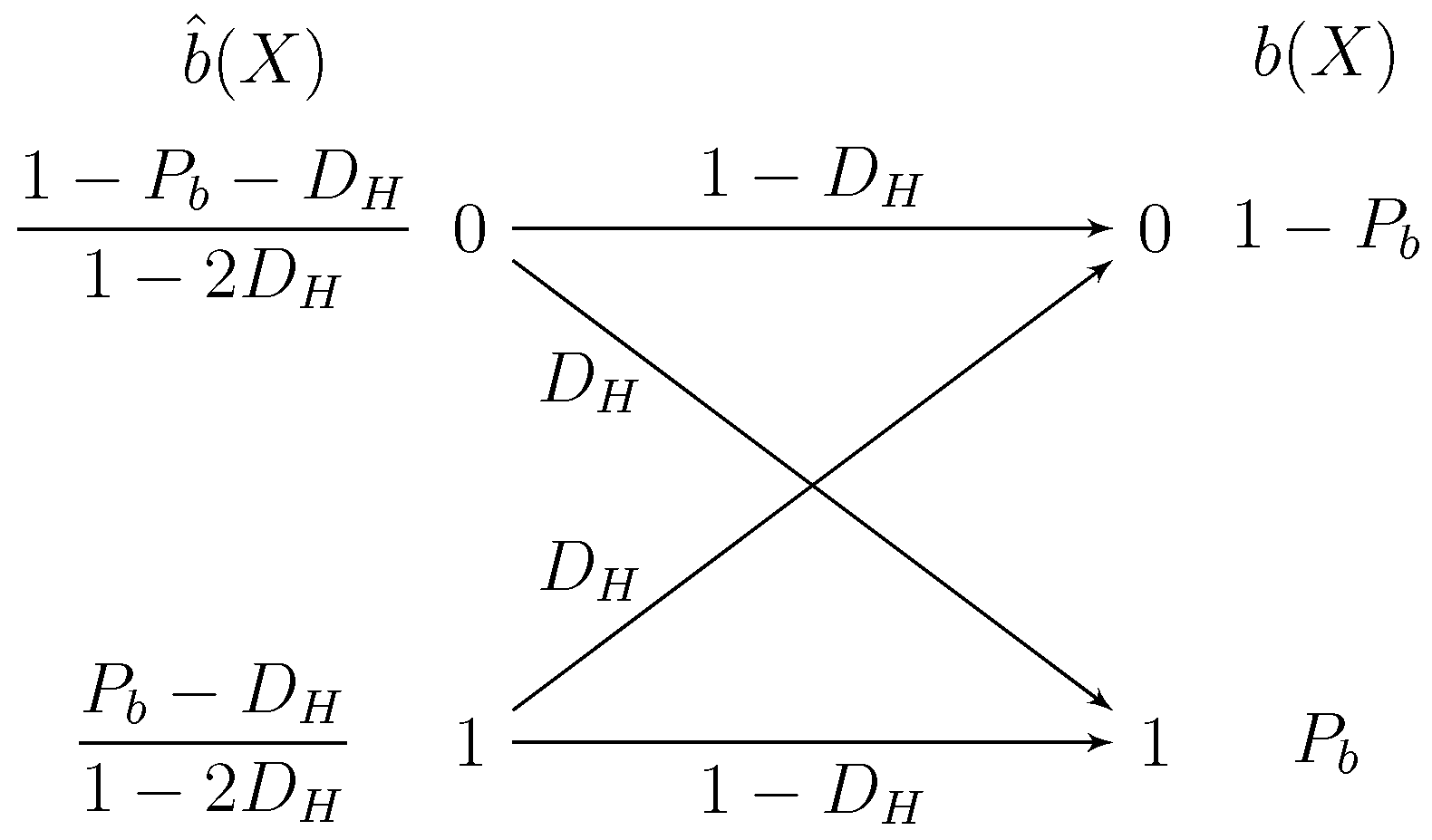1. Introduction
Entropy-constrained scalar quantization (ECSQ) is a well-known compression scheme where a scalar quantizer
is followed by a block lossless entropy-constrained encoder [
1,
2]. The two main quantities characterizing ECSQ are its distortion
D and rate
R. For a real-valued input source
X, the most common distortion measure is the mean squared error between the source
X and its reconstruction
. As the quantizer
is followed by entropy coding, the rate
R is usually defined as the entropy of the random variable at the output of the quantizer, denoted by
.
A natural design problem is how to design
to achieve the lowest possible rate with distortion not greater than
D. While this problem can be solved numerically with various quantizer optimization algorithms [
3,
4,
5], the expressions are only known when
X follows an exponential [
4] or uniform [
6] distribution. The asymptotic limit
constitutes an exception, as it is well known that an infinite-level uniform quantizer is optimal for a broad class of source distributions [
1,
7,
8]. Further, as
, ECSQ with uniform quantizing is only 0.255 bits above Shannon’s lower bound (SLB) to the rate distortion function
. SLB tends to
as
, and is equal to
for a Gaussian distributed source. Beyond scalar quantization,
vector quantization (VQ) is the most common option to improve ECSQ; i.e., to achieve rates closer to
at the same distortion level [
9].
In this communication, we introduce a scalar quantization scheme that, in the limit , reduces the gap to Shannon’s lower bound to the rate distortion function to 0.251 bits. Furthermore, we show that in the low-resolution regime (1-bit quantization), the proposed scheme can remarkably improve ECSQ. The main idea of the proposed scheme is to encode the quantizer output by combining both lossless compression and binary lossy compression at a given Hamming distortion , which offers an additional degree of freedom.
The compression scheme is straightforward, as we only need to expand ECSQ with an additional bit that encodes if the source symbol was in the left half or the right half of the quantization region that contained the source symbol. In other words, this scheme codes the least significant quantization bit lossily, allowing a certain Hamming distortion .
We refer to the proposed method as lossy-bit ECSQ (Lb-ECSQ). Note that Lb-ECSQ contains ECSQ as a particular solution, as ECSQ is recovered when the allowed distortion at the least significant quantization bit is set to zero.
The Lb-ECSQ method resembles works in the field of source-channel coding—namely, channel-optimized quantization [
10]. Interestingly, when the output of a scalar quantizer is coded and transmitted via a very noisy channel, quantizers with a small number of levels (higher distortion) may yield better performance than those with a larger number of levels (lower distortion) [
11]. Several works have addressed the design of scalar quantizers for noisy channels (e.g., [
10,
11,
12]). All these works present conditions and algorithms to optimize the scalar quantizer given that it is followed by a noisy channel. This is similar to the Lb-ECSQ setup, where the lossy binary encoder behaves like a “noisy channel”, with an important and critical difference: in our problem, the distortion introduced by the lossy encoder (the“error probability” of the channel) is a parameter to be optimized, and acts as an additional degree of freedom. Note also that we solely consider the problem of source coding of a continuous source; encoded symbols are transmitted errorless to the receiver that aims at reconstructing the source.
We also study the low-resolution regime, in which we only encode the source with the lossy-bit—namely, 1-bit quantizer followed by a lossy entropy encoder. Results are distribution-dependent for the low-resolution regime, and we focus on the uniform and Gaussian distributions, which are interesting cases that show different behaviors. For example, in this low-resolution regime, the distortion can be reduced by 10% for a uniform distribution when we use 0.2 bits/sample.
In
Section 2 of the paper, we review the analysis of ECSQ for an infinite-level uniform quantizer in the limit
. The asymptotic analysis of Lb-ECSQ for the same quantizer and same limit is presented in
Section 3. In
Section 4, we move to the opposite limit and compare both scalar quantization schemes with 1-bit quantizers.
2. ECSQ and the Uniform Quantizer
Suppose that a source produces the sequence of independent and identically distributed (i.i.d.) real-valued random variables
according to the distribution
. A scalar quantizer is defined as a deterministic mapping
from the source alphabet
to the reconstruction alphabet
, which is assumed to be countable. By Shannon’s source coding theorem,
can be losslessly described by a variable-length code whose expected length is roughly equal to its entropy
. In ECSQ, this quantity constitutes the rate of the quantizer
. Additionally, the mean squared-error distortion incurred by the scalar quantizer
is given by
where
denotes that the expectation is computed w.r.t. the source distribution
. Consider the set of quantizers
for which the squared distortion in Equation (
1) is smaller or equal to
, and let
be the smallest rate achievable among this set; more precisely
Under some constraints on the continuity and decay of
, Gish and Pierce showed that in the limit
,
can asymptotically be achieved by the infinite-level uniform quantizer, whose quantization regions partition the real line into intervals of equal lengths [
1]. Further, they showed that
where
is the rate-distortion function of the source [
13]. In the rest of this section, we briefly review the asymptotic analysis of ECSQ with uniform quantization following the approach described in [
7,
8]. We later rely on intermediate results to analyze the Lb-ECSQ scheme for the uniform quantizer. The following conditions are assumed for the source [
7,
8]:
- C1
is integrable, ensuring that the differential entropy is well-defined and finite; and
- C2
the integer part of the source
X has finite entropy; i.e.,
otherwise,
is infinite [
14].
Denote the infinite-level uniform quantizer by
, and let
δ be the interval length. For
, we have
where
is the reconstruction value for interval
n, and
denotes the indicator function. We define the piecewise-constant probability density function
as follows:
where
is the probability that
x belongs to that interval, and
. To evaluate the squared error distortion, we first decompose
as follows:
As shown in [
7,
8], the absolute value of the second term in the above equation can be upper-bounded by
, and this term vanishes as
according to Lebesgue’s differentiation theorem and Scheffe’s lemma (Th. 16.12) [
15]. Thus,
On the other hand, following [
1], we express the entropy of the quantizer’s output
as follows:
As shown in [
16], the integral in the above expression converges to
as
, hence
where
refers to error terms that vanish as
δ tends to zero. We conclude that the uniform quantizer
with quadratic distortion
and rate
achieves
bits per sample, where
comprises error terms that vanish as
D tends to zero. Further, for sources
X satisfying conditions C1 and C2, the rate-distortion function
can be approximated as [
17]
Without the
term, the right-hand side (RHS) of Equation (11) is referred to the
Shannon lower bound (SLB). By combining Equations (10) and (11), we obtain
3. Uniform Quantization with a Lossy-Compressed Bit
The above results show that—according to Equation (
2)—uniform quantizers are asymptotically optimal as the allowed distortion
D vanishes. In the following, we present a simple scheme that—while maintaining the scalar uniform quantizer—reduces the gap to the rate distortion function of the source below Equation (12). To this end, the quantizer’s output is compressed using both lossless and lossy compression, and thus the compression rate is no longer measured by the entropy of the quantizer’s output. Unlike in [
1], we do not claim that uniform quantization is optimal according to the proposed definition of compression rate. Consider again the uniform quantizer
with interval length
δ. Given
X and
, let
be a binary random variable such that
3.1. Compression with a Lossy-Compressed Bit
Given the random variable , we maintain the lossless variable-length encoder to compress . Moreover, the binary random variable is lossy compressed with a certain Hamming distortion , which is a free parameter to be tuned to minimize the squared error distortion. We refer to this compression scheme as ECSQ with a lossy-compressed bit (Lb-ECSQ).
We assume that lossy-compression of
at a Hamming distortion
is optimally done, achieving the rate distortion function for a Bernoulli source with probability
. While this assumption is somewhat unrealistic, our main goal in this paper is to analyze the fundamental limits of the proposed scheme, as one would do in ECSQ when assuming that the scalar quantizer’s output is compressed at a rate equal to its entropy. For the actual implementation of Lb-ESCQ, practical schemes based on low-density generator-matrix (LDGM) [
18] or lattice codes [
19] could be investigated.
Under the assumption of optimal lossy binary compression, we define the Lb-ECSQ rate of the uniform quantizer
as
where with a slight abuse of notation we use
to denote the rate distortion function of a Bernoulli source with probability
, and
is the binary entropy function. We are interested in evaluating Equation (14) in the limit
. In this regime, it is straightforward to show that for any source distribution
satisfying C1, then
. Using this result and Equation (9), we have
where
comprises error terms that vanish as
δ tends to zero. Observe that if we take
(i.e., lossless compression is used for both
and
), in the limit
the rate
coincides with the entropy of the uniform quantizer in Equation (9) with half the interval length—i.e.,
.
3.2. Reconstruction Values and Squared Distortion with a Lossy-Compressed Bit
Since
is losslessly compressed, upon decompression, it is recovered with no error. Let
be a binary random variable representing the reconstructed value for
. Due to the lossy compression at a certain Hamming distortion, there exists a non-zero reconstruction error; namely,
for
. Given the pair
, we compute the source reconstruction value
as follows
where
is a parameter that—along with
—will be optimized to minimize the squared error distortion
. We note that the reconstruction rule in Equation (16) is possibly suboptimal.
Before evaluating
D as a function of
, and
c, we first need to compute the error probabilities for the
bit. Following [
20] (Chapter 10), if
are jointly distributed according to the binary symmetric channel shown in
Figure 1, then the mutual information
actually coincides with the Bernoulli rate distortion function
. Moreover, by using random coding in [
20] (Chapter 10), it is shown that there exist encoding/decoding schemes that asymptotically (in the block-length) meet the input–output distribution in
Figure 1. Consequently, under the assumption of optimal lossy compression of
with prior probability
, we can compute the error reconstruction probabilities by applying Bayes’ rule in
Figure 1,
Note that in the limit , we have , and thus Equations (17) and (18) are equal to .
Lemma 1. For any source X with a distribution that satisfies conditions C1 and C2,under the assumption that the binary random variable defined in Equation (13) is optimally lossy compressed at a Hamming distortion . Proof. Assuming optimal lossy compression, in the limit
,
is in error with probability
. Further, for any
, it is straightforward to check that both Equations (17) and (18) are upper bounded by
. Therefore, the squared error distortion can be computed as follows:
where
is the conditional distribution of the reconstruction value for
, assuming that the reconstruction error probabilities are equal to
. Equality is achieved at
. According to Equation (16),
can be expressed as follows: for
, then
, and hence
and similarly, if
, then
, and
As in Equation (
7), we expand the integral in Equation (20) using the piecewise-constant distribution
where it can be check that the absolute value of the second term is upper bounded by
, which vanishes as
.
Using Equations (21) and (22), the first term in Equation (23) reads:
where
. The equality is obtained after straight-forward manipulation. The latter expression is minimized if we choose
, Equation (19) being the corresponding distortion. Note that for
, the reconstruction value is at the center of the interval,
. Conversely, if
, the reconstruction point moves closer to the center of the next largest interval, such that the distortion caused by an erroneous transmission is reduced. ☐
3.3. Asymptotic Gap to the Shannon Lower Bound
The following lemma jointly characterizes the rate and squared distortion D of the Lb-ECSQ scheme for the uniform quantizer in the limit :
Lemma 2. For any source X with a distribution that satisfies conditions C1 and C2, the uniform quantizer with interval length δ and Lb-ECSQ compression with quadratic distortion and Hamming distortion of the bit achieveswhere comprises error terms that vanish as D tends to zero, and Proof. The proof is straightforward by combining Equations (15) and (19). More precisely, from Equation (19), we get that as
, the following equality holds
By plugging this equality into Equation (15), we get Equation (28), where
. ☐
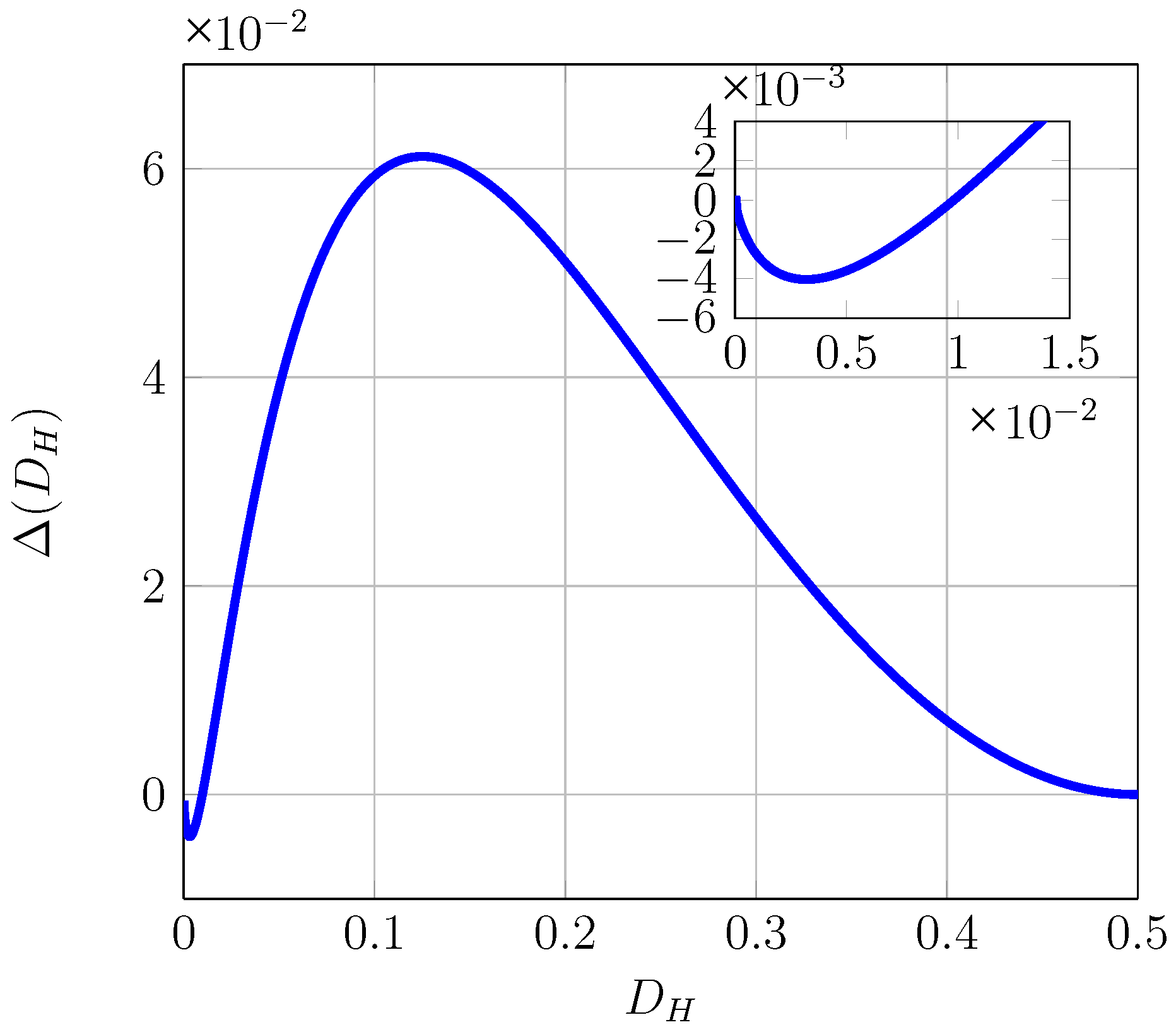
In
Figure 2, we plot
for
. Observe that
is equal to zero at
and
. However, for small values of
,
is actually smaller than zero, achieving its minimum at
×
.
Corollary 1. The uniform quantizer with interval length δ and Lb-ECSQ compression with quadratic distortion achievesbits/sample, where . Finally, by combining Equations (11) and (28),
bits/sample, which proves that Lb-ECSQ is able to outperform ECSQ in the limit
using the uniform quantizer
.
4. Lb-ECSQ in the High Distortion Regime
The above results demonstrate that the use of lossy compression can reduce the gap to SLB in the limit with respect to ECSQ. Improvements can also be observed for low-to-moderate compression rates. The case of a quantizer with only two quantization levels plays a special role that we analyze in this section. While the extension to an arbitrary number N of quantization levels is interesting, preliminary results show that the biggest gain is achieved for a 2-level quantizer, and that the Lb-ECSQ performance tend with N very quickly to the asymptotic gain described in the previous section. We consider a two-level quantizer with quantization regions and for some and two possible source distributions, and .
4.1. Two-Level Quantization of a Uniform Source
For the uniform source
, the ECSQ rate is
where
and
. The squared distortion is minimized if reconstruction points are placed at the center of each quantization region [
6]; i.e.,
if
and
if
, and the distortion incurred is
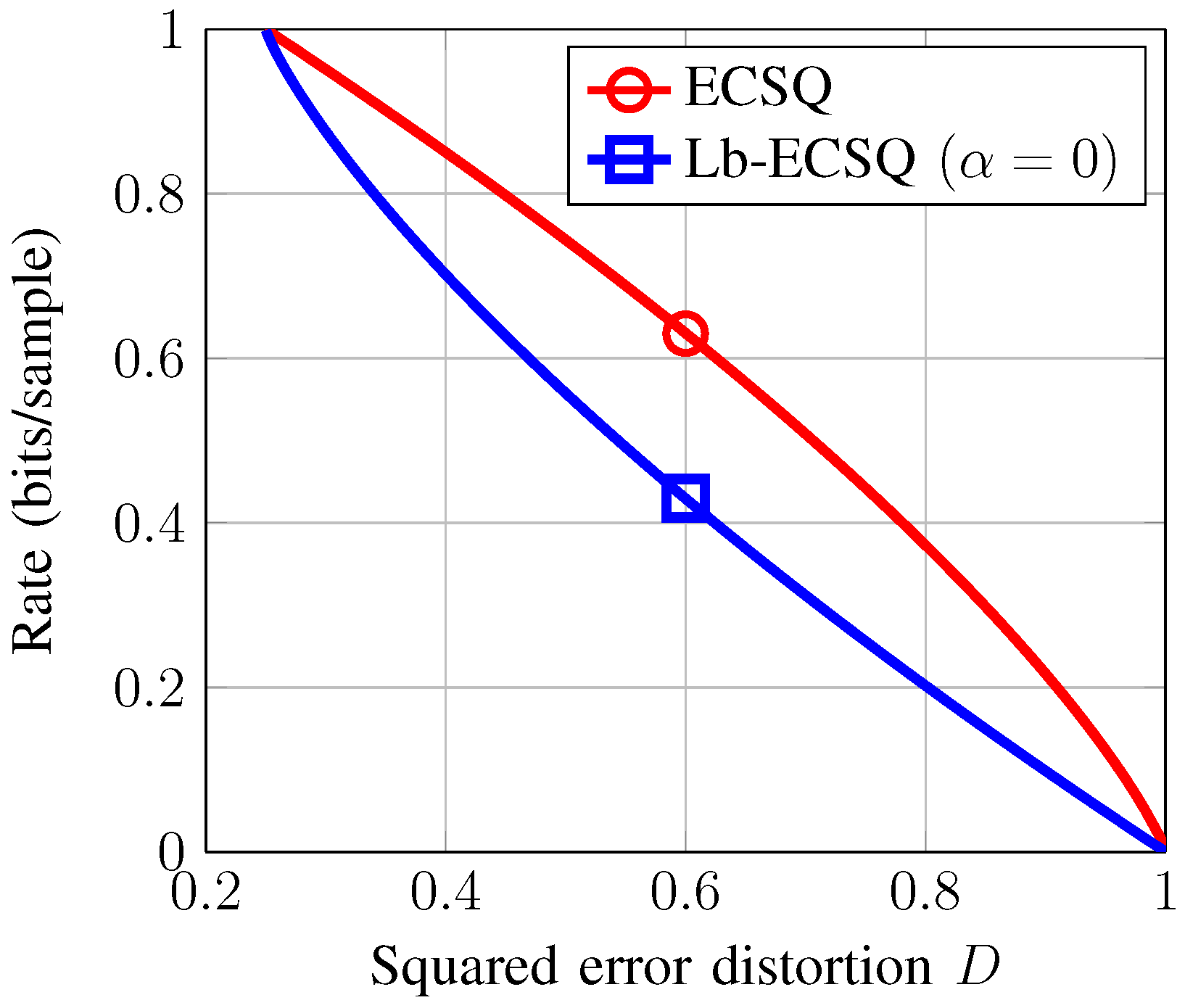
In
Figure 3, we plot
vs.
as we vary
for
(red curve with ∘ marker). As presented in
Section 3, Lb-ECSQ combines lossless compression of
with lossy compression of a random variable
that gathers additional information of the source
X within the quantization region. As now
only partitions the real line in two quantization regions, we implement Lb-ECSQ by directly lossy compressing the quantizer’s output
. To this end, we define the binary R.V.
if
and zero-otherwise. The Lb-ECSQ rate is given by the compression rate of
at a certain Hamming distortion
:
Further, we fix the quantizer threshold to , which implies that takes value either or with uniform probability, and thus . Under optimal lossy compression, the reconstructed bit is in error with the same probability model described in Equations (17) and (18); namely, is in error with probability . We set the source reconstruction if and if , where c is a positive quantity optimized to minimize .
Lemma 3. Given the source , the 1-bit quantizer with threshold and Lb-ECSQ compression achieves a squared distortionunder the assumption that is optimally lossy compressed at a Hamming distortion . Proof. The proof is similar to that of Lemma 1, expanding as done for every quantization region done in and minimizing w.r.t. the reconstruction point c. ☐
In
Figure 3, we plot
in Equation (37) vs.
in Equation (32) for
as we vary
(blue curve with □ marker). Observe that Lb-ECSQ improves ECSQ at all points, except for
and
, as we know they must be equivalent at these two points. The Lb-ECSQ analysis proposed for
can be generalized to an arbitrary threshold
, but simulations for
using numerical optimization show that the obtained rate-distortion function coincides with the one computed for
. This result is dependent on the source distribution, as shown for the Gaussian source case.
4.2. Two-Level Quantization of a Gaussian Source
Now consider the same quantizer
and
. Low-resolution ECSQ for a Gaussian input source was studied in [
21], where the authors showed that the minimum rate is achieved by a quantizer whose unique threshold α goes either to
or to ∞ as
, and the two reconstruction points are the centroids of the quantization regions. The ECSQ rate distortion function for this source is given by the following parametric curve
where
is the cumulative density function of the Gaussian distribution, and
We now study the same Lb-ECSQ scheme analyzed before for the uniform source. First, we fix the quantizer threshold to and define if , and zero otherwise. Note that Lb-ECSQ rate is given in Equation (32).
Lemma 4. Given the source , the quantizer with and Lb-ECSQ compression achieves a squared distortionfor . Proof. The proof is based on expanding as done for every quantization region in Equation (24) and minimizing w.r.t. the reconstruction point c. ☐
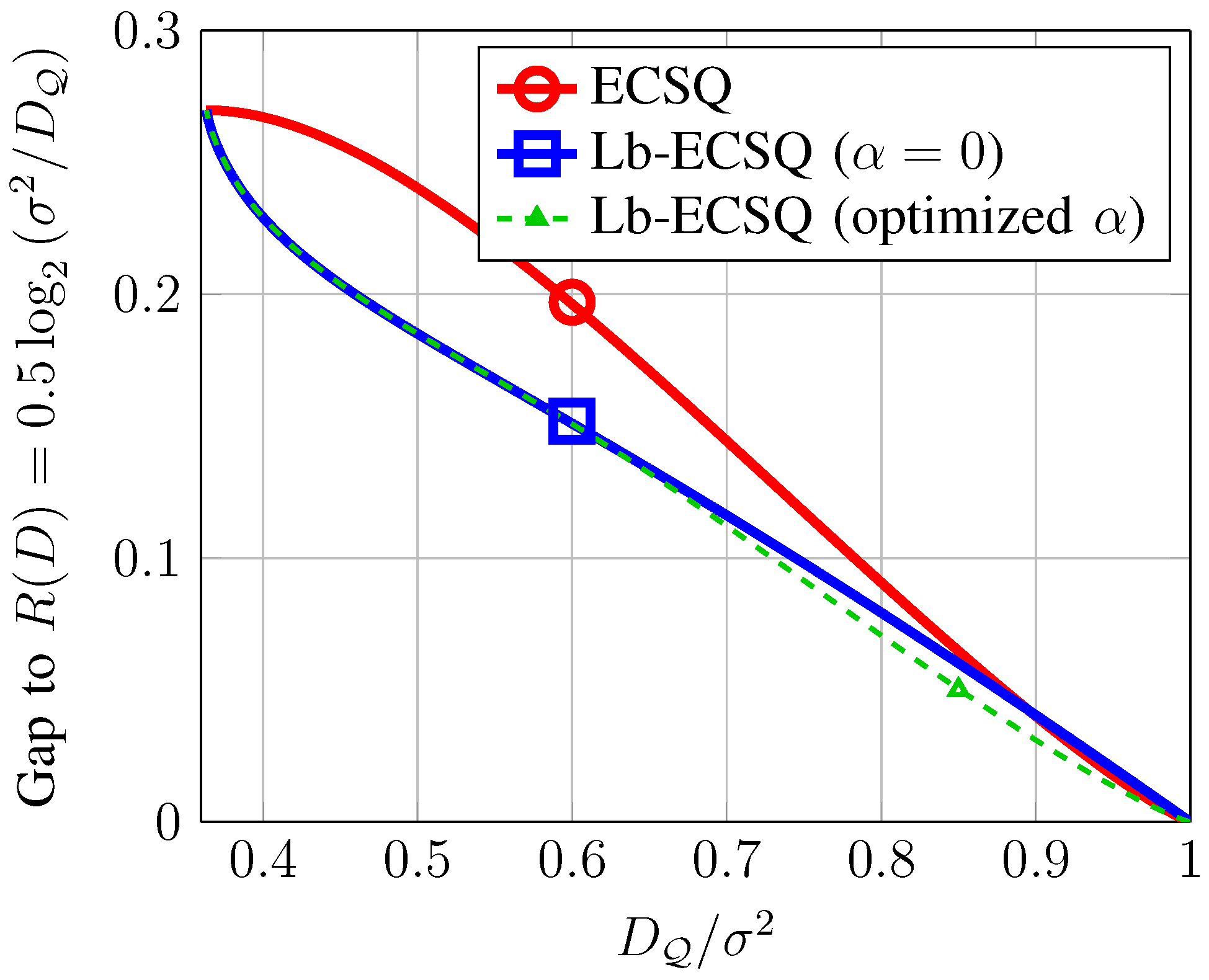
In
Figure 4, we plot the gap between the ECSQ and Lb-ECSQ rate distortion function for a 1-bit quantizer and the rate distortion function for the source; i.e.,
. Observe that, unlike the case of a uniform source, for
, Lb-ECSQ is slightly worse than ECSQ. As discussed before, in the ECSQ solution for a Gaussian input source, the threshold α goes to infinity in the limit
[
21]. By fixing the threshold α to 0 in Lb-ECSQ, we are restraining to an equivalent solution. This can be tackled by generalizing the above equations to an arbitrary threshold α. While the methodology is equivalent, we have to rely on numerical optimization to find the optimal choice of α,
, and
for each value of
. In this case, the bit error reconstruction probabilities take the form given in Equations (17) and (18). Additionally, for an arbitrary threshold α,
is a Bernoulli source with probability
, and hence the compression rate is
. A numerical optimization (gradient descend) procedure has been used to find the minimum distortion for each
. The results are shown in
Figure 4, where we can see that now Lb-ECSQ is able to perform equally to or better than ECSQ in the whole range.