1. Introduction
The natural convection of single phase fluids is an archetypal example of both non-linear dynamics and non-equilibrium thermodynamics. When heated from below and cooled from above, such fluids spontaneously structure themselves into a system of convection rolls, which tend to increase the rate of heat transport through the system (compared to that of diffusive transport alone). It has long been suggested—beginning with the pioneering work of Malkus [
1,
2,
3]—that such phenomena express the system’s attempts to maximize its rate of heat transport, subject to basic physical constraints. If the temperatures at the system’s boundaries are held fixed, maximizing the rate of heat transport and maximizing entropy production become indistinguishable, since only the heat transport rate (to which entropy production rate is proportional) can vary.
Further work since then (including theoretical and numerical studies [
4,
5]) has aimed to establish the scaling relation between the two primary dimensionless groups related to fluid convection: The Rayleigh number (Ra, a measure of thermal driving force), and the Nusselt number (Nu, the ratio of total heat flux to diffusive heat flux). The majority of studies concerning convection made use of fixed temperature (perfectly conducting) boundaries. Such boundary conditions (BCs) are convenient for theoretical treatments, and can be implemented experimentally to a close approximation. A smaller number of works have also considered fixed heat flux boundaries [
5,
6,
7], and the general result appears to be that the scaling relation between Ra and Nu is invariant to the type of BC for turbulent conditions. At low Ra, fixed flux systems achieve a slightly augmented Nu compared to an equivalent fixed temperature system, due to the fact that the boundaries of the fixed flux system are not constrained to have horizontally uniform temperature profiles.
In previous work, we demonstrated (through the use of Lattice Boltzmann Model (LBM) simulations) that one can employ an alternative set of BCs, where neither the boundary temperatures nor heat fluxes are fixed, and still observe the characteristic scaling relation between Ra and Nu. These BCs are described as negative feedback BCs [
8], since the heat flux into each boundary is constrained to be a decreasing function of the instantaneous boundary temperature. A defining characteristic of such BCs is that for any given set of boundary parameters, the system has the freedom to adjust its net heat flux between two well-defined bounds. The entropy production of the system, rather than changing monotonically between these two bounds, actually exhibits a single intermediate peak. It is thus an ideal test case for theories of maximum entropy production (MEP).
MEP is a variational principle which proposes that a non-equilibrium system with many degrees of freedom will adjust its internal dynamics such that its entropy production rate tends to a maximum, subject to any relevant physical constraints or conservation laws [
9,
10]. Negative feedback BCs were applied in the simple box models of Paltridge [
11], which accurately predicted that atmospheric heat transport adheres to states of MEP. This early work catalysed a profusion of further investigations into the applicability, theoretical foundations, and consequences of MEP [
9,
12,
13,
14,
15,
16,
17,
18,
19,
20]. Indeed, it has been proposed that convecting fluids are a prime example of MEP [
21,
22,
23]. In all of the aforementioned works, for the case of single phase fluid convection, only constant temperature BCs were considered. We would like to stress that entropy production should always be carefully distinguished from heat flux. Entropy production is the product of heat flux and the gradient of inverse temperature. Thus, statements about entropy production should include considerations of variable temperature difference, as well as variable heat flux. Alternatively, if an investigation only considers fixed temperature BCs, then it should be cautioned that only statements about the heat flux of those systems can be made.
Convecting fluids are characterized by a series of dynamical bifurcations as the thermal driving force is increased from 0. The first—occurring at the so-called critical Rayleigh number—marks the point at which the linear diffusive state is unstable to perturbations, and the system cascades into a new configuration characterized by spatially structured velocity fields and convective heat transport between diffusive boundary layers. The primary approach of non-linear dynamics is to understand the nature of such bifurcations and why the system adopts a particular branch of steady states instead of alternative branches. In the case of the present work focussing on laminar convection, there are two steady states that the system could adopt—one in which the fluid remains motionless and heat moves by diffusion, and another in which there is sustained convective motion. Hence, variational principles such as MEP should predict which of these two discrete states the system will adopt (by way of comparing the two entropy production values). There is no continuous spectrum of stable states, simply the two branches extending beyond the first bifurcation. So, maximizing or minimizing entropy production in the present work refers to the discrete selection of the branch of states with the higher or lower entropy production.
In fact, the evidence from experimental and theoretical work compels us to conclude that convective systems maximize their entropy production under constant temperature BCs (maximum heat flux), but minimize their entropy production under constant flux BCs (minimum temperature difference) [
24,
25,
26,
27]. The case of minimum entropy production for flux-driven systems is simple to understand: below the critical Rayleigh number, in the linear diffusive regime, the temperature profile through the system is a simple linear extrapolation of the local temperature gradient (defined by the imposed heat flux) at the boundaries. Above the critical Rayleigh number, however, the steady state temperature difference drops below that of the diffusive regime, because the thermal impedance of the system is reduced when convection becomes an additional channel for heat transport. Thus, the system could produce more entropy by having the higher temperature difference of the diffusive regime. Instead, it bifurcates to a mode of convection with a characteristically lower temperature difference, which translates to a lower entropy production than the diffusive mode.
Recalling that the definition of the Nusselt number is (where F is total heat flux, χ is thermal diffusivity, is temperature difference, and H is vertical system dimension), it is clear that above the critical Rayleigh number, the entropy production will go down because we know that and hence . Given that F is fixed by the BCs, the temperature difference must have dropped below what it could be in the diffusive regime. Thus, the fact that the convective branch is stable beyond the bifurcation at the critical Ra implies that the system has chosen the steady state of lower entropy production (for fixed flux BCs).
In our previous numerical investigation, neither the heat flux nor the temperature difference of the system was fixed, since we employed negative feedback BCs [
24]. We found that the system never evolved towards the MEP state. In fact, in all cases, the system’s heat flux was far greater than that pertaining to MEP. It seemed that the steady state transport properties depended solely on the unique set of fluid and boundary parameters of that particular system. The scaling of the Rayleigh and Nusselt numbers was also shown to be identical to that of fixed BCs.
Given that the heat flux values that were exhibited in the previous work were significantly higher than that associated with MEP, it was possible that the boundary parameters we chose were acting as a binding constraint, holding the system away from the state of MEP. We were thus motivated to explore the possibility of systems with different boundary parameters, such that their steady states lie in the vicinity of the MEP peak. If MEP was indeed an attractor, and if our choice of parameters was a constraint preventing the system from reaching that attractor, then we would expect a discrete change in the distribution of steady state operating points of the system as the parameter constraints were relaxed. In other words, we would expect the density of steady state points to be higher near the MEP point.
In fact, it is straightforward to alter the boundary parameters such that the general position of the steady state along the heat flux axis is shifted (as will be shown in the following section). One can then more directly assess whether or not the MEP state represents a local attractor.
Thus, the objective of this work was to explore the steady states of fluid convection systems with negative feedback BCs in the vicinity of MEP (the heat flux value corresponding to MEP). We are thus building upon our previous analysis of entropy production in negative feedback fluid systems [
24] and previous work on the transport properties of convective systems with fixed BCs [
5,
6,
7,
27].
In the following section, we present the details of our model system and the various parameters and variables that characterise it. Since the LBM model employed here has been described in detail elsewhere [
24,
25,
28,
29], we avoid an in-depth description in this paper. In
Section 3 we present the results of our simulations. The paper concludes with a discussion of the implications of our findings for the wider relevance of MEP to fluid dynamical and heat transport systems.
2. Model System
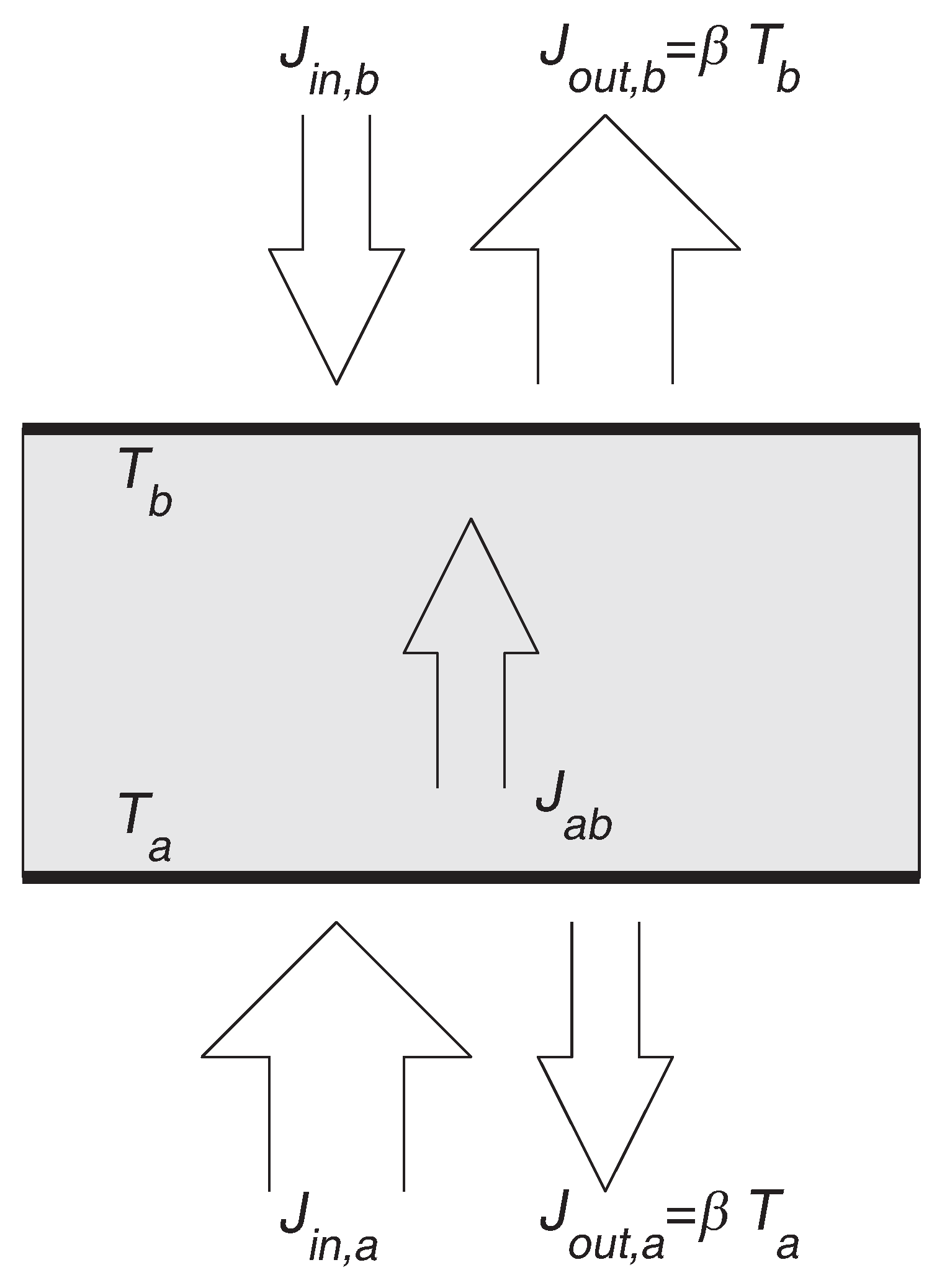
The system in question is a vertically oriented two-dimensional fluid enclosed between solid boundaries at the top and bottom. Periodic BCs were used in the horizontal direction, and a fixed aspect ratio of 2:1 was adopted. The upper and lower boundaries receive inward heat fluxes
and
respectively, and are also able to radiate heat away. Following the example of the box models used by many previous authors [
9,
11,
16], the outward fluxes have the functional form
, where
and
β is a parameter.
Figure 1 shows a schematic of the system.
Heat flows through it by a combination of diffusion and convection. As mentioned in the previous section, simple box models with similar BCs have been used to approximate atmospheric heat transport [
11,
19,
23], and have been explored analytically (e.g., [
9]). Ignoring the internal details of the system and considering it as a black box that has reached a state of dynamic equilibrium, the energy balance at the two boundaries can be written as
Summing these two equations yields
If we write the two temperatures in the form
and
, we can use Equation (
3) to find an expression for the system’s average temperature
,
To find an expression in terms of
, we can subtract Equation (
2) from Equation (
1):
As mentioned previously, we see that the BCs force the heat flux to be a decreasing function of the temperature difference. Furthermore, the constraint of Equation (
5) means that the system has only one macroscopic degree of freedom (despite the fact that neither the temperature difference nor the heat flux are explicitly fixed). To determine the steady state properties exactly, we would require an additional constraint—for example, the relationship between
and
. Such a relationship would be linear for diffusive heat transport. For convective transport, it is generally not known. Various empirical scaling laws have been observed, and theoretical studies have also produced candidate expressions. However, at present, it is still not clear whether a universally valid force-flux relationship exists [
4,
5,
30].
How the system will choose its steady state is not entirely clear, hence the potential utility of a selection mechanism such as MEP. We shall now see how a characteristic peak in entropy production emerges from the boundary energy balance expressions. First let us consider the extrema of
and
, making use of Equation (
5). In the case of zero flux through the fluid,
and the temperature difference is maximized:
. Conversely, if the temperature difference becomes negligible
, the heat flux is maximized:
. The two maxima can be used to calculate dimensionless versions of the heat flux and temperature difference:
and
. We can now find the entropy production as a function of a single dimensionless variable of the system. Noting the dimensions of
β, the dimensionless entropy production can be defined as
:
which, after some manipulation, becomes
We see that the dimensionless entropy production only depends upon the normalized variable
and the inward flux parameters
and
. Compared to our previous study, in this work we used a new value for the parameter
β, and the other parameters remain unchanged (
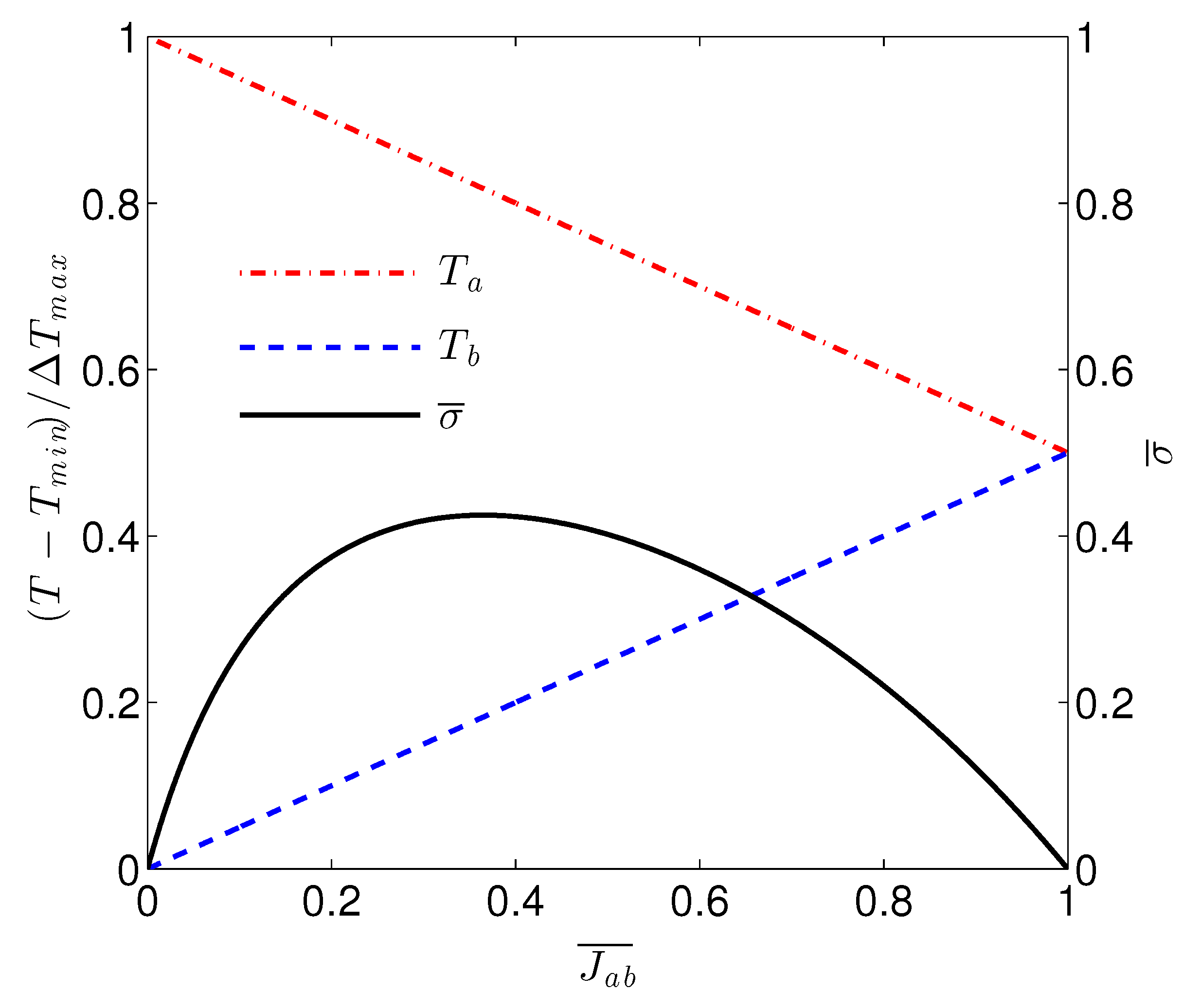
for the present work). MEP corresponds to maximizing
with respect to
. This is displayed graphically in
Figure 2.
We see that the entropy production peak emerges from the compromise of increasing heat flux vs. decreasing temperature gradient.
To simulate the fluid dynamic and thermodynamic behaviour of such a system, we employed a thermal LBM, first introduced by He et al. [
28] and simplified by Peng et al. [
29]. Details of the exact implementation of negative feedback BCs can be found in Bartlett and Bullock [
24], Bartlett [
25]. The numerical parameters of each simulation carried out are given in
Table 1.
The relaxation parameter
defines the fluid viscosity
ν:
where
c is the lattice spacing. The thermal diffusivity
χ is controlled analogously:
The values within the body of
Table 1 are the steady state Rayleigh numbers exhibited by each combination of
and
. As can be seen from these values, we restricted the simulations to laminar flows (the simulation domain size was fixed at
, and the height was
lattice cells). In previous work, we experimented with high Rayleigh number flows (up to
) and found that more turbulent conditions had no effect on whether the system was attracted to states of MEP. This, combined with the large computational burden of turbulent systems, led us to restrict ourselves to laminar flows in the present work.
We also used the
uni-temp BC, wherein the incoming heat flux at each time step is distributed across boundary grid cells, such that the boundary temperature remains horizontally uniform. Note that the use of BCs in which the boundary temperature is free to be non-uniform do not exhibit significantly different results (see Bartlett and Bullock [
24], Bartlett [
25] for details). All simulations had the same boundary parameters.
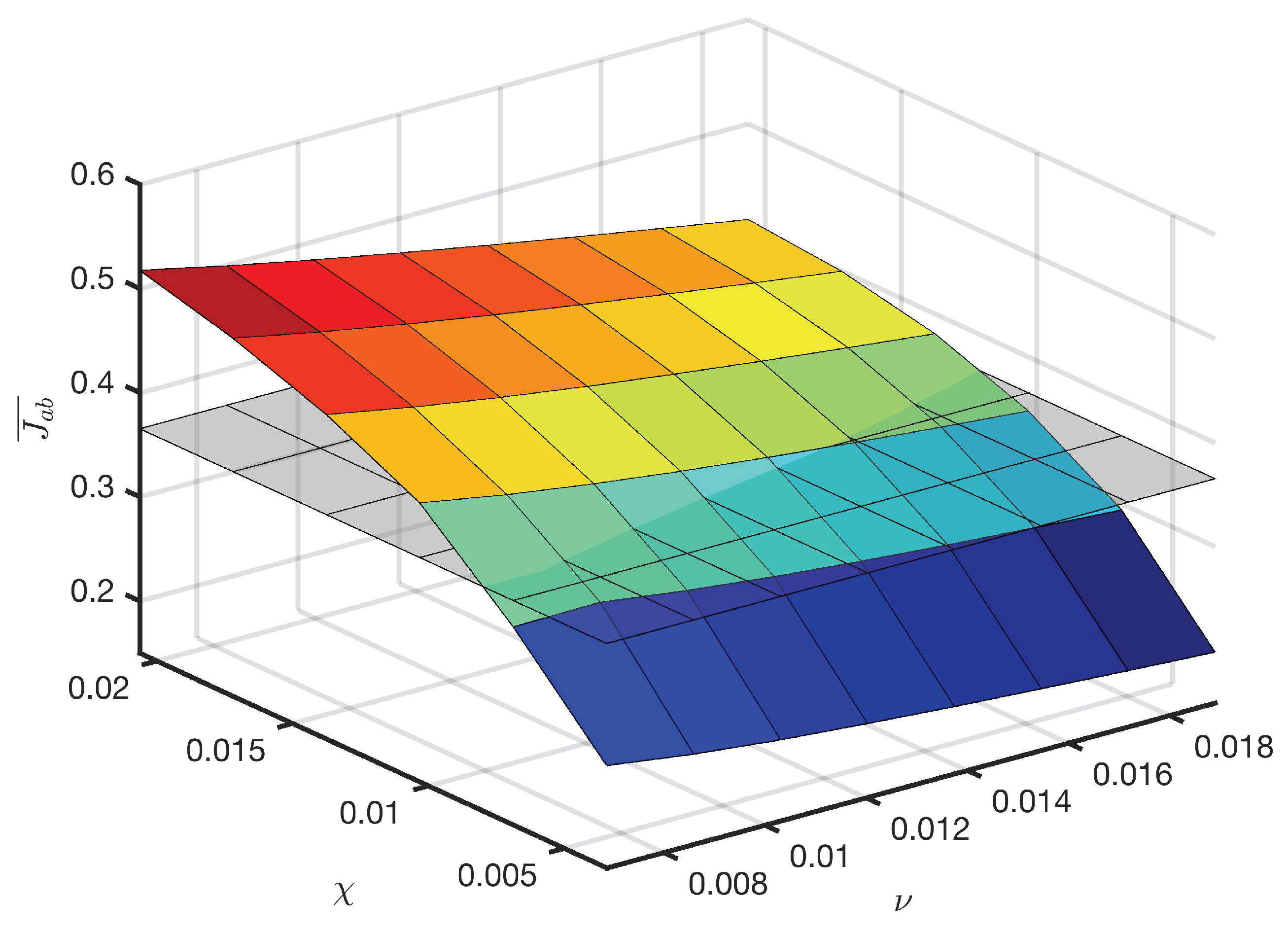
If MEP was indeed an attractor for these systems, and some combination of the fluid viscosity and thermal diffusivity was a constraining factor preventing MEP from being expressed, we should expect a discrete and abrupt adherence to the heat flux value corresponding to MEP as the two fluid parameters are varied and the steady state of the system approaches that of MEP.
4. Discussion
In our previous work, we showed that the use of negative feedback BCs had no influence on the scaling behaviour of the dimensionless parameters Ra and Nu for single phase fluid convection. With the parameter set used in that investigation, simulated heat flux values were far higher than the value corresponding to MEP. In this paper, we modified the boundary parameters such that the steady states of the system lay in the vicinity of the MEP state. This was motivated by the possibility that our previous parameter choices constituted a preventive constraint on the system. Since entropy production can only be maximized subject to constraints, we were compelled to assess whether relaxing the parameter choice constraint might induce a qualitative change in the system’s choice of steady state and allow it to adhere to MEP.
The results of our simulations support the conclusions of our previous work that for single phase fluid convection, MEP does not represent a steady state attractor. We see no reason why this system should be sensitive to its net thermal entropy production, given that it depends only upon boundary parameters, rather than both boundary and fluid parameters. As we have shown, different sets of fluid parameters produce different steady states, and there is no increase in the density of states as the parameters allow the system to approach MEP.
What remains to be elucidated is the connection between our negative result and previous positive results which showed that atmospheric heat transport adheres to MEP [
9,
11,
16,
18,
19]. It could be the case that non-equilibrium systems need a threshold number of degrees of freedom in order to have the ability to express MEP, and the current 2D single-phase system is simply not complex enough (its behaviour is not significantly more complex than a dynamical system with two degrees of freedom, despite being a fluid comprised of a very large number of microscopic degrees of freedom).
It would be desirable to perform similar numerical experiments in the turbulent regime. This would require either a modified LBM algorithm (e.g., [
31]), very high resolution grids, or simply a different simulation technique. However, there is no reason to believe that the conclusion of this and our previous work would be altered. The steady states of all systems analyzed correspond to the point of intersection between the force-flux curve of the fluid and the force-flux curve of the BCs. We believe that this trend of the system finding the single steady state compatible with both the fluid force-flux relationship
and the BC force-flux relationship would continue to higher, turbulent Rayleigh numbers.
The question of a universal extremum principle for nonequilibrium systems remains very much open. We believe it is clear that MEP cannot be interpreted as a general principle of nature. However, there is a combination of variables which is always maximized for all three BCs considered by this and previous work, and this will be discussed in the final section.