1. Introduction
User-created content (UCC, also called user-generated content) are appearing in the era of Web 2.0, encouraging individuals to publish their opinions or reviews on different types of subjects such as e-commerce [
1], tourism industry [
2], software engineering [
3], and so forth. People can easily publish their opinions, comments, or views on online shopping platforms, blogs, and forums. For instance, users’ comments are a must-have section on a shopping website. Potential customers typically view other people’s reviews before making consumption decisions, and they may be strongly influenced by existing users’ opinions. Negative reviews can cause poor reputation to a product or even a brand. On the contrary, positive reviews can impart a noble image to a product and bring about advantages over other products in the market competition.
Some companies purposely post positive reviews to promote their own products in order to make money. Even worse, they even hire an “Online Water Army” [
4] to post negative comments to defame competitors’ products. Since fake reviews can be generated at little cost, a large number of deceptive reviews have arisen with the development of Internet.
In order to get rid of fabricated reviews, researchers propose several approaches to differentiate false reviews from truthful ones. Jindal and Liu [
5] point out that spam reviews are widespread after they analyzed 5.8 million reviews and 2.14 million reviewers from Amazon.com. They categorize spam reviews into three types: untruthful reviews, only-one-brand ones, and irrelevant ones. They also named such fake opinions as “opinion spam”, which is made with vicious incentives and purposes.
According to Jindal and Liu’s work, it is not hard to manually identify only-one-brand reviews and irrelevant reviews. However, it is very difficult for human beings to differentiate purposely fabricated reviews from truthful ones; in other words, it is very difficult to identify deceptive reviews which are deliberately and elaborately crafted by spammers from truthful ones [
5]. Thus, several machine learning techniques are proposed to fulfill the classification task of automatic deceptive review identification. Due to the lack of the golden set of spam reviews, Jindal and Liu assume duplicate reviews as spam information for research. However, Pang and Lee deem it inappropriate to merely regard duplicate reviews as spam reviews because the connotation of the spam review is much more than a duplicate review [
6]. In this paper, we define spam reviews as those reviews that are purposely made to mislead ordinary consumers with fake information on the Internet.
Ott et al. [
7] combine the n-gram feature and psychological feature to identify spam reviews. With support vector machine (SVM) as the base classifier, they claim that they obtain accuracy as high as 90% in the identification task, and this outcome is superior over human beings’ manual decision, which is about 60% accuracy. Other researchers have also proposed several approaches to automatic spam identification, such as Feng et al. [
8], Zhou et al. [
9], and Li et al. [
10].
In our prior work [
11], we examined two base classifiers: SVM and Naïve Bayes. The experimental result indicates that the average accuracy is very similar for each of the two base-classifiers. This conclusion is also consistent with other researchers, like Huang et al. [
12]. For this reason, we only use SVM as the base classifier in this research.
Labeled reviews are crucial to improve the performance of spam identification. However, labeled reviews are expensive to obtain in practice. It requires extensive human labor and a lot of time is spent to produce enough labeled reviews to train the base classifier. In contrast, there are vast amounts of unlabeled reviews available on the Internet. Thus, it is natural to attempt to make use of unlabeled reviews to solve the spam review identification problem by adopting particular assumptions like smoothness assumption, cluster assumption, and so forth [
13].
This paper proposes a novel approach to identifying spam reviews based on entropy and the co-training algorithm by making use of unlabeled reviews. The remainder of this paper is organized as follows.
Section 2 presents related work.
Section 3 proposes the CoFea (Co-training by Features) approach.
Section 4 conducts the experiments on the spam dataset, and
Section 5 concludes the paper.
2. Related Work
2.1. Entropy
The size of information for a message and its uncertainty has a direct relationship. Entropy
of a signal
is defined by Shannon [
14] to measure the amount of information. The entropy can be written explicitly as follows in Equation (1).
where
is the entropy of a discrete variable
.
is the base of the logarithm (generally
, and the unit of entropy is bit).
is the probability of samples where
represents each sample of the data point
. The value of
is taken to be 0 in the case of
.
Based on the idea of entropy, in the proposed CoFea approach, we calculate the entropy
of each term
in Equation (2).
Here, is the total number of reviews. is the number of truthful reviews and is the number of deceptive reviews. is the number of truthful reviews which contain term , and is the number of deceptive reviews which contain term . The result of the summation is the entropy value of term . If one term occurred with same frequency in both truthful and deceptive reviews, we cannot deduce useful information from it for deceptive review identification. However, if one term occurred merely in either truthful or deceptive reviews, then it can provide useful information for deceptive review identification due to the potential link between this term and the label of reviews. Further, as for the former terms, they have larger entropy values than the latter terms. From this point of view, the smaller the entropy is, the greater the amount of information the term contains for deceptive review identification.
We sort the lexical terms of all the reviews by its entropy scores in a descending order. Then we evenly divide the terms of the sequence into two distinct subsets: all odd-numbered terms groups and all even-numbered groups. Feature selection is conducted based on terms’ entropy value—that is, we regard subset as view , and subset as view .
2.2. The Co-Training Algorithm
The Co-training algorithm is a semi-supervised method, invented to combine labeled and unlabeled samples when the data can be regarded as having two distinct views [
15]. Pioneers using the co-training method obtain accuracy as high as 95% for the task of categorizing 788 webpages by using only 12 labeled ones [
16]. Other researchers extend this study into three categories: co-training with multiple views, co-training with multiple classifiers, and co-training with multiple manifolds [
17]. In this paper, we use co-training with multiple views on spam review identification.
We use two feature sets as and to describe a data sample. In other words, we have two different “views” on the data sample , and each view can be represented by a vector . We assume that the two views and are independent of each other and each view in itself can provide sufficient information for the classification task. When we utilize and to denote the classifiers derived from the two views, we will obtain , where is the true label of . We also can describe this idea in another way: for a data point , if we derive two classifiers as and from the training data, and will predict the same label .
2.3. Support Vector Machine (SVM)
SVM is a type of supervised learning model in machine learning proposed by Vapnik et al. [
18]. This method minimizes the structural risk and turns out to provide better performance than the traditional classifiers. Formally, an SVM constructs a hyperplane in a Hilbert space. The Hilbert space has higher dimensions than that of the original one using kernel methods [
19]. A good hyperplane could make the largest distance to the nearest training data point of any class.
The optimum hyperplane can be expressed as a combination of support vectors (i.e., the data samples in the input space). Generally, the optimization problem of hyperplane can be written as follows [
20].
subject to
Here, are the labeled data samples with labels. For each , we use the slack variable to tolerate those outlier samples. Note that , if and only if is the smallest nonnegative number satisfying . is the slope vector of the hyperplane. After the optimal hyperplane problem is solved, the decision function can be used to classify the unlabeled data. Intuitively, the larger the distance of a data point from the hyperplane is, the more confident we will be to classify the data sample using SVM. For this reason, we use the distance as the confidence of the classifying result.
3. CoFea—The Proposed Approach
The co-training algorithm needs two different views to combine labeled and unlabeled reviews. The state-of-the-art co-training techniques usually use different types of views. For instance, Liu et al. [
17] propose combining textual content (lexical terms) of a webpage and the hyperlinks in the webpage as two distinct views for webpage classification using the co-training algorithm. Differing from their method, the CoFea algorithm is proposed to identify spam reviews using two views comprising purely lexical terms. The details of the CoFea algorithm are described in Algorithm 1 as follows.
| Algorithm 1 The CoFea Algorithm |
Input:
: a sized set of truthful or deceptive labeled reviews; : a sized set of unlabeled reviews; : the feature 1 set of terms derived from the words in reviews; : the feature 2 set of terms derived from the words in reviews; : the iteration number; : the number of reviews drawn from ; : the number of selected reviews which are classified as truthful; : the number of selected reviews which are classified as deceptive; : the reviews’ label, i.e. .
Output:
Procedure:
Randomly sample a -sized reviews set from ; Based on the set, train a classifier on the view of and a classifier on the view of ; For iterations: Use to classify the reviews in ; Use to classify the reviews in ; Select reviews from classified by as truthful; Select reviews from classified by as deceptive; Select reviews from classified by as truthful; Select reviews from classified by as deceptive; Add all those selected reviews to , remove them from ; Randomly choose reviews from and merge them to ; Based on the new set, retrain a classifier on the view of and a classifier on the view of ; End for.
|
At the preparatory phase, we produce a lexicon including all those terms appearing in the reviews. Then, the lexicon is divided into two distinct subsets evenly. Here, we take one subset as and the other as . That is, the terms in subset are different from the terms in subset and vice versa. Note that the two subsets are of the same size. Further, we regard subset as view , and subset as view .
With lines 1 and 2, we use the labeled reviews to train our base SVM classifier with two views, and . With lines 4–6, we use the trained classifiers to classify the unlabeled reviews in the test set and select the number of classified reviews from to augment the training set . Then, with line 7, we fetch unlabeled reviews from set to complement the test set . Finally, with line 8, the base classifiers are retrained using the augmented training set . With times of iteration, the CoFea algorithm is trained completely for spam review identification. We adopt the 10-fold cross-validation method to evaluate the accuracy in testing the CoFea algorithm.
There are two different methods for feature selection (in this paper, we use the terms occurring in the reviews as our feature) and those features are used to represent reviews as data samples. That is, each individual review is represented by a numeric vector and each dimension of the vector corresponds to one feature.
The CoFea-T (T abbreviates “total”) strategy is to use all terms in the lexicon for review representation. Under this strategy, we use the subset and the subset of views and as the features to represent each review as two numeric vectors. Then, the two numeric vectors are used to train the base classifier with the CoFea algorithm.
The details of the CoFea-T strategy are shown in Algorithm 2.
| Algorithm 2 The CoFea-T Strategy |
Input:
L: a -sized set of truthful or deceptive labeled reviews; : a -sized set of unlabeled reviews; , : a vector representing one review in the labeled reviews, means the view of a or b; , : a vector representing one review in the unlabeled reviews, means the view of a or b; , : a representation set of , means the view of a or b; , : a representation set of , means the view of a or b;
Output:
Procedure:
Traversing all the reviews without repetition both labeled and unlabeled, we can get a -sized lexicon with the entropy of each term as the term additive attribute; Sort the terms by entropy; Represent every review with vector, use the odd–even order of the terms in the lexicon to divide them. Get , , and . Each vector has the length of , and each vector has nearly the same entropy words; Return , , and .
|
The CoFea-S (S abbreviates “sampling”) strategy uses some of the terms in the subset and the subset for review representation. By the entropy score, we know that some lexical terms in the reviews are of very limited information for spam review identification. That is to say, these terms occur in deceptive and truthful reviews without any difference in frequency. If the terms with limited information were used for review representation, as conducted in the CoFea-T strategy, then it will induce much computation complexity because the length of each review vector would be very long. Thus, it would be wise to reduce the length of each review vector for a time-saving benefit in the CoFea algorithm. This idea motivates the proposal of the CoFea-S strategy. Under this strategy, we rank all terms in the lexicon by its entropy score. Then, we predefine a threshold entropy score to remove the terms in the lexicon and use the new lexicon as a partition to produce the subset and the subset for review representation.
The details of the CoFea-S strategy are shown in Algorithm 3. The difference between the CoFea-T strategy and the CoFea-S strategy is at line 3 in Algorithm 3. Under the CoFea-S strategy, we stipulate that the length of the numeric vector of each review should be
. That is to say, we use the top
terms with minimum entropy scores as the lexicon. Then, the lexicon is further split into two subsets, the subset
and the subset
, for review representation to construct the views
and
. In the experiments, we compare the two strategies embedded with the CoFea algorithm in spam review identification.
| Algorithm 3 The CoFea-S Strategy |
Input:
: a -size set of truthful or deceptive labeled reviews; : a -sized set of unlabeled reviews; , : a vector representing one labeled review, means the view of a or b; , : a vector representing one unlabeled review, means the view of a or b; , : a representation set of , means the view of a or b; , : a representation set of , means the view of a or b;
Output:
Procedure:
Traversing all the reviews without repetition both labeled and unlabeled, we can get a -sized lexicon with the entropy of each term as the term additive attribute; Sort the terms by entropy; Give a certain number to determine the length of a vector, i.e., the top minimum entropy terms will be in the vector; Represent every review with vector, get , , and . Each vector has the length of ; Return , , and .
|
4. Experiments
4.1. The Data Set
The data set we use in the experiments is the spam dataset from Myle Ott et al. [
7]. For each review, we conduct the stop-word elimination, stemming, and term frequency–inverse document frequency (TF-IDF) representation work [
11]. The stop-word list is quoted from the USPTO (United States Patent and Trademark Office) patent full-text and image database [
21]. The Porter stemming algorithm is employed to produce every individual word stem [
22]. We extracted all those sentences from one of the reviews using the sentence boundary-determining method mentioned in Weiss et al.’s paper [
23]. Representing all the terms in reviews by the TF-IDF method, which is a numerical statistical approach, reflects how important a word is in a document in collection or corpus [
24]. We conduct entropy computation of all lexical terms in the reviews to divide them into two subsets as subset
and subset
under the CoFea-T strategy and the CoFea-S strategy, respectively. The basic information about reviews in the spam data set is shown in
Table 1. The data set has 7677 terms (i.e., words including numbers and abbreviations) after preprocessing.
4.2. Experiment Setup
Based on the CoFea algorithm, three parameters,
,
, and
(i.e., the number of iterations, the number of unlabeled reviews classified as truthful, and the number of unlabeled reviews classified as deceptive) must be tuned in order to optimize the performance of the algorithm. On account of our previous work [
11], we know that the value of
and
should be equal to each other. We track accuracies of spam review identifications when we tune the parameter
while fixing the parameter
. We also track accuracies of spam review identifications when we tune the parameter
while fixing the parameter
. Because the CoFea-S strategy needs to predefine a threshold
for feature selection, we use
in this paper. Results of the CoFea-T and CoFea-S strategies for parameter tuning are as shown in
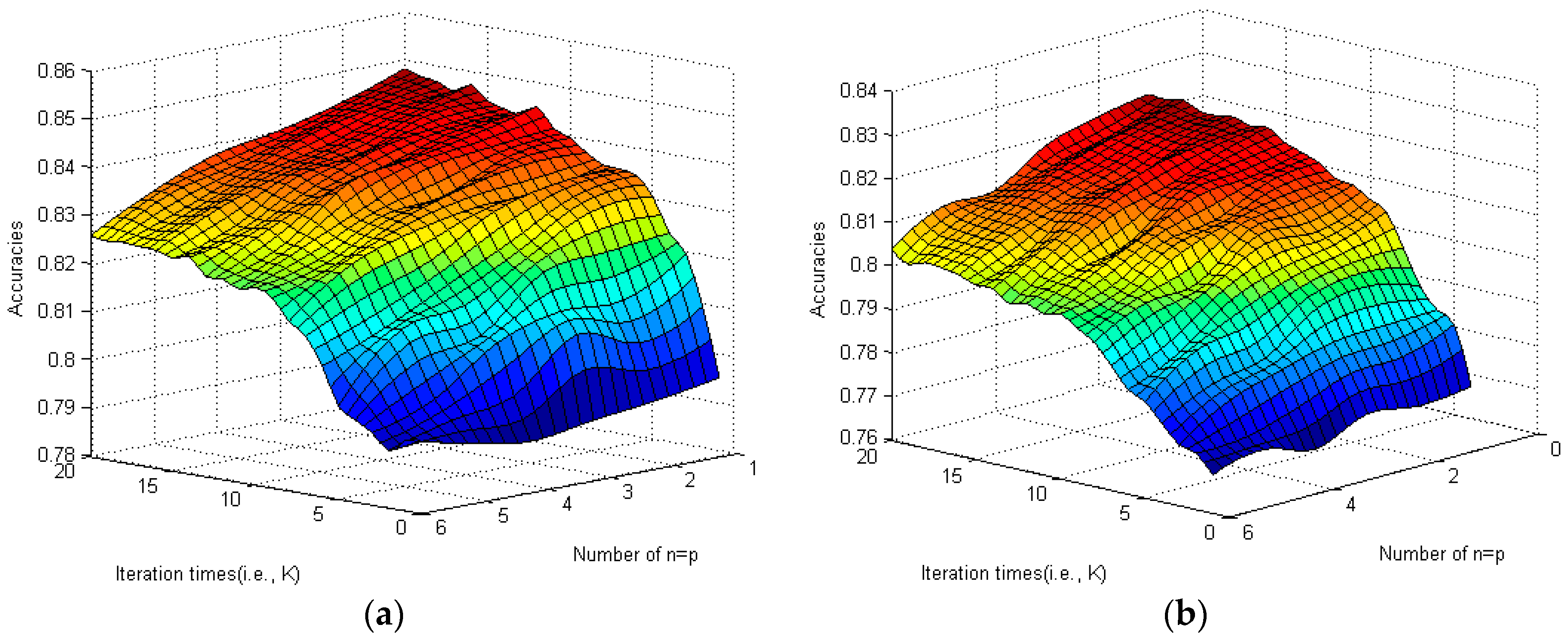
Figure 1a,b, respectively.
In the experiments, we set parameter from 1 to 6 and vary the parameter from 1 to 20. To average the performance, we implement a 5-fold cross-validation. That means we use the training set containing 320 reviews and the test set containing 80 reviews 5 times. Each time we randomly choose 5% of the data (16 data samples) for classifier training, and 15% of the data (48 data samples) for the testing phase.
To compare the CoFea algorithm with other state-of-the-art techniques, we compare the CoFea algorithm and the CoSpa (Another approach for spam review identification based on Co-training algorithm) algorithm [
11] in the experiments. The CoSpa algorithm use lexical terms as one view and probabilistic context-free grammar as another view in co-training for spam review identification. We fix the parameters
in both the CoFea algorithm and the CoSpa algorithm when tuning the parameter
. We fix the parameter
in both algorithms when tuning the parameter
.
4.3. Experimental Results
Figure 1 shows the performances of the CoFea algorithm embedded with the CoFea-T strategy (left) and the CoFea-S strategy (right). In the figure, the warm-toned color lumps represent high accuracy, and the cool-toned color lumps represent low accuracy. We can see from
Figure 1a that, when increasing the iterations, the accuracy of spam review identification has a certain degree of ascension. This approximate phenomenon also happened in the CoFea-S experiment. The accuracy quickly approaches the threshold at the
stage. That means the method (i.e., the CoFea algorithm) has certain limits. In general, the CoFea-T strategy performs better than the CoFea-S strategy.
Figure 2 shows the performances of different co-training algorithms—CoSpa, CoFea-T, and CoFea-S—in spam review identification. The CoSpa algorithm has an average accuracy of 0.8157, with 0.8375 as its highest accuracy. The CoFea-T algorithm has an average accuracy as 0.8202, with 0.8326 as its highest accuracy. The CoFea-S algorithm has an average accuracy as 0.7994, with 0.8105 as its highest accuracy.
In order to better illustrate the effectiveness of CoFea-T, CoFea-S, and CoSpa, we employ Wilcoxon signed-rank test [
25] to examine the statistical significance of experimental results when fixing
. The Wilcoxon signed-rank test indicates the CoFea-T strategy outperforms the CoSpa algorithm with a two-tailed
p-value of 0.0438, the CoFea-S strategy outperforms the CoSpa algorithm with a two-tailed
p-value of 0.0002, and the CoFea-T strategy outperforms the CoFea-S strategy with a two-tailed
p-value of 0.0000.
When fixing , the Wilcoxon signed-rank test indicates that the CoFea-T algorithm and the CoFea-S algorithm outperform the CoSpa algorithm, and the CoFea-T algorithm outperforms the CoFea-S algorithm.
The CoSpa algorithm only has its highest accuracy point without taking the stability into account. The CoFea-T algorithm has the highest mean accuracy among all the algorithms. The CoFea-S strategy has a good performance, very close to the CoFea-T strategy.
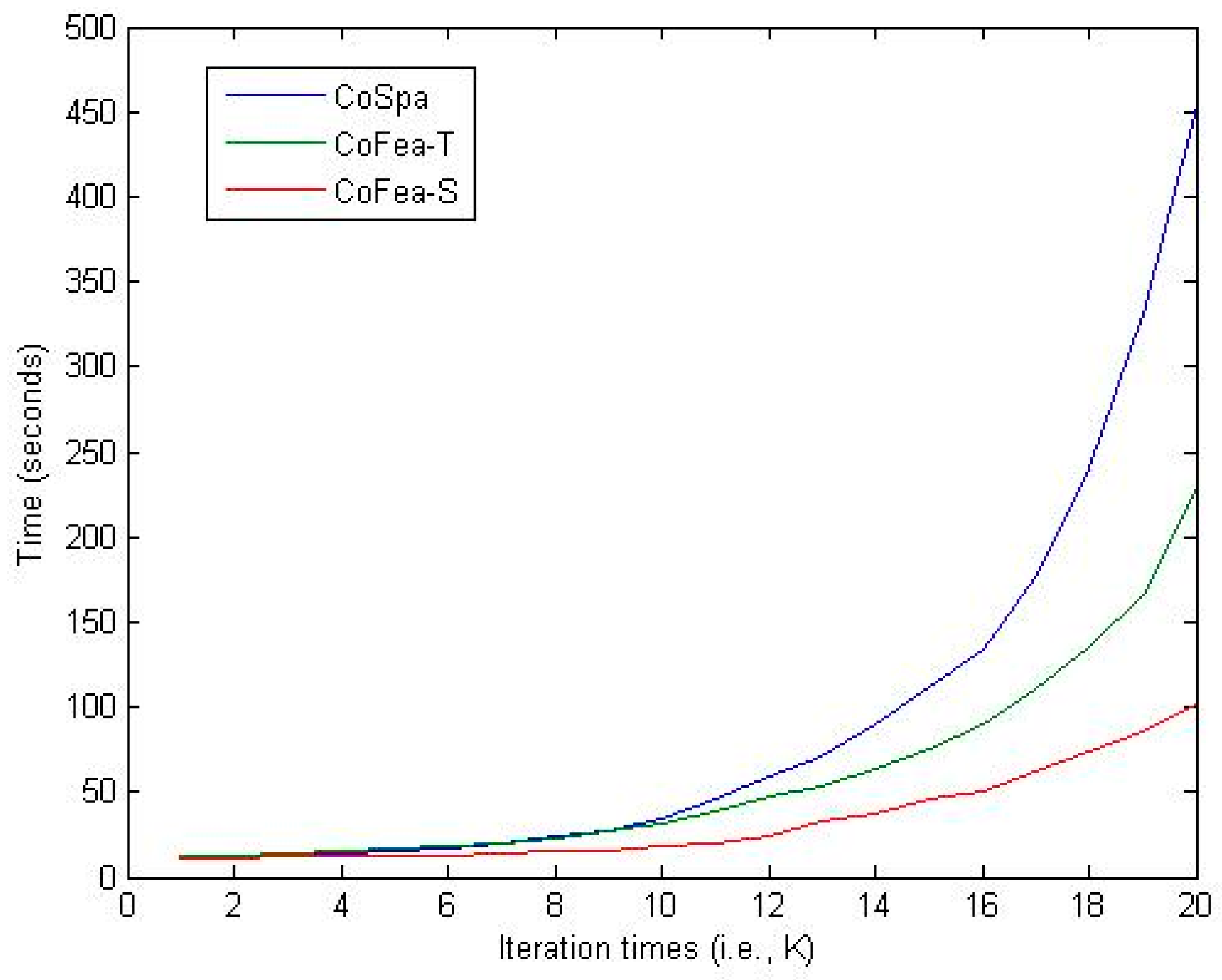
Figure 3 shows the time consumed in conducting the above experiments. The computer machine we use in the experiments had the following settings. CPU: Intel(R) Core(TM) i7-4700MQ @ 2.40 GHz; RAM: Kingston(R) DDR3 1600 MHz 4 × 2 GB; and Hard Drive: HGST(R) 500 GB @ 7200 r/min. The CoFea algorithm apparently has better speed performance in identifying the spam reviews, especially when dealing with a high number of iteration problems. Considering the motivation for proposing the CoFea algorithm (i.e., using terms only without other views), we argue that it is one of the most advisable algorithm among the state-of-the-art techniques in spam review identification domain.
5. Concluding Remarks
In this paper, we propose a new approach, called CoFea, based on entropy and the co-training algorithm to identify spam reviews by making use of unlabeled reviews. The experimental results show some promising aspects of the proposed approach in the paper. The contribution of the paper can be summarized as follows.
First, we sort terms by means of entropy measures. This allows feature selection and can be conducted based on the amount of information a term contains.
Second, we propose two strategies, the CoFea-T strategy and the CoFea-S strategy, with different lengths of vectors of each view to be embedded with the CoFea algorithm for spam review identification.
Third, we conduct experiments on the spam review set to compare the proposed approach with the state-of-the-art techniques in spam review identification. Experimental results show that both the CoFea-T and CoFea-S strategies have produced good performances on spam review identification. The CoFea-T strategy has produced better accuracies than the CoFea-S strategy, while the CoFea-S strategy needs less time for computation than the CoFea-T strategy. Under the condition of lacking other views to implement the co-training algorithm, the CoFea algorithm is a good alternative for spam review identification using textual content only.
Although the paper has shown some promising aspects of using co-training on spam review identification, we admit that this paper is merely the initial step. In the future, on the one hand, we will use more data sets to examine the effectiveness of the proposed CoFea algorithm in spam review identification. On the other hand, we will also extend the co-training algorithm to more research areas such as sentiment analysis [
26], image recognition [
27], and text classification [
28] to explore more fields. In fact, text classification is a basic technique for deceptive review identification. All the techniques mentioned in the paper can be extended to text classification. With the prosperity of e-commerce and online shopping, we regard the deceptive review identification to be a more practical application for users than pure text classification. As for sentiment analysis and image recognition, we cannot apply simple lexical terms as its feature for co-training, and there is no golden theory on how to build its feature sets. For this reason, we will firstly conduct research on feature extraction of the two tasks and further apply the proposed co-training approach on them.
Acknowledgments
This work is supported by the National Natural Science Foundation of China under Grant No. 91218302, 91318301, 61379046 and 61432001; the Fundamental Research Funds for the Central Universities (buctrc201504).
Author Contributions
Wen Zhang and Taketoshi Yoshida conceived and designed the experiments; Wen Zhang performed the experiments; Wen Zhang and Chaoqi Bu analyzed the data; Siguang Zhang contributed analysis tools; Wen Zhang and Chaoqi Bu wrote the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aljukhadar, M.; Senecal, S. The user multifaceted expertise: Divergent effects of the website versuse-commerce expertise. Int. J. Inf. Manag. 2016, 36, 322–332. [Google Scholar] [CrossRef]
- Xiang, Z.; Magnini, V.P.; Fesenmaier, D.R. Information technology and consumer behavior in travel andtourism: Insights from travel planning using the Internet. J. Retail. Consum. Serv. 2015, 22, 244–249. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, S.; Wang, Q. KSAP: An approach to bug report assignment using KNN search and heterogeneous proximity. Inf. Softw. 2016, 70, 68–84. [Google Scholar] [CrossRef]
- Sui, D.Z. Mapping and Modeling Strategic Manipulation and Adversarial Propaganda in Social Media: Towards a tipping point/critical mass model. In Proceedings of the Workshop on Mapping Ideas: Discovering and Information Landscapes, San Diego, CA, USA, 29–30 June 2011.
- Jindal, N.; Liu, B. Opinion spam and analysis. In Proceedings of the 2008 International Conference on Web Search and Data Mining, Palo Alto, CA, USA, 11–12 February 2008; pp. 219–230.
- Pang, B.; Lee, L. Opinion mining and sentiment analysis. Found. Trends Inf. Retr. 2008, 2, 1–134. [Google Scholar] [CrossRef]
- Ott, M.; Choi, Y.; Cardie, C.; Hancock, J.T. Finding Deceptive Opinion Spam by Any Stretch of the Imagination. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics, Portland, OR, USA, 19–24 June 2011; pp. 309–319.
- Feng, V.W.; Hirst, G. Detecting deceptive opinions with profile compatibility. In Proceedings of the International Joint Conference on Natural Language Processing, Nagoya, Japan, 14–18 October 2013.
- Zhou, L.; Shi, Y.; Zhang, D. A Statistical Language Modeling Approach to Online Deception Detection. IEEE Trans. Knowl. Data Eng. 2008, 20, 1077–1081. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z.; Mukherjee, A.; Liu, B.; Shao, J. Analyzing and Detecting Opinion Spam on a Large scale Dataset via Temporal and Spatial Patterns. In Proceedings of the 9th International AAAI Conference on Web and Social Media, Oxford, UK, 26–29 May 2015.
- Zhang, W.; Bu, C.; Yoshida, T.; Zhang, S. CoSpa: A Co-training Approach for Spam Review Identification with Support Vector Machine. Information 2016, 7, 12. [Google Scholar] [CrossRef]
- Huang, J.; Lu, J.; Ling, C.X. Comparing Naive Bayes, Decision Trees, and SVM with AUC and Accuracy. In Proceedings of the 3rd IEEE International Conference on Data Mining, Melbourne, FL, USA, 19–22 November 2003; p. 553.
- Chapelle, O.; Schölkopf, B.; Zien, A. Semi-Supervised Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the Workshop on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998; pp. 92–100.
- Committee on the Fundamentals of Computer Science—Challenges and Opportunities. Computer Science: Reflections on the Field, Reflections from the Field; ISBN 0-309-09301-5. The National Academies Press: Washington, DC, USA, 2004. [Google Scholar]
- Liu, W.; Li, Y.; Tao, D.; Wang, Y. A general framework for co-training and its applications. Neurocomputing 2015, 167, 112–121. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Joachims, T. Transductive Inference for Text Classification using Support Vector Machines. In Proceedings of the 1999 International Conference on Machine Learning, Bled, Slovenia, 27–30 June 1999; pp. 200–209.
- USPTO Stop Words. Available online: http://ftp.uspto.gov/patft/help/stopword.htm (accessed on 1 March 2016).
- Porter Stemming Algorithm. Available online: http://tartarus.org/martin/PorterStemmer/ (accessed on 29 November 2016).
- Weiss, S.M.; Indurkhya, N.; Zhang, T.; Damerau, F. Text Mining: Predictive Methods for Analyzing Unstructured Information; Springer: New York, NY, USA, 2004; pp. 36–37. [Google Scholar]
- Rajaraman, A.; Ullman, J.D. Data Mining. In Mining of Massive Datasets; Cambridge University Press: London, UK, 2011; pp. 1–17. [Google Scholar]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Ravi, K.; Ravi, V. A survey on opinion mining and sentiment analysis: Tasks, approaches and applications. Knowl. Based Syst. 2015, 89, 14–46. [Google Scholar] [CrossRef]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Zhang, W.; Yoshida, T.; Tang, X. Text classification based on multi-word with support vector machine. Knowl. Based Syst. 2008, 21, 879–886. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).