Abstract
A sliding block code between shift spaces is called fiber-mixing if, for every x and in X with , there is which is left asymptotic to x and right asymptotic to . A fiber-mixing factor code from a shift of finite type is a code of class degree 1 for which each point of Y has exactly one transition class. Given an infinite-to-one factor code between mixing shifts of finite type (of unequal entropies), we show that there is also a fiber-mixing factor code between them. This result may be regarded as an infinite-to-one (unequal entropies) analogue of Ashley’s Replacement Theorem, which states that the existence of an equal entropy factor code between mixing shifts of finite type guarantees the existence of a degree 1 factor code between them. Properties of fiber-mixing codes and applications to factors of Gibbs measures are presented.
1. Introduction
It is well known that for any factor code from an irreducible shift of finite type onto a sofic shift with equal topological entropy, there is a uniform upper bound on the number of preimages of the points in Y. In this case, almost all points (including the doubly transitive points) have the same number of preimages. This number is called the degree of π. If the degree of π is 1, π may be considered as a weaker version of a conjugacy (usually called almost invertible), in the sense that π is a measure theoretic isomorphism between any fully supported ergodic invariant measure on X and its push-forward to Y by π. As finding a conjugacy between two shifts of finite type is one of the very difficult problems in the field, finding a factor code of degree 1 has been investigated in many classification problems [1,2,3]. In the early 1990s, Ashley showed that if there is a factor code between equal entropy mixing shifts of finite type, then there also exists a factor code of degree 1 [4]. This was referred to as Replacement Theorem in [5]. Ashley’s result simplified many previous proofs on the existence of degree 1 factor codes.
For a general factor code where the topological entropies of X and Y may differ, there may exist a point of Y with an infinite number of preimages. However, one can define an equivalence relation on each fiber and consider the number of equivalence classes. It turned out that there is a uniform upper bound on the number of equivalence classes (called transition classes), and almost all points (including the right transitive points) have the same number of classes in their fiber [6]. This number is called the class degree of π. Properties of class degree and the structure of fibers and transition classes show that class degree may be regarded as a natural generalization of the degree to not necessarily finite-to-one factor codes [6,7,8].
As the degree gives an upper bound on the number of ergodic measures on X over a fully supported ergodic measure on Y, the class degree gives an upper bound on the number of ergodic measures on X of relative maximal entropy over a fully supported ergodic measure on Y. Hence, if a factor code is of class degree 1, then for each fully supported ergodic measure on Y, there is a unique relative maximal measure over it [6]. A special kind of class degree 1 code, called a fiber-mixing factor code, was first defined in [9]. A fiber-mixing factor code from a shift of finite type is a code of class degree 1 for which each point of Y has exactly one transition class; that is, it is a constant-class-to-one code of class degree 1 [7]. In [9], Yoo proved that a fiber-mixing code sends every fully supported Markov measure on X to a Gibbs measure on Y. Kempton [10] also used factor codes with a similar property for the study of factors of Gibbs measures. It turned out that such code is indeed a 1-block fiber-mixing code defined on a one-sided mixing 1-step shift of finite type (see Proposition 2).
Factor codes of class degree 1 are useful in the study of push-forwards or lifts of invariant measures, and the existence of a finite-to-one factor code guarantees the existence of a factor code of degree 1. Hence, it is natural to ask whether there also exists a kind of Replacement Theorem for infinite-to-one factor codes, which is the motivation of this paper. We state our main results as follows. Denote by the topological entropy of X.
Theorem 1.
Suppose that there is a factor code between mixing shifts of finite type with . Then, there is a fiber-mixing (hence class degree 1) factor code from X onto Y.
In fact, as the proof shows, any code from a proper subshift of X can be extended to a fiber-mixing factor code from X onto Y. By using a reduction to the mixing case, we can state an infinite-to-one analogue of the Replacement Theorem. Denote by the period of X.
Theorem 2.
Suppose that there is a factor code between irreducible shifts of finite type with . Then there is a constant-class-to-one factor code of class degree from X onto Y.
As constant-class-to-one codes are bi-continuing [7], Theorems 1 and 2 also strengthen the main results of [11], in which the existence of an infinite-to-one factor code implies the existence of a bi-continuing factor code.
The paper is organized as follows. In the next section, we present several properties of fiber-mixing codes in view of class degree 1 codes. In Section 3, we complete the proofs of Theorems 1 and 2, and present an equivalent condition for the existence of a fiber-mixing factor code between irreducible shifts of finite type (see Theorem 3). In Section 4 we present a relation between fiber-mixing codes and factor codes defined by Kempton in [10], and an application to factors of Gibbs measures.
2. Preliminaries and Fiber-Mixing Codes
We introduce basic terminology and known results on symbolic dynamics. For further details on symbolic dynamics, see [5]. Properties of class degree and transition classes can be found in [6,7,8].
For a shift space (or subshift) X with the shift map σ, denote by the set of all words of length n appearing in the points of X and ; also let . For , denote by the set of all words with and .
A point is right transitive if the forward orbit of x is dense in X. Two points x and are said to be right asymptotic if for some . Left transitive points and left asymptotic points are defined analogously. X is called irreducible if there is a right transitive point, or equivalently, for all there is a word w with . It is called mixing if for all , there is an integer such that whenever , we can find with . If there is such an N which works for all , then we call N a transition length for X. A word is synchronizing if whenever and are in , we have . If each is synchronizing for some , then X is called a (k-step) shift of finite type. Every shift of finite type is conjugate to an edge shift; i.e., a one-step shift space which consists of all bi-infinite trips on a directed graph. A sofic shift is a factor of a shift of finite type. A mixing sofic shift has a transition length.
The period of a shift space X (denoted by ) is the greatest common divisor of the periods of all periodic points of X. If X is an irreducible shift of finite type of period p, then X has the periodic decomposition: there are disjoint clopen subsets of X so that , , and is mixing for each i. The entropy of a shift space is defined by , which equals the topological entropy of as a dynamical system. If X is a mixing shift of finite type, then for each , where (resp. ) denotes the number of periodic points of period n (resp. least period n).
A (sliding block) code is a continuous σ-commuting map between shift spaces. A factor code is a surjective code. Each code can be recoded to a one-block code; i.e., a code for which determines . For simplicity, we will also use π for the induced map from to . We call π finite-to-one if is finite for all y in Y. Otherwise, π is called infinite-to-one. If is a factor code from an irreducible shift of finite type, then it is well known that if and only if π is finite-to-one (e.g., Section 8 in [5]). If this condition holds, then every doubly transitive point in Y has the same number of preimages (the degree of π), which equals the minimal number of preimages over all points in Y.
Class degree is a generalization of a degree to (possibly infinite-to-one) factor codes, where the entropies of X and Y may differ. We recall the properties of transition classes and class degrees. Details can be found in [6,7,8].
Let be a factor code from a shift of finite type onto an irreducible sofic shift. Given two points , we say if for each integer n there exists a point z in X such that , and for some . Say if and . Then ∼ is an equivalence relation on each fiber . Each equivalence class is called a transition class over y. Denote by the set of transition classes over y. The class degree of π is the minimal number of transition classes over the points of Y. Then, as for the equal entropy case, equals the class degree of π for each right transitive point y in Y [6].
The following properties of factor codes were defined in [7] and [9], respectively. The definition of a fiber-mixing code is rather simple and can be stated without transition classes (see Figure 1).
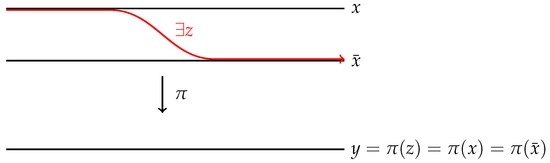
Figure 1.
A fiber-mixing code.
Definition 1.
Let be a factor code between shift spaces.
- Suppose that X is of finite type and Y is irreducible and sofic. π is called constant-class-to-one if is independent of .
- π is called fiber-mixing if, for every with , there is such that z is left asymptotic to x, right asymptotic to and .
These conditions are clearly invariant under conjugacy. A simple example of a fiber-mixing factor code is a projection map: if is a projection, and Z is a mixing sofic shift (more generally if Z has the specification property), then π is fiber-mixing.
The following notion introduces a local condition for codes to be fiber-mixing.
Definition 2.
Let be a 1-block factor code from a 1-step shift of finite type. Let for some and . A path is called a bridge from u to v if , and .
If the domain of a fiber-mixing code is of finite type, there is a uniform bound condition on the code, which appears in Lemma 3.2 in [9] and in Theorem 5.3 in [7] in a very general form. For the completeness of the exposition, we include a proof.
Lemma 1.
Let be a 1-block fiber-mixing factor code from a 1-step shift of finite type. Then, there is such that—for every with —there is a bridge from u to v.
Proof.
Suppose that the assertion of the lemma does not hold. Then, for each , there are such that and there is no bridge from to . By choosing a subsequence, we can assume that there are with and . Then, . Since π is fiber-mixing, there exist and with such that and . Take large so that , and . Define a point by . Then, is a bridge from to , which is a contradiction. ☐
Note that if k satisfies the condition in the above lemma, then every also satisfies the condition.
Corollary 1.
Let be a fiber-mixing factor code from a shift of finite type. Then Y is also of finite type.
Proof.
By recoding, we may assume that X is 1-step and π is 1-block. Let be as in Lemma 1. For each , if , then take and . Then there is a bridge from β to so that . So, each word is synchronizing, and Y is a k-step shift of finite type. ☐
By Lemma 1, the following corollary is immediate.
Corollary 2.
[7] Let be a factor code from a shift of finite type onto an irreducible sofic shift. Then π is fiber-mixing if and only if it is constant-class-to-one and the class degree of π is 1.
Lemma 2.
Let be a fiber-mixing factor code between irreducible shifts of finite type. Then .
Proof.
By usual reduction, we may assume that , i.e., Y is mixing. Let be the periodic decomposition of X. If , since acts transitively on each , is onto for each i. Take any , and . As π is fiber-mixing, there is , which is left asymptotic to x and right asymptotic to . As z is left (resp. right) asymptotic to x (resp. ), we have (resp. ). This is a contradiction. Hence, and . ☐
A π-diamond is a pair of distinct blocks with (). Recall that a 1-block factor code from an irreducible shift of finite type is finite-to-one if and only if there is no π-diamond (e.g., see Section 8 in [5]).
Corollary 3.
Let be a finite-to-one fiber-mixing factor code from an irreducible shift of finite type. Then π is a conjugacy.
Proof.
We may assume that X is 1-step and π is 1-block. Let be as in Lemma 1. If π is not a conjugacy, then there are distinct points with . As π is finite-to-one, there are infinitely many with . Hence, there are indices such that , and . By Lemma 1, there are a bridge u from to and a bridge v from to . Then, two blocks and form a π-diamond, a contradiction. ☐
Given a set of words , denote by the coded system generated by W; that is, the smallest shift space containing the sequences obtained by concatenating words in W. We present two simple fiber-mixing factor codes from shift spaces which are not of finite type.
Example 1.
(1) Let and , where and . Note that Y is the even shift (sofic), while X is a non-sofic (mixing) coded system. Let be a code sending a to 1 and to 0.
Then, π is fiber-mixing. Suppose that . If 1 occurs in y, then we can assume that . Then so that is a desired point. Otherwise, . In this case, we have . By examining each case, for each , one can check that there is with z left asymptotic to x and right asymptotic to .
(2) Let and , where and . Let be the subscript dropping code. Let . If a occurs in y infinitely to the right, then contains only one point. Otherwise, consists of two points x and such that x and differ in only one coordinate. Hence π is an example of a finite-to-one fiber-mixing factor code which is not a conjugacy. Note that X is strictly sofic, while Y is a mixing shift of finite type (Fibonacci).
3. Existence of Fiber-Mixing Codes
In this section, we prove Theorems 1 and 2, and present a characterization of the existence of a fiber-mixing factor code between irreducible shifts of finite type with unequal entropies (Theorem 3).
The following lemma is referred to as the Blowing up Lemma.
Lemma 3.
[12] Let X be a mixing shift of finite type with and . Let . Then there is a mixing shift of finite type such that
- (1)
- ,
- (2)
- , and
- (3)
- for all other i.
Lemma 4.
Let and . Then there is a mixing shift of finite type W such that , for all , and for each .
Proof.
Let be a mixing shift of finite type with (such exists as the set of Perron numbers is dense in . One may construct directly by considering a graph consisting of two long cycles of relatively prime lengths meeting only at a single vertex).
Note that for large enough , we have . Hence, from the definition of the entropy, we have for n large enough. Thus for large enough n. By applying the Blowing up Lemma repeatedly to points in having low periods, we can obtain a mixing shift of finite type W satisfying all the conditions. ☐
Lemma 5.
Let X and Y be mixing shifts of finite type with . Then there exist a mixing shift of finite type and a fiber-mixing factor code .
Proof.
Let . Also let if for all and otherwise. Then there is such that for all . There is also such that for all . Let . By Lemma 4, we can find a mixing shift of finite type W such that , for each and for all . Then we have
for , and for . Thus, for all . Since , there is an embedding by Krieger’s Embedding Theorem [13]. The result follows by letting and be the composite of , followed by the projection code from onto Y. ☐
Lemma 6.
(Theorem 26.17 in [14]) Let X be a mixing shift of finite type and a proper subshift of X. For given , there is a mixing shift of finite type such that and .
Lemma 7.
(Extension Lemma) [12] Let X be a shift space and Y a mixing shift of finite type. If there is a code from X into Y, then any code from a subshift of X to Y can be extended to a code from X to Y.
Now we are ready to prove Theorem 1. The first part of the proof of Theorem 1 follows the line in [11].
Proof of Theorem 1.
Suppose that is a proper subshift of X and is any code. As we have stated in Section 1, we will construct a fiber-mixing factor code so that .
By Lemma 6, there is a mixing shift of finite type disjoint from with ; also by Lemma 5, there exist a mixing shift of finite type and a fiber-mixing factor code . By Lemma 7 used for a subshift , we can find a code such that and . This ψ is a factor code, since is onto. Finally, by Lemma 6 there is a mixing shift of finite type which is disjoint from Z and .
By passing to higher block shifts, we may assume that (a) , and Y are 1-step, (b) and , (c) ψ is a 1-block code, and (d) if and , then . Let be as in Lemma 1 for . Choose N large so that N is a transition length for X, Y, V, and Z.
For each , and , define
Since N is a transition length for , and Z, these sets are nonempty. Now, since , there is such that
for all and . For each and , define surjections from onto . Similarly, define surjections from onto . Finally, for each , define a map such that . This is possible because N is a transition length for Y.
Given , we divide into low and high-stretches, as in [11]. Call a segment of x a low-stretch if it is a maximal Z-word of length . Remaining stretches of maximal length are called high-stretches (of x). By the condition (d), low-stretches of x cannot overlap, and hence x is uniquely decomposed as low and high-stretches. Additionally, if a high-stretch of x is of length greater than , then it is called a long high-stretch. Otherwise, we call it a short high-stretch.
Now, we define a code . Let .
- (i)
- Low-stretches. If is in a low-stretch, then let .
- (ii)
- Long high-stretches. If is in a long high-stretch, let .
- (iii)
- Short high-stretches. If is a short high-stretch, then . Let .
- (iv)
- High–low transition. If is the end of some long high-stretch and is the beginning of some low-stretch, then let
- (v)
- Low–high transition. Similarly as in (iv), using .
These cases cover all parts of x, and π is a well-defined code from X to Y. Note that π has memory and anticipation . Since consists of a single low-stretch and consists of a single high-stretch, we have and , so π is a factor code which is an extension of .
To show that π is fiber-mixing, let . We first prove the following claim.
Claim.
Let , , and satisfy . Then, we can find such that , and .
Proof.
First, suppose that there exists an such that is part of a low-stretch. Then, . Let and . Since , by Lemma 1, there exists with . Define a point z by letting
Note that is part of a low-stretch of z, and therefore rule (i) applies to , and we have .
Next, suppose that the above does not hold. Then, is part of a long high-stretch of x (since the length of this interval is ). Since there is no Z-word of length greater than in this part, by the property (d), there exist and with . Let .
Since is onto, there exists with . Let . Then . Note that is part of a long high-stretch and is a low-stretch ( guarantees no new occurrence of a Z-block of length greater than in ). Therefore, rules (ii), (iv), and (i) apply to , and we have , which proves the claim. ☐
By a symmetric argument, if and satisfy , then we can find such that , and .
To show that π is fiber-mixing, suppose that and . Since π is an extension of a factor code , there is such that . Then, by the claim above, there is such that , and . There is also such that , and . Let . Then, is a desired point, which completes the proof. ☐
Remark 1.
By combining the proof of the above theorem and the argument in Theorem 4.4 in [11], one can prove that the result of Theorem 1 still holds if X is a shift space with the specification property.
For two shift spaces X and Y, we denote by if, whenever x is a periodic point of X, there exists a periodic point of Y whose period divides the period of x. It is well known that given two irreducible shifts of finite type X and Y with , there is a factor code from X onto Y if and only if [5,12].
Theorem 3.
Let X and Y be irreducible shifts of finite type. Then there is a fiber-mixing factor code if and only if one of the following holds.
- X is conjugate to Y, or
- , , and .
Proof.
Suppose that there is a fiber-mixing factor code π from X onto Y. Then it is clear that . We also have by Lemma 2. If π is finite-to-one, then by Corollary 3, it is a conjugacy. Otherwise, π is infinite-to-one and .
Conversely, since a conjugacy is clearly a fiber-mixing factor code, the sufficiency follows from Theorem 1 and a reduction to the mixing case. ☐
Theorem 2 follows from a standard reduction to the mixing case.
Proof of Theorem 2.
By usual reduction, we may assume that . Let be the periodic decomposition of X. Then is an irreducible component of the p-th higher power shift of X and is mixing. Hence, by Theorem 1, there is a -commuting fiber-mixing code . For , let . Then is a constant-class-to-one code of class degree . ☐
Note that is the smallest possible class degree of a factor code from X onto Y.
4. Application: Factors of Gibbs Measures under Fiber-Mixing Codes
As an application, we present the existence of factor codes mapping fully supported Gibbs measures to Gibbs measures. We recall some definitions.
Let X be a mixing shift of finite type. An invariant (probability) measure μ on X is called a Gibbs measure if there are a continuous function , and , such that
for all and . The function f is called a potential of μ. Denote by the set of all Gibbs measures on X.
Denote by the one-sided mixing shift of finite type obtained from X, and by the set of Gibbs measures on . There is a natural identification between the set of invariant measures on and that on X, and this identification maps into . Hence, one may also think about as a measure on X (we will call μ a one-sided Gibbs measure). In fact, if μ is a Gibbs measure on X, then if and only if μ has a one-sided potential (that is, a function on X for which depends only on ). This is the case when μ has a potential function which is Hölder continuous [15], of summable variation [16], or more generally, a Bowen function [17].
In [10], Kempton extended an idea of [18] and showed the following theorem. In what follows, for a set and , denote by the set .
Theorem 4.
[10] Let be a 1-block factor code between one-sided 1-step mixing shifts of finite type. If there is with the following two properties, then for every , we have .
- (i)
- If is nonempty for some , with and , then .
- (ii)
- for each .
The condition (ii) above is indeed related to continuing properties of factor codes defined in [19]. We will soon see that condition (ii) is implied by (i). A code between shift spaces is called right continuing if, whenever , and is left asymptotic to y, then there exists which is left asymptotic to x and . A left continuing code is defined similarly. If π is right and left continuing at the same time, it is called bi-continuing. The following is an easy observation from Lemma 1.
Lemma 8.
[7,9] Let be a fiber-mixing factor code from a shift of finite type. Then it is bi-continuing.
In the case where X is not of finite type, then a fiber-mixing factor code need not be continuing, as the following example shows.
Example 2.
Let be a factor map defined in Example 1(1). Then π is not left continuing: Take and . If is right asymptotic to x, then is in the orbit of , and we have . One can check that π is right continuing.
The proof of Proposition 2.4 in [11] gives the following uniform property for continuing codes.
Proposition 1.
[11] Let be a right continuing code with X of finite type. Then π has a (right continuing) retract; that is, there is so that given and with , we have with and .
Remark 2.
Let satisfy the conditions in Proposition 1. Suppose also that X is 1-step and π is 1-block. Then, given and with , there is such that and .
A factor code between one-sided subshifts naturally induces a factor code between (two-sided) subshifts by the same block map. Thus, say that a factor code is fiber-mixing if the corresponding factor code is fiber-mixing. The fiber-mixing property for a factor code between one-sided subshifts is a conjugacy invariant.
Proposition 2.
Let be a 1-block fiber-mixing factor code from a 1-step shift of finite type. Then it satisfies both conditions in Theorem 4.
Proof.
The induced map between the two-sided subshifts is fiber-mixing and thus bi-continuing. So, take , where k is as in Lemma 1 and M yields the right and left continuing retracts as given in Proposition 1 for . The map , hence also π, satisfies the condition (i) by Lemma 1 and (ii) by Remark 2. ☐
By Proposition 2, Theorem 4, and Theorem 1, we obtain the following corollaries.
Corollary 4.
(1) Let be a fiber-mixing factor code between one-sided mixing shifts of finite type. Then for every , we have .
(2) Let be a fiber-mixing factor code between (two-sided) mixing shifts of finite type. Then for every , we have . In particular, if μ is a Gibbs measure on X with a potential in Bowen class, then is a Gibbs measure on Y.
In Corollary 4(2), we do not know whether for each .
Corollary 5.
Let X and Y be one-sided (resp. two-sided) mixing shifts of finite type with . If there is a factor code from X onto Y, then there is a factor code sending every Gibbs measure (resp. every one-sided Gibbs measure) on X to a Gibbs measure (resp. a one-sided Gibbs measure) on Y.
Acknowledgments
The author would like to thank the referees for their valuable comments. This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2012R1A1A2006874) and by the Ministry of Science, ICT & Future Planning (2015R1C1A1A02037553).
Conflicts of Interest
The author declares no conflict of interest.
References
- Adler, R.L.; Goodwyn, L.W.; Weiss, B. Equivalence of topological Markov shifts. Israel J. Math. 1977, 27, 48–63. [Google Scholar] [CrossRef]
- Adler, R.L.; Marcus, B. Topological entropy and equivalence of dynamical systems. Mem. Am. Math. Soc. 1979, 20, 1–84. [Google Scholar] [CrossRef]
- Boyle, M.; Marcus, B.; Trow, P. Resolving Maps and the Dimension Group for Shifts of Finite Type. Mem. Am. Math. Soc. 1987, 70, 1–146. [Google Scholar] [CrossRef]
- Ashley, J. Bounded-to-1 factors of an aperiodic shift of finite type are 1-to-1 almost everywhere factors also. Ergod. Theory Dyn. Syst. 1990, 10, 615–625. [Google Scholar] [CrossRef]
- Lind, D.; Marcus, B. An Introduction to Symbolic Dynamics and Coding; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Allahbakhshi, M.; Quas, A. Class degree and relative maximal entropy. Trans. Am. Math. Soc. 2013, 365, 1347–1368. [Google Scholar] [CrossRef]
- Allahbakhshi, M.; Hong, S.; Jung, U. Class-closing factor codes and constant-class-to-one factor codes from shifts of finite type. Dyn. Syst. 2015, 30, 485–500. [Google Scholar] [CrossRef]
- Allahbakhshi, M.; Hong, S.; Jung, U. Structure of transition classes for factor codes on shifts of finite type. Ergod. Theory Dyn. Syst. 2015, 35, 2353–2370. [Google Scholar] [CrossRef]
- Yoo, J. On factor maps that send Markov measures to Gibbs measures. J. Stat. Phys. 2010, 141, 1055–1070. [Google Scholar] [CrossRef]
- Kempton, T. Factors of Gibbs measures for subshifts of finite type. Bull. Lond. Math. Soc. 2011, 43, 751–764. [Google Scholar] [CrossRef]
- Jung, U. On the existence of open and bi-continuing codes. Trans. Am. Math. Soc. 2011, 363, 1399–1417. [Google Scholar] [CrossRef]
- Boyle, M. Lower entropy factors of sofic systems. Ergod. Theory Dyn. Syst. 1983, 3, 541–557. [Google Scholar] [CrossRef]
- Krieger, W. On the subsystems of topological Markov chains. Ergod. Theory Dyn. Syst. 1982, 2, 195–202. [Google Scholar] [CrossRef]
- Denker, M.; Grillenberger, C.; Sigmund, K. Ergodic Theory on Compact Spaces; Springer: Berlin/Heidelberg, Germany, 1976; Volume 527. [Google Scholar]
- Bowen, R. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms; Springer: Berlin/Heidelberg, Germany, 1975; Volume 470. [Google Scholar]
- Coelho, Z.; Quas, A. Criteria for -continuity. Trans. Am. Math. Soc. 1998, 350, 3257–3268. [Google Scholar] [CrossRef]
- Walters, P. Convergence of the Ruelle operator for a function satisfying Bowen’s condition. Trans. Am. Math. Soc. 2001, 353, 327–347. [Google Scholar] [CrossRef]
- Pollicott, M.; Kempton, T. Factors of Gibbs Measures for Full Shifts. In Entropy of Hidden Markov Processes and Connections to Dynamical Systems; Cambridge University Press: Cambridge, UK, 2011; pp. 246–257. [Google Scholar]
- Boyle, M.; Tuncel, S. Infinite-to-one codes and Markov measures. Trans. Am. Math. Soc. 1984, 285, 657–684. [Google Scholar] [CrossRef]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).