Anisotropically Weighted and Nonholonomically Constrained Evolutions on Manifolds †
Abstract
:1. Introduction
Background
2. Frame Bundles, Stochastic Development, and Anisotropic Diffusions
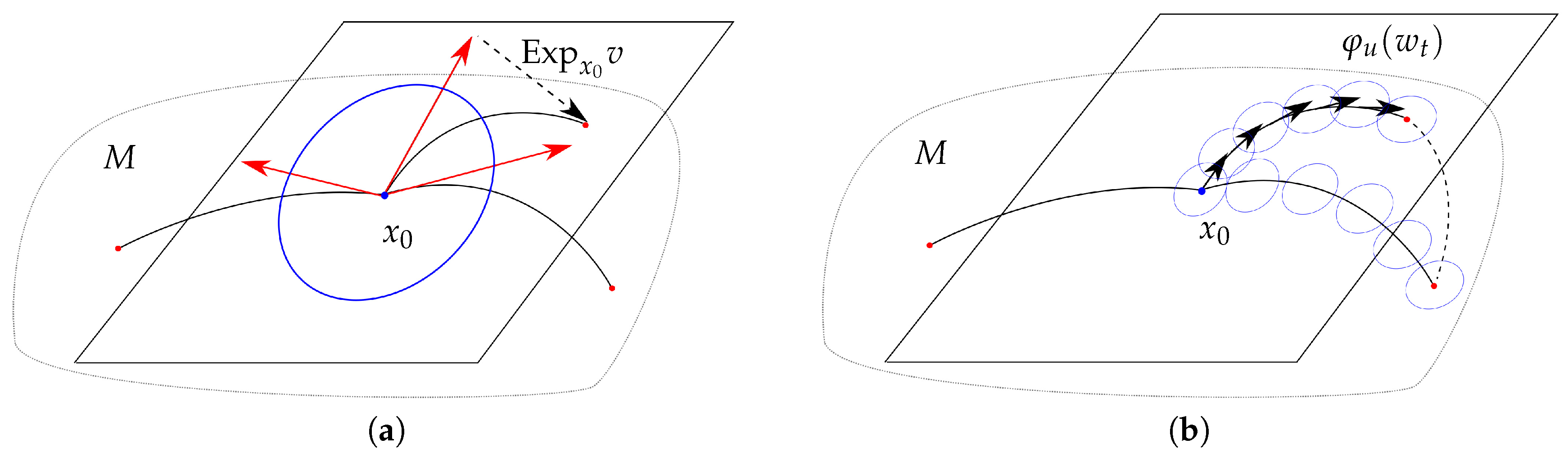
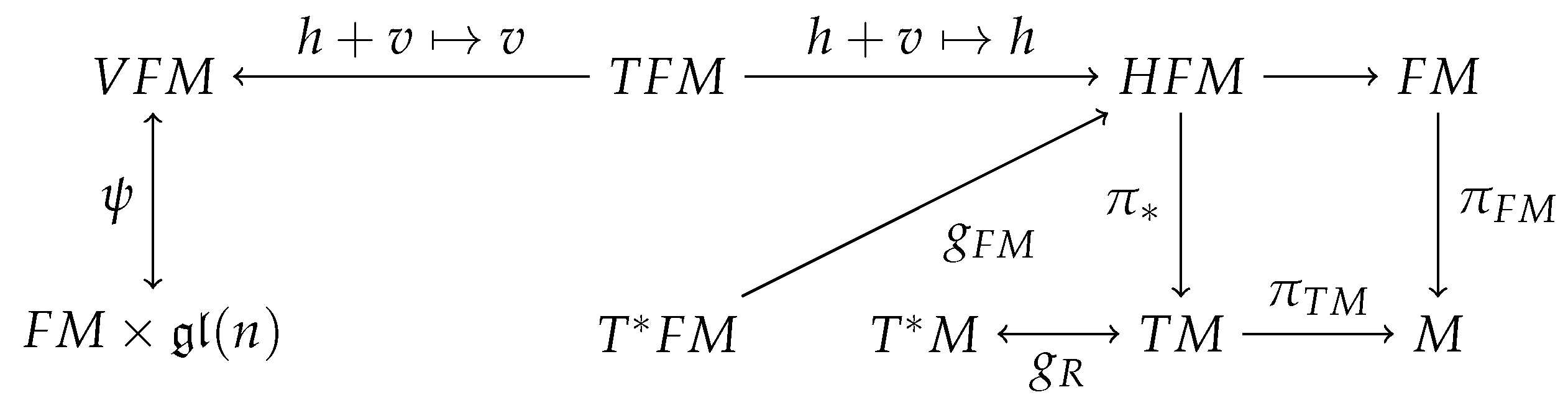
2.1. The Frame Bundle
2.2. Development and Stochastic Development
2.3. Adapted Coordinates
2.4. Connection and Curvature
3. The Anisotropically Weighted Metric
3.1. Sub-Riemannian Metric on the Horizontal Distribution
3.2. Covariance and Nonholonomicity
3.3. Riemannian Metrics on
4. Constrained Evolutions
4.1. Normal Geodesics for
4.2. Evolution in Coordinates
4.3. Acceleration and Polynomials for
5. Cometric Formulation and Low-Rank Generator
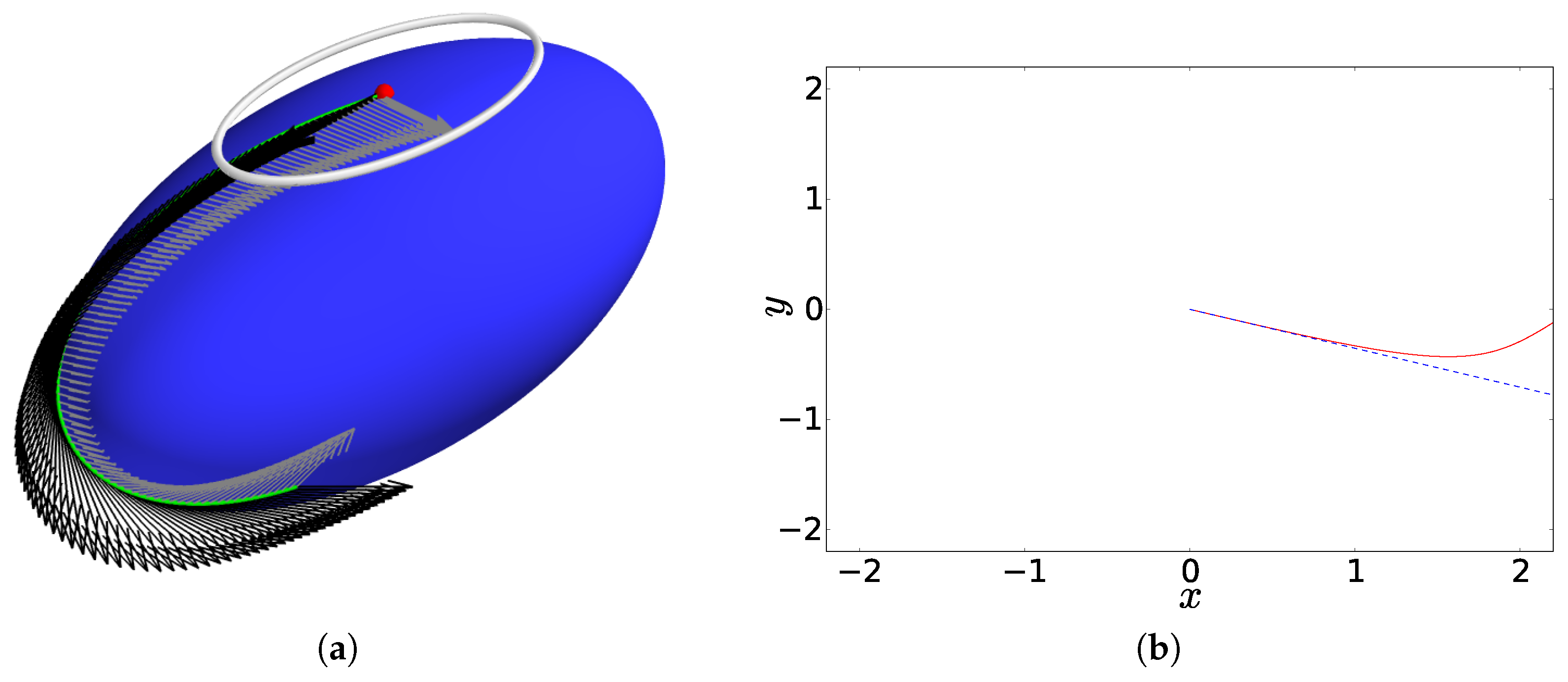
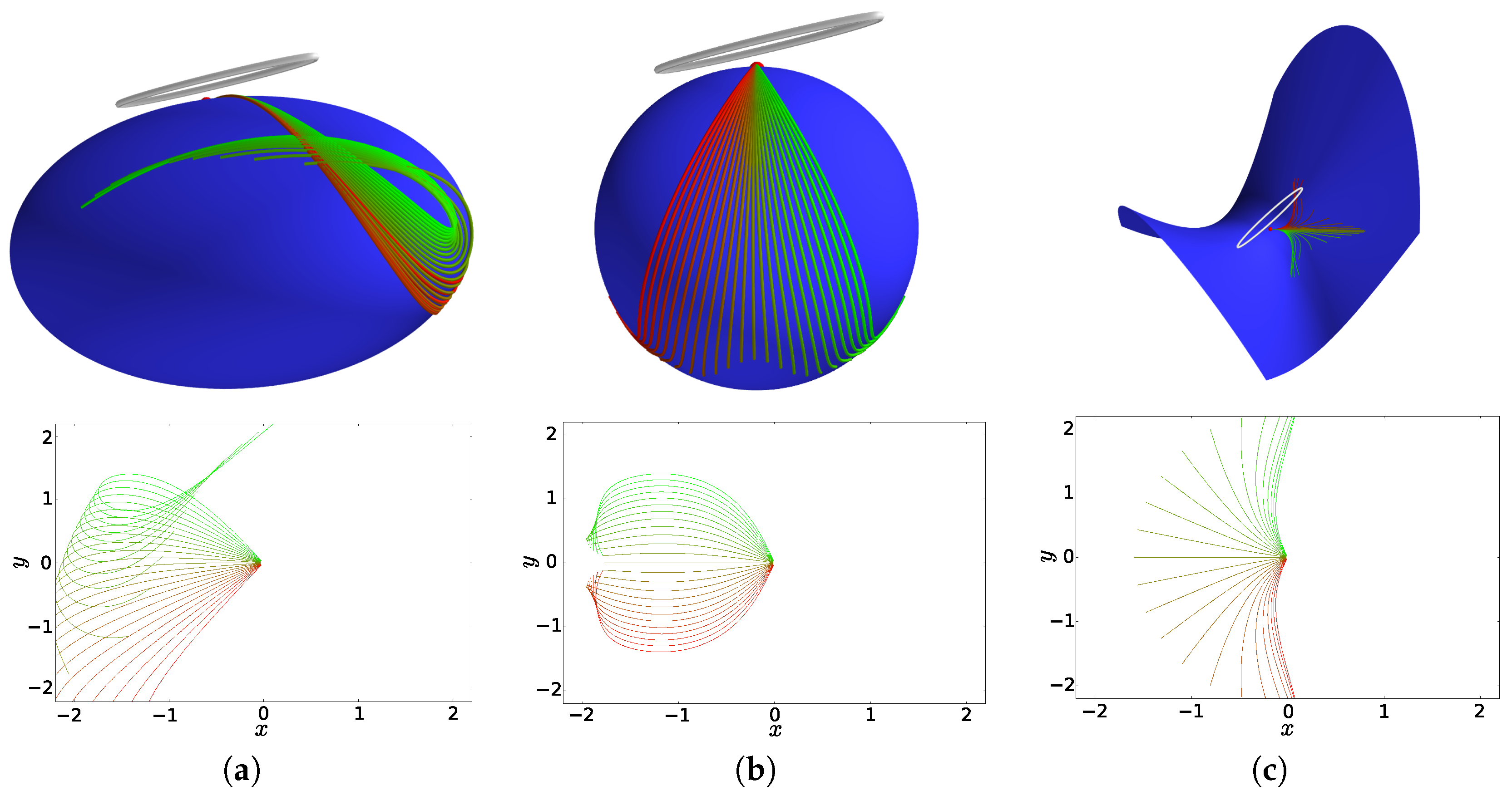
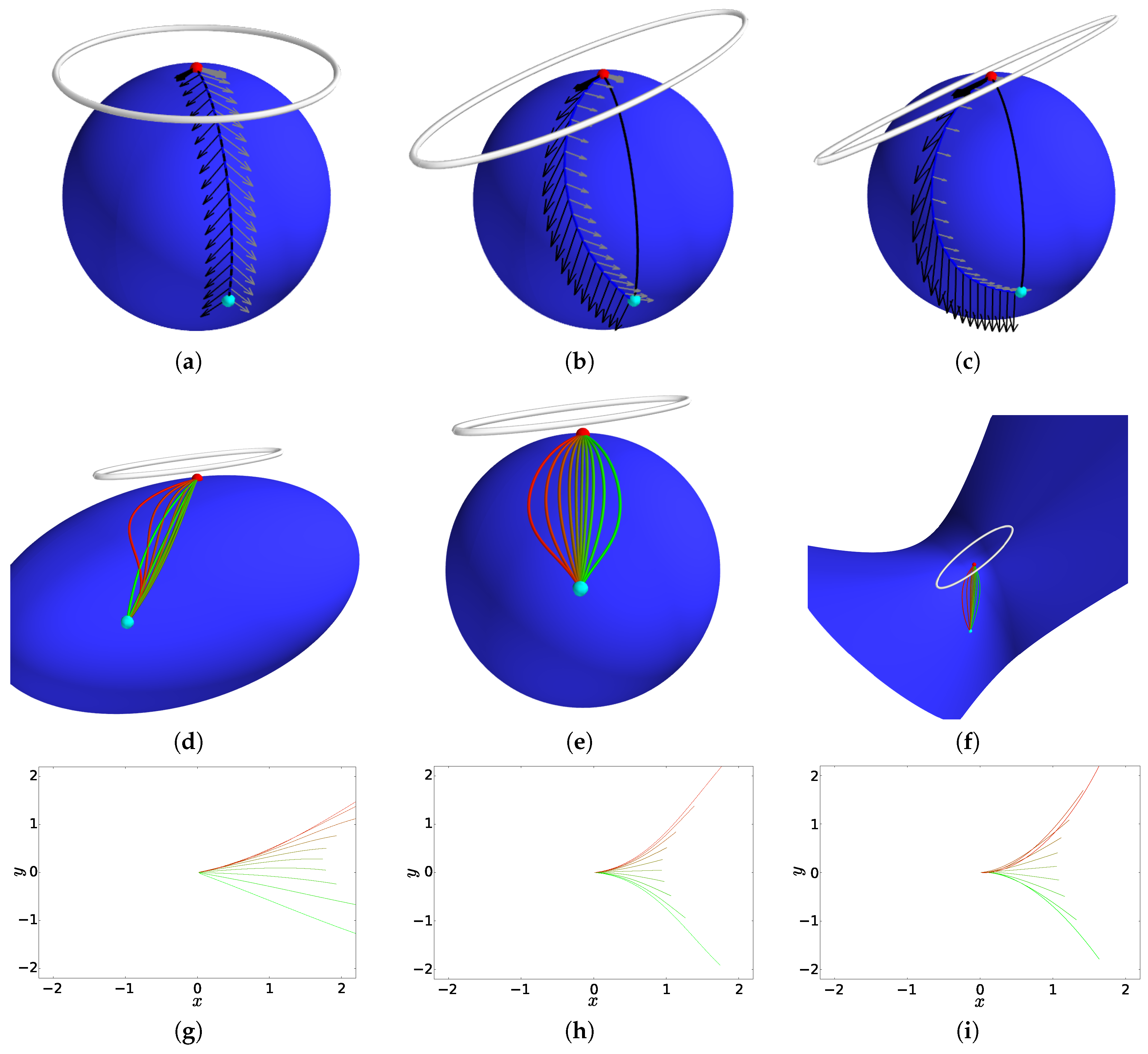
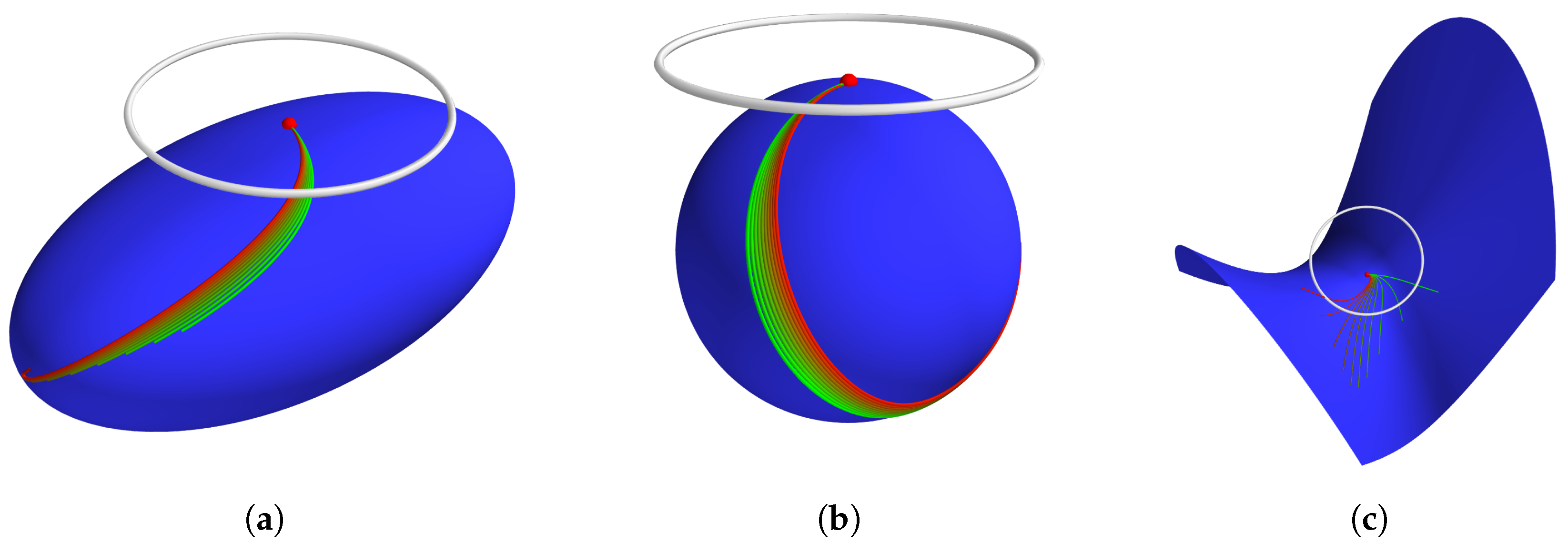
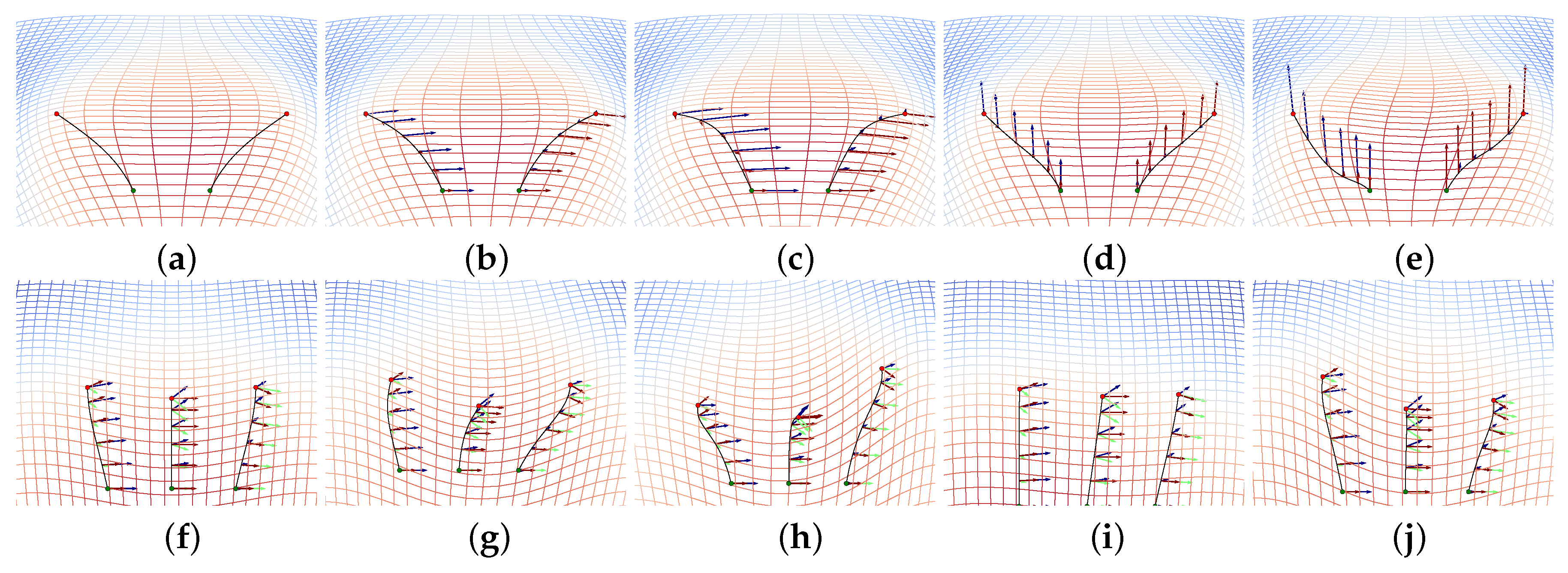
6. Numerical Experiments
6.1. Embedded Surfaces
6.2. LDDMM Landmark Equations
7. Discussion and Concluding Remarks
7.1. Statistical Estimators
7.2. Priors and Low-Rank Estimation
7.3. Conclusions
Acknowledgments
Conflicts of Interest
References
- Sommer, S. Diffusion Processes and PCA on Manifolds. Available online: https://www.mfo.de/document/1440a/OWR_2014_44.pdf (accessed on 24 November 2016).
- Sommer, S. Anisotropic distributions on manifolds: Template estimation and most probable paths. In Information Processing in Medical Imaging; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9123, pp. 193–204. [Google Scholar]
- Sommer, S.; Svane, A.M. Modelling anisotropic covariance using stochastic development and sub-riemannian frame bundle geometry. J. Geom. Mech. 2016, in press. [Google Scholar]
- Hsu, E.P. Stochastic Analysis on Manifolds; American Mathematical Society: Providence, RI, USA, 2002. [Google Scholar]
- Fréchet, M. Les éléments aléatoires de nature quelconque dans un espace distancie. Annales de l’Institut Henri Poincaré 1948, 10, 215–310. [Google Scholar]
- Fletcher, P.; Lu, C.; Pizer, S.; Joshi, S. Principal geodesic analysis for the study of nonlinear statistics of shape. IEEE Trans. Med. Imaging 2004, 23, 995–1005. [Google Scholar] [CrossRef] [PubMed]
- Vaillant, M.; Miller, M.; Younes, L.; Trouvé, A. Statistics on diffeomorphisms via tangent space representations. NeuroImage 2004, 23, S161–S169. [Google Scholar] [CrossRef] [PubMed]
- Younes, L. Shapes and Diffeomorphisms; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Pennec, X. Intrinsic statistics on riemannian manifolds: Basic tools for geometric measurements. J. Math. Imaging Vis. 2006, 25, 127–154. [Google Scholar] [CrossRef]
- Karcher, H. Riemannian center of mass and mollifier smoothing. Commun. Pure Appl. Math. 1977, 30, 509–541. [Google Scholar] [CrossRef]
- Huckemann, S.; Hotz, T.; Munk, A. Intrinsic shape analysis: Geodesic PCA for Riemannian manifolds modulo isometric lie group actions. Stat. Sin. 2010, 20, 1–100. [Google Scholar]
- Jung, S.; Dryden, I.L.; Marron, J.S. Analysis of principal nested spheres. Biometrika 2012, 99, 551–568. [Google Scholar] [CrossRef] [PubMed]
- Pennec, X. Barycentric subspaces and affine spans in manifolds. In Proceedings of the Second International Conference on Geometric Science of Information, Paris, France, 28–30 October 2015; Nielsen, F., Barbaresco, F., Eds.; Lecture Notes in Computer Science. pp. 12–21.
- Sommer, S. Horizontal dimensionality reduction and iterated frame bundle development. In Geometric Science of Information; Springer: Berlin/Heidelberg, Germany, 2013; pp. 76–83. [Google Scholar]
- Zhang, M.; Fletcher, P. Probabilistic principal geodesic analysis. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe, Nevada, 5–10 December 2013; pp. 1178–1186.
- Tipping, M.E.; Bishop, C.M. Probabilistic principal component analysis. J. R. Stat. Soc. Ser. B 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Elworthy, D. Geometric aspects of diffusions on manifolds. In École d’Été de Probabilités de Saint-Flour XV–XVII, 1985–1987; Hennequin, P.L., Ed.; Number 1362 in Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1988; pp. 277–425. [Google Scholar]
- Mok, K.P. On the differential geometry of frame bundles of Riemannian manifolds. J. Reine Angew. Math. 1978, 1978, 16–31. [Google Scholar]
- Taubes, C.H. Differential Geometry: Bundles, Connections, Metrics and Curvature, 1st ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 2011. [Google Scholar]
- Kolář, I.; Slovák, J.; Michor, P.W. Natural Operations in Differential Geometry; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Andersson, L.; Driver, B.K. Finite dimensional approximations to wiener measure and path integral formulas on manifolds. J. Funct. Anal. 1999, 165, 430–498. [Google Scholar] [CrossRef]
- Fujita, T.; Kotani, S.i. The Onsager-Machlup function for diffusion processes. J. Math. Kyoto Univ. 1982, 22, 115–130. [Google Scholar]
- Strichartz, R.S. Sub-Riemannian geometry. J. Differ. Geom. 1986, 24, 221–263. [Google Scholar]
- Bloch, A.M. Nonholonomic mechanics and control. In Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2003; Volume 24. [Google Scholar]
- Marsden, J.E.; Ratiu, T.S. Introduction to mechanics and symmetry. In Texts in Applied Mathematics; Springer: New York, NY, USA, 1999; Volume 17. [Google Scholar]
- Leite, F.S.; Krakowski, K.A. Covariant Differentiation under Rolling Maps; Centro de Matemática da Universidade de Coimbra: Coimbra, Portugal, 2008. [Google Scholar]
- Hinkle, J.; Fletcher, P.T.; Joshi, S. Intrinsic polynomials for regression on riemannian manifolds. J. Math. Imaging Vis. 2014, 50, 32–52. [Google Scholar] [CrossRef]
- Noakes, L.; Heinzinger, G.; Paden, B. Cubic splines on curved spaces. IMA J. Math. Control Inf. 1989, 6, 465–473. [Google Scholar] [CrossRef]
- Camarinha, M.; Silva Leite, F.; Crouch, P. On the geometry of Riemannian cubic polynomials. Differ. Geom. Appl. 2001, 15, 107–135. [Google Scholar] [CrossRef]
- Team, T.T.D.; Al-Rfou, R.; Alain, G.; Almahairi, A.; Angermueller, C.; Bahdanau, D.; Ballas, N.; Bastien, F.; Bayer, J.; Belikov, A.; et al. Theano: A Python framework for fast computation of mathematical expressions. arXiv, 2016; arXiv:1605.02688. [Google Scholar]
- Micheli, M. The Differential Geometry of Landmark Shape Manifolds: Metrics, Geodesics, and Curvature. Ph.D. Thesis, Brown University, Providence, RI, USA, 2008. [Google Scholar]
- Miller, M.; Banerjee, A.; Christensen, G.; Joshi, S.; Khaneja, N.; Grenander, U.; Matejic, L. Statistical methods in computational anatomy. Stat. Methods Med. Res. 1997, 6, 267–299. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Singh, N.; Fletcher, P.T. Bayesian estimation of regularization and atlas building in diffeomorphic image registration. In Information Processing for Medical Imaging (IPMI); Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; pp. 37–48. [Google Scholar]

© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sommer, S. Anisotropically Weighted and Nonholonomically Constrained Evolutions on Manifolds. Entropy 2016, 18, 425. https://doi.org/10.3390/e18120425
Sommer S. Anisotropically Weighted and Nonholonomically Constrained Evolutions on Manifolds. Entropy. 2016; 18(12):425. https://doi.org/10.3390/e18120425
Chicago/Turabian StyleSommer, Stefan. 2016. "Anisotropically Weighted and Nonholonomically Constrained Evolutions on Manifolds" Entropy 18, no. 12: 425. https://doi.org/10.3390/e18120425
APA StyleSommer, S. (2016). Anisotropically Weighted and Nonholonomically Constrained Evolutions on Manifolds. Entropy, 18(12), 425. https://doi.org/10.3390/e18120425





