The Information Geometry of Sparse Goodness-of-Fit Testing
Abstract
:1. Introduction
2. Sampling Distributions in the Sparse Case
- (a)
- and , while:
- (b)
- for as .
3. Divergences and Goodness-of-Fit
3.1. The Power-Divergence Family
3.2. Literature Review
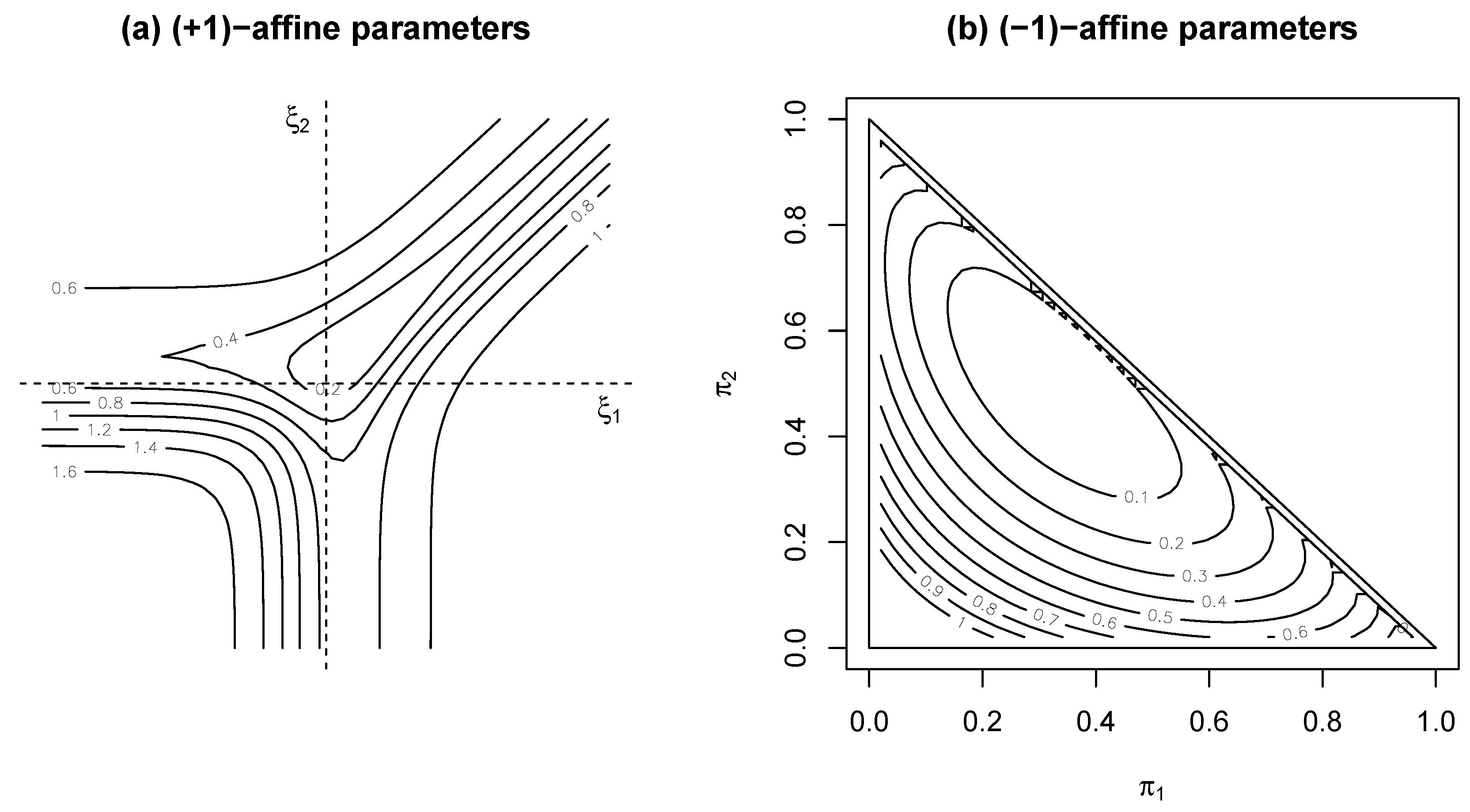
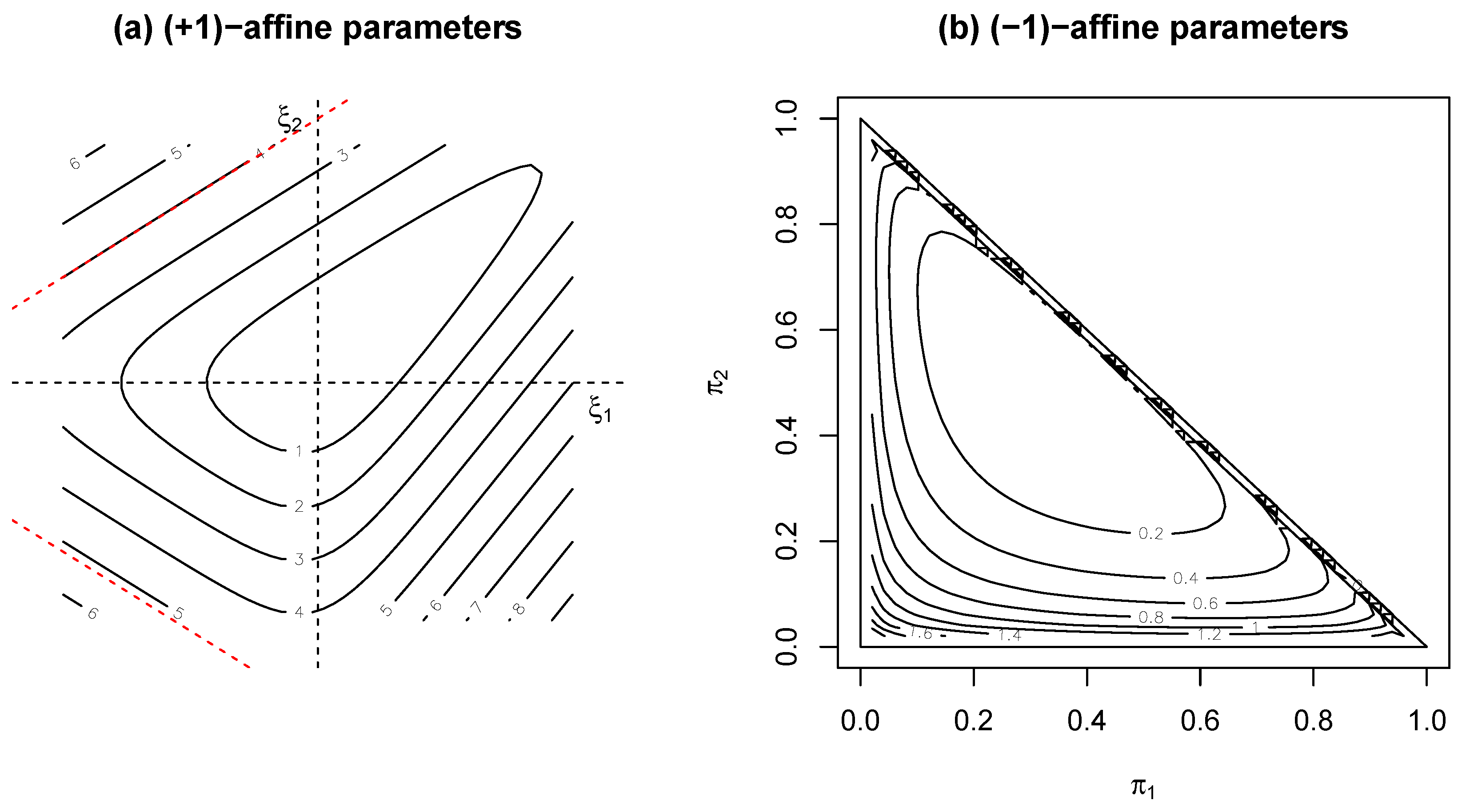
3.3. Links with Information Geometry
3.4. Extended Multinomial Case
4. Simulation Studies
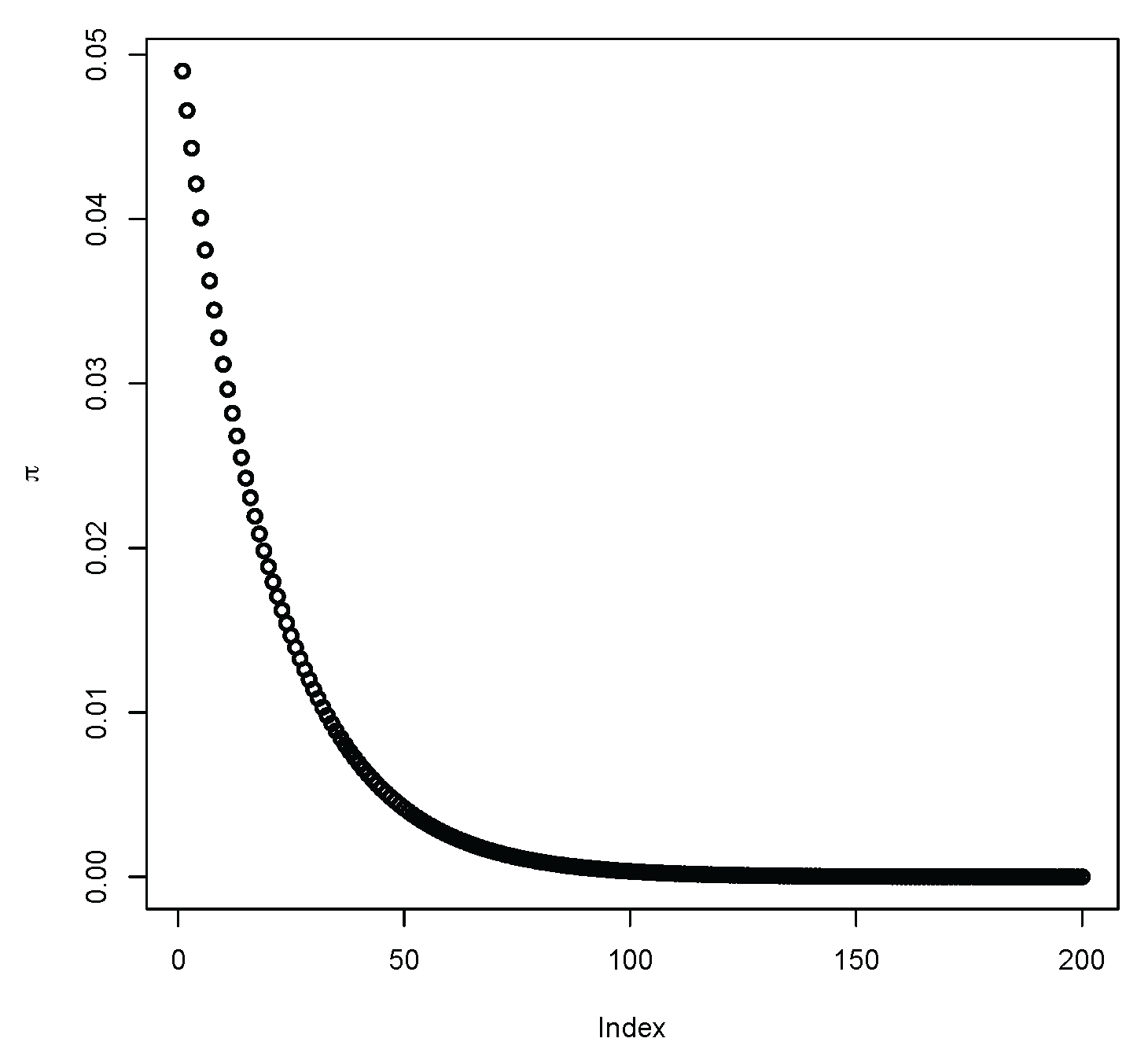
- The transition as varies between discrete and continuous features of the sampling distributions of goodness-of-fit statistics—focusing on the behaviour of the deviance at the uniform discrete distribution;
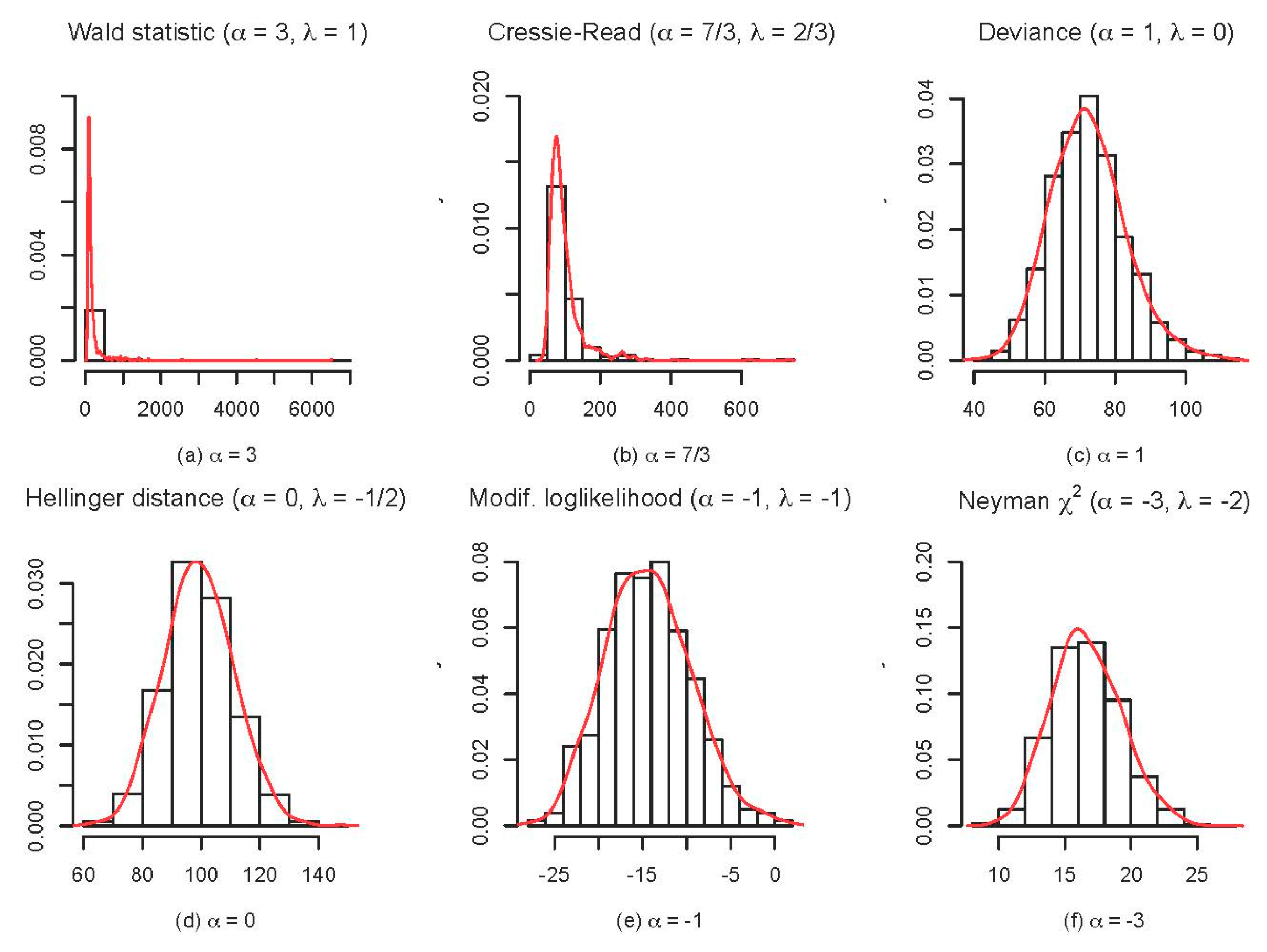
- The comparative behaviour of a range of Power-Divergence statistics—focusing on the relative stability of their sampling distributions near the boundary;
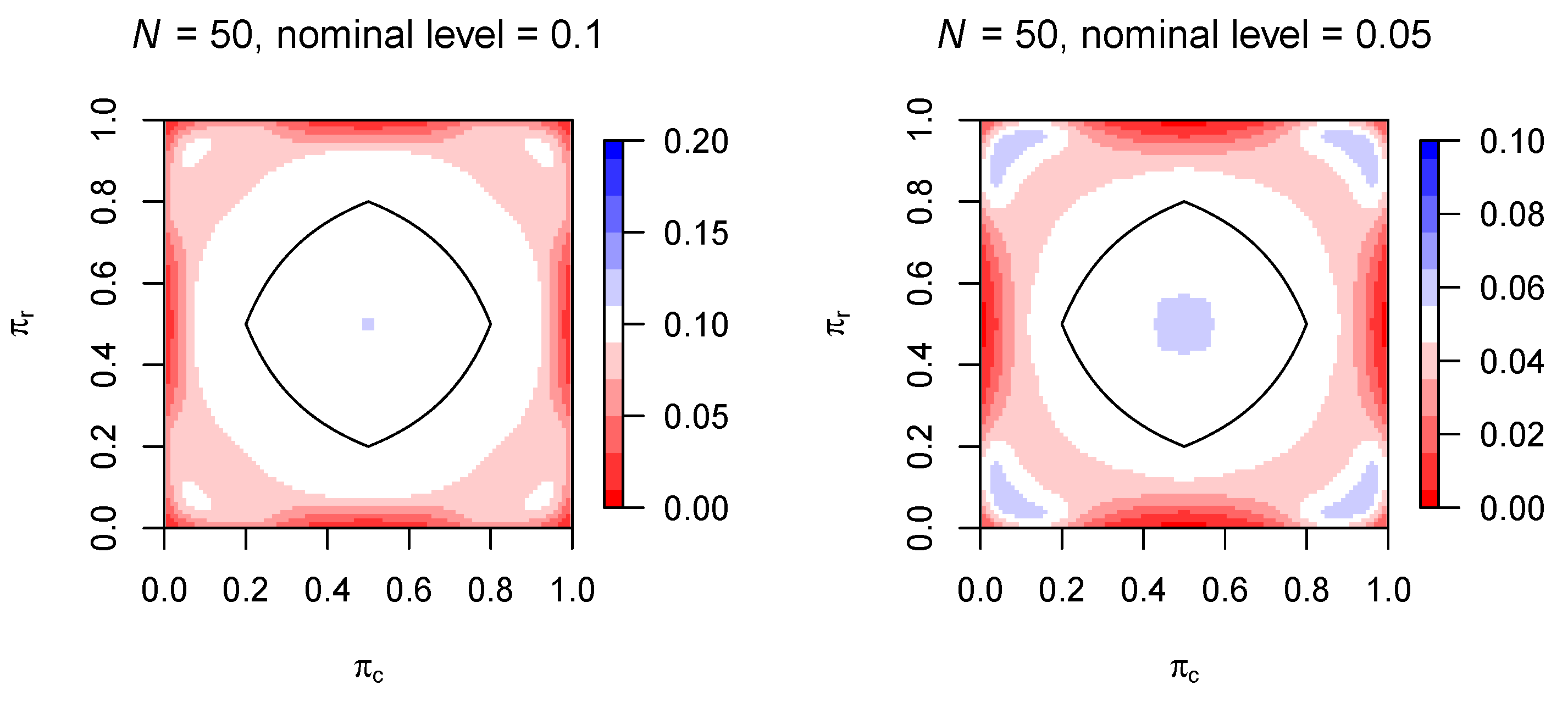
- The lack of uniformity—across the parameter space—of the finite sample adequacy of standard asymptotic sampling distributions, focusing on testing independence in contingency tables.
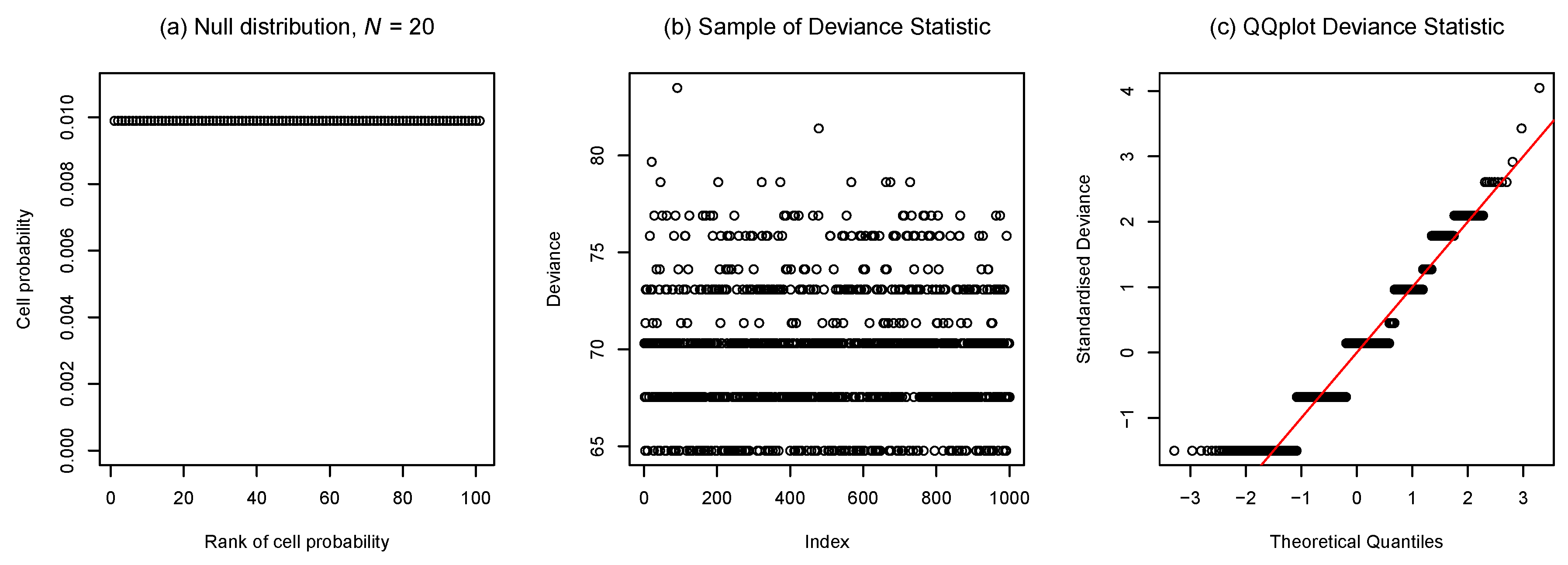
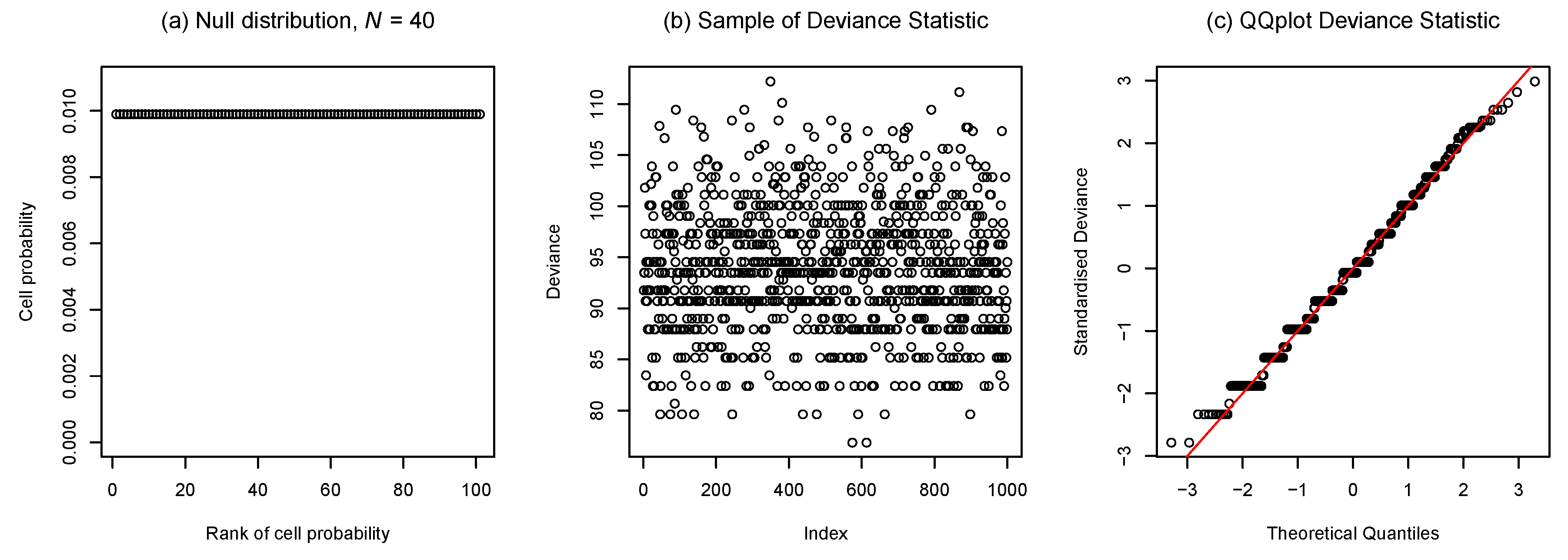
4.1. Transition Between Discrete and Continuous Features of Sampling Distributions
4.2. Comparative Behaviour of Power-Divergence Statistics near the Boundary
4.3. Variation in Finite Sample Adequacy of Asymptotic Distributions across the Parameter Space
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Truncate and Bound Approximations
References
- Critchley, F.; Marriott, P. Computational Information Geometry in Statistics: Theory and practice. Entropy 2014, 16, 2454–2471. [Google Scholar] [CrossRef]
- Marriott, P.; Sabolova, R.; Van Bever, G.; Critchley, F. Geometry of goodness-of-fit testing in high dimensional low sample size modelling. In Geometric Science of Information: Second International Conference, GSI 2015, Palaiseau, France, October 28–30, 2015, Proceedings; Nielsen, F., Barbaresco, F., Eds.; Springer: Berlin, Germany, 2015; pp. 569–576. [Google Scholar]
- Amari, S.-I.; Nagaoka, H. Methods of Information Geometry; Translations of Mathematical Monographs; American Mathematical Society: Providence, RI, USA, 2000. [Google Scholar]
- Cressie, N.; Read, T.R.C. Multinomial goodness-of-fit tests. J. R. Stat. Soc. B 1984, 46, 440–464. [Google Scholar]
- Read, T.R.C.; Cressie, N.A.C. Goodness-of-Fit Statistics for Discrete Multivariate Data; Springer: New York, NY, USA, 1988. [Google Scholar]
- Kass, R.E.; Vos, P.W. Geometrical Foundations of Asymptotic Inference; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1997. [Google Scholar]
- Agresti, A. Categorical Data Analysis, 3rd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Amari, S.-I. Differential-geometrical methods in statistics. In Lecture Notes in Statistics; Springer: New York, NY, USA, 1985; Volume 28. [Google Scholar]
- Barndorff-Nielsen, O.E.; Cox, D.R. Asymptotic Techniques for Use in Statistics; Chapman & Hall: London, UK, 1989. [Google Scholar]
- Anaya-Izquierdo, K.; Critchley, F.; Marriott, P. When are first-order asymptotics adequate? A diagnostic. STAT 2014, 3, 17–22. [Google Scholar] [CrossRef]
- Lauritzen, S.L. Graphical Models; Clarendon Press: Oxford, UK, 1996. [Google Scholar]
- Geyer, C.J. Likelihood inference in exponential families and directions of recession. Electron. J. Stat. 2009, 3, 259–289. [Google Scholar] [CrossRef]
- Fienberg, S.E.; Rinaldo, A. Maximum likelihood estimation in log-linear models. Ann. Stat. 2012, 40, 996–1023. [Google Scholar] [CrossRef]
- Eguchi, S.; Copas, J. Local model uncertainty and incomplete-data bias. J. R. Stat. Soc. B 2005, 67, 1–37. [Google Scholar]
- Copas, J.; Eguchi, S. Likelihood for statistically equivalent models. J. R. Stat. Soc. B 2010, 72, 193–217. [Google Scholar] [CrossRef]
- Anaya-Izquierdo, K.; Critchley, F.; Marriott, P.; Vos, P. On the geometric interplay between goodness-of-fit and estimation: Illustrative examples. In Computational Information Geometry: For Image and Signal Processing; Lecture Notes in Computer Science (LNCS); Nielsen, F., Dodson, K., Critchley, F., Eds.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Morris, C. Central limit theorems for multinomial sums. Ann. Stat. 1975, 3, 165–188. [Google Scholar] [CrossRef]
- Osius, G.; Rojek, D. Normal goodness-of-fit tests for multinomial models with large degrees of freedom. JASA 1992, 87, 1145–1152. [Google Scholar] [CrossRef]
- Holst, L. Asymptotic normality and efficiency for certain goodness-of-fit tests. Biometrika 1972, 59, 137–145. [Google Scholar] [CrossRef]
- Koehler, K.J.; Larntz, K. An empirical investigation of goodness-of-fit statistics for sparse multinomials. JASA 1980, 75, 336–344. [Google Scholar] [CrossRef]
- Koehler, K.J. Goodness-of-fit tests for log-linear models in sparse contingency tables. JASA 1986, 81, 483–493. [Google Scholar] [CrossRef]
- McCullagh, P. The conditional distribution of goodness-of-fit statistics for discrete data. JASA 1986, 81, 104–107. [Google Scholar] [CrossRef]
- Forster, J.J.; McDonald, J.W.; Smith, P.W.F. Monte Carlo exact conditional tests for log-linear and logistic models. J. R. Stat. Soc. B 1996, 58, 445–453. [Google Scholar]
- Kim, D.; Agresti, A. Nearly exact tests of conditional independence and marginal homogeneity for sparse contingency tables. Comput. Stat. Data Anal. 1997, 24, 89–104. [Google Scholar] [CrossRef]
- Booth, J.G.; Butler, R.W. An importance sampling algorithm for exact conditional tests in log-linear models. Biometrika 1999, 86, 321–332. [Google Scholar] [CrossRef]
- Caffo, B.S.; Booth, J.G. Monte Carlo conditional inference for log-linear and logistic models: A survey of current methodology. Stat. Methods Med. Res. 2003, 12, 109–123. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, C.J. Computing highly accurate or exact P-values using importance sampling. Comput. Stat. Data Anal. 2012, 56, 1784–1794. [Google Scholar] [CrossRef]
- Simonoff, J.S. Jackknifing and bootstrapping goodness-of-fit statistics in sparse multinomials. JASA 1986, 81, 1005–1011. [Google Scholar] [CrossRef]
- Gaunt, R.E.; Pickett, A.; Reinert, G. Chi-square approximation by Stein’s method with application to Pearson’s statistic. arXiv, 2015; arXiv:1507.01707. [Google Scholar]
- Fan, J.; Hung, H.-N.; Wong, W.-H. Geometric understanding of likelihood ratio statistics. JASA 2000, 95, 836–841. [Google Scholar] [CrossRef]
- Ulyanov, V.V.; Zubov, V.N. Refinement on the convergence of one family of goodness-of-fit statistics to chi-squared distribution. Hiroshima Math. J. 2009, 39, 133–161. [Google Scholar]
- Asylbekov, Z.A.; Zubov, V.N.; Ulyanov, V.V. On approximating some statistics of goodness-of-fit tests in the case of three-dimensional discrete data. Sib. Math. J. 2011, 52, 571–584. [Google Scholar] [CrossRef]
- Zelterman, D. Goodness-of-fit tests for large sparse multinomial distributions. JASA 1987, 82, 624–629. [Google Scholar] [CrossRef]
- Bregman, L.M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comp. Math. Math. 1967, 7, 200–217. [Google Scholar] [CrossRef]
- Amari, S.-I. Information Geometry and Its Applications; Springer: Tokyo, Japan, 2015. [Google Scholar]
- Csiszár, I. On topological properties of f-divergences. Stud. Sci. Math. Hung. 1967, 2, 329–339. [Google Scholar]
- Csiszár, I. Information measures: A critical survey. In Transactions of the Seventh Prague Conference on Information Theory, Statistical Decision Functions, Random Processes and of the 1974 European Meeting of Statisticians; Kozesnik, J., Ed.; Springer: Houten, The Netherlands, 1977; Volume B, pp. 73–86. [Google Scholar]
- Barndorff-Nielsen, O. Information and Exponential Families in Statistical Theory; John Wiley & Sons, Ltd.: Chichester, UK, 1978. [Google Scholar]
- Brown, L.D. Fundamentals of Statistical Exponential Families with Applications in Statistical Decision Theory; Lecture Notes-Monograph Series; Integrated Media Systems (IMS): Hayward, CA, USA, 1986; Volume 9. [Google Scholar]
- Csiszár, I.; Matúš, F. Closures of exponential families. Ann. Probab. 2005, 33, 582–600. [Google Scholar] [CrossRef]
- Eriksson, N.; Fienberg, S.E.; Rinaldo, A.; Sullivant, S. Polyhedral conditions for the nonexistence of the MLE for hierarchical log-linear models. J. Symb. Comput. 2006, 41, 222–233. [Google Scholar] [CrossRef]
- Rinaldo, A.; Feinberg, S.; Zhou, Y. On the geometry of discrete exponential families with applications to exponential random graph models. Electron. J. Stat. 2009, 3, 446–484. [Google Scholar] [CrossRef]
- Critchley, F.; Marriott, P. Computing with Fisher geodesics and extended exponential families. Stat. Comput. 2016, 26, 325–332. [Google Scholar] [CrossRef]
- Sheather, S.J.; Jones, M.C. A reliable data-based bandwidth selection method for kernel density estimation. J. R. Stat. Soc. B 1991, 53, 683–690. [Google Scholar]

| α:= 1+ 2λ | λ | Formula | Name |
|---|---|---|---|
| 3 | 1 | Pearson | |
| 7/3 | 2/3 | Read–Cressie | |
| 1 | 0 | Twice log-likelihood (deviance) | |
| 0 | Freeman–Tukey or Hellinger | ||
| −1 | −1 | Twice modified log-likelihood | |
| −3 | −2 | Neyman |
| λ | α | Divergence | Divergence Parameter ξ | Potential |
|---|---|---|---|---|
| −1 | −1 | |||
| 0 | 1 | |||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marriott, P.; Sabolová, R.; Van Bever, G.; Critchley, F. The Information Geometry of Sparse Goodness-of-Fit Testing. Entropy 2016, 18, 421. https://doi.org/10.3390/e18120421
Marriott P, Sabolová R, Van Bever G, Critchley F. The Information Geometry of Sparse Goodness-of-Fit Testing. Entropy. 2016; 18(12):421. https://doi.org/10.3390/e18120421
Chicago/Turabian StyleMarriott, Paul, Radka Sabolová, Germain Van Bever, and Frank Critchley. 2016. "The Information Geometry of Sparse Goodness-of-Fit Testing" Entropy 18, no. 12: 421. https://doi.org/10.3390/e18120421
APA StyleMarriott, P., Sabolová, R., Van Bever, G., & Critchley, F. (2016). The Information Geometry of Sparse Goodness-of-Fit Testing. Entropy, 18(12), 421. https://doi.org/10.3390/e18120421





