Kernel Density Estimation on the Siegel Space with an Application to Radar Processing †
Abstract
:1. Introduction
2. The Siegel Space
2.1. The Siegel Upper Half Space
2.2. The Siegel Disk
3. Non Parametric Density Estimation on the Siegel Space
3.1. Histograms
3.2. Orthogonal Series
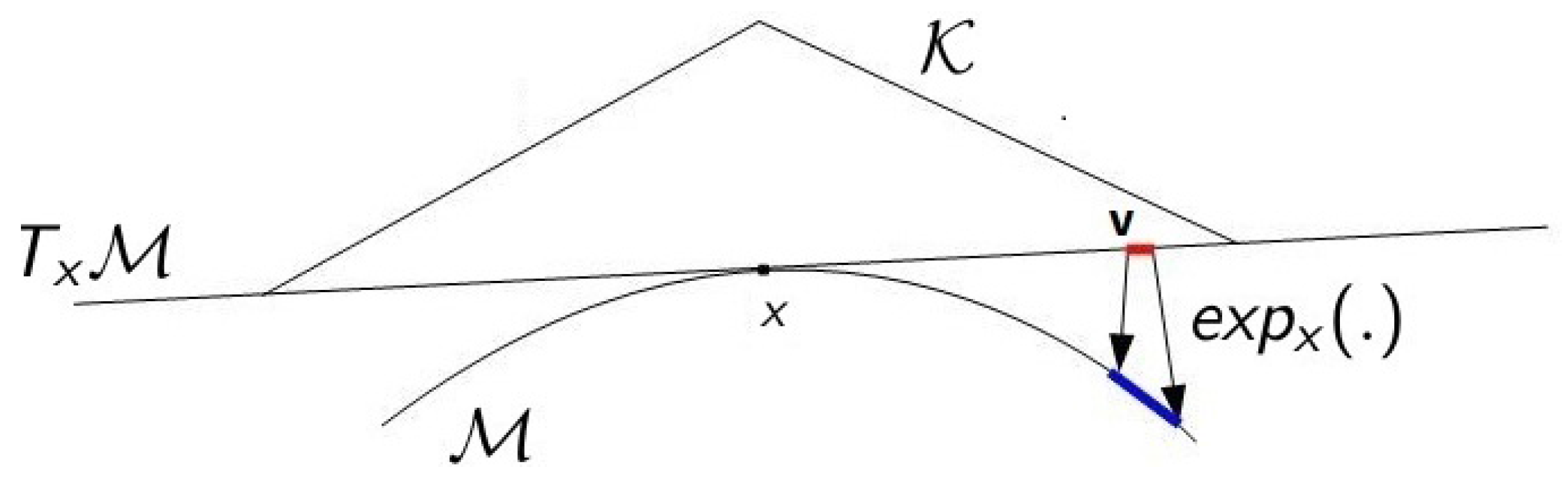
3.3. Kernels
- (i)
- ;
- (ii)
- ;
- (iii)
- ;
- (iv)
- .
4. Application to Radar Processing
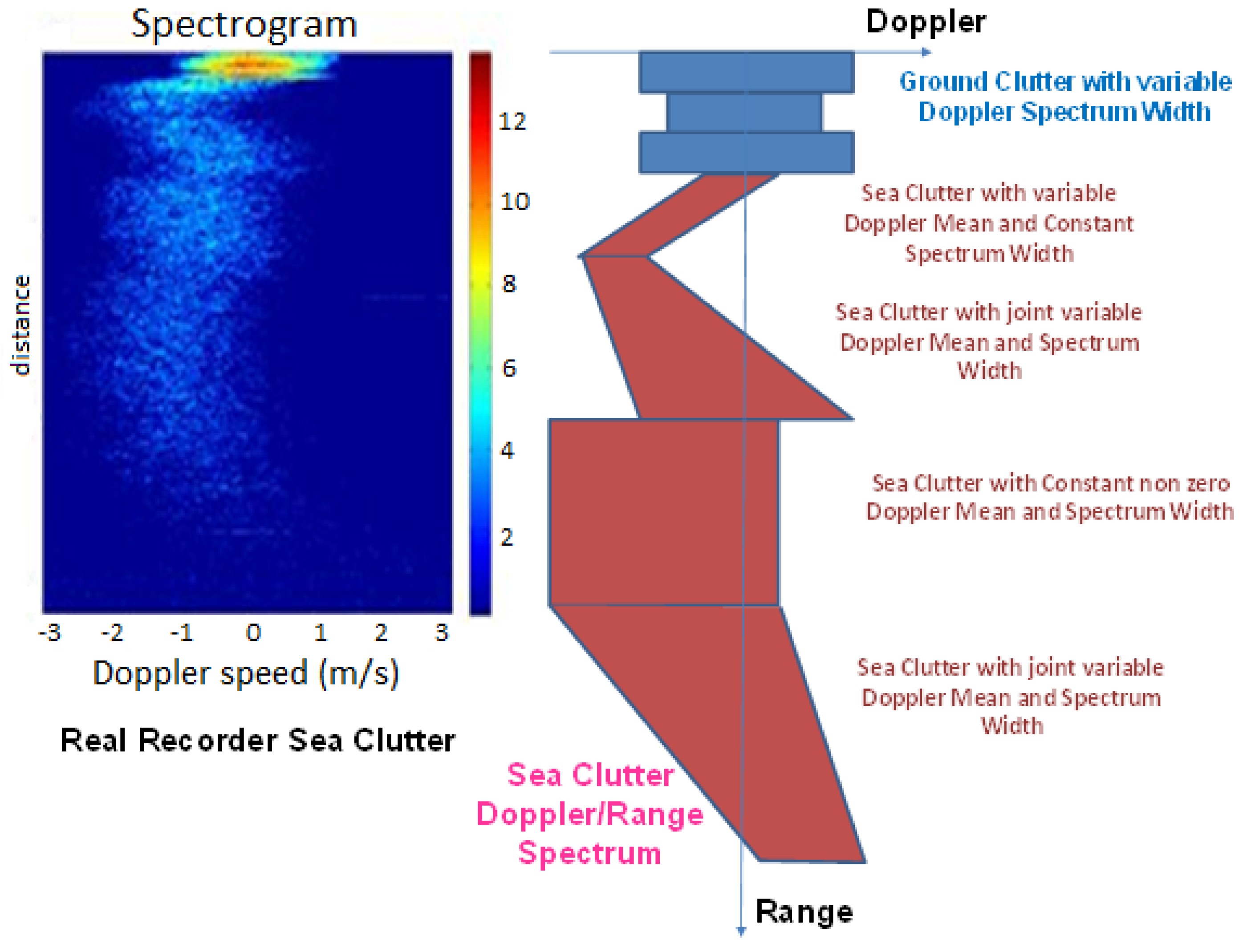
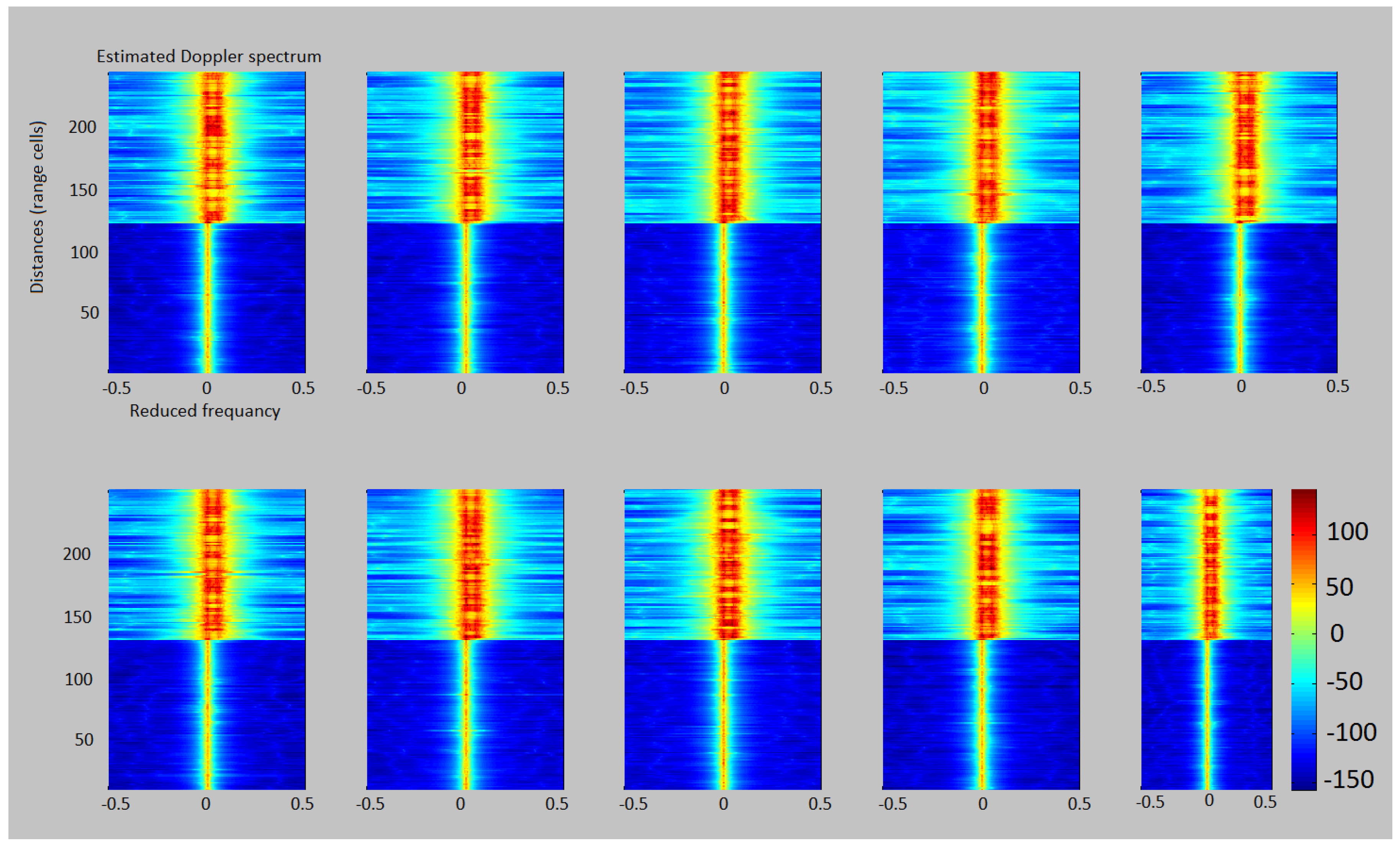
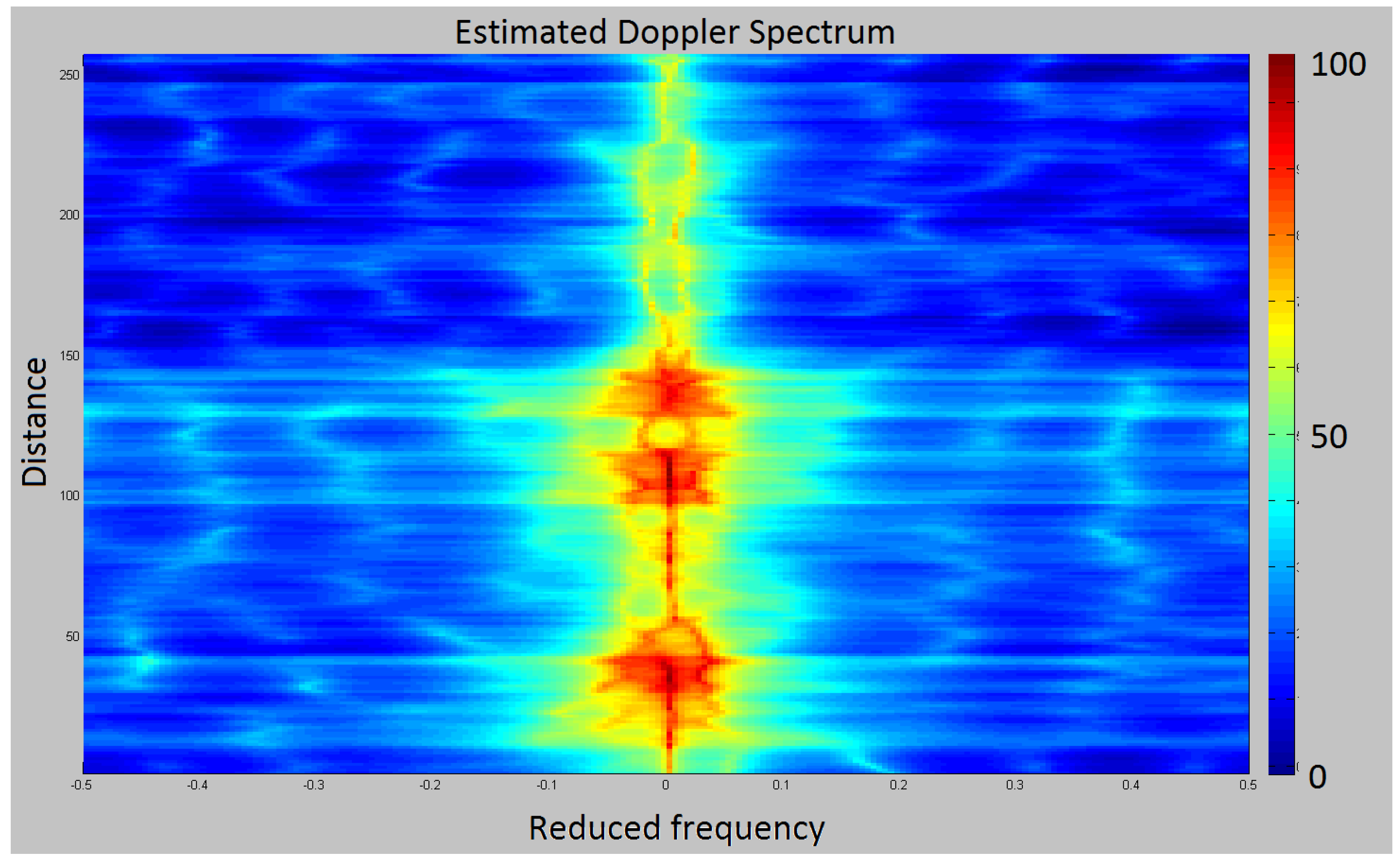
4.1. Radar Data
4.2. Marginal Densities of Reflection Coefficients
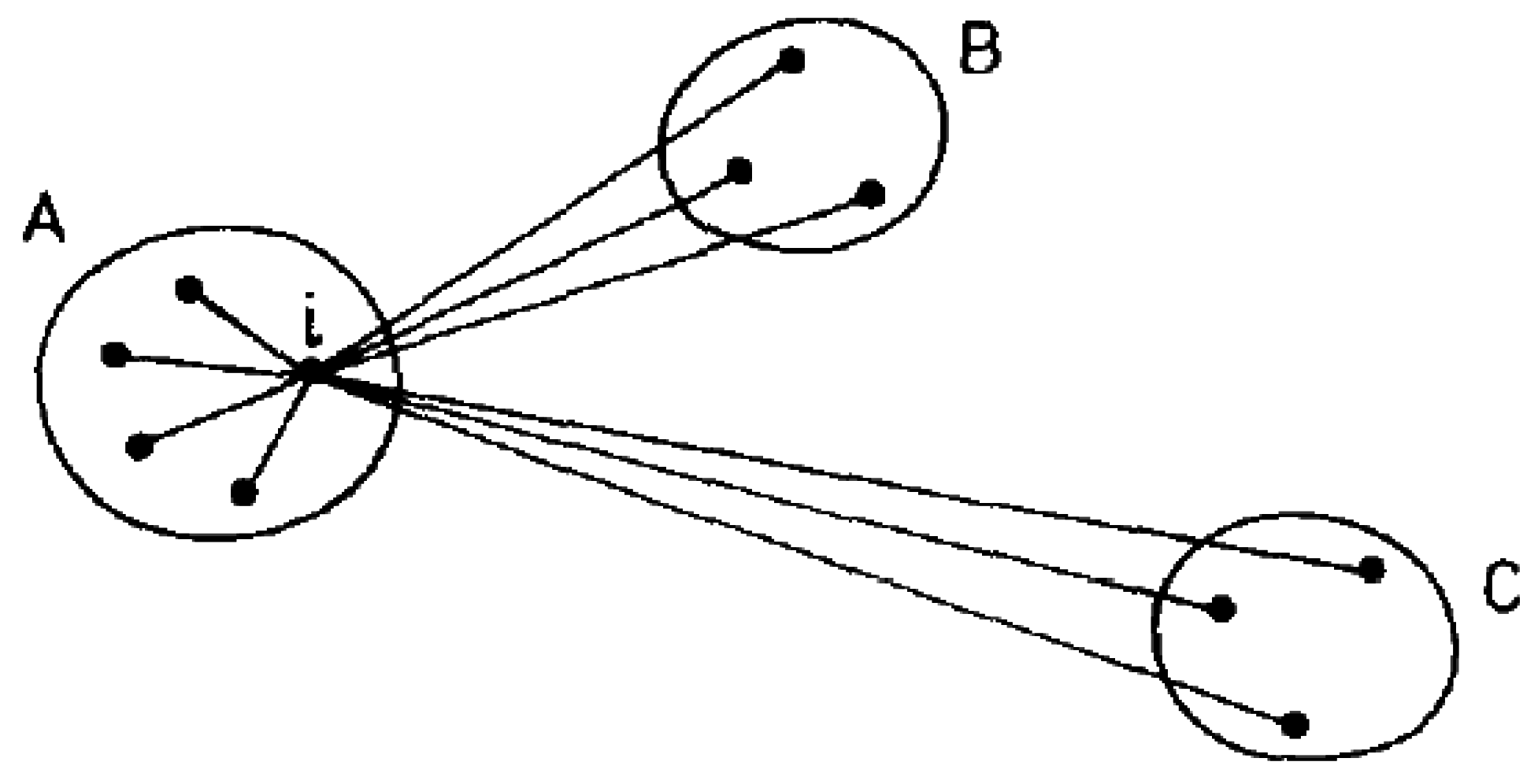
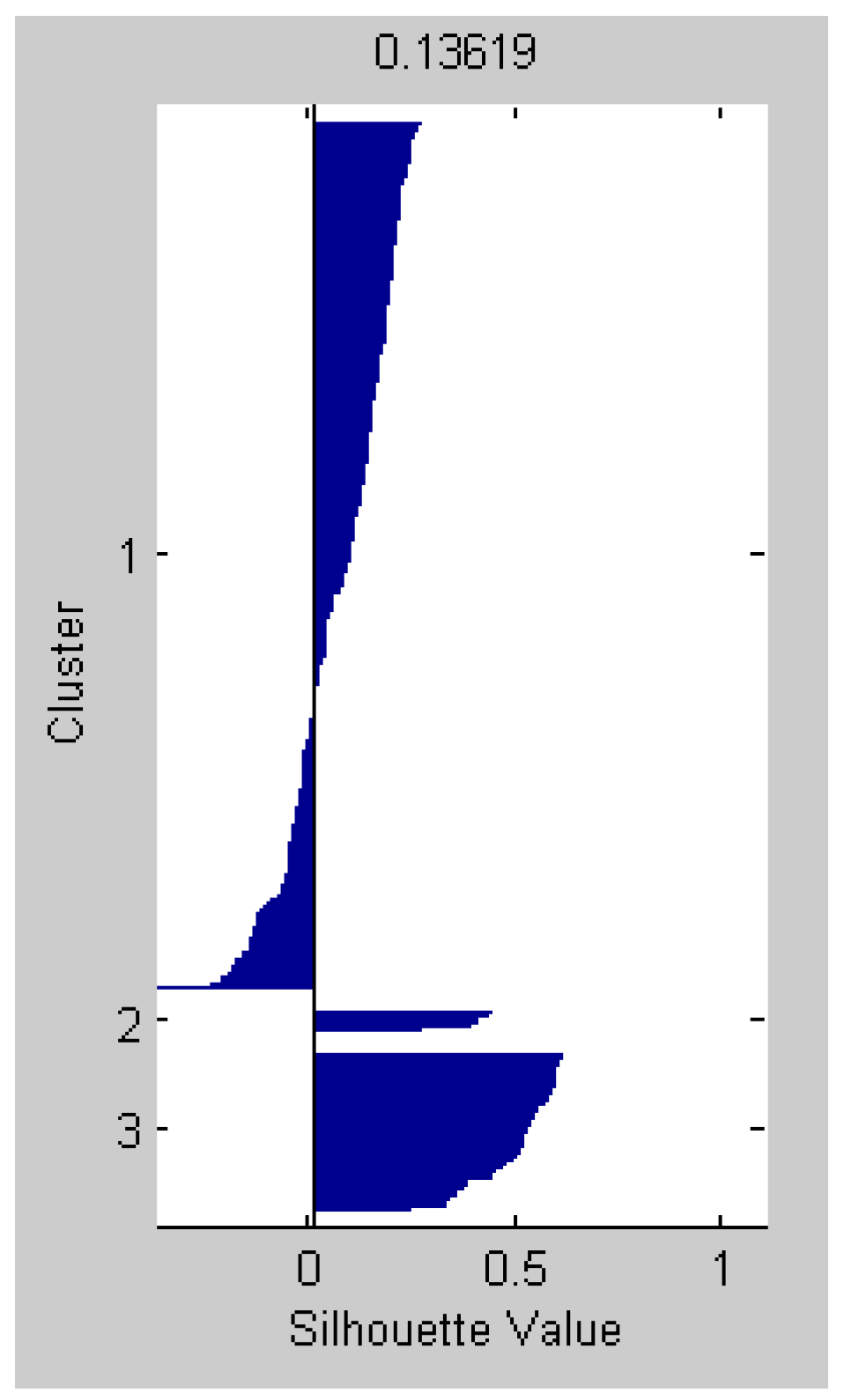
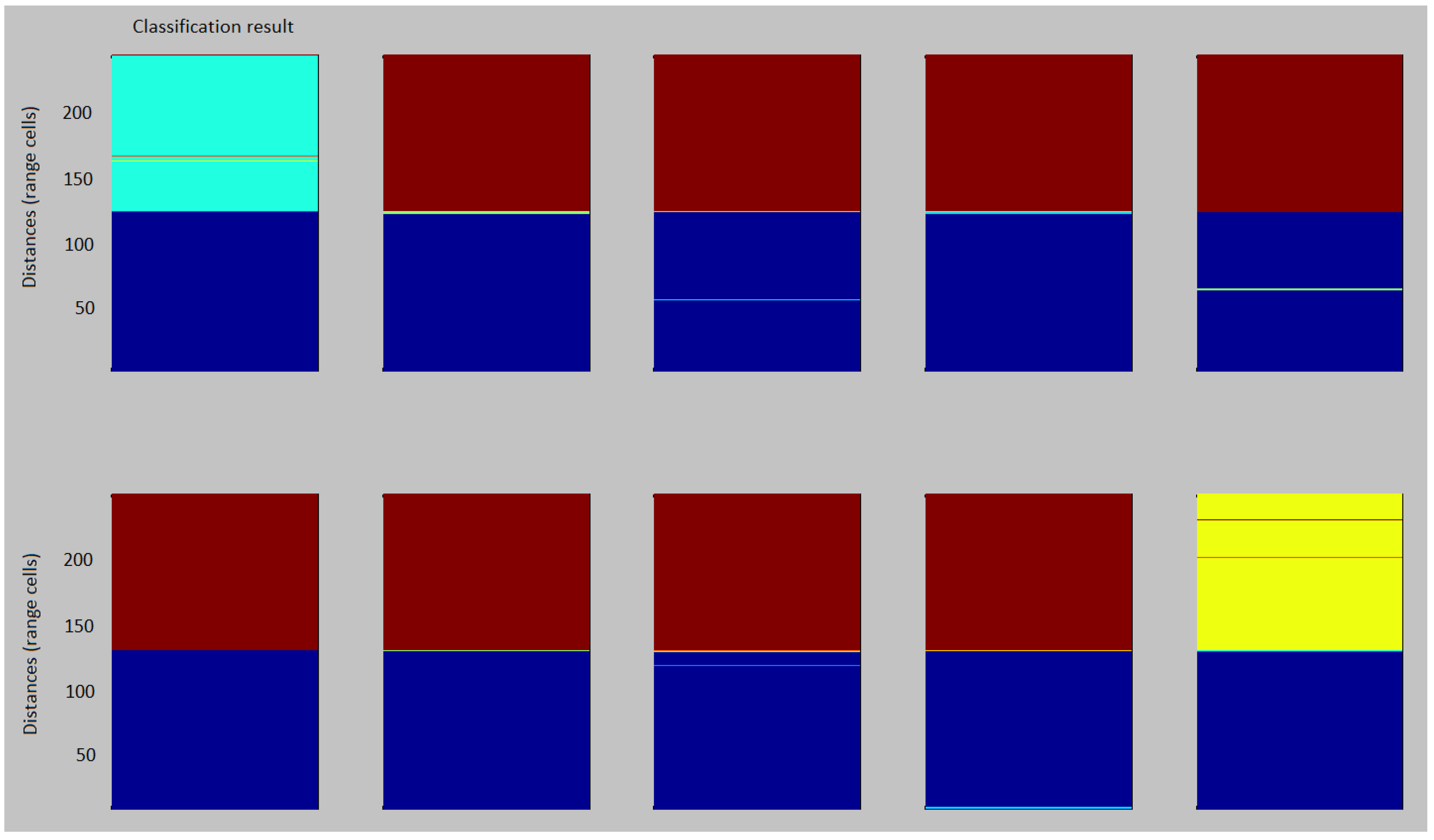
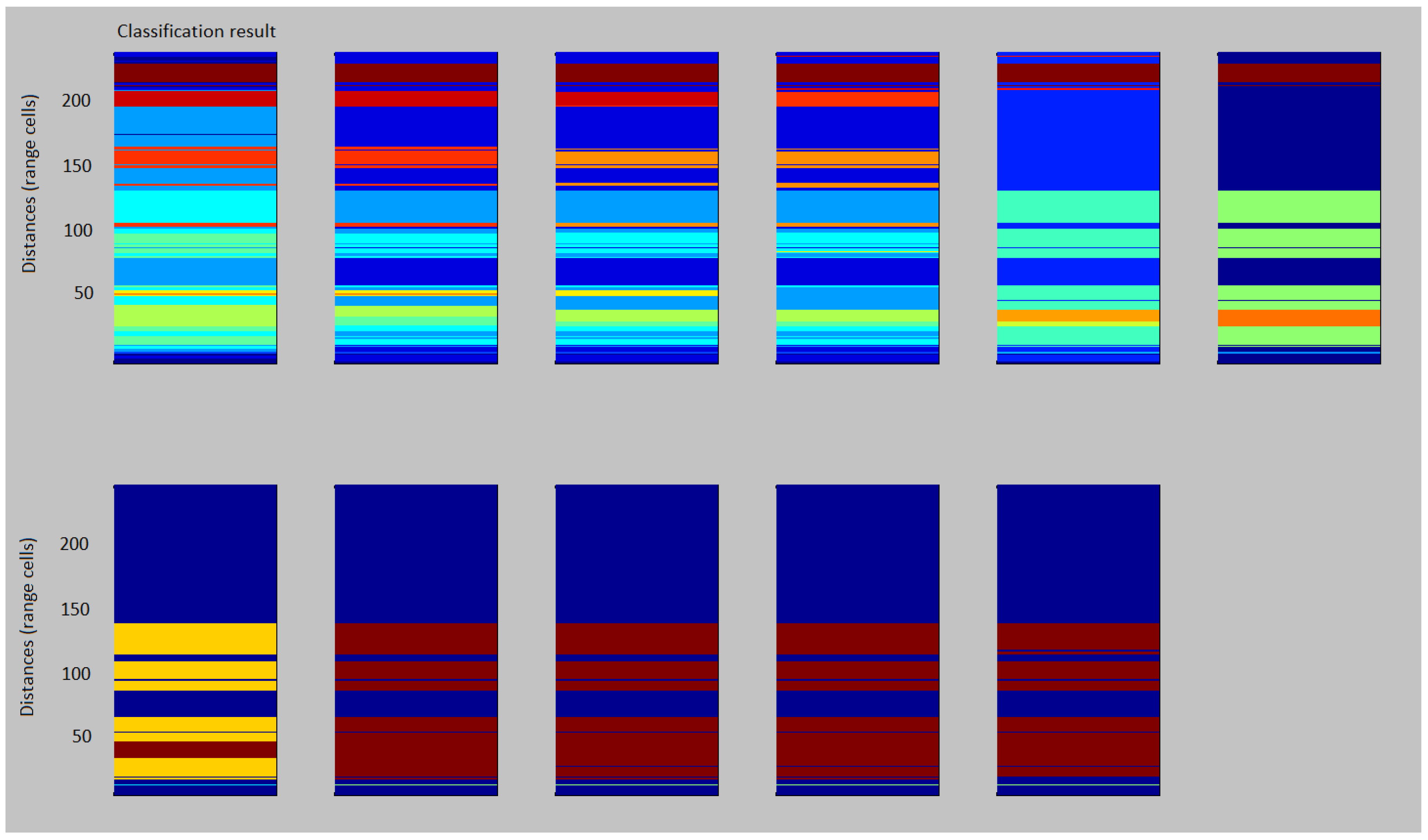
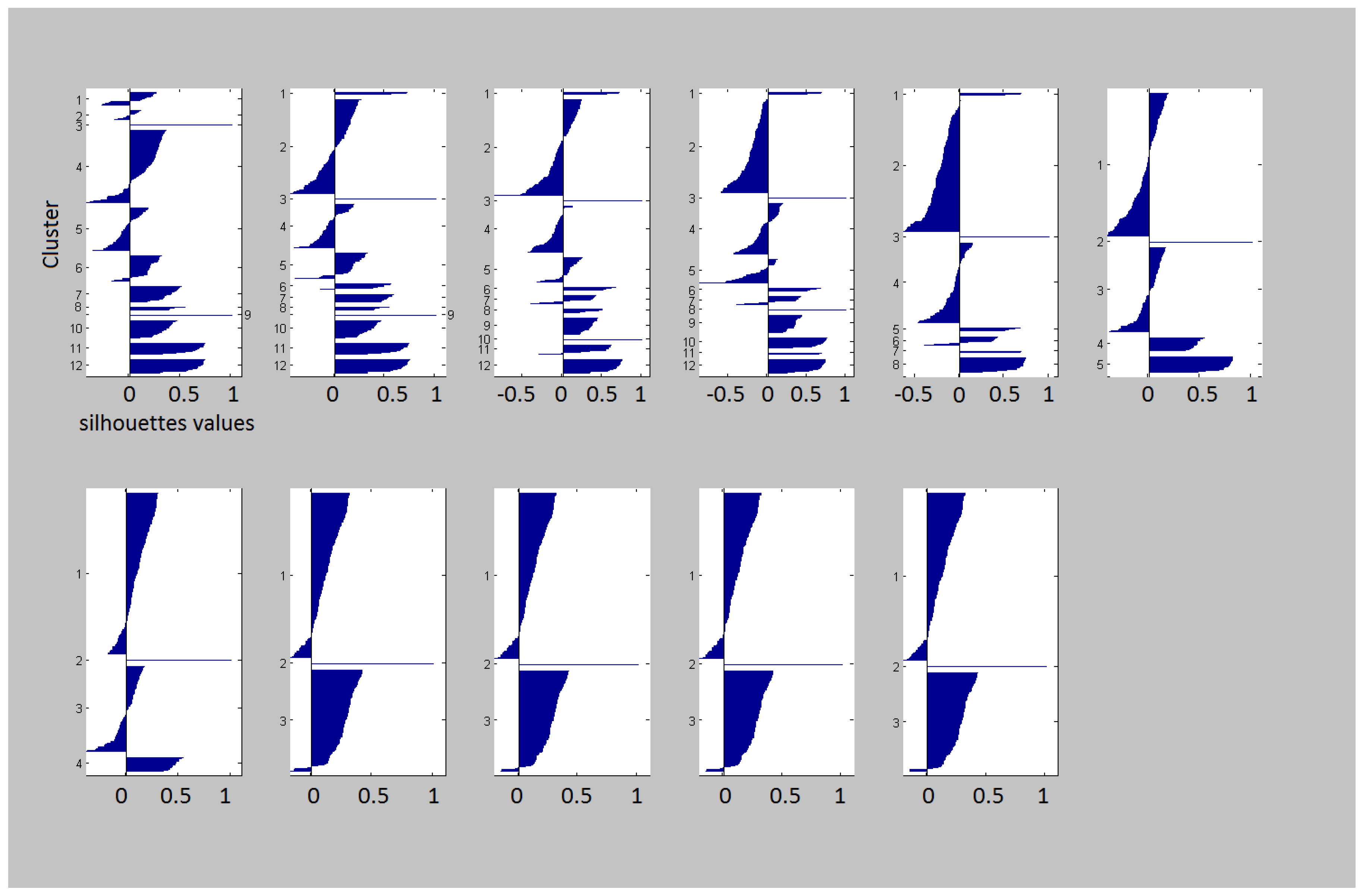
4.3. Radar Clutter Segmentation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Demonstration of Theorem 1
References
- Pelletier, B. Kernel density estimation on Riemannian manifolds. Stat. Probab. Lett. 2005, 73, 297–304. [Google Scholar] [CrossRef]
- Hendriks, H. Nonparametric estimation of a probability density on a Riemannian manifold using Fourier expansions. Ann. Stat. 1990, 18, 832–849. [Google Scholar] [CrossRef]
- Asta, D.M. Kernel Density Estimation on Symmetric Spaces. In Geometric Science of Information; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9389, pp. 779–787. [Google Scholar]
- Barbaresco, F. Robust statistical radar processing in Fréchet metric space: OS-HDR-CFAR and OS-STAP processing in siegel homogeneous bounded domains. In Proceedings of the 2011 12th International Radar Symposium (IRS), Leipzig, Germany, 7–9 Septerber 2011.
- Barbaresco, F. Information Geometry of Covariance Matrix: Cartan-Siegel Homogeneous Bounded Domains, Mostow/Berger Fibration and Fréchet Median. In Matrix Information Geometry; Bhatia, R., Nielsen, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 199–256. [Google Scholar]
- Barbaresco, F. Information geometry manifold of Toeplitz Hermitian positive definite covariance matrices: Mostow/Berger fibration and Berezin quantization of Cartan-Siegel domains. Int. J. Emerg. Trends Signal Process. 2013, 1, 1–87. [Google Scholar]
- Berezin, F.A. Quantization in complex symmetric spaces. Izv. Math. 1975, 9, 341–379. [Google Scholar] [CrossRef]
- Lenz, R. Siegel Descriptors for Image Processing. IEEE Signal Process. Lett. 2016, 25, 625–628. [Google Scholar]
- Barbaresco, F. Robust Median-Based STAP in Inhomogeneous Secondary Data: Frechet Information Geometry of Covariance Matrices. In Proceedings of the 2nd French-Singaporian SONDRA Workshop on EM Modeling, New Concepts and Signal Processing For Radar Detection and Remote Sensing, Cargese, France, 25–28 May 2010.
- Degurse, J.F.; Savy, L.; Molinie, J.P.; Marcos, S. A Riemannian Approach for Training Data Selection in Space-Time Adaptive Processing Applications. In Proceedings of the 2013 14th International Radar Symposium (IRS), Dresden, Germany, 19–21 June 2013; Volume 1, pp. 319–324.
- Degurse, J.F.; Savy, L.; Marcos, S. Information Geometry for radar detection in heterogeneous environments. In Proceedings of the 33rd International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Amboise, France, 21–26 September 2014.
- Barbaresco, F. Koszul Information Geometry and Souriau Geometric Temperature/Capacity of Lie Group Thermodynamics. Entropy 2014, 16, 4521–4565. [Google Scholar] [CrossRef]
- Barbaresco, F. New Generation of Statistical Radar Processing based on Geometric Science of Information: Information Geometry, Metric Spaces and Lie Groups Models of Radar Signal Manifolds. In Proceedings of the 4th French-Singaporian Radar Workshop SONDRA, Lacanau, France, 23 May 2016.
- Jeuris, B.; Vandebril, R. The Kahler mean of Block-Toeplitz matrices with Toeplitz structured block. SIAM J. Matrix Anal. Appl. 2015, 37, 1151–1175. [Google Scholar] [CrossRef]
- Huckemann, S.; Kim, P.; Koo, J.; Munk, A. Mobius deconvolution on the hyperbolic plan with application to impedance density estimation. Ann. Stat. 2010, 38, 2465–2498. [Google Scholar] [CrossRef]
- Asta, D.; Shalizi, C. Geometric network comparison. 2014; arXiv:1411.1350. [Google Scholar]
- Chevallier, E.; Barbaresco, F.; Angulo, J. Probability density estimation on the hyperbolic space applied to radar processing. In Geometric Science of Information; Springer: Berlin/Heidelberg, Germany, 2015; pp. 753–761. [Google Scholar]
- Said, S.; Bombrun, L.; Berthoumieu, Y. New Riemannian Priors on the Univariate Normal Model. Entropy 2014, 16, 4015–4031. [Google Scholar] [CrossRef]
- Said, S.; Hatem, H.; Bombrun, L.; Baba, C.; Vemuri, B.C. Gaussian distributions on Riemannian symmetric spaces: Statistical learning with structured covariance matrices. 2016; arXiv:1607.06929. [Google Scholar]
- Terras, A. Harmonic Analysis on Symmetric Spaces and Applications II; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Siegel, C.L. Symplectic geometry. Am. J. Math. 1943, 65. [Google Scholar] [CrossRef]
- Helgason, S. Differential Geometry, Lie Groups, and Symmetric Spaces; Academic Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Cannon, J.W.; Floyd, W.J.; Kenyon, R.; Parry, W.R. Hyperbolic geometry. In Flavors of Geometry; Cambridge University Press: Cambridge, UK, 1997; Volume 31, pp. 59–115. [Google Scholar]
- Bhatia, R. Matrix Analysis. In Graduate Texts in Mathematics-169; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Kim, P.; Richards, D. Deconvolution density estimation on the space of positive definite symmetric matrices. In Nonparametric Statistics and Mixture Models: A Festschrift in Honor of Thomas P. Hettmansperger; World Scientific Publishing: Singapore, 2008; pp. 147–168. [Google Scholar]
- Loubes, J.-M.; Pelletier, B. A kernel-based classifier on a Riemannian manifold. Stat. Decis. 2016, 26, 35–51. [Google Scholar] [CrossRef]
- Gangolli, R.; Varadarajan, V.S. Harmonic Analysis of Spherical Functions on Real Reductive Groups; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Decurninge, A.; Barbaresco, F. Robust Burg Estimation of Radar Scatter Matrix for Mixtures of Gaussian Stationary Autoregressive Vectors. 2016; arxiv:1601.02804. [Google Scholar]
- Barbaresco, F. Eddy Dissipation Rate (EDR) retrieval with ultra-fast high range resolution electronic-scanning X-band airport radar: Results of European FP7 UFO Toulouse Airport trials. In Proceedings of the 2015 16th International Radar Symposium, Dresden, Germany, 24–26 June 2015.
- Oude Nijhuis, A.C.P.; Thobois, L.P.; Barbaresco, F. Monitoring of Wind Hazards and Turbulence at Airports with Lidar and Radar Sensors and Mode-S Downlinks: The UFO Project; Bulletin of the American Meteorological Society, 2016; submitted for publication. [Google Scholar]
- Barbaresco, F.; Forget, T.; Chevallier, E.; Angulo, J. Doppler spectrum segmentation of radar sea clutter by mean-shift and information geometry metric. In Proceedings of the 17th International Radar Symposium (IRS), Krakow, Poland, 10–12 May 2016; pp. 1–6.
- Fukunaga, K.; Hostetler, L.D. The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition. Proc. IEEE Trans. Inf. Theory 1975, 21, 32–40. [Google Scholar] [CrossRef]
- Arias-Castro, E.; Mason, D.; Pelletier, B. On the estimation of the gradient lines of a density and the consistency of the mean-shift algorithm. J. Mach. Learn. Res. 2000, 17, 1–28. [Google Scholar]
- Subbarao, R.; Meer, P. Nonlinear Mean Shift over Riemannian Manifolds. Int. J. Comput. Vis. 2009, 84. [Google Scholar] [CrossRef]
- Wang, Y.H.; Han, C.Z. PolSAR Image Segmentation by Mean Shift Clustering in the Tensor Space. Acta Autom. Sin. 2010, 36, 798–806. [Google Scholar] [CrossRef]
- Rousseeuw, P. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 1, 53–65. [Google Scholar] [CrossRef]
- Barbaresco, F. Geometric Theory of Heat from Souriau Lie Groups Thermodynamics and Koszul Hessian Geometry: Applications in Information Geometry for Exponential Families. Entropy 2016, 18, 386. [Google Scholar] [CrossRef]
- Wanga, Y.; Huang, X.; Wua, L. Clustering via geometric median shift over Riemannian manifolds. Inf. Sci. 2013, 220, 292–305. [Google Scholar] [CrossRef]
- Munkres, J.R. Elementary Differential Topology. In Annals of Mathematics Studies-54; Princeton University Press: Princeton, NJ, USA, 1967. [Google Scholar]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chevallier, E.; Forget, T.; Barbaresco, F.; Angulo, J. Kernel Density Estimation on the Siegel Space with an Application to Radar Processing. Entropy 2016, 18, 396. https://doi.org/10.3390/e18110396
Chevallier E, Forget T, Barbaresco F, Angulo J. Kernel Density Estimation on the Siegel Space with an Application to Radar Processing. Entropy. 2016; 18(11):396. https://doi.org/10.3390/e18110396
Chicago/Turabian StyleChevallier, Emmanuel, Thibault Forget, Frédéric Barbaresco, and Jesus Angulo. 2016. "Kernel Density Estimation on the Siegel Space with an Application to Radar Processing" Entropy 18, no. 11: 396. https://doi.org/10.3390/e18110396
APA StyleChevallier, E., Forget, T., Barbaresco, F., & Angulo, J. (2016). Kernel Density Estimation on the Siegel Space with an Application to Radar Processing. Entropy, 18(11), 396. https://doi.org/10.3390/e18110396






