Geometric Theory of Heat from Souriau Lie Groups Thermodynamics and Koszul Hessian Geometry: Applications in Information Geometry for Exponential Families
Abstract
:Lorsque le fait qu’on rencontre est en opposition avec une théorie régnante, il faut accepter le fait et abandonner la théorie, alors même que celle-ci, soutenue par de grands noms, est généralement adoptée—Claude Bernard in “Introduction à l’Étude de la Médecine Expérimentale” [1]
Au départ, la théorie de la stabilité structurelle m’avait paru d’une telle ampleur et d’une telle généralité, qu’avec elle je pouvais espérer en quelque sorte remplacer la thermodynamique par la géométrie, géométriser en un certain sens la thermodynamique, éliminer des considérations thermodynamiques tous les aspects à caractère mesurable et stochastiques pour ne conserver que la caractérisation géométrique correspondante des attracteurs.—René Thom in “Logos et théorie des Catastrophes” [2]
1. Introduction
- The Souriau model of Lie group thermodynamics is presented with standard notations of Lie group theory, in place of Souriau equations using less classical conventions (that have limited understanding of his work by his contemporaries).
- We prove that Souriau Riemannian metric introduced with symplectic cocycle is a generalization of Fisher metric (called Souriau-Fisher metric in the following) that preserves the property to be defined as a hessian of partition function logarithm as in classical information geometry. We then establish the equality of two terms, the first one given by Souriau’s definition from Lie group cocycle and parameterized by “geometric heat” Q (element of dual Lie algebra) and “geometric temperature” β (element of Lie algebra) and the second one, the hessian of the characteristic function with respect to the variable β:A dual Souriau-Fisher metric, the inverse of this last one, could be also elaborated with the hessian of “geometric entropy” with respect to the variable Q:For the maximum entropy density (Gibbs density), the following three terms coincide: that describes the convexity of the log-likelihood function, the Fisher metric that describes the covariance of the log-likelihood gradient, whereas that describes the covariance of the observables.
- This Souriau-Fisher metric is also identified to be proportional to the first derivative of the heat , and then comparable by analogy to geometric “specific heat” or “calorific capacity”.
- We observe that the Souriau metric is invariant with respect to the action of the group , due to the fact that the characteristic function after the action of the group is linearly dependent to . As the Fisher metric is proportional to the hessian of the characteristic function, we have the following invariance:
- We have proposed, based on Souriau’s Lie group model and on analogy with mechanical variables, a variational principle of thermodynamics deduced from Poincaré-Cartan integral invariant. The variational principle holds on the Lie algebra, for variations , where is an arbitrary path that vanishes at the endpoints, :where the Poincaré-Cartan integral invariant is defined with , the Massieu characteristic function, with the 1-form
- We have deduced Euler-Poincaré equations for the Souriau model:where is the Souriau geometric heat (element of dual Lie algebra) and is the Souriau geometric temperature (element of the Lie algebra). The second equation is linked to the result of Souriau based on the moment map that a symplectic manifold is always a coadjoint orbit, affine of its group of Hamiltonian transformations (a symplectic manifold homogeneous under the action of a Lie group, is isomorphic, up to a covering, to a coadjoint orbit; symplectic leaves are the orbits of the affine action that makes the moment map equivariant).
- We have established that the affine representation of Lie group and Lie algebra by Jean-Marie Souriau is equivalent to Jean-Louis Koszul’s affine representation developed in the framework of hessian geometry of convex sharp cones. Both Souriau and Koszul have elaborated equations requested for Lie group and Lie algebra to ensure the existence of an affine representation. We have compared both approaches of Souriau and Koszul in a table.
- We have applied the Souriau model for exponential families and especially for multivariate Gaussian densities.
- We have applied the Souriau-Koszul model Gibbs density to compute the maximum entropy density for symmetric positive definite matrices, using the inner product , given by Cartan-Killing form. The Gibbs density (generalization of Gaussian law for theses matrices and defined as maximum entropy density):
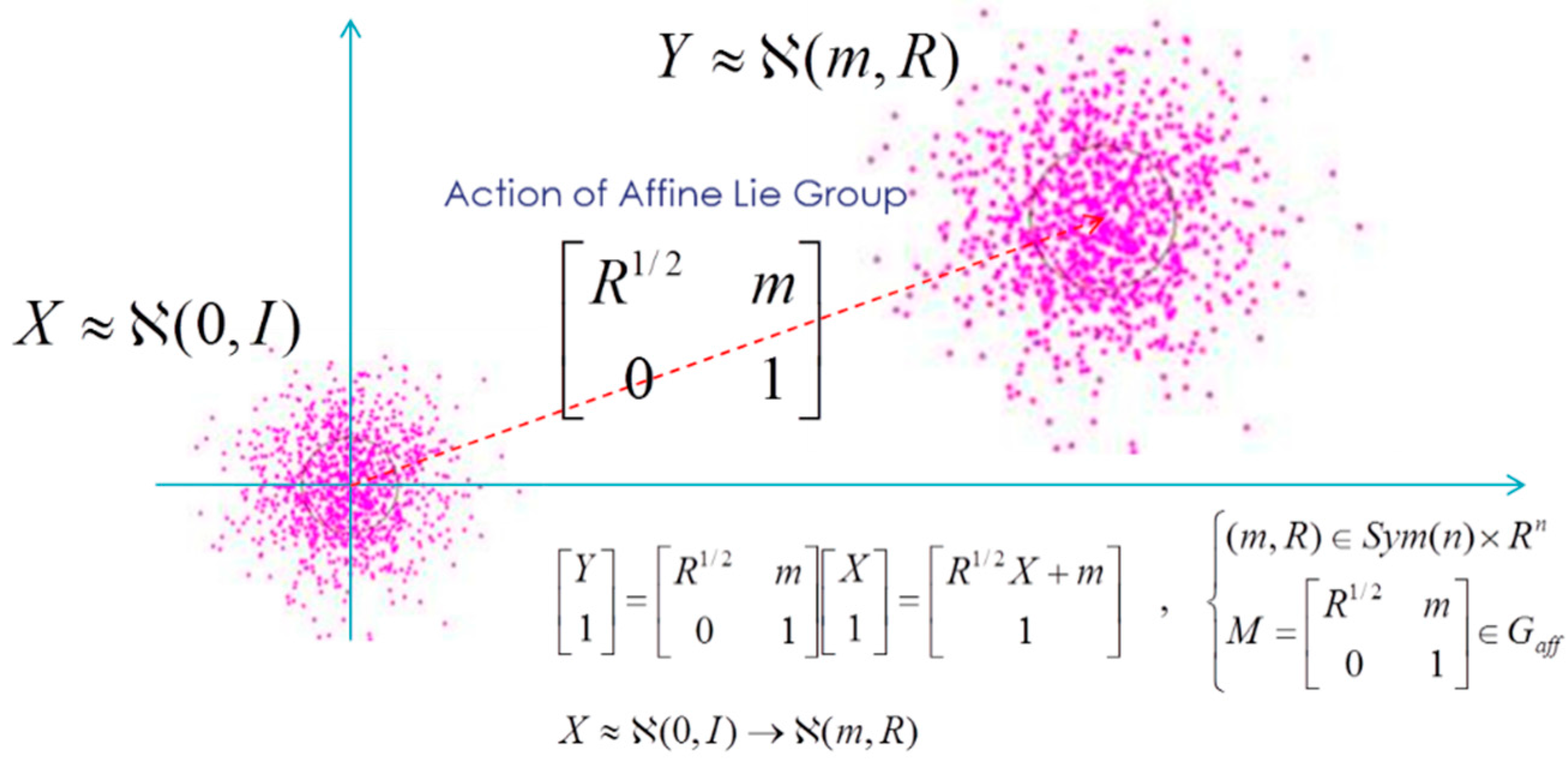
- For the case of multivariate Gaussian densities, we have considered a sub-group of affine group, that we defined by a (n + 1) × (n + 1) embedding in matrix Lie group , and that acts for multivariate Gaussian laws by:
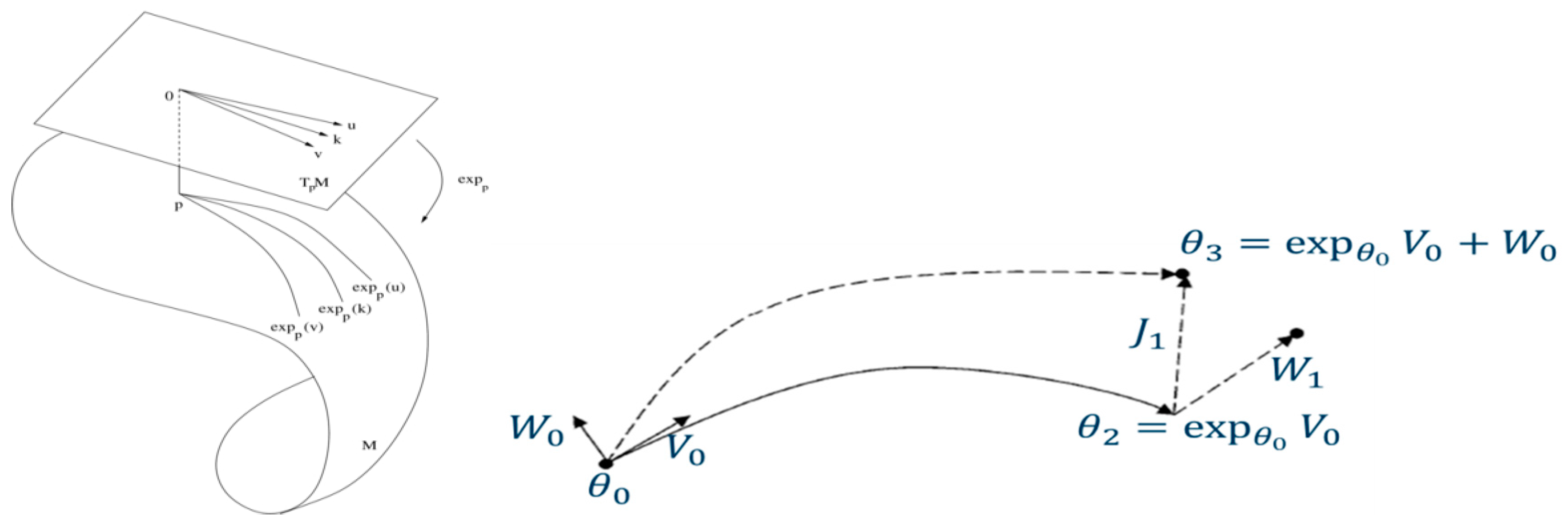
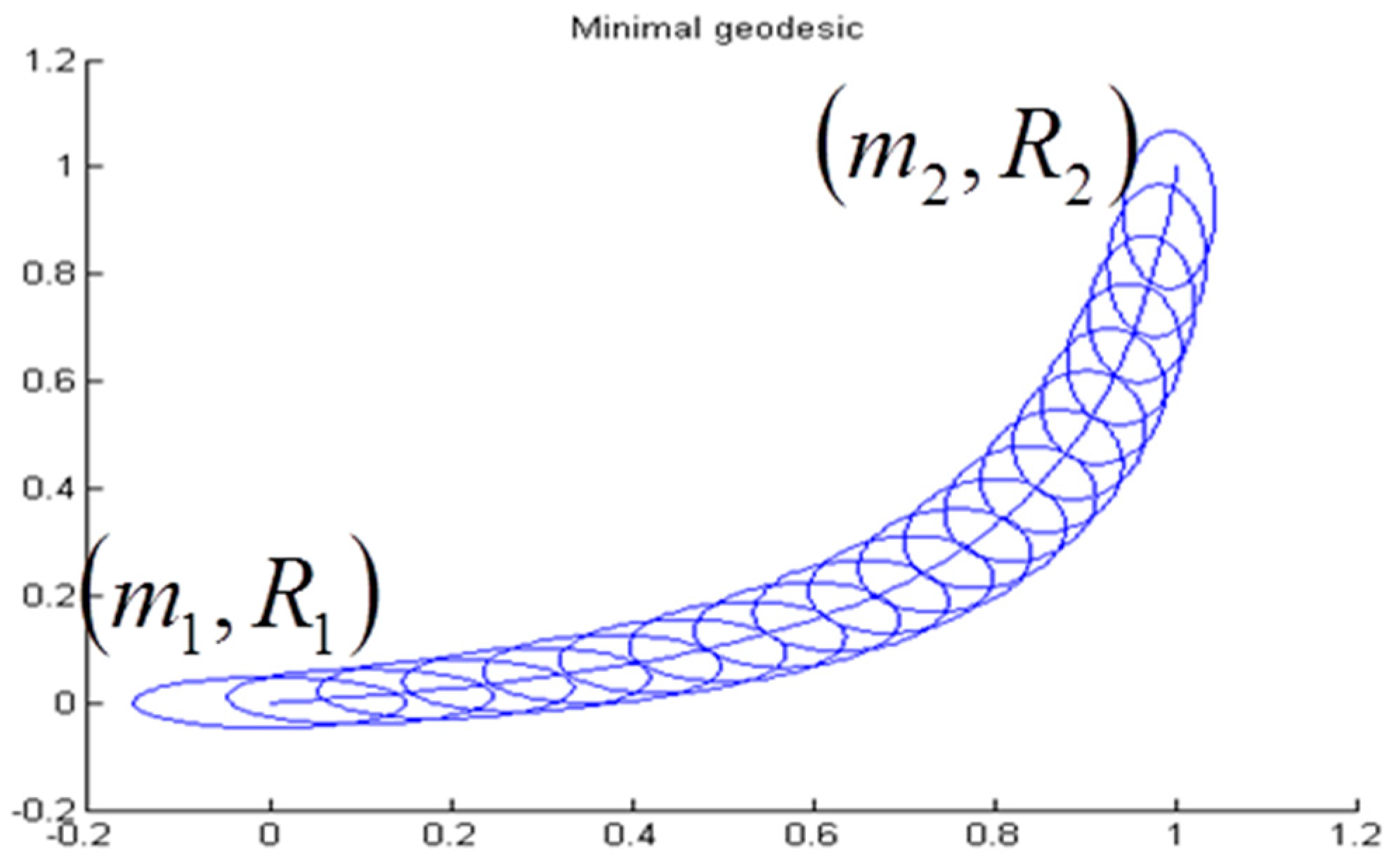
- For multivariate Gaussian densities, as we have identified the acting sub-group of affine group , we have also developed the computation of the associated Lie algebras and , adjoint and coadjoint operators, and especially the Souriau “moment map” :Using Souriau Theorem (geometrization of Noether theorem), we use the property that this moment map is constant (its components are equal to Noether invariants):to reduce the Euler-Lagrange equation of geodesics between two multivariate Gaussian densities:to this reduced equation of geodesics:that we solve by “geodesic shooting” technic based on Eriksen equation of exponential map.
- For the families of multivariate Gaussian densities, that we have identified as homogeneous manifold with the associated sub-group of the affine group , we have considered the elements of exponential families, that play the role of geometric heat in Souriau Lie group thermodynamics, and the geometric (Planck) temperature:We have considered that these elements are homeomorph to the (n + 1) × (n + 1) matrix elements:to compute the Souriau symplectic cocycle of the Lie group:where the adjoint operator is equal to:withand the co-adjoint operator:
- Finally, we have computed the Souriau-Fisher metric for multivariate Gaussian densities, given by:with element of Lie algebra given by .
2. Position of Souriau Symplectic Model of Statistical Physics in Historical Developments of Thermodynamic Concepts
3. Revisited Souriau Symplectic Model of Statistical Physics
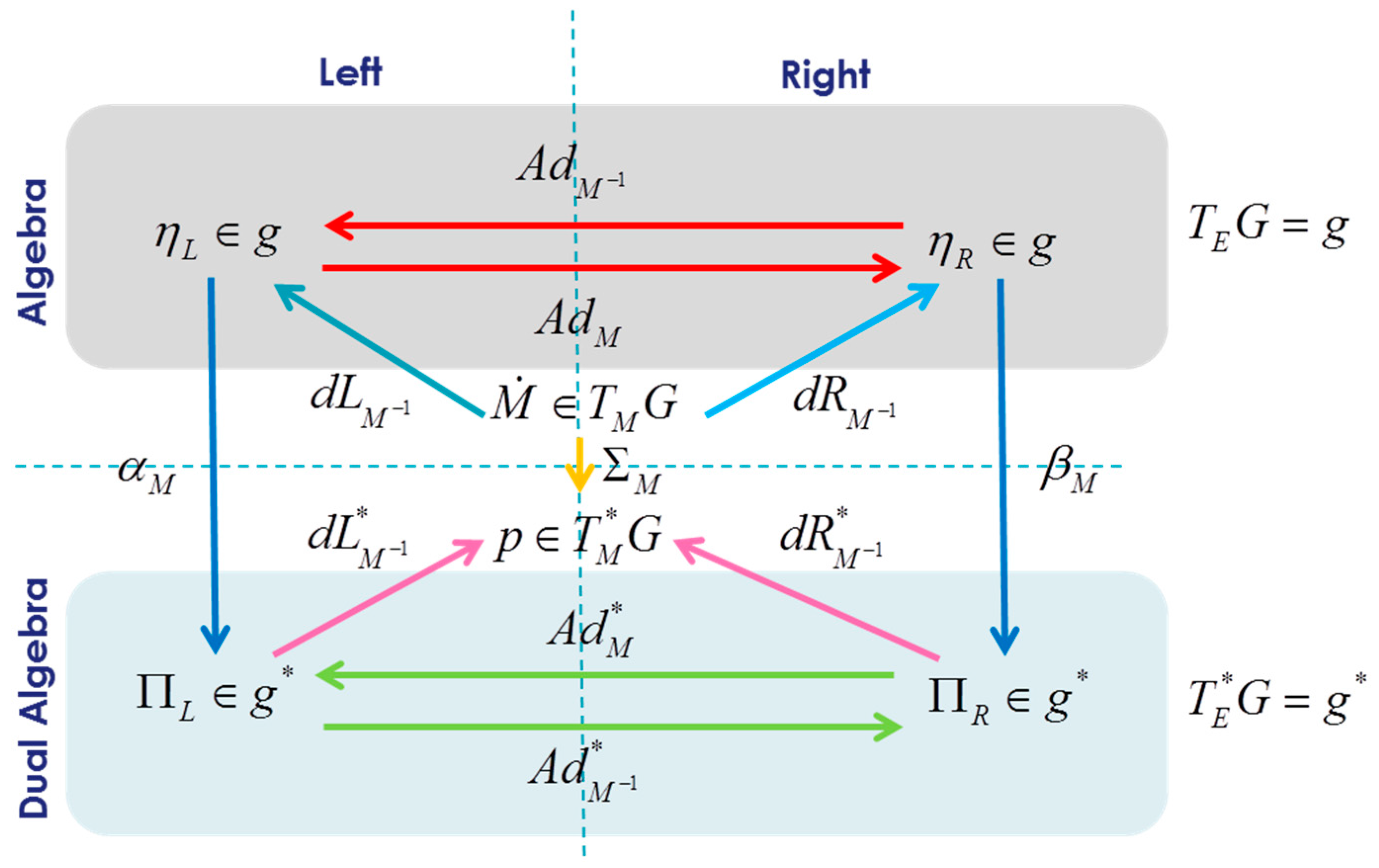
- The coadjoint representation of is the contragredient of the adjoint representation. It associates to each the linear isomorphism , which satisfies, for each and :
- The adjoint representation of the Lie algebra is the linear representation of into itself which associates, to each , the linear map . Tangent application of at neutral element of :
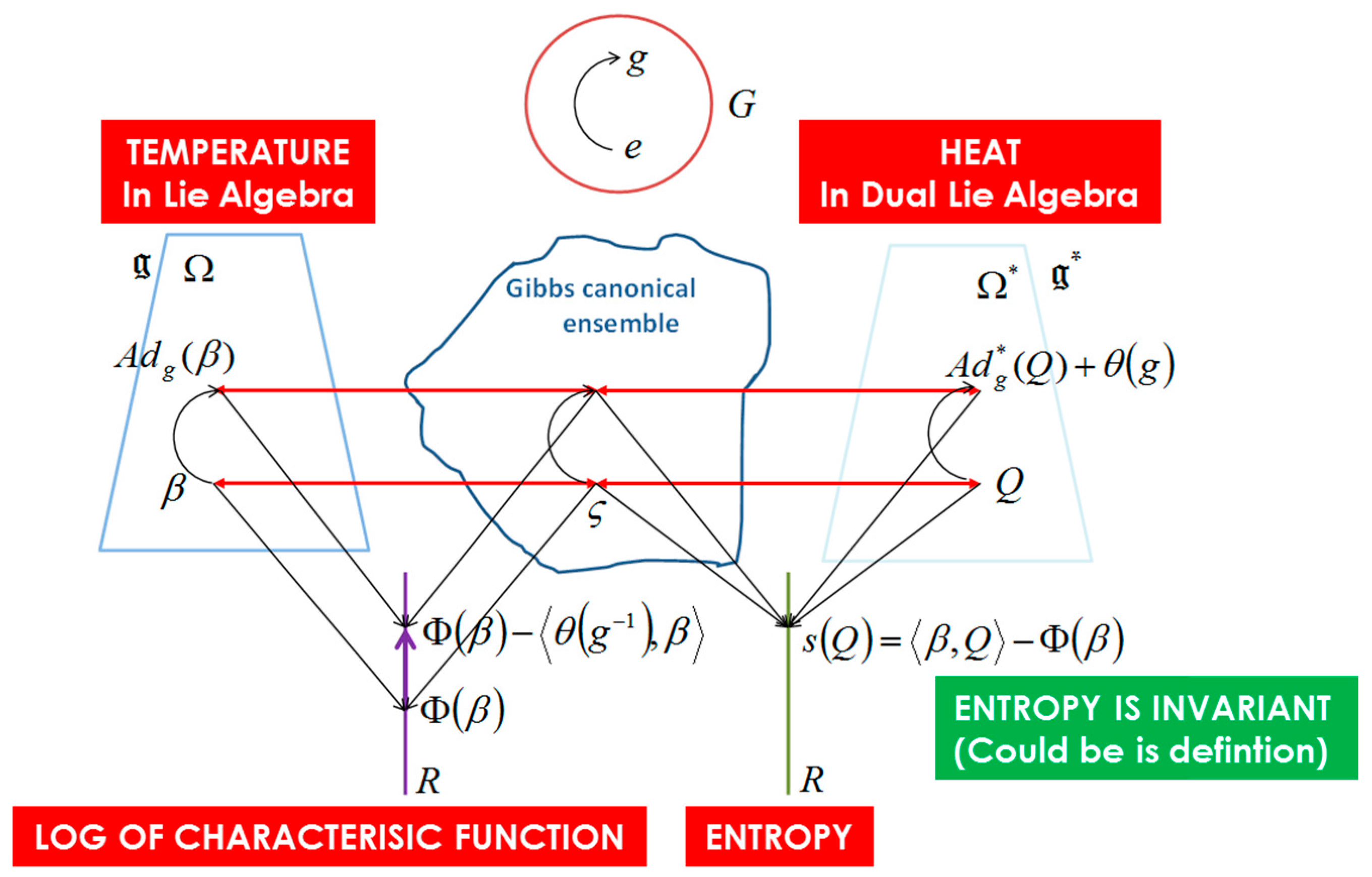
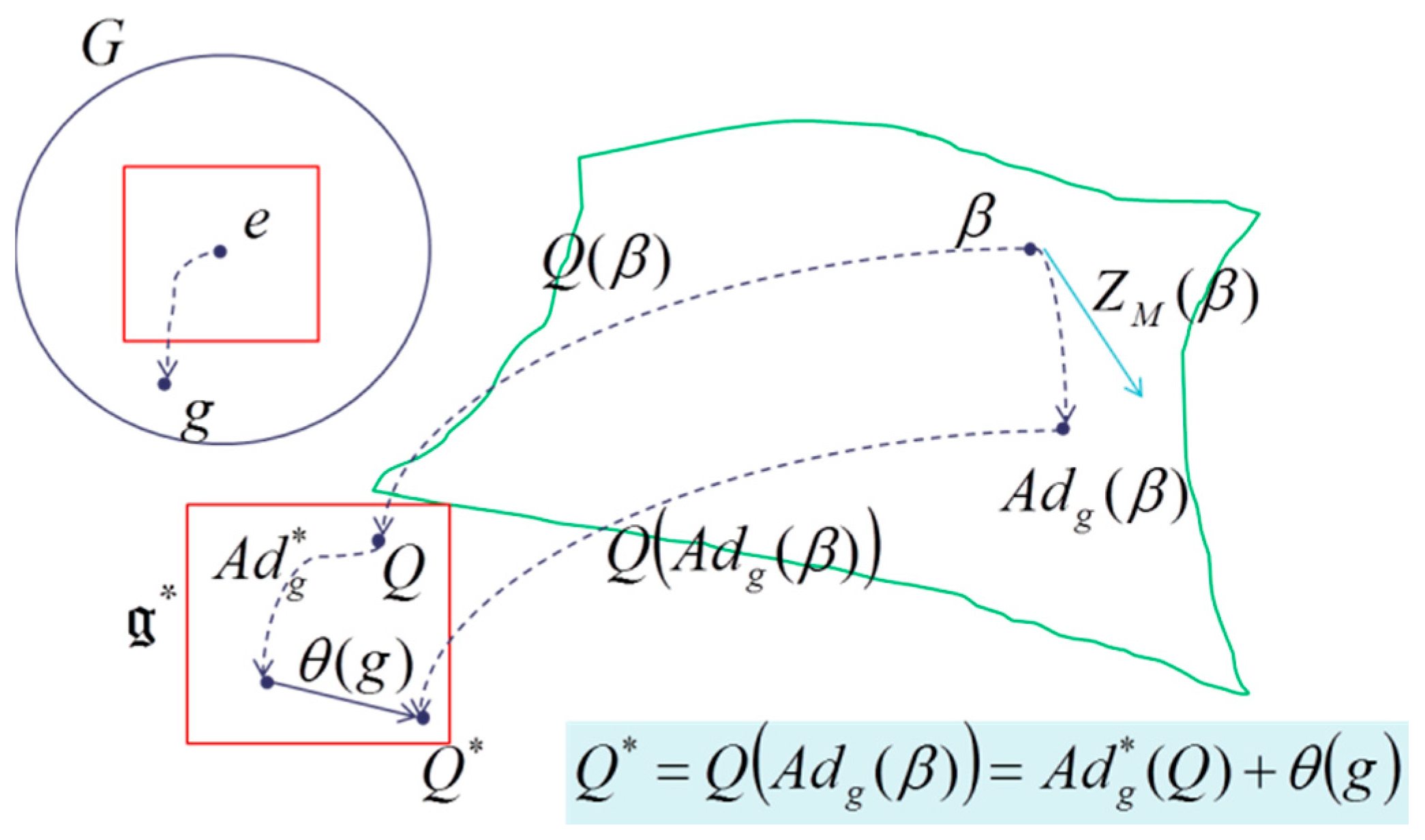
- The coadjoint representation of the Lie algebra is the contragredient of the adjoint representation. It associates, to each , the linear map which satisfies, for each and :We can illustrate for group of matrices for with .Then, the curve from tangent to is given by and transform by :For each temperature , element of the Lie algebra , Souriau has introduced a tensor , equal to the sum of the cocycle and the heat coboundary (with [.,.] Lie bracket):This tensor has the following properties:
- where the map is the one-cocycle of the Lie algebra with values in , with where the one-cocycle of the Lie group G. is constant on M and the map is a skew-symmetric bilinear form, and is called the symplectic cocycle of Lie algebra associated to the moment map , with the following properties:where linear application from to differential function on : and the associated differentiable application , called moment(um) map:If instead of we take the following moment map:where is constant, the symplectic cocycle is replaced bywhere is one-coboundary of with values in . We also have properties and .
- The geometric temperature, element of the algebra , is in the thekernel of the tensor :
- The following symmetric tensor , defined on all values of is positive definite:where the linear map is the adjoint representation of the Lie algebra defined by , and the co-adjoint representation of the Lie algebra the linear map which satisfies, for each and :These equations are universal, because they are not dependent on the symplectic manifold but only on the dynamical group G, the symplectic cocycle , the temperature and the heat . Souriau called this model “Lie groups thermodynamics”.
- Action of Lie group on Lie algebra:
- Transformation of characteristic function after action of Lie group:
- Invariance of entropy with respect to action of Lie group:
- Action of Lie group on geometric heat, element of dual Lie algebra:
It is obvious that one can only define average values on objects belonging to a vector (or affine) space; Therefore—so this assertion may seem Bourbakist—that we will observe and measure average values only as quantity belonging to a set having physically an affine structure. It is clear that this structure is necessarily unique—if not the average values would not be well defined. (Il est évident que l’on ne peut définir de valeurs moyennes que sur des objets appartenant à un espace vectoriel (ou affine); donc—si bourbakiste que puisse sembler cette affirmation—que l’on n’observera et ne mesurera de valeurs moyennes que sur des grandeurs appartenant à un ensemble possédant physiquement une structure affine. Il est clair que cette structure est nécessairement unique—sinon les valeurs moyennes ne seraient pas bien définies.).
4. The Souriau-Fisher Metric as Geometric Heat Capacity of Lie Group Thermodynamics
5. Euler-Poincaré Equations and Variational Principle of Souriau Lie Group Thermodynamics
6. Souriau Affine Representation of Lie Group and Lie Algebra and Comparison with the Koszul Affine Representation
6.1. Affine Representations and Cocycles
6.2. Souriau Moment Map and Cocycles
6.3. Equivariance of Souriau Moment Map
6.4. Action of Lie Group on a Symplectic Manifold
6.5. Dual Spaces of Finite-Dimensional Lie Algebras
6.6. Koszul Affine Representation of Lie Group and Lie Algebra
6.7. Comparison of Koszul and Souriau Affine Representation of Lie Group and Lie Algebra
6.8. Additional Elements on Koszul Affine Representation of Lie Group and Lie Algebra
- If is quasi-compact, then the universal covering manifold of M is affinely isomorphic to a convex domain of an affine space not containing any full straight line.
- If is compact, then is a sharp convex cone.
7. Souriau Lie Group Model and Koszul Hessian Geometry Applied in the Context of Information Geometry for Multivariate Gaussian Densities
8. Affine Group Action for Multivariate Gaussian Densities and Souriau’s Moment Map: Computation of Geodesics by Geodesic Shooting
9. Souriau Riemannian Metric for Multivariate Gaussian Densities
10. Conclusions
Lorsque il y un tremblement de terre, nous assistons à la mort de l’Espace. … Nous vivons avec nos habitudes que nous pensons universelles. … La neuroscience s’occupe rarement de la géométrie … Pour les singes qui vivent dans les arbres, certaines propriétés du groupe d’Euclide sont mieux câblées dans leurs cerveaux (When there is an earthquake, we are witnessing the death of Space … We live with our habits that we think are universal.... Neuroscience rarely is interested in geometry … For the monkeys that live in trees, some properties of the Euclid group are better coded in their brains).
L’élève demanda à Bohr qu’il ne comprenait pas le principe de correspondance. Bohr lui demanda de s’assoir et il tourna autour de lui. Bohr lui dit tu dois commencer à avoir mal au cœur, c’est que tu commences à comprendre ce qu’est le principe de correspondance (The student said to Bohr that he did not understand the principle of correspondence. Bohr asked him to sit and he turned around. Bohr said, you should start to be seasick, it is then that you begin to understand what the correspondence principle is.).
Acknowledgments
Si on ajoute que la critique qui accoutume l’esprit, surtout en matière de faits, à recevoir de simples probabilités pour des preuves, est, par cet endroit, moins propre à le former, que ne le doit être la géométrie qui lui fait contracter l’habitude de n’acquiescer qu’à l’évidence; nous répliquerons qu’à la rigueur on pourrait conclure de cette différence même, que la critique donne, au contraire, plus d’exercice à l’esprit que la géométrie: parce que l’évidence, qui est une et absolue, le fixe au premier aspect sans lui laisser ni la liberté de douter, ni le mérite de choisir; au lieu que les probabilités étant susceptibles du plus et du moins, il faut, pour se mettre en état de prendre un parti, les comparer ensemble, les discuter et les peser. Un genre d’étude qui rompt, pour ainsi dire, l’esprit à cette opération, est certainement d’un usage plus étendu que celui où tout est soumis à l’évidence; parce que les occasions de se déterminer sur des vraisemblances ou probabilités, sont plus fréquentes que celles qui exigent qu’on procède par démonstrations: pourquoi ne dirions –nous pas que souvent elles tiennent aussi à des objets beaucoup plus importants?—Joseph de Maistre in L’Espit de Finesse [221]
Le cadavre qui s’acoutre se méconnait et imaginant l’éternité s’en approrie l’illusion … C’est pourquoi j’abandonnerai ces frusques et jetant le masque de mes jours, je fuirai le temps où, de concert avec les autres, je m’éreinte à me trahir.—Emile Cioran in Précis de decomposition [222]
Conflicts of Interest
Appendix A. Clairaut(-Legendre) Equation of Maurice Fréchet Associated to “Distinguished Functions” as Fundamental Equation of Information Geometry
Clairaut Equation and Legendre Transform
Appendix B. Balian Gauge Model of Thermodynamics and its Compliance with Souriau Model
Appendix C. Casalis-Letac Affine Group Invariance for Natural Exponential Families
References and Notes
- Bernard, C. Introduction à l’Étude de la Médecine Expérimentale. Available online: http://classiques.uqac.ca/classiques/bernard_claude/intro_etude_medecine_exp/intro_medecine_exper.pdf (accessed on 17 October 2016).
- Thom, R. Logos et Théorie des Catastrophes; Editions Patiño: Genève, Switzerland, 1988. [Google Scholar]
- Barbaresco, F. Symplectic structure of information geometry: Fisher metric and Euler-Poincaré equation of souriau lie group thermodynamics. In Geometric Science of Information, Second International Conference GSI 2015; Nielsen, F., Barbaresco, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9389, pp. 529–540. [Google Scholar]
- De Saxcé, G.; Vallée, C. Galilean Mechanics and Thermodynamics of Continua; Wiley-ISTE: London, UK, 2016. [Google Scholar]
- Vallée, C. Relativistic thermodynamics of continua. Int. J. Eng. Sci. 1981, 19, 589–601. [Google Scholar] [CrossRef]
- Vallée, C.; Lerintiu, C. Convex analysis and entropy calculation in statistical mechanics. Proc. A Razmadze Math. Inst. 2005, 137, 111–129. [Google Scholar]
- Marle, C.M. From Tools in Symplectic and Poisson Geometry to J.-M. Souriau’s Theories of Statistical Mechanics and Thermodynamics. Entropy 2016, 18, 370. [Google Scholar] [CrossRef]
- De Saxcé, G. Link between lie group statistical mechanics and thermodynamics of continua. In Special Issue MDPI Entropy “Differential Geometrical Theory of Statistics”; MDPI: Basel, Switzerland, 2016; Volume 18, p. 254. [Google Scholar]
- Barbaresco, F. Koszul information geometry and souriau geometric temperature/capacity of lie group thermodynamics. Entropy 2014, 16, 4521–4565. [Google Scholar] [CrossRef]
- Souriau, J.M. Structure des Systèmes Dynamiques; Editions Jacques Gabay: Paris, France, 1970. (In French) [Google Scholar]
- Souriau, J.M. Structure of Dynamical Systems, volume 149 of Progress in Mathematics. In A Symplectic View of Physics; Birkhäuser: Basel, Switzerland, 1997. [Google Scholar]
- Nielsen, F.; Barbaresco, F. Geometric Science of Information; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Kosmann-Schwarzbach, Y. La géométrie de Poisson, création du XXième siècle. In Siméon-Denis Poisson; Ecole Polytechnique: Paris, France, 2013; pp. 129–172. [Google Scholar]
- Bismut, J.M. Mécanique Aléatoire; Springer: Berlin/Heidelberg, Germany, 1981; Volume 866. [Google Scholar]
- Casas-Vázquez, J.; Jou, D. Temperature in non-equilibrium states: A review of open problems and current proposals. Rep. Prog. Phys. 2003, 66, 1937–2023. [Google Scholar] [CrossRef]
- Streater, R.F. The information manifold for relatively bounded potentials. Tr. Mat. Inst. Steklova 2000, 228, 217–235. [Google Scholar]
- Arnold, V.I. Sur la géométrie différentielle des groupes de Lie de dimension infinie et ses applications à l’hydrodynamique des fluides parfaits. Ann. Inst. Fourier 1966, 16, 319–361. [Google Scholar] [CrossRef]
- Arnold, V.I.; Givental, A.B. Symplectic geometry. In Dynamical Systems IV: Symplectic Geometry and Its Applications, Encyclopaedia of Mathematical Sciences; Arnol’d, V.I., Novikov, S.P., Eds.; Springer: Berlin, Germany, 1990; Volume 4, pp. 1–136. [Google Scholar]
- Marle, C.M.; de Saxcé, G.; Vallée, C. L’oeuvre de Jean-Marie Souriau, Gazette de la SMF, Hommage à Jean-Marie Souriau. 2012; Published by SMF, Paris. [Google Scholar]
- Patrick Iglesias, Itinéraire d’un Mathématicien: Un entretien Avec Jean-Marie Souriau, Le Journal de Maths des Elèves. Available online: http://www.lutecium.fr/jp-petit/science/gal_port/interview_Souriau.pdf (accessed on 27 October 2016). (In French)
- Iglesias, P. Symétries et Moment; Hermann: Paris, France, 2000. [Google Scholar]
- Kosmann-Schwarzbach, Y. Groupes et Symmetries; Ecole Polytechnique: Paris, France, 2006. [Google Scholar]
- Kosmann-Schwarzbach, Y. En homage à Jean-Marie Souriau, quelques souvenirs. Gazette des Mathématiciens 2012, 133, 105–106. [Google Scholar]
- Ghys, E. Actions localement libres du groupe affine. Invent. Math. 1985, 82, 479–526. [Google Scholar] [CrossRef]
- Rais, M. La representation coadjointe du groupe affine. Ann. Inst. Fourier 1978, 28, 207–237. (In French) [Google Scholar] [CrossRef]
- Souriau, J.M. Mécanique des états condensés de la matière. In Proceedings of the 1st International Seminar of Mechanics Federation of Grenoble, Grenoble, France, 19–21 May 1992. (In French)
- Souriau, J.M. Géométrie de l’espace de phases. Commun. Math. Phys. 1966, 374, 1–30. (In French) [Google Scholar]
- Souriau, J.M. Définition covariante des équilibres thermodynamiques. Nuovo Cimento 1966, 1, 203–216. (In French) [Google Scholar]
- Souriau, J.M. Mécanique Statistique, Groupes de Lie et Cosmologie; Colloques Internationaux du CNRS Numéro 237: Paris, France, 1974; pp. 59–113. (In French) [Google Scholar]
- Souriau, J.M. Géométrie Symplectique et Physique Mathématique; Éditions du C.N.R.S.: Paris, France, 1975. (In French) [Google Scholar]
- Souriau, J.M. Thermodynamique Relativiste des Fluides; Centre de Physique Théorique: Marseille, France, 1977. (In French) [Google Scholar]
- Souriau, J.M. Interpretation Géometrique des Etatsquantiques; Springer: Berlin/Heidelberg, Germany, 1977; Volume 570. (In French) [Google Scholar]
- Souriau, J.M. Thermodynamique et géométrie. In Differential Geometrical Methods in Mathematical Physics II; Bleuler, K., Reetz, A., Petry, H.R., Eds.; Springer: Berlin/Heidelberg, Germany, 1978; pp. 369–397. (In French) [Google Scholar]
- Souriau, J.M. Dynamic Systems Structure, Chapters 16–19. Unpublished work. 1980.
- Souriau, J.M.; Iglesias, P. Heat Cold and Geometry. Differential Geometry and Mathematical Physics, Mathematical Physics Studies Volume; Springer: Amsterdam, The Netherlands, 1983; pp. 37–68. [Google Scholar]
- Souriau, J.M. Mécanique classique et géométrie symplectique. CNRS Marseille. Cent. Phys. Théor. Report ref. CPT-84/PE-1695 1984. (In French)
- Souriau, J.M. On Geometric Mechanics. Discret. Cont. Dyn. Syst. J. 2007, 19, 595–607. [Google Scholar] [CrossRef]
- Laplace, P.S. Mémoire sur la probabilité des causes sur les évènements. In Mémoires de Mathématique et de Physique; De l’Imprimerie Royale: Paris, France, 1774. (In French) [Google Scholar]
- Gibbs, J.W. Elementary principles in statistical mechanics. In The Rational Foundation of Thermodynamics; Scribner: New York, NY, USA, 1902. [Google Scholar]
- Ruelle, D.P. Thermodynamic Formalism; Addison-Wesley: New York, NY, USA, 1978. [Google Scholar]
- Ruelle, D.P. Extending the definition of entropy to nonequilibrium steady states. Proc. Natl. Acad. Sci. USA 2003, 100, 3054–3058. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E.T. Prior probabilities. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 227–241. [Google Scholar] [CrossRef]
- Jaynes, E.T. The well-posed problem. Found. Phys. 1973, 3, 477–493. [Google Scholar] [CrossRef]
- Jaynes, E.T. Where do we stand on maximum entropy? In The Maximum Entropy Formalism; Levine, R.D., Tribus, M., Eds.; MIT Press: Cambridge, MA, USA, 1979; pp. 15–118. [Google Scholar]
- Jaynes, E.T. The minimum entropy production principle. Annu. Rev. Phys. Chem. 1980, 31, 579–601. [Google Scholar] [CrossRef]
- Jaynes, E.T. On the rationale of maximum entropy methods. IEEE Proc. 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Jaynes, E.T. Papers on Probability, Statistics and Statistical Physics; Reidel: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Ollivier, Y. Aspects de l’entropie en Mathématiques et en Physique (Théorie de l’information, Systèmes Dynamiques, Grandes Déviations, Irréversibilité). Available online: http://www.yann-ollivier.org/entropie/entropie.pdf (accessed on 7 August 2015). (In French)
- Villani, C. (Ir)rréversibilité et Entropie. Available online: http://www.bourbaphy.fr/villani.pdf (accessed on 5 August 2015). (In French)
- Godement, R. Introduction à la Théorie des Groupes de Lie; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Guichardet, A. Cohomologie des Groups Topologiques et des Algèbres de Lie; Cedic/Fernand Nathan: Paris, France, 1980. [Google Scholar]
- Guichardet, A. La method des orbites: Historiques, principes, résultats. In Leçons de Mathématiques D’aujourd’hui; Cassini: Paris, France, 2010; Volume 4, pp. 33–59. [Google Scholar]
- Guichardet, A. Le Problème de Kepler, Histoire et Théorie; Ecole Polytechnique: Paris, France, 2012. [Google Scholar]
- Dubois, J.G.; Dufour, J.P. La théorie des catastrophes. V. Transformées de Legendre et thermodynamique. In Annales de l’IHP Physique Théorique; Institut Henri Poincaré: Paris, France, 1978; Volume 29, pp. 1–50. [Google Scholar]
- Monge, G. Sur le Calcul Intégral des Equations aux Différences Partielles; Mémoires de l’Académie des Sciences: Paris, France, 1784; pp. 118–192. (In French) [Google Scholar]
- Moreau, J.J. Fonctions convexes duales et points proximaux dans un espace hilbertien. C. R. Acad. Sci. 1962, 255, 2897–2899. (In French) [Google Scholar]
- Plastino, A.; Plastino, A.R. On the Universality of thermodynamics’ Legendre transform structure. Phys. Lett. A 1997, 226, 257–263. [Google Scholar] [CrossRef]
- Friedrich, T. Die fisher-information und symplectische strukturen. Math. Nachr. 1991, 153, 273–296. (In German) [Google Scholar] [CrossRef]
- Massieu, F. Sur les Fonctions caractéristiques des divers fluides. C. R. Acad. Sci. 1869, 69, 858–862. (In French) [Google Scholar]
- Massieu, F. Addition au précédent Mémoire sur les Fonctions caractéristiques. C. R. Acad. Sci. 1869, 69, 1057–1061. (In French) [Google Scholar]
- Massieu, F. Exposé des Principes Fondamentaux de la Théorie Mécanique de la Chaleur (note Destinée à Servir D’introduction au Mémoire de L’auteur sur les Fonctions Caractéristiques des Divers Fluides et la Théorie des Vapeurs); Académie des Sciences: Paris, France, 1873; p. 31. (In French) [Google Scholar]
- Massieu, F. Thermodynamique: Mémoire sur les Fonctions Caractéristiques des Divers Fluides et sur la Théorie des Vapeurs; Académie des Sciences: Paris, France, 1876; p. 92. (In French) [Google Scholar]
- Massieu, F. Sur les Intégrales Algébriques des Problèmes de Mécanique. Suivie de Sur le Mode de Propagation des Ondes Planes et la Surface de L’onde Elémentaire dans les Cristaux Biréfringents à Deux Axes. Ph.D. Thesis, Faculté des Sciences de Paris, Paris, France, 1861. [Google Scholar]
- Nivoit, E. Notice sur la vie et les Travaux de M. Massieu, Inspecteur Général des Mines. Available online: http://facultes19.ish-lyon.cnrs.fr/fiche.php?indice=1153 (accessed 27 October).
- Gibbs, J.W. Graphical Methods in the Thermodynamics of Fluids. In The Scientific Papers of J. Willard Gibbs; Dover: New York, NY, USA, 1961. [Google Scholar]
- Brillouin, L. Science and Information Theory; Academic Press: New York, NY, USA, 1956. [Google Scholar]
- Brillouin, L. Maxwell’s demon cannot operate: Information and entropy. J. Appl. Phys. 1951, 22, 334–337. [Google Scholar] [CrossRef]
- Brillouin, L. Physical entropy and information. J. Appl. Phys. 1951, 22, 338–343. [Google Scholar] [CrossRef]
- Brillouin, L. Negentropy principle of information. J. Appl. Phys. 1953, 24, 1152–1163. [Google Scholar] [CrossRef]
- Duhem, P. Sur les équations générales de la thermodynamique. In Annales scientifiques de l’École Normale Supérieure; Ecole Normale Supérieure: Paris, France, 1891; Volume 8, pp. 231–266. (In French) [Google Scholar]
- Duhem, P. Commentaire aux principes de la Thermodynamique—Première partie. J. Math. Appl. 1892, 8, 269–330. (In French) [Google Scholar]
- Duhem, P. Commentaire aux principes de la Thermodynamique—Troisième partie. J. Math. Appl. 1894, 10, 207–286. (In French) [Google Scholar]
- Duhem, P. Les théories de la chaleur. Revue des deux Mondes 1895, 130, 851–868. [Google Scholar]
- Carathéodory, C. Untersuchungen über die Grundlagen der Thermodynamik (Examination of the foundations of thermodynamics). Math. Ann. 1909, 67, 355–386. [Google Scholar] [CrossRef]
- Carnot, S. Réflexions sur la Puissance Motrice du feu; Dover: New York, NY, USA, 1960. [Google Scholar]
- Clausius, R. On the Mechanical Theory of Heat; Browne, W.R., Translator; Macmillan: London, UK, 1879. [Google Scholar]
- Darrigol, O. The Origins of the Entropy Concept. Available online: http://www.bourbaphy.fr/darrigol.pdf (accessed on 5 August 2015). (In French)
- Gromov, M. In a Search for a Structure, Part 1: On Entropy. Available online: http://www.ihes.fr/~gromov/PDF/structre-serch-entropy-july5-2012.pdf (accessed on 6 August 2015).
- Gromov, M. Six Lectures on Probability, Symmetry, Linearity. Available online: http://www.ihes.fr/~gromov/PDF/probability-huge-Lecture-Nov-2014.pdf (accessed on 6 August 2015).
- Gromov, M. Metric Structures for Riemannian and Non-Riemannian Spaces (Modern Birkhäuser Classics), 3rd ed.Lafontaine, J., Pansu, P., Eds.; Birkhäuser: Basel, Switzerland, 2006. [Google Scholar]
- Kozlov, V.V. Heat equilibrium by Gibbs and poincaré. Dokl. RAN 2002, 382, 602–606. (In French) [Google Scholar]
- Poincaré, H. Sur les tentatives d’explication mécanique des principes de la thermodynamique. C. R. Acad. Sci. 1889, 108, 550–553. [Google Scholar]
- Poincaré, H. Thermodynamique, Cours de Physique Mathématique. Available online: http://gallica.bnf.fr/ark:/12148/bpt6k2048983 (accessed on 24 October 2016). (In French)
- Poincaré, H. Calcul des Probabilités; Gauthier-Villars: Paris, France, 1896. (In French) [Google Scholar]
- Poincaré, H. Réflexions sur la théorie cinétique des gaz. J. Phys. Theor. Appl. 1906, 5, 369–403. [Google Scholar] [CrossRef]
- Fourier, J. Théorie Analytique de la Chaleur; Chez Firmin Didot: Paris, France, 1822. (In French) [Google Scholar]
- Clausius, R. Théorie Mécanique de la Chaleur; Lacroix: Paris, France, 1868. (In French) [Google Scholar]
- Poisson, S.D. Théorie Mathématique de la Chaleur; Bachelier: Paris, France, 1835. (In French) [Google Scholar]
- Kosmann-Schwarzbach, Y. Siméon-Denis Poisson: Les Mathématiques au Service de la Science; Ecole Polytechnique: Paris, France, 2013. (In French) [Google Scholar]
- Smale, S. Topology and Mechanics. Invent. Math. 1970, 10, 305–331. [Google Scholar] [CrossRef]
- Cushman, R.; Duistermaat, J.J. The quantum mechanical spherical pendulum. Bull. Am. Math. Soc. 1988, 19, 475–479. [Google Scholar] [CrossRef]
- Guillemin, V.; Sternberg, S. The moment map and collective motion. Ann. Phys. 1980, 1278, 220–253. [Google Scholar] [CrossRef]
- De Saxcé, G.; Vallée, C. Bargmann group, momentum tensor and Galilean invariance of Clausius-Duhem Inequality. Int. J. Eng. Sci. 2012, 50, 216–232. [Google Scholar] [CrossRef]
- De Saxcé, G. Entropy and structure for the thermodynamic systems. In Geometric Science of Information, Second International Conference GSI 2015 Proceedings; Nielsen, F., Barbaresco, F., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9389, pp. 519–528. [Google Scholar]
- Kapranov, M. Thermodynamics and the moment map. 2011; arXiv:1108.3472v1. [Google Scholar]
- Pavlov, V.P.; Sergeev, V.M. Thermodynamics from the differential geometry standpoint. Theor. Math. Phys. 2008, 157, 1484–1490. [Google Scholar] [CrossRef]
- Cartier, P.; DeWitt-Morette, C. Functional Integration. Action and Symmetries; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Libermann, P.; Marle, C.M. Symplectic Geometry and Analytical Mechanics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Lichnerowicz, A. Espaces homogènes Kähleriens. In Colloque de Géométrie Différentielle; CNRSP: Paris, France, 1953; pp. 171–184. (In French) [Google Scholar]
- Lichnerowicz, A. Représentation Coadjointe Quotient et Espaces Homogènes de Contact, cours du Collège de France; Springer: Berlin/Heidelberg, Germany, 1986. (In French) [Google Scholar]
- Balian, R.; Valentin, P. Hamiltonian structure of thermodynamics with gauge. Eur. Phys. J. B 2001, 21, 269–282. [Google Scholar] [CrossRef]
- Marle, C.M. On Henri Poincaré’s note “Sur une forme nouvelle des équations de la mécanique”. J. Geom. Symmetry Phys. 2013, 29, 1–38. [Google Scholar]
- Poincaré, H. Sur une forme nouvelle des équations de la Mécanique. C. R. Acad. Sci. 1901, 7, 369–371. (In French) [Google Scholar]
- Sternberg, S. Symplectic homogeneous spaces. Trans. Am. Math. Soc. 1975, 212, 113–130. [Google Scholar] [CrossRef]
- Bourguignon, J.P. Calcul Variationnel; Ecole Polytechnique: Paris, France, 2007. (In French) [Google Scholar]
- Dedecker, P. A property of differential forms in the calculus of variations. Pac. J. Math. 1957, 7, 1545–1549. [Google Scholar] [CrossRef]
- Marle, C.M. On mechanical systems with a Lie group as configuration space. In Jean Leray ’99 Conference Proceedings; De Gosson, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 183–203. [Google Scholar]
- Marle, C.M. Symmetries of Hamiltonian systems on symplectic and poisson manifolds. In Similarity and Symmetry Methods; Springer: Berlin/Heidelberg, Germany, 2014; pp. 185–269. [Google Scholar]
- Kirillov, A.A. Merits and demerits of the orbit method. Bull. Am. Math. Soc. 1999, 36, 433–488. [Google Scholar] [CrossRef]
- Cartan, E. La structure des groupes de transformations continus et la théorie du trièdre mobile. Bull. Sci. Math. 1910, 34, 250–284. (In French) [Google Scholar]
- Cartan, E. Leçons sur les Invariants Intégraux; Hermann: Paris, France, 1922. (In French) [Google Scholar]
- Cartan, E. Les récentes généralisations de la notion d’espace. Bull. Sci. Math. 1924, 48, 294–320. (In French) [Google Scholar]
- Cartan, E. Le rôle de la Théorie des Groupes de Lie dans L’évolution de la Géométrie Modern; C.R. Congrès International: Oslo, Norway, 1936; Volume 1, pp. 92–103. (In French) [Google Scholar]
- Libermann, P. La géométrie différentielle d’Elie Cartan à Charles Ehresmann et André Lichnerowicz. In Géométrie au XXe siècle, 1930-2000: Histoire et Horizons; Hermann: Paris, France, 2005. (In French) [Google Scholar]
- Koszul, J.L. Sur la forme hermitienne canonique des espaces homogènes complexes. Can. J. Math. 1955, 7, 562–576. (In French) [Google Scholar] [CrossRef]
- Koszul, J.L. Exposés sur les Espaces Homogènes Symétriques; Publicação da Sociedade de Matematica de São Paulo: São Paulo, Brazil, 1959. (In French) [Google Scholar]
- Koszul, J.L. Domaines bornées homogènes et orbites de groupes de transformations affines. Bull. Soc. Math. Fr. 1961, 89, 515–533. (In French) [Google Scholar]
- Koszul, J.L. Ouverts convexes homogènes des espaces affines. Math. Z. 1962, 79, 254–259. (In French) [Google Scholar] [CrossRef]
- Koszul, J.L. Variétés localement plates et convexité. Osaka J. Math. 1965, 2, 285–290. (In French) [Google Scholar]
- Koszul, J.L. Lectures on Groups of Transformations; Tata Institute of Fundamental Research: Bombay, India, 1965. [Google Scholar]
- Koszul, J.L. Déformations des variétés localement plates. Ann. Inst. Fourier 1968, 18, 103–114. (In French) [Google Scholar] [CrossRef]
- Koszul, J.L. Trajectoires convexes de groupes affines unimodulaires. In Essays on Topology and Related Topics; Springer: Berlin, Germany, 1970; pp. 105–110. [Google Scholar]
- Vinberg, E.B. The theory of homogeneous convex cones. Trudy Moskovskogo Matematicheskogo Obshchestva 1963, 12, 303–358. [Google Scholar]
- Vinberg, E.B. Structure of the group of automorphisms of a homogeneous convex cone. Trudy Moskovskogo Matematicheskogo Obshchestva 1965, 13, 56–83. (In Russian) [Google Scholar]
- Byande, P.M.; Ngakeu, F.; Boyom, M.N.; Wolak, R. KV-cohomology and differential geometry of affinely flat manifolds. Information geometry. Afr. Diaspora J. Math. 2012, 14, 197–226. [Google Scholar]
- Byande, P.M. Des Structures Affines à la Géométrie de L’information; Omniscriptum: Saarbrücken, France, 2012. [Google Scholar]
- Nguiffo Boyom, M. Sur les structures affines homotopes à zéro des groupes de Lie. J. Differ. Geom. 1990, 31, 859–911. (In French) [Google Scholar]
- Nguiffo Boyom, M. Structures localement plates dans certaines variétés symplectiques. Math. Scand. 1995, 76, 61–84. (In French) [Google Scholar] [CrossRef]
- Nguiffo Boyom, M. The cohomology of Koszul-Vinberg algebras. Pac. J. Math. 2006, 225, 119–153. [Google Scholar] [CrossRef]
- Nguiffo Boyom, M. Some Lagrangian Invariants of Symplectic Manifolds, Geometry and Topology of Manifolds; Banach Center Institute of Mathematics, Polish Academy of Sciences: Warsaw, Poland, 2007; Volume 76, pp. 515–525. [Google Scholar]
- Nguiffo Boyom, M. Métriques kählériennes affinement plates de certaines variétés symplectiques. I. Proc. Lond. Math. Soc. 1993, 2, 358–380. (In French) [Google Scholar] [CrossRef]
- Nguiffo Boyom, M.; Byande, P.M. KV Cohomology in Information Geometry Matrix Information Geometry; Springer: Heidelberg, Germany, 2013; pp. 69–92. [Google Scholar]
- Nguiffo Boyom, M. Transversally Hessian foliations and information geometry I. Am. Inst. Phys. Proc. 2014, 1641, 82–89. [Google Scholar]
- Nguiffo Boyom, M.; Wolak, R. Transverse Hessian metrics information geometry MaxEnt 2014. AIP. Conf. Proc. Am. Inst. Phys. 2015. [Google Scholar] [CrossRef]
- Vey, J. Sur une Notion D’hyperbolicité des Variables Localement Plates. Thèse de Troisième Cycle de Mathématiques Pures; Faculté des Sciences de l’université de Grenoble: Grenoble, France, 1969. (In French) [Google Scholar]
- Vey, J. Sur les Automorphismes affines des ouverts convexes saillants. Annali della scuola normale superiore di pisa. Classe Sci. 1970, 24, 641–665. (In French) [Google Scholar]
- Barbaresco, F. Koszul information geometry and Souriau Lie group thermodynamics. In AIP Conference Proceedings, Proceedings of MaxEnt’14 Conference, Amboise, France, 21–26 September 2014.
- Lesne, A. Shannon entropy: A rigorous notion at the crossroads between probability, information theory, dynamical systems and statistical physics. Math. Struct. Comput. Sci. 2014, 24, e240311. [Google Scholar] [CrossRef]
- Fréchet, M.R. Sur l’extension de certaines évaluations statistiques au cas de petits échantillons. Rev. Inst. Int. Stat. 1943, 11, 182–205. (In French) [Google Scholar] [CrossRef]
- Fréchet, M.R. Les espaces abstraits topologiquement affines. Acta Math. 1925, 47, 25–52. [Google Scholar] [CrossRef]
- Fréchet, M.R. Les éléments aléatoires de nature quelconque dans un espace distancié. Ann. Inst. Henri Poincaré 1948, 10, 215–310. [Google Scholar]
- Fréchet, M.R. Généralisations de la loi de probabilité de Laplace. Ann. Inst. Henri Poincaré 1951, 12, 1–29. (In French) [Google Scholar]
- Shima, H. The Geometry of Hessian Structures; World Scientific: Singapore, 2007. [Google Scholar]
- Shima, H. Geometry of Hessian Structures. In Springer Lecture Notes in Computer Science; Nielsen, F., Frederic, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8085, pp. 37–55. [Google Scholar]
- Crouzeix, J.P. A relationship between the second derivatives of a convex function and of its conjugate. Math. Program. 1977, 3, 364–365. [Google Scholar] [CrossRef]
- Hiriart-Urruty, J.B. A new set-valued second-order derivative for convex functions. In Mathematics for Optimization; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Bakhvalov, N.S. Memorial: Nikolai Nikolaevitch Chentsov. Theory Probab. Appl. 1994, 38, 506–515. [Google Scholar] [CrossRef]
- Chentsov, N.N. Statistical Decision Rules and Optimal Inference; American Mathematical Society: Providence, RI, USA, 1982. [Google Scholar]
- Berezin, F. Quantization in complex symmetric spaces. Izv. Akad. Nauk SSSR Ser. Math. 1975, 9, 363–402. [Google Scholar] [CrossRef]
- Bhatia, R. Positive Definite Matrices; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Bhatia, R. The bipolar decomposition. Linear Algebra Appl. 2013, 439, 3031–3037. [Google Scholar] [CrossRef]
- Bini, D.A.; Garoni, C.; Iannazzo, B.; Capizzano, S.S.; Sesana, D. Asymptotic Behaviour and Computation of Geometric-Like Means of Toeplitz Matrices. In SLA14 Conference, Kalamata, Greece, September 2014; Available online: http://noether.math.uoa.gr/conferences/sla2014/sites/default/files/Iannazzo.pdf (accessed on 8–12 September 2014).
- Bini, D.A.; Garoni, C.; Iannazzo, B.; Capizzano, S.S. Geometric means of toeplitz matrices by positive parametrizations. 2016, in press. [Google Scholar]
- Calvo, M.; Oller, J.M. An explicit solution of information geodesic equations for the multivariate normal model. Stat. Decis. 1991, 9, 119–138. [Google Scholar] [CrossRef]
- Calvo, M.; Oller, J.M. A distance between multivariate normal distributions based in an embedding into the Siegel group. J. Multivar. Anal. Arch. 1990, 35, 223–242. [Google Scholar] [CrossRef]
- Calvo, M.; Oller, J.M. A distance between elliptical distributions based in an embedding into the Siegel group. J. Comput. Appl. Math. 2002, 145, 319–334. [Google Scholar] [CrossRef]
- Chevallier, E.; Barbaresco, F.; Angulo, J. Probability density estimation on the hyperbolic space applied to radar processing. In Geometric Science of Information Proceedings; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9389, pp. 753–761. [Google Scholar]
- Chevallier, E.; Forget, T.; Barbaresco, F.; Angulo, J. Kernel Density Estimation on the Siegel Space Applied to Radar Processing. Available online: https://hal-ensmp.archives-ouvertes.fr/hal-01344910/document (accessed on 24 October 2016).
- Costa, S.I.R.; Santosa, S.A.; Strapasson, J.E. Fisher information distance: A geometrical reading. Discret. Appl. Math. 2015, 197, 59–69. [Google Scholar] [CrossRef]
- Jeuris, B.; Vandebril, R.; Vandereycken, B. A survey and comparison of contemporary algorithms for computing the matrix geometric mean. Electron. Trans. Numer. Anal. 2012, 39, 379–402. [Google Scholar]
- Jeuris, B. Riemannian Optimization for Averaging Positive Definite Matrices. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2015. [Google Scholar]
- Jeuris, B.; Vandebril, R. The Kähler Mean of Block-Toeplitz Matrices with Toeplitz Structured Blocks; Department of Computer Science, KU Leuven: Leuven, Belgium, 2015. [Google Scholar]
- Maliavin, P. Invariant or quasi-invariant probability measures for infinite dimensional groups, Part II: Unitarizing measures or Berezinian measures. Jpn. J. Math. 2008, 3, 19–47. [Google Scholar] [CrossRef]
- Strapasson, J.E.; Porto, J.P.S.; Costa, S.I.R. On bounds for the Fisher-Rao distance between multivariate normal distributions. AIP Conf. Proc. 2015, 1641, 313–320. [Google Scholar]
- Hua, L.K. Harmonic Analysis of Functions of Several Complex Variables in the Classical Domains; American Mathematical Society: Providence, RI, USA, 1963. [Google Scholar]
- Siegel, C.L. Symplectic geometry. Am. J. Math. 1943, 65, 1–86. [Google Scholar] [CrossRef]
- Yoshizawa, S.; Tanabe, K. Dual differential geometry associated with the Kullback-Leibler information on the Gaussian distributions and its 2-parameters deformations. SUT J. Math. 1999, 35, 113–137. [Google Scholar]
- Skovgaard, L.T. A Riemannian Geometry of the Multivariate Normal Model; Technical Report for Stanford University: Stanford, CA, USA, April 1981. [Google Scholar]
- Deza, M.M.; Deza, E. Encyclopedia of Distances, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2013; p. 242. [Google Scholar]
- Casalis, M. Familles exponentielles naturelles invariantes par un groupe de translations. C. R. Acad. Sci. Ser. I Math. 1988, 307, 621–623. (In French) [Google Scholar]
- Casalis, M. Familles Exponentielles Naturelles Invariantes par un Groupe. Ph.D. Thesis, Thèse de l’Université Paul Sabatier, Toulouse, France, 1990. [Google Scholar]
- Casalis, M. Familles exponentielles naturelles sur rd invariantes par un groupe. Int. Stat. Rev. 1991, 59, 241–262. (In French) [Google Scholar] [CrossRef]
- Casalis, M. Les familles exponentielles à variance quadratique homogène sont des lois de Wishart sur un cône symétrique. C. R. Acad. Sci. Ser. I Math. 1991, 312, 537–540. (In French) [Google Scholar]
- Casalis, M.; Letac, G. Characterization of the Jørgensen set in generalized linear models. Test 1994, 3, 145–162. [Google Scholar] [CrossRef]
- Casalis, M.; Letac, G. The Lukacs-Olkin-Rubin characterization of the Wishart distributions on symmetric cone. Ann. Stat. 1996, 24, 763–786. [Google Scholar] [CrossRef]
- Casalis, M. The 2d + 4 simple quadratic natural exponential families on Rd. Ann. Stat. 1996, 24, 1828–1854. [Google Scholar]
- Letac, G. A characterization of the Wishart exponential families by an invariance property. J. Theor. Probab. 1989, 2, 71–86. [Google Scholar] [CrossRef]
- Letac, G. Lectures on Natural Exponential Families and Their Variance Functions, Volume 50 of Monografias de Matematica (Mathematical Monographs); Instituto de Matematica Pura e Aplicada (IMPA): Rio de Janeiro, Brazil, 1992. [Google Scholar]
- Letac, G. Les familles exponentielles statistiques invariantes par les groupes du Cône et du paraboloïde de revolution. In Journal of Applied Probability, Volume 31, Studies in Applied Probability; Takacs, L., Galambos, J., Gani, J., Eds.; Applied Probability Trust: Sheffield, UK, 1994; pp. 71–95. [Google Scholar]
- Barndorff-Nielsen, O.E. Differential geometry and statistics: Some mathematical aspects. Indian J. Math. 1987, 29, 335–350. [Google Scholar]
- Barndorff-Nielsen, O.E.; Jupp, P.E. Yokes and symplectic structures. J. Stat. Plan Inference 1997, 63, 133–146. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Jupp, P.E. Statistics, yokes and symplectic geometry. Annales de la Faculté des sciences de Toulouse: Mathématiques 1997, 6, 389–427. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E. Information and Exponential Families in Stattistical Theory; Wiley: New York, NY, USA, 2014. [Google Scholar]
- Jespersen, N.C.B. On the structure of transformation models. Ann. Stat. 1999, 17, 195–208. [Google Scholar]
- Skovgaard, L.T. A Riemannian geometry of the multivariate normal model. Scand. J. Stat. 1984, 11, 211–223. [Google Scholar]
- Han, M.; Park, F.C. DTI segmentation and fiber tracking using metrics on multivariate normal distributions. J. Math. Imaging Vis. 2014, 49, 317–334. [Google Scholar] [CrossRef]
- Imai, T.; Takaesu, A.; Wakayama, M. Remarks on geodesics for multivariate normal models. J. Math. Ind. 2011, 3, 125–130. [Google Scholar]
- Inoue, H. Group theoretical study on geodesics for the elliptical models. In Geometric Science of Information Proceedings; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9389, pp. 605–614. [Google Scholar]
- Pilté, M.; Barbaresco, F. Tracking quality monitoring based on information geometry and geodesic shooting. In Proceedings of the 17th International Radar Symposium (IRS), Krakow, Poland, 10–12 May 2016; pp. 1–6.
- Eriksen, P.S. (k, 1) Exponential transformation models. Scand. J. Stat. 1984, 11, 129–145. [Google Scholar]
- Eriksen, P. Geodesics Connected with the Fisher Metric on the Multivariate Normal Manifold; Technical Report 86-13; Institute of Electronic Systems, Aalborg University: Aalborg, Denmark, 1986. [Google Scholar]
- Eriksen, P.S. Geodesics connected with the Fisher metric on the multivariate normal manifold. In Proceedings of the GST Workshop, Lancaster, UK, 28–31 October 1987.
- Feragen, A.; Lauze, F.; Hauberg, S. Geodesic exponential kernels: When curvature and linearity conflict. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 8–10 June 2015; pp. 3032–3042.
- Besse, A.L. Einstein Manifolds, Ergebnisse der Mathematik und ihre Grenzgebiete; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Tumpach, A.B. Infinite-dimensional hyperkähler manifolds associated with Hermitian-symmetric affine coadjoint orbits. Ann. Inst. Fourier 2009, 59, 167–197. [Google Scholar] [CrossRef]
- Tumpach, A.B. Classification of infinite-dimensional Hermitian-symmetric affine coadjoint orbits. Forum Math. 2009, 21, 375–393. [Google Scholar] [CrossRef]
- Tumpach, A.B. Variétés Kählériennes et Hyperkählériennes de Dimension Infinie. Ph.D. Thesis, Ecole Polytechnique, Paris, France, 26 July 2005. [Google Scholar]
- Neeb, K.-H. Infinite-dimensional groups and their representations. In Lie Theory; Birkhäuser: Basel, Switzerland, 2004. [Google Scholar]
- Gauduchon, P. Calabi’s Extremal Kähler Metrics: An Elementary Introduction. Available online: germanio.math.unifi.it/wp-content/uploads/2015/03/dercalabi.pdf (accessed on 27 October 2016).
- Biquard, O.; Gauduchon, P. Hyperkähler Metrics on Cotangent Bundles of Hermitian Symmetric Spaces. Available online: https://www.math.ens.fr/~biquard/aarhus96.pdf (accessed on 27 October 2016).
- Biquard, O.; Gauduchon, P. La métrique hyperkählérienne des orbites coadjointes de type symétrique d’un groupe de Lie complexe semi-simple. Comptes Rendus de l’Académie des Sciences 1996, 323, 1259–1264. (In French) [Google Scholar]
- Biquard, O.; Gauduchon, P. Géométrie hyperkählérienne des espaces hermitiens symétriques complexifiés. Séminaire de Théorie Spectrale et Géométrie 1998, 16, 127–173. [Google Scholar] [CrossRef]
- Chaperon, M. Jets, Transversalité, Singularités: Petite Introduction aux Grandes Idées de René Thom; Kouneiher, J., Flament, D., Nabonnand, P., Szczeciniarz, J.-J., Eds.; Géométrie au Vingtième Siècle, Histoire et Horizons: Hermann, Paris, 2005; pp. 246–256. [Google Scholar]
- Chaperon, M. Generating maps, invariant manifolds, conjugacy. J. Geom. Phys. 2015, 87, 76–85. [Google Scholar] [CrossRef]
- Viterbo, C. Symplectic topology as the geometry of generating functions. Math. Ann. 1992, 292, 685–710. [Google Scholar] [CrossRef]
- Viterbo, C. Generating functions, symplectic geometry and applications. In Proceedings of the International Congress of Mathematics, Zürich, Switzerland, 3–11 August 1994.
- Dazord, P.; Weinstein, A. Symplectic, Groupoids, and Integrable Systems; Springer: Berlin/Heidelberg, Germany, 1991; pp. 99–128. [Google Scholar]
- Drinfeld, V.G. Hamiltonian structures on Lie groups. Sov. Math. Dokl. 1983, 27, 68–7l. [Google Scholar]
- Thom, R. Une théorie dynamique de la Morphogenèse. In Towards a Theoretical Biology I; Waddington, C.H., Ed.; University of Edinburgh Press: Edinburgh, UK, 1966; pp. 52–166. [Google Scholar]
- Thom, R. Stabilité Structurelle et Morphogénèse, 2nd ed.; Inter Editions: Paris, France, 1977. [Google Scholar]
- Ingarden, R.S.; Nakagomi, T. The second order extension of the Gibbs state. Open Syst. Inf. Dyn. 1992, 1, 243–258. [Google Scholar] [CrossRef]
- Ingarden, R.S.; Meller, J. Temperatures in Linguistics as a Model of Thermodynamics. Open Syst. Inf. Dyn. 1994, 2, 211–230. [Google Scholar] [CrossRef]
- Nencka, H.; Streater, R.F. Information Geometry for some Lie algebras. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 1999, 2, 441–460. [Google Scholar] [CrossRef]
- Burdet, G.; Perrin, M.; Perroud, M. Generating functions for the affine symplectic group. Comm. Math. Phys. 1978, 3, 241–254. [Google Scholar] [CrossRef]
- Berthoz, A. Le Sens du Movement; Odile Jacob Edirot: Paris, France, 1997. (In French) [Google Scholar]
- Afgoustidis, A. Invariant Harmonic Analysis and Geometry in the Workings of the Brain. Available online: https://hal-univ-diderot.archives-ouvertes.fr/tel-01343703 (accessed on 17 October 2016).
- Souriau, J.M. Innovaxiom—Interview of Jean-Marie Souriau. Available online: https://www.youtube.com/watch?v=Lb_TWYqBUS4 (accessed on 27 October 2016).
- Souriau, J.M. Quantique ? Alors c’est Géométrique. Available online: http://www.ahm.msh-paris.fr/Video.aspx?domain=84fa1a68-95c0-4c74-aed7-06055edaca16&language=fr&metaDescriptionId=dd3bd275-8372-4130-976b-847c36156a83&mediatype=VideoWithShots (accessed on 27 October 2016).
- Masseau, D. Les marges des Lumières Françaises (1750–1789); Dix-huitième Siècle Année: Paris, France, 2005; Volume 37, pp. 638–639. (In French) [Google Scholar]
- Cioran, E. Précis de Décomposition Poche; Gallimard: Paris, France, 1977. [Google Scholar]
- Rao, C.R. Information and the accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 1945, 37, 81–91. [Google Scholar]
- Burbea, J.; Rao, C.R. Entropy differential metric, distance and divergence measures in probability spaces: A unified approach. J. Multivar. Anal. 1982, 12, 575–596. [Google Scholar] [CrossRef]
- Legendre, A.M. Mémoire Sur L’intégration de Quelques Equations aux Différences Partielles; Mémoires de l’Académie des Sciences: Paris, France, 1787; pp. 309–351. (In French) [Google Scholar]
- Darboux, G. Leçons sur la Théorie Générale des Surfaces et les Applications Géométriques du Calcul Infinitésimal: Premiere Partie (Généralités, Coordonnées Curvilignes, Surface Minima); Gauthier-Villars: Paris, France, 1887. (In French) [Google Scholar]
- Balian, R.; Alhassid, Y.; Reinhardt, H. Dissipation in many-body systems: A geometric approach based on information theory. Phys. Rep. 1986, 131, 1–146. [Google Scholar] [CrossRef]
- Balian, R.; Balazs, N. Equiprobability, inference and entropy in quantum theory. Ann. Phys. 1987, 179, 97–144. [Google Scholar] [CrossRef]
- Balian, R. On the principles of quantum mechanics. Am. J. Phys. 1989, 57, 1019–1027. [Google Scholar] [CrossRef]
- Balian, R. From Microphysics to Macrophysics: Methods and Applications of Statistical Physics; Springer: Heidelberg, Germany, 1991 & 1992; Volumes I and II. [Google Scholar]
- Balian, R. Incomplete descriptions and relevant entropies. Am. J. Phys. 1999, 67, 1078–1090. [Google Scholar] [CrossRef]
- Balian, R. Entropy, a protean concept. In Poincaré Seminar 2003; Dalibard, J., Duplantier, B., Rivasseau, V., Eds.; Birkhauser: Basel, Switzerland, 2004; pp. 119–144. [Google Scholar]
- Balian, R. Information in statistical physics. In Studies in History and Philosophy of Modern Physics, Part B; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Balian, R. The entropy-based quantum metric. Entropy 2014, 16, 3878–3888. [Google Scholar] [CrossRef]
- Balian, R. François Massieu et les Potentiels Thermodynamiques, Évolution des Disciplines et Histoire des Découvertes; Académie des Sciences: Avril, France, 2015. [Google Scholar]
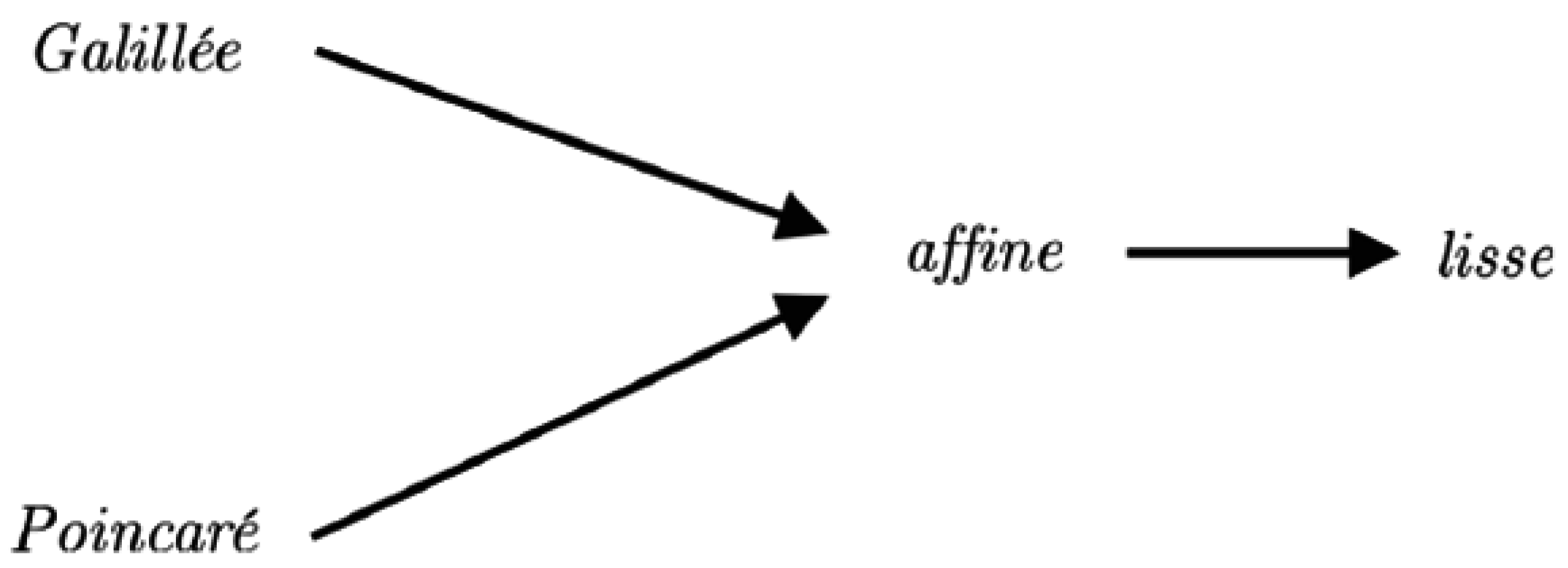




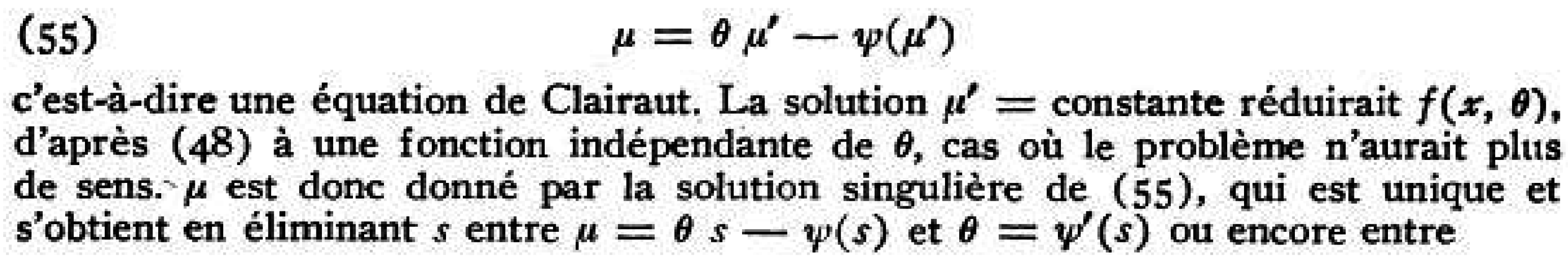


| Souriau Model of Affine Representation of Lie Groups and Algebra | Koszul Model of Affine Representation of Lie Groups and Algebra |
|---|---|
| and | |
| with is a one-cocycle of G with values in E, | |
The linear map is a one-cocycle of G with values in E: | and the differential of and respectively |
| none | |
| none |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbaresco, F. Geometric Theory of Heat from Souriau Lie Groups Thermodynamics and Koszul Hessian Geometry: Applications in Information Geometry for Exponential Families. Entropy 2016, 18, 386. https://doi.org/10.3390/e18110386
Barbaresco F. Geometric Theory of Heat from Souriau Lie Groups Thermodynamics and Koszul Hessian Geometry: Applications in Information Geometry for Exponential Families. Entropy. 2016; 18(11):386. https://doi.org/10.3390/e18110386
Chicago/Turabian StyleBarbaresco, Frédéric. 2016. "Geometric Theory of Heat from Souriau Lie Groups Thermodynamics and Koszul Hessian Geometry: Applications in Information Geometry for Exponential Families" Entropy 18, no. 11: 386. https://doi.org/10.3390/e18110386
APA StyleBarbaresco, F. (2016). Geometric Theory of Heat from Souriau Lie Groups Thermodynamics and Koszul Hessian Geometry: Applications in Information Geometry for Exponential Families. Entropy, 18(11), 386. https://doi.org/10.3390/e18110386






