Point Information Gain and Multidimensional Data Analysis
Abstract
:1. Introduction
2. Mathematical Description and Properties of Point Information Gain
2.1. Point Information Gain and Its Relation to Other Information Entropies
2.2. Point Information Gain for Typical Distributions
2.3. Point Information Gain Entropy and Point Information Gain Entropy Density
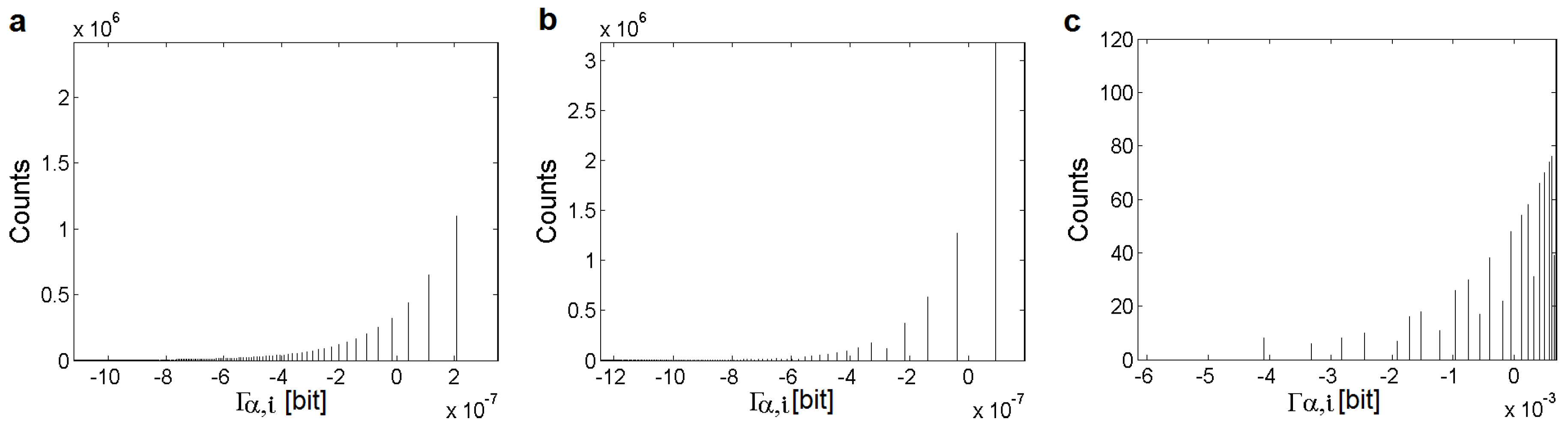
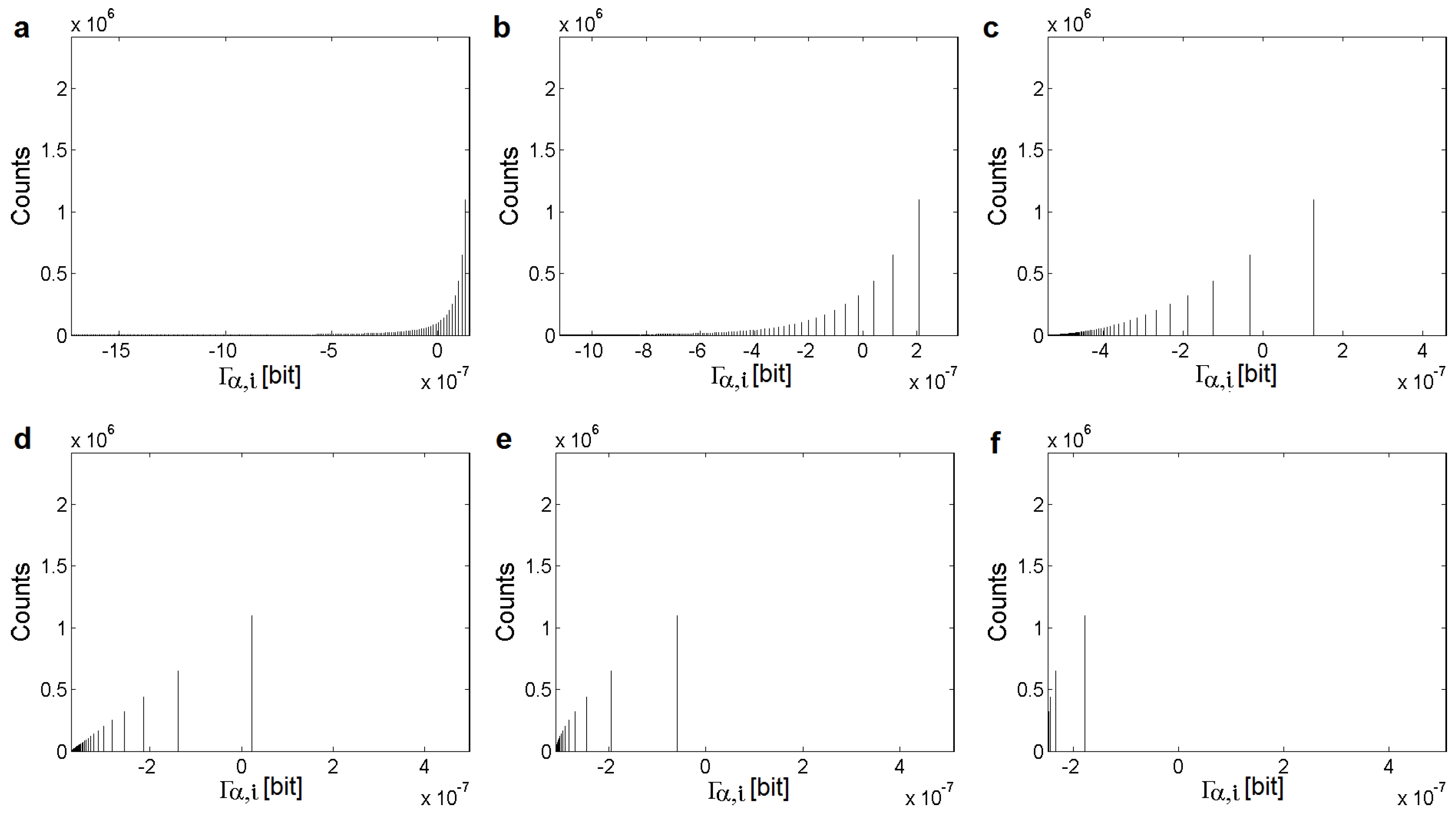
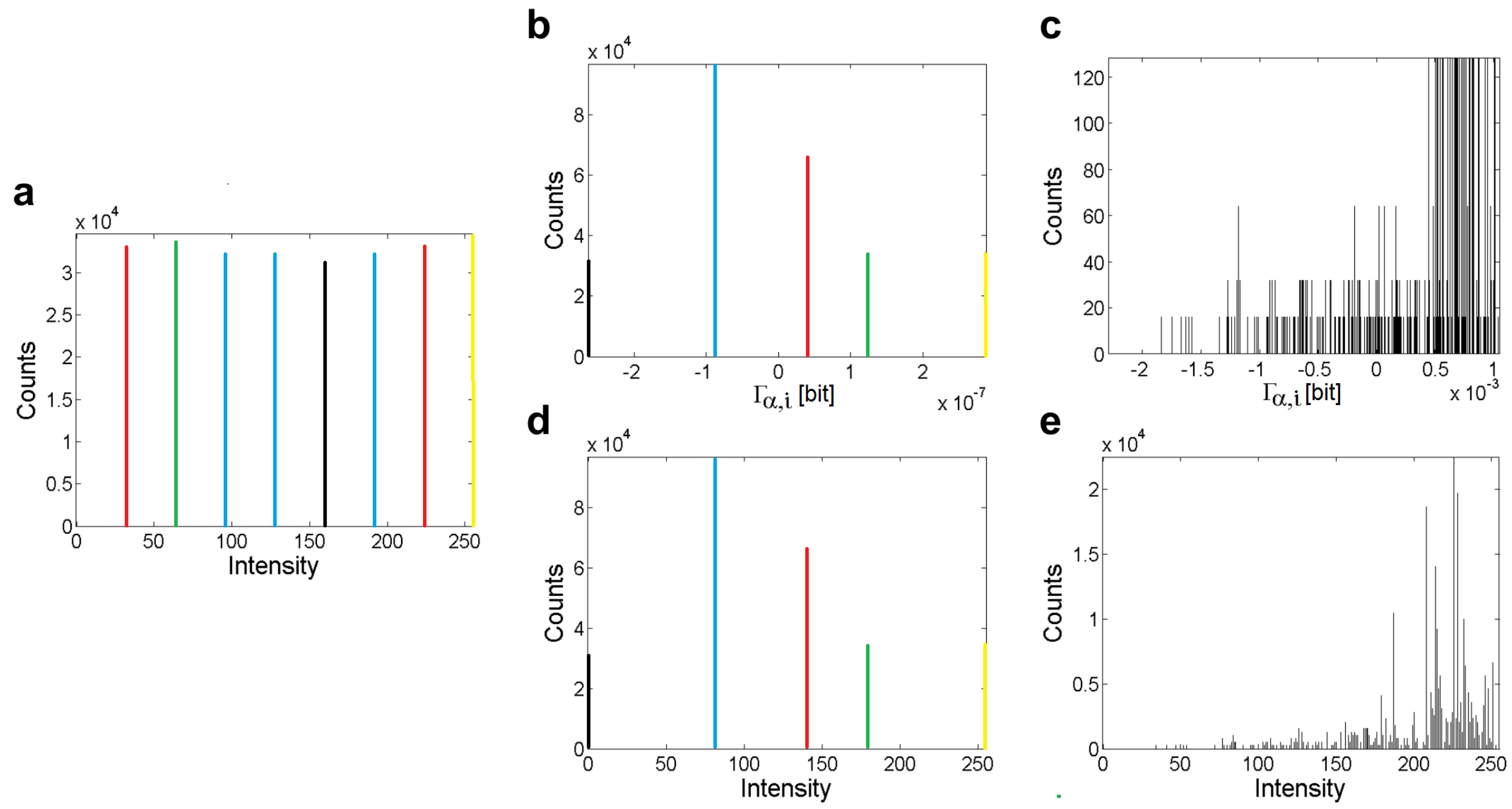
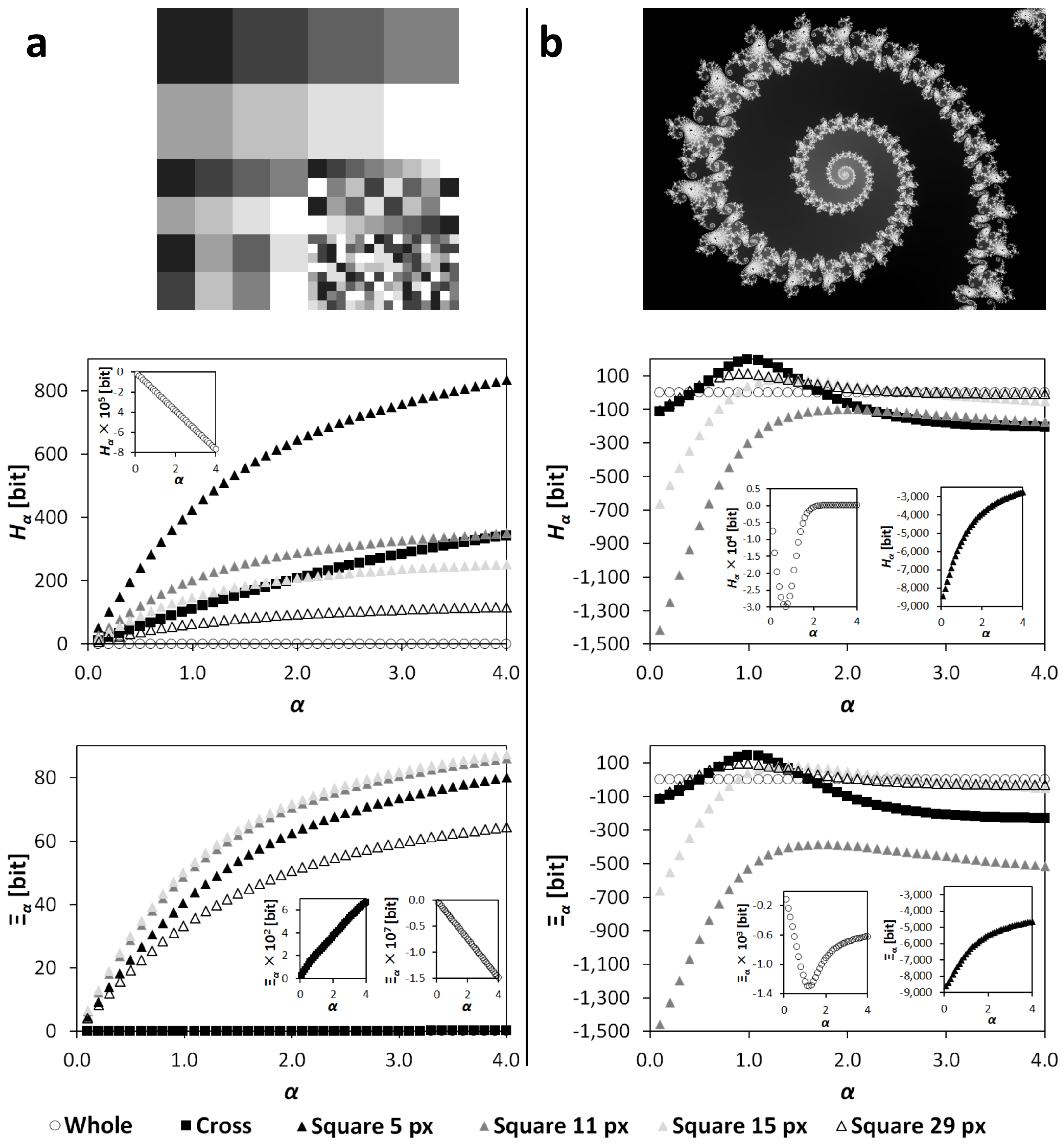
3. Estimation of Point Information Gain in Multidimensional Datasets
3.1. Point Information Gain in the Context of Whole Image
| Algorithm 1: Point information gain vector (), point information gain entropy (), and point information gain entropy density () calculations for global (Whole image) information and typical histograms. |
| Input: n-bin histogram ; α, where α ≥ 0 ∧ α ≠ 1 |
| Output: ; ; |
| 1 sum; % explain the frequency histogram as a probability histogram |
| 2 zeros; % create a zero matrix of the size of the histogram |
| 3 for to n do |
 |
| 10 end |
| 11 ; |
| % calculate as a sum of the element-by-element multiplication of and |
| 12 ; % calculate as a sum of all unique values in (Equation (20)); |
3.2. Local Point Information Gain
| Algorithm 2: Point information gain matrix (), point information gain entropy (), and point information gain entropy density () calculations for local kinds of information. Parameters a and b are semiaxes of the ellipse surroundings and a half-width of the rectangle surroundings, respectively, a = 0 and b = 0 for the cross surroundings. |
| Input: 2D discrete data ; α, where α ≥ 0 ∧ α ≠ 1; parameters of surroundings |
| Output: ; ; |
| 1 zeros; % create a zero matrix of the size of the matrix |
| 2 containers.Map; % declare an empty hash-map (the key-value array) |
| 3 for to do |
 |
| 16 end |
| 17 ; % calculate as a sum of all elements in the matrix (Equation (19)) |
| 18 ; % calculate as a sum of all elements in the matrix |
| (Equation (20)) |
3.3. Point Information Gain Entropy and Point Information Gain Entropy Density
4. Materials and Methods
4.1. Processing of Images and Typical Histograms
- (a)
- Lévy distribution:
- (b)
- Cauchy distribution:
- (c)
- Gauss distribution:
4.2. Calculation Algorithms
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
- Folder “Figures” contains subfolders with results of , , and calculations for “RGB” (4.1.07.tiff, wash-ir.tiff) and “gray” (texmos2.s512.png, wd950112.png, 6ASCP011.png) standard images calculated for 40 values α. The results are separated into subfolders according to the type of extracted information.
- Folder “H_Xi” stores the PIE_PIED.xlsx and PIE_PIED2.xlsx files with dependencies of and on α as exported from the PIE.mat files (in folder “Figures”). Titles of the graphs, which are in agreement with the computed variables and extracted kinds of information, are written in the sheets.
- Folder “Histograms” stores the histograms of the occurrences of values for the Cauchy (two types), Lévy (three types), and Gauss (four types) distributions. The parameters of the original distributions are saved in the equation.txt files. All histograms were recalculated using 13 values α.
- Folder “Software” contains a 32- and 64-bit version of an Image Info Extractor Professional v. b9 software (ImageExtractor_b9_xxbit.zip; supported by OS Win7) and a pig_histograms.m Matlab® script for recalculation of the typical probability density functions. A script pie_ec.m serves for the extraction of and from the folders (outputs from the Image Info Extractor Professional) over α. In the software and script, the variables , , and are called , , and , respectively. Manuals for the software and scripts are also attached.
References
- Štys, D.; Urban, J.; Vaněk, J.; Císař, P. Analysis of biological time-lapse microscopic experiment from the point of view of the information theory. Micron 2011, 42, 3360–3365. [Google Scholar] [CrossRef] [PubMed]
- Urban, J.; Vaněk, J.; Štys, D. Preprocessing of microscopy images via Shannon’s entropy. In Proceedings of the Pattern Recognition and Information Processing, Minsk, Belarus, 19–21 May 2009; pp. 183–187.
- Boer, P.T.D.; Kroese, D.P.; Mannor, S.; Rubinstein, R. A tutorial on the cross-entropy method. Ann. Oper. Res. 2005, 134, 19–67. [Google Scholar] [CrossRef]
- Baez, J.C.; Fritz, T.; Leinster, T. A characterization of entropy in terms of information loss. Entropy 2011, 13, 1945–1957. [Google Scholar] [CrossRef]
- Marcolli, M.; Tedeschi, N. Entropy algebras and Birkhoff factorization. J. Geom. Phys. 2015, 97, 243–265. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Jizba, P.; Arimitsu, T. The world according to Rényi: Thermodynamics of multifractal systems. Ann. Phys. 2004, 312, 17–59. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J. Multifractal diffusion entropy analysis: Optimal bin width of probability histograms. Physica A 2014, 413, 438–458. [Google Scholar] [CrossRef]
- Hentschel, H.G.E.; Procaccia, I. The infinite number of generalized dimensions of fractals and strange attractors. Physcia D 1983, 8, 435–444. [Google Scholar] [CrossRef]
- Campbel, L.L. A coding theorem and Rényi’s entropy. Inf. Control 1965, 8, 423–429. [Google Scholar] [CrossRef]
- Štys, D.; Jizba, P.; Papáček, S.; Náhlik, T.; Císař, P. On measurement of internal variables of complex self-organized systems and their relation to multifractal spectra. In Proceedings of the 6th IFIP TC 6 International Workshop (WSOS 2012), Delft, The Netherlands, 15–16 March 2012; pp. 36–47.
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; pp. 547–561.
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Csiszár, I. I-divergence geometry of probability distributions and minimization problems. Ann. Prob. 1975, 3, 146–158. [Google Scholar] [CrossRef]
- Harremoes, P. Interpretations of Rényi entropies and divergences. Physica A 2006, 365, 57–62. [Google Scholar] [CrossRef]
- Van Erven, T.; Harremoes, P. Rényi divergence and Kullback–Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Van Erven, T.; Harremoës, P. Rényi divergence and majorization. In Proceedings of the 2010 IEEE International Symposium on Information Theory Proceedings (ISIT), Austin, TX, USA, 13–18 June 2010.
- Jizba, P.; Kleinert, H.; Shefaat, M. Rényi’s information transfer between financial time series. Physica A 2012, 391, 2971–2989. [Google Scholar] [CrossRef]
- Havrda, J.; Charvát, F. Quantification method of classification processes. Concept of structural α-entropy. Kybernetika 1967, 3, 30–35. [Google Scholar]
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Physica D 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346. [Google Scholar] [CrossRef]
- Costa, M. A new entropy power inequality. IEEE Trans. Inf. Theory 1985, 31, 751–760. [Google Scholar] [CrossRef]
- Jizba, P.; Dunningham, J.A.; Joo, J. Role of information theoretic uncertainty relations in quantum theory. Ann. Phys. 2015, 355, 87–114. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Jizba, P.; Arimitsu, T. On observability of Rényi’s entropy. Phys. Rev. E 2004, 69, 026128. [Google Scholar] [CrossRef] [PubMed]
- The USC-SIPI Image Database. Available online: http://sipi.usc.edu/database/database.php?volume=textures &image=61#top (accessed on 17 October 2016).
- Shalizi, C.R.; Crutchfield, J.P. Computational mechanics: Pattern and prediction, structure and simplicity. J. Stat. Phys. 2001, 104, 817–879. [Google Scholar] [CrossRef]
- Shalizi, C.R.; Shalizi, K.L. Quantifying self-organization in cyclic cellular automata. In Noise in Complex Systems and Stochastic Dynamics; Society of Photo Optical: Bellingham, WA, USA, 2003. [Google Scholar]
- Shalizi, C.R.; Shalizi, K.L.; Haslinger, R. Quantifying self-organization with optimal predictors. Phys. Rev. Lett. 2004, 93, 118701. [Google Scholar] [CrossRef] [PubMed]
- Crutchfield, J.P. Between order and chaos. Nat. Phys. 2012, 8, 17–24. [Google Scholar] [CrossRef]
- Explore Fractals Beautiful, Colorful Fractals, and More! Available online: https://www.pinterest.com/pin/254031235202385248/ (accessed on 17 October 2016).
- Zhyrova, A.; Štys, D.; Císař, P. Macroscopic description of complex self-organizing system: Belousov–Zhabotinsky reaction. In ISCS 2013: Interdisciplinary Symposium on Complex Systems; Sanayei, A., Zelinka, N., Rössler, O.E., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 109–115. [Google Scholar]
- Rychtarikova, R. Clustering of multi-image sets using Rényi information entropy. In Bioinformatics and Biomedical Engineering; Ortuño, F., Rojas, I., Eds.; Springer: Cham, Switzerland, 2016; pp. 517–526. [Google Scholar]
- Štys, D.; Vaněk, J.; Náhlík, T.; Urban, J.; Císař, P. The cell monolayer trajectory from the system state point of view. Mol. BioSyst. 2011, 42, 2824–2833. [Google Scholar] [CrossRef] [PubMed]
- Available online: http://cims.nyu.edu/ kiryl/Photos/Fractals1/ascp011et.html (accessed on 17 October 2016).
- Point Information Gain Supplementary Data. Available online: ftp://160.217.215.251/pig (accessed on 17 October 2016).

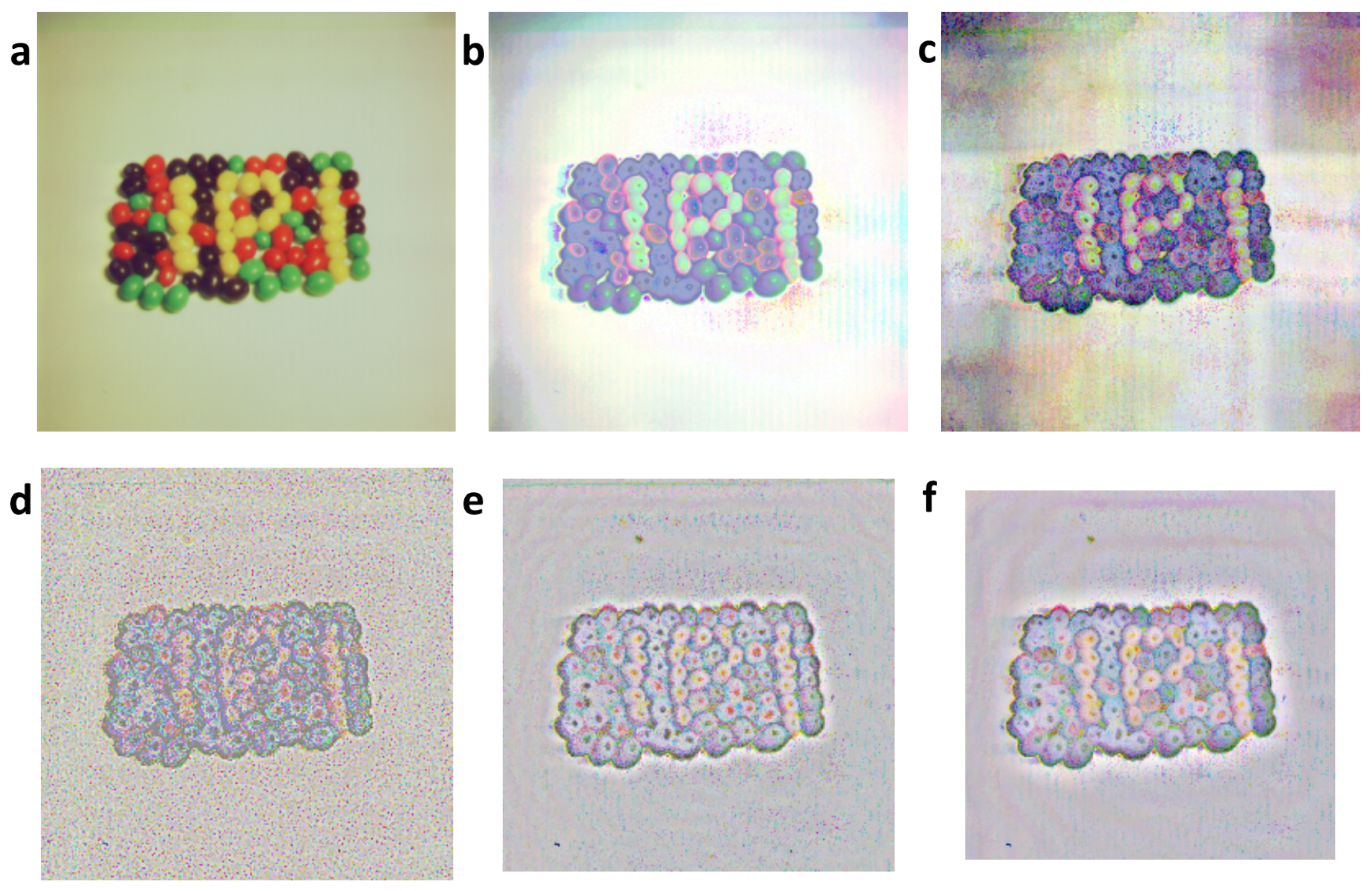
| Image | Source | Colors | Resolution | Geometry | Origin |
|---|---|---|---|---|---|
| texmos2.s512.png | [26] | mono | 512 × 512 | unifractal | computer-based |
| 4.1.07.tiff | [26] | RGB | 256 × 256 | unifractal | photograph |
| wash-ir.tiff | [26] | RGB | 2250 × 2250 | unifractal | computer-based |
| wd950112.png | [31] | mono | 1024 × 768 | multifractal | computer-based |
| 6ASCP011.png | [35] | mono | 1600 × 1200 | multifractal | computer-based |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rychtáriková, R.; Korbel, J.; Macháček, P.; Císař, P.; Urban, J.; Štys, D. Point Information Gain and Multidimensional Data Analysis. Entropy 2016, 18, 372. https://doi.org/10.3390/e18100372
Rychtáriková R, Korbel J, Macháček P, Císař P, Urban J, Štys D. Point Information Gain and Multidimensional Data Analysis. Entropy. 2016; 18(10):372. https://doi.org/10.3390/e18100372
Chicago/Turabian StyleRychtáriková, Renata, Jan Korbel, Petr Macháček, Petr Císař, Jan Urban, and Dalibor Štys. 2016. "Point Information Gain and Multidimensional Data Analysis" Entropy 18, no. 10: 372. https://doi.org/10.3390/e18100372
APA StyleRychtáriková, R., Korbel, J., Macháček, P., Císař, P., Urban, J., & Štys, D. (2016). Point Information Gain and Multidimensional Data Analysis. Entropy, 18(10), 372. https://doi.org/10.3390/e18100372







