Generalized Thermodynamic Optimization for Iron and Steel Production Processes: Theoretical Exploration and Application Cases
Abstract
:1. Introduction
2. Emergence and Development of the Finite Time Thermodynamics
3. Emergence and Development of the Generalized Thermodynamic Optimization
4. Emergence and Development of the Constructal Theory
5. Emergence and Development of the Entransy Theory
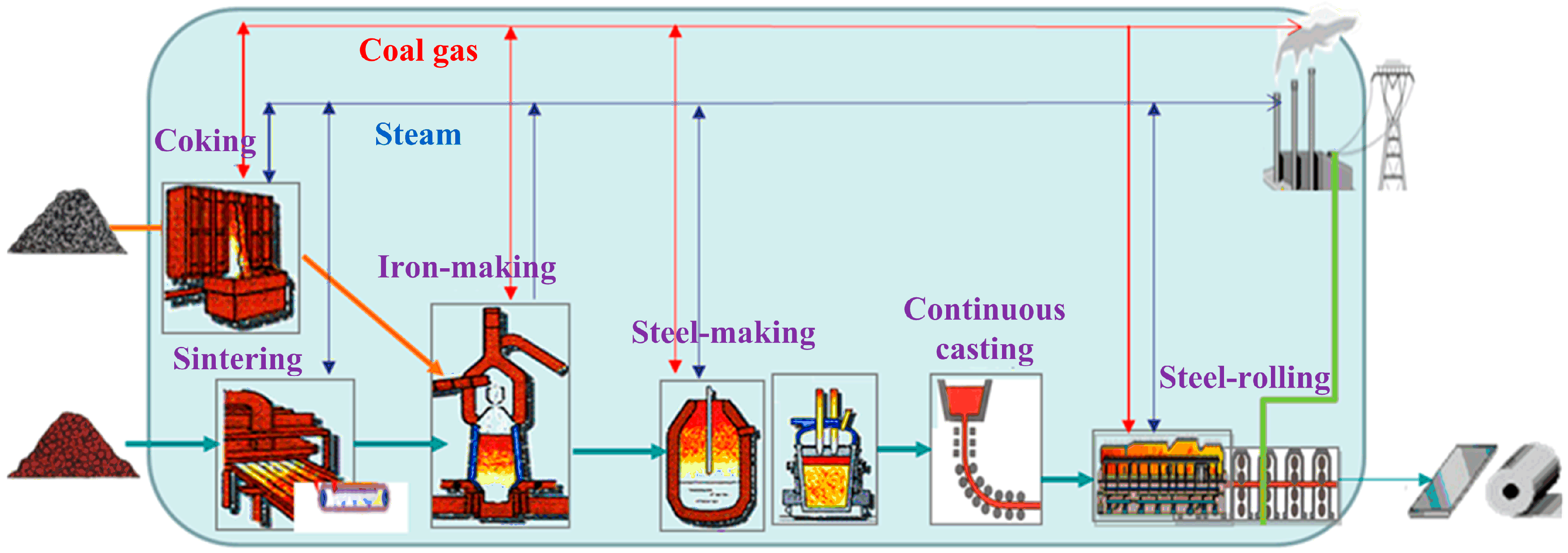
6. Emergence and Development of the Metallurgical Process Engineering
7. Generalized Thermodynamic Optimization Theory for ISPP and Its Applications
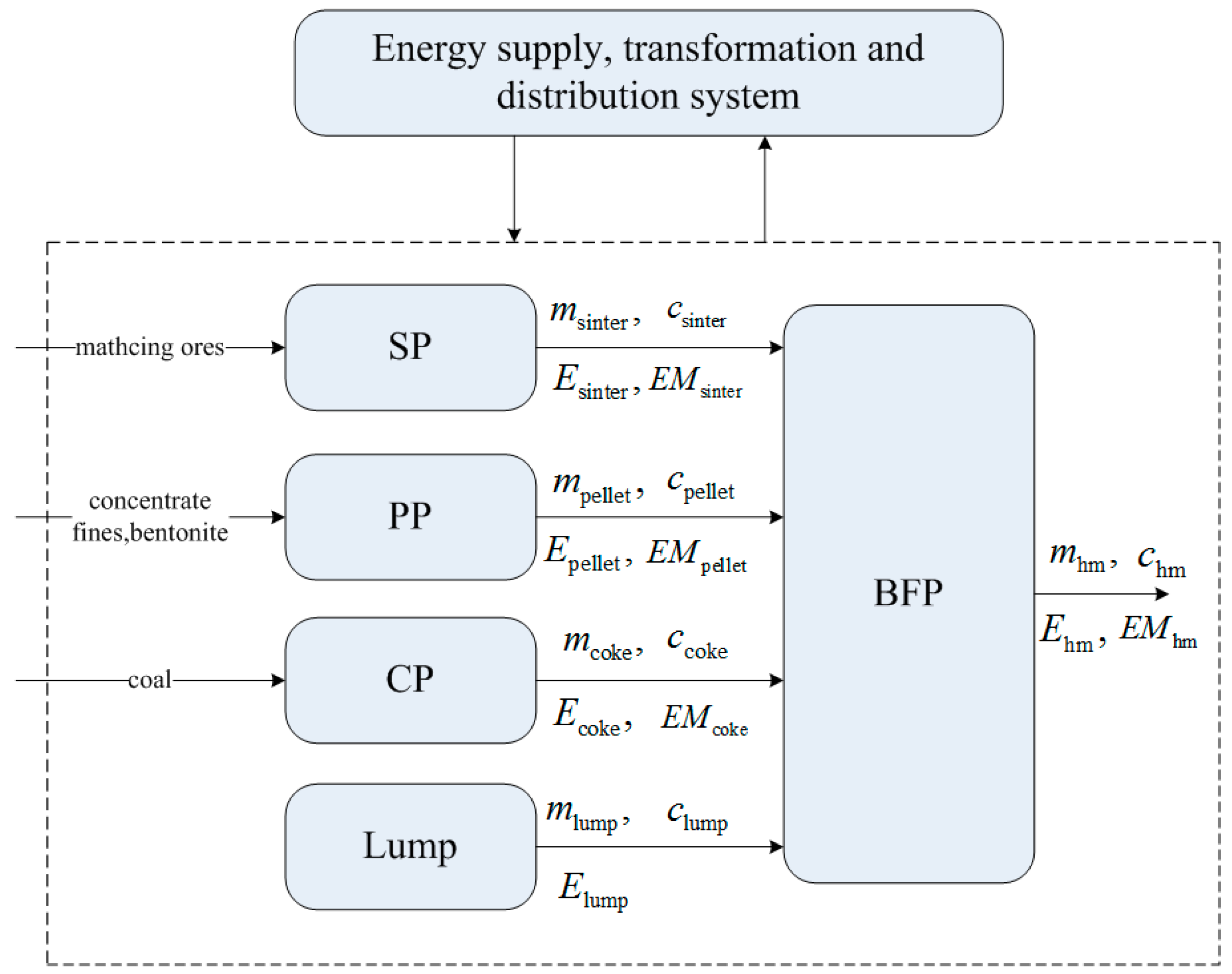
7.1. Generalized Thermodynamic Optimization Theory for ISPP
7.2. Generalized Thermodynamic Optimizations for Elemental and Working Procedure Modules of ISPP
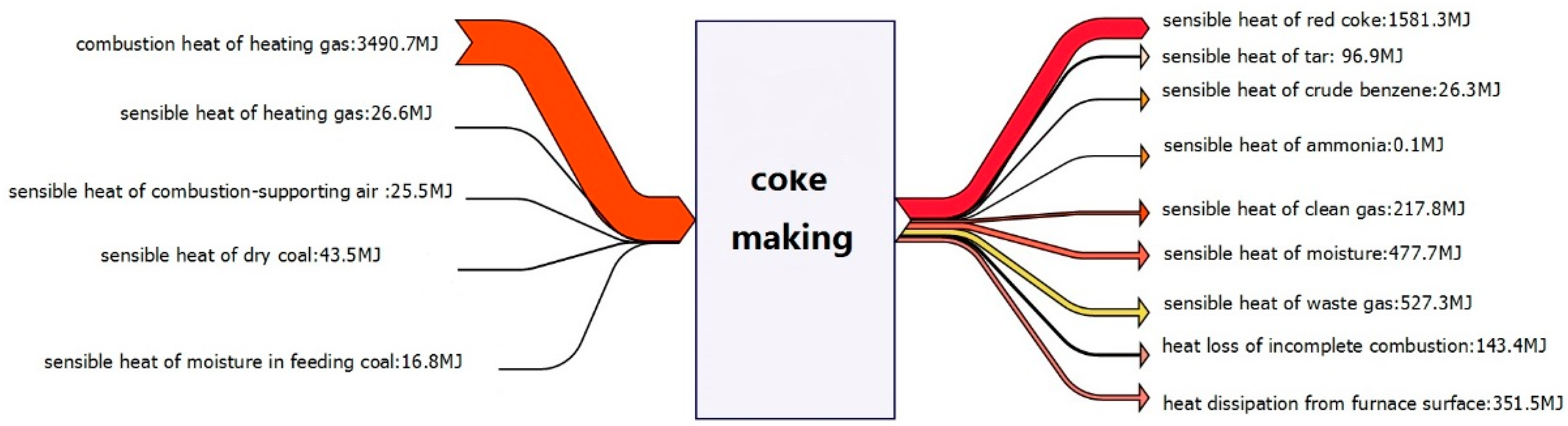
7.2.1. Investigations for Coking Procedures
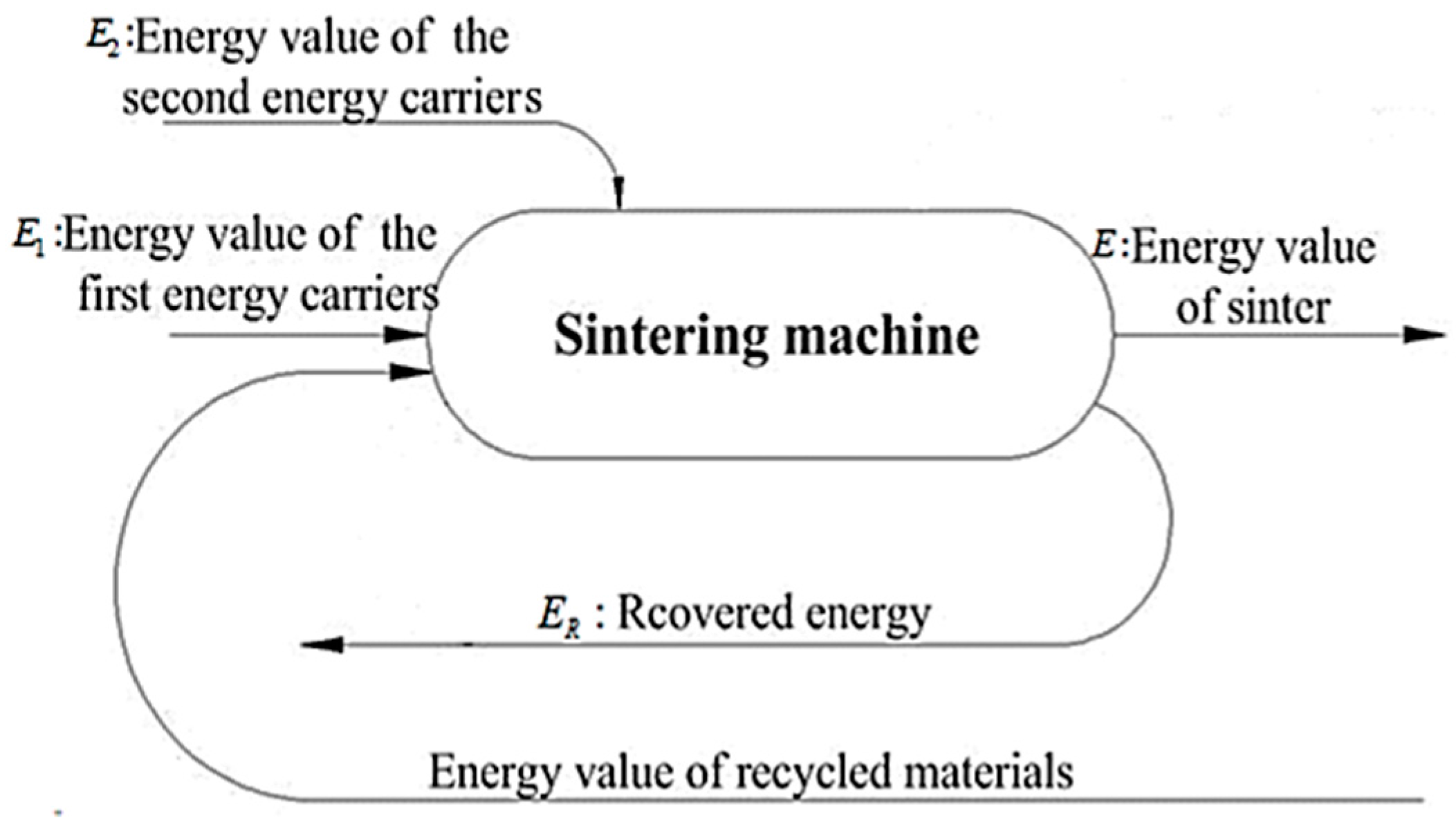
7.2.2. Investigations of Sintering Procedures
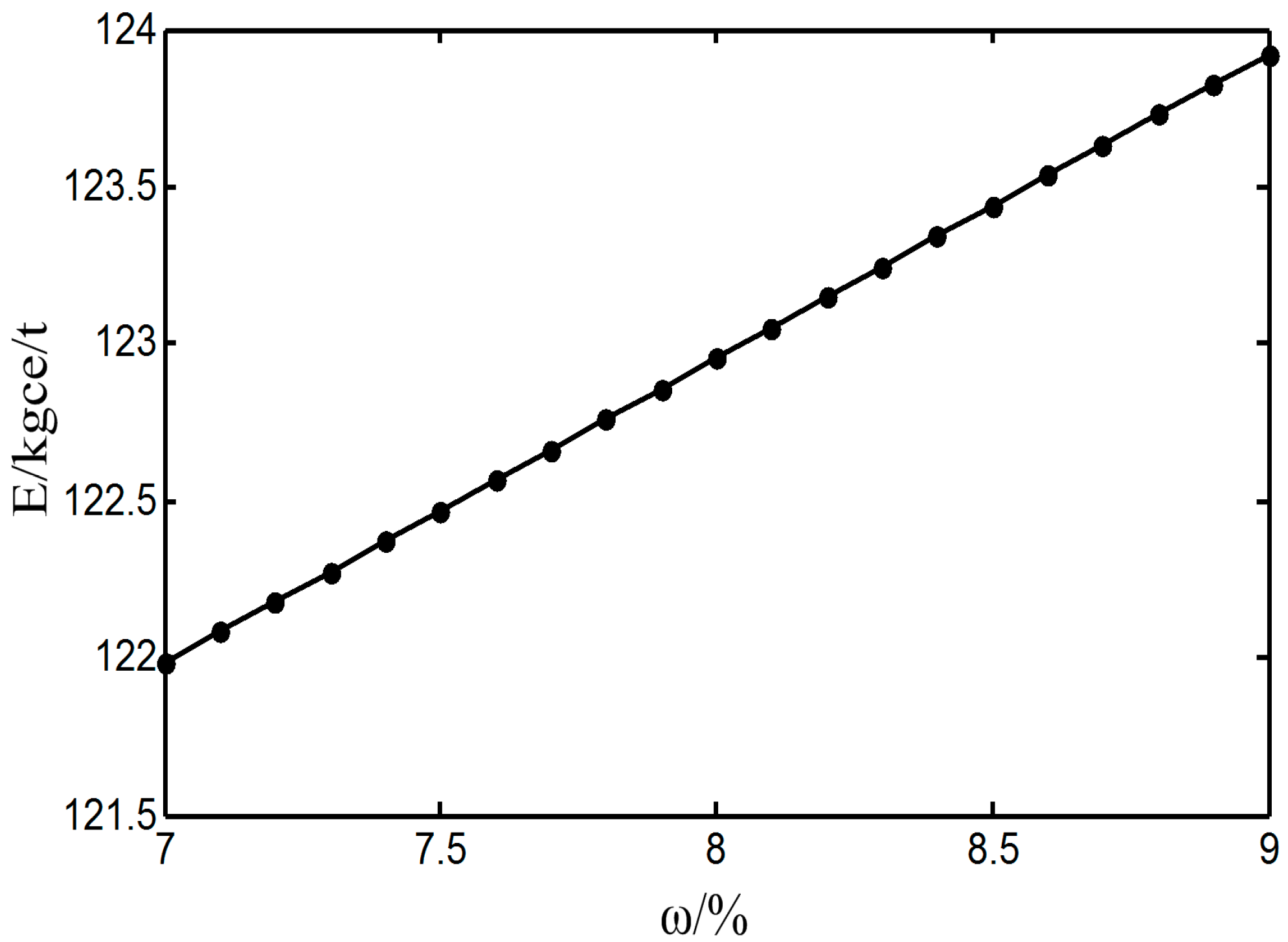
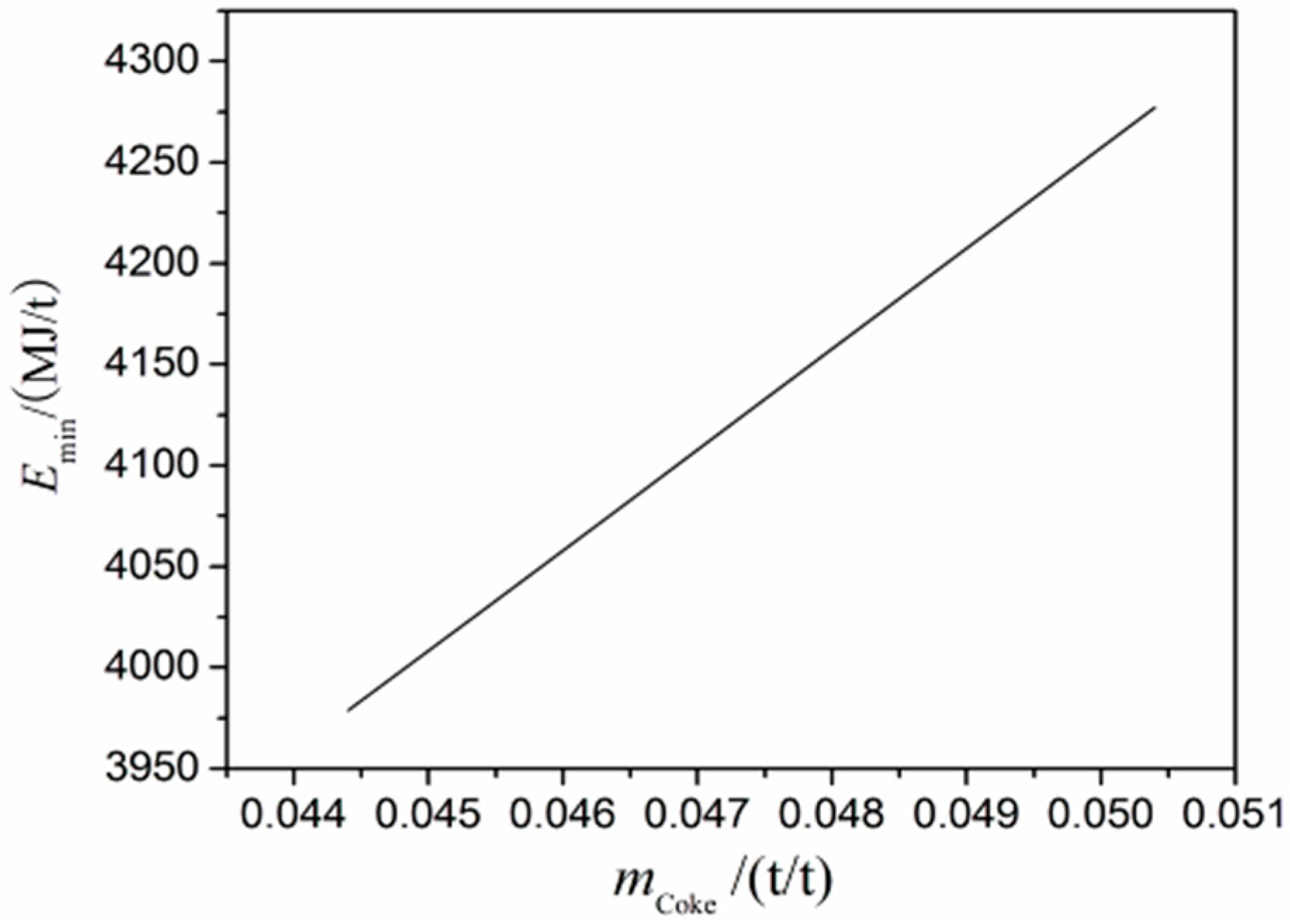
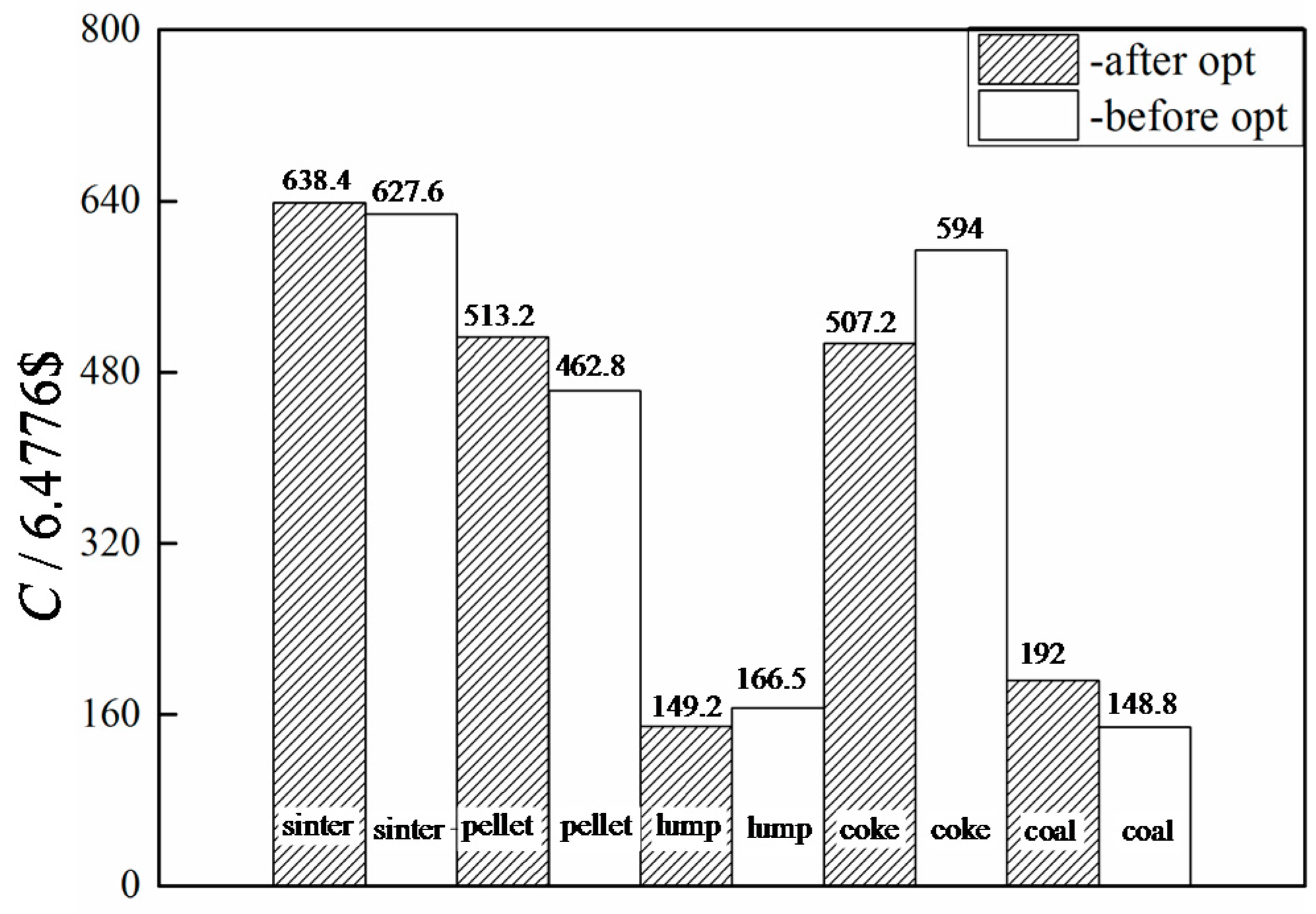
Optimization of Sintering Proportioning
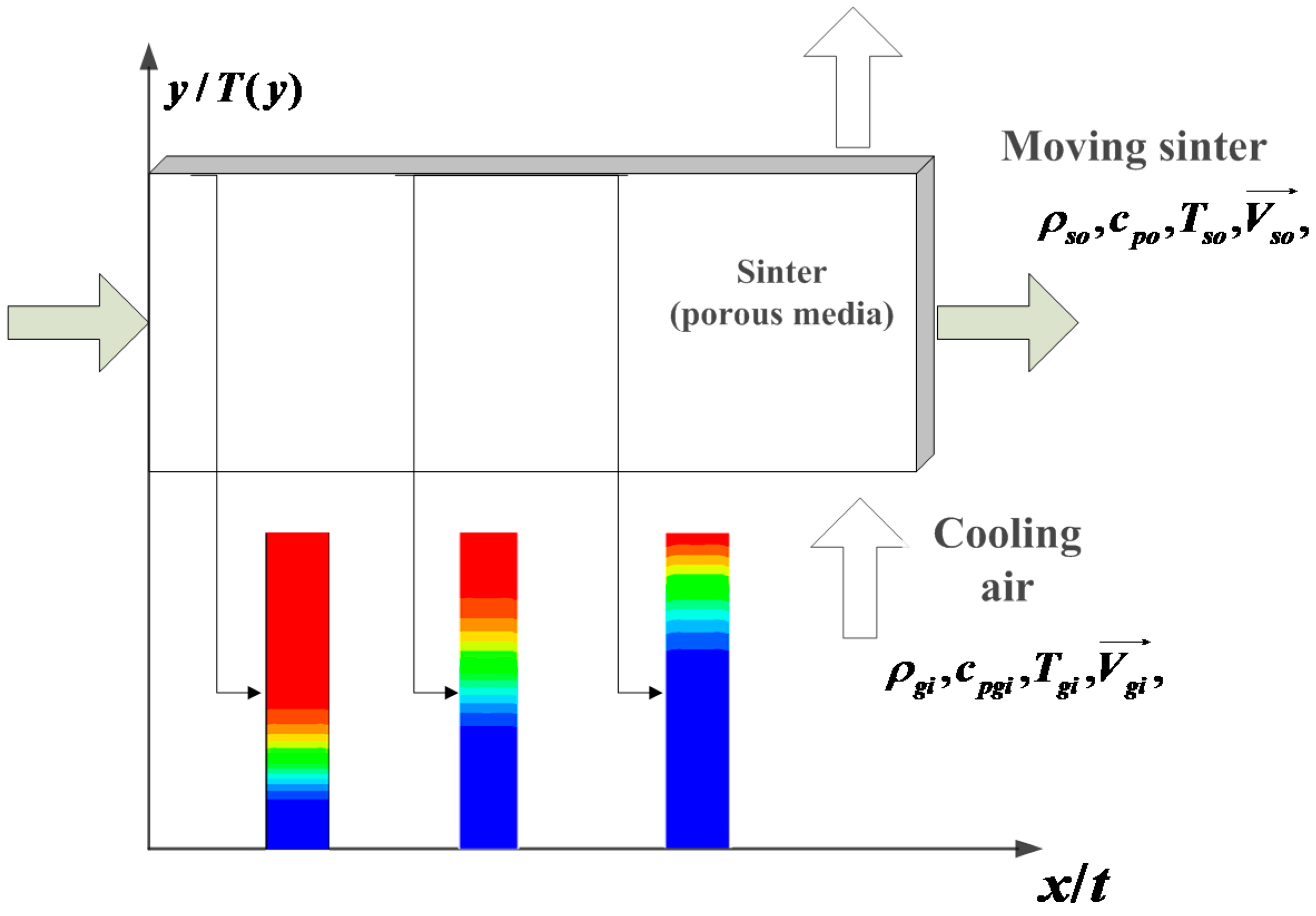
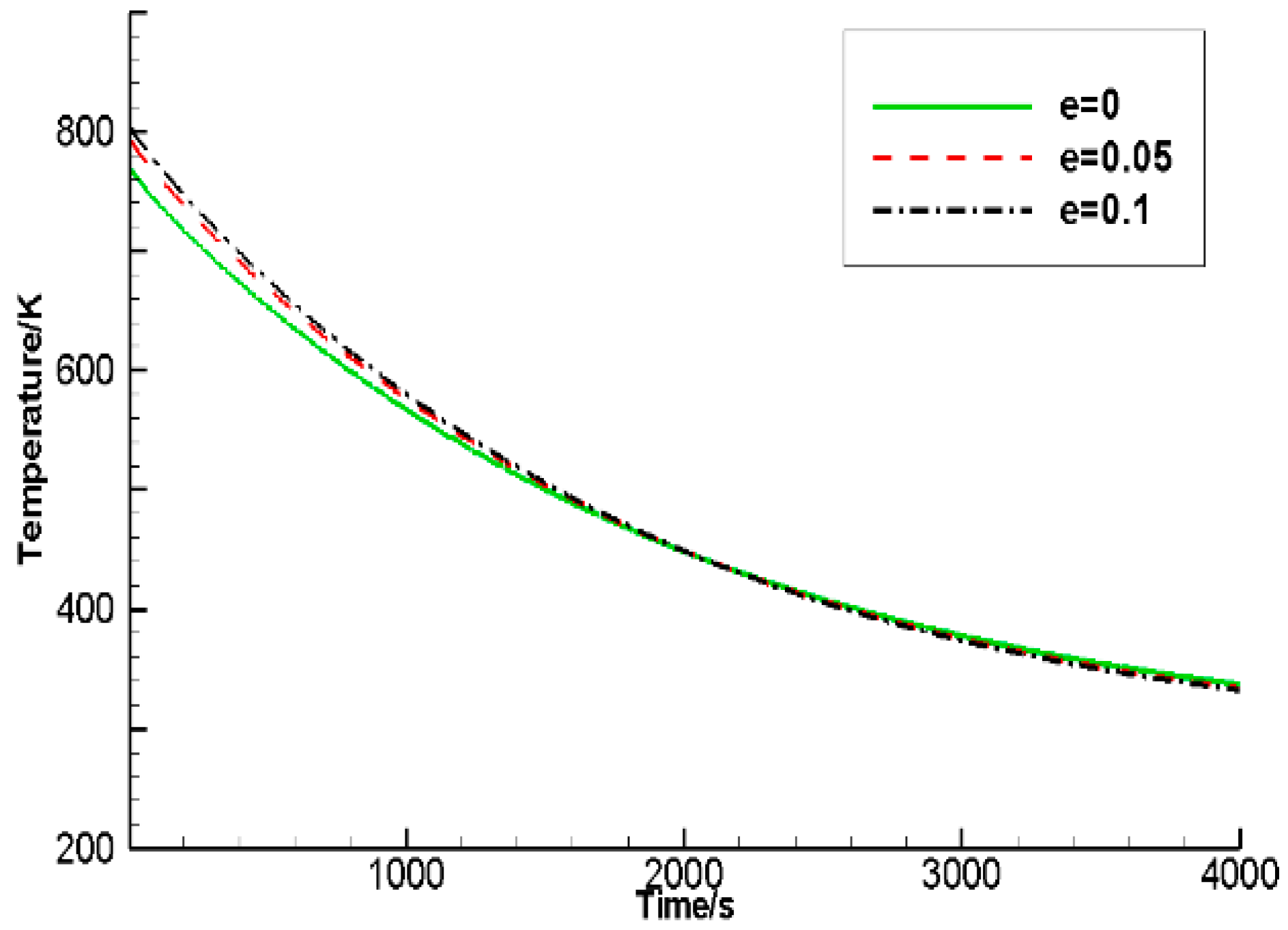
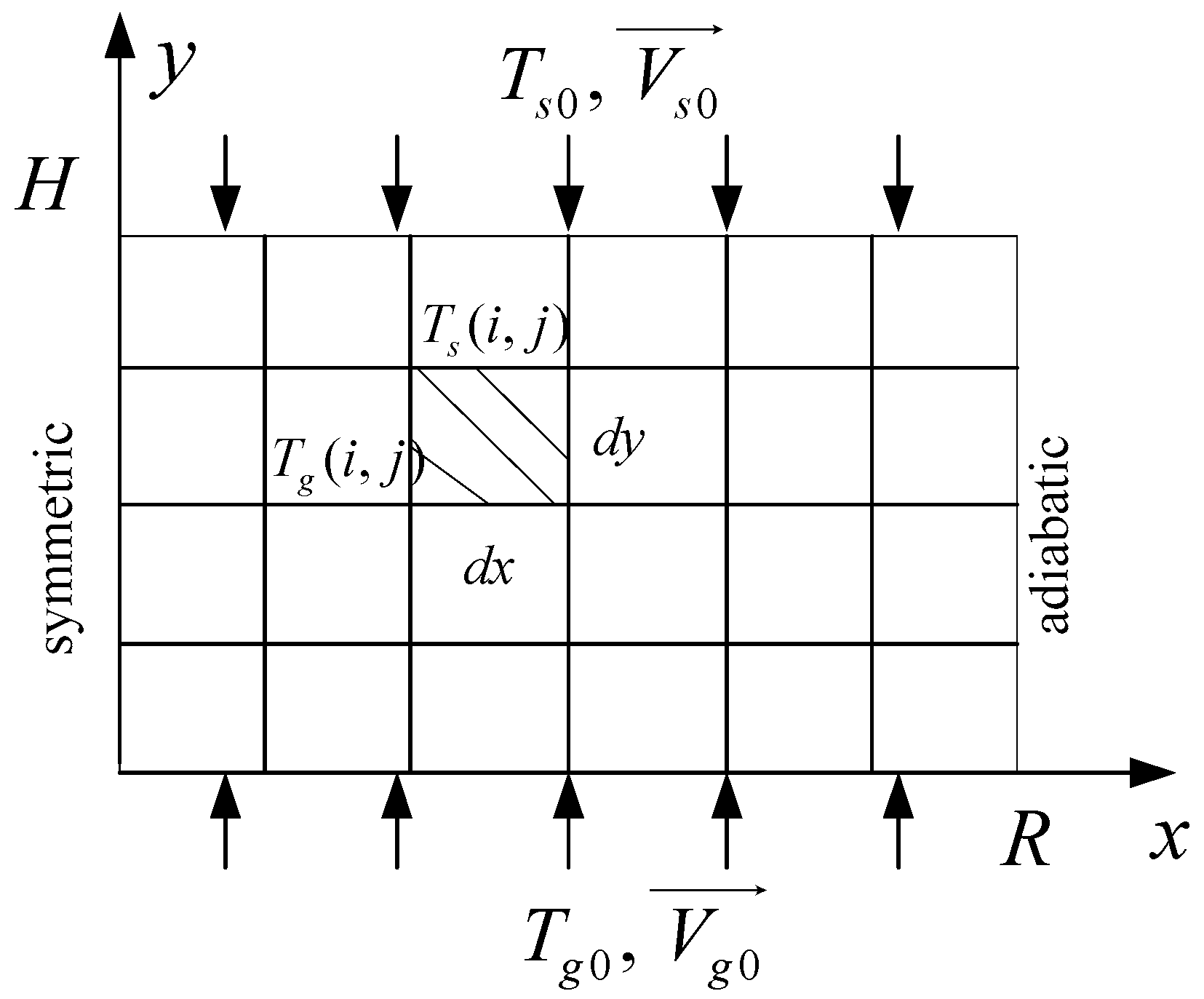
Analyses of Heat Transfer in Sinter Cooling Processes
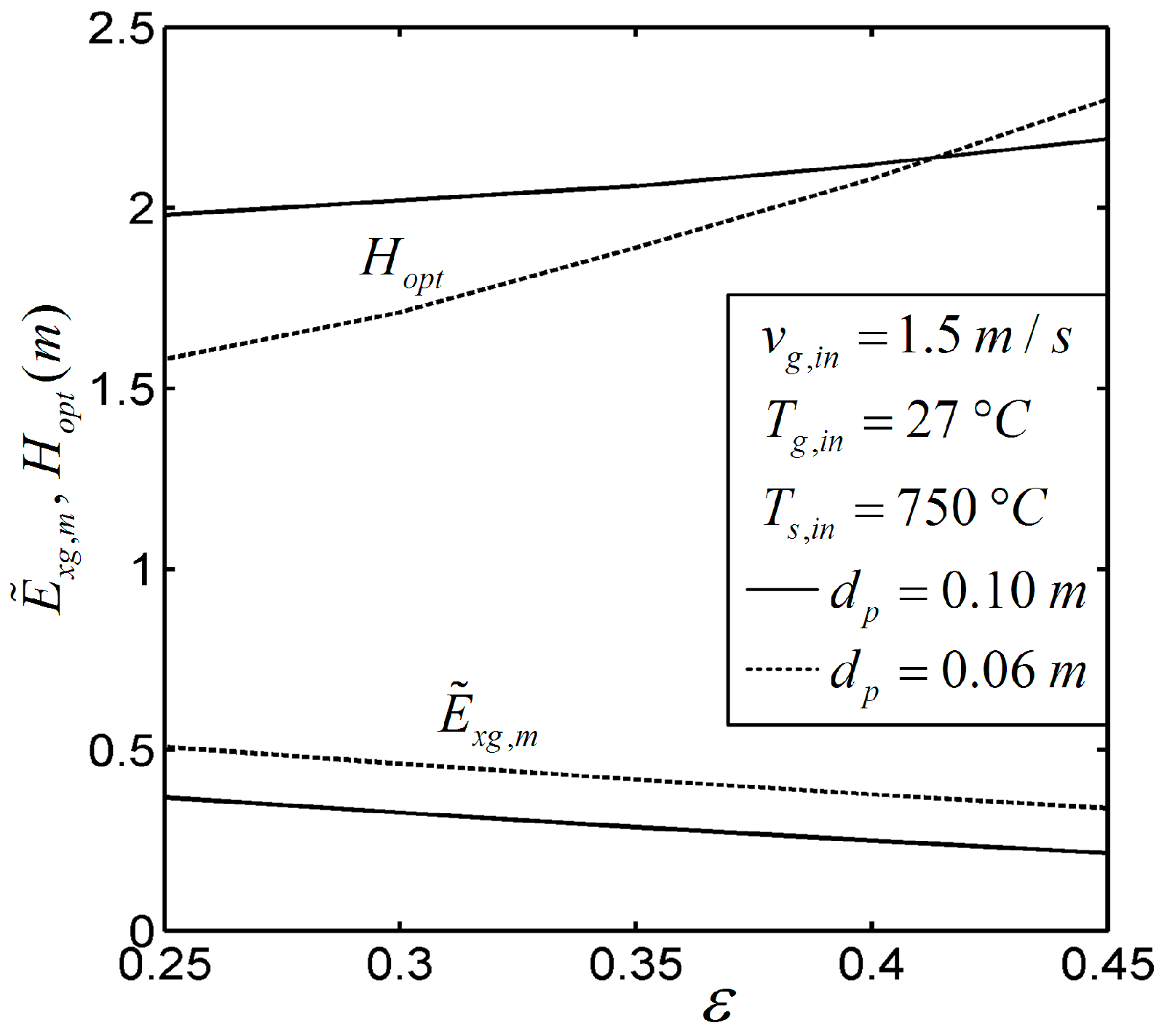
Constructal Optimization of Sinter Cooling Processes Based on Exergy Output Maximization
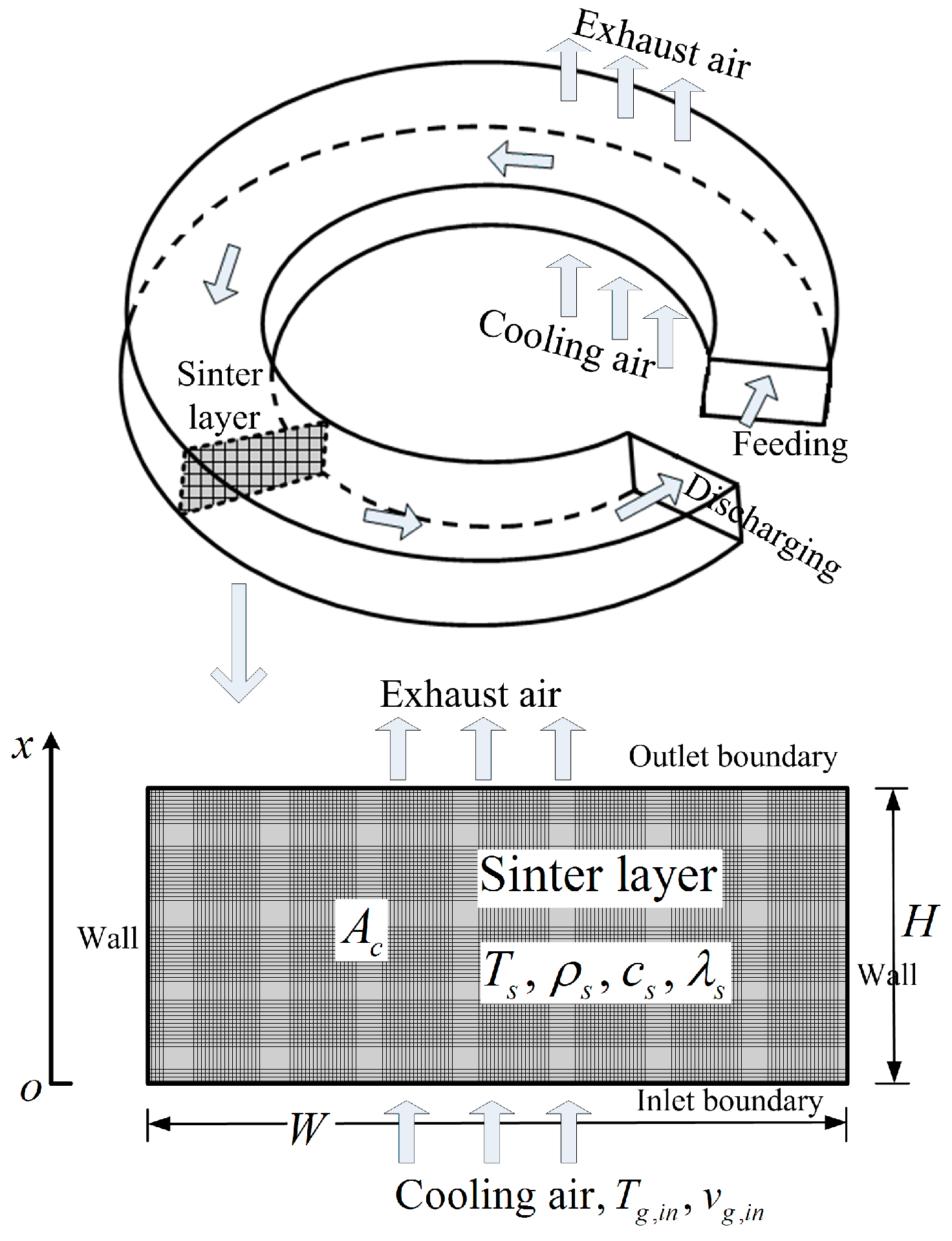
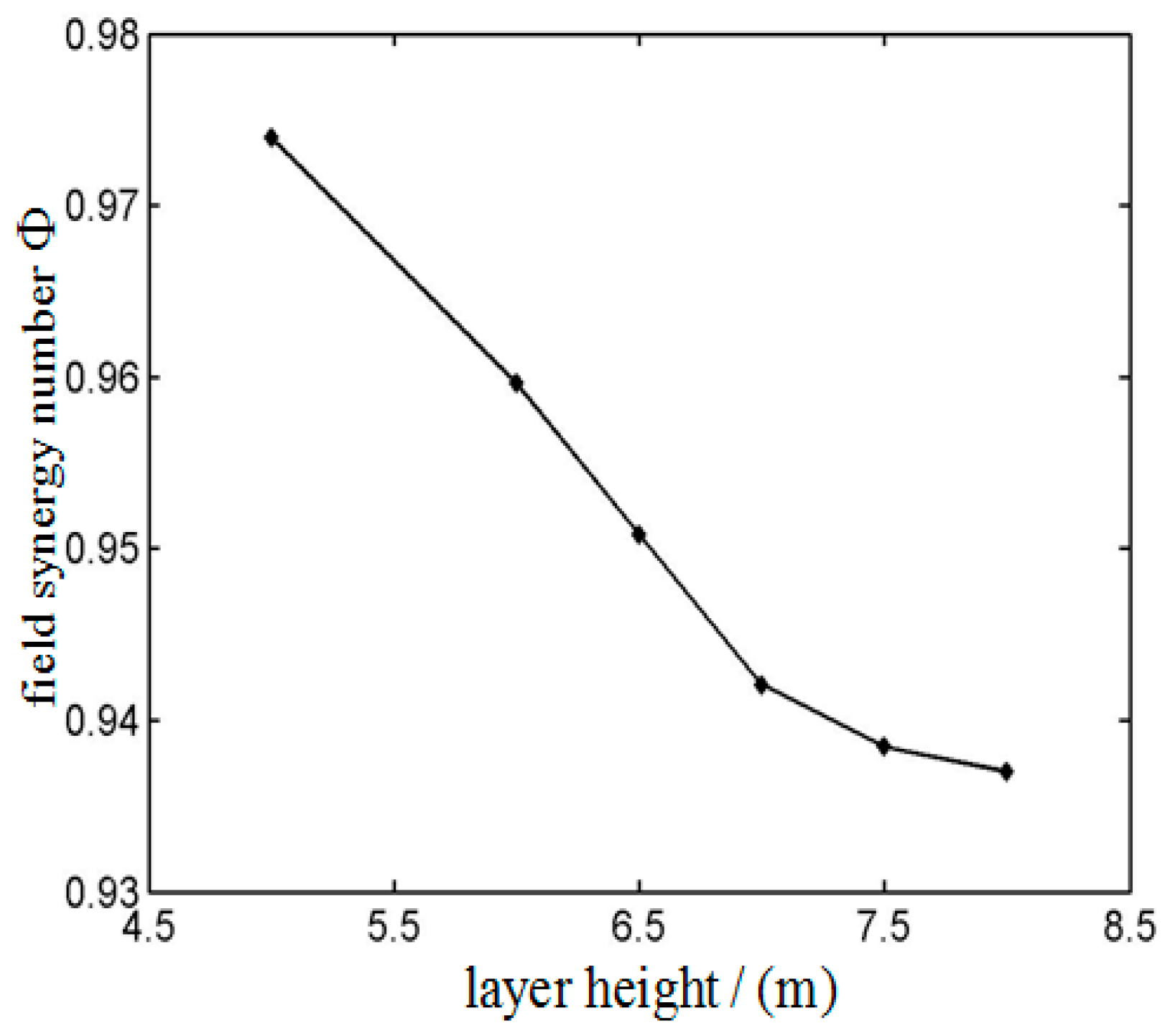
Field Synergy Analyses of Sinter Cooling Processes in Annular Coolers and Vertical Tanks
7.2.3. Investigations of Iron-Making Procedure
Constructal Optimization of Thermal Insulation Processes for Blast Furnace Walls
Optimizations for Blast Furnace Iron-Making Elemental Packages Based on Nonlinear Programming Methods
Optimizations for Blast Furnace Iron-Making Procedures Based on Nonlinear Programming Methods
Generalized Constructal Optimization for a Blast Furnace Iron-Making Elemental Package
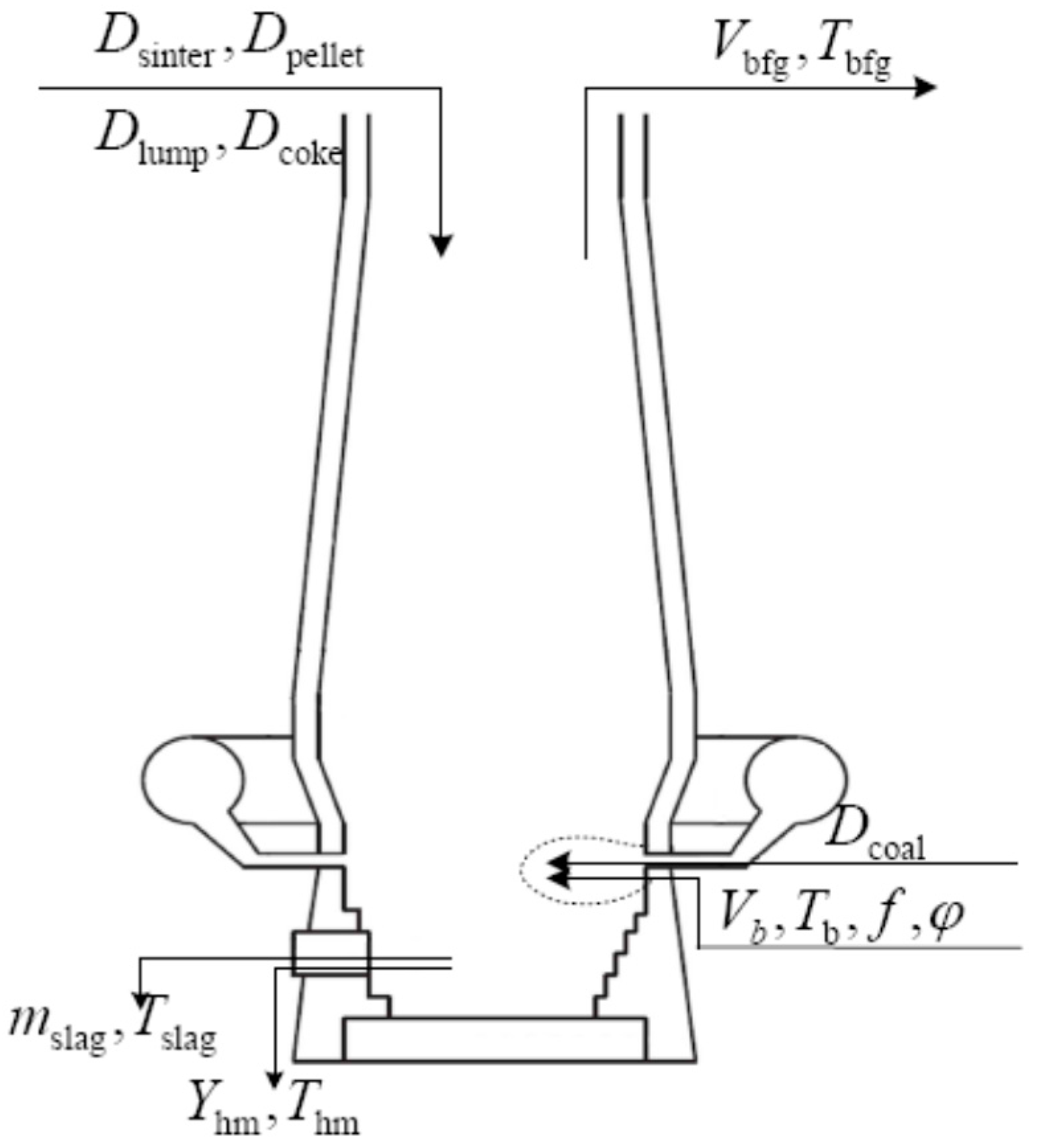
Generalized Constructal Optimization for a Blast Furnace Iron-Making Procedure
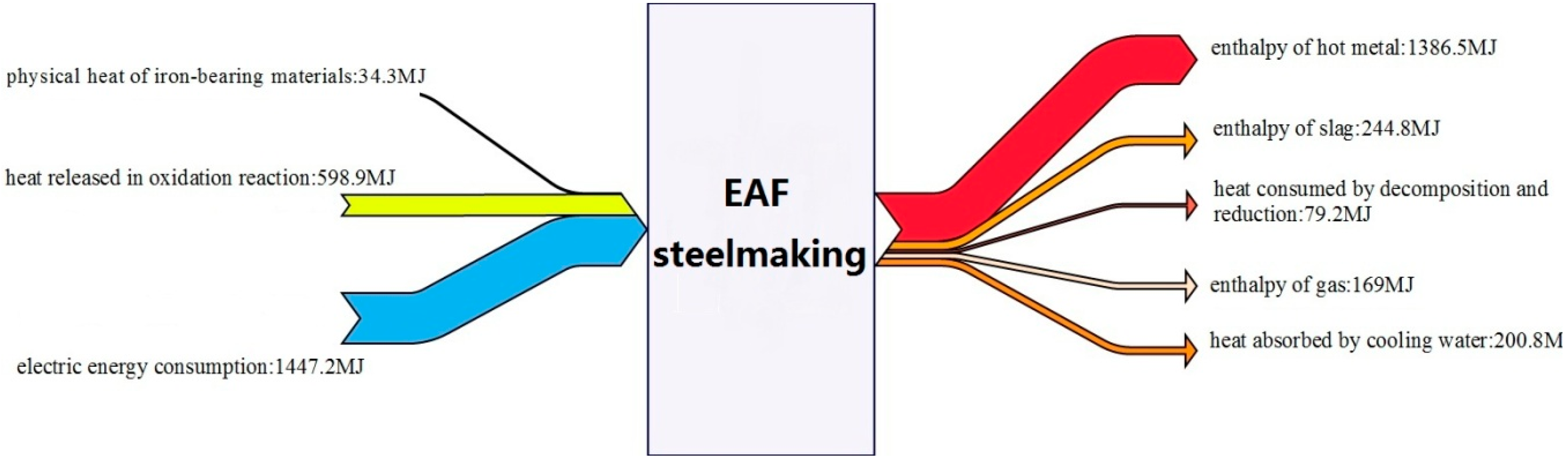
7.2.4. Steel-Making Procedure Investigations
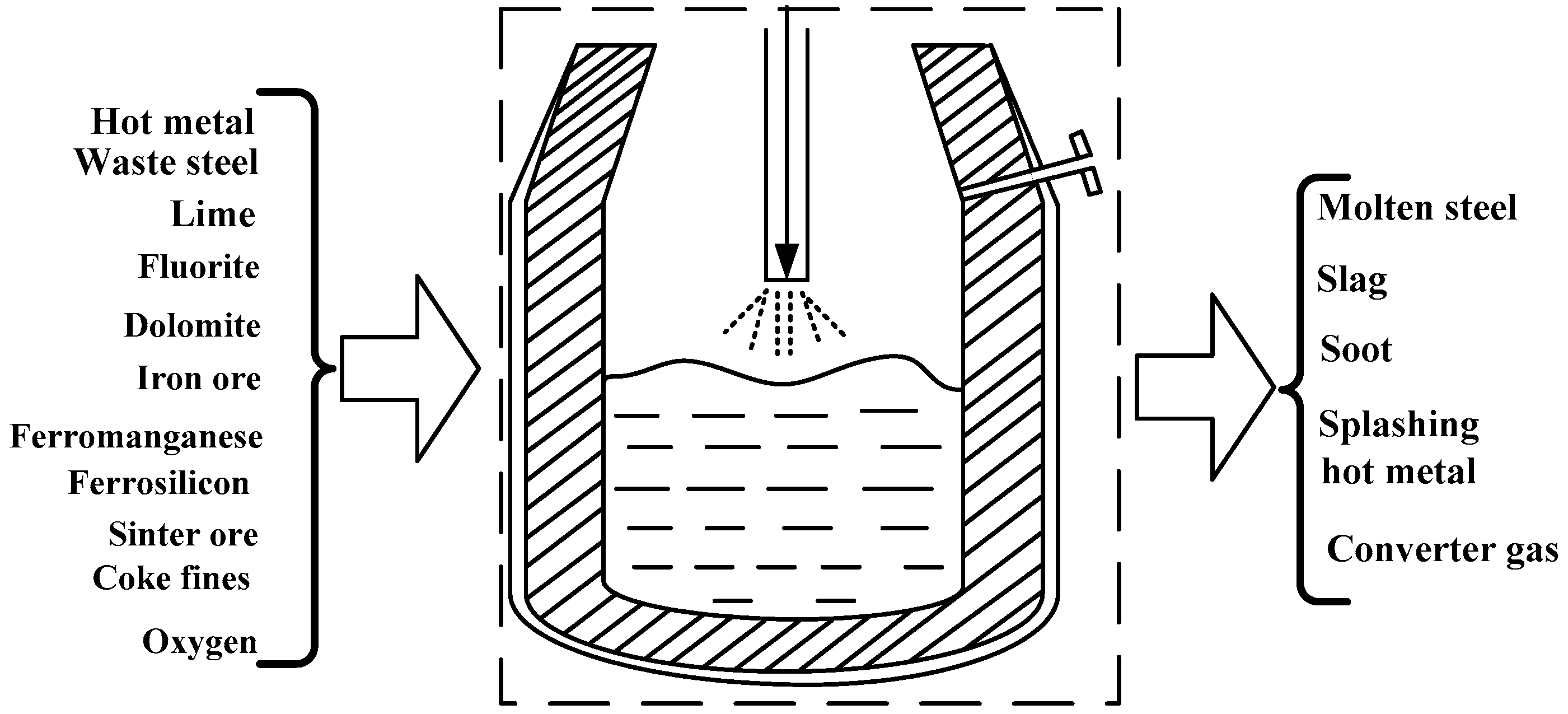
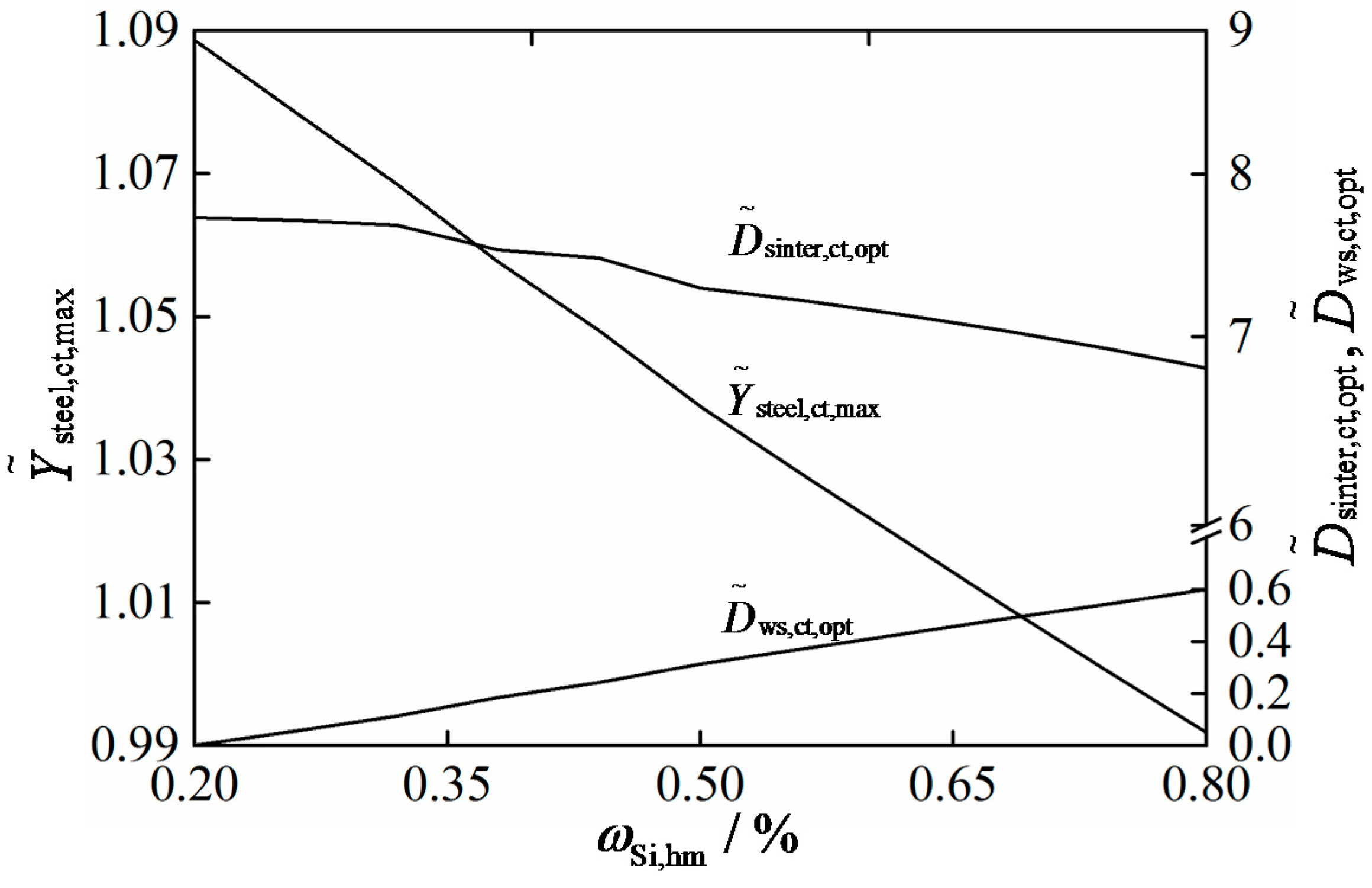
Generalized Constructal Optimization for a Converter Steel-Making Elemental Package
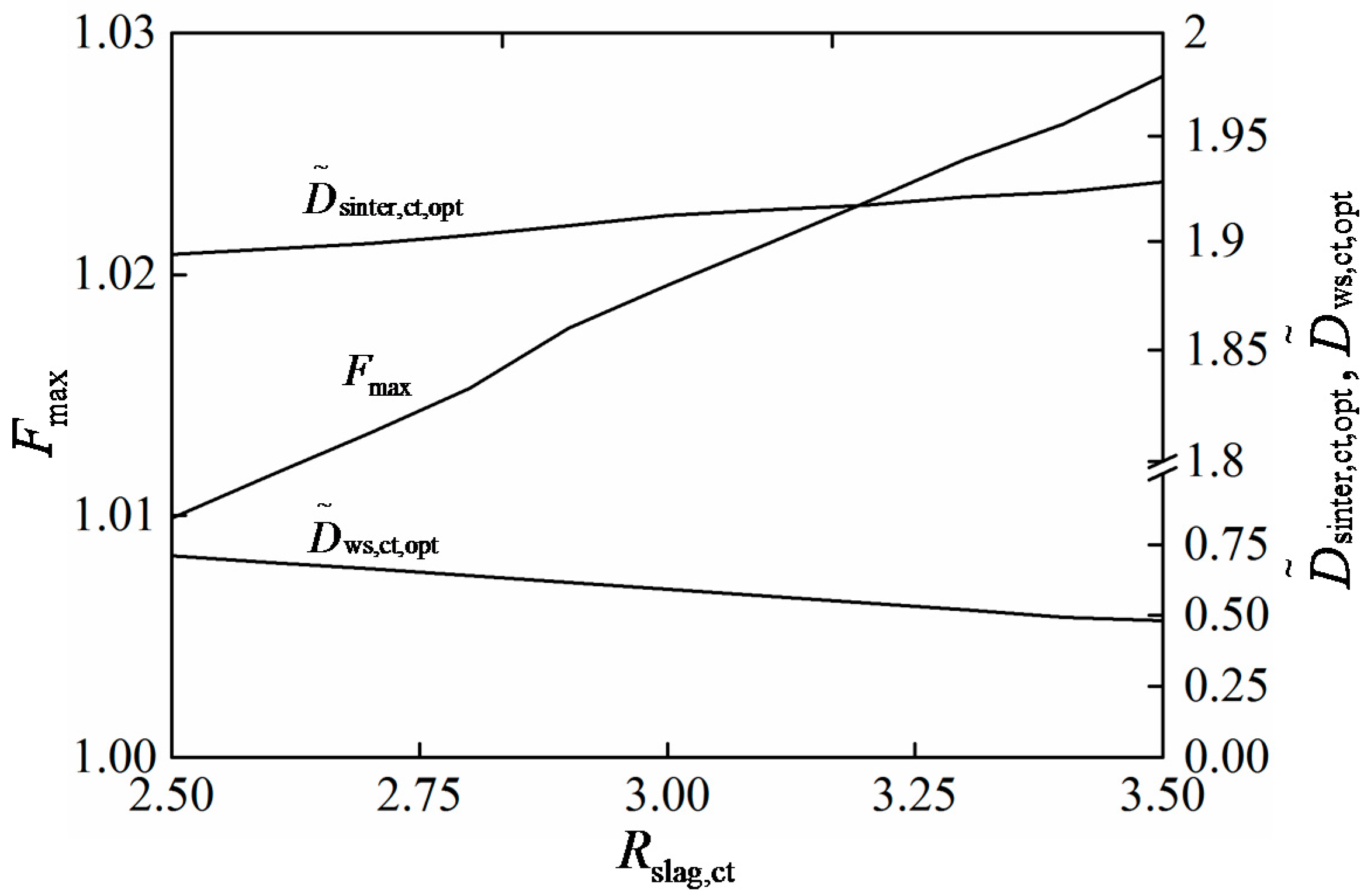
Generalized Constructal Optimization for a Converter Steel-Making Procedure
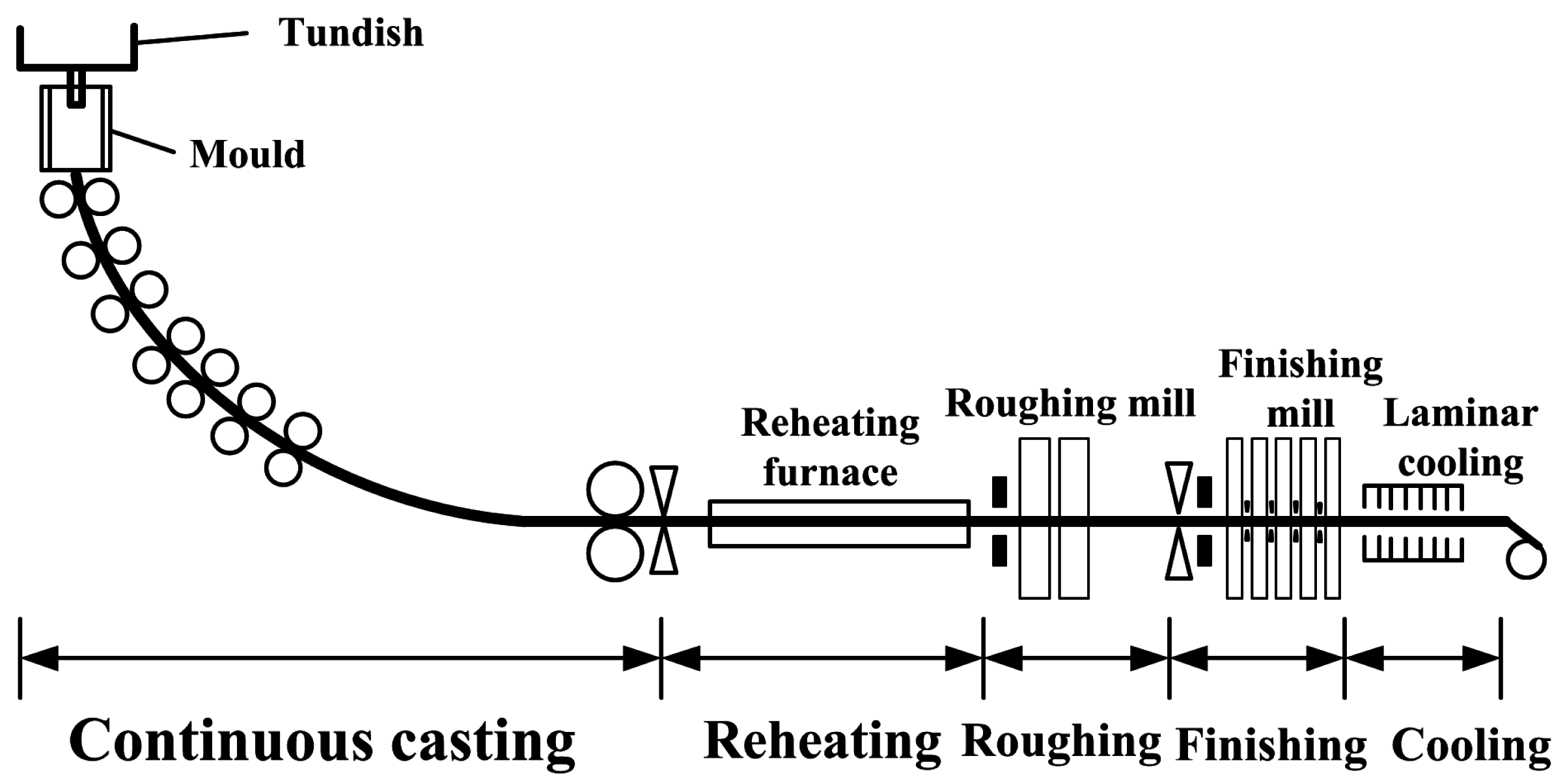
7.2.5. Investigations of Continuous Casting and Rolling Procedures
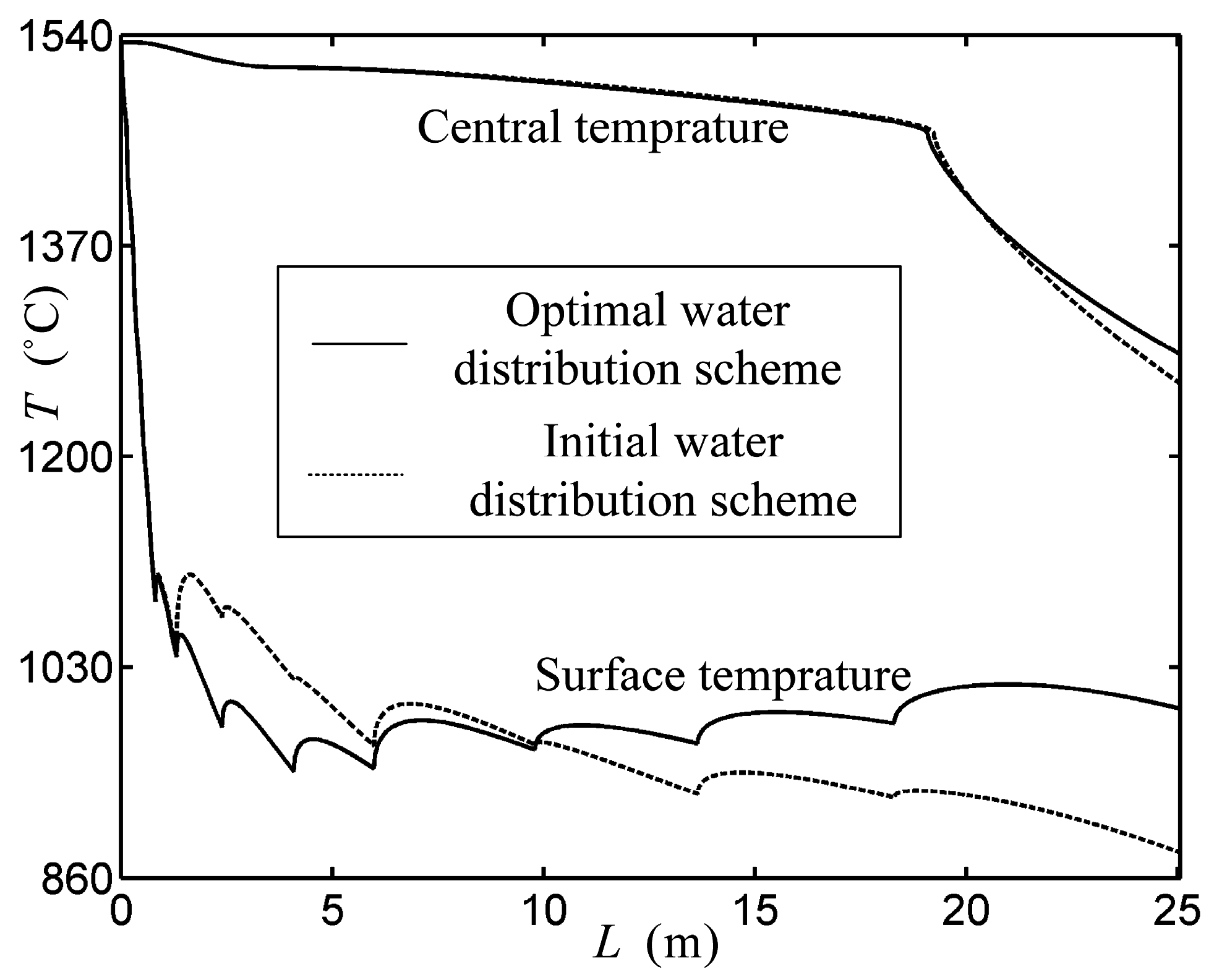
Temperature Field Investigation of Thin Slab Continuous Casting and Rolling Procedures
Generalized Constructal Optimization of Slab Continuous Casting Elemental Packages
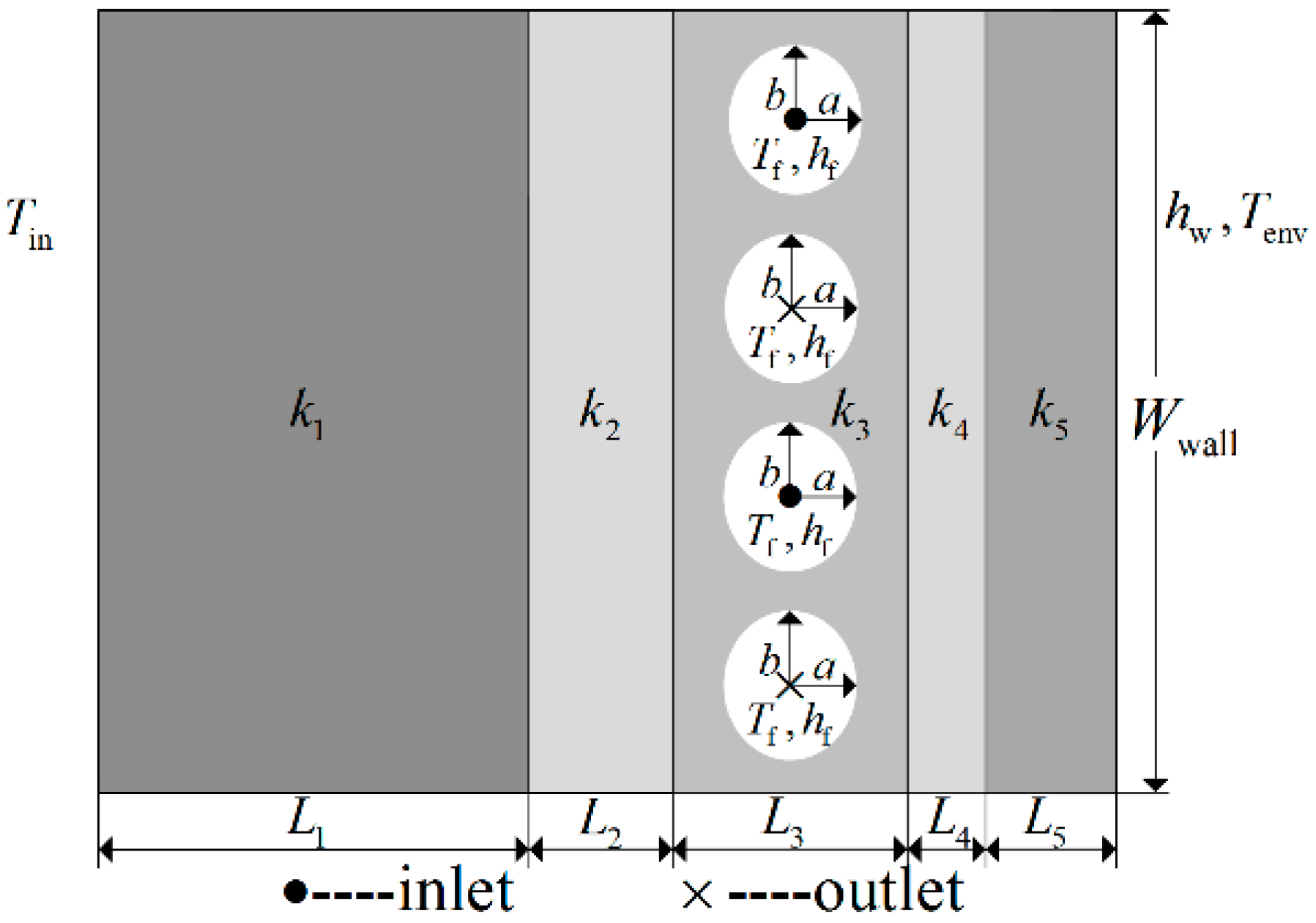
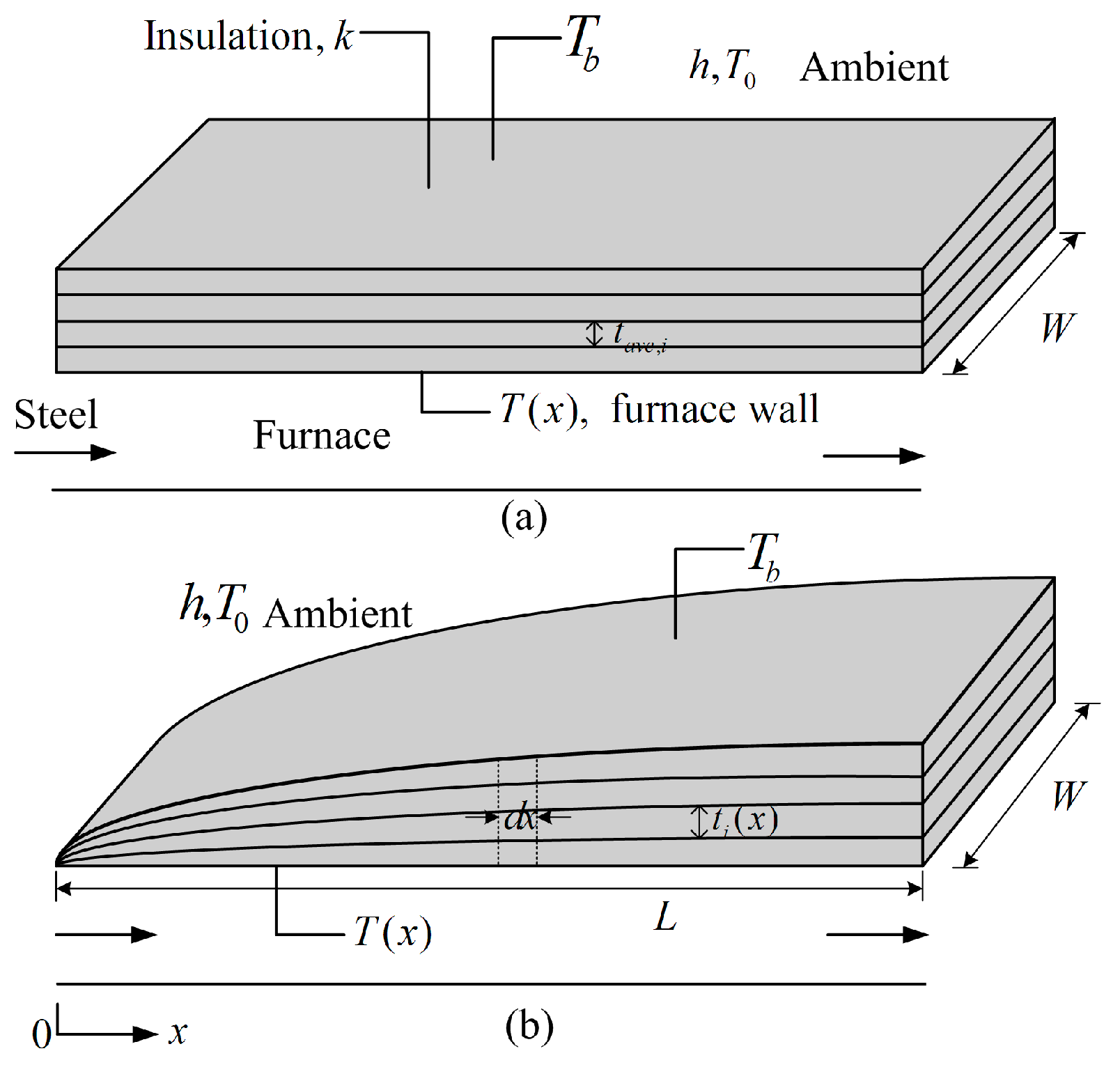
Constructal Optimizations for Thermal Insulation Processes of Steel Rolling Reheating Furnace Walls
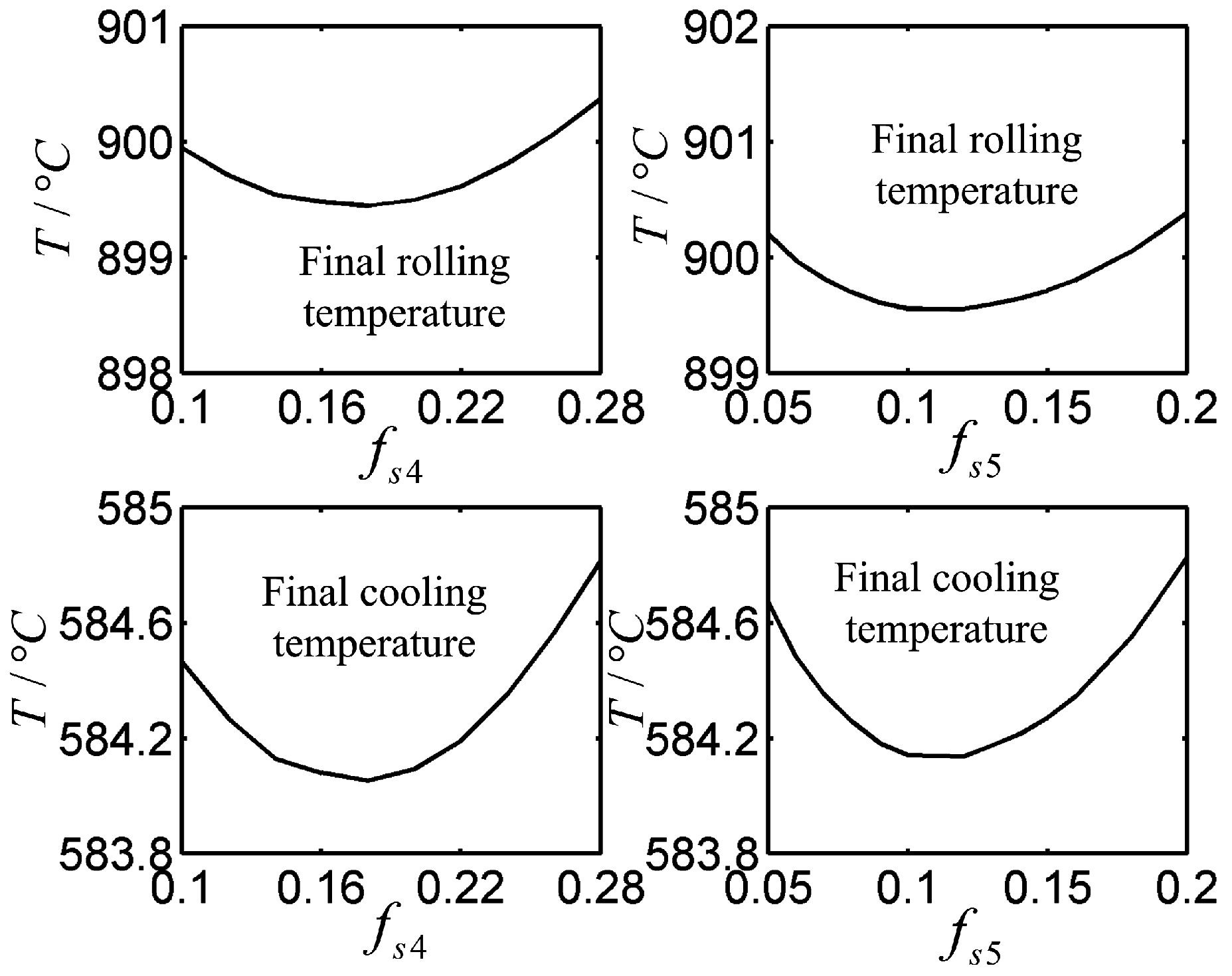
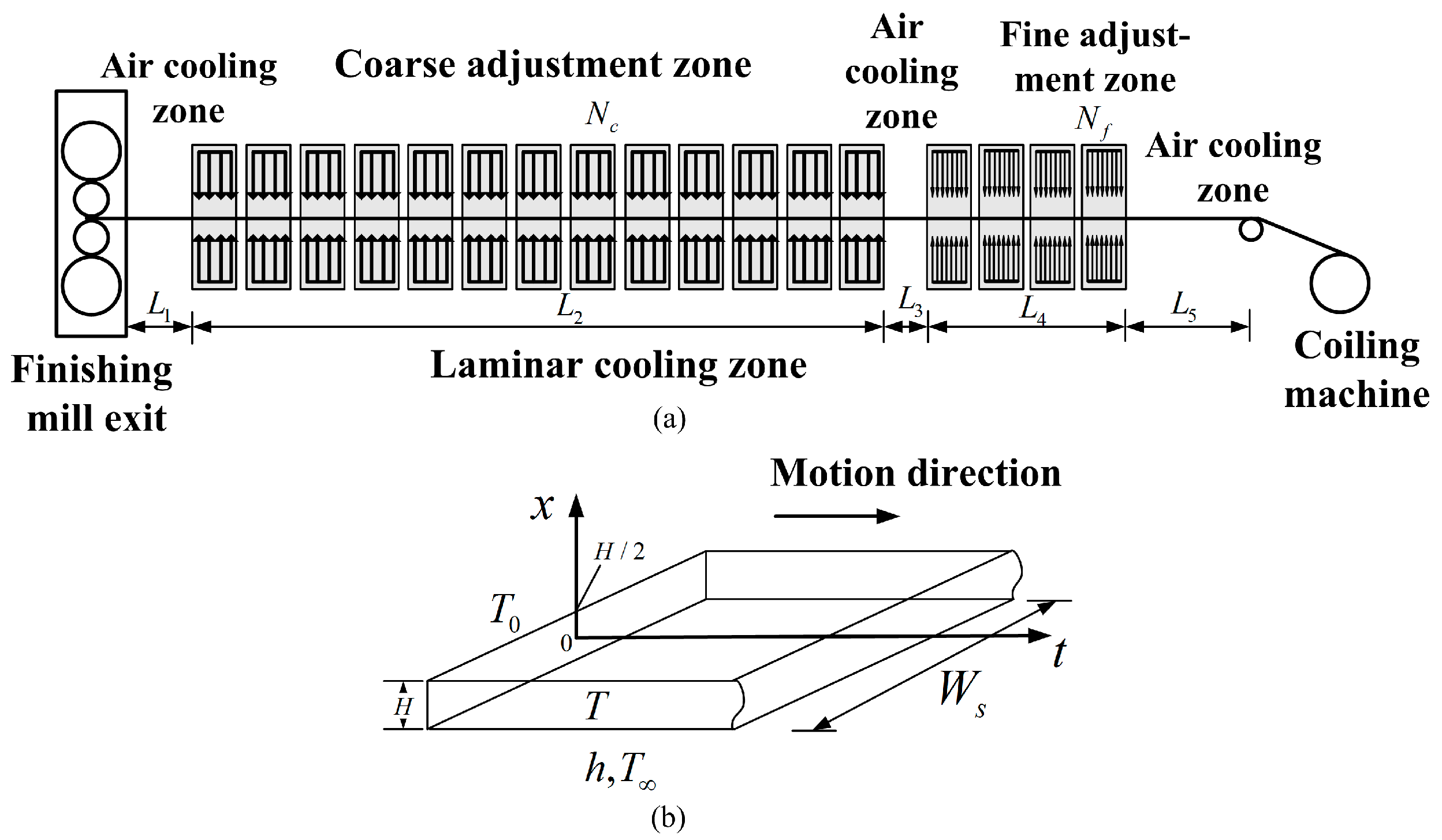
Constructal Optimizations for Laminar Cooling Elemental Packages
7.3. Generalized Thermodynamic Optimizations for Functional Subsystems of ISPP
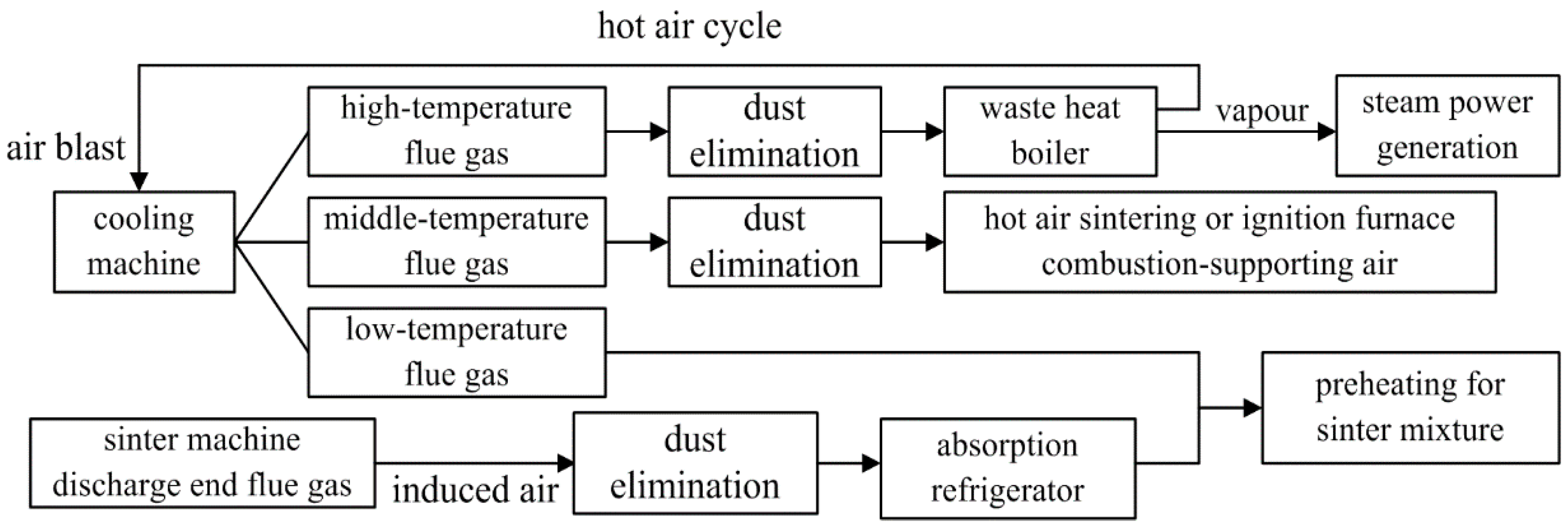
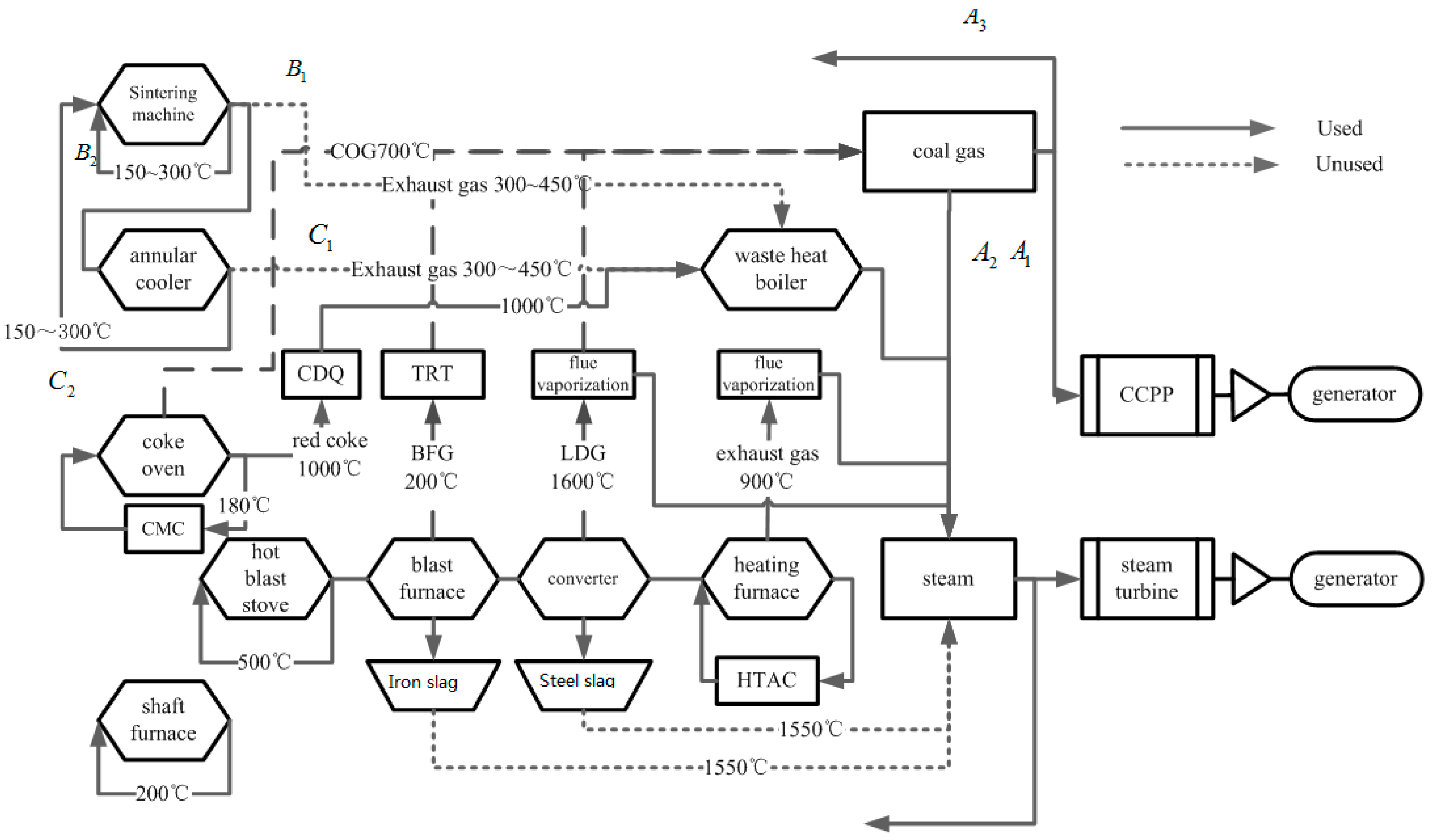
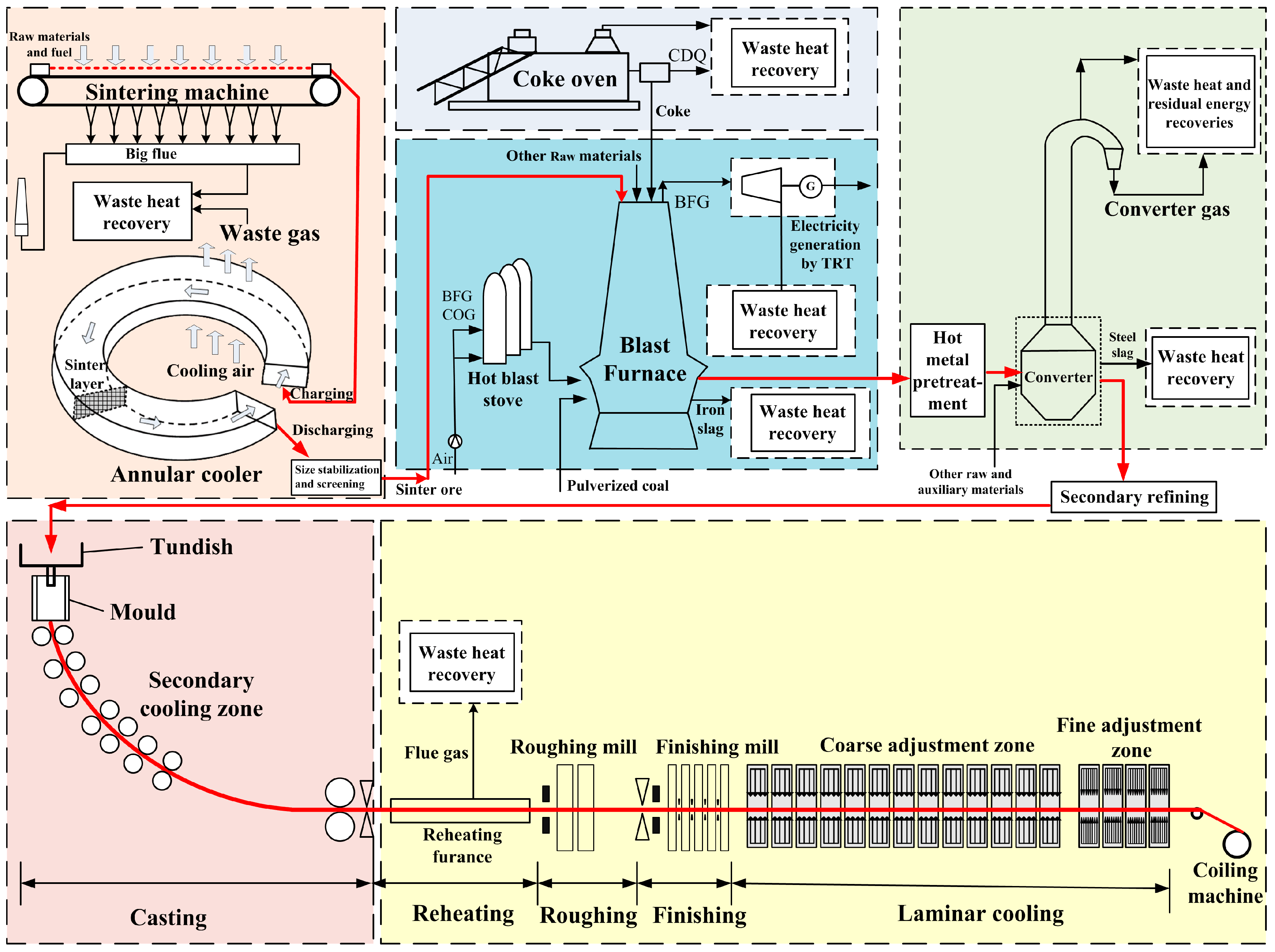
7.3.1. Potential Analyses of Thermodynamic Optimizations in Waste Heat and Residual Energy Recoveries of China’s Iron and Steel Industry
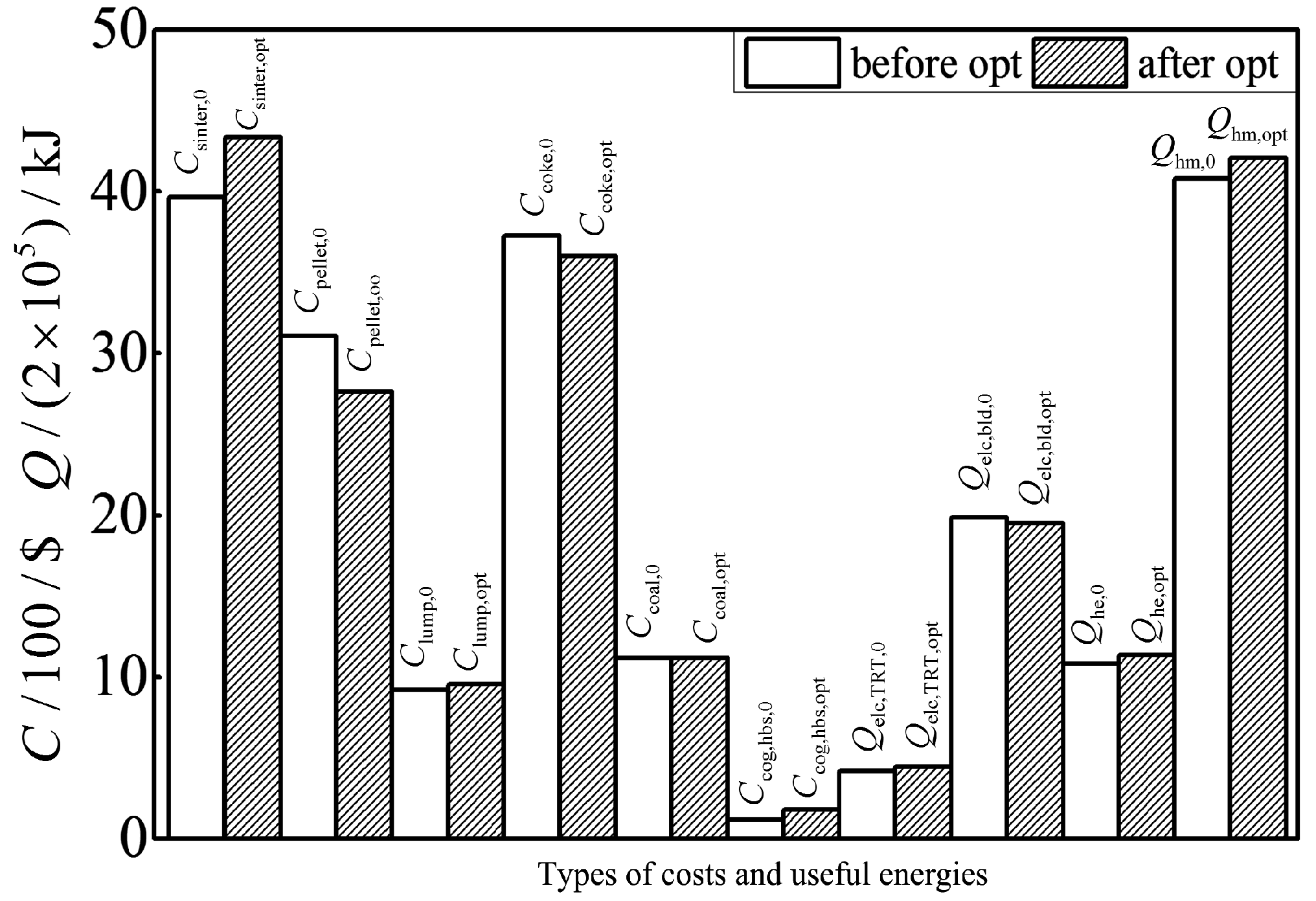
7.3.2. Recovery and Utilization of Residual Energy and Heat for Sintering Procedure: A Case Study
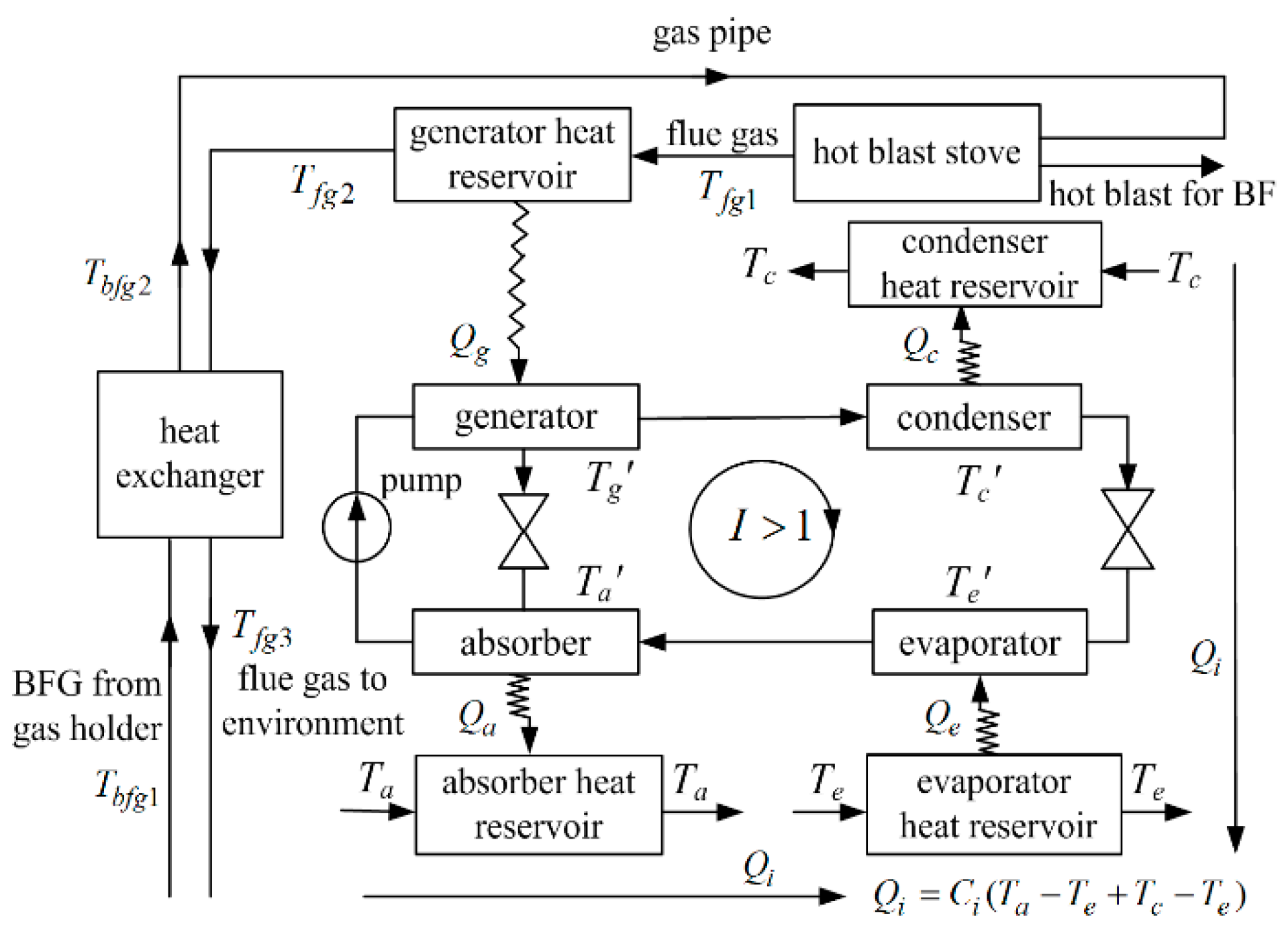
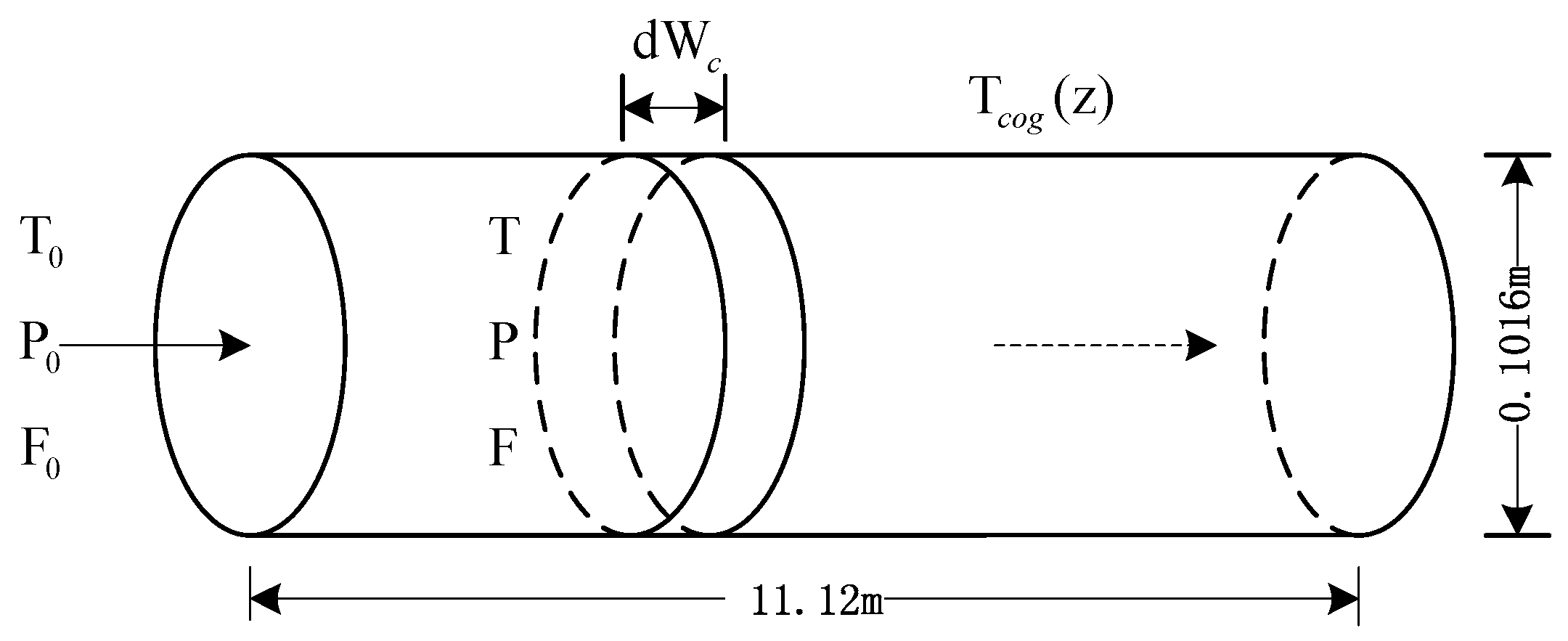
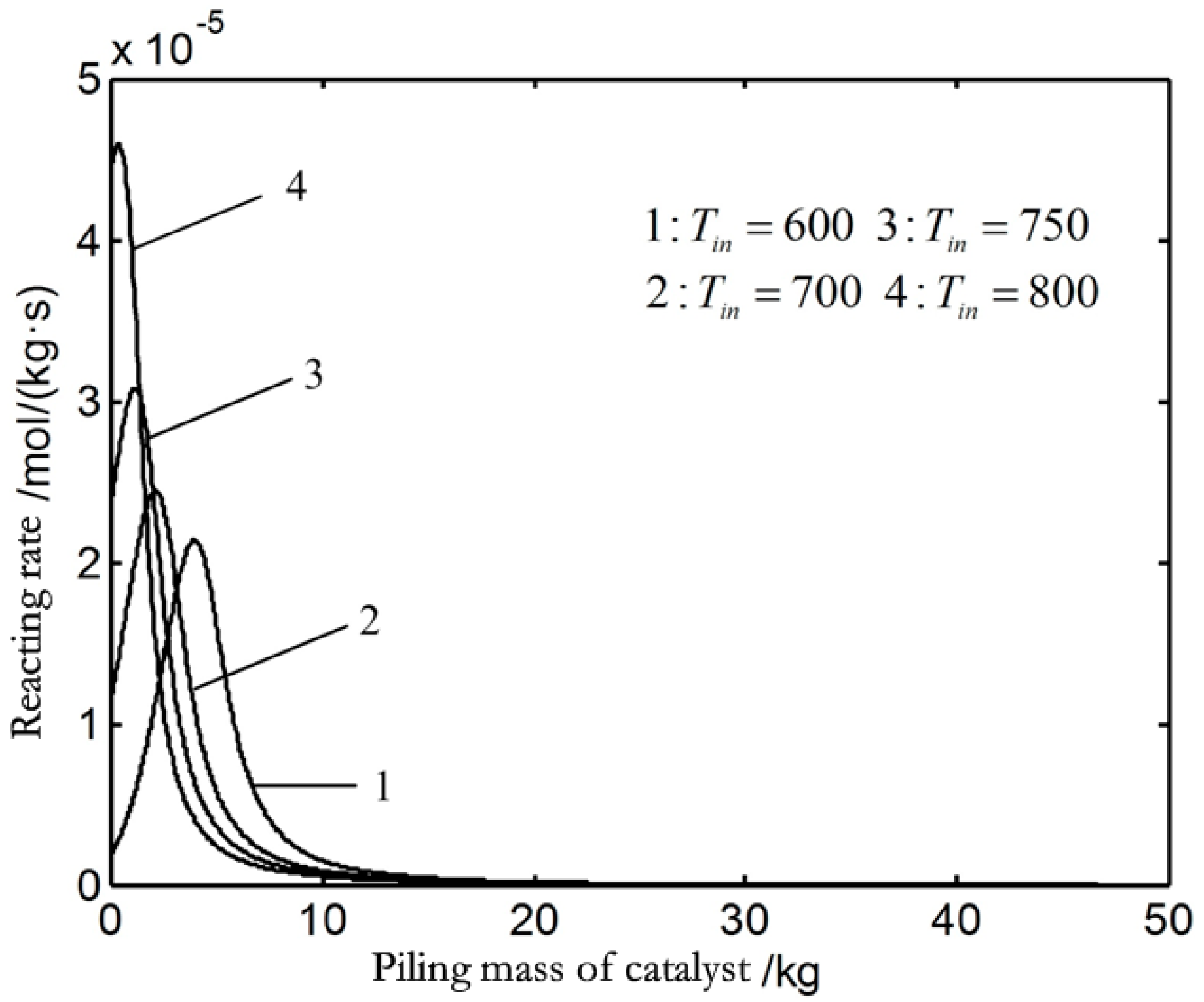
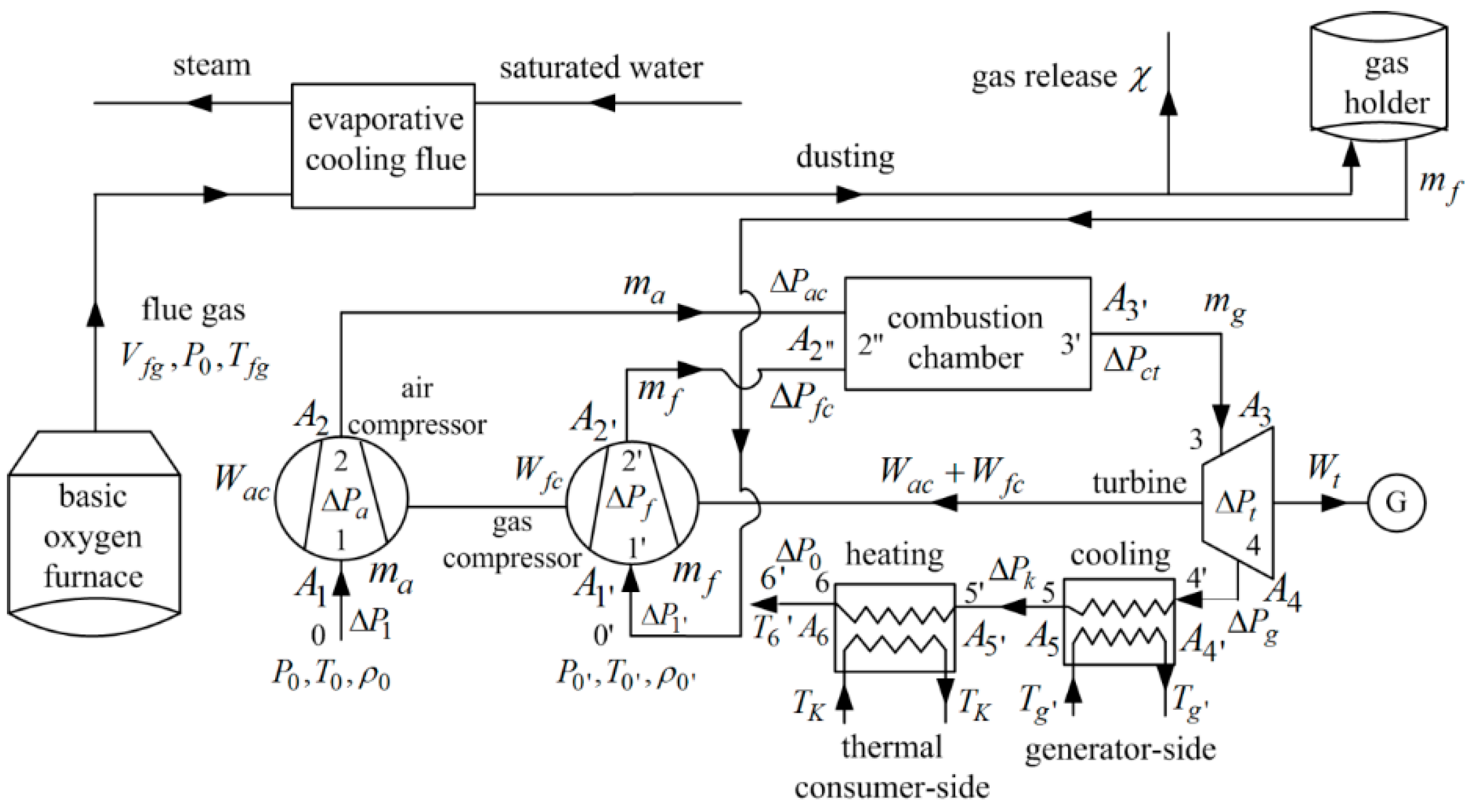
7.3.3. Heat Recovery and Utilization of High Temperature BOG Based on Thermochemical Method
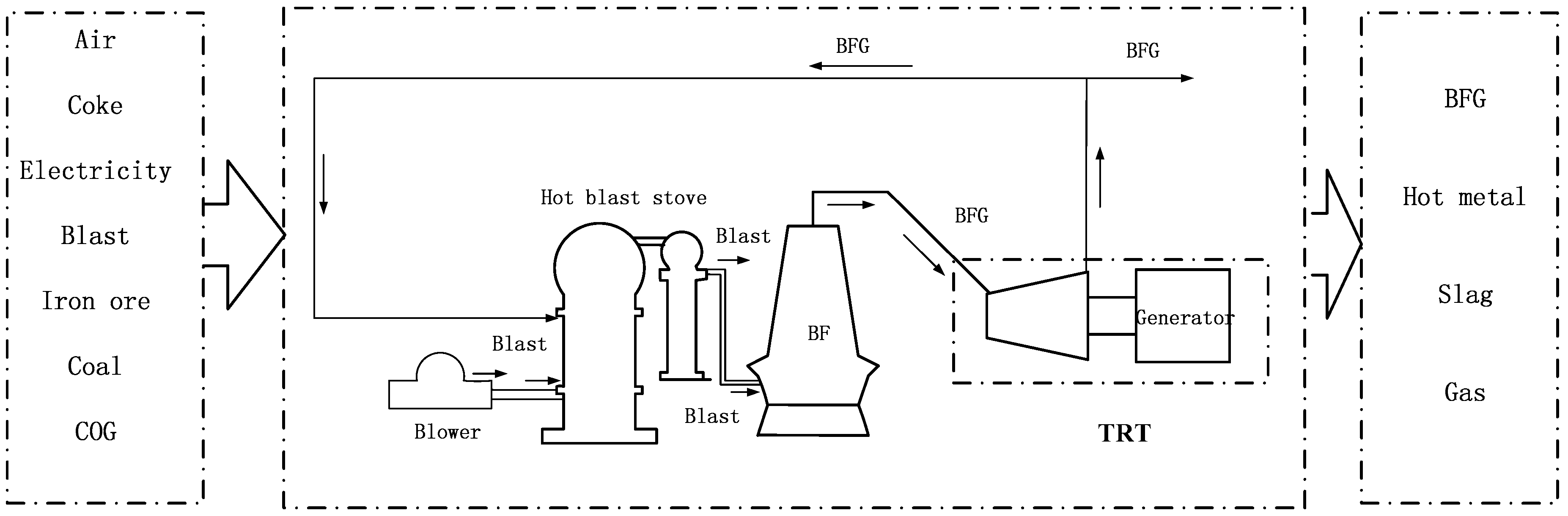
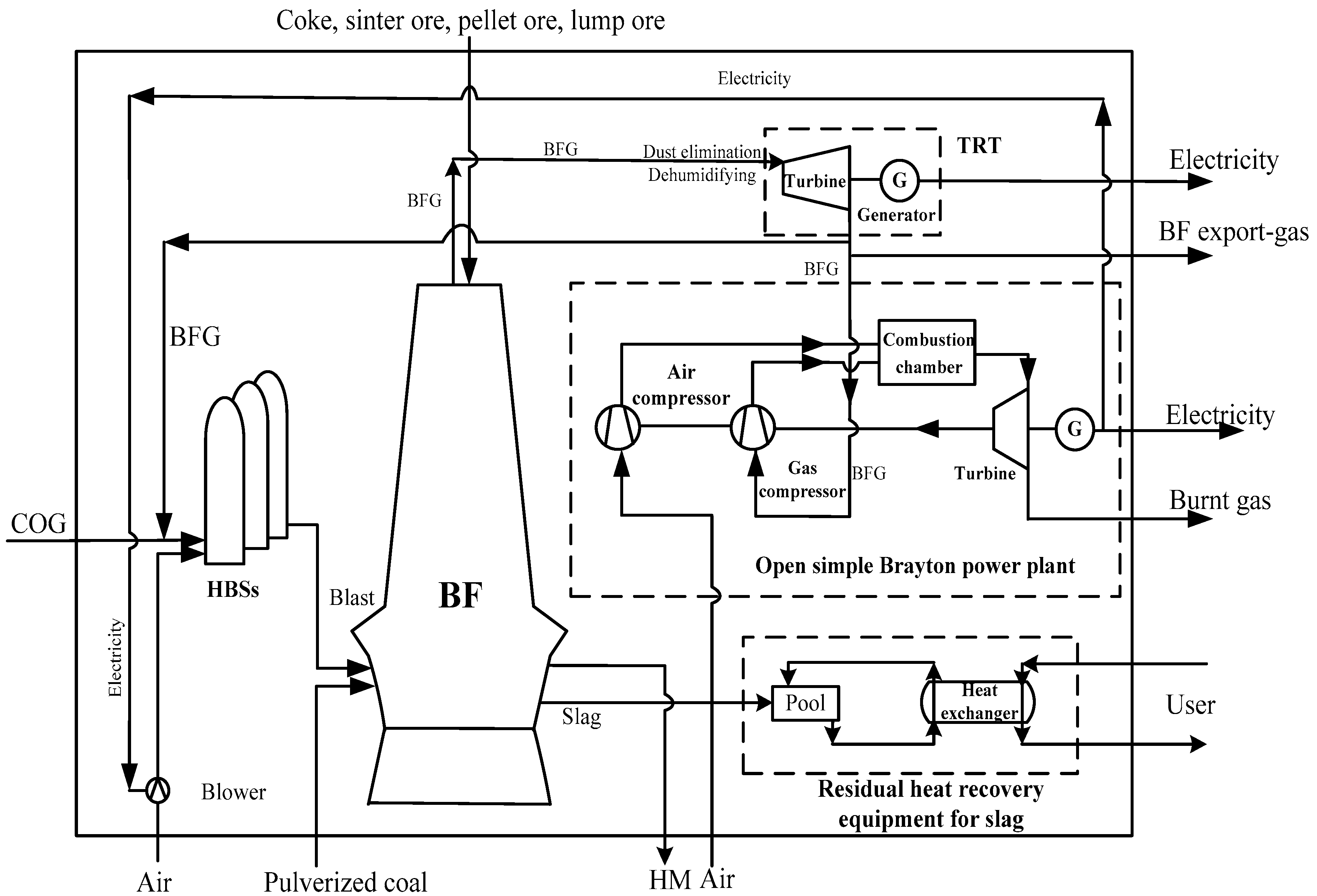
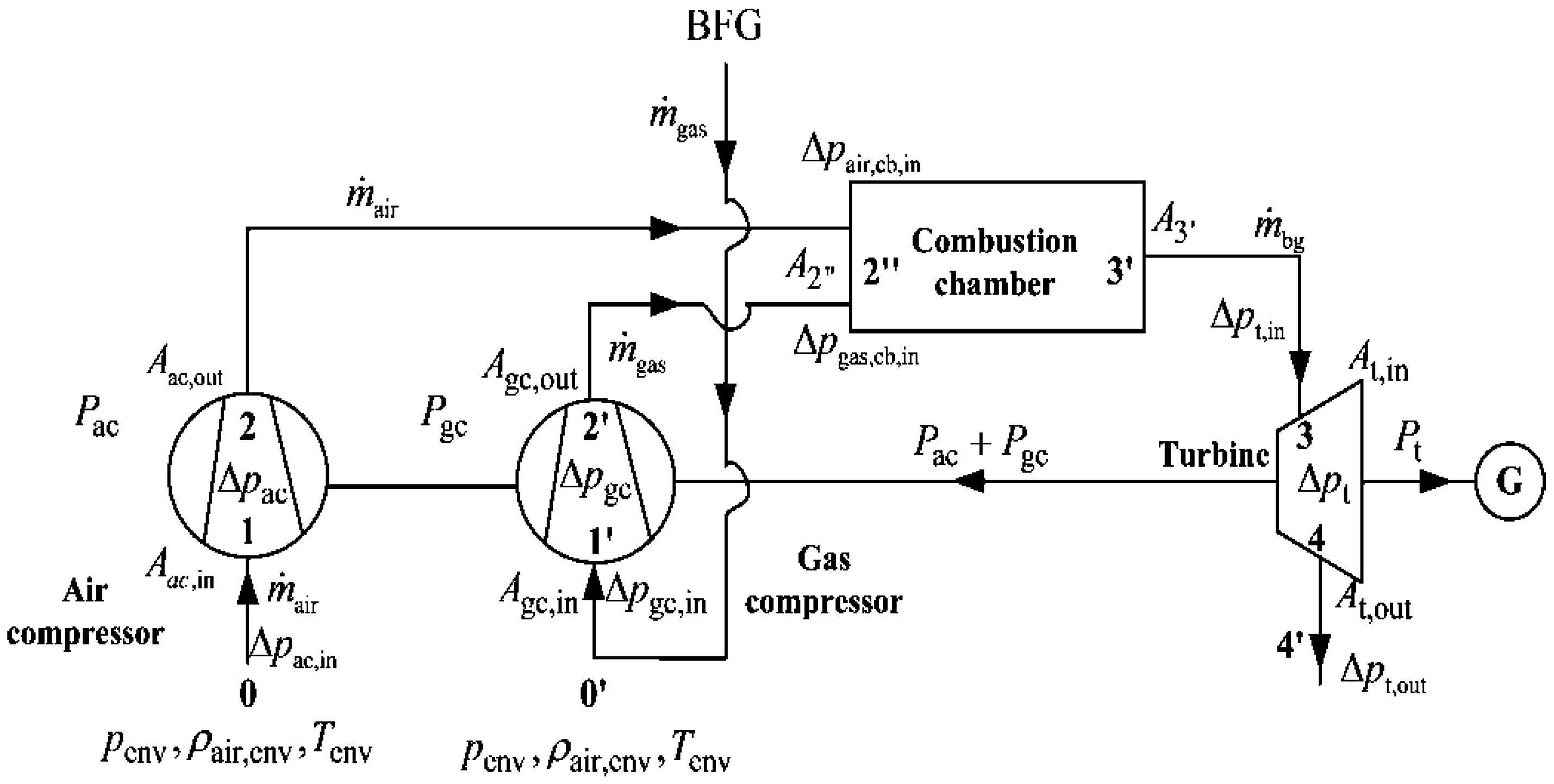
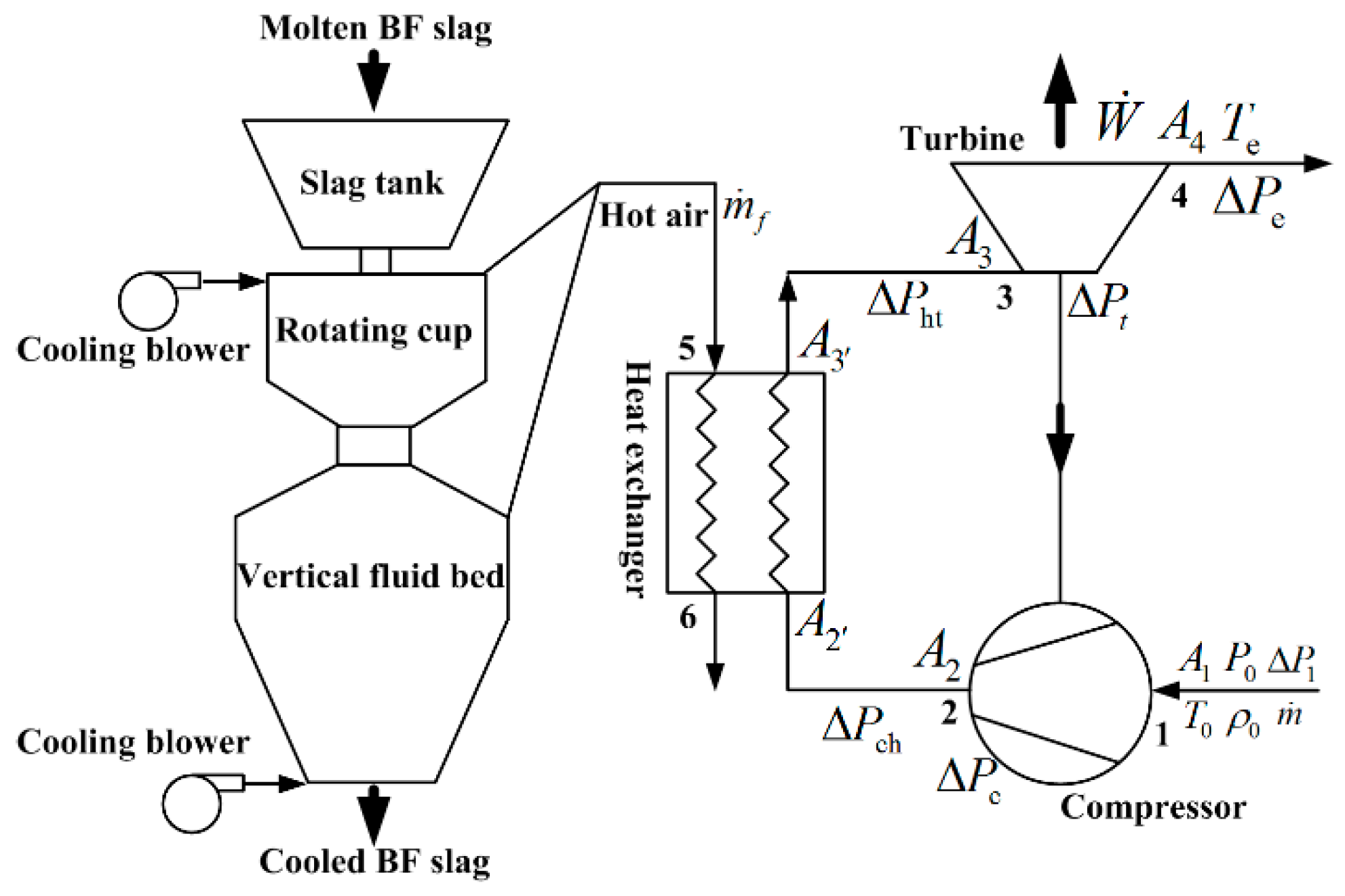
7.3.4. Thermodynamic Optimizations of Residual Energy and Heat Based on Gas Turbine Technology
7.3.5. Low Temperature Waste Heat Recovery with Constructal Disc-Shaped Solid-Gas Reactors
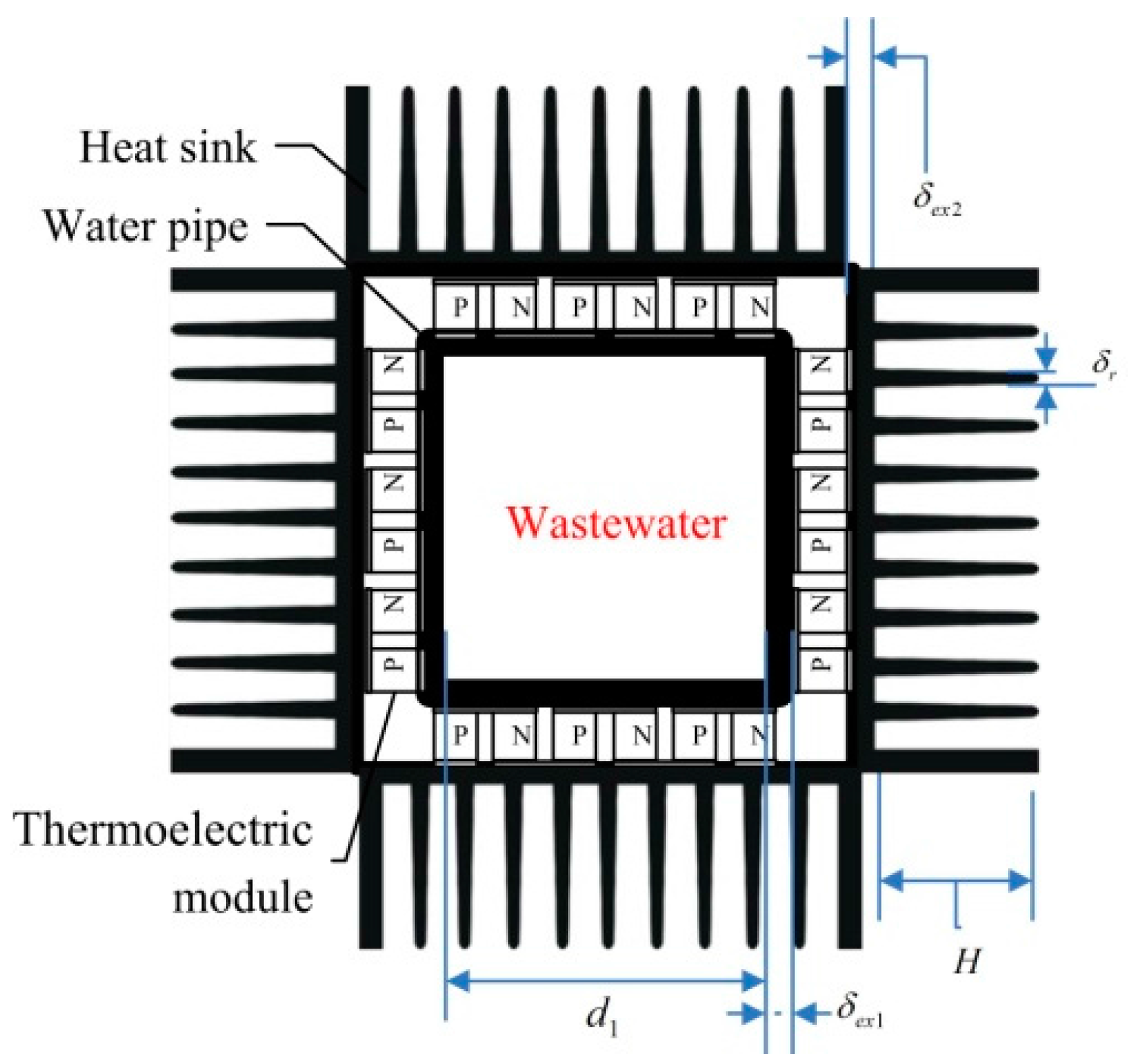
7.3.6. Heat Recovery Based on Thermoelectric Device and Its Evaluation
7.4. Generalized Thermodynamic Optimizations for Sections and Whole Process of ISPP
7.4.1. Performance Optimization of Sintering and Iron-Making Section
7.4.2. Study of Reasonable Process Route for BF-CC Section Based on the MPE
- (1)
- The most reasonable process route for plain construction steel production is “small BF-KR desulphurization (S > 0.03%)→small converter→ladle argon stirring and wire feeding/(CAS-OB) billet caster”.
- (2)
- The reasonable process route for machinery steel production is “small BF-KR desulphurization→small BOF-LF-VD/RH-billet caster, adding process carburetion of catching carbon at blowing endpoint of converter (C ≥ 0.6%)”.
- (3)
- The reasonable process route for HR thin slab production is “large BF-KR desulphurization (full hot metal pretreatment, namely KR desulphurization and dephosphorization BOF)→large decarburization converter-(CAS-OB)/RH (ladle argon stirring for plain carbon steel, LF-RH for pipe line steel)→thin slab caster”.
- (4)
- The reasonable process route for CR thin slab production is “large BF-KR desulphurization (full hot metal pretreatment, namely KR desulphurization and dephosphorization BOF)→large decarburization converter-RH (CAS-OB for plain carbon steel)→thin slab caster”. Moreover, the RH light treatment should be applied in the low carbon Al-killed steel production with RH refining.
- (5)
- The reasonable process route for plain construction steel production is “medium sized BF-KR desulphurization→medium sized converter-LF-VD or RH-slab caster”.
7.4.3. Calculations of Theoretical Minimum Energy Consumption and CO2 Emission and Exergy Analysis for ISPP
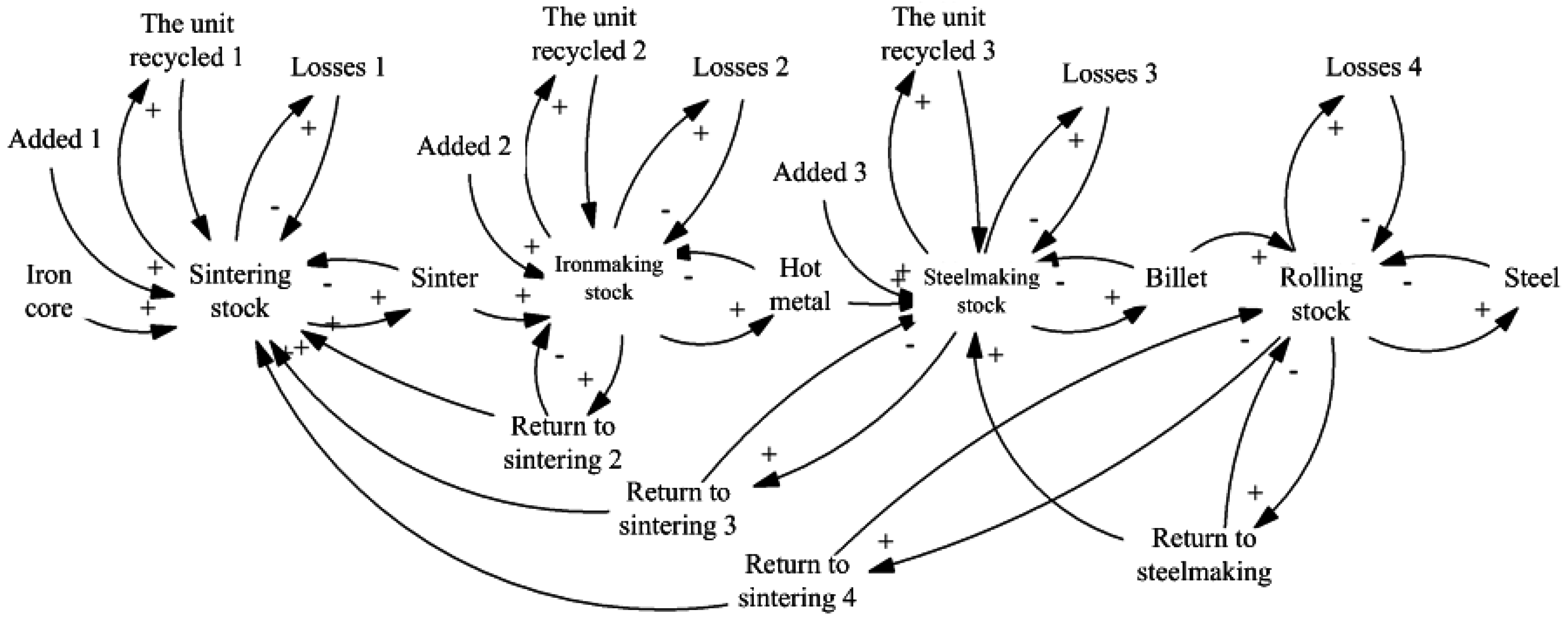
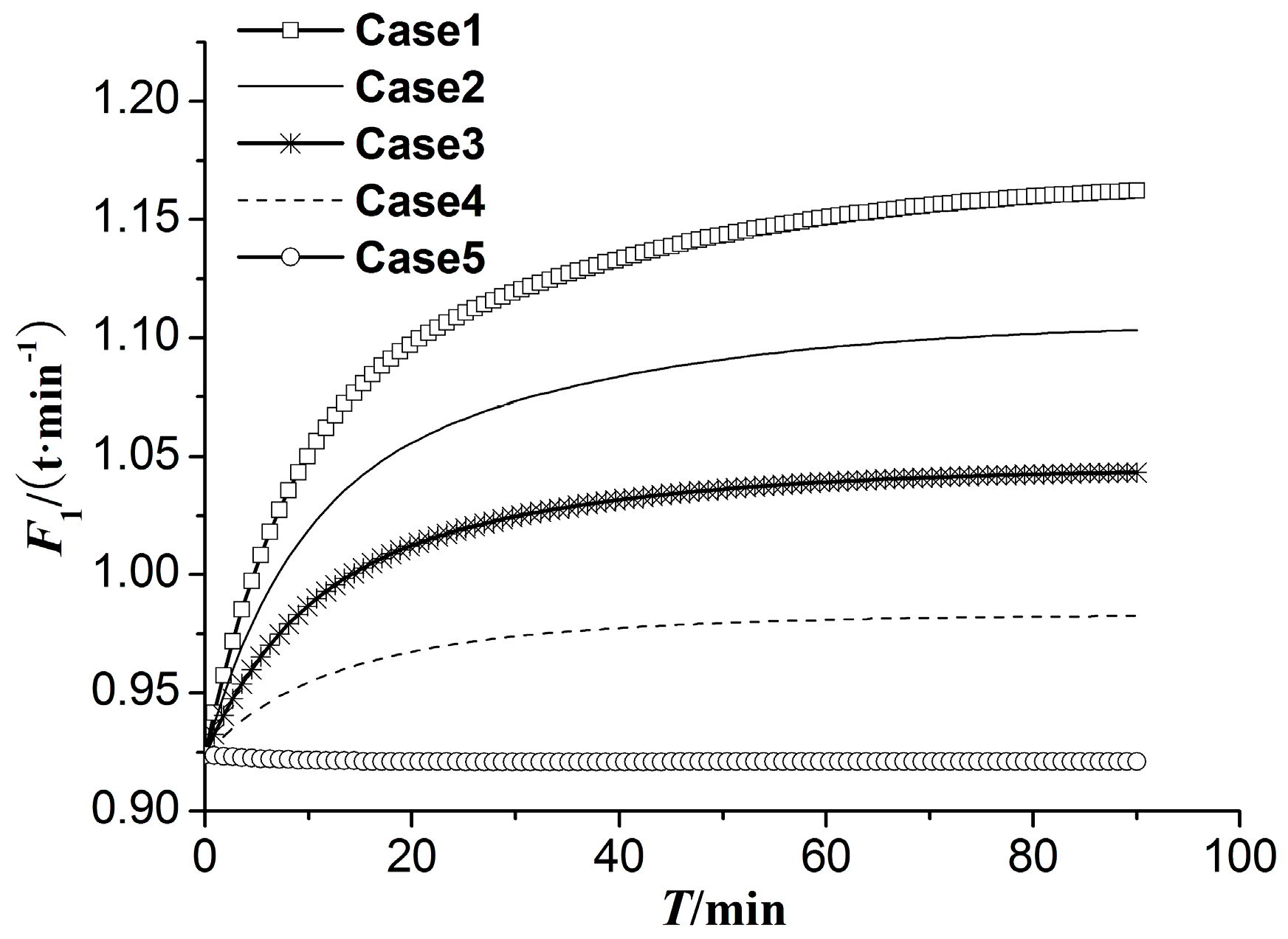
7.4.4. Investigations of the Dynamic Characteristics of Iron Flow for ISPP
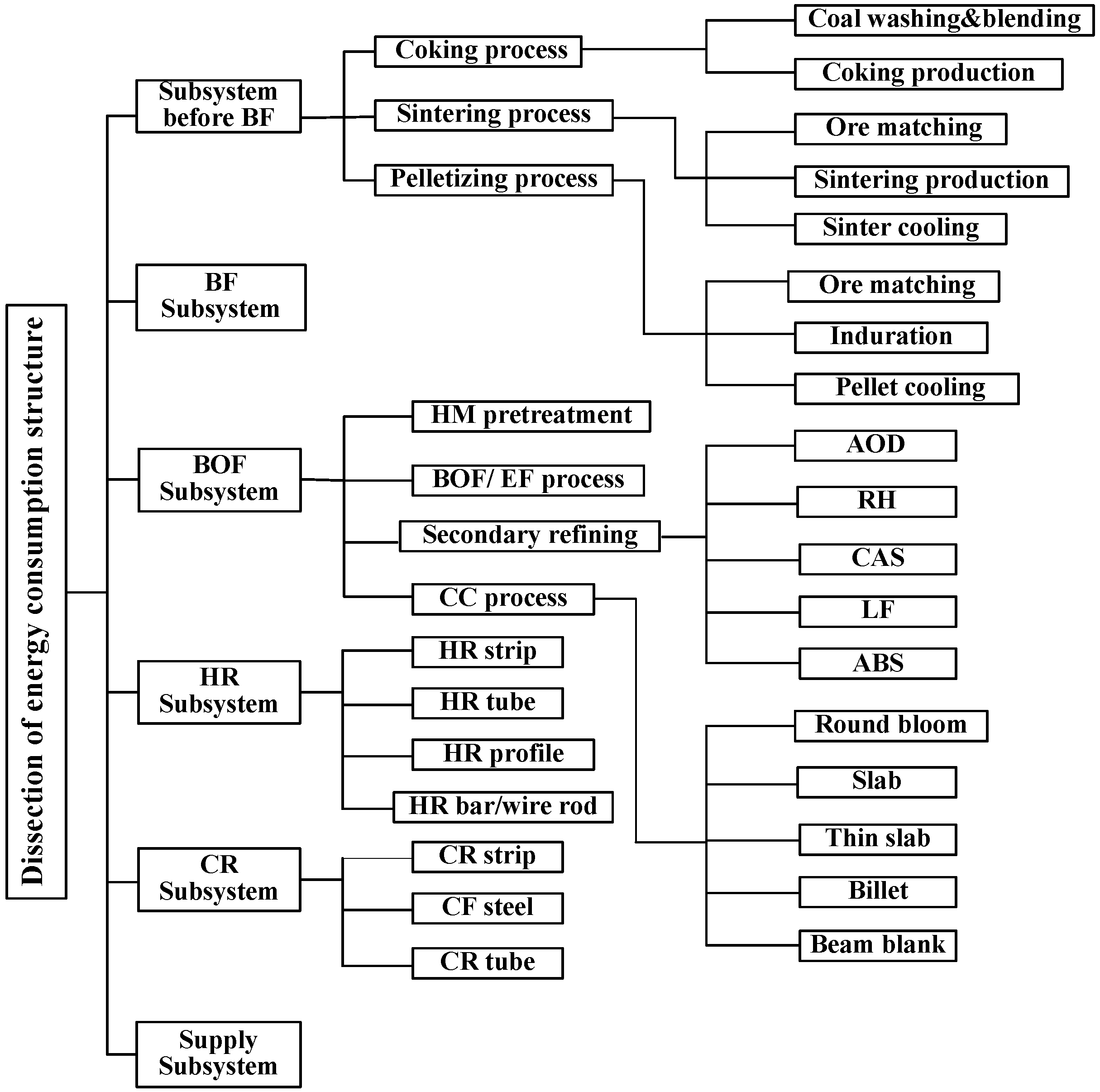
7.4.5. Generalized Energy Consumption Structure Analysis and Systematic Optimization for ISPP
7.4.6. Generalized Constructal Optimization for ISPP
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lin, B.Q.; Wang, X.L. Carbon emissions from energy intensive industry in China: Evidence from the iron & steel industry. Renew. Sustain. Energy Rev. 2015, 47, 746–754. [Google Scholar]
- Wang, X.L.; Lin, B.Q. How to reduce CO2 emissions in China’s iron and steel industry. Renew. Sustain. Energy Rev. 2016, 57, 1496–1505. [Google Scholar] [CrossRef]
- Yin, R.Y. The essence, functions, and future development mode of steel manufacturing process. Sci. China Ser. E-Tech. Sci. 2008, 38, 1365–1377. (In Chinese) [Google Scholar]
- Yin, R.Y. Metallurgical Process Engineering; Springer: New York, NY, USA, 2011. [Google Scholar]
- Yin, R.Y. Theory and Method of Metallurgical Process Integration; Metallurgical Industry Press: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures, 2nd ed.; Wiley: Chichester, UK, 2014. [Google Scholar]
- Andresen, B. Finite-Time Thermodynamics; Physics Laboratory II, University of Copenhagen: Copenhagen, Denmark, 1983. [Google Scholar]
- Chen, L.G.; Wu, C.; Sun, F.R. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Chen, L.G.; Sun, F.R. Advances in Finite Time Thermodynamics: Analysis and Optimization; Nova Science: New York, NY, USA, 2004. [Google Scholar]
- Chen, L.G. Finite-Time Thermodynamic Analysis of Irreversible Processes and Cycles; Higher Education Press: Beijing, China, 2005. [Google Scholar]
- Andresen, B. Current trends in finite-time thermodynamics. Angew. Chem. Int. Ed. 2011, 50, 2690–2704. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.G.; Xia, S.J. Generalized Thermodynamic Dynamic-Optimization for Irreversible Processes; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Chen, L.G.; Xia, S.J.; Li, J. Generalized Thermodynamic Dynamic-Optimization for Irreversible Cycles; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Ge, Y.L.; Chen, L.G.; Sun, F.R. Progress in finite time thermodynamic studies for internal combustion engine cycles. Entropy 2016, 18, 139. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Bejan, A. Entropy Generation Minimization; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bejan, A.; Lorente, S. Design with Constructal Theory; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chen, L.G. Progress in study on constructal theory and its application. Sci. China Technol. Sci. 2012, 55, 802–820. [Google Scholar] [CrossRef]
- Bejan, A.; Lorente, S. Constructal law of design and evolution: Physics, biology, technology, and society. J. Appl. Phys. 2013, 113, 151301. [Google Scholar] [CrossRef]
- Bejan, A. The Physics of Life: The Evolution of Everything; St. Martin’s Press: New York, NY, USA, 2016. [Google Scholar]
- Chen, L.G.; Feng, H.J. Multi-Objective Constructal Optimizations for Fluid Flow, Heat and Mass Transfer Processes; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Guo, Z.Y.; Zhu, H.Y.; Liang, X.G. Entransy—A physical quantity describing heat transfer ability. Int. J. Heat Mass Transf. 2007, 50, 2545–2556. [Google Scholar] [CrossRef]
- Chen, L.G. Progress in entransy theory and its applications. Chin. Sci. Bull. 2012, 57, 4404–4426. [Google Scholar] [CrossRef]
- Chen, Q.; Liang, X.G.; Guo, Z.Y. Entransy theory for the optimization of heat transfer—A review and update. Int. J. Heat Mass Transf. 2013, 63, 65–81. [Google Scholar] [CrossRef]
- Chen, L.G. Progress in optimization of mass transfer processes based on mass entransy dissipation extremum principle. Sci. China Technol. Sci. 2014, 57, 2305–2327. [Google Scholar] [CrossRef]
- Radcenco, V. Generalized Thermodynamics; Editura Technica: Bucharest, Romania, 1994. [Google Scholar]
- Chen, L.G.; Bi, Y.H.; Wu, C. Influence of nonlinear flow resistance relation on the power and efficiency from fluid flow. J. Phys. D Appl. Phys. 1999, 32, 1346–1349. [Google Scholar] [CrossRef]
- Carnot, S. Reflection on the Motive Power of Fire; Bachelier: Paris, France, 1824. [Google Scholar]
- Reitlinger, H.B. Sur L’utilisation de la Chaleur Dans les Machines à Feu; Vaillant-Carmanne: Liège, Belgium, 1929. (In German) [Google Scholar]
- Novikov, I.I. The efficiency of atomic power stations (A review). Atommaya Energiya 1957, 3, 409–412. [Google Scholar] [CrossRef]
- Chambadal, P. Les Centrales Nucleaires; Armand Colin: Paris, France, 1957. (In French) [Google Scholar]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Bejan, A. Street network theory of organization in nature. J. Adv. Transp. 1996, 30, 85–107. [Google Scholar] [CrossRef]
- Bejan, A. Constructal-theory network of conducting paths for cooling a heat generating volume. Int. J. Heat Mass Transf. 1997, 40, 799–816. [Google Scholar] [CrossRef]
- Chen, Q. Irreversibility and Its Optimization of Convective Heat Transfer Processes. Ph.D. Thesis, Tsinghua University, Beijing, China, 2008. [Google Scholar]
- Chen, Q.; Ren, J.X.; Guo, Z.Y. The extremum principle of mass entransy dissipation and its application to decontamination ventilation designs in space station cabins. Chin. Sci. Bull. 2009, 54, 2862–2870. [Google Scholar] [CrossRef]
- Liu, X.B.; Wang, M.; Meng, J.A.; Ben-Naim, E.; Guo, Z.Y. Minimum entransy dissipation principle for the optimization of transport networks. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 113–120. [Google Scholar] [CrossRef]
- Chen, L.G.; Tian, F.H.; Xiao, Q.H.; Sun, F.R. Constructal entransy dissipation minimization for mass transfer based on rectangular element with constant channel. J. Therm. Sci. Tech. 2012, 11, 136–141. (In Chinese) [Google Scholar]
- Cheng, X.T.; Xu, X.H.; Liang, X.G. Principles of potential entransy in generalized flow. Acta Phys. Sin. 2011, 60, 118103. (In Chinese) [Google Scholar]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Thermal insulation constructal optimization for steel rolling reheating furnace wall based on entransy dissipation extremum principle. Sci. China Technol. Sci. 2012, 55, 3322–3333. [Google Scholar] [CrossRef]
- Cai, J.J.; Dong, H.; Du, T.; Xu, C.B.; Zhou, J.W.; Lin, K. Study on grade recovery and cascade utilization of waste heat from sintering-cooling process. Iron Steel 2011, 46, 88–92. (In Chinese) [Google Scholar]
- Zhang, Q.; Cai, J.J.; Shen, F.M. Application of process integration on systemic energy saving and emission reduction in iron and steel works. China Metall. 2011, 20, 3–6. (In Chinese) [Google Scholar]
- Chen, G.; Yang, T.; Ding, Y.; Wang, W. Energy flow analysis and the application of it to the coking unit in iron and steel enterprise. Energy Metall. Ind. 2013, 32, 3–8. (In Chinese) [Google Scholar]
- Xu, W.; Cao, W.; Wan, B.; Ye, M.; Zhu, T. Emission calculation and reduction measures of CO2 from coking based on carbon flow analysis. Clean Coal Technol. 2015, 2, 10–13. (In Chinese) [Google Scholar]
- Liu, Z.M.; Xie, Z.H.; Zhang, Z.L.; Sun, F.R. Calculation of energy consumption and CO2 emission and investigation of the parameter influences for coking process. Res. Iron Steel 2016, 44, 1–4. (In Chinese) [Google Scholar]
- Liu, C.X.; Xie, Z.H.; Sun, F.R.; Chen, L.G. Optimization for sintering proportioning based on energy value. Appl. Therm. Eng. 2016, 103, 1087–1094. [Google Scholar] [CrossRef]
- Shen, X.; Chen, L.G.; Xia, S.J.; Sun, F.R. Numerical simulation and analyses for sinter cooling process with convective and radiative heat transfer. Int. J. Energy Environ. 2016, 7, 303–316. [Google Scholar]
- Feng, H.J.; Chen, L.G.; Liu, X.; Xie, Z.H.; Sun, F.R. Constructal optimization of a sinter cooling process based on exergy output maximization. Appl. Therm. Eng. 2016, 96, 161–166. [Google Scholar] [CrossRef]
- Shen, X.; Chen, L.G.; Xia, S.J.; Sun, F.R. Numerical simulation of sinter cooling processes in vertical tank and annular cooler. Sci. China Technol. Sci. 2016, 46, 36–45. (In Chinese) [Google Scholar]
- Liu, X.; Chen, L.G.; Feng, H.J.; Sun, F.R. Constructal design for blast furnace wall based on the entransy theory. Appl. Therm. Eng. 2016, 100, 798–804. [Google Scholar] [CrossRef]
- Mitra, T.; Helle, M.; Pettersson, F.; Saxén, H. Multiobjective optimization of top gas recycling conditions in the blast furnace by genetic algorithms. Mater. Manuf. Proc. 2011, 26, 475–480. [Google Scholar] [CrossRef]
- Qin, X.Y.; Liu, X.; Chen, L.G.; Sun, F.R. Utilization coefficient optimization model for blast furnace iron–making process. China Metall. 2014, 25, 5–10. (In Chinese) [Google Scholar]
- Liu, X. Thermodynamic Optimization Model and Analyses of Blast Furnace Iron-Making Process. Master’s Thesis, Naval University of Engineering, Wuhan, China, 2013. [Google Scholar]
- Liu, X.; Chen, L.G.; Qin, X.Y.; Sun, F.R. Exergy loss minimization for a blast furnace with comparative analyses for energy flows and exergy flows. Energy 2015, 93, 10–19. [Google Scholar] [CrossRef]
- Zhang, Z.Y. Thermodynamic Analyses and Optimization of Blast Furnace Iron-Making Process. Master’s Thesis, Naval University of Engineering, Wuhan, China, 2014. [Google Scholar]
- Zhang, Z.Y.; Qin, X.Y.; Chen, L.G.; Sun, F.R. Performance optimization of blast furnace iron-making process taking energy consumption reducing as the objective. Steel Res. 2016, 44, 1–5. (In Chinese) [Google Scholar] [CrossRef]
- Liu, X.; Chen, L.G.; Feng, H.J.; Sun, F.R. Hot metal yield optimization of a blast furnace based on constructal theory. Energy 2016, 104, 33–41. [Google Scholar] [CrossRef]
- Liu, X.; Feng, H.J.; Chen, L.G.; Qin, X.Y.; Sun, F.R. Constructal design of a blast furnace iron-making process based on multi-objective optimization. Energy 2016, 109, 137–151. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Wagner, D.; Patisson, F. Modelling a new, low CO2 emissions, hydrogen steelmaking process. J. Clean. Prod. 2013, 46, 27–35. [Google Scholar] [CrossRef]
- Lu, B.H.; Li, Y.K.; Qu, B.Z. Optimization research on converter steelmaking process parameters based on DOE. Key Eng. Mater. 2014, 579/580, 128–132. [Google Scholar] [CrossRef]
- Rajashekar, Y.; Alex, T.C.; Sahoo, D.P.; Babu, G.A.; Balakrishnan, V.; Venugopalan, T.; Kumar, S. Iron ore slime as an alternate coolant in steelmaking: Performance evaluation at commercial scale. J. Clean. Prod. 2016, 139, 886–893. [Google Scholar] [CrossRef]
- Chen, L.G.; Liu, X.; Feng, H.J.; Ge, Y.L.; Xie, Z.H.; Sun, F.R. Molten steel yield optimization of a converter based on constructal theory. Renew. Sustain. Energy Rev. 2016. submitted for publication. [Google Scholar]
- Liu, X.; Feng, H.J.; Chen, L.G.; Ge, Y.L.; Xie, Z.H.; Sun, F.R. Constructal design of a converter steel-making process based on multi-objective optimization. Appl. Therm. Eng. 2016. submitted for publication. [Google Scholar]
- Feng, H.J.; Chen, L.G.; Sun, F.R. Numerical analyses of thin slab continuous casting and rolling process. Res. Iron Steel 2015, 43, 23–27. (In Chinese) [Google Scholar]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Generalized constructal optimization for solidification heat transfer process of slab continuous casting based on heat loss rate. Energy 2014, 66, 991–998. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Ding, Z.M.; Sun, F.R. Solidification heat transfer process and its heat loss of slab continuous casting based on Matlab. Contin. Cast. Technol. 2013, 6, 16–22. (In Chinese) [Google Scholar]
- Feng, H.J.; Chen, L.G.; Ding, Z.M.; Sun, F.R. Generalized constructal optimization for secondary cooling process of slab continuous casting based on entransy theory. Sci. China Technol. Sci. 2014, 57, 784–795. [Google Scholar] [CrossRef]
- Kang, D.H.; Lorente, S.; Bejan, A. Constructal architecture for heating a stream by convection. Int. J. Heat Mass Transf. 2010, 53, 2248–2255. [Google Scholar] [CrossRef]
- Kang, D.H.; Lorente, S.; Bejan, A. Constructal distribution of multi-layer insulation. Int. J. Energy Res. 2013, 37, 153–160. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructalentransy optimizations for insulation layer of steel rolling reheating furnace wall with convective and radiative boundary conditions. Chin. Sci. Bull. 2014, 59, 2470–2477. [Google Scholar] [CrossRef]
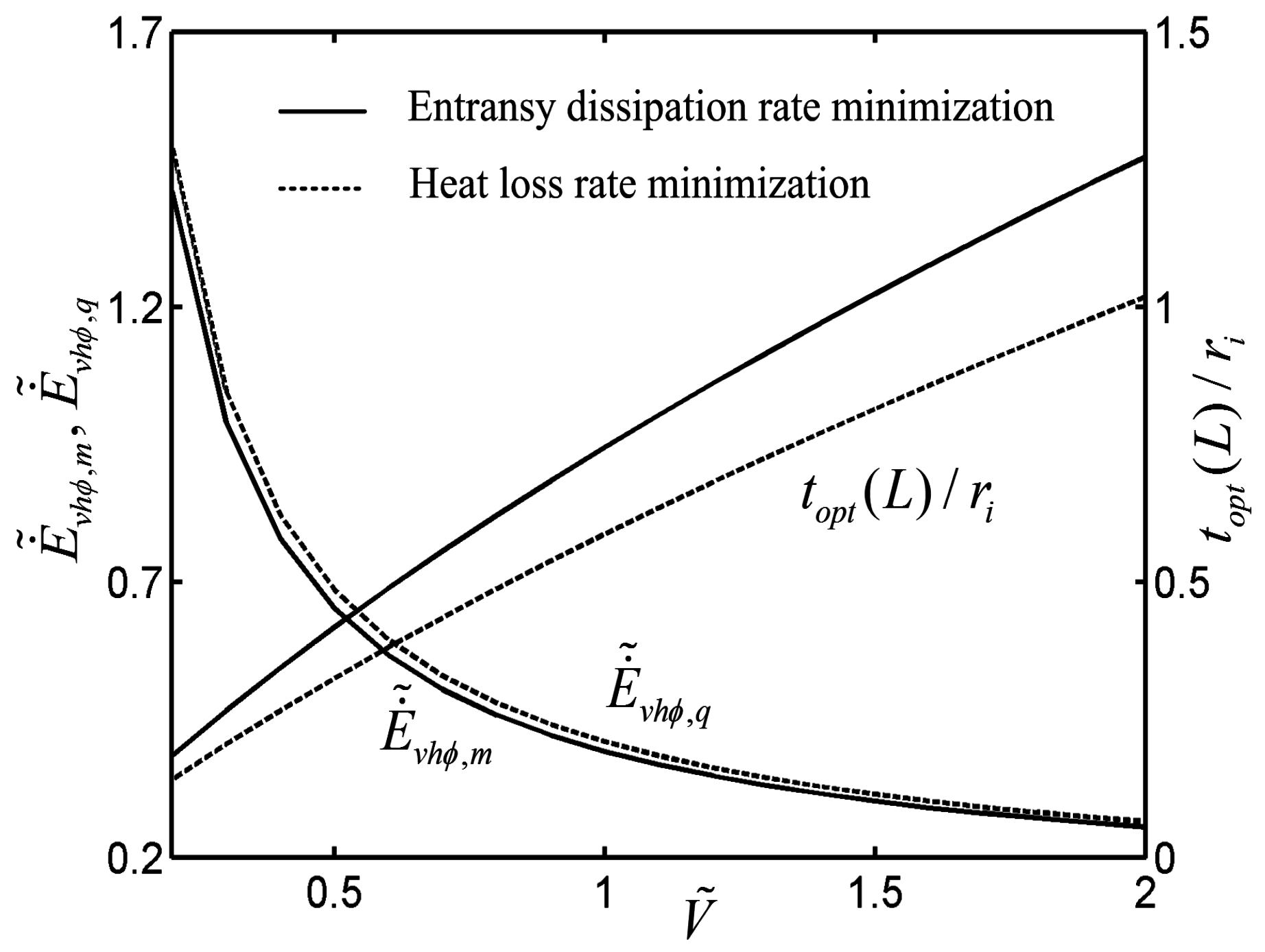
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructalentransy dissipation rate minimization for variable cross-section insulation layer of the steel rolling reheating furnace wall. Int. Commun. Heat Mass Transf. 2014, 52, 26–32. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal designs for insulation layers of steel rolling reheating furnace wall with convective and radiative boundary conditions. Appl. Therm. Eng. 2016, 100, 925–931. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal optimization of variable cross-section insulation layer of steel rolling reheating furnace wall based on entransy theory. Acta Phys. Sin. 2015, 64, 054402. (In Chinese) [Google Scholar]
- Feng, H.J.; Chen, L.G.; Sun, F.R. Temperature field of steel plate cooling process after plate rolling. Int. J. Energy Environ. 2015, 6, 255–264. [Google Scholar]
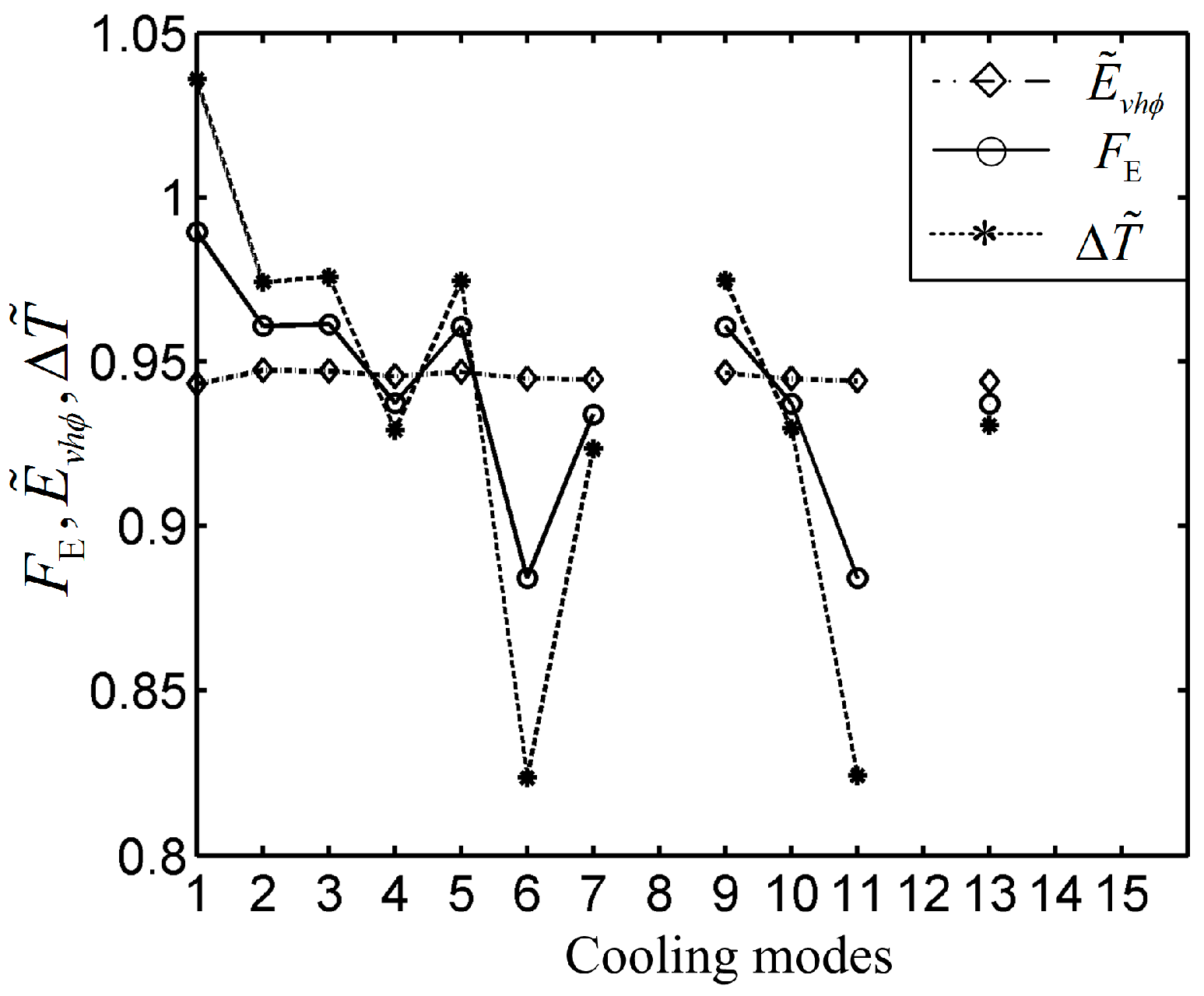
- Feng, H.J.; Chen, L.G.; Liu, X.; Xie, Z.H.; Sun, F.R. Generalized constructal optimization of strip laminar cooling process based on entransy theory. Sci. China Technol. Sci. 2016. [Google Scholar] [CrossRef]
- Chen, L.G.; Yang, B.; Shen, X.; Xie, Z.H.; Sun, F.R. Thermodynamic optimization opportunities for the recovery and utilization of residual energy and heat in China’s iron and steel industry: A case study. Appl. Therm. Eng. 2015, 86, 151–160. [Google Scholar] [CrossRef]
- Shen, X.; Xia, S.J.; Chen, L.G.; Sun, F.R. Thermodynamic analyses for recovering waste heat of high temperature BOG by the methane reforming with carbon dioxide reaction. In Proceedings of the 22th National Academic Conference on Engineering Thermodynamics of Higher Education Institutions, Haerbin, China, 26–29 May 2016.
- Yang, B. Finite Time Thermodynamic Analyses and Optimizations for Brayton CHP (Combined Heat and Power) and CCHP (Combined Cooling, Heating and Power) Plants. Ph.D. Thesis, Naval University of Engineering, Wuhan, China, 2014. [Google Scholar]
- Zhang, Z.L. Thermodynamic Analyses and Optimizations of Brayton Cycles for Recovering Residual Heat and Energy in Steel Plants. Ph.D. Thesis, Naval University of Engineering, Wuhan, China, 2015. [Google Scholar]
- Zhang, Z.L.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Thermodynamic analysis of an air Brayton cycle for recovering waste heat of BF slag. Appl. Therm. Eng. 2015, 9, 742–748. [Google Scholar] [CrossRef]
- Yang, B.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Exergy performance optimization of an irreversible closed intercooled regenerative Brayton cogeneration plant. Arab. J. Sci. Eng. 2014, 39, 6385–6397. [Google Scholar] [CrossRef]
- Yang, B.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Finite time exergoeconomic performance of a real intercooled regenerated gas turbine cogeneration plant. Part 2: Heat conductance distribution and pressure ratio optimization. Int. J. Low-Carbon Technol. 2014, 9, 262–267. [Google Scholar] [CrossRef]
- Yang, B.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Exergy performance analysis of an irreversible two-stage intercooled regenerative reheated closed Brayton CHP plant. Int. J. Exergy 2014, 14, 459–483. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Thermodynamic analysis for a regenerative gas turbine cycle in coking process. Int. J. Energy Environ. 2014, 5, 701–708. [Google Scholar]
- Wang, J.H.; Chen, L.G.; Ge, Y.L.; Sun, F.R. Power and power density analyzes of an end reversible modified variable-temperature reservoir Brayton cycle with isothermal heat addition. Int. J. Low-Carbon Technol. 2016, 11, 42–53. [Google Scholar]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. “Disc-point” heat and mass transfer constructal optimization for solid-gas reactors based on entropy generation minimization. Energy 2015, 83, 431–437. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Constructal entransy dissipation rate minimization for solid-gas reactors with heat and mass transfer in a disc-shaped body. Int. J. Heat Mass Transf. 2015, 89, 24–32. [Google Scholar] [CrossRef]
- Chen, L.G.; Meng, F.K.; Sun, F.R. Analysis on energy-saving potential of recycling iron and steel industry waste heat based on thermoelectric power generation technology. Res. Iron Steel 2013, 41, 41–43. (In Chinese) [Google Scholar]
- Meng, F.K.; Chen, L.G.; Yang, B.; Sun, F.R. Sintering flue gas waste heat driven thermoelectric power generation model and numerical simulation. J. Eng. Thermophys. 2014, 35, 2323–2328. (In Chinese) [Google Scholar]
- Meng, F.K.; Chen, L.G.; Sun, F.R.; Yang, B. Thermoelectric power generation driven by blast furnace slag flushing water. Energy 2014, 66, 965–972. [Google Scholar] [CrossRef]
- Xiong, B.; Chen, L.G.; Meng, F.K.; Sun, F.R. Modeling and performance analysis of a two-stage thermoelectric energy harvesting system from blast furnace slag water waste heat. Energy 2014, 77, 562–569. [Google Scholar] [CrossRef]
- Xiong, B.; Chen, L.G.; Meng, F.K.; Sun, F.R. Thermodynamic analysis and optimization for a two-stage thermoelectric generator device with cylindrical tubes driven by sintering flue gas heat. Sci. China Technol. Sci. 2016, 46, 293–301. (In Chinese) [Google Scholar]
- Meng, F.K.; Chen, L.G.; Xiong, B.; Sun, F.R. Comprehensive evaluation of waste heat recovery technologies in iron and steel industry. Chin. Metal. 2015, 25, 76–81. (In Chinese) [Google Scholar]
- Meng, F.K.; Chen, L.G.; Xie, Z.H.; Sun, F.R. Energy utilization rationality evaluation of waste heat recovery processes in iron and steel industry. In Proceedings of the Chinese Society of Engineering Thermophysics on Engineering Thermophysics and Energy Utility, Xiamen, China, 27–30 November 2015.
- Helle, H.; Helle, M.; Saxen, H. Optimization of top gas recycling conditions under high oxygen enrichment in the blast furnace. ISIJ Int. 2010, 50, 931–938. [Google Scholar] [CrossRef]
- Shen, X.; Chen, L.G.; Xia, X.J.; Sun, F.R. Iron ores matching analysis and optimization for iron-making system by taking energy consumption, CO2 emission or cost minimization as the objective. Renew. Sustain. Energy Rev. 2016. submitted for publication. [Google Scholar]
- Xia, S.J.; Chen, L.G.; Sun, F.R. Reasonable process route for BF-CC section based on the metallurgical process engineering. Appl. Math. Model. 2016. submitted for publication. [Google Scholar]
- Fruehan, R.J.; Fortini, O.; Paxton, H.W. Theoretical Minimum Energies to Produce Steel for Selected Conditions; Carnegie Mellon University: Pittsburgh, PA, USA, 2000. [Google Scholar]
- Hajidavalloo, E.; Dashti, H. Exergy analysis of steel electric arc furnace. In Proceedings of the 10th Biennial Conference on Engineering Systems Design and Analysis, Istanbul, Turkey, 12–14 July 2010.
- Qiu, X.L. Research and Development of Mathematical Model of Process Energy Consumption and Technology Database for Iron and Steel Production. Master’s Thesis, Shanghai University, Shanghai, China, 2007. [Google Scholar]
- Liu, Z.M. Modelling and Analysis of the Energy Consumption and the CO2 Emission of Iron and Steel Manufactering Process. Master’s Thesis, Naval University of Engineering, Wuhan, China, 2015. [Google Scholar]
- Liu, C.X.; Xie, Z.H.; Sun, F.R.; Chen, L.G. System dynamics analysis on characteristics of iron-flow in sintering process. Appl. Therm. Eng. 2015, 82, 206–211. [Google Scholar] [CrossRef]
- Liu, C.X. Study on Characteristics of Iron-flow in Iron and Steel Production Process Based on System Dynamics. Master’s Thesis, Naval University of Engineering, Wuhan, China, 2013. [Google Scholar]
- Feng, H.J.; Chen, L.G.; Xie, Z.H. Generalized constructal optimization for iron and steel production process. Energy 2016. submitted for publication. [Google Scholar]
- Liu, X. Multi-objective Generalized Constructal Optimizations for Iron and Steel Production Processes. Ph.D. Thesis, Naval University of Engineering, Wuhan, China, 2016. [Google Scholar]
- De Souza, S.A.; de Queiroz Lamas, W. Thermoeconomic and ecological analysis applied to heating industrial process in chemical reactors. Renew. Sustain. Energy Rev. 2014, 29, 96–107. [Google Scholar] [CrossRef]
- Teodoros, L.; Andresen, B. Thermoeconomic optimization of a combined heating and humidification coil for HVAC systems. J. Non-Equilib. Thermodyn. 2016, 41, 237–247. [Google Scholar] [CrossRef]
- Reini, M. Constructal law & thermoeconomics. Int. J. Heat Technol. 2016, 34, S141–S146. [Google Scholar]


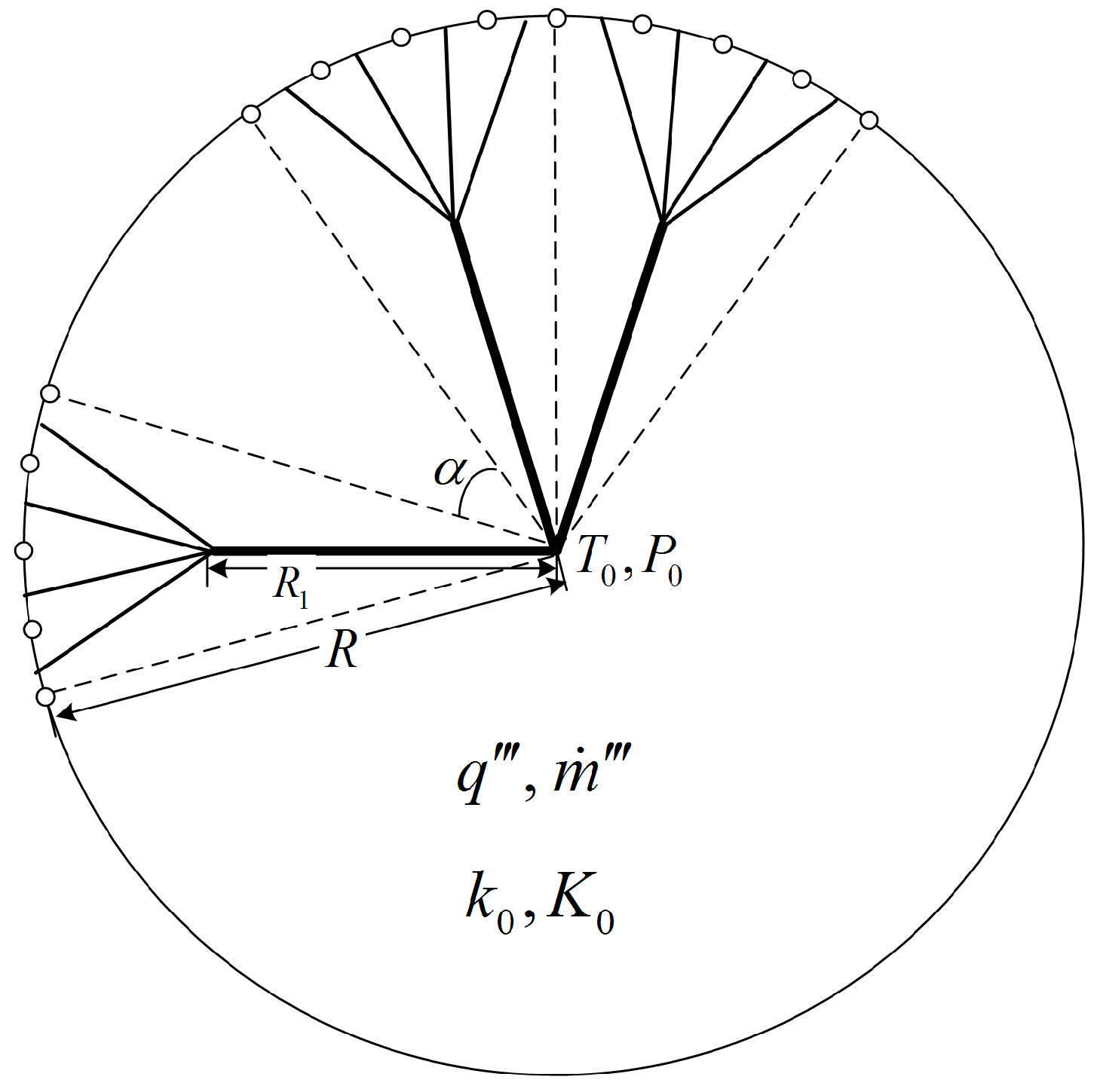
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Feng, H.; Xie, Z. Generalized Thermodynamic Optimization for Iron and Steel Production Processes: Theoretical Exploration and Application Cases. Entropy 2016, 18, 353. https://doi.org/10.3390/e18100353
Chen L, Feng H, Xie Z. Generalized Thermodynamic Optimization for Iron and Steel Production Processes: Theoretical Exploration and Application Cases. Entropy. 2016; 18(10):353. https://doi.org/10.3390/e18100353
Chicago/Turabian StyleChen, Lingen, Huijun Feng, and Zhihui Xie. 2016. "Generalized Thermodynamic Optimization for Iron and Steel Production Processes: Theoretical Exploration and Application Cases" Entropy 18, no. 10: 353. https://doi.org/10.3390/e18100353
APA StyleChen, L., Feng, H., & Xie, Z. (2016). Generalized Thermodynamic Optimization for Iron and Steel Production Processes: Theoretical Exploration and Application Cases. Entropy, 18(10), 353. https://doi.org/10.3390/e18100353






