1. Introduction
With the rapid development of wideband Internet services and the requirement of data processing at a great capacity, the efficient use of the optical signal spectrum and capacity are continuously being enhanced by upgrading the signal modulation format in the optical transport network (OTN) [
1]. On the other hand, the former modulation formats are not eliminated immediately due to the cost saving and holding on to existing services. Consequently, many kinds of modulation formats are used together to make the best of the available resources in the current OTN. Hence, the recognition of optical signal modulation is an urgent need for the OTN multiple signal monitoring. Similarly, it is useful for the realization of cognitive optical networking (CON) [
2], where the net nodes have the capability to blindly demodulate the received data.
During the past few years, there have been many research papers on wireless signal modulation recognition [
3,
4,
5,
6,
7], but few published papers can be found for the optical signal. Eric
et al. [
8] have demonstrated the usage of physical layer characteristics coupled with a digital coherent detection technique for the received optical signal modulation format recognition. However, the advanced modulation formats [
9], such as polarization multiplexed (PM) modulation and quadrature amplitude modulation (QAM), are limited due to the range of the test parameters of the transmitter laser in their work. Khan and his colleagues [
10,
11] adopt an artificial neutral network (ANN), which is trained by an asynchronous amplitude histogram (AAH) or an asynchronous delay-tap plot (ADTP) of the received optical signal, to recognize six optical modulation formats with various data rates. One disadvantage of this approach is that ANN-based classification processes involve the selection of the most suitable ANN, which will cause an increase in computation time and a risk of over-fitting. On the other side, the approach only supports the offline modulation format recognition with stringent impairment limitation. Thus, it is not easy to meet the requirement of real-time recognition in the next generation OTN and CON.
In this paper, a method is proposed for multiple optical modulation format recognition through employing multidimensional asynchronous delay-tap plot entropy (ADTPE) and multiclass SVM. It is noteworthy that the support vector machine (SVM) is a popular machine learning application for data classification with many advantages of small dependence on samples and excellent generalization. The most important aspect is that SVM guarantees that the local optimal solution is exactly the global optimal solution [
12,
13,
14]. Therefore, it can be anticipated that SVM is preferred to ANN for real-time modulation format recognition. The simulations are performed on VPI 9.1 software [
15] to simulate an optical transmission system that consists of six channels with different commonly-used modulation formats and various data rates, including 10-Gb return-to-zero (RZ) on-off keying (OOK), 40-Gb not-return-zero (NRZ) differential phase-shift keying (DPSK), 40-Gb duo-binary optical (DUO), 40-Gb RZ differential quadrature phase-shift keying (DQPSK), 100-Gb polarization-multiplexed (PM) RZ quadrature phase-shift keying (QPSK) and 200-Gb PM-NRZ 16 quadrature amplitude modulation (16QAM) [
16]. Considering transmission impairments, the multidimensional ADTPEs are extracted by varying the size of steps in the wide range of optical signal-to-noise ratios (OSNR), chromatic dispersion (CD) and polarization mode dispersion (PMD), respectively. The results of the simulations show that the overall recognition accuracy can reach 99.05%, while the recognition time can keep within 332 ms for these six commonly-used optical modulation formats. At last, we further prove that the method with flexible expansion can implement real-time recognition of the new advanced optical modulation formats.
2. Multidimensional Asynchronous Delay-Tap Plot Entropy
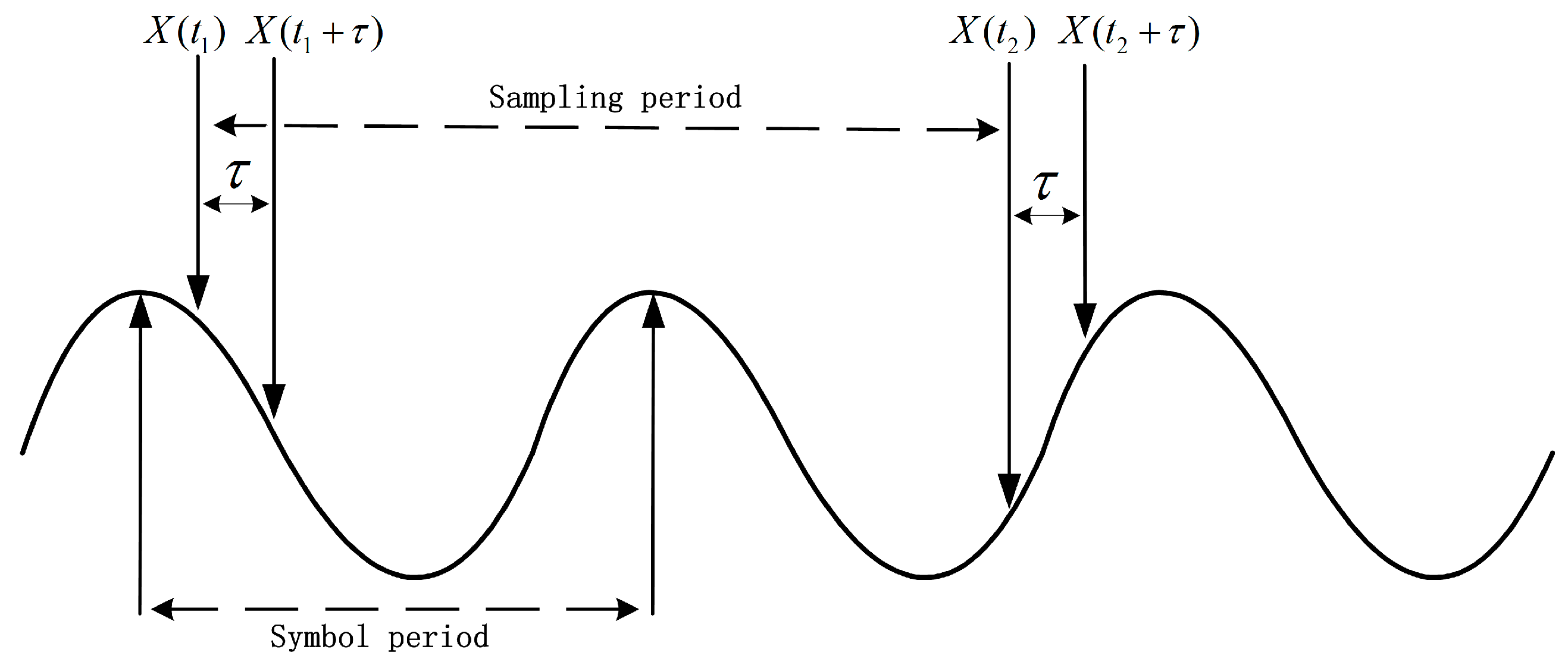
In the principle of ADTP [
11], the detection signal is asynchronously sampled in pairs with a fixed delay time between the two sampling points, as shown in
Figure 1. According to the figure, asynchronous sampling can be defined such that although
and
are sampled at the same time, the locations of two sampling points on the signal waveform are different because of delay-tap
[
17]. Then, asynchronous sampling pairs are utilized to plot a two-dimensional histogram having
bins. Essentially, an ADTP is a joint probability distribution of closely-located samples, which is the reflex of the distribution of the signal waveform’s slopes.
Figure 1.
Asynchronous fixed delay time sampling for asynchronous delay-tap plot.
Figure 1.
Asynchronous fixed delay time sampling for asynchronous delay-tap plot.
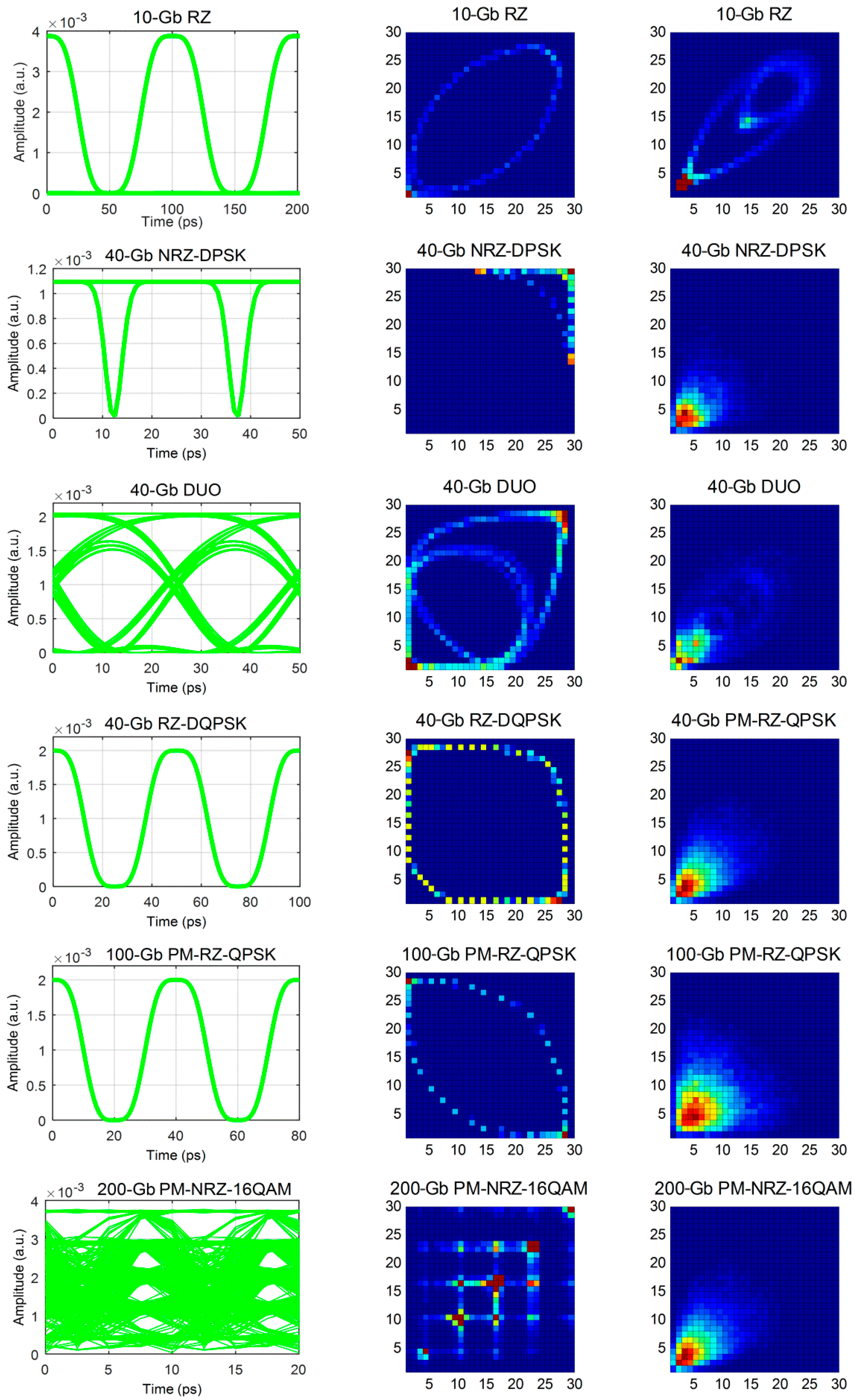
Figure 2 shows eye diagrams and ADTPs for six types of modulation formats under two different detection conditions. Each ADTP is made up of
bins. It can be found that ADTPs corresponding to various formats appear as distinctive portraits when OSNR = 20 dB without CD impairment, whereas they are difficult to distinguish when the received optical signals are impaired by large CD. To tackle this problem, we introduce four types of classical entropies into ADTP as the features for the enhancement of recognition performance and impairment tolerance.
Figure 2.
The left and middle columns show eye diagrams and asynchronous delay-tap plots (ADTPs) when the optical SNR (OSNR) = 20 dB without chromatic dispersion (CD) for 10-Gb return-to-zero (RZ), 40-Gb NRZ-differential phase-shift keying (DPSK), 40-Gb duo-binary optical (DUO), 40-Gb RZ-differential quadrature phase-shift keying (DQPSK), 100-Gb polarization-multiplexed (PM)-RZ-QPSK and 200-Gb PM-NRZ-16 quadrature amplitude modulation (16QAM), while the right column shows ADTPs when OSNR = 20 dB and CD = 500 ps/nm.
Figure 2.
The left and middle columns show eye diagrams and asynchronous delay-tap plots (ADTPs) when the optical SNR (OSNR) = 20 dB without chromatic dispersion (CD) for 10-Gb return-to-zero (RZ), 40-Gb NRZ-differential phase-shift keying (DPSK), 40-Gb duo-binary optical (DUO), 40-Gb RZ-differential quadrature phase-shift keying (DQPSK), 100-Gb polarization-multiplexed (PM)-RZ-QPSK and 200-Gb PM-NRZ-16 quadrature amplitude modulation (16QAM), while the right column shows ADTPs when OSNR = 20 dB and CD = 500 ps/nm.
It has been successfully proven that the value of entropy indicates information-related properties for an accurate representation of a given image [
18,
19,
20]. Usually, the entropy
E must be an additive cost function, such that
. In this paper, an ADTP with pixel intensity is presented as a
matrix. Then, four types of ADTPE are defined as below:
The exponent entropy:
with the convention
and
, where
(
).
is the value of the pixel intensity, which here is obtained from the amplitude of the two-dimensional asynchronous delay-tap histogram.
The singular Shannon entropy:
The singular exponent entropy:
where
(
), and the singular vector
is decomposed from a matrix of ADTPs.
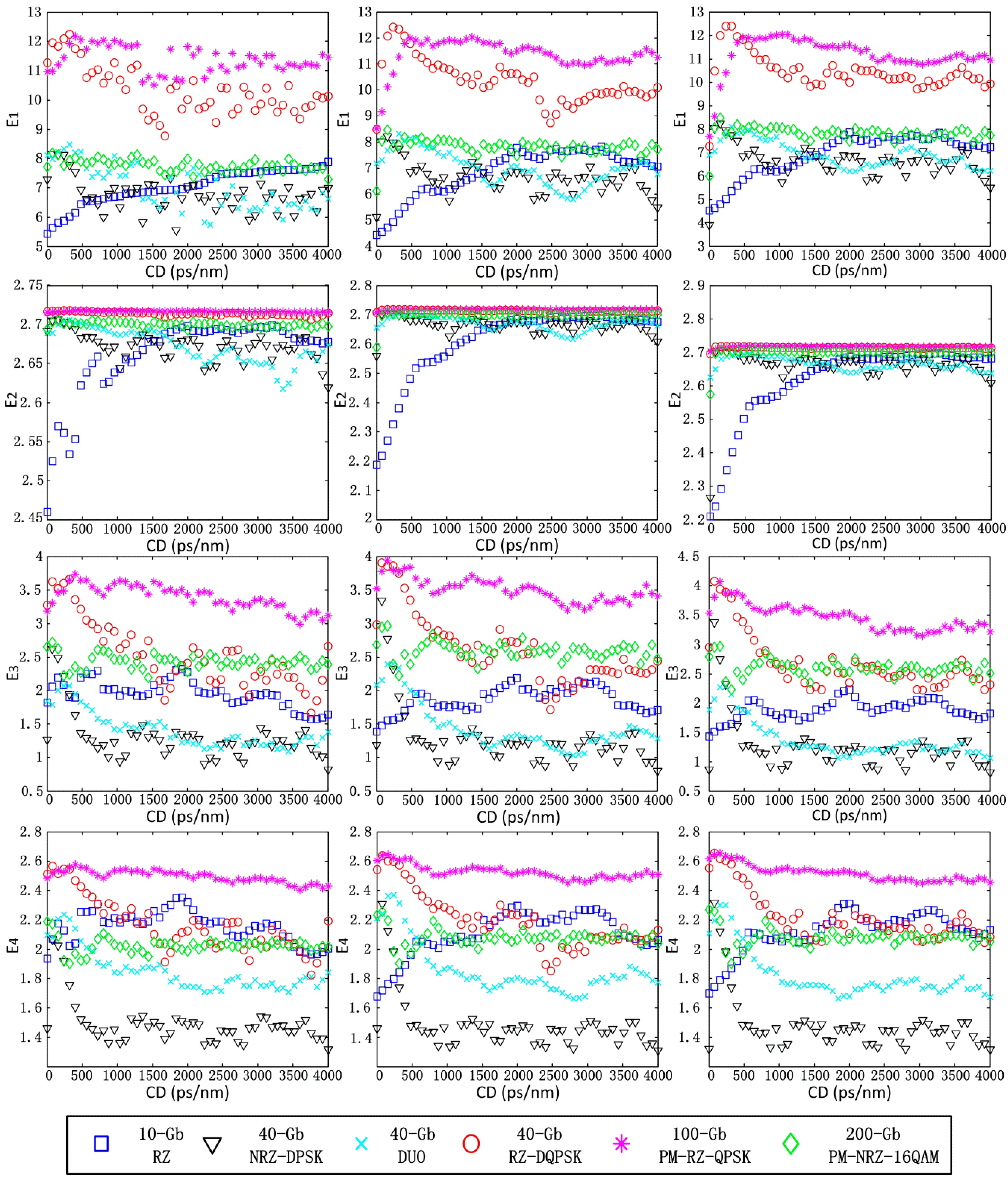
Considering the negative and positive CD influence over the received signal waveform with the same magnitude, but the sign,
Figure 3 only shows that four types of ADTPE corresponding to six different modulation formats change along with the increase of positive CD in the range from 0 to 4000 ps/nm in steps of 80 ps/nm under different OSNR levels. According to the figure, it is worth emphasizing that the four types of ADTPE corresponding to respective modulation formats fluctuate in a certain domain after the CD value increases more than 500 ps/nm. The domains for different modulation formats are distinctive in
Figure 3. For example, the value of
for 100-Gb PM-RZ-QPSK always fluctuates in the range from three to four. This is because the eye diagram of the received signal gradually closes until a steady state with the CD accumulation. Then, the asynchronous delay-tap sampling pairs of the signal waveform concentrate in the bottom left of the ADTP for all six modulation formats, as shown in
Figure 2 (right column), but different modulation formats induce the different distribution of pixel intensities. As a result, ADTPEs corresponding to different modulation formats can be identified. Although there is overlapping in some types of ADTPE for different modulation formats in
Figure 3, we can choose the most proper one for recognition by directly judging the selected ADTPE values in the domain. Additionally, it can be found from the figure that the variations of four types of ADTPE remain almost unaffected while changing the OSNR level from low to high. This implies that the ADTPEs are insensitive to amplified spontaneous emission (ASE) noise. From the above results, it is predicted that four types of ADTPE with large tolerance to transmission impairments can be exploited for the recognition of multiple modulation formats and different data rates.
Figure 3.
Variations of four types of asynchronous delay-tap plot entropy (ADTPE) for six different modulation formats along with positive CD varying from 0 to 4000 ps/nm under different OSNR levels. The ADTPEs in the left, middle and right column correspond to 10-dB, 20-dB and 30-dB OSNRs, respectively.
Figure 3.
Variations of four types of asynchronous delay-tap plot entropy (ADTPE) for six different modulation formats along with positive CD varying from 0 to 4000 ps/nm under different OSNR levels. The ADTPEs in the left, middle and right column correspond to 10-dB, 20-dB and 30-dB OSNRs, respectively.
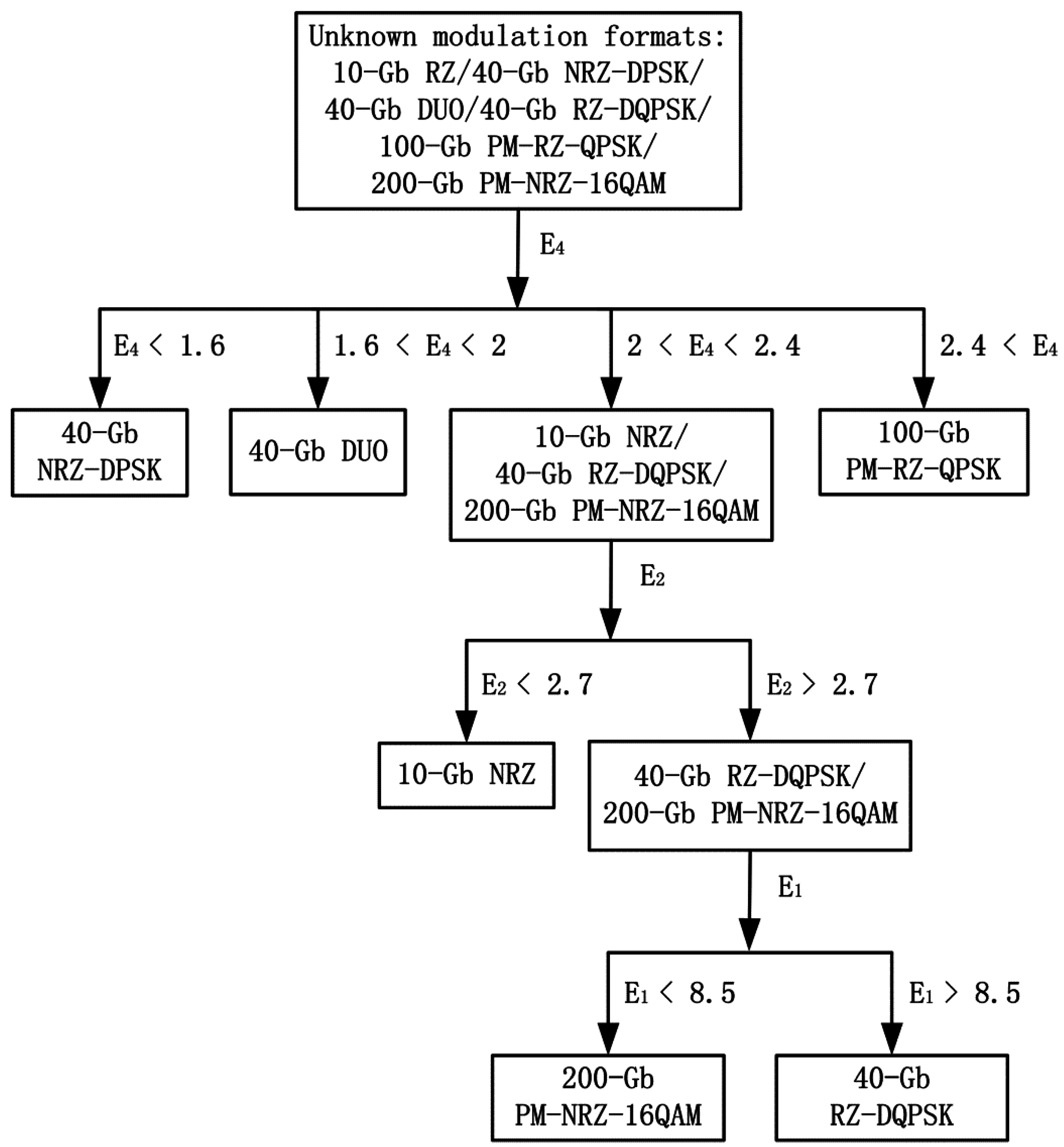
Figure 4 depicts a viable recognition process directly using the multidimensional ADTPE step by step. All six unknown modulation formats are separated into four groups by
(singular exponent entropy): {40-Gb NRZ-DPSK}, {40-Gb DUO}, {100-Gb PM-RZ-QPSK} and {10-Gb NRZ, 40-Gb RZ-DQPSK, 200-Gb PM-NRZ-16QAM}. Then, 10-Gb NRZ in the last group can be directly distinguished by
(exponent entropy), while 40-Gb RZ-DQPSK and 200-Gb PM-NRZ-16QAM can be distinguished by
(Shannon entropy). Additionally, the sequence and the types of selected entropies in
Figure 4 are not fixed. However, it is impractical that every recognition is according to continuously finding the most appropriate type of ADTPE. To solve this problem, four types of ADTPE are used as a four-dimensional eigenvector, and one type of ADTPE represents one dimension of the eigenvector. Each dimension of the eigenvector corresponding to different modulation formats is compared simultaneously and separately in the trained SVM. Modulation formats can be distinguished as long as the difference in any dimension exceeds the threshold, which is determined by the trained SVM. In addition, it is noted that the new modulation format can be recognized only after it is trained by SVM with four types of ADTPE.
Figure 4.
A viable procedure of recognition directly using multidimensional ADTPE.
Figure 4.
A viable procedure of recognition directly using multidimensional ADTPE.
3. Support Vector Machine for Modulation Format Classification
In the basic SVM approach with extraction features [
21,
22,
23,
24,
25], the classifier separates the input feature vectors into two classes based on the maximal distance algorithm using the most powerful classifying functions, which defines the judgment boundary (two-dimensional space) or hyperplane (multidimensional space). The mathematical expression for the two classes of linear SVM classifiers can be defined as below:
where
is the input vector,
represents two classes labels,
is the vector of weight coefficient and b is the correction coefficient. To obtain the maximum distance,
has to be minimized subject to the condition in (5). The linear input vectors cannot be separated in some cases, whereas SVM can map inseparable input vectors into a higher dimensional feature space through a kernel function. The kernel function could be one of many types of functions, such as linear, quadratic, radial basis function (RBF), polynomial and multilayer perceptron (MLP). In this paper, four popularly-used kernel functions, including linear, polynomial, RBF and sigmoid, are selected. Their expressions are given as below [
26,
27,
28]:
The linear kernel function:
The polynomial kernel function:
The sigmoid kernel function:
where
are input vectors,
is the reciprocal of the number of modulation formats (
),
is default zero and
is the order of the polynomial function. It is noted that the polynomial kernel changes to a linear kernel when the order equals one. The comparison of overall recognition accuracies for different kernel functions is given in the following section. For multiclass classification, a multiclass SVM comprising fifteen two-class sub-SVMs is designed. The number of sub-SVMs is calculated through
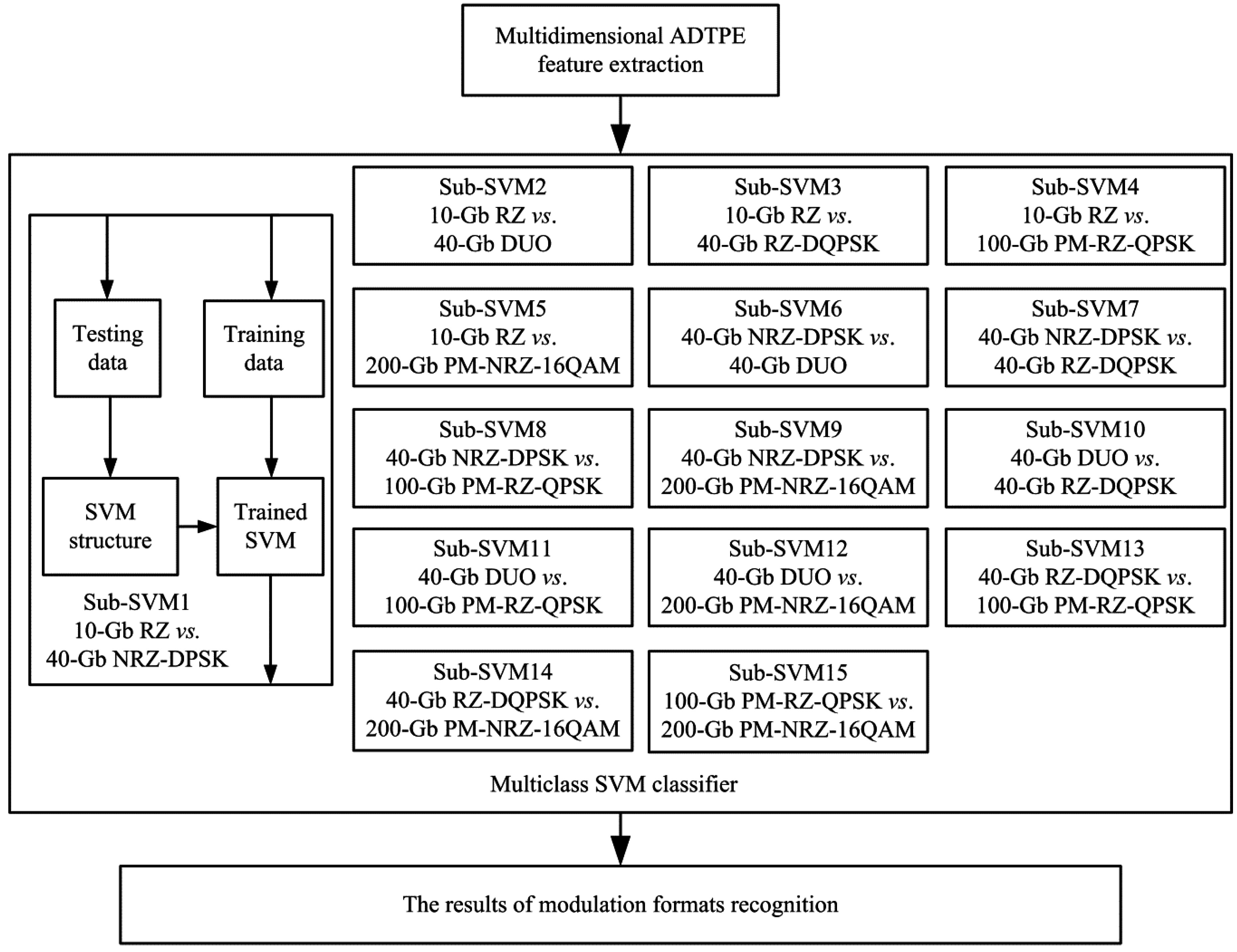
, where n is the number of the modulation format.
Figure 5 depicts the structure of the recognition procedure using multidimensional ADTPE and a multiclass SVM. Multidimensional ADTPEs are divided into two parts: testing database and training database. The training database is utilized to train each sub-SVM, while the testing database is processed as the SVM structure for the trained sub-SVM testing. Each trained sub-SVM separates testing data into two parts, which can be labeled +1 and −1. The accuracy based on the one-
versus-one algorithm is computed as below:
where
is the recognition accuracy,
is the correct part for labeled +1 testing data,
is the correct part for labeled −1 testing data,
is the error part for labeled +1 testing data and
is the error part for labeled −1 testing data. Finally, the recognition results are output from each sub-SVM, and the overall accuracy is calculated by the average value of all 15 sub-SVM results.
Figure 5.
The structure of multiclass SVM comprised of fifteen sub-SVMs based on the one-versus-one algorithm.
Figure 5.
The structure of multiclass SVM comprised of fifteen sub-SVMs based on the one-versus-one algorithm.
4. The Structural Process of the Real-Time Modulation Format Recognition System and Database Formation
In the fiber backbone transmission link, the 10-Gb RZ OOK format still presents in the metropolitan area network, and later, the speed will increase to 40 Gb with RZ-DPSK, DUO or RZ-DQPSK formats; the selection depends on many factors, such as cost and link distance. On the other side, the 100-Gb PM-RZ-QPSK format has been commercially applied in optical fiber international communication, while 200-Gb PM-NRZ-16QAM, which is a potential format for the next generation international backbone network, has proven its feasibility experimentally [
9,
16]. To sum up, these six kinds of modulation formats are selected as a result of wide application. The structure of the real-time recognition system for the proposed method is shown in
Figure 6. Six different modulated optical signals as mentioned before are transmitted in the pseudo-random bit sequence (PRBS) at the same laser power of 1 MW over a single-mode fiber (SMF). The OSNR is regulated in the range of 10 to 30 dB (in steps of 2 dB) by using an erbium-doped fiber amplifier (EDFA) and a variable optical attenuator (VOA). The CD is considered in the range of 0 to 4000 ps/nm (in steps of 100 ps/nm) by using a CD emulator. With the large CD accumulation, the first-order PMD should be considered for our proposed method in practice. Thus, the differential group delay (DGD) is changed in the range of 0 ps to 10 ps (in steps of 1 ps) by using a first-order PMD emulator. The angle
between the principle state-of-polarization (SOP) of the PMD emulator and the different modulation optical SOP is varied randomly. The random value of
corresponding to different PMDs is selected in the range of 0 to 90 degrees. The initial azimuth angle between the two same bit-rate polarization modulation signals is 90 degrees. Then, the optical signal is split by a coupler at static power and filtered by an optical band-pass filter (OBPF) with a bandwidth of 0.8 nm to get the demand channel signal. After that, the filtered optical signal inputs a 600-ps/nm fixed dispersion module (FDM) to ensure the ADTPE with the best available characteristics of identification. Finally, the optical signal is transformed into an electrical signal by a photodiode detector with a 50-GHz bandwidth. The received electrical signal is asynchronously sampled at
GHz/symbol rate, much slower than the symbol rates of all modulation formats.
Figure 6.
The structure of the real-time modulation format recognition system. PMD, polarization mode dispersion; SMF, single mode fiber; EDFA, erbium-doped fiber amplifier; VOA, variable optical attenuator; OBPF, optical band-pass filter; FDM, fixed dispersion module; PIN, positive intrinsic-negative diode; Async., asynchronous.
Figure 6.
The structure of the real-time modulation format recognition system. PMD, polarization mode dispersion; SMF, single mode fiber; EDFA, erbium-doped fiber amplifier; VOA, variable optical attenuator; OBPF, optical band-pass filter; FDM, fixed dispersion module; PIN, positive intrinsic-negative diode; Async., asynchronous.
It is noted that the extraction of multidimensional ADTPE and the training of SVM take up much response time when applying the proposed method to the real-time modulation recognition system. To reduce the response time, a DDR3 SDRAM module is added to cache the sampling data and implement a serial-to-parallel function after the asynchronous delay-tap sampling and analog-to-digital converter (ADC), as shown in
Figure 6. In this system, the received serial data at a bit-rate of
are de-multiplexed into 15 parallel data channels at a bit-rate of
, and hence, the response time can be anticipated to be much shorter than the direct use of serial sampling data for recognition in sequence. This is due to the fact that the extraction of multidimensional ADTPE can be accomplished in 15 parallel sub-modules with 1/15 of the original time, and the training time is the largest one rather than the sum of all sub-SVMs. Each ADTP is formulated by 100,000 pairs (
) with delayed time
ps between
and
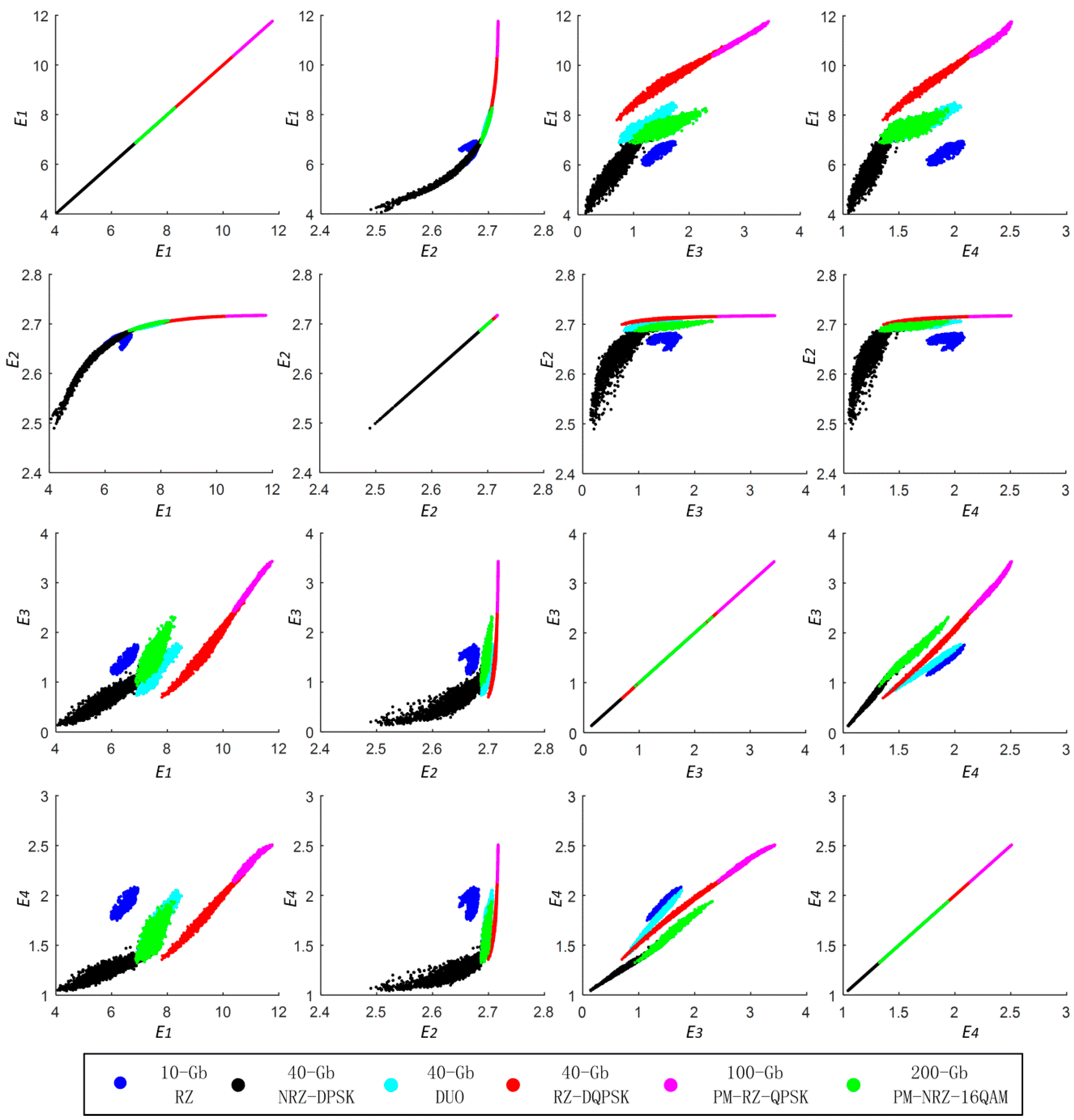
. A four-dimensional eigenvector is comprised of four types of ADTPE only extracted from an ADTP without any other information about the channel impairment. Then, a set of 43,296 eigenvectors to different OSNR, CD, DGD, initial angle and different modulation formats are obtained. The scatter points of four types of ADTPEs for multiple modulation formats are shown in
Figure 7, which is called a “plot matrix” here. From the figure, it is clear that several existing sub-matrices (for example,
-
versus-
) can be used to immediately identify 10-GB NRZ from others formats. For 40-Gb DUO,
-
versus-
is firstly used to divide the six formats into three groups, including {10-Gb NRZ}, {40-Gb RZ-DQPSK, 100-Gb PM-RZ-QPSK} and {40-Gb NRZ-DPSK, 40-Gb DUO, 200-Gb PM-NRZ-16QAM}, and then,
-
versus-
can be utilized to recognize 40-Gb DUO. Therefore, we can also expect good recognition accuracy for these two modulation formats. Nevertheless, there is an overlap more or less between 40-Gb RZ-DQPSK and 100-Gb PM-RZ-QPSK in all sub-matrices, while 40-Gb NRZ-DPSK and 200-Gb PM-NRZ-16QAM are the same situation. Consequently, a few estimation errors are anticipated for these four modulation formats.
Figure 7.
The scatter points of four types of ADTPEs for multiple modulation formats.
Figure 7.
The scatter points of four types of ADTPEs for multiple modulation formats.
5. Results and Discussion
To evaluate the performance of different kernel functions for multiclass SVM, we use the N-fold stratified cross-validation (SCV) technique [
29]. In this study, the obtained eigenvectors are randomly divided into 10 mutually-exclusive subsets with close lengths; after that, 10-1 subsets are used for training and the rest for testing. The procedure repeats 10 times, and each subset is utilized only once for testing. The 10 testing results from the 10 times are then combined together so as to decrease the variance of the estimation of classification performance. The comparison results of the overall recognition accuracy are shown in the following
Table 1. The simulations are implemented on a computer with a center process unit (CPU) of Intel(R) Core(TM) 3.2 Ghz i5-4570 and 8-Gb RAM, under the 64-bit Microsoft Windows operation system. The multiclass SVM is accomplished via MATLAB 2015a (The Mathworks ©, Natick, MA, USA). It can be found from the table that the multiclass SVM using the polynomial kernel function with nine-order or each sub-SVM can achieve the highest overall recognition accuracy.
Table 1.
Comparison of different kernel functions for overall accuracy.
Table 1.
Comparison of different kernel functions for overall accuracy.
| Kernel Function | Overall Accuracy (%) |
|---|
| Polynomial with 1-order (linear function) | 97.87 |
| Polynomial with 2-order | 97.99 |
| Polynomial with 3-order | 98.22 |
| Polynomial with 4-order | 98.36 |
| Polynomial with 5-order | 98.45 |
| Polynomial with 6-order | 98.69 |
| Polynomial with 7-order | 98.82 |
| Polynomial with 8-order | 98.94 |
| Polynomial with 9-order | 99.05 |
| RBF | 97.88 |
| Sigmoid | 97.54 |
To validate the real-time recognition system using the proposed method in a short response time, the recognition time of each sub-SVM is shown in
Table 2. According to the table, the total testing time of all sub-SVMs is 3360 ms, which can be considered as the serial-based multiclass SVM testing time. However, the usage time for the parallel-based multiclass SVM is actually 332 ms, which is the maximum one among all sub-SVMs thanks to the parallel process. It is noteworthy that whatever the recognition system is based on, serial or parallel, the computation time of voting in multiclass SVM can be predicted to be equal. Because the voting scheme can only start after all sub-SVM proceedings finish, therefore we deem that the voting time can be ignored here, so as to highlight the advantage of time saving by the parallel design of the recognition system. As a result, the recognition time in this study only includes sub-SVM testing time. In addition, although the recognition simulations are simulated in the computer, the final goal is that the proposed method can be implemented with DSP for practical applications. Thus, considering the realization in the DSP with hardware language, we should carefully think over the time sequence for each sub-module processing, which corresponds to one-
versus-one sub-SVM in the designed real-time recognition system. Each sub-SVM testing time is advisable to be estimated before the testing results of all sub-SVMs feeding in the voting scheme, and the largest testing time is chosen to ensure all testing results without absence [
30,
31,
32].
Table 2.
Each sub-SVM recognition time in the real-time recognition system.
Table 2.
Each sub-SVM recognition time in the real-time recognition system.
| Sub-SVM | Time (ms) |
|---|
| 10-Gb RZ vs. 40-Gb NRZ-DPSK | 213 |
| 10-Gb RZ vs. 40-Gb DUO | 192 |
| 10-Gb RZ vs. 40-Gb RZ-DQPSK | 196 |
| 10-Gb RZ vs. 100-Gb PM-RZ-QPSK | 251 |
| 10-Gb RZ vs. 200-Gb PM-NRZ-16QAM | 191 |
| 40-Gb NRZ-DPSK vs. 40-Gb DUO | 183 |
| 40-Gb NRZ-DPSK vs. 40-Gb RZ-DQPSK | 203 |
| 40-Gb NRZ-DPSK vs. 100-Gb PM-RZ-QPSK | 189 |
| 40-Gb NRZ-DPSK vs. 200-Gb PM-NRZ-16QAM | 197 |
| 40-Gb DUO vs. 40-Gb RZ-DQPSK | 234 |
| 40-Gb DUO vs. 100-Gb PM-RZ-QPSK | 308 |
| 40-Gb DUO vs. 200-Gb PM-NRZ-16QAM | 250 |
| 40-Gb RZ-DQPSK vs. 100-Gb PM-RZ-QPSK | 187 |
| 40-Gb RZ-DQPSK vs. 200-Gb PM-NRZ-16QAM | 234 |
| 100-Gb PM-RZ-QPSK vs. 200-Gb PM-NRZ-16QAM | 332 |
| Total time: 3360 |
To compare the performance of our proposed method with the ADTP-based method, the sizes of the training and testing subsets are chosen to be 50% and 50% of the overall eigenvector set, respectively, while the size of training, validating and testing datasets are chosen to be 56%, 19% and 25% of the overall dataset in [
11]. Namely, the number of training and testing eigenvectors for each modulation format is 3608 respectively in this study.
Table 3 shows the recognition accuracies of the respective optical modulation format using multidimensional ADTPE and a multiclass SVM when the order of the polynomial kernel function is nine for each of sub-SVM. An overall recognized accuracy of 99.05% is a little lower than the research [
11] claimed 99.95%. However, the enhancement of recognition accuracy can be expected by introducing new ADTPE (e.g., wavelet exponent entropy) into ADTP in order to increase the dimension of the eigenvector, as well as the complexity of computation and response time. Moreover, the stringent 500 ps/nm CD restraint in [
11] has been freed up to 4000 ps/nm, while the range of OSNR is expanded to 10 to 30 dB. Considering the typical coefficient 17 ps/nm/km of single mode fiber (SMF), 4000 ps/nm CD equates to a 235.2-km transmission distance in realty, which can meet the requirements of long-haul optical fiber communication. The reasons are two-fold. First, compared to the ADTP-based feature, multidimensional ADTPE described the physical properties of the modulation format are the counterparts of two distinct and entirely different aspects, which will lead to the precise distinction in the large CD situation. Second, entropy is the statistical feature with the advantage of insensitivity to amplified spontaneous emission (ASE) noise. Meanwhile, it is effective at describing the uncertainty and complexity of a two-dimensional image.
Table 3.
The recognition accuracies of the optical modulation format using multidimensional ADTPE and a multiclass SVM. The overall recognized accuracy is about 99.05%.
Table 3.
The recognition accuracies of the optical modulation format using multidimensional ADTPE and a multiclass SVM. The overall recognized accuracy is about 99.05%.
| Actual Bit-Rate and Modulation Format | Recognized Accuracy of Optical Modulation Format |
|---|
| 10-Gb RZ | 40-Gb NRZ-DPSK | 40-Gb DUO | 40-Gb RZ-DQPSK | 100-Gb PM-RZ-QPSK | 200-Gb PM-NRZ-16QAM |
|---|
| 10-Gb RZ | 100% | - | - | - | - | - |
| 40-Gb NRZ-DPSK | - | 97.67% | - | - | - | 2.73% |
| 40-Gb DUO | - | - | 100% | - | - | - |
| 40-Gb RZ-DQPSK | - | - | - | 99.72% | 0.34% | - |
| 100-Gb PM-RZ-QPSK | - | - | - | 0.27% | 99.66% | - |
| 200-Gb PM-NRZ-16QAM | - | 2.32% | - | - | - | 97.26% |
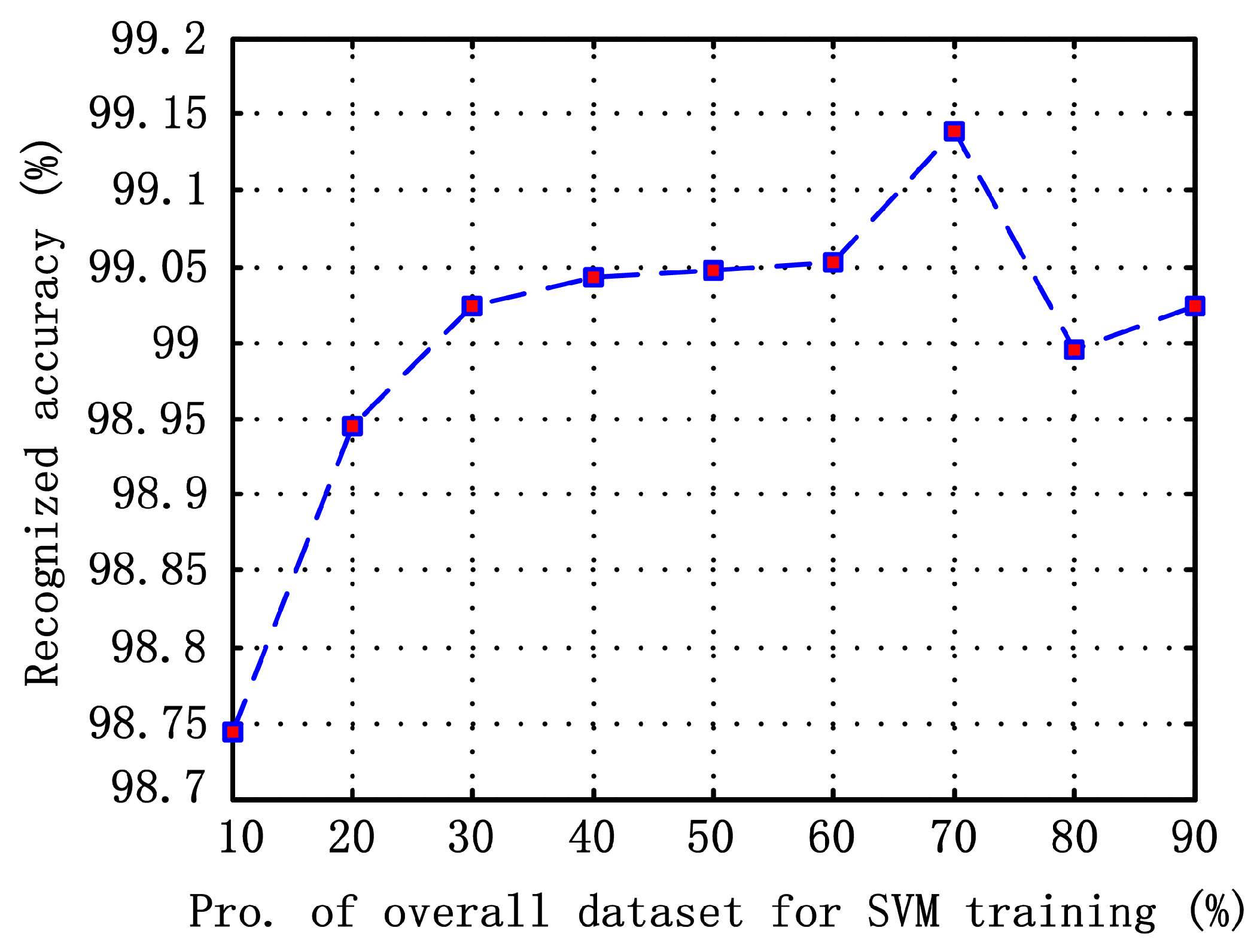
To investigate the influence of the proportion between the training and testing eigenvector set, we change the size of the training eigenvector from 10% to 90% in steps of 10% of the overall eigenvector set. The remaining eigenvectors are used to test, and
Figure 8 shows the overall recognition results. It is evident from the figure that the accuracy rapidly increases in the range from 10% to 70%, whereas the accuracy decreases when the proportion of the training set is greater than 70%. Because the size of the overall eigenvector set is fixed, the increase of the training eigenvectors causes the decrease of the testing eigenvectors. As a result, “over-training” occurs when there is not enough testing data for SVM. On the other hand, it is noted that the recognized accuracy for different proportions fluctuates by a small absolute value of 0.1434%. This proves that the SVM can classify multiclasses with high and steady performance using a small number of samples [
20].
Figure 8.
Recognized accuracy as a function of the proportion of the overall eigenvector for the SVM training.
Figure 8.
Recognized accuracy as a function of the proportion of the overall eigenvector for the SVM training.
Furthermore, we increase the number of unknown modulation formats to prove the flexible expansion of the proposed method. The method is capable of distinguishing the modulation formats with various bit rates, recognition time and correct accuracies, as listed in
Table 4. It can be found that the recognition accuracy of each modulation format is decreased a little, but the overall accuracy can still be up to 98.21%, and the recognition time keeps within 397 ms. Thus, we believe that the proposed method can be compatible with large numbers of emerging new optical modulation formats through simply adding the corresponding sub-SVM module in the digital signal processer (DSP) when it is applied in the real OTN system.
Table 4.
The correct recognition rates and time for more various bit rates and modulation formats using multidimensional ADTPE and SVM.
Table 4.
The correct recognition rates and time for more various bit rates and modulation formats using multidimensional ADTPE and SVM.
| Modulation Formats | Time (ms) | Correct Recognition Accuracy of Modulation Formats (%) |
|---|
| 10-Gb RZ | 264 | 99.69 |
| 20-Gb RZ | 231 | 96.32 |
| 10-Gb NRZ | 259 | 99.84 |
| 40-Gb PM-RZ-QPSK | 172 | 93.99 |
| 100-Gb PM-RZ-QPSK | 164 | 94.69 |
| 40-Gb PM-NRZ-QPSK | 186 | 99.1 |
| 100-Gb PM-NRZ-QPSK | 191 | 98.71 |
| 100-Gb PM-NRZ-QAM | 267 | 99.23 |
| 200-Gb PM-NRZ-QAM | 196 | 98.59 |
| 10-Gb NRZ-DPSK | 165 | 100 |
| 40-Gb NRZ-DPSK | 397 | 99.6 |
| 40-Gb NRZ-QPSK | 161 | 99.15 |
| 40-Gb RZ-QPSK | 193 | 99.37 |
| 20-Gb DUO | 166 | 99.1 |
| 40-Gb DUO | 179 | 95.78 |
| Overall accuracy: 98.21 |