Approximate Analytical Solutions of Time Fractional Whitham–Broer–Kaup Equations by a Residual Power Series Method
Abstract
:1. Introduction
2. Preliminaries
3. Residual Power Series for Time Fractional WBK
4. Applications
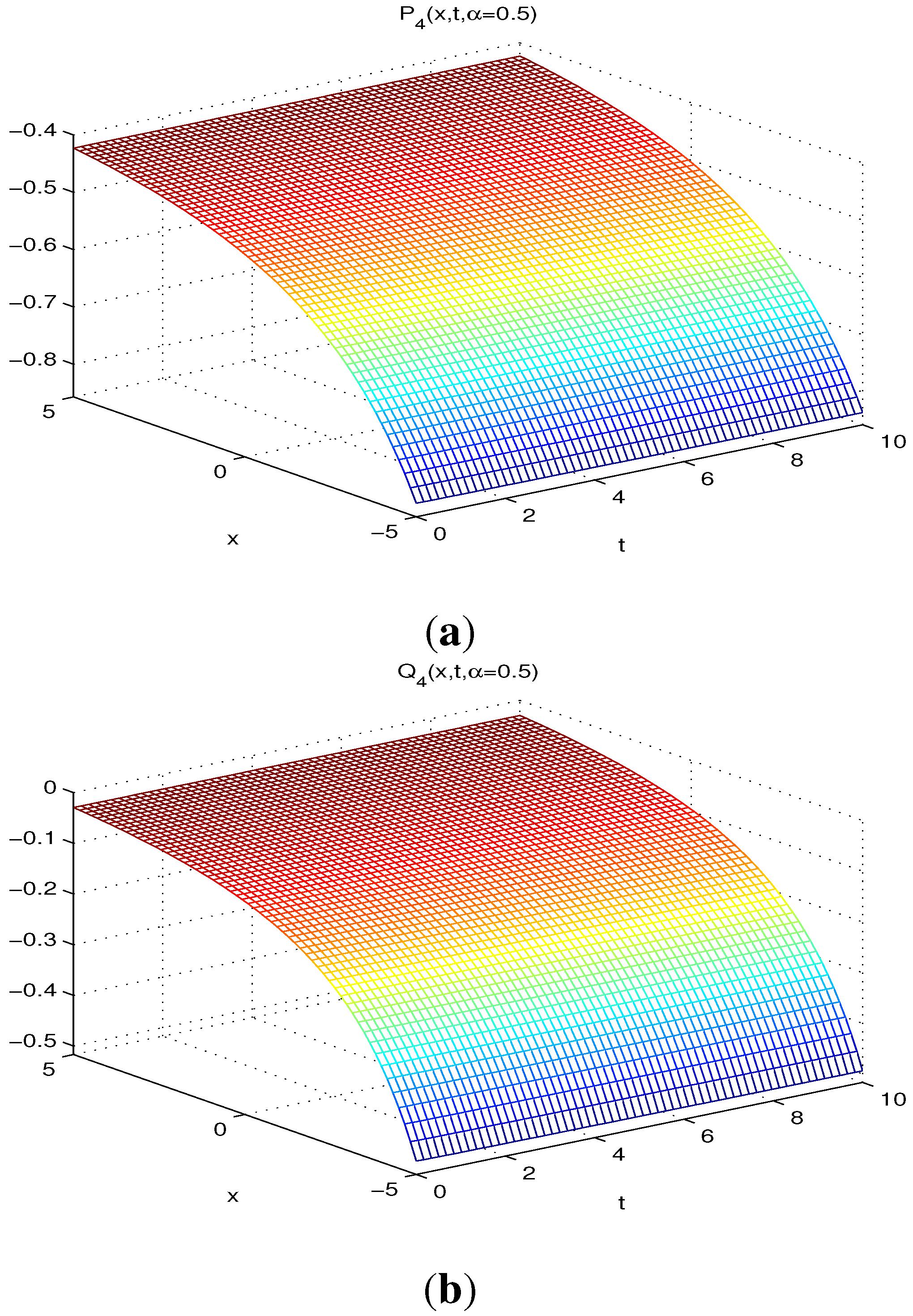
| (0.1,0.1) | 1.04892 | 1.23033 | 1.07078 | 4.69624 | 1.11022 | |
| (0.1,0.3) | 9.64474 | 3.69597 | 3.04565 | 1.26521 | 1.11022 | |
| (0.1,0.5) | 8.88312 | 6.16873 | 4.81303 | 5.85787 | 1.11022 | |
| (0.2,0.1) | 4.25408 | 1.19869 | 1.04388 | 4.49640 | 0 | |
| (0.2,0.3) | 3.91098 | 3.60098 | 2.97260 | 1.21614 | 1.11022 | |
| (0.2,0.5) | 3.60161 | 6.01006 | 4.70138 | 5.63161 | 1.11022 | |
| (0.3,0.1) | 9.71922 | 1.16789 | 1.01776 | 4.34097 | 1.11022 | |
| (0.3,0.3) | 8.93309 | 3.50866 | 2.90150 | 1.16984 | 0 | |
| (0.3,0.5) | 8.22452 | 5.85610 | 4.59590 | 5.41645 | 1.11022 | |
| (0.4,0.1) | 1.75596 | 1.13829 | 9.92418 | 4.18554 | 1.66533 | |
| (0.4,0.3) | 1.61430 | 3.41948 | 2.83229 | 1.12560 | 5.55111 | |
| (0.4,0.5) | 1.48578 | 5.70710 | 4.49118 | 5.21133 | 5.55111 | |
| (0.5,0.1) | 2.79519 | 1.10936 | 9.67808 | 4.00791 | 5.55111 | |
| (0.5,0.3) | 2.56714 | 3.33274 | 2.76492 | 1.08330 | 0 | |
| (0.5,0.5) | 2.36184 | 5.56235 | 4.38895 | 5.01577 | 1.11022 |
| (0.1,0.1) | 6.41419 | 1.10430 | 5.86860 | 6.37142 | 4.29274 | |
| (0.1,0.3) | 5.99783 | 3.31865 | 3.04565 | 1.71937 | 2.55237 | |
| (0.1,0.5) | 5.61507 | 5.54071 | 3.08812 | 7.96097 | 3.23499 | |
| (0.2,0.1) | 1.33181 | 1.07016 | 5.56884 | 6.06144 | 3.78170 | |
| (0.2,0.3) | 1.24441 | 3.21601 | 2.97260 | 1.63713 | 7.59809 | |
| (0.2,0.5) | 1.16416 | 5.36927 | 2.92626 | 7.58015 | 1.12757 | |
| (0.3,0.1) | 2.07641 | 1.03737 | 5.28609 | 5.77301 | 1.53762 | |
| (0.3,0.3) | 1.93852 | 3.11737 | 2.90150 | 1.55956 | 1.34853 | |
| (0.3,0.5) | 1.81209 | 5.20447 | 2.77382 | 7.22117 | 3.19298 | |
| (0.4,0.1) | 2.88100 | 1.00579 | 5.01929 | 5.50600 | 2.06725 | |
| (0.4,0.3) | 2.68724 | 3.02245 | 2.83229 | 1.48644 | 1.95189 | |
| (0.4,0.5) | 2.50985 | 5.04593 | 2.63019 | 6.88241 | 1.72117 | |
| (0.5,0.1) | 3.75193 | 9.75385 | 4.76741 | 5.25135 | 2.76894 | |
| (0.5,0.3) | 3.49617 | 2.93107 | 2.76492 | 1.41738 | 1.32826 | |
| (0.5,0.5) | 3.26239 | 4.89335 | 2.49480 | 6.56265 | 1.22244 |
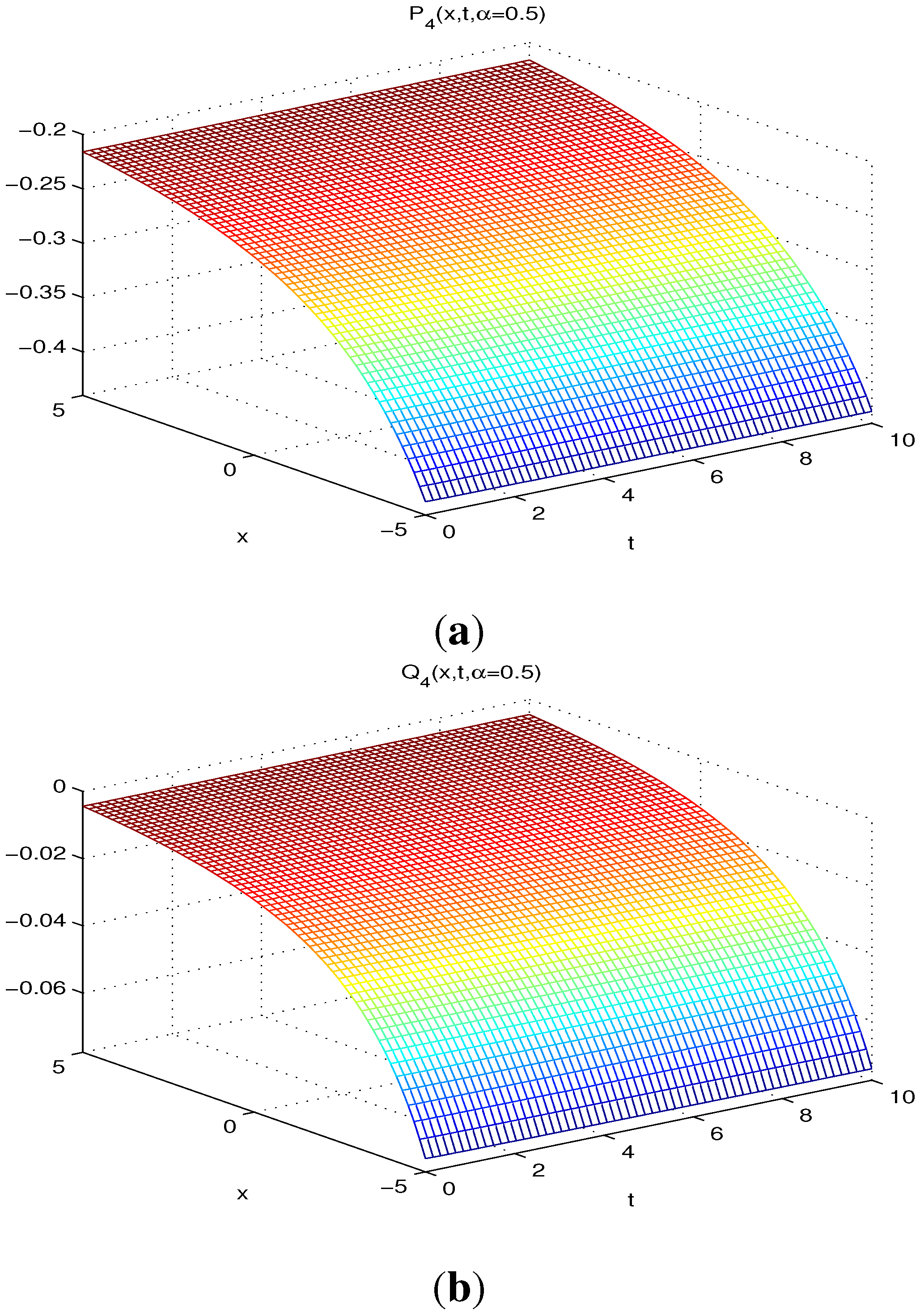
| (0.1,0.1) | 8.16297 | 6.35269 | 6.35267 | 2.42082 | 1.34780 | |
| (0.1,0.3) | 7.64245 | 1.90854 | 1.90854 | 6.53345 | 2.17823 | |
| (0.1,0.5) | 7.16083 | 3.18549 | 3.18548 | 3.02494 | 2.24972 | |
| (0.2,0.1) | 3.26243 | 6.18930 | 6.18931 | 2.32705 | 9.38089 | |
| (0.2,0.3) | 3.05458 | 1.85945 | 1.85945 | 6.28096 | 1.43996 | |
| (0.2,0.5) | 2.86226 | 3.10352 | 3.10352 | 2.90822 | 1.97731 | |
| (0.3,0.1) | 7.33445 | 6.03095 | 6.03098 | 2.24143 | 4.24677 | |
| (0.3,0.3) | 6.86758 | 1.81187 | 1.81187 | 6.04127 | 2.87822 | |
| (0.3,0.5) | 6.43557 | 3.02408 | 3.02408 | 2.79704 | 2.11487 | |
| (0.4,0.1) | 1.30286 | 5.87746 | 5.87749 | 2.16117 | 8.72342 | |
| (0.4,0.3) | 1.22000 | 1.76574 | 1.76574 | 5.81296 | 7.90451 | |
| (0.4,0.5) | 1.14333 | 2.94707 | 2.94708 | 2.69115 | 6.79998 | |
| (0.5,0.1) | 2.03415 | 5.72867 | 5.72865 | 2.07126 | 4.07931 | |
| (0.5,0.3) | 1.90489 | 1.72102 | 1.72102 | 5.59417 | 1.19703 | |
| (0.5,0.5) | 1.78528 | 2.87241 | 2.87240 | 2.59014 | 6.07085 |
| (0.1,0.1) | 5.88676 | 1.65942 | 1.65942 | 9.57047 | 3.17215 | |
| (0.1,0.3) | 5.56914 | 4.98691 | 4.98691 | 2.58365 | 1.08813 | |
| (0.1,0.5) | 5.27169 | 8.32598 | 8.26491 | 1.19628 | 2.73648 | |
| (0.2,0.1) | 1.18213 | 1.60813 | 1.60812 | 9.10730 | 2.42893 | |
| (0.2,0.3) | 1.11833 | 4.83269 | 4.83269 | 2.46008 | 1.39638 | |
| (0.2,0.5) | 1.05858 | 8.06837 | 7.94290 | 1.13906 | 3.50926 | |
| (0.3,0.1) | 1.78041 | 1.55880 | 1.55880 | 8.67709 | 1.18742 | |
| (0.3,0.3) | 1.68429 | 4.68440 | 4.68439 | 2.34354 | 8.35230 | |
| (0.3,0.5) | 1.59428 | 7.82068 | 7.63646 | 1.08512 | 4.22825 | |
| (0.4,0.1) | 2.38356 | 1.51135 | 1.51135 | 8.27463 | 3.41750 | |
| (0.4,0.3) | 2.25483 | 4.54174 | 4.54174 | 2.23366 | 3.80156 | |
| (0.4,0.5) | 2.13430 | 7.58243 | 7.34471 | 1.03421 | 2.18005 | |
| (0.5,0.1) | 2.99162 | 1.46569 | 1.46569 | 7.89473 | 7.77731 | |
| (0.5,0.3) | 2.83001 | 4.40448 | 4.40448 | 2.12988 | 1.82067 | |
| (0.5,0.5) | 2.67868 | 7.35317 | 7.06678 | 9.86164 | 4.18858 |
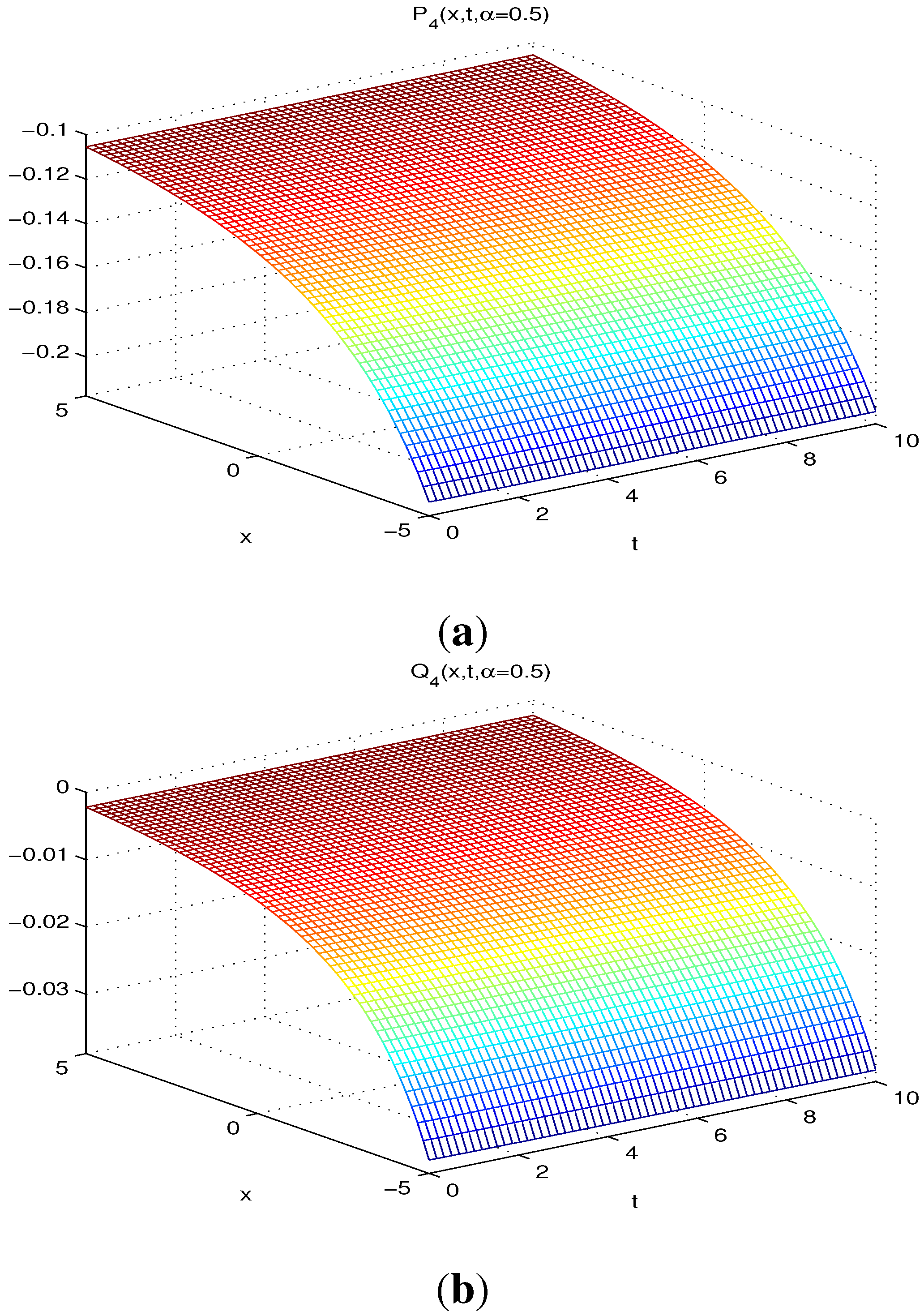
| (0.1,0.1) | 8.02989 | 3.17634 | 3.17634 | 1.21041 | 6.73913 | |
| (0.1,0.3) | 7.38281 | 9.54273 | 9.54269 | 3.26673 | 1.08892 | |
| (0.1,0.5) | 6.79923 | 1.59274 | 1.59274 | 1.51247 | 1.12040 | |
| (0.2,0.1) | 3.23228 | 3.09466 | 3.09465 | 1.16352 | 4.72239 | |
| (0.2,0.3) | 2.97172 | 9.29725 | 9.29723 | 3.14048 | 7.10655 | |
| (0.2,0.5) | 2.73673 | 1.55176 | 1.55176 | 1.45411 | 1.00389 | |
| (0.3,0.1) | 7.32051 | 3.01549 | 3.01549 | 1.12072 | 2.12448 | |
| (0.3,0.3) | 6.73006 | 9.05935 | 9.05932 | 3.02063 | 1.44235 | |
| (0.3,0.5) | 6.19760 | 1.51204 | 1.51204 | 1.39852 | 1.06299 | |
| (0.4,0.1) | 1.31032 | 2.93874 | 2.93874 | 1.08059 | 4.36379 | |
| (0.4,0.3) | 1.20455 | 8.82871 | 8.82870 | 2.90648 | 3.95777 | |
| (0.4,0.5) | 1.10919 | 1.47354 | 1.47354 | 1.34557 | 3.40839 | |
| (0.5,0.1) | 2.06186 | 2.86433 | 2.86432 | 1.03563 | 2.05053 | |
| (0.5,0.3) | 1.89528 | 8.60509 | 8.60506 | 2.79708 | 5.94932 | |
| (0.5,0.5) | 1.74510 | 1.43620 | 1.43620 | 1.29507 | 3.02966 |
| (0.1,0.1) | 4.81902 | 8.29712 | 8.29711 | 4.78523 | 1.58608 | |
| (0.1,0.3) | 4.50818 | 2.49346 | 2.49345 | 1.29182 | 5.43944 | |
| (0.1,0.5) | 4.22221 | 4.16299 | 4.16298 | 5.98141 | 1.36881 | |
| (0.2,0.1) | 9.76644 | 8.04063 | 8.04063 | 4.55365 | 1.21449 | |
| (0.2,0.3) | 9.13502 | 2.41634 | 2.41634 | 1.23004 | 1.68513 | |
| (0.2,0.5) | 8.55426 | 4.03419 | 4.03418 | 5.69530 | 1.75768 | |
| (0.3,0.1) | 1.48482 | 7.79401 | 7.79400 | 4.33854 | 5.93717 | |
| (0.3,0.3) | 1.38858 | 2.34220 | 2.34219 | 1.17177 | 4.17842 | |
| (0.3,0.5) | 1.30009 | 3.91034 | 3.91034 | 5.42558 | 2.11323 | |
| (0.4,0.1) | 2.00705 | 7.55675 | 7.55675 | 4.13732 | 1.70872 | |
| (0.4,0.3) | 1.87661 | 2.27087 | 2.27087 | 1.11683 | 1.89994 | |
| (0.4,0.5) | 1.75670 | 3.79121 | 3.79121 | 5.17105 | 1.08612 | |
| (0.5,0.1) | 2.54396 | 7.32847 | 7.32846 | 3.94736 | 3.88866 | |
| (0.5,0.3) | 2.37815 | 2.20224 | 2.20224 | 1.06494 | 9.10368 | |
| (0.5,0.5) | 2.22578 | 3.67658 | 3.67658 | 4.93082 | 2.09445 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Beyer, H.; Kempfle, S. Definition of physical consistent damping laws with fractional derivatives. Z. Angew. Math. Mech. 1995, 75, 623–635. [Google Scholar] [CrossRef]
- He, J.H. Some applications of nonlinear fractional differential equations and their approximations. Sci. Technol. Soc. 1999, 15, 86–90. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.A.T.; Pinto, C.M.A.; Galhano, A.M.S.F. Fractional dynamics and MDS visualization of earthquake phenomena. Comput. Math. Appl. 2013, 66, 647–658. [Google Scholar] [CrossRef]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
- Prehl, J.; Boldt, F.; Essex, C.; Hoffmann, K.H. Time evolution of relative entropies for anomalous diffusion. Entropy 2013, 15, 2989–3006. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Willy and Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Guo, S.M.; Mei, L.Q.; Li, Y.; Sun, Y.F. The improved fractional sub-equation method and its applications to the space-time fractional differential equations in fluid mechanics. Phys. Lett. A 2012, 376, 407–411. [Google Scholar] [CrossRef]
- Machado, J.A.T. Optimal tuning of fractional controllers using genetic algorithms. Nonlinear Dyn. 2010, 62, 447–452. [Google Scholar]
- Jumarie, G. Path probability of random fractional systems defined by white noises in coarse-grained time applications of fractional entropy. Frac. Differ. Eq. 2011, 1, 45–87. [Google Scholar] [CrossRef]
- Machado, J.A.T. Entropy analysis of integer and fractional dynamical system. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar]
- Prehl, J.; Essex, C.; Hoffmann, K.H. Tsallis relative entropy and anomalous diffusion. Entropy 2012, 14, 701–706. [Google Scholar] [CrossRef]
- Sommacal, L.; Melchior, P.; Dossat, A.; Cabelguen, J.M.; Oustaloup, A.; Ijspeert, A.J. Improvement of the muscle fractional multimodel for low-rate stimulation. Biomed. Signal Process. Control 2007, 2, 226–233. [Google Scholar] [CrossRef]
- Xie, F.; Yan, Z.; Zhang, H.Q. Explicit and exact traveling wave solutions of Whitham–Broer–Kaup shallow water equations. Phys. Lett. A 2001, 285, 76–80. [Google Scholar] [CrossRef]
- EI-Sayed, S.M.; Kaya, D. Exact and numerical traveling wave solutions of Whitham–Broer–Kaup equations. Appl. Math. Comput. 2005, 167, 1339–1349. [Google Scholar] [CrossRef]
- Rafei, M.; Daniali, H. Application of the variational iteration method to the Whitham–Broer–Kaup equations. Comput. Math. Appl. 2007, 54, 1079–1085. [Google Scholar] [CrossRef]
- Haq, S.; Ishaq, M. Solution of coupled Whitham–Broer–Kaup equations using optimal homotopy asymptotic method. Ocean Eng. 2014, 84, 81–88. [Google Scholar] [CrossRef]
- Machado, J.T. Fractional order generalized information. Entropy 2014, 16, 2350–2361. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. A method based on the Jacobi tau approximation for solving multi-term time-space fractional partial differential equations. J. Comput. Phys. 2015, 281, 876–895. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Abdelkawy, M.A. A fully spectral collocation approximation for multi-dimensional fractional Schrodinger equations. J. Comput. Phys. 2015, 294, 462–483. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Doha, E.H.; Ezz-Eldien, S.S.; Abdelkawy, M.A. A numerical technique based on the shifted Legendre polynomials for solving the time-fractional coupled KdV equation. Calcolo 2015. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation. Nonlinear Dyn. 2015, 80, 101–116. [Google Scholar] [CrossRef]
- Bhrawy, A.H. A highly accurate collocation algorithm for 1+1 and 2+1 fractional percolation equations. J. Vib. Control 2015. [Google Scholar] [CrossRef]
- Bhrawy, A.H. An efficient Jacobi pseudospectral approximation for nonlinear complex generalized Zakharov system. Appl. Math. Comput. 2014, 247, 30–46. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Taha, T.M.; Machado, J.A.T. A Review of Operational Matrices and Spectral Techniques for Fractional Calculus. Nonlinear Dyn. 2015, 81, 1023–1052. [Google Scholar] [CrossRef]
- Fu, Z.J.; Chen, W.; Yang, H.T. Boundary particle method for Laplace transformed time fractional diffusion equations. J. Comput. Phys. 2013, 235, 52–66. [Google Scholar] [CrossRef]
- Pang, G.F.; Chen, W.; Fu, Z.J. Space-fractional advection-dispersion equations by the Kansa method. J. Comput. Phys. 2015, 293, 280–296. [Google Scholar] [CrossRef]
- Abu Arqub, O. Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 2013, 5, 31–52. [Google Scholar] [CrossRef]
- EI-Ajou, A.; Abu Arqub, O.; Momani, S. Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: A new iterative algorithm. J. Comput. Phys. 2015, 293, 81–94. [Google Scholar] [CrossRef]
- Alquran, M. Analytical solutions of fractional foam drainage equation by residual power series method. Math. Sci. 2014, 8, 153–160. [Google Scholar] [CrossRef]
- Alquran, M. Analytical solutions of time-fractional two-component evolutionary system of order 2 by residual power series method. J. Appl. Anal. Comput. 2015, 5, 589–599. [Google Scholar]
- Abu Arqub, O.; EI-Ajou, A.; Al Zhour, Z.; Momani, S. Multiple solutions of nonlinear boundary value problems of fractional order: A new analytic iterative technique. Entropy 2014, 16, 471–493. [Google Scholar] [CrossRef]
- Abu Arqub, O.; EI-Ajou, A.; Al Zhour, Z.; Momani, S. New results on fractional power series: Theories and applications. Entropy 2013, 15, 5305–5323. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Chen, X. Approximate Analytical Solutions of Time Fractional Whitham–Broer–Kaup Equations by a Residual Power Series Method. Entropy 2015, 17, 6519-6533. https://doi.org/10.3390/e17096519
Wang L, Chen X. Approximate Analytical Solutions of Time Fractional Whitham–Broer–Kaup Equations by a Residual Power Series Method. Entropy. 2015; 17(9):6519-6533. https://doi.org/10.3390/e17096519
Chicago/Turabian StyleWang, Linjun, and Xumei Chen. 2015. "Approximate Analytical Solutions of Time Fractional Whitham–Broer–Kaup Equations by a Residual Power Series Method" Entropy 17, no. 9: 6519-6533. https://doi.org/10.3390/e17096519
APA StyleWang, L., & Chen, X. (2015). Approximate Analytical Solutions of Time Fractional Whitham–Broer–Kaup Equations by a Residual Power Series Method. Entropy, 17(9), 6519-6533. https://doi.org/10.3390/e17096519





