A Novel Image Encryption Algorithm Based on DNA Encoding and Spatiotemporal Chaos
Abstract
:1. Introduction
2. Related Work
2.1. DNA Coding and Complementary Rule
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| A | 00 | 00 | 01 | 01 | 10 | 10 | 11 | 11 |
| T | 11 | 11 | 10 | 10 | 01 | 01 | 00 | 00 |
| G | 01 | 10 | 00 | 11 | 00 | 11 | 01 | 10 |
| C | 10 | 01 | 11 | 00 | 11 | 00 | 10 | 01 |
2.2. NCA Map
2.3. Spatiotemporal Chaotic System
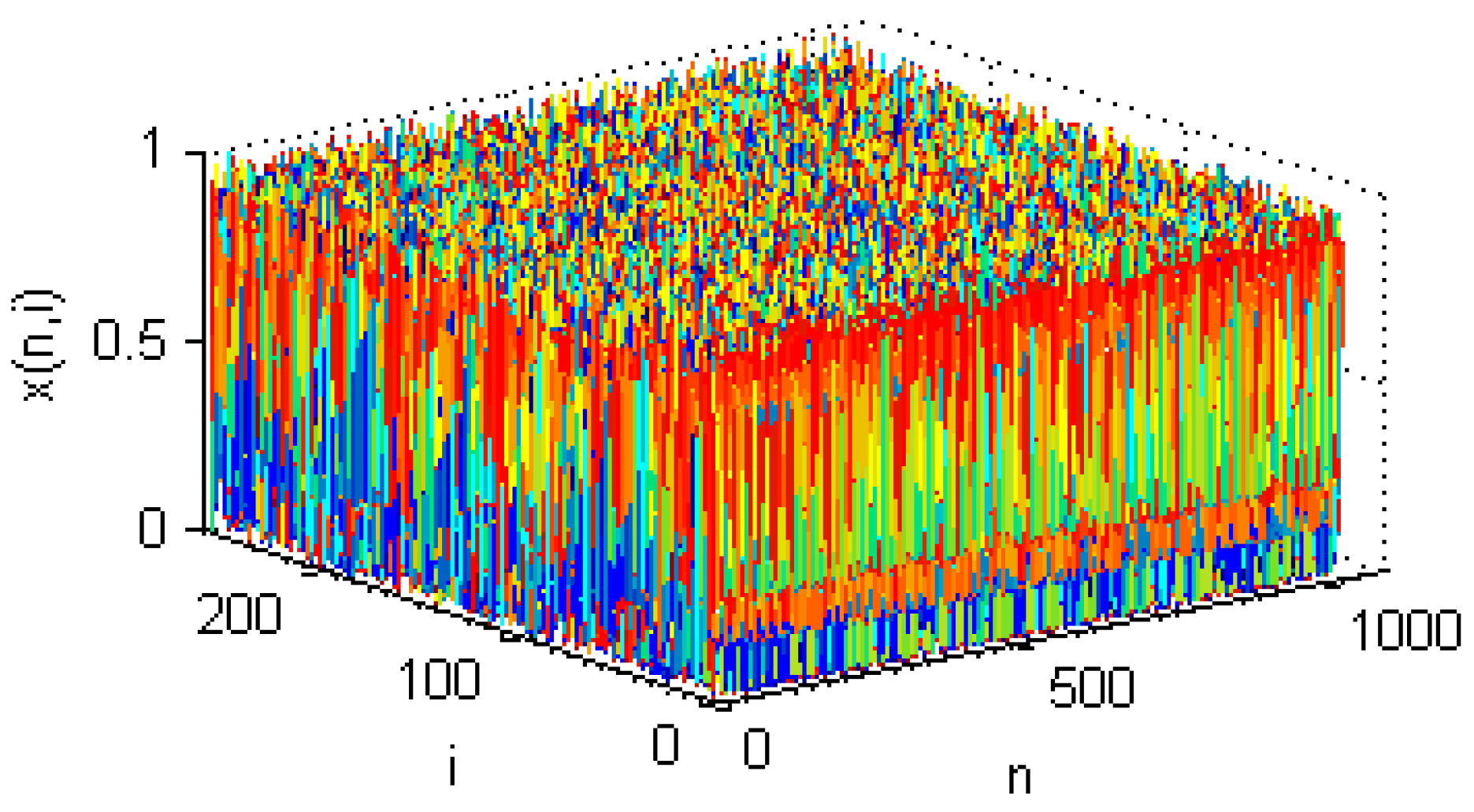
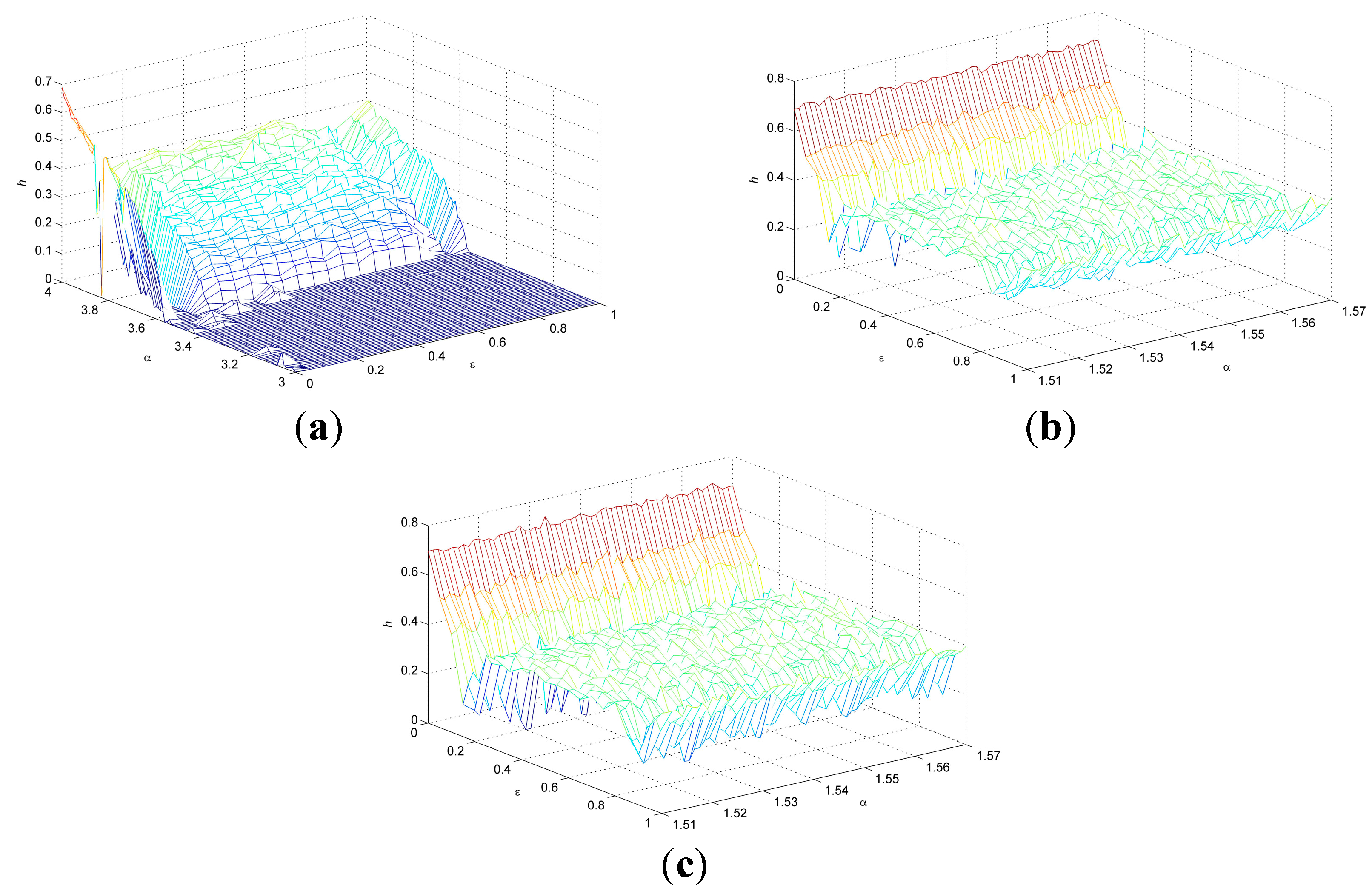
3. Proposed Image Encryption Algorithm
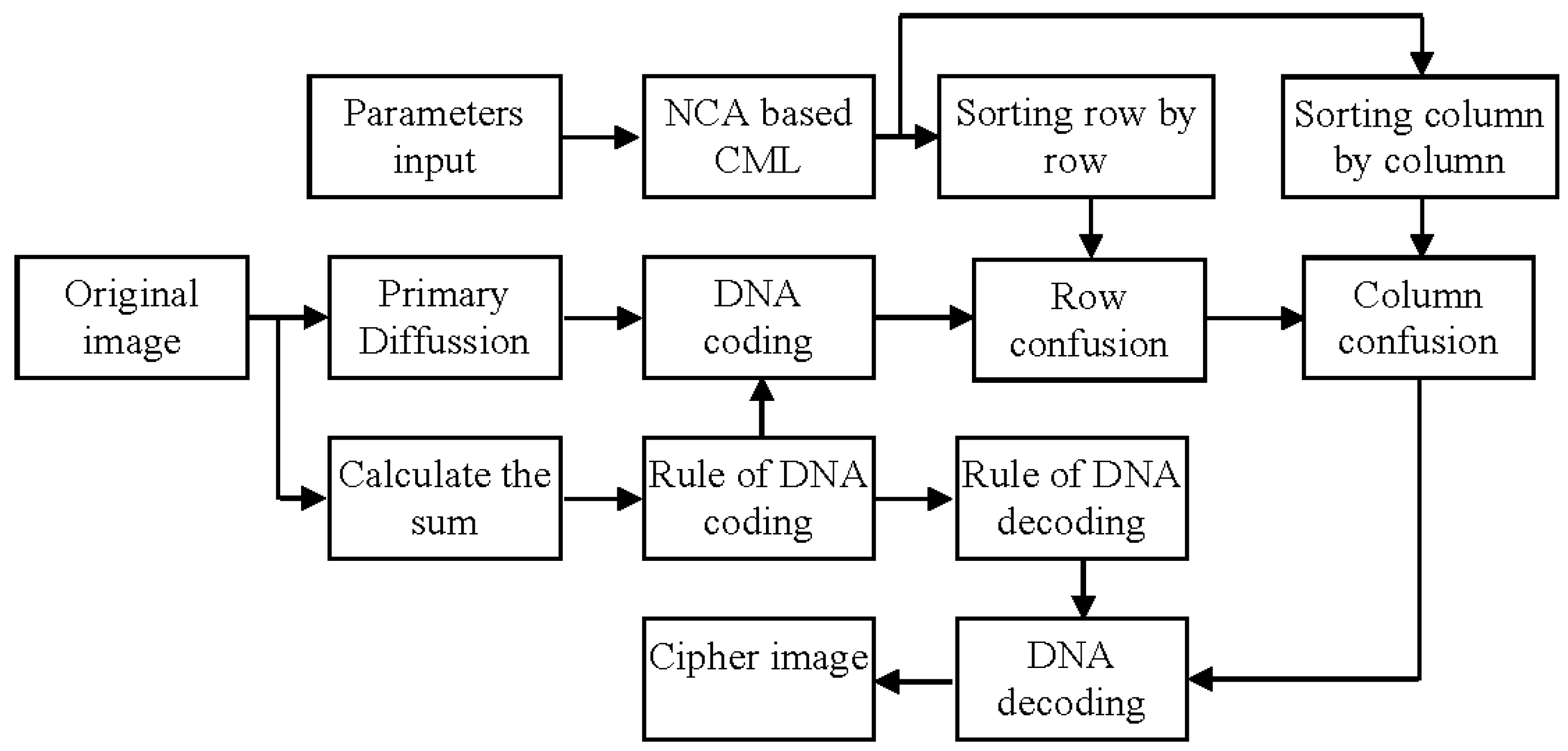
4. Experimental Results

5. Security Analysis
5.1. Gray Histogram Analysis
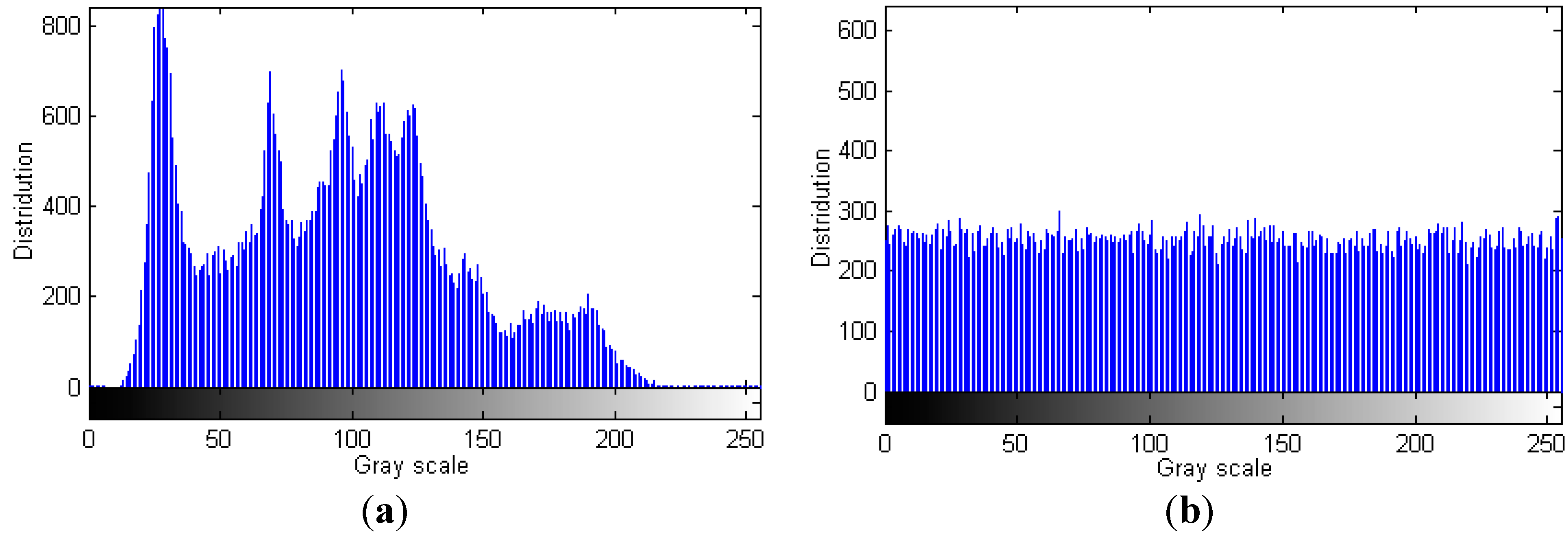
5.2. Information Entropy Analysis
| Lenna | House | Couple | Airplane | Peppers | Camera | Aerial | Boats | |
|---|---|---|---|---|---|---|---|---|
| Entropy | 7.9967 | 7.9933 | 7.9975 | 7.9974 | 7.9973 | 7.9958 | 7.9974 | 7.9973 |
5.3. Correlation Analysis
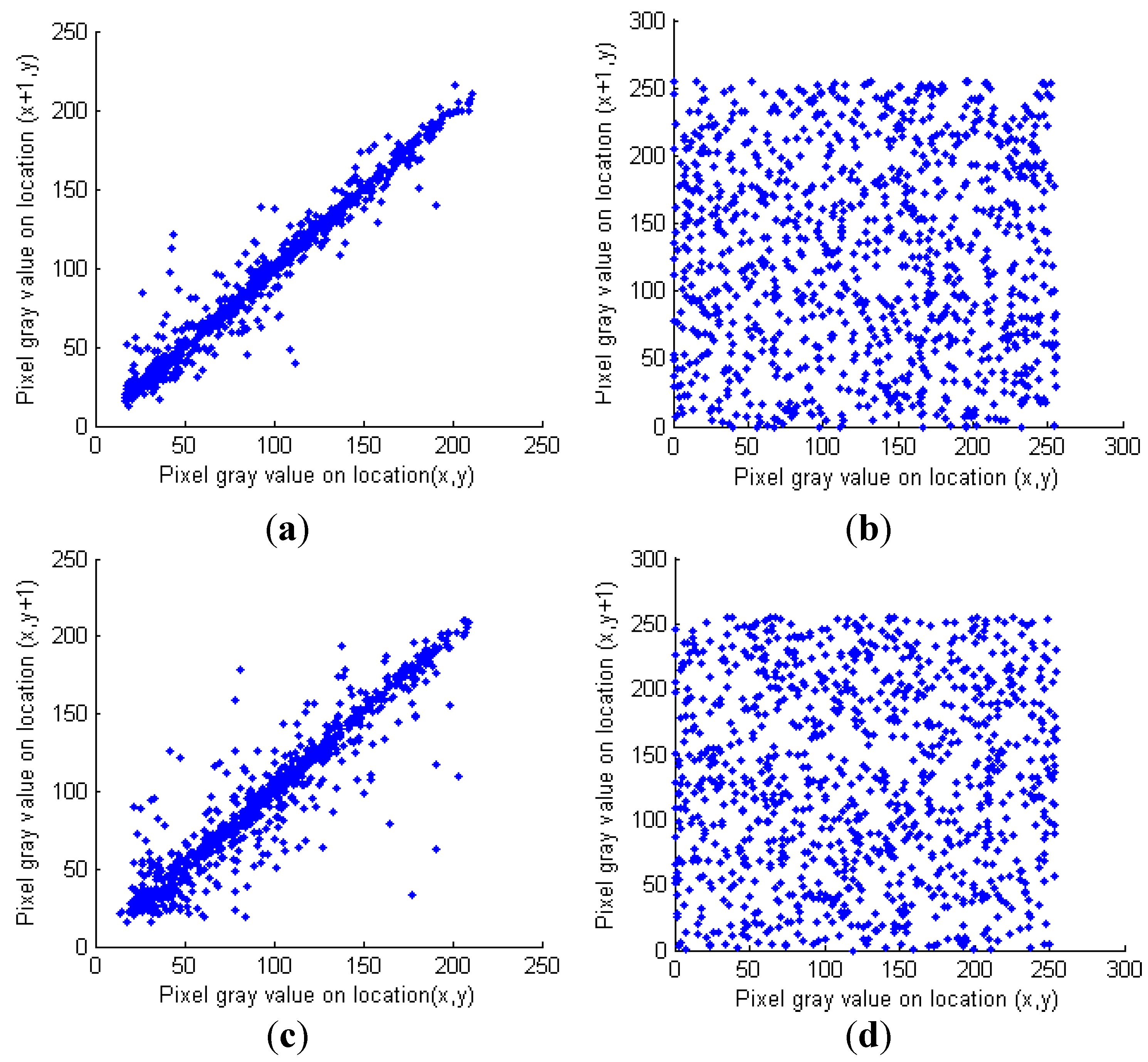
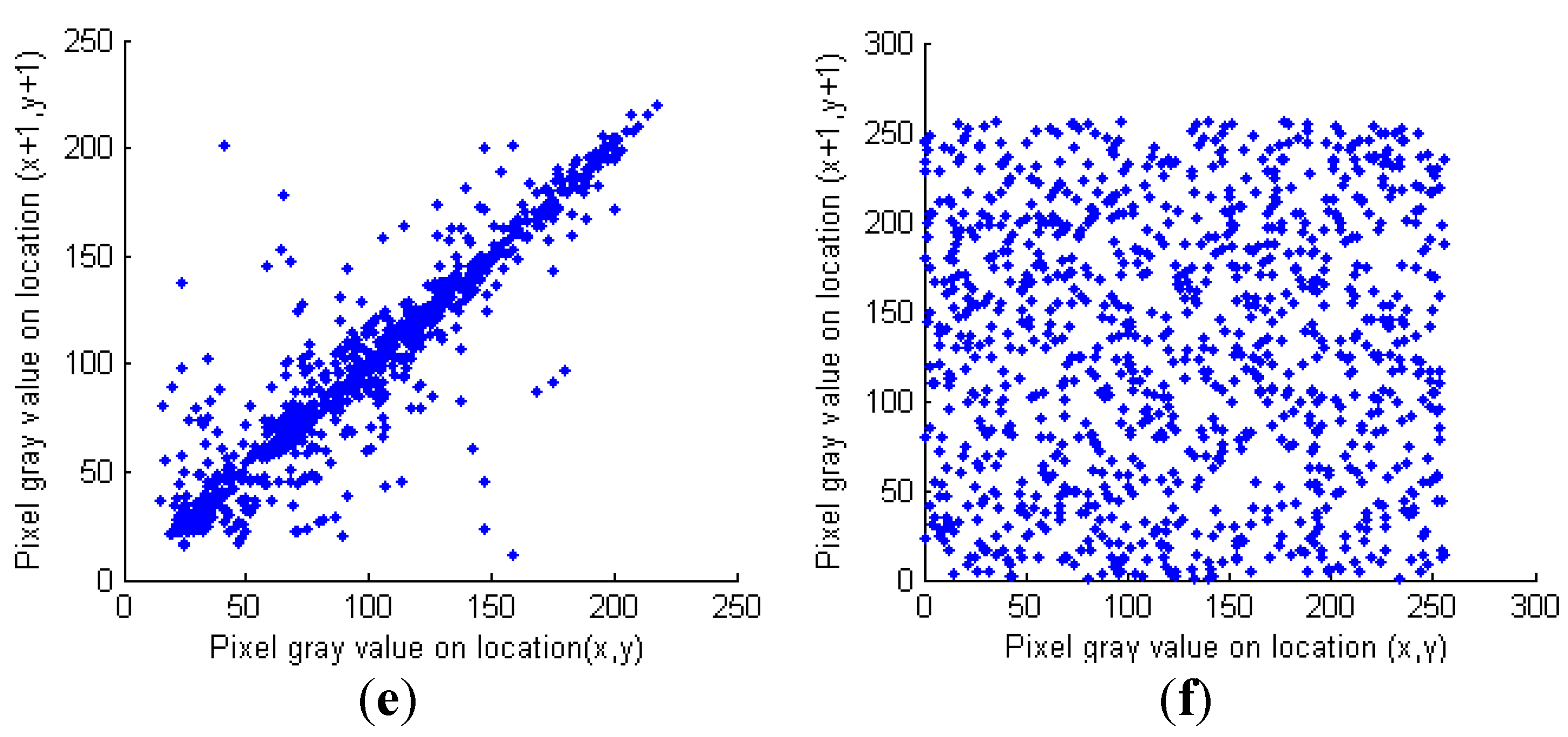
| Horizontal | Vertical | Diagonal | ||
|---|---|---|---|---|
| Lenna | Plain image | 0.9787 | 0.9502 | 0.9332 |
| Cipher image | −0.0021 | −0.0032 | 0.0037 | |
| House | Plain image | 0.9792 | 0.9746 | 0.9602 |
| Cipher image | 0.0616 | −0.0067 | −0.0072 | |
| Couple | Plain image | 0.9402 | 0.9171 | 0.8693 |
| Cipher image | −0.0055 | 0.0317 | −0.0108 | |
| Airplane | Plain image | 0.9269 | 0.9322 | 0.8792 |
| Cipher image | 0.0169 | −0.0212 | 0.0086 | |
| Peppers | Plain image | 0.9757 | 0.9468 | 0.9133 |
| Cipher image | 0.0054 | 0.0060 | −0.0094 | |
| Camera | Plain image | 0.9547 | 0.9308 | 0.8942 |
| Cipher image | −0.0082 | −0.0012 | −0.0179 | |
| Aerial | Plain image | 0.7706 | 0.8096 | 0.6619 |
| Cipher image | −0.0223 | −0.0069 | 0.0285 | |
| Boats | Plain image | 0.9483 | 0.9263 | 0.8883 |
| Cipher image | −0.0201 | 0.0021 | 0.0046 | |
| Correlation | Horizontal | Vertical | Diagonal |
|---|---|---|---|
| Plain Lenna image | 0.9787 | 0.9502 | 0.9332 |
| Ref. [17] | 0.0023 | 0.0036 | 0.0039 |
| Ref. [15] | 0.0004 | 0.0021 | −0.0038 |
| Ref. [11] | 0.0055 | 0.0041 | 0.0002 |
| Proposed algorithm * (Figure 3b) | 0.0007 | 0.0015 | 0.0014 |
5.4. Differential Analysis

| Lenna | House | Couple | Airplane | Peppers | Camera | Aerial | Boats | |
|---|---|---|---|---|---|---|---|---|
| NPCR | 0.9958 | 0.9957 | 0.9958 | 0.9961 | 0.9956 | 0.9961 | 0.9964 | 0.9960 |
| UACI | 0.3349 | 0.3343 | 0.3347 | 0.3327 | 0.3323 | 0.3338 | 0.3342 | 0.3348 |
5.5. Key Sensitivity Analysis

5.6. Key Space Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, S.; Chen, G.; Zheng, X. Chaos-based encryption for digital images and videos. In Multimedia Security Handbook; Furht, B., Kirovski, D., Eds.; CRC Press: Boca Raton, FL, USA, 2004; pp. 133–167. [Google Scholar]
- Mazloom, S.; Eftekhari-Moghadam, A.M. Color image encryption based on coupled nonlinear chaotic map. Chaos Soliton Fract. 2009, 42, 1745–1754. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X. Optical image encryption based on multiple-region plaintext and phase retrieval in three-dimensional space. Opt. Laser Eng. 2013, 51, 128–133. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X. Optical multiple-image authentication based on modified Gerchberg-Saxton algorithm with random sampling. Opt. Commun. 2014, 318, 128–132. [Google Scholar] [CrossRef]
- Matthews, R. On the derivation of a chaotic encryption algorithm. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.K.; Sud, K. Image encryption using chaotic logistic map. Image Vision Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Wang, X.; Teng, L.; Qin, X. A novel colour image encryption algorithm based on chaos. Signal Process. 2012, 92, 1101–1108. [Google Scholar] [CrossRef]
- Liu, H.J.; Wang, X.Y. Color image encryption based on one-time keys and robust chaotic maps. Comput. Math. Appl. 2010, 59, 3320–3327. [Google Scholar] [CrossRef]
- Wang, X.Y.; Lei, Y.; Liu, R.; Kadir, A. A chaotic image encryption algorithm based on perceptron model. Nonlinear Dyn. 2010, 62, 615–621. [Google Scholar] [CrossRef]
- Liu, H.J.; Wang, X.Y. Color image encryption using spatial bit-level permutation and high-dimension chaotic system. Opt. Commun. 2011, 284, 3895–3903. [Google Scholar] [CrossRef]
- Song, C.Y.; Qiao, Y.L.; Zhang, X.Z. An image encryption scheme based on new spatiotemporal chaos. Optik 2013, 124, 3329–3334. [Google Scholar] [CrossRef]
- Adleman, L.M. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. [Google Scholar] [CrossRef] [PubMed]
- Xiao, G.; Lu, M.; Qin, L.; Lai, X. New field of cryptography: DNA cryptography. Chin. Sci. Bull. 2006, 51, 1413–1420. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, L.H.B. Research on DNA cryptography. In Applied Cryptography and Network Security; Sen, J., Ed.; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Liu, H.; Wang, X.; Kadir, A. Image encryption using DNA complementary rule and chaotic maps. Appl. Soft Comput. 2012, 12, 1457–1466. [Google Scholar] [CrossRef]
- Gehani, A.; LaBean, T.H.; Reif, J.H. DNA-Based Cryptography. In DIMACS Series in Discrete Mathematics and Theoretical Computer Science, Proceedings of the 5th DIMACS Workshop on DNA Based Computers V, MIT, Cambridge, MA, USA; Winfree, E., Gifford, D.K., Eds.; 1999; Volume 54, pp. 233–249. [Google Scholar]
- Zhang, Q.; Guo, L.; Wei, X.P. Image encryption using DNA addition combining with chaotic maps. Math. Comput. Model. 2010, 52, 2028–2035. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Liang, S.; Li, D. A new chaotic algorithm for image encryption. Chaos Soliton Fract. 2006, 29, 393–399. [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, M.J. A hyperchaos generated from Lorenz system. Physica A 2008, 387, 3751–3758. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, X.Y. A symmetric image encryption algorithm based on mixed linear-nonlinear coupled map lattice. Inf. Sci. 2014, 273, 329–351. [Google Scholar] [CrossRef]
- Behnia, S.; Akhshani, A.; Ahadpour, S.; Mahmodi, H.; Akhavan, A. A fast chaotic encryption scheme based on piecewise nonlinear chaotic maps. Phys. Lett. A 2007, 366, 391–396. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Fu, C.; Lin, B.; Miao, Y.; Liu, X.; Chen, J. A novel chaos-based bit-level permutation scheme for digital image encryption. Opt. Commun. 2011, 284, 5415–5423. [Google Scholar] [CrossRef]
- Ye, R. A novel chaos-based image encryption scheme with an efficient permutation-diffusion mechanism. Opt. Commun. 2011, 284, 5290–5298. [Google Scholar] [CrossRef]
- Akhavan, A.; Samsudin, A.; Akhshani, A. A symmetric image encryption scheme based on combination of nonlinear chaotic maps. J. Franklin Inst. 2011, 348, 1797–1813. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar]
- IEEE Computer Society. IEEE Standard for Binary Floating-Point Arithmetic. Available online: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=30711 (accessed on 14 October 2015).
- Niu, Y.; Wang, X. An anonymous key agreement protocol based on chaotic maps. Commun. Nonlinear Sci. 2011, 16, 1986–1992. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.; Qiao, Y. A Novel Image Encryption Algorithm Based on DNA Encoding and Spatiotemporal Chaos. Entropy 2015, 17, 6954-6968. https://doi.org/10.3390/e17106954
Song C, Qiao Y. A Novel Image Encryption Algorithm Based on DNA Encoding and Spatiotemporal Chaos. Entropy. 2015; 17(10):6954-6968. https://doi.org/10.3390/e17106954
Chicago/Turabian StyleSong, Chunyan, and Yulong Qiao. 2015. "A Novel Image Encryption Algorithm Based on DNA Encoding and Spatiotemporal Chaos" Entropy 17, no. 10: 6954-6968. https://doi.org/10.3390/e17106954
APA StyleSong, C., & Qiao, Y. (2015). A Novel Image Encryption Algorithm Based on DNA Encoding and Spatiotemporal Chaos. Entropy, 17(10), 6954-6968. https://doi.org/10.3390/e17106954





