Modeling of a Mass-Spring-Damper System by Fractional Derivatives with and without a Singular Kernel

1. Introduction

In recent years, fractional calculus (FC) has been increasingly applied in different fields of science [1,2,3,4,5,6,7]. Physical phenomena related to electromagnetism, propagation of energy in dissipative systems, thermal stresses, models of porous electrodes, relaxation vibrations, viscoelasticity and thermoelasticity are successfully described by fractional differential equations [8,9,10,11,12,13,14,15,16,17,18,19]. FC allows for the investigation of the nonlocal response of mechanical systems, this is the main advantage when compared to the classical calculus. Some research concerning classical mechanics introduces FC, for example in [20], the authors investigated the relationship of the Fourier transform of fractional order to harmonic oscillation. Ryabov in [21] studied the fractional oscillator engaging the Riemann–Liouville fractional derivative. In [22], the authors found the analytical solution of the fractional damped oscillator equation using the Caputo derivative. In [23], Stanislavsky dealt with generalization of the mechanical oscillator using fractional derivatives. Tarasov in [24] considered the oscillator of fractional order as a system with memory; the author suggested independent harmonic oscillators to define the environment. Caputo in [25] studied the classic second order differential equation of the damped oscillator; using this model, the author quantifies the response and the decaying oscillations of a seismograph and applied the FC approach; this model introduces the mathematical memory operator represented by the fractional order derivative in order to model the response curves of more complex instruments realistically. Recently, in [26], the mass-spring and the spring-damper systems without the source term were analyzed; the authors considered fractional time derivatives of the Caputo type. Other applications of FC to mechanical oscillators are given in [27,28,29].

In the literature, a number of definitions of the fractional derivatives have been introduced, namely the Hadamard, Erdelyi–Kober, Riemann–Liouville, Riesz, Weyl, Grünwald–Letnikov, Jumarie and the Caputo representation [30,31,32,33]. A thorough analysis of fractional dynamical systems is necessary to achieve an appropriate definition of the fractional derivative. For example, the Riemann–Liouville definition entails physically unacceptable initial conditions (fractional order initial conditions) [34]; conversely, for the Caputo representation, the initial conditions are expressed in terms of integer-order derivatives having direct physical significance [35]; this definition is mainly used to include memory effects. Recently, Michele Caputo and Mauro Fabrizio in [36] presented a new definition of the fractional derivative without a singular kernel; this derivative possesses very interesting properties, for instance the possibility to describe fluctuations and structures with different scales. Furthermore, this definition allows for the description of mechanical properties related to damage, fatigue and material heterogeneities. The properties of this new fractional derivative are reviewed in detail in the paper [37]. Recently, Abdon Atangana and Badr Alkahtani [38,39] studied the resistor–inductor–capacitor electrical circuit and the Keller–Segel model based on the Caputo–Fabrizio definition; in both works, the authors showed the application of the new proposed fractional derivative without a singular kernel.

In the present work, we use both the Caputo and the Caputo–Fabrizio fractional derivatives to present the analytical and numerical solutions of the mass-spring-damper systems for different source terms; the idea proposed in [26] is applied to construct the fractional differential equations, and our representation preserves the physical units of the physical system for any value by the fractional derivative exponent. The main reason for this work is to investigate and model the displacement of the oscillator in fractal geometries using the fractional derivative with a singular kernel (Caputo approach) and the fractional derivative without a singular kernel (Caputo–Fabrizio approach).

The manuscript is organized as follows: Section 2 explains the basic concepts of the FC; Section 3 presents the analytic solution of the systems and the simulations with different source terms; and the conclusions are given in Section 4.

2. Basic Concepts

The Caputo derivative (CD) is defined as follows [32]:

$${}_0^C{D}_t^{\gamma }f\left(t\right)=\frac{1}{\Gamma (n-\gamma )}{\int }_0^t\frac{f^{\left(n\right)}\left(\alpha \right)}{{(t-\alpha )}^{\gamma -n+1}}d\alpha ,$$

(1)

where $\frac{d^{\phi }}{d{t}^{\phi }}$=${}_a^C{D}_t^{\phi }$ is a CD with respect to t, φϵR is the order of the fractional derivative and $\Gamma (·)$ represents the gamma function.

The Laplace transform of the CD has the form [32]:

$$L{[}_0^C{D}_t^{\gamma }f\left(t\right)]=S^{\gamma }F\left(S\right)-\sum _{k=0}^{m-1}{S}^{\gamma -k-1}{f}^{\left(k\right)}\left(0\right).$$

(2)

Some common Laplace transforms are:

$$\frac{1}{s^{\alpha }+a}=t^{\alpha -1}{E}_{\alpha ,\alpha }(-a{t}^{\alpha })$$

(3)

$$\frac{s^{\alpha }}{s(s^{\alpha }+a)}=E_{\alpha }(-a{t}^{\alpha }),$$

(4)

$$\frac{a}{s(s^{\alpha }+a)}=1-E_{\alpha }(-a{t}^{\alpha }).$$

(5)

The Mittag–Leffler function [40] is defined by a power as:

$$E_a\left(t\right)=\sum _{m=0}^{\infty }\frac{t^m}{\Gamma (am+1)},(a>0),$$

(6)

The Caputo–Fabrizio derivative (CF) is defined as follows [36,37]:

$${}_0^{CF}{\mathcal{D}}_t^{\gamma }f\left(t\right)=\frac{M\left(\gamma \right)}{1-\gamma }{\int }_0^t\dot{f}\left(\alpha \right)exp\left[-\frac{\gamma (t-\alpha )}{1-\gamma }\right]d\alpha ,$$

(7)

where $\frac{d^{\gamma }}{d{t}^{\gamma }}$=${}_0^{CF}{D}_t^{\gamma }$ is a CF with respect to t, $M\left(\gamma \right)$ is a normalization function, such that $M\left(0\right)=M\left(1\right)=1$; in this definition, the derivative of a constant is equal to zero, but unlike the usual Caputo definition (1), the kernel does not have a singularity at $t=\alpha$.

If $n\ge 1$ and $\gamma \in [0,1]$, the CF fractional derivative, ${}_0^{CF}{\mathcal{D}}_t^{(\gamma +n)}f\left(t\right)$, of order $(n+\gamma )$ is defined by:

$${}_0^{CF}{\mathcal{D}}_t^{(\gamma +n)}f\left(t\right){=}_0^{CF}{\mathcal{D}}_t^{\left(\gamma \right)}{(}_0^{CF}{\mathcal{D}}_t^{\left(n\right)}f\left(t\right)).$$

(8)

The Laplace transform of (7) is defined as follows [36,37]:

$$\begin{array}{ccc}\hfill L{[}_0^{CF}{\mathcal{D}}_t^{(\gamma +n)}f\left(t\right)]& =& \frac{1}{1-\gamma }L\left[f^{(\gamma +n)}t\right]L\left[exp\left(-\frac{\gamma }{1-\gamma }t\right)\right]\hfill \end{array}$$

(9)

$$\begin{array}{ccc}& =& \frac{s^{n+1}L\left[f\left(t\right)\right]-s^{n}f\left(0\right)-s^{n-1}{f}^{\prime }\left(0\right)\dots -f^{\left(n\right)}\left(0\right)}{s+\gamma (1-s)},\hfill \end{array}$$

(10)

for this representation in the time domain, it is suitable to use the Laplace transform [36,37].

From this expression, we have:

$$L{[}_0^{CF}{\mathcal{D}}_t^{\gamma }f\left(t\right)]=\frac{sL\left[f\right(t\left)\right]-f\left(0\right)}{s+\gamma (1-s)},n=0,$$

(11)

$$L{[}_0^{CF}{\mathcal{D}}_t^{(\gamma +1)}f\left(t\right)]=\frac{s^{2}L\left[f\left(t\right)\right]-sf\left(0\right)-\dot{f}\left(0\right)}{s+\gamma (1-s)},n=1.$$

(12)

3. Mass-Spring-Damper System

According to [26], to be consistent with the dimensionality of the physical equation, an auxiliary parameter σ is introduced into the fractional temporal operator:

$$\frac{d}{dt}\to \frac{1}{{\sigma }^{1-\gamma }}·\frac{d^{\gamma }}{d{t}^{\gamma }},m-1<\gamma \le m,m\in M=1,2,3,\dots$$

(13)

and:

$$\frac{d^2}{d{t}^2}\to \frac{1}{{\sigma }^{2(1-\gamma )}}·\frac{d^{2\gamma }}{d{t}^{2\gamma }},m-1<\gamma \le m,m\in M=1,2,3,\dots$$

(14)

where γ represents the order of the fractional temporal operator and σ has the dimension of seconds. The auxiliary parameter σ is associated with the temporal components in the system (these components change the time constant of the system) [41]; for the case $\gamma =1$, Expressions (13) and (14) become ordinary temporal operators. Following this idea, the equation of the mass-spring-damper system represented in Figure 1 is given by:

$$\frac{m}{{\sigma }^{2(1-\gamma )}}{}_0^C{D}_t^{2\gamma }x\left(t\right)+\frac{\beta }{{\sigma }^{1-\gamma }}{}_0^C{D}_t^{\gamma }x\left(t\right)+kx\left(t\right)=F\left(t\right),0<\gamma \le 1,$$

(15)

and for the CF, we have:

$$\frac{m}{{\sigma }^{2(1-\gamma )}}{}_0^{CF}{\mathcal{D}}_t^{2\gamma }x\left(t\right)+\frac{\beta }{{\sigma }^{1-\gamma }}{}_0^{CF}{\mathcal{D}}_t^{\gamma }x\left(t\right)+kx\left(t\right)=F\left(t\right),0<\gamma \le 1,$$

(16)

where the mass is m, the damping coefficient is β, the spring constant is k and $F\left(t\right)$ represents the forcing function.

Figure 1. Mass-spring-damper system.

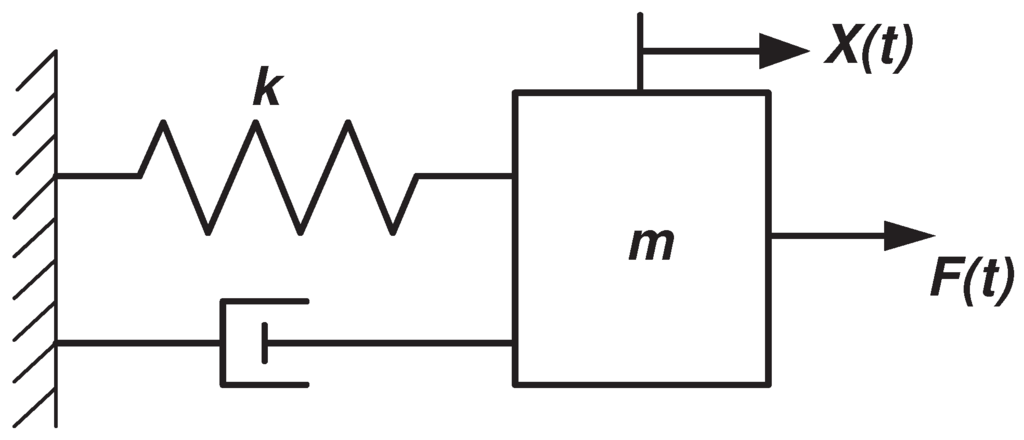
Figure 1. Mass-spring-damper system.

From Equations (15) and (16), we derive the particular cases:

• Mass-spring system, $\beta =0$

  $${}_0^C{D}_t^{2\gamma }x\left(t\right)+\frac{k}{m}{\sigma }^{2(1-\gamma )}x\left(t\right)=\frac{F\left(t\right)}{m}{\sigma }^{2(1-\gamma )},0<\gamma \le 1,$$

  (17)

  and:

  $${}_0^{CF}{\mathcal{D}}_t^{2\gamma }x\left(t\right)+\frac{k}{m}{\sigma }^{2(1-\gamma )}x\left(t\right)=\frac{F\left(t\right)}{m}{\sigma }^{2(1-\gamma )},0<\gamma \le 1.$$

  (18)
• Damper-spring system, $m=0$:

  $${}_0^C{D}_t^{\gamma }x\left(t\right)+\frac{k}{\beta }{\sigma }^{1-\gamma }x\left(t\right)=\frac{F\left(t\right)}{\beta }{\sigma }^{1-\gamma },0<\gamma \le 1,$$

  (19)

  and:

  $${}_0^{CF}{\mathcal{D}}_t^{\gamma }x\left(t\right)+\frac{k}{\beta }{\sigma }^{1-\gamma }x\left(t\right)=\frac{F\left(t\right)}{\beta }{\sigma }^{1-\gamma },0<\gamma \le 1.$$

  (20)

Now, we obtain the analytic and numerical solutions of Equations (15)–(16) corresponding to the particular Cases 1 and 2 for different source terms.

3.1. Mass-Spring System

Case 1: Consider a constant source, $F\left(t\right)=f_0$, $x\left(0\right)=x_0$, $(x_0>0)$, $\dot{x}\left(0\right)=0$; Equation (17) may be written as follows:

$${}_0^C{D}_t^{2\gamma }x\left(t\right)=\frac{{\eta }^2}{k}{f}_0-{\eta }^{2}x\left(t\right),$$

(21)

where:

$${\eta }^2=\frac{k{\sigma }^{2(1-\gamma )}}{m}={\eta }_0^2·{\sigma }^{2(1-\gamma )},$$

(22)

is the fractional angular frequency and ${\eta }_0^2=\frac{k}{m}$ is the frequency in the classical case.

The solution of (21) is:

$$x\left(t\right)=(x_0-\frac{f_0}{k})·E_{2\gamma }\left\{-{\eta }^2{t}^{2\gamma }\right\}+\frac{f_0}{k},$$

(23)

where $E_{2\gamma }$ is given by (6).

Concerning the classical case, from (22), we have ${\eta }^2={\eta }_0^2=\frac{k}{m}$; then, the solution of Equation (21) is:

$$x\left(t\right)=(x_0-\frac{f_0}{k})·\cos \left({\eta }_{0}t\right)+\frac{f_0}{k},$$

(24)

In this case, a physical relationship exists between Equation (17), the order γ and σ:

$$\gamma =\frac{k}{m}\sigma .$$

(25)

For Expression (25), the solution (23) is given by:

$$x\left(t\right)=(x_0-\frac{f_0}{k})·E_{2\gamma }\left\{-{\gamma }^{2(1-\gamma )}{t}^{2\gamma }\right\}+\frac{f_0}{k}.$$

(26)

The plots for different values of the fractional order γ are shown in Figure 2.

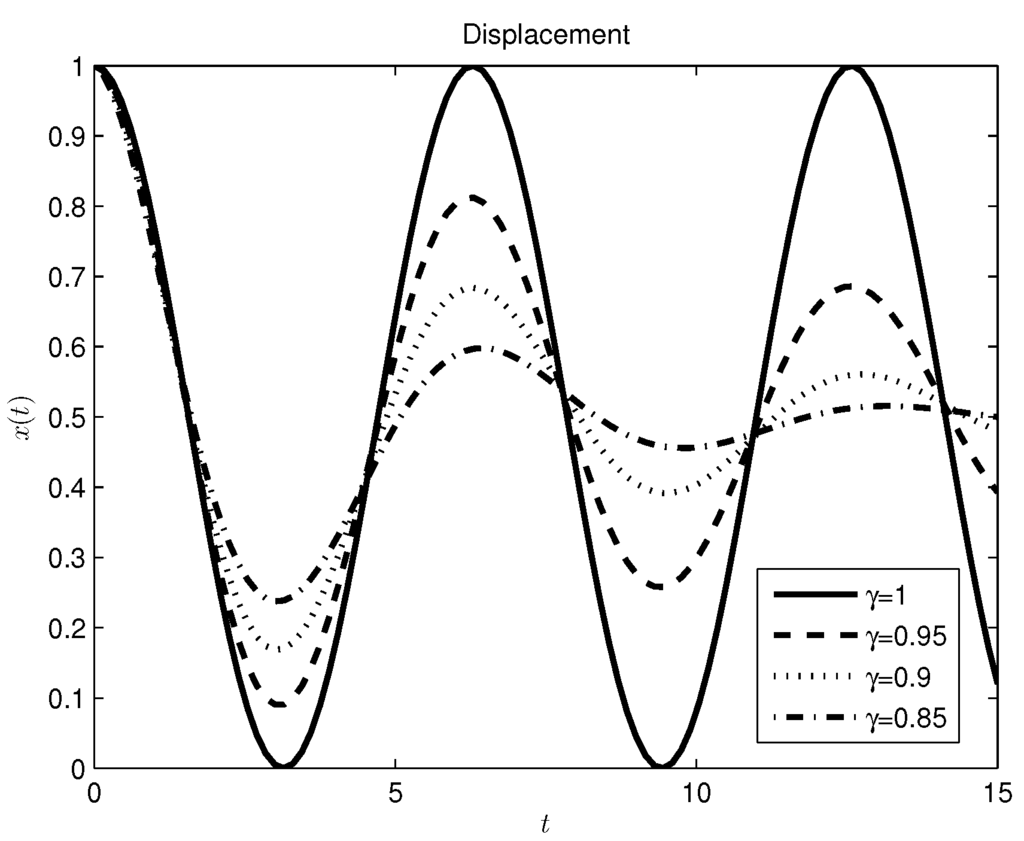
Figure 2. Mass-spring system with a constant source, Caputo derivative approach.

Figure 2. Mass-spring system with a constant source, Caputo derivative approach.

For Equation (18), we have:

$${}_0^{CF}{\mathcal{D}}_t^{2\gamma }x\left(t\right)=\frac{{\eta }^2}{k}{f}_0-{\eta }^{2}x\left(t\right),$$

(27)

the Laplace transform (10) of (27) yields:

$$x\left(s\right)=x_0·\frac{s^{2\gamma -1}}{s^2+{\eta }^2[s+\gamma (1-s)]}+\frac{{\eta }^2{f}_0}{k}\left(\frac{s+\gamma (1-s)}{s(s^2+{\eta }^2[s+\gamma (1-s)])}\right),$$

(28)

applying the numerical inverse Laplace transform algorithm [42] to (28), we obtain the time response. The plots for different values of the fractional order γ are shown in Figure 3.

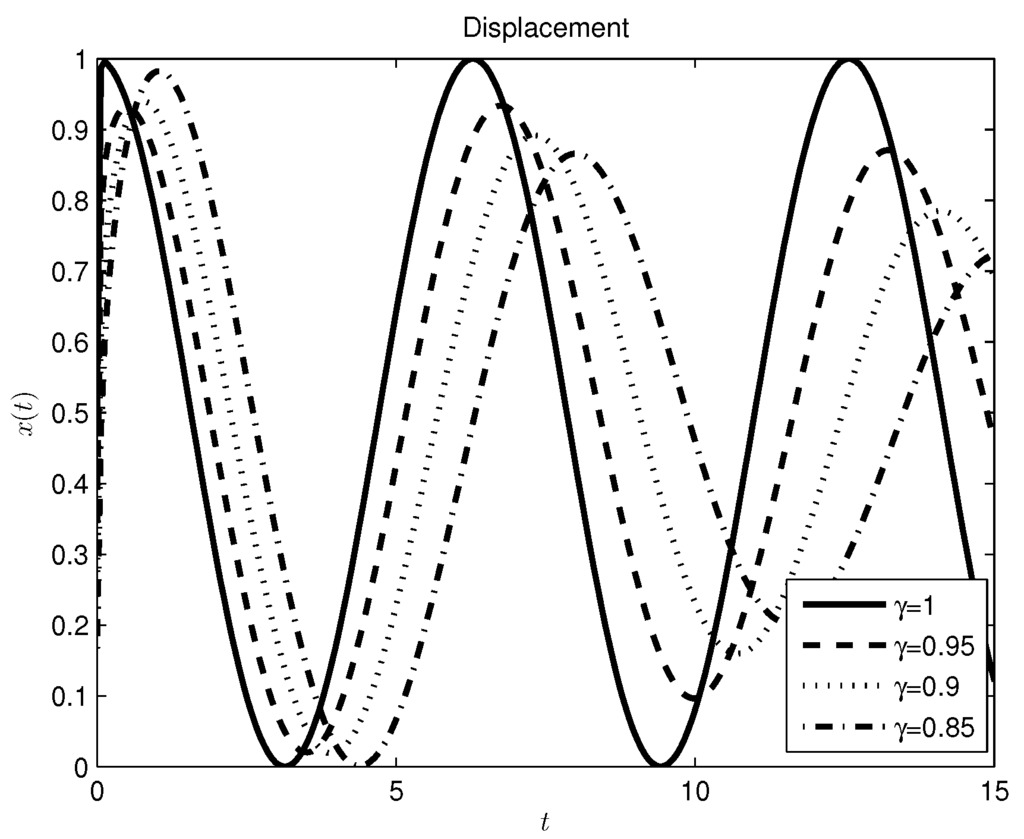
Figure 3. Mass-spring system with a constant source, Caputo–Fabrizio derivative approach.

Figure 3. Mass-spring system with a constant source, Caputo–Fabrizio derivative approach.

Case 2: Consider a periodic source, $F\left(t\right)=f_{0}cos\left(\omega t\right)$, $x\left(0\right)=x_0$, $(x_0>0)$, $\dot{x}\left(0\right)=0$; Equation (17) may be written as follows:

$${}_0^C{D}_t^{2\gamma }x\left(t\right)=\frac{{\eta }^2}{k}{f}_{0}cos\left(\omega t\right)-{\eta }^{2}x\left(t\right),$$

(29)

where ${\eta }^2$ is given by (22).

The solution of Equation (29) is:

$$x\left(t\right)=x_0·E_{2\gamma }\left\{-{\eta }^2{t}^{2\gamma }\right\}-\frac{f_0}{k}{\int }_0^{t}cos\omega (t-u)E_{2\gamma }\left\{-{\eta }^2{u}^{2\gamma }\right\}du,$$

(30)

where $E_{2\gamma }$ is given by (6).

For the classical case, from (22), we have ${\eta }^2={\eta }_0^2=\frac{k}{m}$; the solution of Equation (29) is:

$$x\left(t\right)=x_0·cos\left({\eta }_{0}t\right)-\frac{f_0}{k}{\int }_0^{t}cos\omega (t-u)cos\left({\eta }_{0}u\right)du,$$

(31)

Taking into account Expression (25), the solution (30) is:

$$x\left(t\right)=x_0·E_{2\gamma }\left\{-{\gamma }^{2(1-\gamma )}{t}^{2\gamma }\right\}-\frac{f_0}{k}{\int }_0^{t}cos\omega (t-u)E_{2\gamma }\left\{-{\gamma }^{2(1-\gamma )}{u}^{2\gamma }\right\}du.$$

(32)

The plots for different values of the fractional order γ are shown in Figure 4.

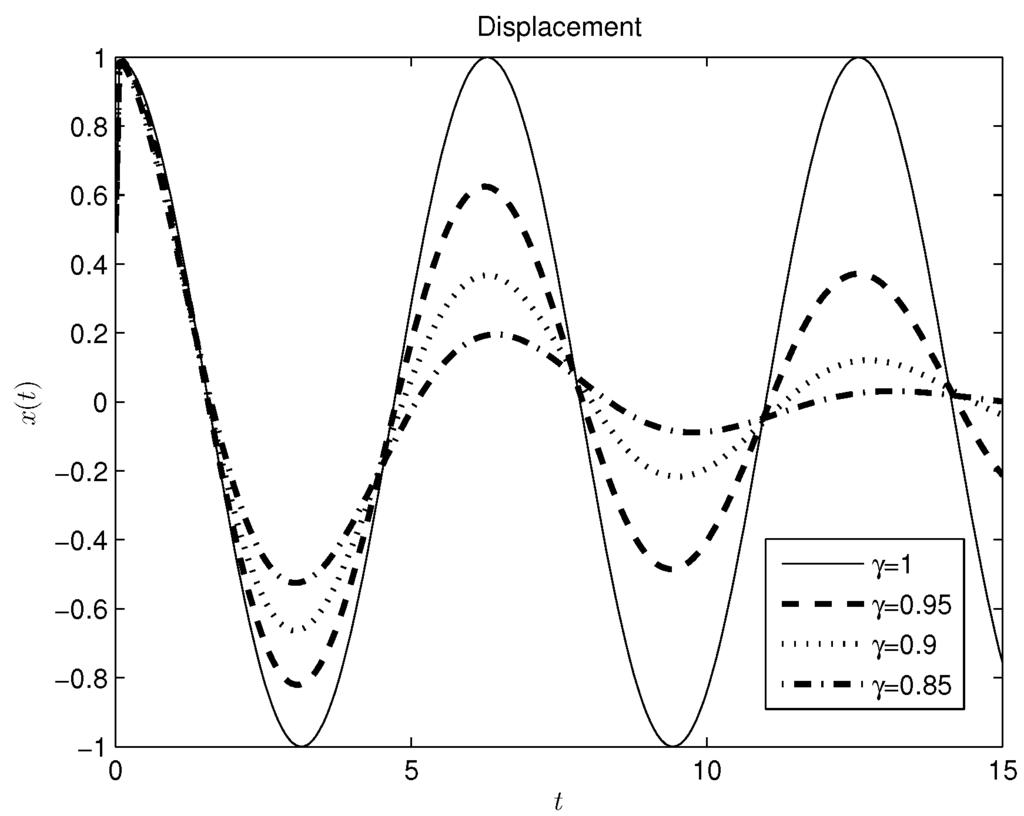
Figure 4. Mass-spring system with a periodic source, Caputo derivative approach.

Figure 4. Mass-spring system with a periodic source, Caputo derivative approach.

For Equation (18), we have:

$${}_0^{CF}{\mathcal{D}}_t^{2\gamma }x\left(t\right)=\frac{{\eta }^2}{k}{f}_0·cos\left(\omega t\right)-{\eta }^{2}x\left(t\right),$$

(33)

the Laplace transform (10) of (33) yields:

$$x\left(s\right)=x_0·\frac{s^{2\gamma -1}}{s^2+{\eta }^2[s+\gamma (1-s)]}+\frac{{\eta }^2{f}_0}{k}\left(\frac{s(s+\gamma (1-s\left)\right)}{(s^2+{\omega }^2)(s^2+{\eta }^2[s+\gamma (1-s)])}\right),$$

(34)

applying the numerical inverse Laplace transform algorithm [42] to (34), we obtain the time response. The plots for different values of the fractional order γ are shown in Figure 5.

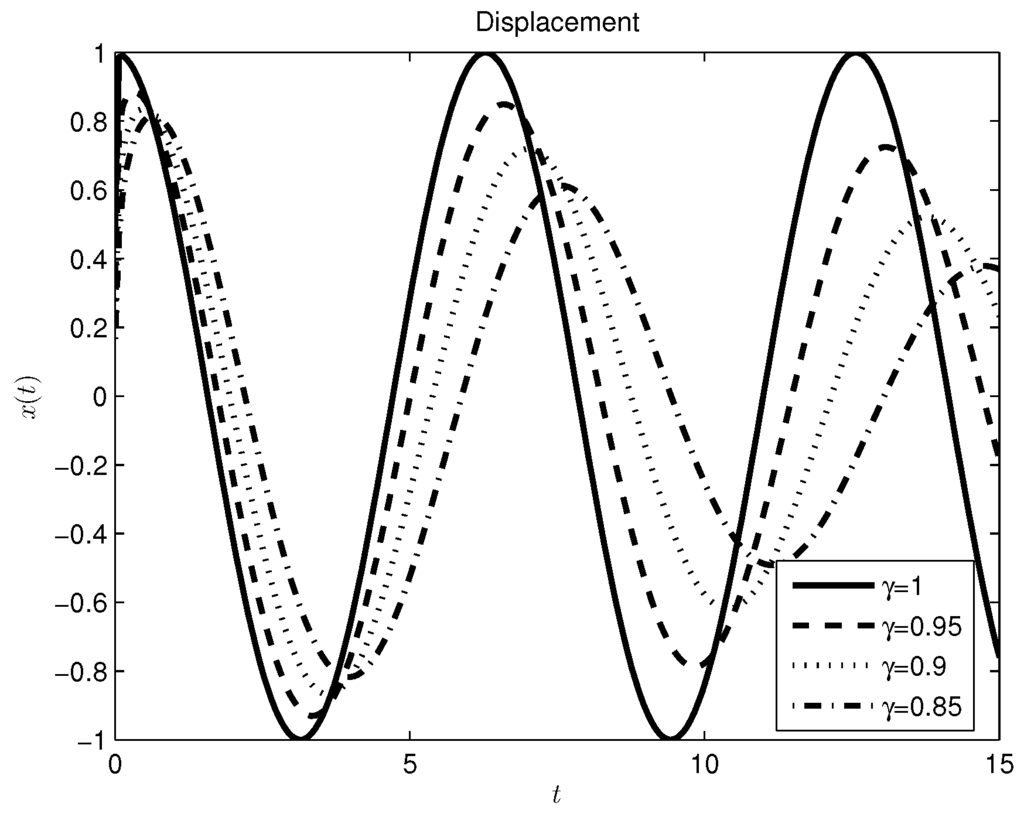
Figure 5. Mass-spring system with a periodic source, Caputo–Fabrizio derivative approach.

Figure 5. Mass-spring system with a periodic source, Caputo–Fabrizio derivative approach.

3.2. Damper-Spring System

Case 1: Consider a constant source, $F\left(t\right)=f_0$, $x\left(0\right)=x_0$, $(x_0>0)$; Equation (19) may be rewritten as follows:

$${}_0^C{D}_t^{\gamma }x\left(t\right)=\frac{\tau }{k}{f}_0-\tau x\left(t\right),$$

(35)

where:

$$\tau =\frac{k}{\beta }{\sigma }^{1-\gamma }.$$

(36)

The solution for Equation (35) is:

$$x\left(t\right)=(x_0-\frac{f_0}{k})·E_{\gamma }\left\{-\tau t^{\gamma }\right\}+\frac{f_0}{k},$$

(37)

where $E_{\gamma }$ is given by (6).

For the classical case, Expression (37) becomes:

$$x\left(t\right)=(x_0-\frac{f_0}{k})·exp(-\tau t)+\frac{f_0}{k},$$

(38)

In this case, there is a physical relation between Equation (19), the order γ and σ:

$$\gamma =\frac{k}{\beta }\sigma ,$$

(39)

considering Expression (39); the solution (37) is:

$$x\left(t\right)=(x_0-\frac{f_0}{k})·E_{\gamma }\left\{-{\gamma }^{1-\gamma }{t}^{\gamma }\right\}+\frac{f_0}{k}.$$

(40)

The plots for different values of the fractional order γ are shown in Figure 6.

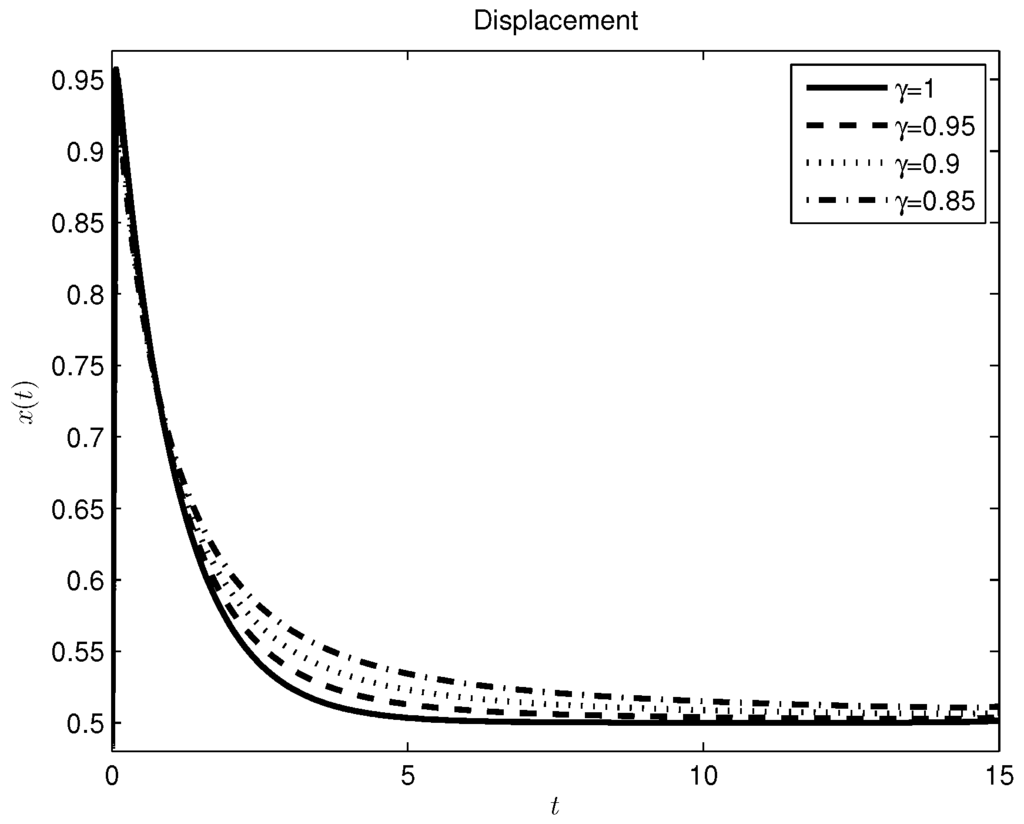
Figure 6. Damper-spring system with a constant source, Caputo derivative approach.

Figure 6. Damper-spring system with a constant source, Caputo derivative approach.

For Equation (20), we have:

$${}_0^{CF}{\mathcal{D}}_t^{\gamma }x\left(t\right)=\frac{\tau }{k}{f}_0-\tau x\left(t\right),$$

(41)

the Laplace transform (10) of (41) yields:

$$x\left(s\right)=x_0·\frac{s^{\gamma -1}}{s+\tau [s+\gamma (1-s\left)\right]}+\frac{\tau f_0}{k}\left(\frac{s+\gamma (1-s)}{s(s+\tau [s+\gamma (1-s)\left]\right)}\right),$$

(42)

applying the numerical inverse Laplace transform algorithm [42] to (42), we obtain the time response. The plots for different values of the fractional order γ are shown in Figure 7.

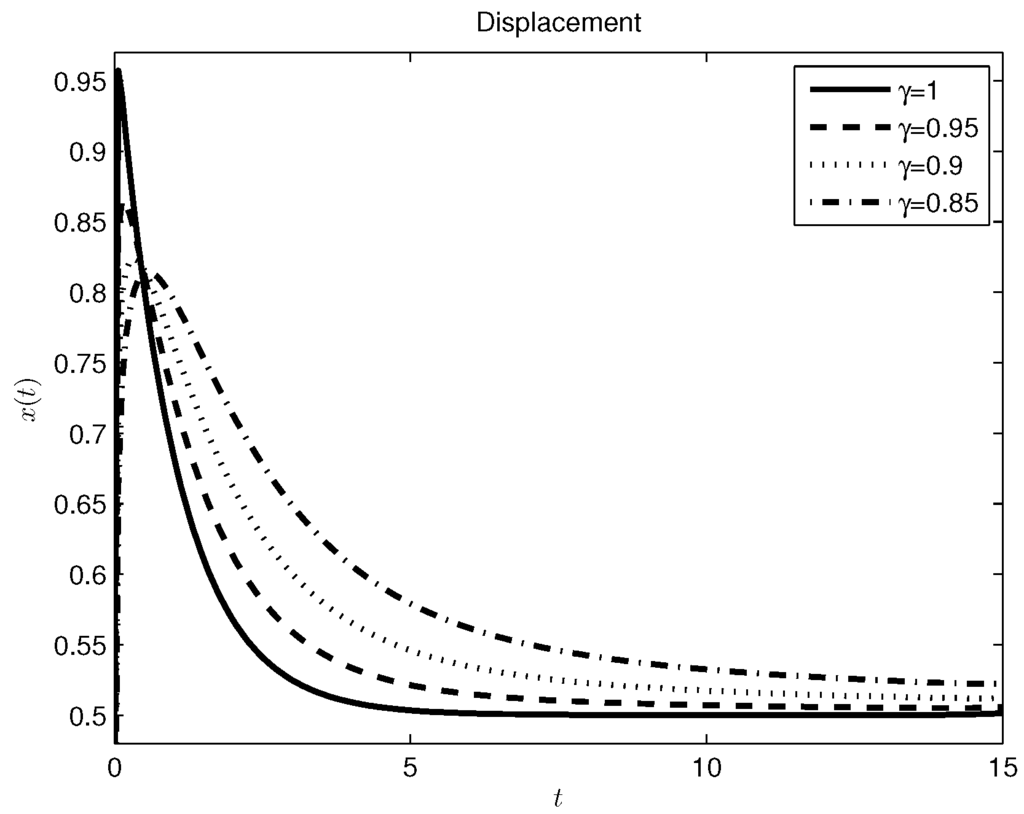
Figure 7. Damper-spring system with a constant source, Caputo–Fabrizio derivative approach.

Figure 7. Damper-spring system with a constant source, Caputo–Fabrizio derivative approach.

Case 2: Consider a periodic source, $F\left(t\right)=f_{0}cos\left(\omega t\right)$, $x\left(0\right)=x_0$, $(x_0>0)$; Equation (19) may be written as follows:

$${}_0^C{D}_t^{\gamma }x\left(t\right)=\frac{\tau }{k}{f}_{0}cos\left(\omega t\right)-\tau x\left(t\right),$$

(43)

the solution for Equation (43) is:

$$x\left(t\right)=x_0·E_{\gamma }\left\{-\tau t^{\gamma }\right\}-\frac{f_0}{k}{\int }_0^{t}cos\omega (t-u)E_{\gamma }\left\{-\tau u^{\gamma }\right\}du,$$

(44)

where $E_{\gamma }$ is given by (6).

For the classical case, Expression (44) becomes:

$$x\left(t\right)=x_0·exp(-\tau t)-\frac{f_0}{k}{\int }_0^{t}cos\omega (t-u)exp(-\tau u)du,$$

(45)

considering Expression (39), the solution (44) is:

$$x\left(t\right)=x_0·E_{\gamma }\left\{-{\gamma }^{1-\gamma }{t}^{\gamma }\right\}-\frac{f_0}{k}{\int }_0^{t}cos\omega (t-u)E_{\gamma }\left\{-{\gamma }^{1-\gamma }{u}^{\gamma }\right\}du,$$

(46)

the plots for different values of the fractional order γ are shown in Figure 8.

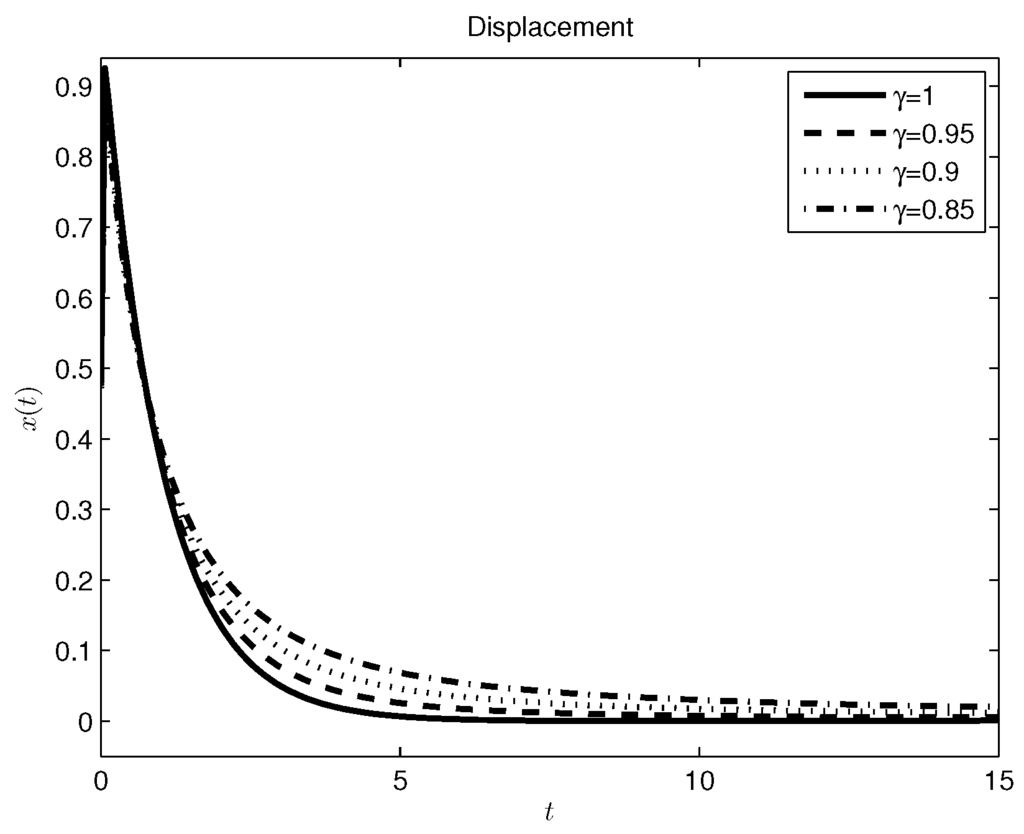
Figure 8. Damper-spring system with a periodic source, Caputo derivative approach.

Figure 8. Damper-spring system with a periodic source, Caputo derivative approach.

For Equation (20), we have:

$${}_0^{CF}{\mathcal{D}}_t^{\gamma }x\left(t\right)=\frac{\tau }{k}{f}_{0}cos\left(\omega t\right)-\tau x\left(t\right),$$

(47)

the Laplace transform (10) of (47) is:

$$x\left(s\right)=x_0·\frac{s^{\gamma -1}}{s+\tau [s+\gamma (1-s\left)\right]}+\frac{\tau f_0}{k}\left(\frac{s(s+\gamma (1-s)}{(s^2+{\omega }^2)(s+\tau [s+\gamma (1-s)])}\right),$$

(48)

applying the numerical inverse Laplace transform algorithm [42] to (48), we obtain the time response. The plots for different values of the fractional order γ are shown in Figure 9.

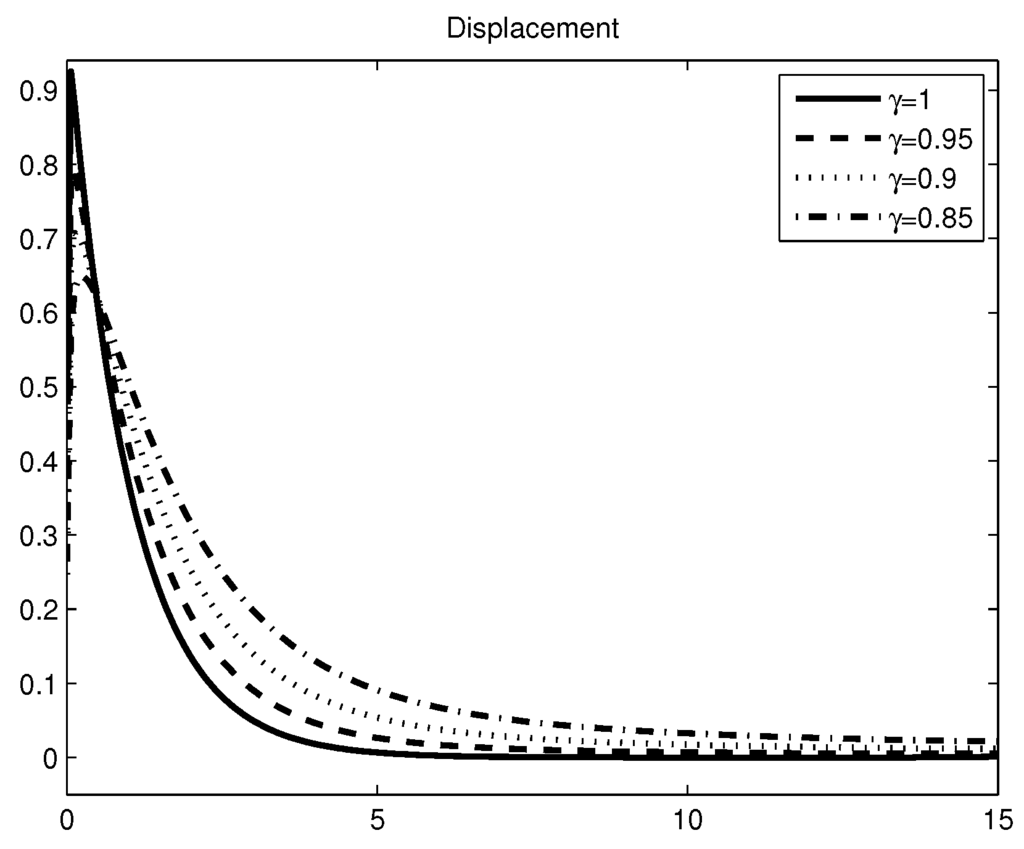
Figure 9. Damper-spring system with periodic source, Caputo–Fabrizio derivative approach.

Figure 9. Damper-spring system with periodic source, Caputo–Fabrizio derivative approach.

3.3. Mass-Spring-Damper System

Case 3: Consider $F\left(t\right)=0$ and initial conditions equal to zero; Equation (15) may be written as follows:

$${}_0^C{D}_t^{2\gamma }x\left(t\right)+\tau {}_0^C{D}_t^{\gamma }x\left(t\right)={\eta }^{2}x\left(t\right),$$

(49)

where ${\eta }^2$ and τ are given by (22) and (36), respectively. The solution of Equation (49) is:

$$x\left(t\right)=x_0·E_{\gamma }\left\{-\frac{\beta }{2m}{\sigma }^{1-\gamma }{t}^{\gamma }\right\}·E_{2\gamma }\left\{-\left[\frac{k}{m}-\frac{{\beta }^2}{4m^2}\right]{\sigma }^{2(1-\gamma )}{t}^{2\gamma }\right\}$$

(50)

where $E_{\gamma }$ is given by (6).

For the classical case, Expression (50) becomes:

$$x\left(t\right)=x_0·exp\left(-\frac{\beta }{2m}t\right)·cos\left(\sqrt{\frac{k}{m}-\frac{{\beta }^2}{4m^2}}t\right),$$

(51)

In this case, there is a physical relation between Equation (15), the order γ and σ:

$$\gamma =\sqrt{\frac{k}{m}-\frac{{\beta }^2}{4m^2}}\sigma ,$$

(52)

considering Expression (52), the solution (50) is:

$$x\left(t\right)=x_0·E_{\gamma }\left\{-{\gamma }^{1-\gamma }{t}^{\gamma }\right\}·E_{2\gamma }\left\{-{\gamma }^{2(1-\gamma )}{t}^{2\gamma }\right\}.$$

(53)

The plots for different values of the fractional order γ are shown in Figure 10.

Figure 10. Mass-spring-damper system without a source, Caputo derivative approach.

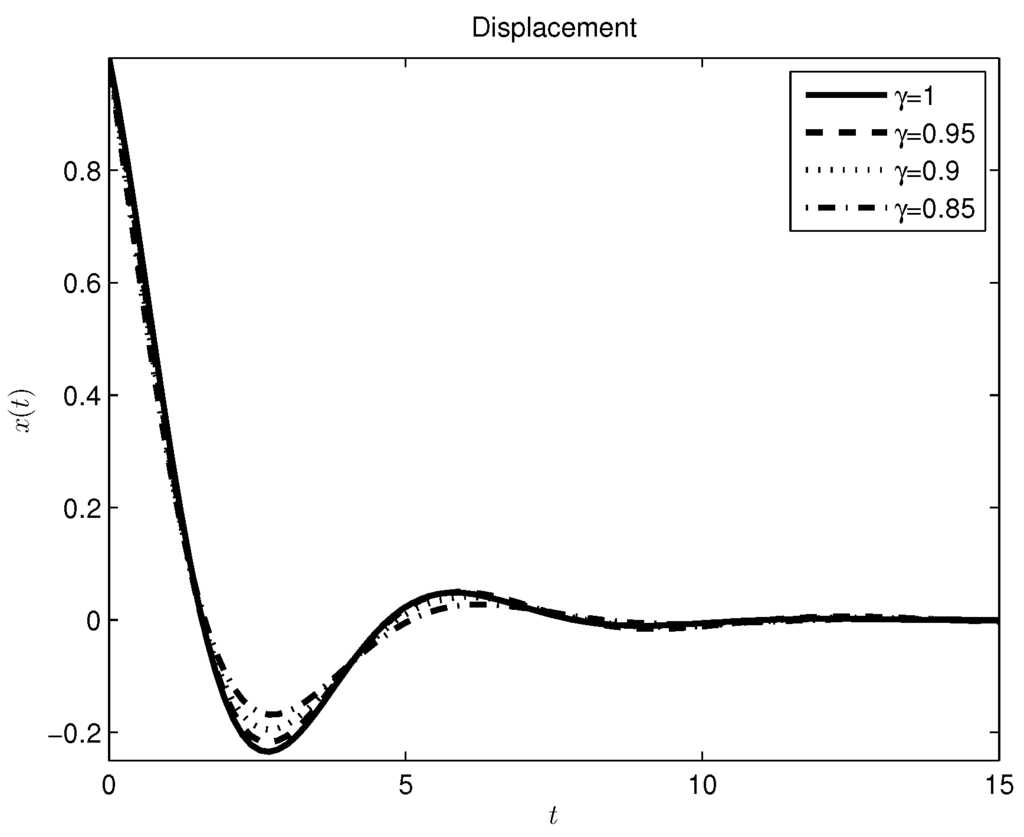
Figure 10. Mass-spring-damper system without a source, Caputo derivative approach.

For Equation (16), we have:

$${}_0^{CF}{\mathcal{D}}_t^{2\gamma }x\left(t\right)+\tau {}_0^{CF}{\mathcal{D}}_t^{\gamma }x\left(t\right)={\eta }^{2}x\left(t\right),$$

(54)

and the Laplace transform (10) of (54) yields:

$$x\left(s\right)=x_0·\left(\frac{s+a}{s^2+\tau s+{\eta }^2(s+\gamma (1-s)}\right),$$

(55)

where ${\eta }^2$ and τ are given by (22) and (36), respectively. Applying the numerical inverse Laplace transform algorithm [42] to (55), we obtain the time response. The plots for different values of the fractional order γ are shown in Figure 11.

Figure 11. Mass-spring-damper system without a source, Caputo–Fabrizio derivative approach.

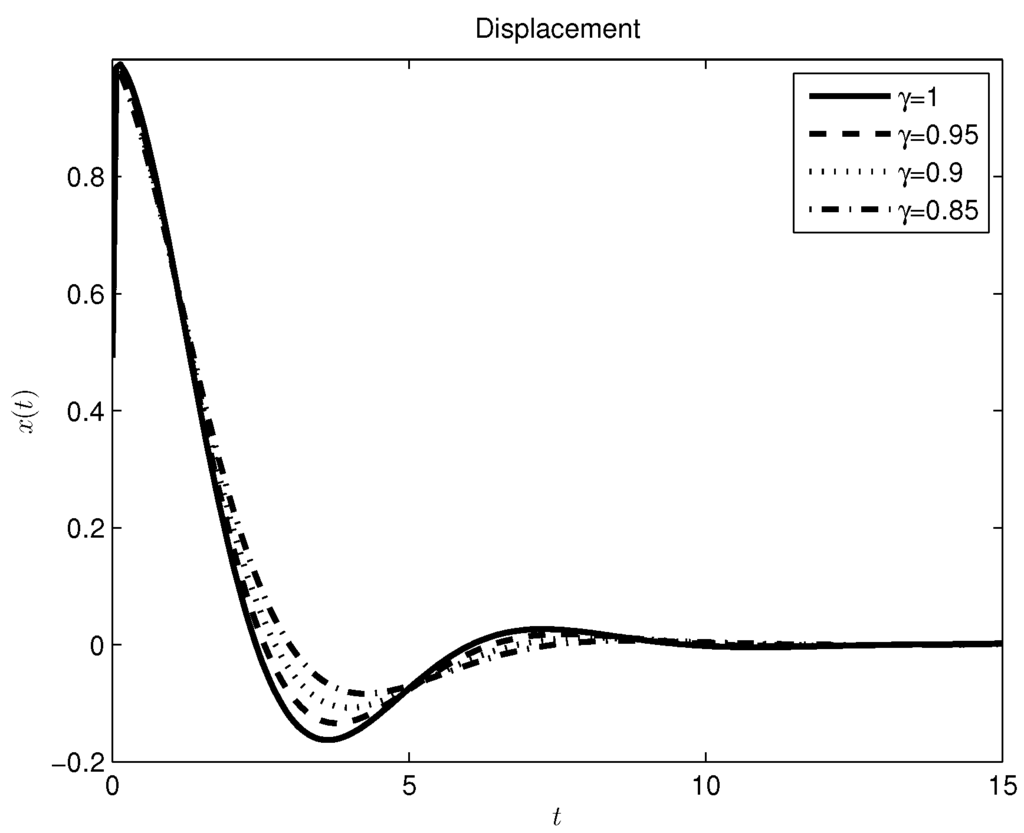
Figure 11. Mass-spring-damper system without a source, Caputo–Fabrizio derivative approach.

4. Conclusion

In this work, we present alternative fractional differential equations using Caputo and Caputo–Fabrizio fractional derivatives for modeling oscillating systems. The proposed equations provide a universal behavior (see Equations (25), (39) and (52)); the solutions presented preserve the dimensionality of the studied system for any value of the exponent of the fractional derivative. The advantage of this alternative representation when compared to the models presented in the literature is the physical compatibility of the solutions.

For the classical Caputo approach, the solutions incorporate and describe long-term memory effects (attenuation or dissipation); these effects are related to an algebraic decay related to the Mittag–Leffler function; when γ is less than one, the fractional differentiation with respect to time represents the non-local displacement effects of dissipation of energy (internal friction) represented by the fractional order γ, which is related to the displacement of the oscillator in fractal geometries. For the Caputo–Fabrizio fractional derivative, the numerical solutions show a change of the amplitude variation and the phase; these behaviors depend on the fractional derivative order and modify the constant time; particularly, when the fractional operator is less than one, the systems exhibit a fast stabilization. This new fractional definition allows describing the relaxation phenomena characteristic of viscoelastic materials, and the numerical solution exhibits temporal fractality at different scales, as well as the existence of material heterogeneities in the mechanical components. The two definitions of fractional derivatives must apply conveniently depending on the materials treated; the choice of the fractional derivative depends upon the problem studied and on the phenomenological behavior of the system. For both definitions, when $\gamma =1$, the displacement has the ordinary behavior.

The results gathered in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 briefly show that when $\gamma =1$, the system displays the Markovian nature. However, for values of $\gamma <1$, the equations describe systems that are non-conservative (non-local in time); in this context, the different γ values are modified the time constant of the systems and exhibit fractional structures (components that show an intermediate behavior between a system that is conservative and dissipative). In the range $\gamma \in (0.85,1)$, the figures show that the system presents dissipative effects that correspond to the nonlinear situation of the physical process (realistic behavior that is non-local in time). In these cases, the systems modified the damping capacity, for example when $\gamma =0.85$, the damping capacity is bigger than when $\gamma =0.95$. Furthermore, the figures show that the Caputo fractional derivative is more affected by the past compared to the Caputo–Fabrizio fractional derivative, which shows a rapid stabilization.

The resulting equations represent a generalization of the classical mass-spring-damper model; the proposed representation can be used to describe a wide variety of systems, which had not been addressed due to the limitations of the classical calculus. In this context, we consider that these results are useful to understand the behavior of dynamical complex systems, mechanical vibrations, control theory, relaxation phenomena, viscoelasticity, viscoelastic damping and oscillatory processes.