Abstract
This work introduces for the first time the application of wavelet entropy (WE) to detect episodes of the most common cardiac arrhythmia, atrial fibrillation (AF), automatically from the electrocardiogram (ECG). Given that AF is often asymptomatic and usually presents very brief initial episodes, its early automatic detection is clinically relevant to improve AF treatment and prevent risks for the patients. After discarding noisy TQ intervals from the ECG, the WE has been computed over the median TQ segment obtained from the 10 previous noise-free beats under study. In this way, the P-waves or the fibrillatory waves present in the recording were highlighted or attenuated, respectively, thus enabling the patient’s rhythm identification (sinus rhythm or AF). Results provided a discriminant ability of about 95%, which is comparable to previous works. However, in contrast to most of them, which are mainly based on quantifying RR series variability, the proposed algorithm is able to deal with patients under rate-control therapy or with a reduced heart rate variability during AF. Additionally, it also presents interesting properties, such as the lowest delay in detecting AF or sinus rhythm, the ability to detect episodes as brief as five beats in length or its integration facilities under real-time beat-by-beat ECG monitoring systems. Consequently, this tool may help clinicians in the automatic detection of a wide variety of AF episodes, thus gaining further knowledge about the mechanisms initiating this arrhythmia.
1. Introduction
Entropy, defined as a measure of the amount of information within a random process, has been playing an important role in biomedical signal and image analysis during the last few years. Indeed, numerous entropy-based metrics have recently provided a significant ability to reveal useful information from diseases that still represent a clinical challenge, such as Alzheimer’s [1], schizophrenia [2], myocardial infarction [3] or atrial fibrillation (AF) [4], among others. The information provided by these metrics is mainly related to underlying mechanisms that cannot be quantified directly by clinicians in an exploratory examination, thus providing a significant knowledge increase of those diseases, as well as improving their diagnosis and treatment [5,6]. Within this context, wavelet entropy (WE) has demonstrated very interesting results because it combines entropy and wavelet decomposition to increase its robustness to non-stationarities, noise and artifacts [7]. Given that physiological signals are often non-stationary, WE has proven to be widely successful in quantifying clinically-relevant events from electroencephalograms (EEG) [7,8], electrocardiograms (ECG) [9], intracranial pressure recordings [10] and evoked related potentials [11]. In the present work, a new application of WE to detect automatically the onset of the most common cardiac arrhythmia will be introduced.
Atrial fibrillation (AF) has been described by physicians as the commonest cardiac arrhythmia in clinical routine, with an estimated prevalence of 1.5%–2% of the general population in the developed world [12]. More than six million people in Europe and three million people in the USA suffer currently from this arrhythmia [12]. It is also expected that its prevalence will double in the next 50 years [13]. Today, three different types of AF are clinically stratified depending on the episode duration. The arrhythmia can then be classified into paroxysmal AF (PAF), persistent or long-standing persistent AF and, finally, permanent AF [14]. In the first stage, PAF terminates spontaneously, at most within seven days of onset. In general, paroxysmal episodes usually increase in frequency and duration over time. On the other hand, persistent AF duration is longer than seven days, evolving to its long-standing form if it lasts more than 12 months. An external intervention, such as electrical cardioversion or catheter ablation, is normally required to revert the arrhythmia [12]. Finally, in the more evolved stage of AF and with the aim of avoiding the risks of further unsuccessful attempts of restoring sinus rhythm (SR), both the patient and the clinician make a joint decision considering the arrhythmia as permanent AF. In this case, only interventions to control the heart rate are pursued [14].
Although AF itself does not represent a life-threatening condition, it adversely affects the blood flow dynamics and predisposes to thrombus formation within the atrium [12]. In fact, the presence of AF is associated with a five-fold risk of stroke and a three-fold incidence of congestive heart failure, thus provoking that AF patients have twice the risk of death than healthy people of the same age [12]. Within this context, an early detection of AF may help with reducing that risk by restoring normal heart rhythm or by improving the blood flow with antithrombotic therapy [14,15]. This early diagnosis may also involve notable benefits for healthcare services around the world, because the high hospitalization rates of AF, as well as its considerable burden on health resources could be significantly limited [16].
However, early AF detection is not an easy task, because the initial PAF episodes are often extremely brief, some of them consisting of only a few beats in length [14]. Additionally, current AF diagnosis is mainly based on the presence of typical symptoms, such as dyspnea, chest pain, dizziness and palpitations [17], but not every single patient always presents these signs. Indeed, previous works have reported that up to 90% of PAF episodes may be asymptomatic [18]. Similarly, a poor correlation between symptoms and AF occurrence have also been described by several authors [19,20]. Hence, to avoid an ischemic stroke as the first manifestation of AF in a considerable number of patients, the development of automatic AF detectors able to be embedded into continuous monitoring systems constitutes a significant challenge [21].
Currently, a wide variety of methods to detect AF automatically can be found in the literature. These algorithms are mostly based on the two main characteristics manifested by AF on the ECG. On the one hand, AF occurs when electrical impulses provided by the sinus node are replaced by multiple and irregular wavefronts, which continuously excite the atria [12]. As a result, the normal P-wave during SR is replaced by fibrillatory waves that are randomly propagated (f-waves) [22]. Taking advantage of this alteration in the atrial electrical activity, a first limited group of algorithms have been proposed [23,24]. However, the low signal-to-noise ratio in the ECG of atrial activation waves can sometimes hamper the proper performance of these methods. Indeed, only a modest result has been obtained by Slocum et al.’s algorithm [23] in the presence of noise [25]. Nonetheless, it is worth noting that the most recent P-wave-based method has reported a high accuracy even within this context [24].
On the other hand, the chaotic and fragmented atrial excitation during AF can reach activation rates of 400 per minute and above. Such a high rate involves a massive bombardment of the atrioventricular (AV) node, which will conduct the electrical impulses from the atria down to the ventricles. Given its intrinsic refractory period, the AV node will only conduct some of these atrial activations, but still provoking the fast and irregular ventricular rhythm, which is commonly observed during AF [26]. By considering ventricular response, numerous authors have proposed AF detectors based on analyzing RR series variability [27,28,29,30,31,32]. However, although these methods have provided a high ability to identify long AF episodes, they have also manifested their weakness when dealing with very short AF events. Indeed, a time length of at least 30 s is required to provide reliable AF detections, such that shorter episodes cannot be uncovered. However, this is a major limitation for these methods, because brief episodes are very common in the first stages of PAF [14]. Moreover, recent works have provided a close relationship between the presence of brief episodes and a high risk of thrombus formation [33].
To overcome the need of long enough episodes for reliable AF detection, several authors have recently combined information from the RR series variability together with the P-wave absence analysis [34,35,36,37,38,39]. In this way, brief PAF episodes of only a few beats in length (≥ 5 beats) have been successfully detected. However, these algorithms still present an important limitation, such as their inability to properly work when regular RR intervals occur. In fact, this situation is very frequent in AF during the presence of AV block, as well as in ventricular or AV junctional tachycardia [40]. Furthermore, the use of pacemakers, as well as drugs to stabilize the heart rate during AF also eliminate the RR series irregularity associated with the arrhythmia [24]. As a consequence, these algorithms would not be able to provide reliable AF detection under these scenarios.
In the present work, a novel algorithm with the ability to detect automatically both long and brief PAF episodes, regardless of the patient’s heart rate regularity, is introduced. It is based on a robust identification of the presence or absence of the P-wave in every single beat of the ECG. For that purpose, WE, as well as the energy associated with several wavelet scales will be computed from the ECG interval containing atrial activity, i.e., the TQ interval, corresponding to the beat under analysis. To improve its signal-to-noise ratio, a signal-averaging approach is used. This technique has been widely considered for P-wave characterization, thus revealing clinically useful information, such as the identification of patients prone to PAF [41] or the prediction of AF recurrence after electrical cardioversion [42] or catheter ablation [43].
The remainder of manuscript is organized as follows. Section 2 describes the database used, as well as the processing applied to the recordings and the algorithm for WE computation. Section 3 summarizes the obtained results, which are then discussed in Section 4. Finally, Section 5 presents the concluding remarks.
2. Materials and Methods
2.1. Study Population
To evaluate the proposed algorithm performance, the MIT-BIH AF Database was used. It is freely available from PhysioNet [44] and has been widely used to validate the automatic detection of AF in previous works [24,28,29,31,32,36,38]. The dataset contains 23 fully-annotated 10-hour length ECG recordings mainly from PAF patients, which were acquired with a sampling rate of 250 Hz and 12-bit resolution over a range of ± 10 mV. More precisely, it includes 605 episodes related to four different rhythms, from which the used R-peak detector identified 1,124,391 beats: 291 AF episodes (474,670 beats), 14 atrial flutter episodes (12,081 beats), 12 episodes of junctional rhythm (3603 beats) and 288 episodes of all other rhythms (633,317 beats). In the current study, 1,107,987 beats were analyzed from all the episodes, apart from those related to atrial flutter and junctional rhythm. These latter episodes were not included in the study, because discerning between AF and atrial flutter is a clinical challenge that merits an exclusive and thorough study, such as has been addressed in [45,46]. Furthermore, the duration of these episodes was too limited compared to the remaining ones.
On the other hand, although each ECG recording contained two leads, only the one providing the largest P-waves was analyzed. Nonetheless, when both leads presented P-waves with a similar amplitude, they were visually inspected, and the one presenting apparently less noise was selected, because noise is a common nuisance artifact in long-term ambulatory recordings [39]. Moreover, to increase the proposed algorithm’s noise immunity, beats where completely noise-masked P- or f-waves were manually identified and annotated from the selected lead. This process was carried out by two different experts, such that those cases of disagreement were discarded. Finally, a total number of 114,460 noisy beats was detected, i.e., 10.60% of all the beats considered for the study. For all the patients, these noisy beats meant 9.72% ± 10.61% on average.
2.2. Data Processing
The selected lead was first preprocessed to improve later analysis. Thus, baseline wander was removed making use of a bidirectional high-pass filtering with a 0.5 Hz cut-off frequency [47]. Muscle noise and power-line interference were reduced by applying an eighth order, bidirectional IIR Chebyshev low-pass filtering with a 50-Hz cut-off frequency [48]. Thereafter, a phasor transform-based algorithm was used to detect every single R-peak [49]. This algorithm has been validated with databases manually annotated by expert cardiologists, providing sensitivity and positive predictivity higher than 99.65% and 99.70%, respectively. Furthermore, this algorithm has the ability to deal with ectopics in the same way as normal beats [49]. Hence, complexes originated from atrial and ventricular premature activations were automatically detected without any additional requirement and were then considered for the study.
After every single R-peak identification, its preceding TQ interval was computed as a variable length segment located 60 ms before the corresponding R-peak. To make the duration of this interval as insensitive to ectopic and errors in R-peak detection as possible, it was adaptively computed as a quarter of the median RR interval associated with the last 10 beats. Several experiments carried out on all of the analyzed signals proved that this TQ interval only contained atrial activity information regardless of the heart rate and its variability.
Finally, every selected TQ interval was analyzed from the wavelet domain following two steps, such as Figure 1 shows. First, WE was computed from the TQ interval under analysis and, then, compared to a threshold to determine whether the noise level exceeded the P- or f-wave amplitude. In case of a noisy TQ interval, it was flagged and discarded. For the remaining beats, a second step computing the median TQ interval from the last L noise-free beats was performed for every single beat. For this purpose, all the single TQ segments were shortened down to the shortest TQ duration. The point located 60 ms before the R-peak was considered as a reference to reach a proper alignment of the P-waves. Hence, every single TQ interval was reduced from the closest side to the T-wave offset. As the last step, the WE, as well as the relative energy in the analyzed wavelet scales were computed from this median interval to discern between SR and AF. It has to be remarked that the use of this signal-averaging approach leads to a tiny delay in AF detection. Indeed, during the transition from SR to AF or vice versa, both P- and f-waves are jointly considered to generate the median TQ interval. Therefore, its waveform will mainly depend on which wave (P or f) is predominant. This delay will increase with the number of averaged beats generating the median TQ interval, such that the larger L, the longer the induced delay. Hence, with the aim to assess how the transition delay affects the classification’s performance, the number of averaged beats was analyzed within a range of beats.
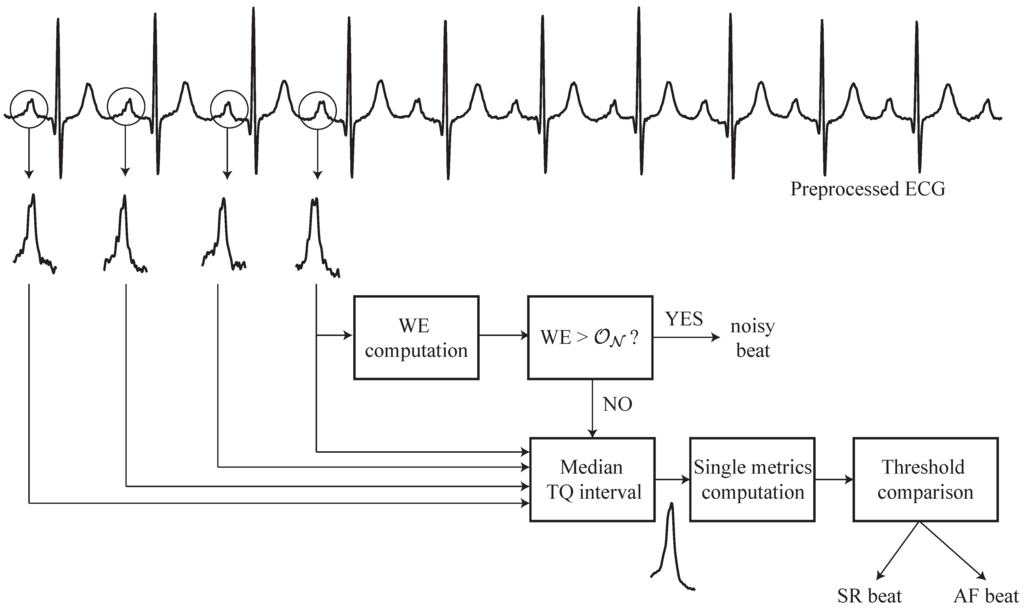
Figure 1.
Block diagram describing the main steps of the proposed algorithm able to detect atrial fibrillation (AF) automatically, regardless of episode duration and heart rate.
2.3. Wavelet Entropy Analysis
The wavelet transform (WT) characterizes a signal in terms of translated and dilated versions of another signal, named the mother wavelet [50]. Hence, a wavelet family is the set of functions generated by translations and dilations, using the scale and translation parameters a and b, of a single mother wavelet, such that:
where , and t is time. Low a values are related to a dilated wavelet and, therefore, focused on low frequencies. Then, the continuous wavelet transform (CWT) of a signal is defined as the correlation between and the wavelet family , such that:
The sampled version of this transform is called discrete wavelet transform (DWT). In this case, is sampled, and dyadic translations and scales are only allowed. Hence, the mother wavelet is only shifted and scaled by powers of two, such that:
where n is the discrete time and j and k are the new scale and shift parameters, respectively. The result of this transformation is a series of wavelet coefficients, , which depend on the value of scale and translation. More precisely, these coefficients can be interpreted as a measure of correlation between the analyzed signal and the wavelet function , such that:
M being the length of . These wavelet coefficients do not contain redundant information, thus making complete reconstruction of the original signal possible whenever an orthogonal function is used as the mother wavelet [50]. Moreover, it should also be noted that coefficients provide a direct estimation of the signal energy at each analyzed scale [7]. Thus, the relative energy associated with the scale j can be computed as:
N and being the number of wavelet decomposition levels and the length of C(j,k), respectively. Obviously, and the distribution can be considered as a time-scale density, which is a suitable tool for detecting and characterizing specific phenomena both in time and frequency domains [7]. Therefore, by computing Shannon’s entropy from this distribution, the WE can be defined, such that:
thus providing useful information about the underlying time-frequency dynamical processes associated with the signal [7]. More precisely, WE yields a measure of the degree of order/disorder of the signal. Thus, for a very organized signal, such as a periodic mono-frequency event, WE will provide a very low value close to zero. In fact, its wavelet decomposition will show a relative wavelet energy close to one for the level containing the representative frequency and a very limited relative energy for the remaining wavelet levels. In contrast, a very disorganized signal, such as those generated by totally random processes, will have a wavelet representation with significant contributions from all the frequency bands, thus providing a high WE value near its maximum.
In the present work, with the aim to compute WE from the median TQ interval, a four-level wavelet decomposition was chosen (). Bearing in mind that the P-wave spectral content is usually considered as a low-frequency (below 10–15 Hz) [48] and recordings were acquired with a sampling rate of 250 Hz, the P-wave relative wavelet energy will be mainly concentrated on the fourth scale. With regard to the mother wavelet selection, there are no available guidelines for this purpose; thus, an exploratory approach by testing different functions is proposed [51,52]. Indeed, all the functions from Haar, Daubechies, Coiflet, Biorthogonal, Reverse Biorthogonal and Symlet wavelet families were tested. Although no huge differences were noticed, the best outcomes were provided by the sixth-order Daubechies function. Hence, this wavelet function was selected, and its main results will be presented later in Section 3.
2.4. Performance Assessment and Statistical Analysis
The optimal threshold to identify noisy beats was obtained by using a learning/test approach. Thus, to avoid results being dependent on the choice for the learning/test split [53], half of the noisy beats manually annotated from each patient (i.e., 57,230 beats) were randomly selected to train the method. A receiver operating characteristic (ROC) curve was then computed from this set. This plot is the result of plotting the fraction of true positives (TP) out of positives (sensitivity) against the fraction of false positives out of the negatives (1−specificity) at various threshold settings. Sensitivity was here considered as the percentage of TQ intervals manually annotated as noisy that were correctly classified. In a similar way, the rate of the remaining TQ intervals available in the studied dataset (i.e., SR and AF beats) properly identified was considered as the specificity. The optimal threshold was selected as the one providing the highest percentage of TQ intervals correctly classified (i.e., accuracy). Finally, the remaining half of the noisy beats was used to test the method. Only classification results provided from this set will be presented in the next section.
An ROC curve was also used to assess the diagnostic ability of WE, as well as of the relative energies , , and , computed from the median TQ interval, to discern between SR and AF beats. In this case, noisy beats were discarded, and the remaining ones were divided into two equally-sized, stratified groups. Thus, as for noisy beats, half the AF (237, 335) and SR (316, 658) beats from each patient were randomly selected as a learning set to compute the optimal threshold from each single metric. The rate of AF beats properly identified was considered as the true positive rate (i.e., sensitivity), whereas the percentage of SR beats successfully classified was considered as the true negative rate (i.e., specificity). As before, the threshold maximizing the accuracy (i.e., the number of beats correctly identified) was selected as optimal and was used to check out the single metric over the test group. Thus, sensitivity, specificity and accuracy were computed from this test set.
On the other hand, a stepwise discriminant analysis (SDA) was also performed with the objective of improving AF automatic detection. For each iteration, the discriminant power provided by each selected subset of features was assessed by the Lawley–Hotelling trace (Rao’s V). This generalized distance measure quantifies the separation of group centroids and does not concern itself with cohesiveness within the groups. Thus, a variable selected on the basis of this index may be decreasing within group cohesion, while it adds to the overall separation. As for the single metrics, SDA was trained with the learning set and validated with the test set.
Finally, all the metrics provided normal and homoscedastic distributions from Kolmogorov–Smirnov and Levene tests, respectively. As a consequence, results were expressed as the mean ± standard deviation for all the patients belonging to the same group, and statistical differences between SR and AF beats were assessed by using a Student’s t-test. A two-tailed value of statistical significance was considered statistically significant.
3. Results
The WE optimal threshold obtained to identify noisy beats was 1.096. This value provided a sensitivity and specificity of 96.70% and 97.95%, respectively. Figure 2 shows an example where noisy beats were properly detected by comparing WE with . As can be observed, noisy beats provided WE values notably higher (1.193 ± 0.083) than the remaining ones (0.687 ± 0.234), the differences between them being statistically significant (). It is worth noting that no transition delay is observed in this figure, since noisy TQ intervals were detected by computing WE in a beat-to-beat fashion.
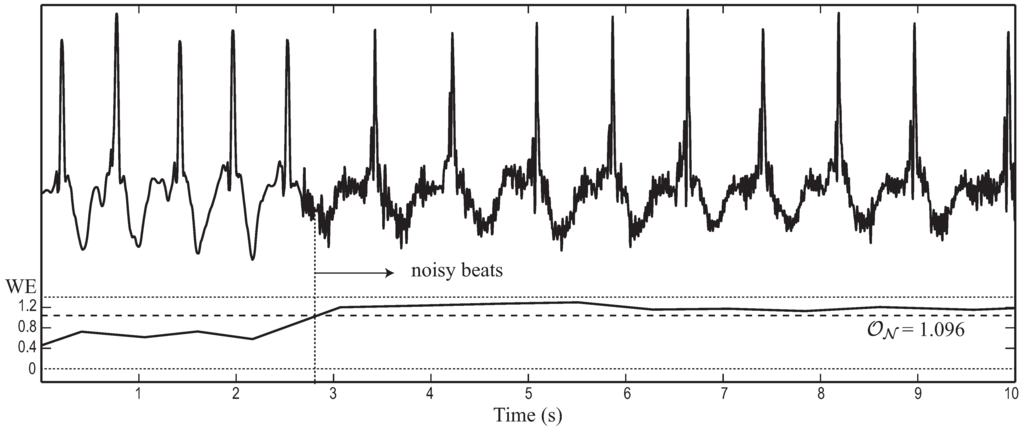
Figure 2.
Example of a typical ECG segment where noisy TQ intervals are properly identified by computing wavelet entropy (WE). In this case, the metric was obtained in a beat-to-beat manner and compared to the optimal threshold to decide the presence or absence of noise.
Once noisy beats were identified and rejected, the improvement in AF detection achieved by the median of consecutive TQ intervals was assessed from the learning set. Thus, Figure 3a displays the WE diagnostic accuracy for the median TQ interval computed from beats. As can be seen, the higher the value of L, the higher the accuracy. In a similar way, Figure 3b shows the delay, as a function of L, in detecting the transition from SR to AF and vice versa. In this case, as L increases, a greater number of beats is also required to identify a change of rhythm. By considering the increasing delay with L together with the limited improvement in accuracy for , a value of beats was selected as an optimal trade-off between both aspects. In fact, a reduced improvement in accuracy lower than 1.5% was provided for , as can be observed in Figure 3a. For the case of , Figure 4 shows an example where WE is able to detect transition from AF to SR with a tiny delay of only five beats. Furthermore, it has to be mentioned that a regular RR series can be observed in both AF and SR. Thus, although the mean RR series is slightly higher for SR than for AF, every algorithm based on quantifying the RR irregularity could not discern between both episodes. Finally, note that these experiments were also repeated for the metrics , , and , and similar results were obtained.
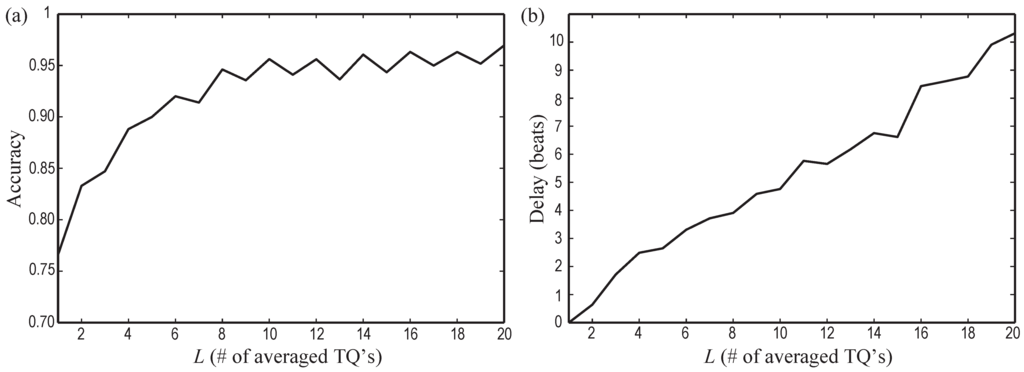
Figure 3.
Variation of (a) wavelet entropy (WE) diagnostic accuracy and (b) transition delay as a function of the number of beats L participating in the averaged TQ interval.
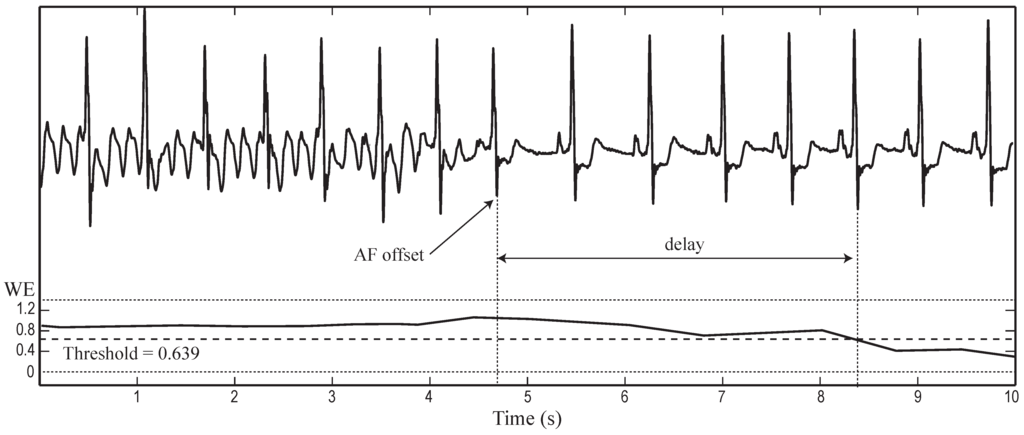
Figure 4.
Example of the transition from atrial fibrillation (AF) to sinus rhythm (SR) where wavelet entropy (WE) presents a tiny delay of five beats. The median TQ interval was computed with beats.
Regarding the classification into SR and AF beats from the median TQ interval (being beats), Table 1 and Table 2 show the learning and test sets results, respectively. For both sets, while WE, , and provided higher values for AF beats, yielded a reverse trend. This finding is also noticeable in Figure 5 and Figure 6, which display boxplots for the analyzed metrics from the learning and test sets, respectively. It should be remarked that notable statistically-significant differences were reported in every case. In addition, all the metrics provided a high accuracy (≥ 85%) from both datasets, but WE showed to be the most powerful single metric to detect AF, although it was closely followed by the relative wavelet energy of the fourth scale .
Finally, the SDA did not improve the accuracy reported by the single metric WE, because any other metric was able to provide extra information to the classifier. Nonetheless, it has to be mentioned that a statistically-significant correlation higher than 50% was observed between WE and the relative energy in all the wavelet scales.

Table 1.
Classification results provided by the analyzed single metrics for the learning group.
| Metric | SR beats | AF beats | p | Threshold | Accuracy (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|---|---|---|
| WE | 0.431 ± 0.135 | 0.952 ± 0.240 | 0.639 | 95.62 | 96.07 | 95.23 | |
| 0.881 ± 0.051 | 0.601 ± 0.190 | 0.804 | 94.89 | 94.61 | 95.19 | ||
| 0.089 ± 0.040 | 0.215 ± 0.105 | 0.110 | 87.60 | 94.78 | 81.03 | ||
| 0.023 ± 0.015 | 0.125 ± 0.096 | 0.038 | 91.04 | 90.69 | 91.35 | ||
| 0.007 ± 0.006 | 0.060 ± 0.057 | 0.011 | 88.75 | 92.10 | 85.68 |

Table 2.
Classification results provided by the analyzed single metrics for the test group.
| Metric | SR beats | AF beats | p | Accuracy (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|---|---|
| WE | 0.420 ± 0.124 | 1.017 ± 0.208 | 95.28 | 96.47 | 94.19 | |
| 0.886 ± 0.044 | 0.546 ± 0.183 | 94.48 | 93.19 | 95.89 | ||
| 0.086 ± 0.032 | 0.249 ± 0.118 | 85.51 | 81.66 | 89.03 | ||
| 0.022 ± 0.017 | 0.141 ± 0.089 | 90.84 | 88.15 | 93.29 | ||
| 0.007 ± 0.006 | 0.065 ± 0.060 | 87.69 | 81.80 | 93.03 |
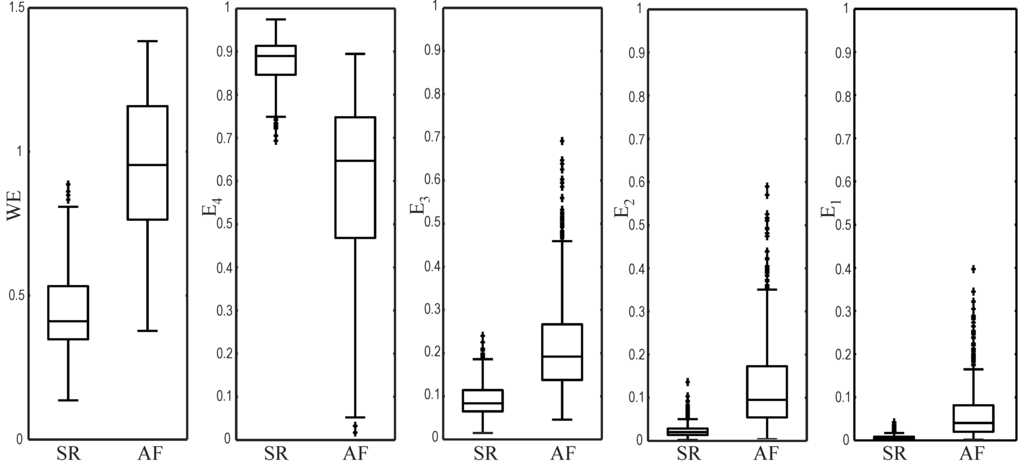
Figure 5.
Boxplots showing the distribution of all the analyzed metrics from the learning set.
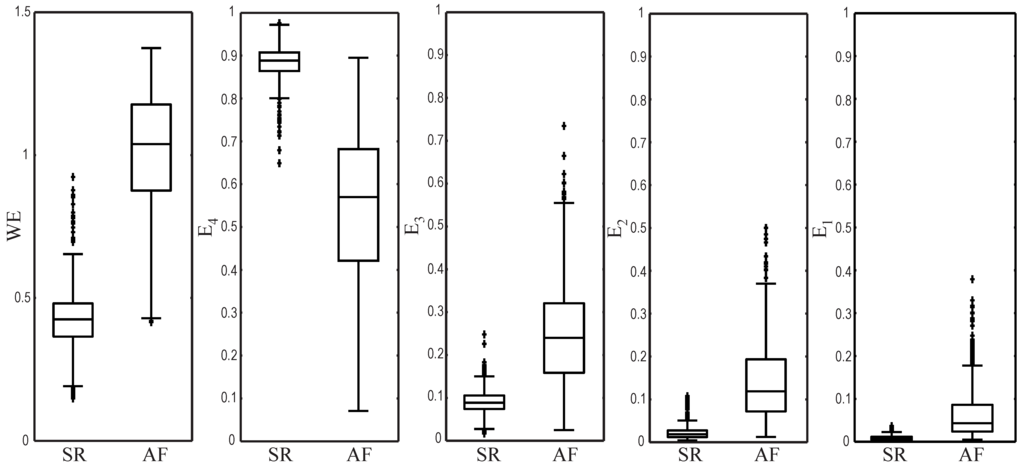
Figure 6.
Boxplots showing the distribution of all the analyzed metrics from the test set.
4. Discussion
To the best of our knowledge, the present work has introduced for the first time the application of WE to detect the rhythm transition from SR to AF and vice versa automatically. Basically, this metric has served to quantify the TQ interval waveform regularity, thus being able to discern among noise, P-waves and f-waves. Although noise robustness is of paramount relevance in AF long-term monitoring, it has not received much attention in previous works [39]. Nonetheless, every short-time method relying on the atrial activity analysis reflected by the ECG will have to consider very carefully the presence of noise. In fact, P- or f-waves can only be properly detected when they are not completely masked by noise. A proper noise identification methodology also plays a key role in AF patients presenting a regular heart rate. To this respect, given that noise does not affect the RR interval, previous algorithms have only paid attention to heart rate variability with the aim to discern the patient’s rhythm [39]. However, these methods will fail for those patients under pharmacologically-controlled heart rate, as well as in those cases lacking significant heart rate variability. An example in this line is illustrated by the two ECG segments presented in Figure 7. Both excerpts show a regular RR series, but the first interval contains an SR episode, whereas the second one is AF. As can be observed, the proper patient’s rhythm identification by using both RR series variability and P-wave-based algorithms is impossible in the presence of noise.
In the proposed algorithm, noisy beats were firstly detected by computing WE in a beat-to-beat fashion (see Figure 1). This approach allowed the successful identification of about 97% of the noisy TQ intervals manually annotated, with an error rate of misclassified non-noisy beats of about 2%. It should also be mentioned that a very similar result was obtained when another entropy metric, such as sample entropy (SampEn), was used instead of WE. SampEn was tested because it has proven recently to have a high ability to identify noise in the ECG [54]. On the other hand, it is interesting to remark that although the method has been developed for single-lead ECG recordings, detection of noisy beats could be helpful in multi-lead ECG environments to improve the proposed method’s robustness. Thus, when a TQ interval is marked as noisy from the studied lead, it could be analyzed from other leads, which eventually would have been less affected by noise [24].
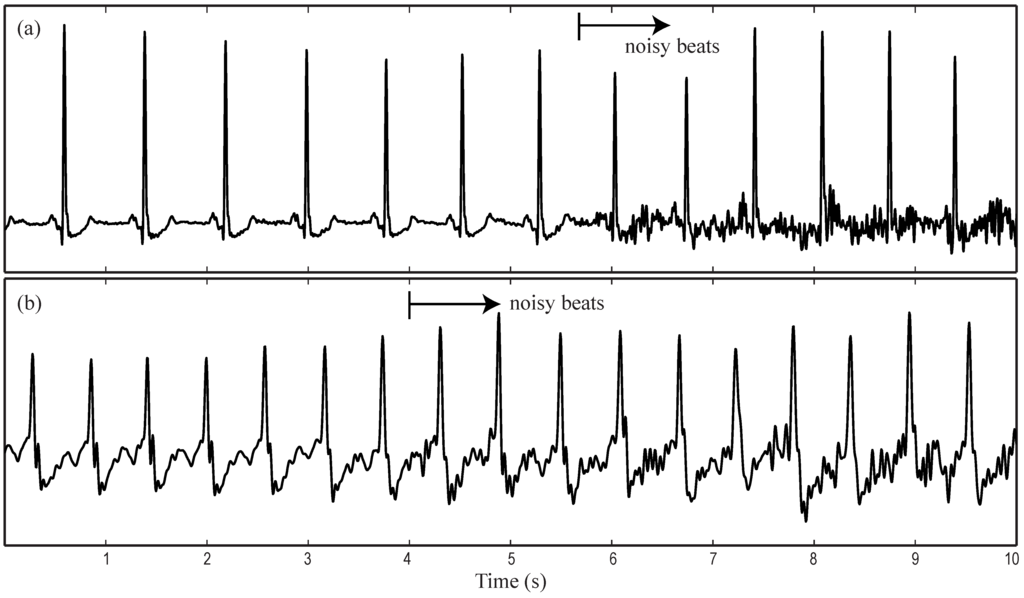
Figure 7.
ECG intervals with regular RR series and noise presence obtained from (a) sinus rhythm (SR) and (b) atrial fibrillation (AF) episodes.
In contrast to the beat-to-beat strategy to detect noisy beats, the second stage of the proposed algorithm allowed the discrimination between SR and AF beats by computing the median of 10 noise-free TQ intervals. Although WE results from signal-averaged and beat-to-beat approaches should not be strictly compared, it is interesting to note that an increasing trend in WE from SR beats to AF beats and then to noisy beats was clearly observed. This behavior could be expected because the P-wave normally presents a well-known Gaussian waveform [48]; the f-waves present rapid variations in time, shape and timing [22]; and finally, the noise contains completely chaotic variations. Furthermore, results from the relative energy for the four analyzed wavelet scales also lend support to this idea. Indeed, as can be observed from Table 1 and Table 2 and Figure 5 and Figure 6, whereas the P-wave presented its energy mainly concentrated on the fourth scale, AF beats provided a wider energy distribution among all the scales.
Analysis of the median TQ interval is justified from the results displayed in Figure 3a. It can be seen that WE computed beat-to-beat (i.e., for beat) only provided an accuracy of about 75%. However, the classification rate directly increased as a function of L up to a value of about 97% for L = 20 beats. A reasonable explanation for this trend is due to the improvement in the signal-to-noise ratio of a P-wave as the number of considered TQ intervals in SR increases; thus, a clearer P-wave can be obtained [55]. Conversely, when TQ intervals only related to AF are considered to obtain their median, f-waves tend to be attenuated because, as previously mentioned, they present random morphological variations [22]. Hence, the proposed methodology is also able to expand the contrast between TQ intervals belonging to SR and AF beats as a function of L. Precisely, this way of working makes the method able to discern appropriately between very low amplitude P- and f-waves. Thus, whenever a distinguishable P-wave can be found in the TQ interval, it will be highlighted by the signal-averaging approach. On the contrary, if low amplitude and variable f-waves are presented, their median will result in a more chaotic signal.
However, the median TQ interval computation also provoked a transition delay in rhythm detection (see Figure 4), being greater as the number of considered beats increased (see Figure 3b). Thus, a proper trade-off between accuracy and transition delay is a key aspect for the algorithm. In fact, the highest accuracy can only be achieved at the cost of some transition delay, which may cause very short AF episodes to remain unseen [29]. Nonetheless, the chosen value of beats provided a high accuracy of 95.28% with a transition delay lower than previous works. Indeed, whereas the proposed algorithm provided a mean delay of about five beats, other methods have reported delays of seven beats [24], 12 beats [30], 18 beats [28], 70 beats [29] or greater [27]. Moreover, although Lee et al. [56] were able to decrease the transition delay down to only six beats; an accuracy lower than 92% was reported in this case. It is also significant to note that the transition delay for the proposed algorithm increased notably with beats, but its accuracy was only improved by 1%, approximately.
It should be remarked that any proposed method will be unable to detect AF episodes shorter than its transition delay. Hence, for a value of beats, only SR and AF episodes shorter than five beats could remain unseen. This result improves most of the previous works where only episodes with several tens of beats in length were appropriately identified [28,29]. Only a recent work has reported comparable results being able to detect AF episodes as short as five beats under some special circumstances [39]. The method requires two ECG leads, one of them close to the atria, like V1, and the other one positioned away from the atria, like V6. This requirement would involve de facto standard ECG recordings of 12 leads, in contrast to the proposed method based on a single lead. Furthermore, Petrenas et al. [39] did not make use of the MIT-BIH database, in which two leads’ noisy problematic recordings sampled at 250 Hz and 12-bit resolution can be found. They used a 12-lead ECG database with recordings sampled at 1 kHz and 16-bit resolution, thus preventing a direct comparison with other methods.
Regarding previous works validated on the same database used here, i.e., the MIT-BIH AF database, Table 3 summarizes the best performing AF detectors. In general terms, the proposed method provided comparable sensitivity, specificity and accuracy values to most of them. Indeed, it was equally sensitive, but slightly less specific. The present algorithm also improved the accuracy reported by the two previous methods based on analyzing the P-wave absence [23,24]. Furthermore, in contrast to Ladavich and Ghoraani [24], it does not require an initial long-term training (at least 35 min) for every patient under analysis.

Table 3.
Performance comparison of AF detectors that have been validated making use of the MIT-BIH AF Database.
| Algorithm | Sensitivity | Specificity | Accuracy | Delay | Methodology |
|---|---|---|---|---|---|
| Slocum et al. [23] | 62.80% | 77.46% | – | – | Frequency analysis of the residual signal after QRST cancellation. |
| Tateno and Glass [27] | 94.40% | 97.20% | – | – | Kolmogorov–Smirnov test from histograms of difference between two successive RR intervals. |
| Dash et al. [28] | 94.40% | 95.10% | – | 18 beats | Analysis of randomness, variability and complexity of RR interval combined by simple rules. |
| Babaeizadeh et al. [34] | 92.00% | 95.50% | – | – | Information combined by a decision tree from RR and PR intervals variability and the P-wave similarity. |
| Huang et al. [29] | 96.10% | 98.10% | – | 70 beats | Analysis of the density histogram of delta RR intervals with several statistical features. |
| Lake and Moorman [30] | 91.00% | 94.00% | – | 12 beats | Analysis of RR interval regularity by using the coefficient of sample entropy. |
| Jiang et al. [36] | 98.20% | 97.50% | – | – | Analysis of RR interval density histograms combined with the P-wave presence study. |
| Lee et al. [56] | 98.20% | 97.70% | – | ≈ 12 beats | Analysis of RR interval variability with time-varying coherence functions and Shannon entropy. |
| Zhou et al. [32] | 96.89% | 98.25% | 97.67% | – | Analysis of RR interval regularity by applying nonlinear/linear integer filters, symbolic dynamics and Shannon entropy. |
| Ladavich and Ghoraani [24] | 98.09% | 91.66% | 93.22% | 7 beats | Analysis of the P-wave absence by using a Gaussian mixture model. |
| This work | 96.47% | 94.19% | 95.28% | 5 beats | Analysis of the median TQ interval by using WE. |
The effect of including noisy beats on the classification performance was also analyzed. Thus, for every beat, WE was computed from the median TQ interval obtained by considering its preceding L beats, such that normal and noisy beats could be included. In this case, sensitivity, specificity and accuracy were 96.22%, 89.89% and 91.26%, respectively. As expected, whereas sensitivity was only decreased by 0.25%, the decrease in specificity was greater (4.3%). Indeed, noise increases notably the WE values computed from the TQ interval, and therefore, there is a high probability that noisy beats are classified into the AF group. Thus, because most of the noisy beats related to AF were properly classified, sensitivity was not significantly altered. On the contrary, specificity was decreased given that most of the noisy beats related to SR were inappropriately identified as AF beats. Anyway, accuracy was only decreased by 4.02%, and therefore, it is still comparable to most of the previous works.
Moreover, although the step of rejection of noisy beats improved the classification results, rejecting some beats that will make no contribution either to AF nor to SR detection seems reasonable. In fact, most of the previous works also required discarding some beats for an appropriate validation of the algorithms. In this respect, Ladavich and Ghoraani [24] did not consider three entire recordings, because they did not contain sufficient SR data to train the method. Similarly, other methods also discarded several full recordings, since their R-peak annotations available from PhysioNet contained errors [28,31,32]. Finally, most of the algorithms based on quantifying RR variability required a filtering of ectopic beats [28,29,31]. In this line, atrial and ventricular premature complexes often provoke heart rate alterations, which can lead to numerous false AF detections [30,34]. Hence, since these ectopics occur quite commonly in AF patients [39], these algorithms required a first step to identify and exclude atrial and ventricular premature complexes. As another advantage of the proposed algorithm, it precludes this requirement, because the presence of an ectopic does not significantly alter the median TQ interval, and hence, the abnormal beat will be classified according to its L preceding normal complexes.
The transition delay from SR to AF and vice versa was also studied without rejecting noisy beats. The obtained results showed that delay only increased slightly for every value of L (0.306 ± 0.148 beats on average). This excellent result can be explained by the fact that the probability of finding noisy beats around the transition of SR to AF or vice versa is quite limited. Indeed, most of the patients (15 out of 23) presented less than eight AF episodes and only about 10% of noisy beats. This argument is also coherent with the finding that the difference between delays with or without rejection of noisy beats increased as a function of L. Thus, whereas the mean delay difference was 0.26 beats for , it was 0.32 beats for .
Finally, some limitations merit consideration. First, the proposed method validation was conducted on a limited group of patients. Nonetheless, the studied MIT-BIH AF Database is the most popular available dataset for AF detection, and therefore, its use is required to honestly compare the obtained results with previously-published algorithms. On the other hand, only one lead was analyzed, thus rejecting the possible information contained in the other available lead. However, it is important to note that the method could work successfully under multi-lead scenarios, because the P-wave is present in every ECG lead. Hence, it could be applied over the most interesting lead, from the atrial activity point of view. Thus, the method should analyze Lead V1 or Lead II, because they present higher P-wave amplitudes than the remaining standard ECG leads. These leads are commonly acquired by Holter systems, even in the case of recording a limited number of leads. In this respect, the signal selection strategy in the present work was based on getting the lead with the largest P-wave, because no information about the acquired leads was provided from PhysioNet. Lastly, it should be mentioned that the proposed method is computationally expensive, because WE has to be computed twice for each beat. Nevertheless, because it only requires information from the last 10 noise-free beats to identify the patient’s rhythm, it could be implemented to work in a real-time beat-by-beat way, thus providing continuous ECG monitoring facilities.
5. Conclusions
This work has proven for the first time how the application of WE is able to discern successfully between SR and AF by only analyzing the atrial electrical activity from single-lead ECGs. The proposed algorithm could be used in a wide range of patients, including those under rate-control therapy or with a reduced heart rate variability during AF. Compared to previous AF detectors, the algorithm reported a similar classification performance with the additional advantages of a shorter transition delay, as well as the ability to detect episodes as brief as five beats in length. Furthermore, the method relies on a single metric, which is able to provide an easily-interpretable result. Finally, it presents significant integration facilities under real-time beat-by-beat ECG monitoring systems, thus allowing clinicians the automatic detection of very brief AF episodes, which are very common during the initial stages of the arrhythmia.
Acknowledgments
This work was supported by the projects TEC2014–52250–R from the Spanish Ministry of Economy and Competitiveness and PPII–2014–026–P from Junta de Comunidades de Castilla La Mancha.
Author Contributions
Juan Ródenas and Manuel García designed the study, analyzed the data, interpreted the results and drafted the manuscript. Raúl Alcaraz and José J. Rieta designed the study, interpreted the results and wrote the final manuscript. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Drachman, D.A. Aging of the Brain, Entropy, and Alzheimer Disease. Neurology 2006, 67, 1340–1352. [Google Scholar] [CrossRef] [PubMed]
- Schulz, S.; Bär, K.J.; Voss, A. Analyses of Heart Rate, Respiration and Cardiorespiratory Coupling in Patients with Schizophrenia. Entropy 2015, 17, 483–501. [Google Scholar] [CrossRef]
- Du, Q.; Nie, K.; Wang, Z. Application of Entropy-Based Attribute Reduction and an Artificial Neural Network in Medicine: A Case Study of Estimating Medical Care Costs Associated with Myocardial Infarction. Entropy 2014, 16, 4788–4800. [Google Scholar] [CrossRef]
- Alcaraz, R.; Rieta, J.J. A Review on Sample Entropy Applications for the Non-invasive Analysis of Atrial Fibrillation Electrocardiograms. Biomed. Signal Process. Control 2010, 5, 1–14. [Google Scholar] [CrossRef]
- Umar, H. Clinical Decision-Making Using Computers: Opportunities and Limitations. Dent. Clin. North Am. 2002, 46, 521–538. [Google Scholar] [CrossRef]
- Belle, A.; Kon, M.A.; Najarian, K. Biomedical Informatics for Computer-Aided Decision Support Systems: A Survey. Sci. World J. 2013, 2013, 769639. [Google Scholar] [CrossRef] [PubMed]
- Rosso, O.A.; Blanco, S.; Yordanova, J.; Kolev, V.; Figliola, A.; Schürmann, M.; Başar, E. Wavelet Entropy: A New Tool for Analysis of Short Duration Brain Electrical Signals. J. Neurosci. Methods 2001, 105, 65–75. [Google Scholar] [CrossRef]
- Frantzidis, C.A.; Vivas, A.B.; Tsolaki, A.; Klados, M.A.; Tsolaki, M.; Bamidis, P.D. Functional Disorganization of Small-World Brain Networks in Mild Alzheimer’s Disease and Amnestic Mild Cognitive Impairment: An EEG Study Using Relative Wavelet Entropy (RWE). Front. Aging Neurosci. 2014, 6. [Google Scholar] [CrossRef] [PubMed]
- Alcaraz, R.; Rieta, J.J. Application of Wavelet Entropy to Predict Atrial Fibrillation Progression from the Surface ECG. Comput. Math. Methods Med. 2012, 2012, 245213. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Hu, X.; Yao, D. Improved Wavelet Entropy Calculation with Window Functions and Its Preliminary Application to Study Intracranial Pressure. Comput. Biol. Med. 2013, 43, 425–433. [Google Scholar] [CrossRef] [PubMed]
- Cek, M.E.; Ozgoren, M.; Savaci, F.A. Continuous Time Wavelet Entropy of Auditory Evoked Potentials. Comput. Biol. Med. 2010, 40, 90–96. [Google Scholar] [PubMed]
- Fuster, V.; Rydén, L.E.; Cannom, D.S.; Crijns, H.J.; Curtis, A.B.; Ellenbogen, K.A.; Halperin, J.L.; Kay, G.N.; Le Huezey, J.Y.; Lowe, J.E.; et al. 2011 ACCF/AHA/HRS Focused Updates Incorporated into the ACC/AHA/ESC 2006 Guidelines for the Management of Patients with Atrial Fibrillation: A Report of the American College of Cardiology Foundation/American Heart Association Task Force on Practice Guidelines. Circulation 2011, 123, e269–e367. [Google Scholar] [PubMed]
- Gillis, A.M.; Krahn, A.D.; Skanes, A.C.; Nattel, S. Management of Atrial Fibrillation in the Year 2033: New Concepts, Tools, and Applications Leading to Personalized Medicine. Can. J. Cardiol. 2013, 29, 1141–1146. [Google Scholar] [CrossRef] [PubMed]
- January, C.T.; Wann, L.S.; Alpert, J.S.; Calkins, H.; Cigarroa, J.E.; Cleveland, J.C., Jr.; Conti, J.B.; Ellinor, P.T.; Ezekowitz, M.D.; Field, M.E.; et al. 2014 AHA/ACC/HRS Guideline for the Management of Patients with Atrial Fibrillation: Executive Summary: A Report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines and the Heart Rhythm Society. Circulation 2014, 130, e199–e267. [Google Scholar] [CrossRef] [PubMed]
- Hart, R.G.; Pearce, L.A.; Aguilar, M.I. Meta-analysis: Antithrombotic Therapy to Prevent Stroke in Patients Who Have Nonvalvular Atrial Fibrillation. Ann. Intern. Med. 2007, 146, 857–867. [Google Scholar] [CrossRef] [PubMed]
- Blomstrom Lundqvist, C.; Lip, G.Y.H.; Kirchhof, P. What Are the Costs of Atrial Fibrillation? Europace 2011, 13, ii9–ii12. [Google Scholar] [CrossRef] [PubMed]
- Asgari, S.; Mehrnia, A.; Moussavi, M. Automatic Detection of Atrial Fibrillation Using Stationary Wavelet Transform and Support Vector Machine. Comput. Biol. Med. 2015, 60, 132–142. [Google Scholar] [CrossRef] [PubMed]
- Israel, C.W.; Grönefeld, G.; Ehrlich, J.R.; Li, Y.G.; Hohnloser, S.H. Long-Term Risk of Recurrent Atrial Fibrillation as Documented by an Implantable Monitoring Device: Implications for Optimal Patient Care. J. Am. Coll. Cardiol. 2004, 43, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Q.; Proietti, M.; Senoo, K.; Lip, G.Y.H. Asymptomatic versus Symptomatic Atrial Fibrillation: A Systematic Review of Age/Gender Differences and Cardiovascular Outcomes. Int. J. Cardiol. 2015, 191, 172–177. [Google Scholar] [CrossRef] [PubMed]
- Strickberger, S.A.; Ip, J.; Saksena, S.; Curry, K.; Bahnson, T.D.; Ziegler, P.D. Relationship between Atrial Tachyarrhythmias and Symptoms. Heart Rhythm 2005, 2, 125–131. [Google Scholar] [CrossRef] [PubMed]
- Quinn, F.R.; Gladstone, D. Screening for Undiagnosed Atrial Fibrillation in the Community. Curr. Opin. Cardiol. 2014, 29, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Petrutiu, S.; Ng, J.; Nijm, G.M.; Al-Angari, H.; Swiryn, S.; Sahakian, A.V. Atrial Fibrillation and Waveform Characterization. A Time Domain Perspective in the Surface ECG. IEEE Eng. Med. Biol. Mag. 2006, 25, 24–30. [Google Scholar] [CrossRef] [PubMed]
- Slocum, J.; Sahakian, A.; Swiryn, S. Diagnosis of Atrial Fibrillation from Surface Electrocardiograms Based on Computer-Detected Atrial Activity. J. Electrocardiol. 1992, 25, 1–8. [Google Scholar] [CrossRef]
- Ladavich, S.; Ghoraani, B. Rate-independent Detection of Atrial Fibrillation by Statistical Modeling of Atrial Activity. Biomed. Signal Process. Control 2015, 18, 274–281. [Google Scholar] [CrossRef]
- Larburu, N.; Lopetegi, T.; Romero, I. Comparative Study of Algorithm for Atrial Fibrillation Detection. In Proceedings of the 2011 Computing in Cardiology, Hangzhou, China, 18–21 September 2011; Vol. 38, pp. 265–268.
- Zhang, Y.; Mazgalev, T.N. Ventricular Rate Control during Atrial Fibrillation and AV Node Modifications: Past, Present, and Future. Pacing Clin. Electrophysiol. 2004, 27, 382–393. [Google Scholar] [CrossRef] [PubMed]
- Tateno, K.; Glass, L. Automatic Detection of Atrial Fibrillation Using the Coefficient of Variation and Density Histograms of RR and ΔRR Intervals. Med. Biol. Eng. Comput. 2001, 39, 664–671. [Google Scholar] [CrossRef] [PubMed]
- Dash, S.; Chon, K.H.; Lu, S.; Raeder, E.A. Automatic Real Time Detection of Atrial Fibrillation. Ann. Biomed. Eng. 2009, 37, 1701–1709. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Ye, S.; Chen, H.; Li, D.; He, F.; Tu, Y. A Novel Method for Detection of the Transition between Atrial Fibrillation and Sinus Rhythm. IEEE Trans. Biomed. Eng. 2011, 58, 1113–1139. [Google Scholar] [CrossRef] [PubMed]
- Lake, D.E.; Moorman, J.R. Accurate Estimation of Entropy in very Short Physiological Time Series: The Problem of Atrial Fibrillation Detection in Implanted Ventricular Devices. Am. J. Physiol. Heart Circ. Physiol. 2011, 300, H319–H325. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Reyes, B.A.; McManus, D.D.; Maitas, O.; Mathias, O.; Chon, K.H. Atrial Fibrillation Detection Using an iPhone 4S. IEEE Trans. Biomed. Eng. 2013, 60, 203–206. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Ding, H.; Ung, B.; Pickwell-MacPherson, E.; Zhang, Y. Automatic Online Detection of Atrial Fibrillation Based on Symbolic Dynamics and Shannon Entropy. Biomed. Eng. Online 2014, 13. [Google Scholar] [CrossRef] [PubMed]
- Seet, R.C.S.; Friedman, P.A.; Rabinstein, A.A. Prolonged Rhythm Monitoring for the Detection of Occult Paroxysmal Atrial Fibrillation in Ischemic Stroke of Unknown Cause. Circulation 2011, 124, 477–486. [Google Scholar] [CrossRef] [PubMed]
- Babaeizadeh, S.; Gregg, R.E.; Helfenbein, E.D.; Lindauer, J.M.; Zhou, S.H. Improvements in Atrial Fibrillation Detection for Real-time Monitoring. J. Electrocardiol. 2009, 42, 522–526. [Google Scholar] [CrossRef] [PubMed]
- De Carvalho, P.; Henriques, J.; Couceiro, R.; Harris, M.; Antunes, M. Model-Based Atrial Fibrillation Detection. In ECG Signal Processing, Classification and Interpretation; Springer: London, UK, 2012; pp. 99–133. [Google Scholar]
- Jiang, K.; Huang, C.; Ye, S.M.; Chen, H. High Accuracy in Automatic Detection of Atrial Fibrillation for Holter Monitoring. J. Zhejiang Univ. Sci. B. 2012, 13, 751–756. [Google Scholar] [CrossRef] [PubMed]
- Pürerfellner, H.; Pokushalov, E.; Sarkar, S.; Koehler, J.; Zhou, R.; Urban, L.; Hindricks, G. P-Wave Evidence as a Method for Improving Algorithm to Detect Atrial Fibrillation in Insertable Cardiac Monitors. Heart Rhythm 2014, 11, 1575–1583. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Rao, N.; Qian, M.; Liu, D.; Li, J.; Feng, W.; Yin, L.; Chen, X. A Novel Method for Real-Time Atrial Fibrillation Detection in Electrocardiograms Using Multiple Parameters. Ann. Noninvasive Electrocardiol. 2014, 19, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Petrėnas, A.; Sörnmo, L.; Lukoševičius, A.; Marozas, V. Detection of Occult Paroxysmal Atrial Fibrillation. Med. Biol. Eng. Comput. 2015, 53, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Lévy, S.; Breithardt, G.; Campbell, R.W.; Camm, A.J.; Daubert, J.C.; Allessie, M.; Aliot, E.; Capucci, A.; Cosio, F.; Crijns, H.; et al. Atrial Fibrillation: Current Knowledge and Recommendations for Management. Working Group on Arrhythmias of the European Society of Cardiology. Eur. Heart J. 1998, 19, 1294–1320. [Google Scholar] [CrossRef] [PubMed]
- Holmqvist, F.; Carlson, J.; Waktare, J.E.P.; Platonov, P.G. Noninvasive Evidence of Shortened Atrial Refractoriness during Sinus Rhythm in Patients with Paroxysmal Atrial Fibrillation. Pacing Clin. Electrophysiol. 2009, 32, 302–307. [Google Scholar] [CrossRef] [PubMed]
- Blanche, C.; Tran, N.; Carballo, D.; Rigamonti, F.; Burri, H.; Zimmermann, M. Usefulness of P-Wave Signal Averaging to Predict Atrial Fibrillation Recurrences after Electrical Cardioversion. Ann. Noninvasive Electrocardiol. 2014, 19, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Blanche, C.; Tran, N.; Rigamonti, F.; Burri, H.; Zimmermann, M. Value of P-Wave Signal Averaging to Predict Atrial Fibrillation Recurrences after Pulmonary Vein Isolation. Europace 2013, 15, 198–204. [Google Scholar] [CrossRef] [PubMed]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Taha, B.; Reddy, S.; Xue, Q.; Swiryn, S. Automated Discrimination between Atrial Fibrillation and Atrial Flutter in the Resting 12-Lead Electrocardiogram. J. Electrocardiol. 2000, 33, 123–125. [Google Scholar] [CrossRef] [PubMed]
- Christov, I.; Bortolan, G.; Daskalov, I. Automatic Detection of Atrial Fibrillation and Flutter by Wave Rectification Method. J. Med. Eng. Technol. 2001, 25, 217–221. [Google Scholar] [CrossRef] [PubMed]
- Dotsinsky, I.; Stoyanov, T. Optimization of Bi-directional Digital Filtering for Drift Suppression in Electrocardiogram Signals. J. Med. Eng. Technol. 2004, 28, 178–180. [Google Scholar] [CrossRef] [PubMed]
- Sörnmo, L.; Laguna, P. Biomedical Signal Processing in Cardiac and Neurological Applications (Biomedical Engineering); Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Martínez, A.; Alcaraz, R.; Rieta, J.J. Application of the Phasor Transform for Automatic Delineation of Single-Lead ECG Fiducial Points. Physiol. Meas. 2010, 31, 1467–1485. [Google Scholar] [CrossRef] [PubMed]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: Waltham, MA, USA, 1999. [Google Scholar]
- Addison, P.S. Wavelet Transforms and the ECG: A Review. Physiol. Meas. 2005, 26, R155–R199. [Google Scholar] [CrossRef] [PubMed]
- Rafiee, J.; Rafiee, M.A.; Prause, N.; Schoen, M.P. Wavelet Basis Functions in Biomedical Signal Processing. Expert Syst. Appl. 2011, 38, 6190–6201. [Google Scholar] [CrossRef]
- Arlot, S. A Survey of Cross-Validation Procedures for Model Selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Liu, C.; Li, P.; Di Maria, C.; Zhao, L.; Zhang, H.; Chen, Z. A Multi-step Method with Signal Quality Assessment and Fine-Tuning Procedure to Locate Maternal and Fetal QRS Complexes from Abdominal ECG Recordings. Physiol. Meas. 2014, 35, 1665–1683. [Google Scholar] [CrossRef] [PubMed]
- Censi, F.; Ricci, C.; Calcagnini, G.; Triventi, M.; Ricci, R.P.; Santini, M.; Bartolini, P. Time-Domain and Morphological Analysis of the P-Wave. Part I: Technical Aspects for Automatic Quantification of P-Wave Features. Pacing Clin. Electrophysiol. 2008, 31, 874–883. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Nam, Y.; McManus, D.D.; Chon, K.H. Time-Varying Coherence Function for Atrial Fibrillation Detection. IEEE Trans. Biomed. Eng. 2013, 60, 2783–2793. [Google Scholar] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).