Self-Similar Solutions of Rényi’s Entropy and the Concavity of Its Entropy Power
Abstract
:1. Introduction
2. Preliminaries
- (a)
- is a continuous () and strictly decreasing function in α unless f is the uniform density, in which case it is constant.Proof: By Hölder’s inequality, there is a family of relations:holding whenever and . Taking and assuming f to be a pdf, we have:Let and . Then, for , the previous inequality becomes:which, using that the logarithmic function is an increasing function, implies that . The same proof holds for .
- (b)
- as a function of α converges to the following limits:where is the Shannon entropy of f.
- (c)
- If the norm is invariant under the homogeneous dilations:then , for , scales as:
3. Formulation of the First Problem and Its Solutions
- (3α)
- The solution (). The requirement that is a pdf and the second moment constraint lead to the relation:We adopt the abbreviation for Euler’s beta function defined by for . Using (25), the exact solution can be expressed as:This one-parameter family of local maxima of is unique, and it remains to prove that it is actually also a one-parameter family of global maxima in . For this, we use the notion of the relative α-Rényi entropy of two densities and g, defined in [17] by:where g satisfies the same second moment constraint as . The first term in the right-hand side of (27) equals , as one may check, since . Therefore:by applying Hölder’s inequality to the functions and . The same result holds in the case.
- (3β)
- The l-differentiable compactly-supported solution (). In this case, following steps similar to the previous one, the solution turns out to be:where is the unit-step function and the arbitrary constant is specified as usual by imposing the requirement that be a pdf:
4. Formulation of the Second Problem and Its Solutions
- (4α)
- The solution (). The positivity of the solution requires and . The pdf, the mean value and the variance constraints lead to the conditions:Finally, the solution is written as:which is identical to the solution derived from the equivalent problem.
- (4α)
- The l-differentiable compactly-supported solution (). In this case, the polynomial should be positive between its real roots. This occurs provided that and . Using the indicator function , with the roots of the polynomial, we find the previous solution with a relative minus sign between the terms inside the parentheses, while the power is now positive.
5. Comparison with the FDE and PME Solutions
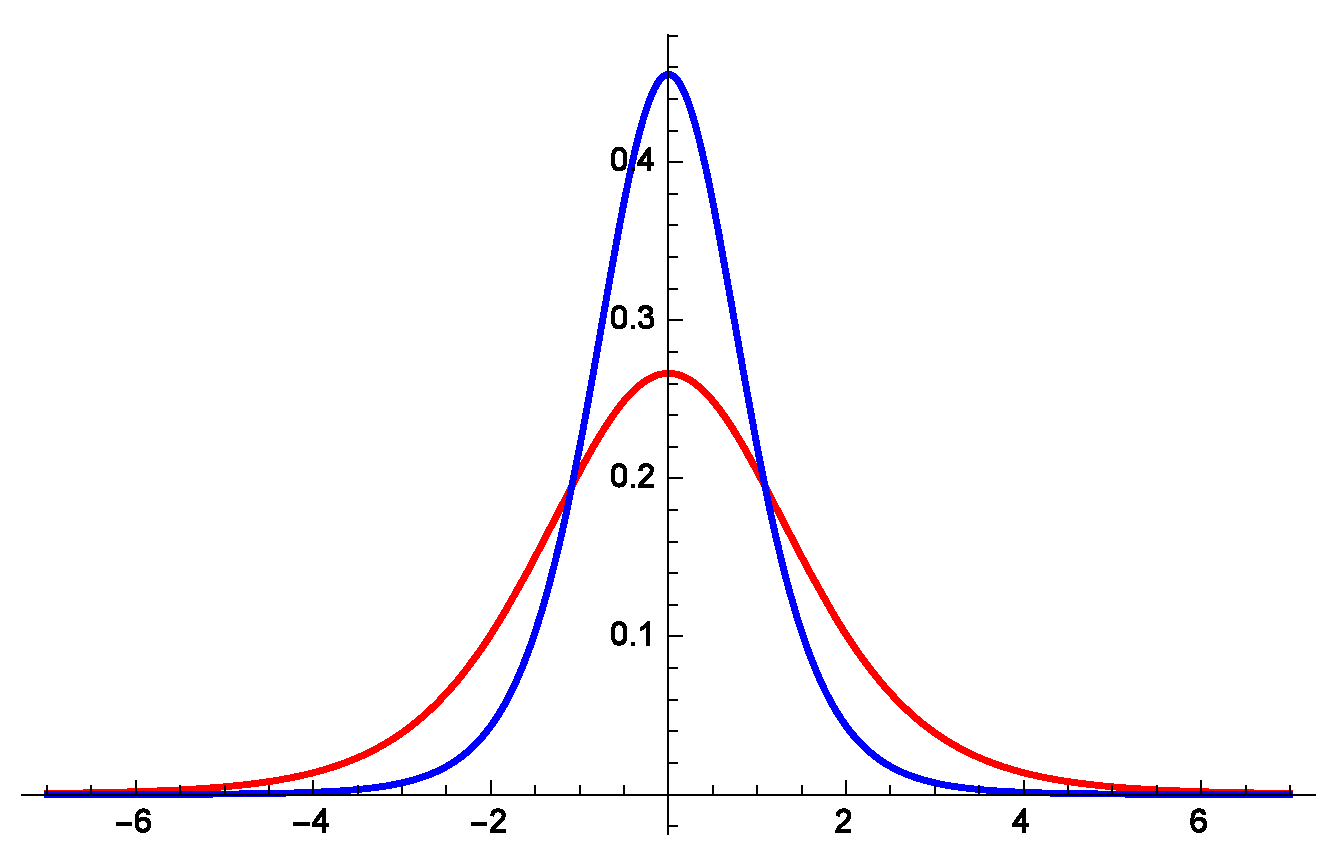
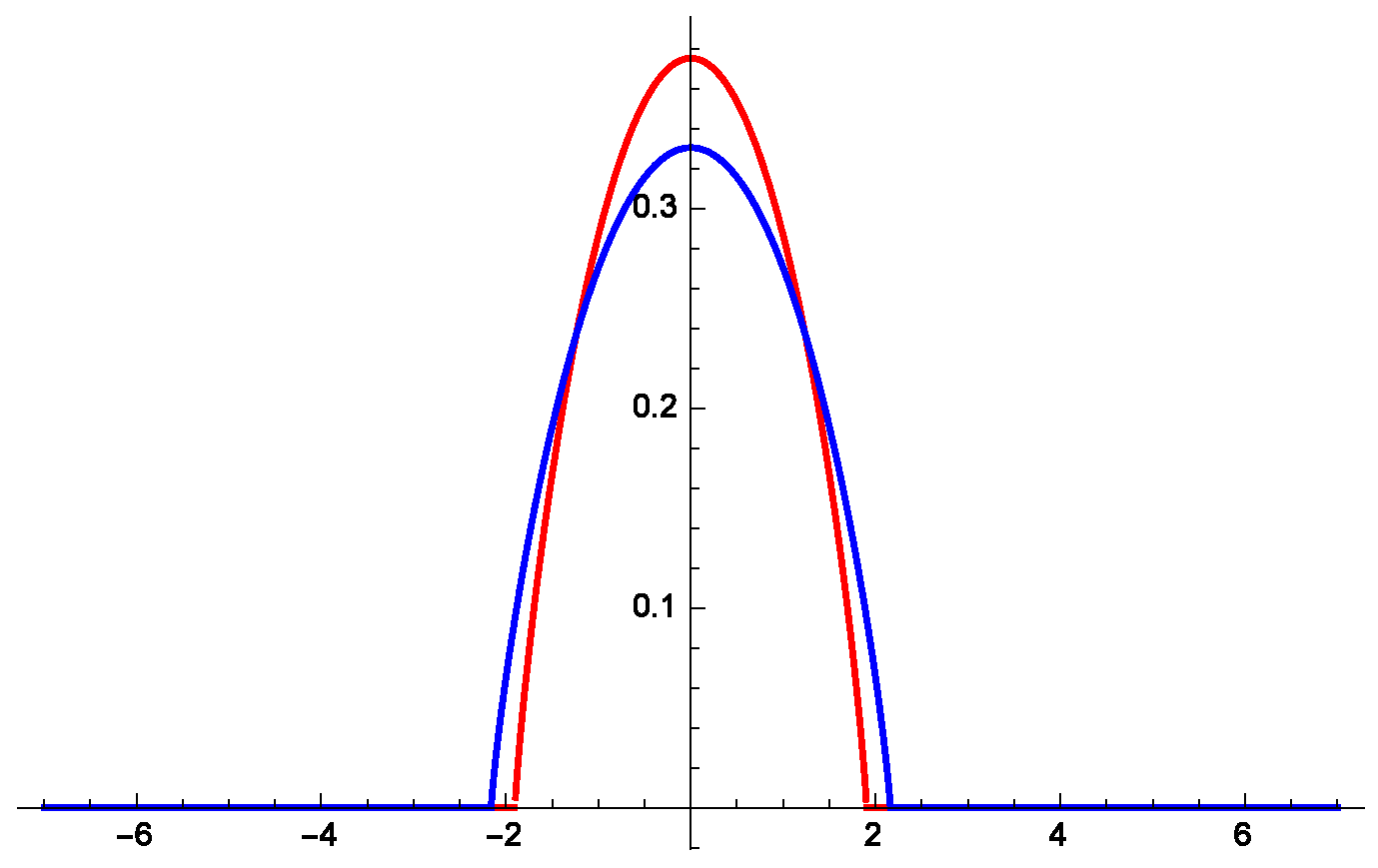
6. The Concavity of Rényi’s Entropy Power
7. Conclusion
Acknowledgements
Conflicts of Interest
Appendix A
References
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Evangelisti, S. Quantum Correlations in Field Theory and Integrable Systems; Minkowski Institute Press: Montreal, QC, Canada, 2013. [Google Scholar]
- Geman, D.; Jedynak, B. An active testing model for tracking roads in satellite images. IEEE Trans. Pattern Anal. Machine Intell. 1996, 1, 10–17. [Google Scholar] [CrossRef]
- Jenssen, R.; Hild, K.E.; Erdogmus, D.; Principe, J.C.; Eltoft, T. Clustering using Renyi’s Entropy. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; pp. 523–528.
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Maurer, U.M. Generalized privacy amplification. IEEE Trans. Inf. Theory 1995, 41, 1915–1923. [Google Scholar] [CrossRef]
- Sahoo, P.; Wilkins, V.; Yeager, J. Threshold selection using Reny’is entropy. Pattern Recognit. 1997, 30, 71–84. [Google Scholar] [CrossRef]
- Sankur, B.; Sezgin, M. Image thresholding techniques: A survey over categories. Pattern Recognit. 2001, 34, 1573–1607. [Google Scholar]
- Johnson, O.; Vignat, C. Some results concerning maximum Rényi entropy distributions. Annales de l’Institut Henri Poincare (B) 2007, 43, 339–351. [Google Scholar] [CrossRef]
- Barenblatt, G.I. On some unsteady motions of a liquid and gas in a porous medium. Prikl. Mat. Mec. 1952, 16, 67–78. [Google Scholar]
- Barenblatt, G.I. Scaling, Self-Similarity and Intermediate Asymptotics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Zeld’dovich, Y.B.; Kompaneets, A.S. Towards a theory of heat conduction with thermal conductivity depending on the temperature. In Collection of Papers Dedicated to 70th Birthday of Academician A. F. Ioffe; Izd. Akad. Nauk SSSR: Moscow, Russia, 1950; pp. 61–71. [Google Scholar]
- Villani, C. A short proof of the “concavity of entropy power”. IEEE Trans. Inf. Theory 2000, 46, 1695–1696. [Google Scholar] [CrossRef]
- Savaré, G.; Toscani, G. The concavity of Rényi entropy power. IEEE Trans. Inf. Theory 2014, 60, 2687–2693. [Google Scholar] [CrossRef]
- Liberzon, D. Calculus of Variations and Optimal Control Theory; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Havrda, M.; Charvát, F. Quantification method of classification processes: Concept of structural α-entropy. Kybernetika 1967, 3, 30–35. [Google Scholar]
- Tsallis, C. Possible generalizations of Boltzmann and Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Lutwak, E.; Yang, D.; Zhang, G. Cramér-Rao and moment-entropy inequalities for Rényi entropy and generalized Fisher information. IEEE Trans. Inf. Theory 2005, 51, 473–478. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Boston, MA, USA, 1994. [Google Scholar]
- Vázquez, J.L. The Porous Medium Equation: Mathematical Theory; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Aronson, D.G.; Bénilan, P. Régularité des solutions de l’équation des milieux poreux dans ℝn. C. R. Acad. Sci. Paris. Sér. 1979, A-B 288, 103–105. [Google Scholar]
- Li, P.; Yau, S.T. On the parabolic kernel of the Schrödinger operator. Acta Math. 1986, 56, 153–201. [Google Scholar] [CrossRef]
- Lu, P.; Ni, N.; Vázquez, L.J.; Villani, C. Local Aronson-Bénilan estimates and entropy formulae for porous medium and fast diffusion equations on manifolds. J. Math. Pures Appl. 2009, 91, 1–19. [Google Scholar] [CrossRef]
- Otto, F. The geometry of dissipative evolution equations: The porous medium equation. Commun. Partial Differ. Equ. 2001, 26, 101–174. [Google Scholar] [CrossRef]
- Tricomi, F.G.; Erdélyi, A. The asymptotic expansion of a ratio of gamma functions. Pacific J. Math. 1951, 1, 133–142. [Google Scholar] [CrossRef]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatzinikitas, A.N. Self-Similar Solutions of Rényi’s Entropy and the Concavity of Its Entropy Power. Entropy 2015, 17, 6056-6071. https://doi.org/10.3390/e17096056
Hatzinikitas AN. Self-Similar Solutions of Rényi’s Entropy and the Concavity of Its Entropy Power. Entropy. 2015; 17(9):6056-6071. https://doi.org/10.3390/e17096056
Chicago/Turabian StyleHatzinikitas, Agapitos N. 2015. "Self-Similar Solutions of Rényi’s Entropy and the Concavity of Its Entropy Power" Entropy 17, no. 9: 6056-6071. https://doi.org/10.3390/e17096056
APA StyleHatzinikitas, A. N. (2015). Self-Similar Solutions of Rényi’s Entropy and the Concavity of Its Entropy Power. Entropy, 17(9), 6056-6071. https://doi.org/10.3390/e17096056




