Binary Classification with a Pseudo Exponential Model and Its Application for Multi-Task Learning †
Abstract
:1. Introduction
2. Settings
3. Itakura–Saito Distance and Pseudo Model
3.1. Parameter Estimation with the Pseudo Model
3.2. Characterization of the Itakura–Saito Distance
3.3. Relationship with AdaBoost
4. Application for Multi-Task Learning
- Case 1 :
- There is a target dataset , and our interest is to construct a discriminant function utilizing remaining datasets () or a priori constructed discriminant functions ().
- Case 2 :
- Our interest is to simultaneously construct better discriminant functions using all J datasets by utilizing shared information among datasets.
4.1. Case 1
- (1)
- Initialize the function to , and define weights for the i-th example with a function F as:where:
- (2)
- For
- (a)
- Select a weak classifier , which minimizes the following quantity:where and .
- (b)
- Calculate a coefficient of by .
- (c)
- Update the discriminant function as .
- (3)
- Output .
4.2. Case 2
- (1)
- Initialize functions .
- (2)
- For :
- (a)
- Randomly choose a target index .
- (b)
- Update the function using the algorithm in Case 1 by S steps, with fixed functions ().
- (3)
- Output learned functions .
4.3. Statistical Properties of the Proposed Methods
4.4. Comparison of Regularization Terms
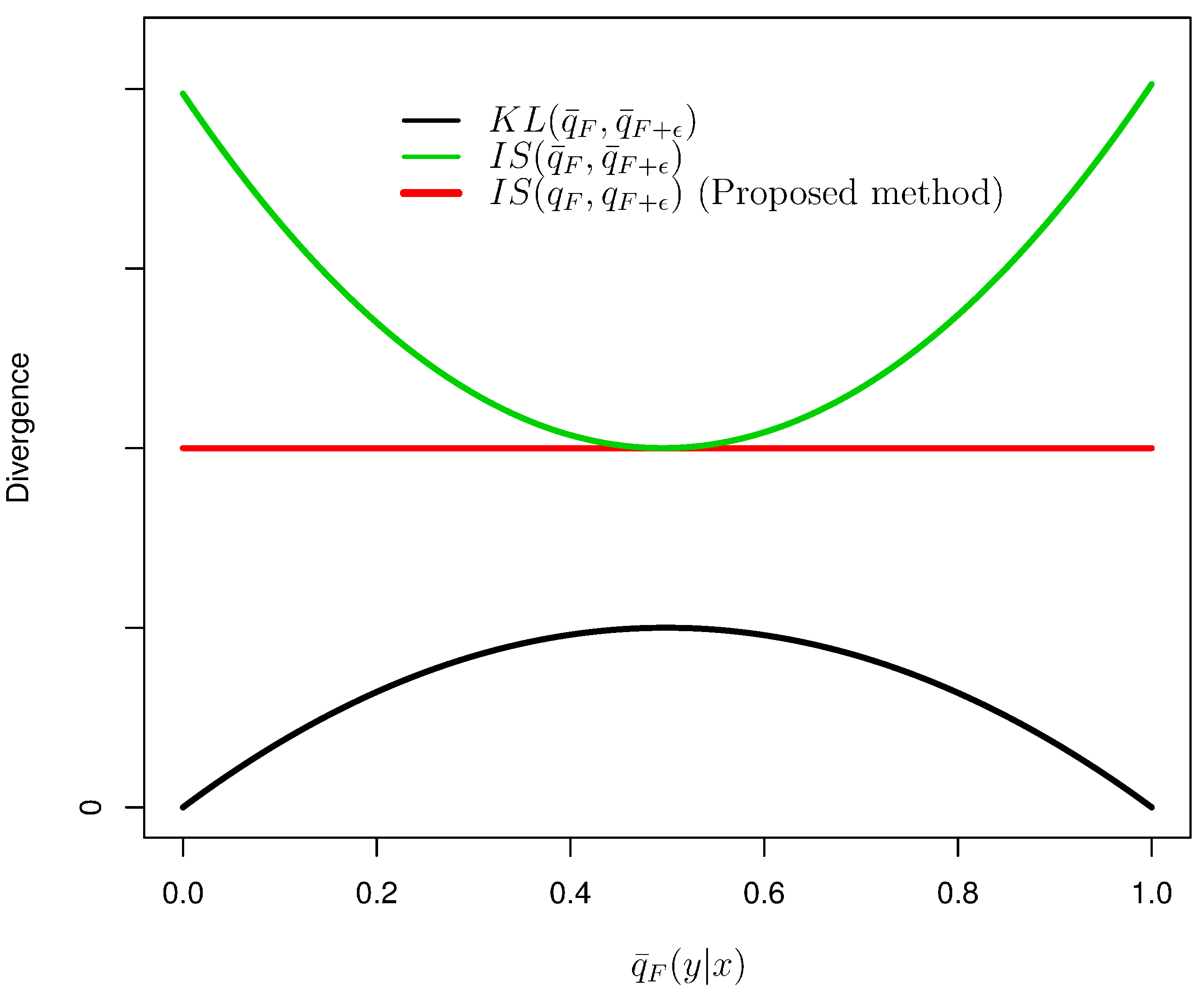
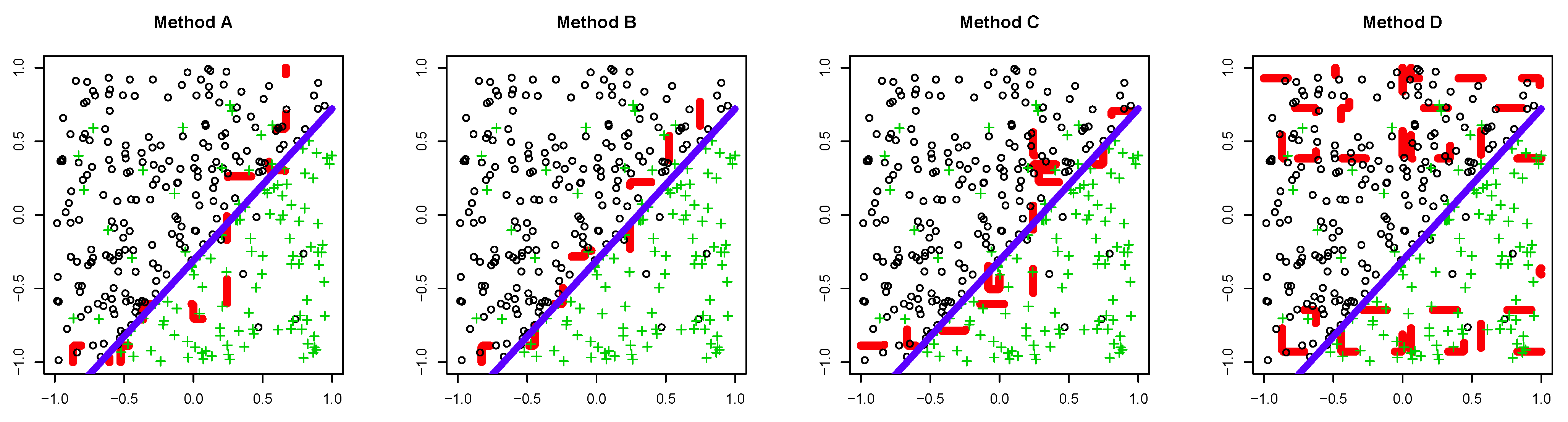
5. Experiments
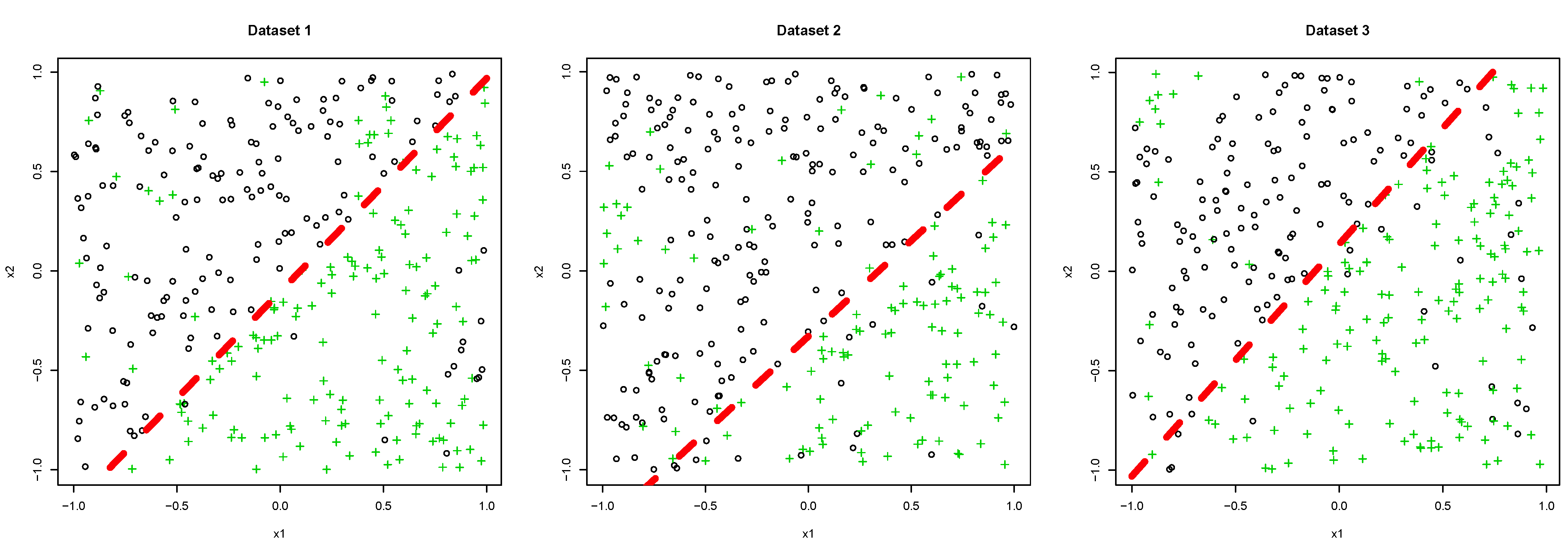
5.1. Synthetic Dataset
- We set that for all and determined λ.
- We set that where is a discriminant function constructed by AdaBoost with the dataset and determined λ.
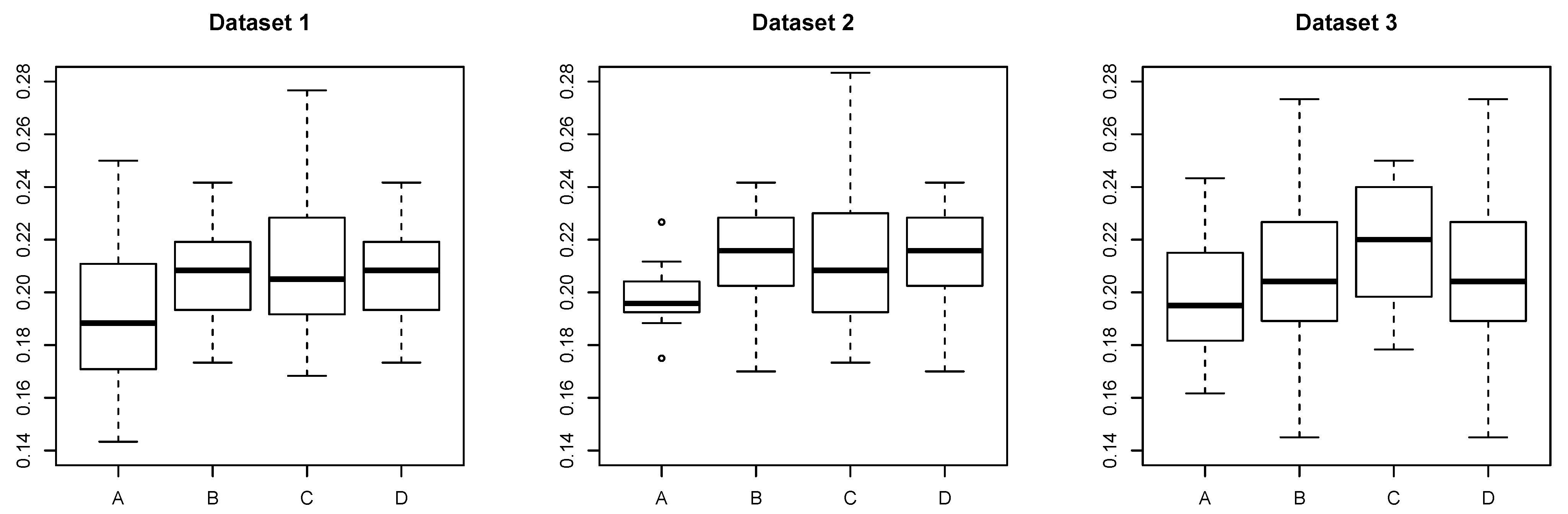
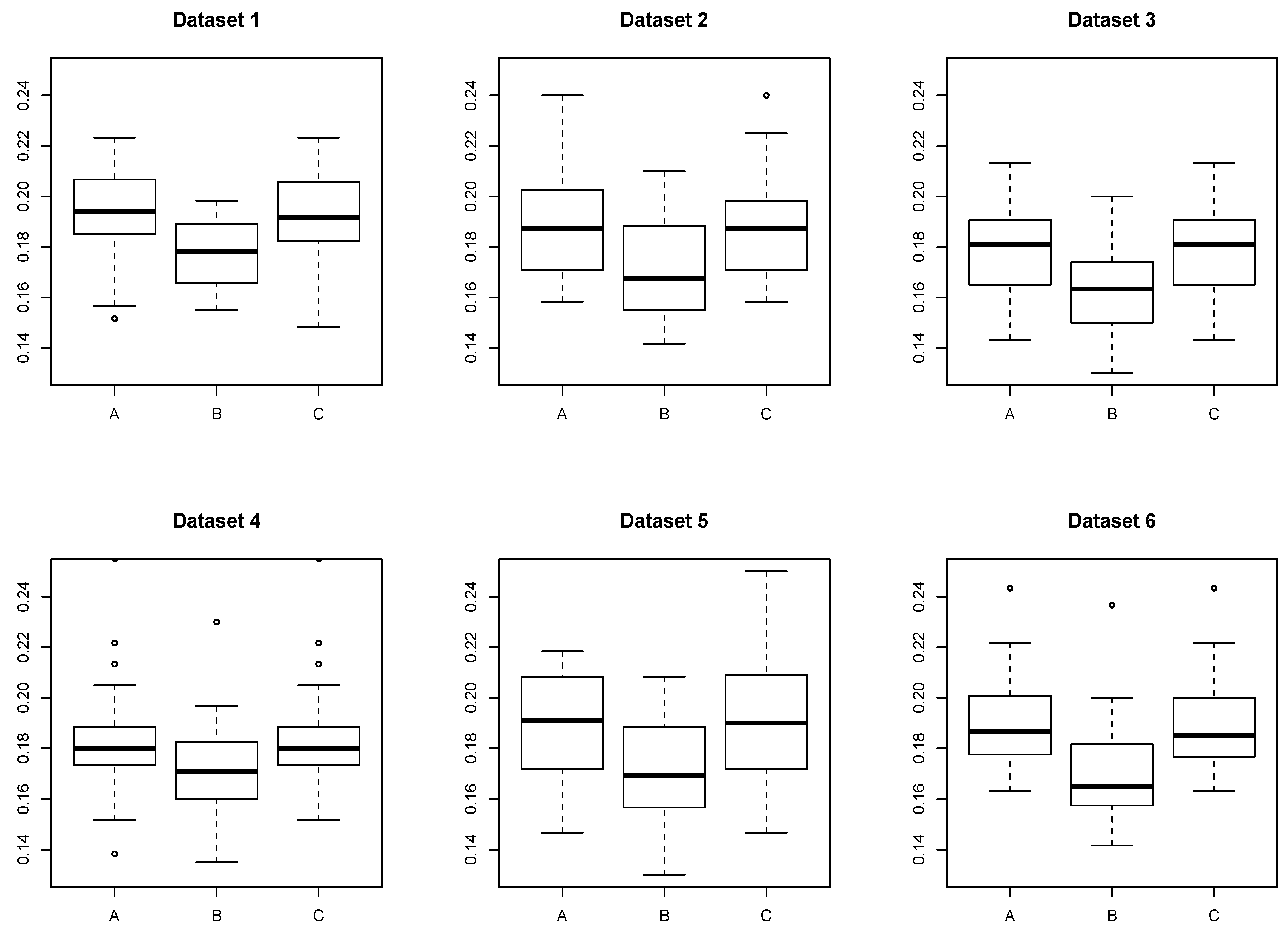
- A:
- The proposed method with determined by Scenario 1.
- B:
- The proposed method with determined by Scenario 2.
- C:
- AdaBoost trained with an individual dataset.
- D:
- AdaBoost trained with all datasets simultaneously.
5.1.1. Dataset 1
5.1.2. Dataset 2

5.2. Real Dataset: School Dataset
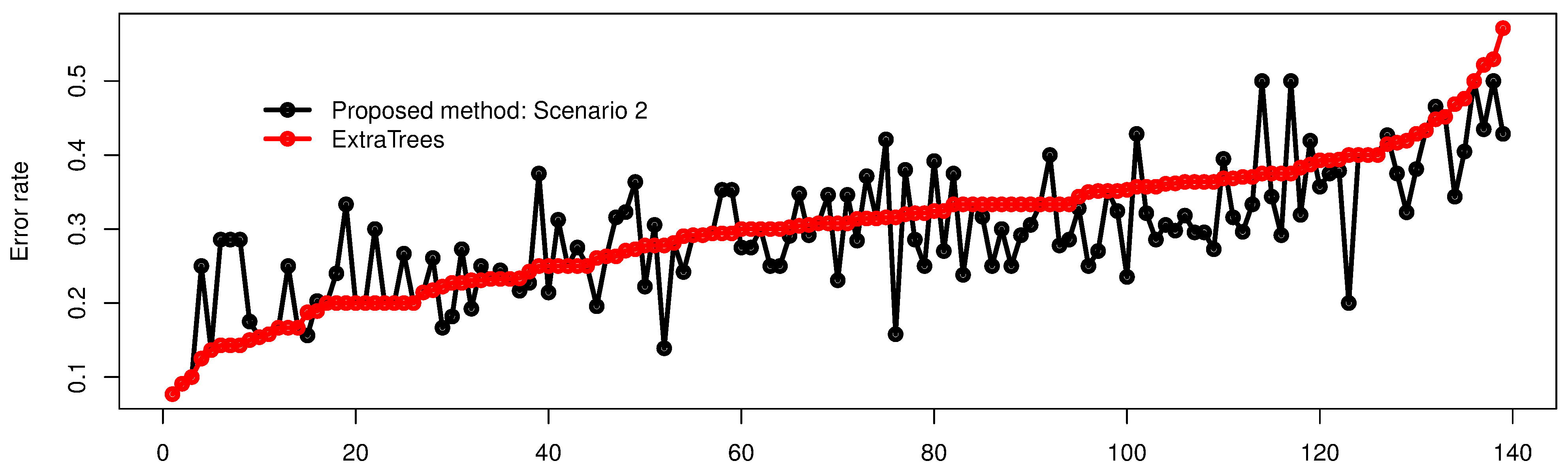
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
A. Proof of Proposition 1
B. Proof of Proposition 2
C. Proof of Lemma 4
D. Proof of Theorem 5
E. Proof of Proposition 7
F. Proof of Proposition 8
G. Proof of Proposition 9
References
- Caruana, R. Multitask learning. Mach. Learn. 1997, 28, 41–75. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Argyriou, A.; Pontil, M.; Ying, Y.; Micchelli, C.A. A spectral regularization framework for multi-task structure learning. In Advances in Neural Information Processing Systems 19; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Evgeniou, A.; Pontil, M. Multi-task feature learning. In Advances in Neural Information Processing Systems 19; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Dai, W.; Yang, Q.; Xue, G.R.; Yu, Y. Boosting for transfer learning. In Proceedings of the 24th International Conference on Machine Learning, Corvallis, OR, USA, 20–24 June 2007; pp. 193–200.
- Wang, X.; Zhang, C.; Zhang, Z. Boosted multi-task learning for face verification with applications to web image and video search. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 142–149.
- Chapelle, O.; Shivaswamy, P.; Vadrevu, S.; Weiinberger, K.; Zhang, Y.; Tseng, B. Multi-task learning for boosting with application to web search ranking. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 1189–1198.
- Cichocki, A.; Amari, S. Families of alpha- beta- and gamma-divergences: Flexible and robust measures of similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Févotte, C.; Bertin, N.; Durrieu, J.L. Nonnegative matrix factorization with the Itakura–Saito divergence: With application to music analysis. Neural Comput. 2009, 21, 793–830. [Google Scholar] [CrossRef] [PubMed]
- Lefevre, A.; Bach, F.; Févotte, C. Itakura–Saito nonnegative matrix factorization with group sparsity. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech, 22–27 May 2011; pp. 21–24.
- Takenouchi, T.; Komori, O.; Eguchi, S. A novel boosting algorithm for multi-task learning based on the Itakura–Saito divergence. In Proceedings of the Bayesian Inference and Maximum Entropy Methods in Science and Engineering (MaxEnt 2014), Amboise, France, 21–26 September 2014; pp. 230–237.
- Murata, N.; Takenouchi, T.; Kanamori, T.; Eguchi, S. Information geometry of U-boost and Bregman divergence. Neural Comput. 2004, 16, 1437–1481. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Amari, S.; Nagaoka, H. Methods of Information Geometry of Translations of Mathematical Monographs; Oxford University Press: Providence, RI, USA, 2000; Volume 191. [Google Scholar]
- Mihoko, M.; Eguchi, S. Robust blind source separation by beta divergence. Neural Comput. 2002, 14, 1859–1886. [Google Scholar] [CrossRef] [PubMed]
- Cichocki, A.; Cruces, S.; Amari, S.I. Generalized alpha-beta divergences and their application to robust nonnegative matrix factorization. Entropy 2011, 13, 134–170. [Google Scholar] [CrossRef]
- Takenouchi, T.; Eguchi, S. Robustifying AdaBoost by adding the naive error rate. Neural Comput. 2004, 16, 767–787. [Google Scholar] [CrossRef] [PubMed]
- Takenouchi, T.; Eguchi, S.; Murata, T.; Kanamori, T. Robust boosting algorithm against mislabeling in multi-class problems. Neural Comput. 2008, 20, 1596–1630. [Google Scholar] [CrossRef] [PubMed]
- Lafferty, G.L.J. Boosting and maximum likelihood for exponential models. In Advances in Neural Information Processing Systems 14; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Evgeniou, T.; Pontil, M. Regularized multi-task learning. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; pp. 109–117.
- Xue, Y.; Liao, X.; Carin, L.; Krishnapuram, B. Multi-task learning for classification with Dirichlet process priors. J. Mach. Learn. Res. 2007, 8, 35–63. [Google Scholar]
- Mason, L.; Baxter, J.; Bartlett, P.; Frean, M. Boosting algorithms as gradient decent in function space. In Advances in Neural Information Processing Systems 11; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Goldstein, H. Multilevel modelling of survey data. J. R. Stat. Soc. Ser. D 1991, 40, 235–244. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takenouchi, T.; Komori, O.; Eguchi, S. Binary Classification with a Pseudo Exponential Model and Its Application for Multi-Task Learning. Entropy 2015, 17, 5673-5694. https://doi.org/10.3390/e17085673
Takenouchi T, Komori O, Eguchi S. Binary Classification with a Pseudo Exponential Model and Its Application for Multi-Task Learning. Entropy. 2015; 17(8):5673-5694. https://doi.org/10.3390/e17085673
Chicago/Turabian StyleTakenouchi, Takashi, Osamu Komori, and Shinto Eguchi. 2015. "Binary Classification with a Pseudo Exponential Model and Its Application for Multi-Task Learning" Entropy 17, no. 8: 5673-5694. https://doi.org/10.3390/e17085673
APA StyleTakenouchi, T., Komori, O., & Eguchi, S. (2015). Binary Classification with a Pseudo Exponential Model and Its Application for Multi-Task Learning. Entropy, 17(8), 5673-5694. https://doi.org/10.3390/e17085673




