1. Introduction
Fractional-order systems have attracted noticeable interest and have been well studied for their potential applications in assorted fields, like engineering, physics, finance, chemistry and bioengineering [
1,
2,
3,
4,
5]. Recently, the research on fractional-order chaotic systems has become a hot issue. The efforts have been devoted to chaotic behavior, chaos control and chaos synchronization. Some fractional-order systems behave chaotically or hyperchaotically, such as the fractional-order Chua system [
6], the fractional-order hyperchaotic Chen system [
7], the fractional-order hyperchaotic Rössler system [
8], and so on. Most recently, many authors have found some fractional-order chaotic systems, including the fractional-order reverse butterfly-shaped chaotic system [
9], the fractional-order stretch-twist-fold (STF) flow chaotic system [
10], a four-dimensional fractional-order chaotic system without an equilibrium point [
11],
etc. Synchronization of fractional-order chaotic systems has been widely investigated due to its potential applications in secure communication, encryption, signal and control processing [
9,
10,
12,
13,
14]. Therefore, a variety of effective methods have been proposed to synchronize various fractional-order chaotic systems. For instance, Agrawal
et al. [
15] realized synchronization of fractional-order chaotic systems via active control. A linear control method was proposed to synchronize the fractional-order chaotic systems in [
16]. By employing the active control method, the phase and anti-phase synchronization of two fractional-order chaotic systems were studied in [
17]. Si
et al. [
18] achieved the projective synchronization between two fractional-order chaotic systems with non-identical orders. Some more attempts to realize the synchronization of fractional-order chaotic systems can be found in [
19,
20].
Recently, with the development of fractional-order real systems and integer-order complex systems, fractional-order chaotic complex systems have attracted a great deal of attention, and many interesting and important results have been researched. For example, the fractional-order complex Lorenz system and its complete synchronization were discussed in [
21]. Luo and Wang presented the fractional-order complex Chen system and applied its hybrid synchronization to digital secure communication [
22]. The fractional-order complex T system was presented, and its function projective synchronization was realized in [
23]. Jiang
et al. [
24] introduced the fractional-order complex Lü system and achieved its anti-synchronization. Complex modified hybrid projective synchronization was investigated between the fractional-order complex chaos and real hyper-chaos in [
25].
However, in the aforementioned literature on the synchronization of the fractional-order chaotic systems, many authors are concerned with the usual drive-response synchronization within one drive system and one response system, and three or more chaotic systems are rarely involved. As a matter of fact, synchronization of multi-chaotic systems can enhance the security in communication, because the transmitted signals can be split into several parts loaded in the different drive systems or the same drive system with different initial conditions. Therefore, many researchers have made an endeavor to analyze the synchronization of multi-chaotic systems and present some new types of synchronization, including combination synchronization [
26,
27,
28], combination complex synchronization [
29], combination-combination synchronization [
30,
31], compound synchronization [
32], and so forth. Amongst the above-mentioned synchronization, combination complex synchronization, characterized by two scaling matrices that three chaotic systems synchronize proportionally, was proposed and studied on the basis of three integer-order chaotic complex systems with the same dimensions.
To the best of our knowledge, there are few results on combination complex synchronization of the fractional-order chaotic complex systems with different dimensions. Motivated by this, we proposed generalized combination complex synchronization among three different dimensional fractional-order chaotic complex systems. By virtue of the stability of the fractional-order linear systems, some sufficient conditions for generalized combination complex synchronization are obtained. Besides, we investigate generalized combination complex synchronization between the fractional-order real chaos and complex chaos. There are some kinds of synchronization that are special cases from our definition, which are complex projective synchronization, combination synchronization and combination complex synchronization. Consequently, our work will extend previous results.
The remainder of this paper is organized as follows.
Section 2 recalls the relevant definitions and stability results of the fractional-order systems. In
Section 3, we present generalized combination complex synchronization and design a scheme to realize the new form of chaos synchronization. By means of two scaling matrices, we establish a link between fractional-order chaotic real systems and chaotic complex systems with different dimensions.
Section 4 provides three examples to exhibit the feasibility and effectiveness of the proposed control technique. Finally, some conclusions are drawn in
Section 5.
2. Preliminaries
In this section, we introduce mathematical definitions of the fractional derivative and the stability results of the fractional-order systems. The fractional-order integro-differential operator is the generalized concept of the integer-order integro-differential operator, which can be denoted by a general fundamental operator as follows:
where
α is the fractional-order, which can be a complex number,
is the real part of
α and
a and
t are the limits of the operation. As we know, there are several definitions of fractional derivatives, including the Grunwald–Letnikov definition, the Riemann–Liouville definition and the Caputo definition.
The Grunwald–Letnikov (GL) derivative with fractional order
α is given by:
where
means the integer part.
The Riemann–Liouville (RL) fractional derivative is defined by:
where
is the Gamma function
The Caputo (C) fractional derivative [
33] is defined as:
In the rest of this paper, the notation is chosen as the Riemann–Liouville derivative operator , and we mainly consider the order .
Consider a fractional-order autonomous system:
where
,
and
.
The stability results for the fractional-order linear system [
34] are given as follows:
Lemma 1.
System (1) is:
- (I)
Asymptotically stable if and only if:
where denotes the argument of the eigenvalue of A. In this case, the component of the state decay towards to zero like .
- (II)
Stable if and only if:
and those critical eigenvalues that satisfy have geometric multiplicity one.
4. Numerical Simulations
In this section, three examples are performed to illustrate the validity and feasibility of the proposed schemes. Firstly, we work out generalized combination complex synchronization between the fractional-order complex Lorenz system, the fractional-order complex Lü system and the fractional-order complex Chen system.
4.1. Synchronization among Three Fractional-Order Chaotic Complex Systems
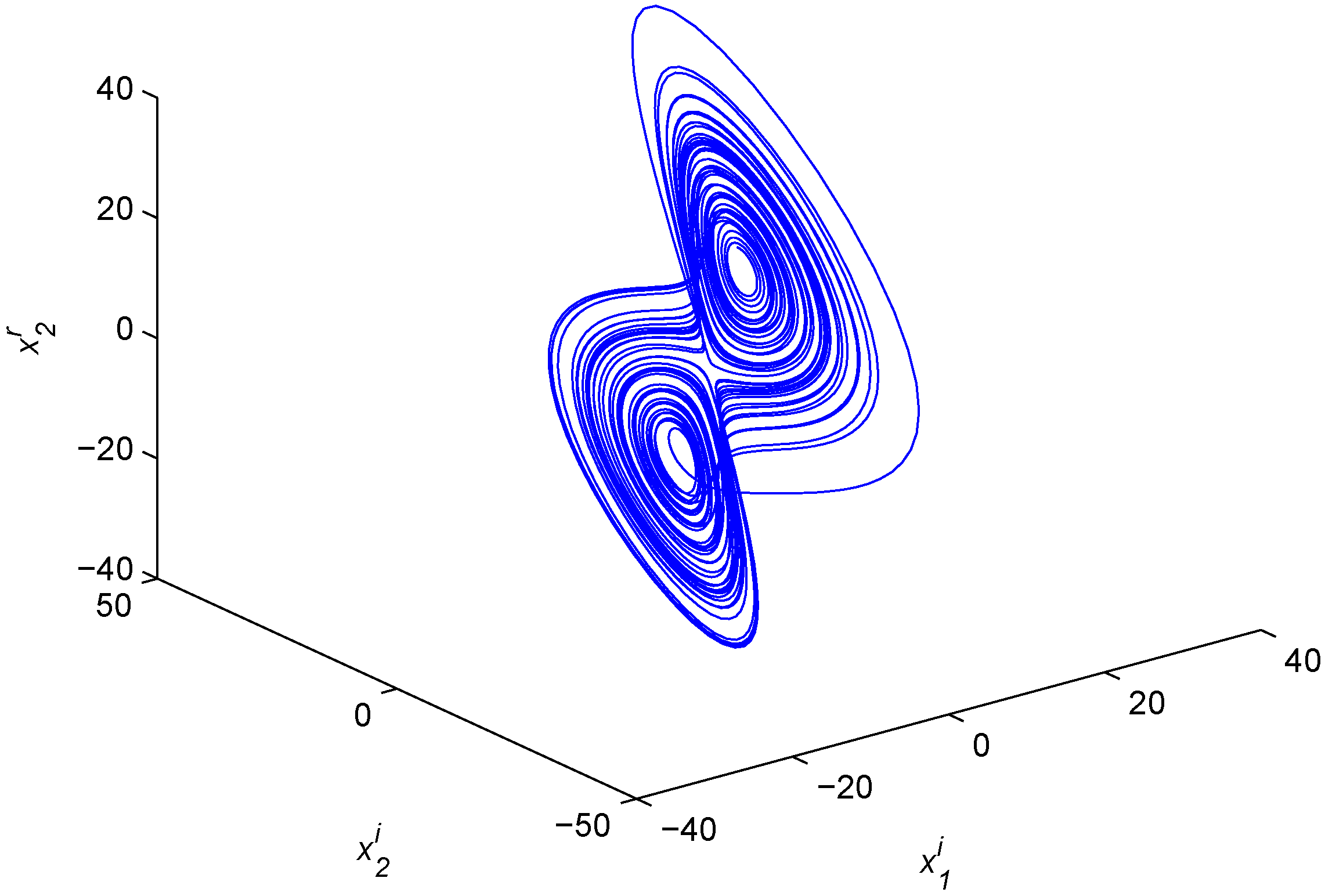
Now, let us consider the fractional-order complex Lorenz system as the first drive system:
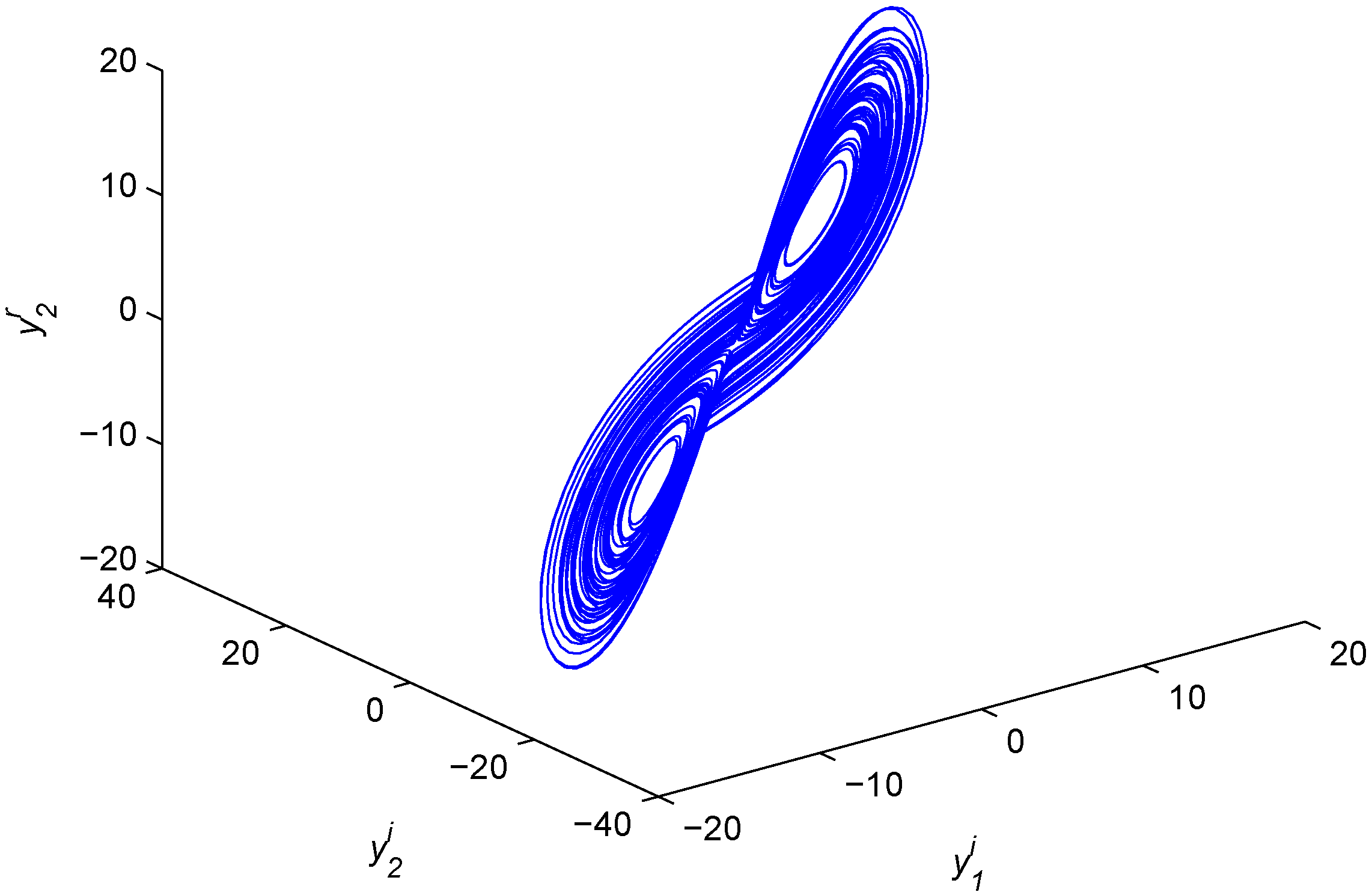
and the fractional-order complex Lü system as the second drive system:
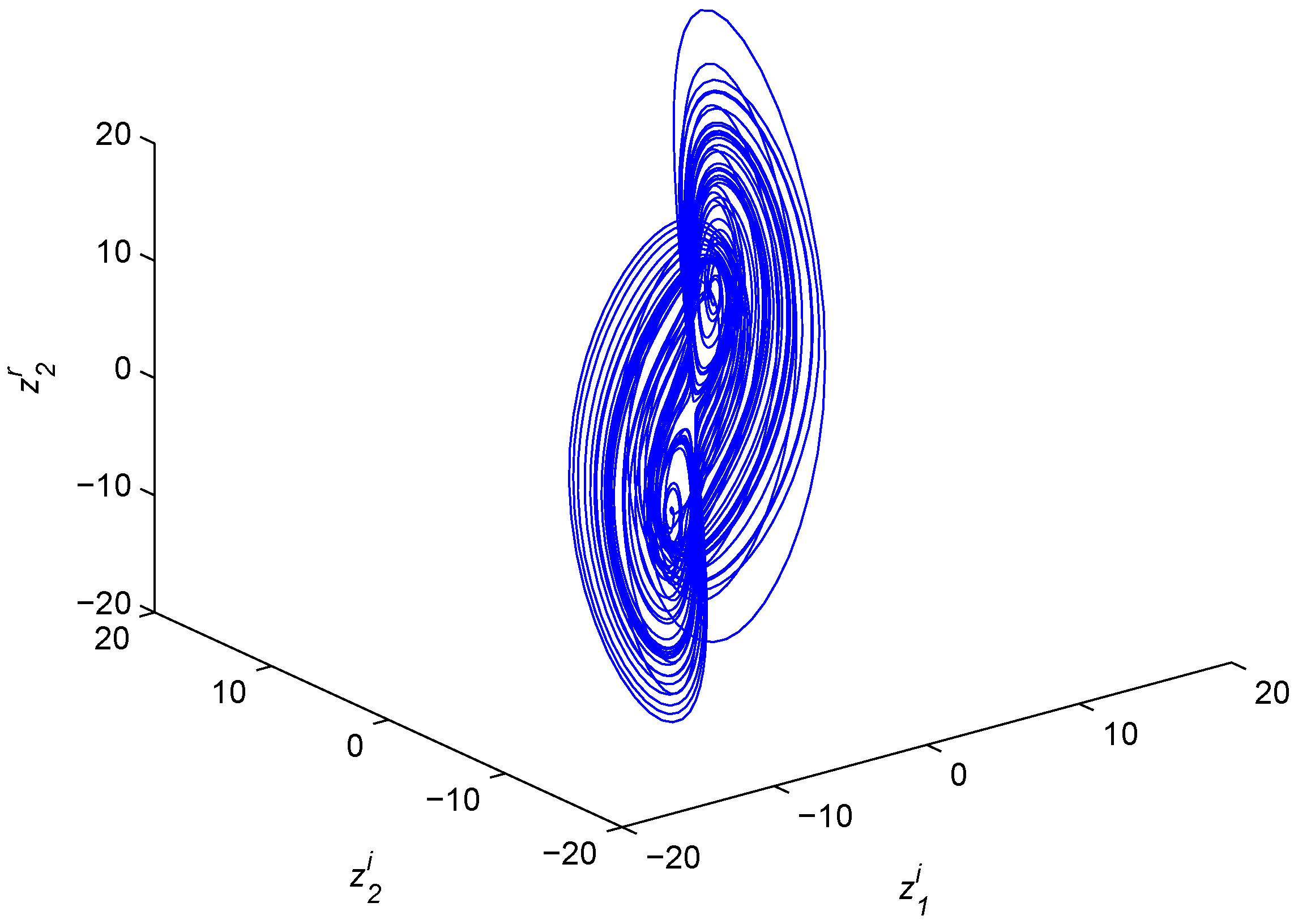
while the response system is the fractional-order complex Chen system:
where
,
,
,
,
,
;
,
,
,
,
and
are complex variables,
,
and
are real variables and
,
and
are complex and real control functions, respectively. Systems (
8)–(
10) behave chaotically with the given parameters
,
,
and
, respectively; see
Figure 1,
Figure 2 and
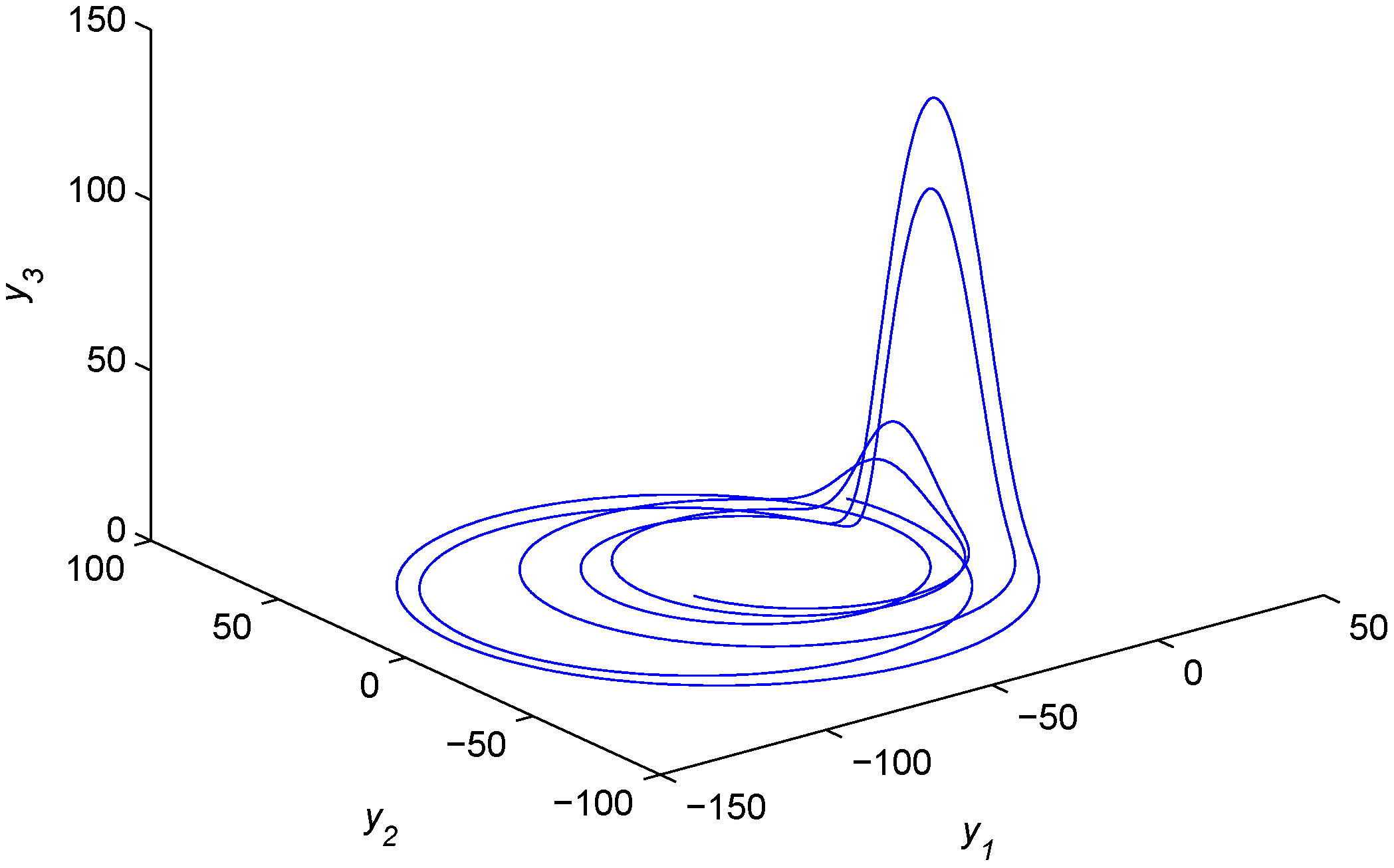
Figure 3. In what follows, we will select the above system parameters and fractional orders in our synchronization analysis.
Figure 1.
Chaotic attractor of the fractional-order complex Lorenz system.
Figure 1.
Chaotic attractor of the fractional-order complex Lorenz system.
Figure 2.
Chaotic attractor of the fractional-order complex Lü system.
Figure 2.
Chaotic attractor of the fractional-order complex Lü system.
Figure 3.
Chaotic attractor of the fractional-order complex Chen system.
Figure 3.
Chaotic attractor of the fractional-order complex Chen system.
Assume that
,
. Then, we obtain the synchronization error functions as follows:
A control matrix is chosen as ; then, we have for the choice of . It is not difficult to see that all eigenvalues of are and , which satisfy , .
According to Theorem 1, the controller is designed as:
In the numerical simulations, the initial values of Systems (
8)–(
10) are taken as
,
and
. Thus, we obtain simulation results by means of the Adams–Bashforth–Moulton predictor-correctors [
35]. The synchronization process of Systems (
8)–(
10) is displayed in
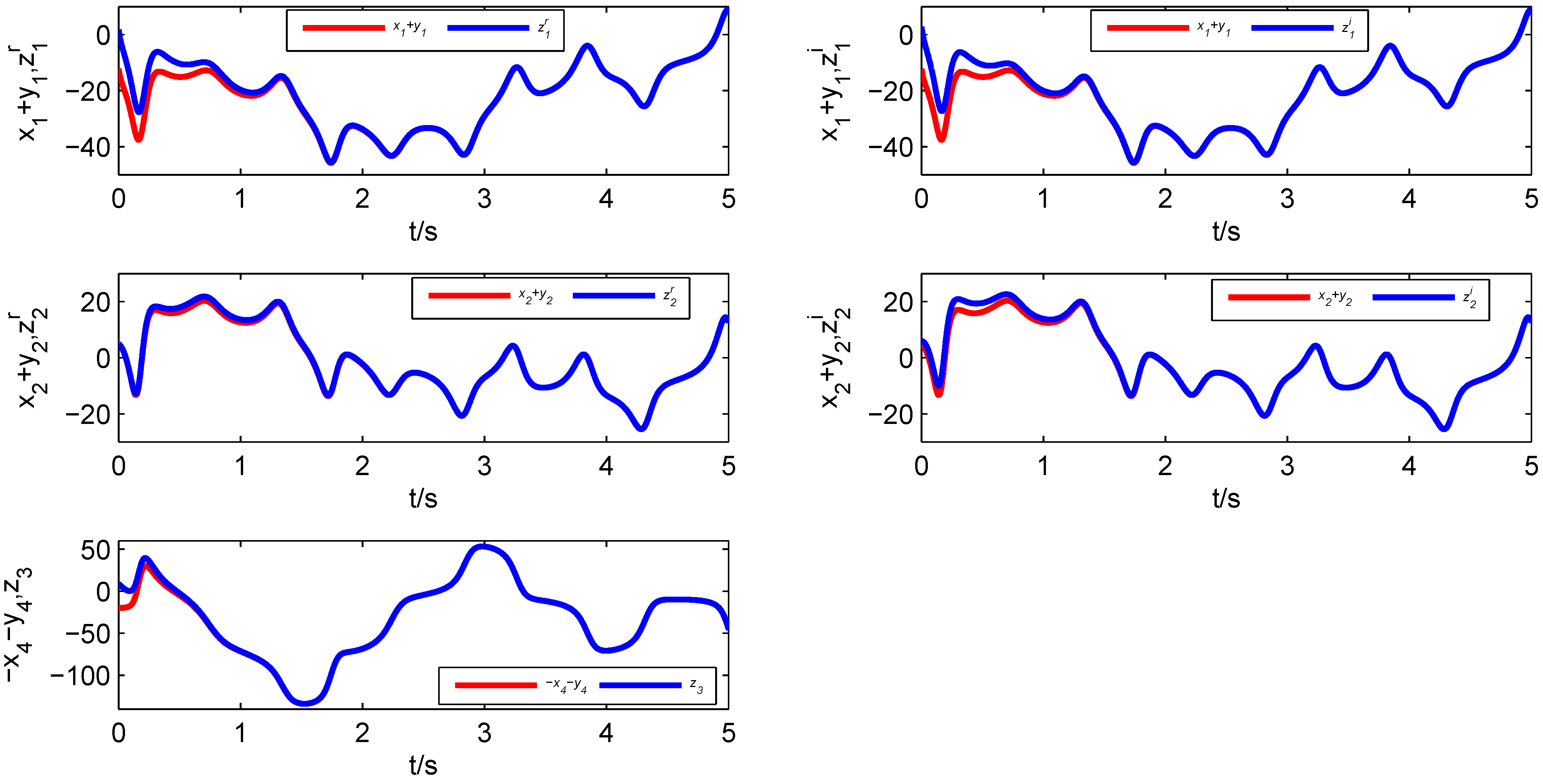
Figure 4, where the red line presents the states of two drive systems and the blue line shows the states of one response system. From
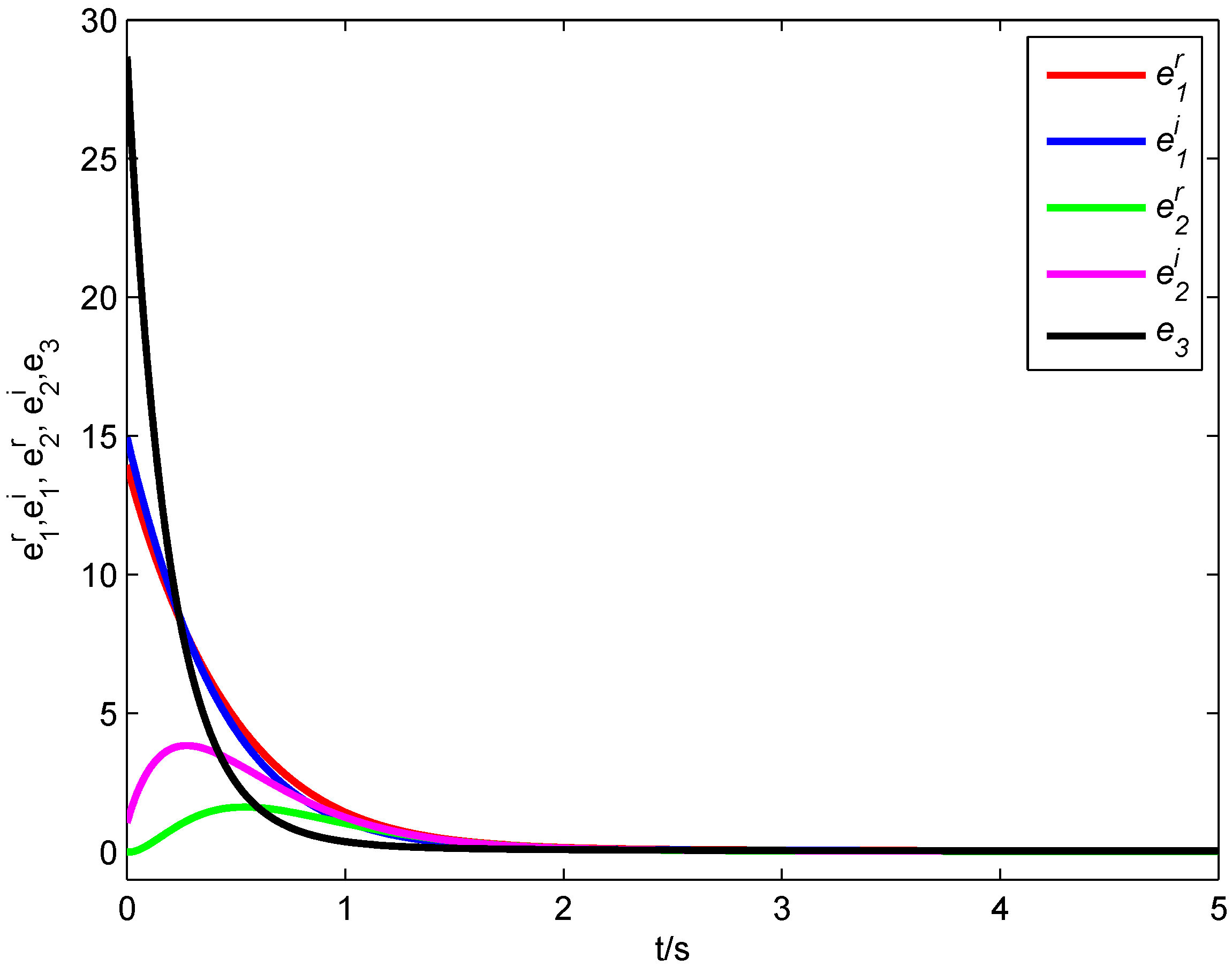
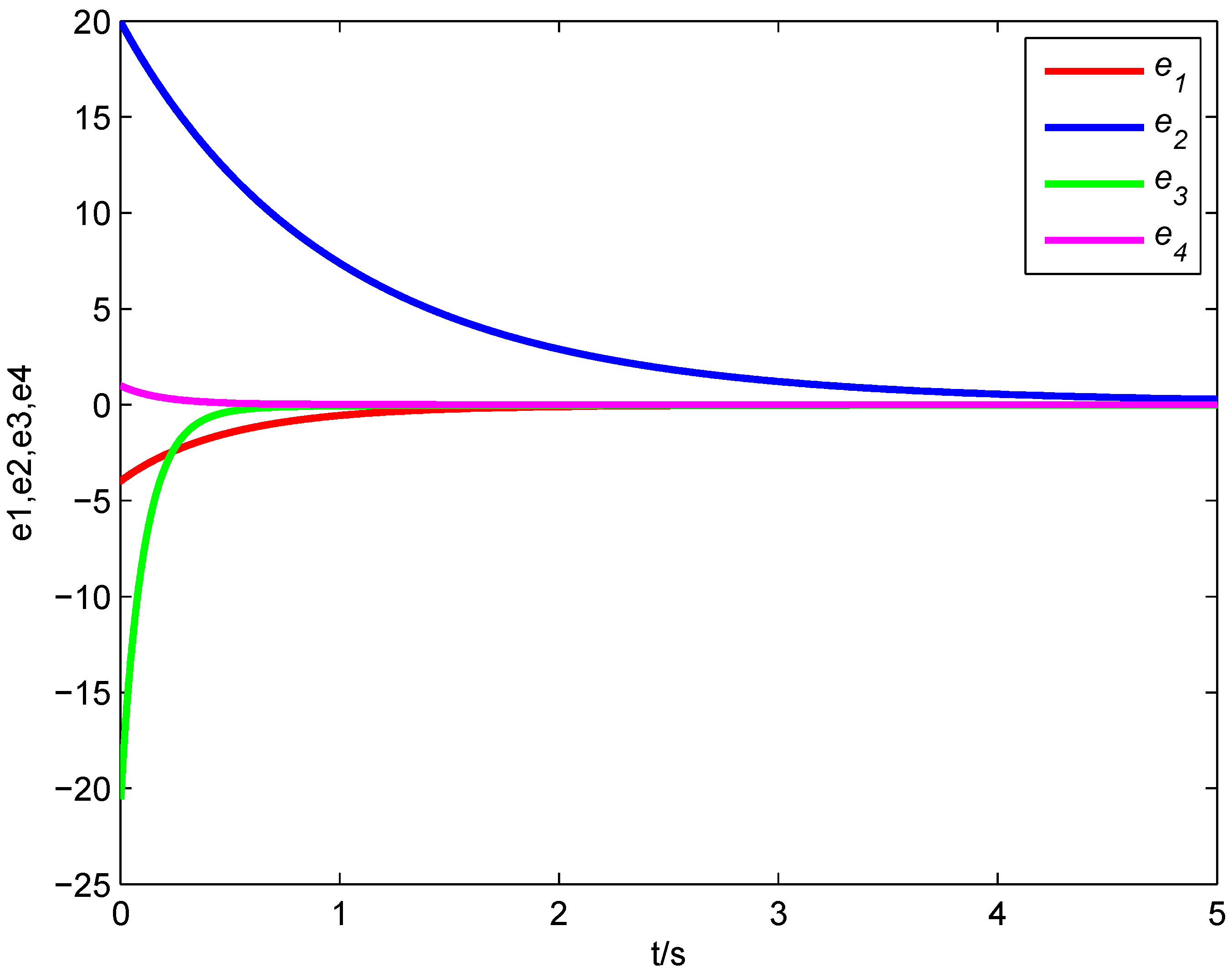
Figure 5, it is clear that all error states converge asymptotically to zero,
i.e., the fractional-order complex Lorenz system, the fractional-order complex Lü system and the fractional-order complex Chen system achieve synchronization with the designed controller.
Figure 4.
State variables of the fractional-order complex Systems (
8)–(
10).
Figure 4.
State variables of the fractional-order complex Systems (
8)–(
10).
Figure 5.
Synchronization errors of the fractional-order complex Systems (
8)–(
10).
Figure 5.
Synchronization errors of the fractional-order complex Systems (
8)–(
10).
4.2. Synchronization between Two Fractional-Order Hyperchaotic Real Drive Systems and a Fractional-Order Chaotic Complex Response System
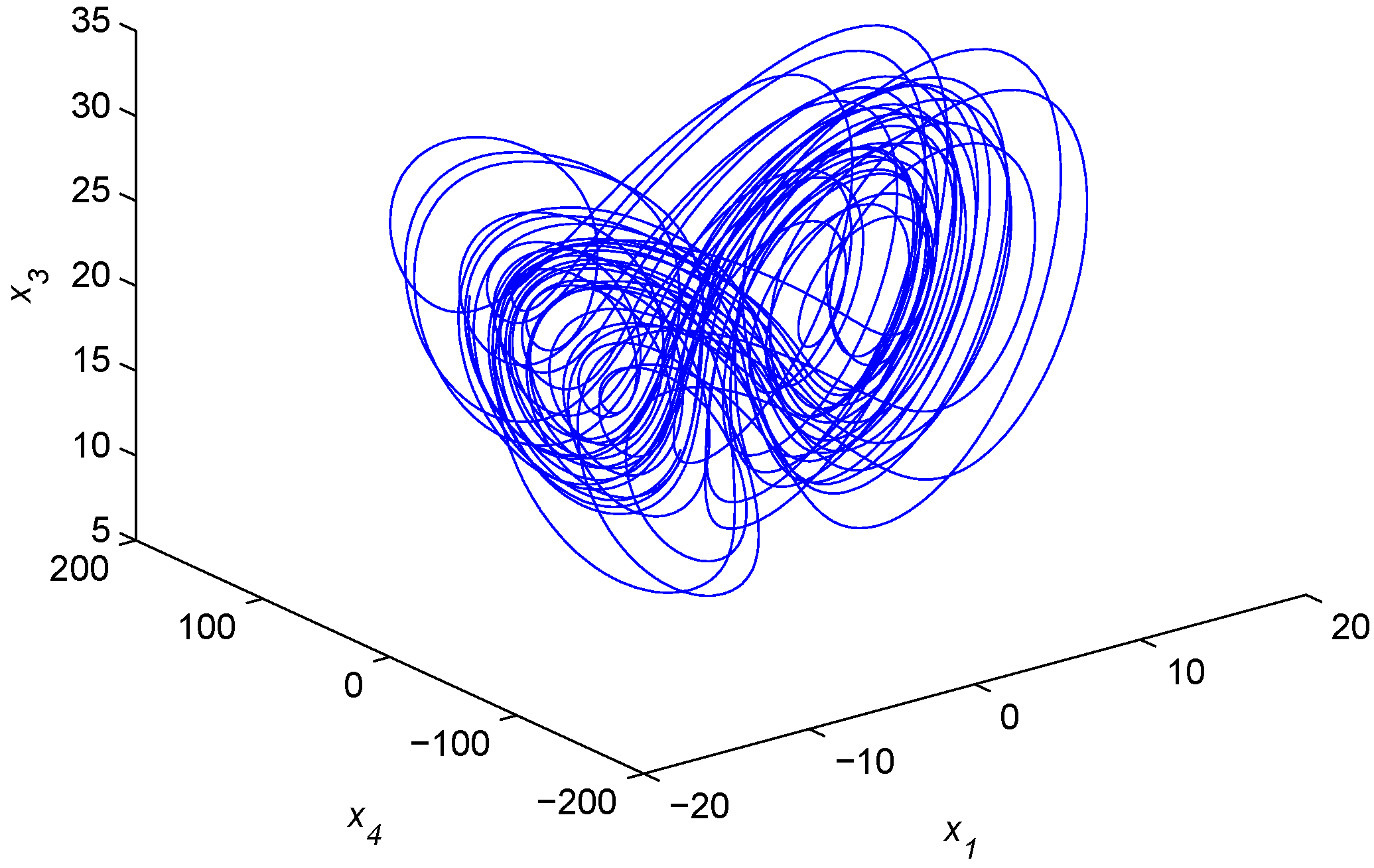
In order to observe generalized combination complex synchronization between two fractional-order hyperchaotic real drive systems and a fractional-order chaotic complex response system, we assume that the fractional-order hyperchaotic real Chen system and the fractional-order hyperchaotic real Rössler system drive the fractional-order chaotic complex Lorenz system. Two drive systems are introduced below:
and:
while the response system with the controller is depicted as follows:
where
,
,
,
,
,
;
and
are complex variables,
,
and
are real variables (
) and
,
and
are complex and real control functions, respectively.
For two given scaling matrices
, the synchronization error is described as follows:
Taking a control matrix as , we get with . Thus, when , all eigenvalues of are and , which lie in the region ().
From Corollary 1, the control law is obtained as follows:
In the following,
, the initial values of Systems (11)–(13) are taken as
,
,
, and the parameters are chosen as
,
,
. Then, Systems (
11) and (
12) exhibit chaotic attractors, as shown in
Figure 6 and
Figure 7.
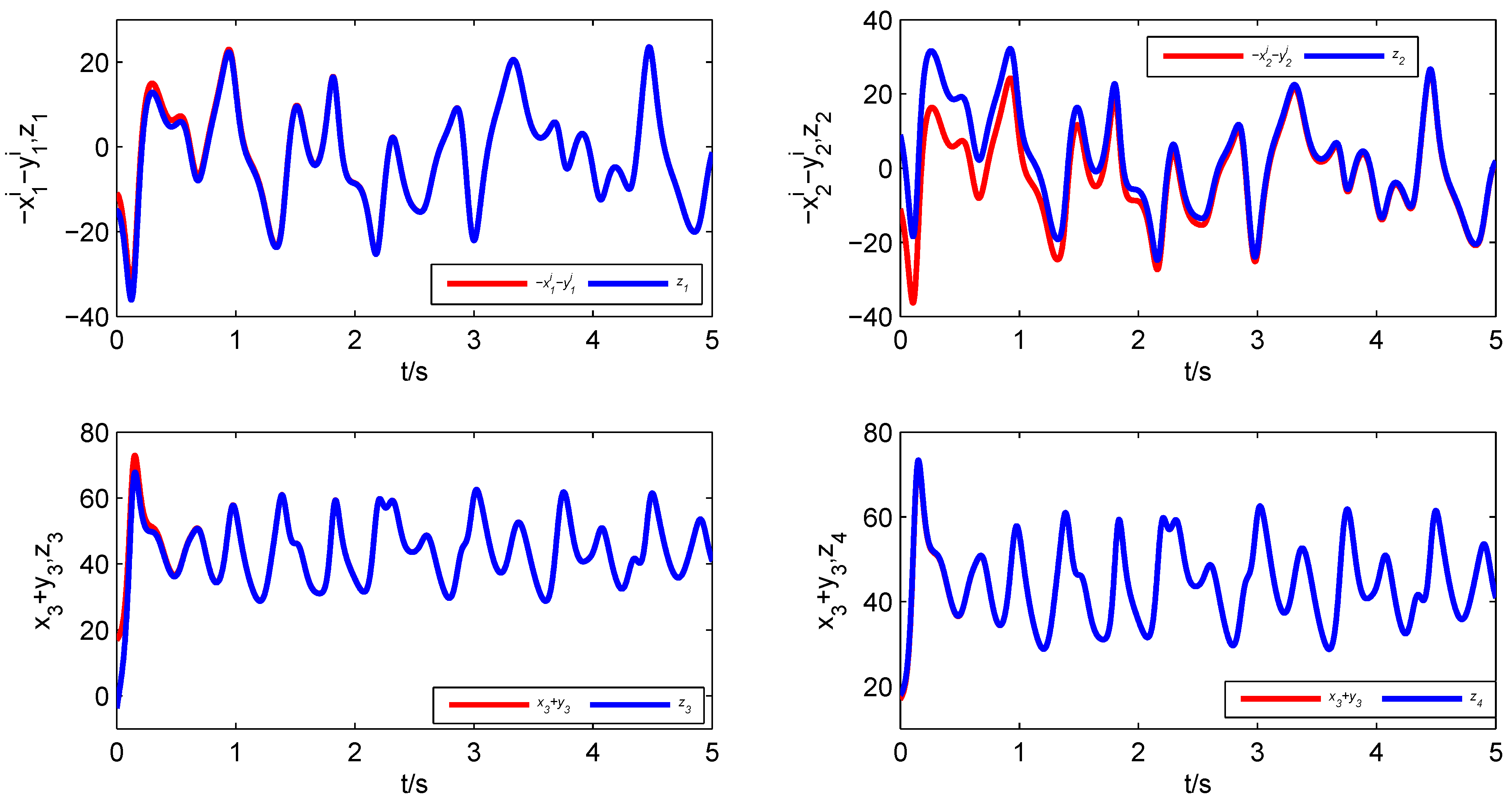
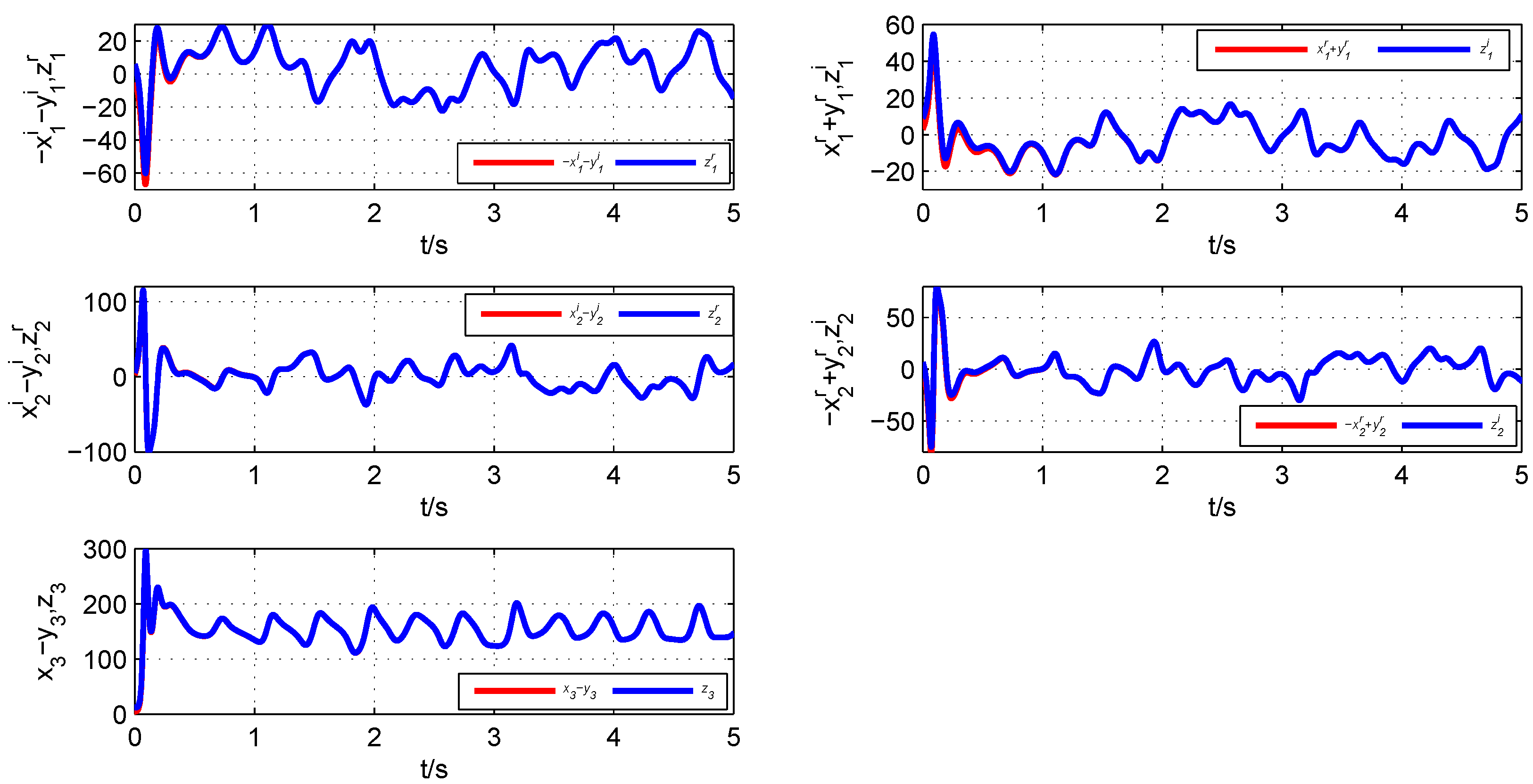
Figure 8 demonstrates the synchronization process and error states of Systems (
11)–(
13). According to
Figure 9, it is obvious that all error states tend asymptotically to zero. Hence, the four-dimensional fractional-order real Chen system, the four-dimensional fractional-order real Rössler system and the three-dimensional fractional-order complex Lorenz system realize generalized combination complex synchronization.
Figure 6.
Chaotic attractor of the fractional-order hyperchaotic real Chen system.
Figure 6.
Chaotic attractor of the fractional-order hyperchaotic real Chen system.
Figure 7.
Chaotic attractor of the fractional-order hyperchaotic real Rössler system.
Figure 7.
Chaotic attractor of the fractional-order hyperchaotic real Rössler system.
Figure 8.
State variables of the fractional-order nonlinear Systems (11)–(13).
Figure 8.
State variables of the fractional-order nonlinear Systems (11)–(13).
Figure 9.
Synchronization errors of the fractional-order Systems (11)–(13).
Figure 9.
Synchronization errors of the fractional-order Systems (11)–(13).
4.3. Synchronization between Two Fractional-Order Chaotic Complex Drive Systems and a Fractional-Order Hyperchaotic Real Response System
In this subsection, we design the control law to achieve generalized combination complex synchronization between the fractional-order complex Lü system, the fractional-order complex Chen system and the fractional-order hyperchaotic real Rössler system. The first drive system is defined as:
and the second drive system is given as:
while the response system with the controller is described as follows:
where
,
,
,
,
,
;
,
,
and
are complex variables,
,
and
are real variables and
are real control functions (
).
Suppose two scaling matrices
. The real synchronization error is defined as follows:
Select a control matrix as , where are real and satisfy , .
The real controller is derived from Corollary 3 as follows:
In what follows,
, the initial values are
,
,
, and the parameters are
,
,
. we choose
,
,
and
, such that all eigenvalues of
lie in region
(
).
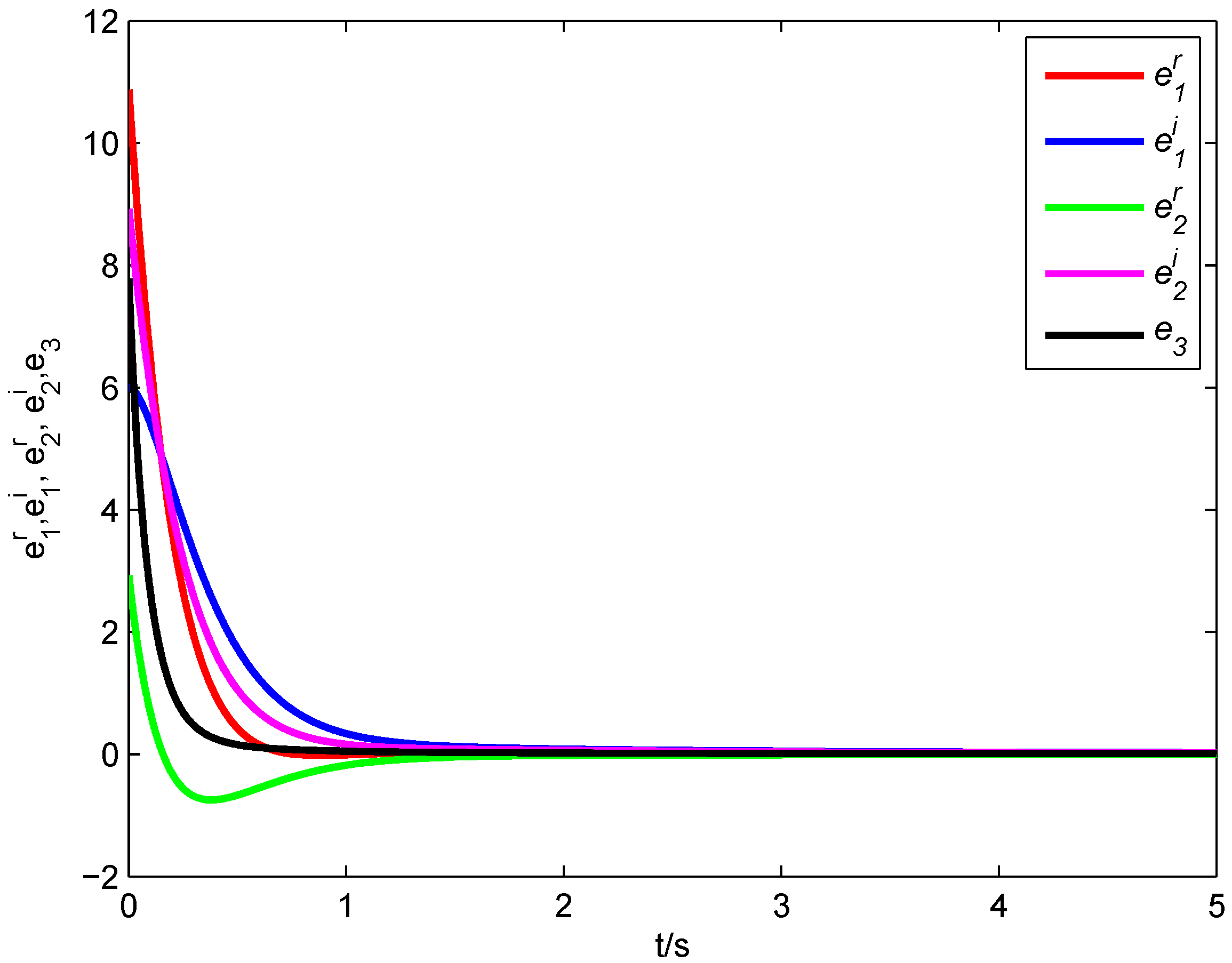
Figure 10 describes the synchronization process of Systems (14)–(16). According to
Figure 11, it can be seen that all error states converge asymptotically to zero. Therefore, the fractional-order chaotic complex Lü system, the fractional-order chaotic complex Chen system and the fractional-order hyperchaotic real Rössler achieve generalized combination complex synchronization.
Figure 10.
State variables of the fractional-order nonlinear Systems (14)–(16).
Figure 10.
State variables of the fractional-order nonlinear Systems (14)–(16).
Figure 11.
Synchronization errors of the fractional-order Systems (14)–(16).
Figure 11.
Synchronization errors of the fractional-order Systems (14)–(16).
5. Conclusions
This paper presents generalized combination complex synchronization between two fractional-order complex drive systems and one fractional-order complex response system with different dimensions. In this proposed scheme, two drive systems and one response system can be synchronized to two complex constant scaling matrices which are non-square matrices. The special cases, such as combination complex synchronization, combination synchronization and complex projective synchronization, are discussed, as well. Based on the stability of fractional-order linear systems, a general controller is obtained to achieve generalized combination complex synchronization among three different dimensional fractional-order chaotic complex systems. Through this scheme, we study generalized combination complex synchronization between fractional-order real chaos and complex chaos. Furthermore, this scheme is successfully applied to three examples. Corresponding simulations verify the feasibility of the proposed scheme. Moreover, the proposed synchronization has advantages over the usual drive-response synchronization, such as being able to provide greater security in secure communication. Therefore, it is believed that the proposed scheme will play an important role in secure communication.