Adaptive Fuzzy Control for Nonlinear Fractional-Order Uncertain Systems with Unknown Uncertainties and External Disturbance

Abstract

In this paper, the problem of robust control of nonlinear fractional-order systems in the presence of uncertainties and external disturbance is investigated. Fuzzy logic systems are used for estimating the unknown nonlinear functions. Based on the fractional Lyapunov direct method and some proposed Lemmas, an adaptive fuzzy controller is designed. The proposed method can guarantee all the signals in the closed-loop systems remain bounded and the tracking errors converge to an arbitrary small region of the origin. Lastly, an illustrative example is given to demonstrate the effectiveness of the proposed results.

1. Introduction

During the past two decades, fractional-order dynamic systems have received lots of attention due to their broad range of application in dielectric polarization, viscoelastic systems, electromagnetic waves, chaotic systems and so on [1]. A distinguished feature of fractional-order systems is their memory effects, which can be utilized to characterize some physical phenomena or complex systems more precisely. Furthermore, fractional order controllers have so far been implemented to enhance the robustness and the performance of the closed loop control systems.

It is well known that stability analysis is one of the most important problems in control system including fractional-order systems. There have been many stability results for fractional-order systems. For Caputo fractional derivative-based linear system, the stability results are formulated with fractional commensurate order of $0<\alpha <1$ and $1<\alpha <2$ in [2] and [3] respectively. In [4,5], the stability of fractional-order linear systems with Riemann-Liouville derivative is discussed with fractional commensurate order of $0<\alpha <1$ and $1<\alpha <2$. However, the results on the stability of fractional-order nonlinear systems are relatively few. In [6], the definition of Mittag-Leffler stability of nonlinear fractional-order dynamic systems is proposed. In [7], the stability of nonlinear fractional-order dynamical systems with fractional-order $0<\alpha <1$ is considered. In [8], sufficient conditions for the locally asymptotical stability of nonlinear fractional-order dynamical systems with fractional-order $0<\alpha <1$ are derived. However, the obtained results only ensure that fractional-order nonlinear dynamical systems are stable. In [9], the sufficient conditions of the stability and stabilization for a class of fractional-order nonlinear systems with fractional-order $0<\alpha <1$ and $1<\alpha <2$ respectively are derived. Based on the sliding mode control technique, a robust control scheme is designed for a class of fractional-order economical system with uncertainties and external disturbance in [10]. In [11], a finite-time control method is introduced for control of a class of non-autonomous fractional-order nonlinear systems in the presence of uncertainties and external noises. However, the uncertainties and external noises are assumed to be bounded in [10,11]. In addition, as discussed in [12], the finite-time synchronization is not possible.

On the other hand, as a fundamental tool to analyze the stability of nonlinear systems, the Lyapunov method has been introduced in [13]. However, how to construct a simple direct Lyapunov function remains an open problem [12]. The stability of fractional-order nonlinear systems by using the Lyapunov direct method is firstly investigated in [14]. Some authors have proposed Lyapunov functions to prove the stability of fractional-order nonlinear systems, for example, a new property for Caputo fractional derivative which allows to find a simple Lyapunov candidate function for many fractional-order systems is presented in [15]. However, either they have neglected the consideration of the effects of both system uncertainties and external noises, or they have not applied the fractional Lyapunov stability theory to guarantee the stability of the overall system. To date and to the best of our knowledge, the problem of robust control of nonlinear fractional-order systems whose model uncertainty and external noises are unknown has not been fully investigated and still remain challenging, which motivates the study of this paper.

In this paper, an adaptive fuzzy control method for fractional-order nonlinear systems in the presence of model uncertainty and external noises is proposed. Fuzzy logic systems are used for estimating the unknown nonlinear functions. Based on the fractional Lyapunov direct method, an adaptive fuzzy controller is designed. Fractional adaptation laws are proposed to update the parameters of the fuzzy systems. The proposed method can guarantee all the signals in the closed-loop systems remain bounded and the tracking errors converge to an arbitrary small region of the origin. The main contributions are given as follows: (1) The adaptive fuzzy control approach is used to control nonlinear fractional-order systems in the presence of uncertainties and external noises. (2) A fractional adaptation law is proposed to update the fuzzy parameter. (3) A direct Lyapunov function method is proposed to analyze the stability of the fractional-order systems.

2. Problem formulation and preliminaries

Several definitions exist regarding the fractional derivative of order $a>0$, but the Caputo definition is used in most of the engineering applications, since this definition incorporates initial conditions for $f\left(t\right)$ and its integer order derivatives, i.e., initial conditions that are physically appealing in the traditional way.

Definition 1 (Caputo Fractional Derivative).

The Caputo fractional derivative of order $\alpha \in R^{+}$ on the half axis $R^{+}$ is defined as follows

$$D^{\alpha }f\left(t\right)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_a^t\frac{f^{\left(n\right)}\left(\tau \right)}{{(t-\tau )}^{\alpha -n+1}}d\tau ,t>0,$$

(1)

where $n-1\le \alpha <n$, and $\Gamma (·)$ denotes the Gamma function.

Definition 2 (Mittag–Leffler Function).

The Mittag-Leffler function with two parameters is defined as

$$E_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\mathrm{\Gamma }(\alpha k+\beta )}$$

(2)

where $\alpha , \beta$ are positive complex numbers and z is a complex number.

In the paper, we consider the following n-dimensional fractional-order system with model uncertainties external disturbances and control inputs

$$\begin{array}{cc}\hfill D^{\alpha }{x}_1& =f_1\left(x\right)+\mathrm{\Delta }{f}_1\left(x\right)+\sum _{j=1}^n{g}_{1j}{u}_j\left(t\right)+d_1\left(t\right)\hfill \\ \hfill D^{\alpha }{x}_2& =f_2\left(x\right)+\mathrm{\Delta }{f}_2\left(x\right)+\sum _{j=1}^n{g}_{2j}{u}_j\left(t\right)+d_2\left(t\right)\hfill \\ \hfill \cdots & \cdots \hfill \\ \hfill D^{\alpha }{x}_n& =f_n\left(x\right)+\mathrm{\Delta }{f}_n\left(x\right)+\sum _{j=1}^n{g}_{nj}{u}_j\left(t\right)+d_n\left(t\right)\hfill \end{array}$$

(3)

where $x={[x_1,x_2,\cdots ,x_n]}^T\in R^n$ is the system state vector which is assumed to be available for measurement. $f_i\left(x\right),i=1,\cdots ,n$ are unknown nonlinear functions and $\mathrm{\Delta }{f}_i\left(x\right),i=1,\cdots ,n$ represent unknown model uncertainty. $u\left(t\right)={[u_1\left(t\right),\cdots ,u_n\left(t\right)]}^T\in R^n$ is the control input and $d_i\left(t\right),i=1,\cdots ,n$ are external perturbations. $g_{ij},i,j=1,\cdots ,n$ are known constant control gains.

Denote

$$f\left(x\right)={[f_1\left(x\right),\cdots ,f_n\left(x\right)]}^T$$

$$d\left(x\right)={[d_1\left(t\right),\cdots ,d_n\left(t\right)]}^T$$

$$G=\left[\begin{array}{ccc}{g}_{11}& \cdots & g_{1n}\\ ⋮& \ddots & ⋮\\ g_{n1}& \cdots & g_{nn}\end{array}\right]$$

$$\mathrm{\Delta }f\left(x\right)={[\mathrm{\Delta }{f}_1\left(x\right),\cdots ,\mathrm{\Delta }{f}_n\left(x\right)]}^T$$

Then, the system (3) can be rewritten as

$$D^{\alpha }x=f\left(x\right)+\mathrm{\Delta }f\left(x\right)+Gu+d\left(t\right).$$

(4)

The main objective is to construct an adaptive fuzzy controller $u\left(t\right)$ such that the state vector $x\left(t\right)$ tracks the following referenced signal with all involved signals keeping bounded in the closed-loop system.

$$x_d\left(t\right)=\left[x_{d1}\left(t\right),x_{d2}\left(t\right),\cdots ,x_{dn}\left(t\right)\right]$$

(5)

The tracking error vector is defined as

$$e\left(t\right)=x_d\left(t\right)-x\left(t\right)$$

(6)

Thus the dynamic of the tracking error can be written as

$$D^{\alpha }e\left(t\right)=D^{\alpha }{x}_d\left(t\right)-f\left(x\right)-\mathrm{\Delta }f\left(x\right)-d\left(t\right)-Gu\left(t\right)$$

(7)

Lemma 1 

(see [16]). If $x\left(t\right)$ is continuous and derivable, then

$$\frac{1}{2}{D}^{\alpha }{x}^T\left(t\right)Px\left(t\right)\le x^T\left(t\right)P{D}^{\alpha }x\left(t\right)$$

(8)

where P is an $n\times n$ positive definite constant matrix.

Lemma 2. 

Consider the following fractional-order system

$$D^{\alpha }y\left(t\right)\le -ay\left(t\right)+b$$

(9)

then there exists a constant $t_0>0$ such that for all $t\in (t_0,\infty )$

$$\parallel y\left(t\right)\parallel \le \frac{2b}{a}$$

(10)

where $y\left(t\right)$ is the state variable, and a, b are two positive constants.

Proof. 

In view of (9), there exists a nonnegative function $m\left(t\right)$ such that

$$D^{\alpha }y\left(t\right)=-ay\left(t\right)+m\left(t\right)+b$$

(11)

Taking Laplace transform on (11) yields

$$Y\left(s\right)=\frac{s^{\alpha -1}}{s^{\alpha }+a}y\left(0\right)+\frac{L\left(m\right(t)+b)}{s^{\alpha }+a}$$

(12)

where $y\left(0\right)$ is initial condition. Then we have

$$y\left(t\right)=y\left(0\right)E_{\alpha ,1}(-a{t}^{\alpha })+{\int }_0^t{(t-\tau )}^{\alpha -1}{E}_{\alpha ,\alpha }(-a{(t-\tau )}^{\alpha })(m\left(\tau \right)+b)d\tau$$

(13)

which yields that

$$\parallel y\left(t\right)\parallel \le \parallel y\left(0\right)\parallel E_{\alpha ,1}(-a{t}^{\alpha })+b{\int }_0^t{(t-\tau )}^{\alpha -1}{E}_{\alpha ,\alpha }(-a{(t-\tau )}^{\alpha })d\tau$$

(14)

Note that

$${\int }_0^t{\tau }^{\beta -1}{E}_{\alpha ,\beta }(-a{\tau }^{\alpha })d\tau =t^{\beta }{E}_{\alpha ,\beta +1}(-a{\tau }^{\alpha })$$

(15)

Then we can obtain

$$\parallel y\left(t\right)\parallel \le \parallel y\left(0\right)\parallel E_{\alpha ,1}(-a{t}^{\alpha })+b{t}^{\alpha }{E}_{\alpha ,\alpha +1}(-a{\tau }^{\alpha })$$

(16)

Thus there exists a constant $t_0>0$ such that (10) is satisfied for all $t\in (t_0,\infty )$.

3. Description of the Fuzzy Logic System

The basic configuration of a fuzzy logic system consists of a fuzzifier, some fuzzy IF-THEN rules, a fuzzy inference engine and a defuzzifier. The fuzzy inference engine uses the fuzzy IF-THEN rules to perform a mapping from an input vector $x={[x_1,x_2,\cdots ,x_n]}^T\in R^n$ to an output $\zeta \left(x\right)\in R$. The ith fuzzy rule is written as

$$\text{Rule} i: \text{if} x_1 \text{is} F_1^i \text{and} \cdots \text{and} x_n \text{is} F_n^i \text{then} \zeta \left(x\right) \text{is} {\alpha }_i.$$

where $F_1^i,F_2^i,\cdots$ and $F_n^i$ are fuzzy sets and ${\alpha }_i$ is the fuzzy singleton for the output in the ith rule. By using the singleton fuzzifier, product inference and the center of gravity defuzzification, the output of the fuzzy system can be expressed as follows:

$$\zeta \left(x\right)=\frac{{\sum }_{j=1}^N{\alpha }_j{\prod }_{i=1}^n{\mu }_{F_i^j}\left(x_i\right)}{{\sum }_{j=1}^N\left[{\prod }_{i=1}^n{\mu }_{F_i^j}\left(x_i\right)\right]}={\theta }^T\psi \left(x\right),$$

(17)

where ${\mu }_{F_i^j}\left(x_i\right)$ is the degree of membership of $x_i$ to $F_i^j$, N is the number of fuzzy rules, $\theta ={[{\alpha }_1,\cdots ,{\alpha }_N]}^T$ is the adjustable parameter vector, and $\psi \left(x\right)={[p_1\left(x\right),p_2\left(x\right),\cdots ,p_N\left(x\right)]}^T$, where

$$p_j\left(x\right)=\frac{{\prod }_{i=1}^n{\mu }_{F_i^j}\left(x_i\right)}{{\sum }_{j=1}^N\left[{\prod }_{i=1}^n{\mu }_{F_i^j}\left(x_i\right)\right]}$$

(18)

is the fuzzy basis function. It is assumed that fuzzy basis functions are selected so that there is always at least one active rule.

4. Adaptive Fuzzy Controller Design

In this section, we will design an adaptive fuzzy controller, such that not only all the signals of the closed-loop system (7) are bounded, but also the tracking error tends to the origin asymptotically. In order to solve the problem, the following theorem will be essential. Denote $P=G^{-1}$. Then (7) can be written as

$$P{D}^{\alpha }e\left(t\right)=\mu \left(x\left(t\right)\right)-u\left(t\right)$$

(19)

where

$$\mu \left(x\left(t\right)\right)=P(D^{\alpha }{x}_d\left(t\right)-f\left(x\right)-\mathrm{\Delta }f\left(x\right)-d\left(t\right))$$

(20)

Since the model uncertainty $\mathrm{\Delta }f\left(x\right)$ and the external perturbations $d\left(t\right)$ are unknown, which lead to the nonlinear function $\mu \left(x\right(t\left)\right)$ is unknown. Thus we need to design an adaptive fuzzy controller, precisely, we will apply the fuzzy systems (17) to approximate the unknown nonlinear functions $\mu \left(x\right(t\left)\right)$ in the following manner:

$${\widehat{\mu }}_i({\theta }_i\left(t\right),x\left(t\right))={\theta }_i^T\left(t\right){\psi }_i\left(x\left(t\right)\right),i=1,2,\cdots ,n,$$

(21)

where ${\mu }_i\left(x\left(t\right)\right)$ is the ith element of the nonlinear function $\mu \left(x\right(t\left)\right)$. Let us define the ideal parameters of ${\theta }_i$ as

$${\theta }_i^{*}=\arg \underset{{\theta }_i}{min}\left[sup|{\mu }_i\left(x\left(t\right)\right)-{\widehat{\mu }}_i\left(x\left(t\right)\right)|\right].$$

(22)

Defining the parameter estimation errors and the fuzzy approximation errors as follows:

$$\widetilde{{\theta }_i}={\theta }_i-{\theta }_i^{*},$$

(23)

$${\epsilon }_i\left(x\right)={\mu }_i\left(x\left(t\right)\right)-{\widehat{\mu }}_i({\theta }_i^{*},x\left(t\right)),$$

(24)

with ${\widehat{\mu }}_i({\theta }_i^{*},x\left(t\right))={\theta }_i^{*}{\psi }_i\left(x\left(t\right)\right)$. We can assume that the fuzzy approximation error is bounded for all x, i.e., $|{\epsilon }_i\left(x\right)|<{\overline{\epsilon }}_i$, where ${\overline{\epsilon }}_i$ is unknown constant. Let $\epsilon ={[{\epsilon }_1\left(x\right),\cdots ,{\epsilon }_n\left(x\right)]}^T$, $\overline{\epsilon }={[{\overline{\epsilon }}_1,\cdots ,{\overline{\epsilon }}_n]}^T$. Then we can get $\left|\epsilon \left(x\right)\right|\le \overline{\epsilon }$. From the above analysis, we have

$$\begin{array}{cc}\hfill \widehat{\mu }({\theta }_i\left(t\right),x\left(t\right))-\mu \left(x\left(t\right)\right)& =\widehat{\mu }({\theta }_i\left(t\right),x\left(t\right))-\widehat{\mu }({\theta }^{*},x\left(t\right))+\widehat{\mu }({\theta }^{*},x\left(t\right))-\mu \left(x\left(t\right)\right)\hfill \\ & =\widehat{\mu }({\theta }_i\left(t\right),x\left(t\right))-\widehat{\mu }({\theta }^{*},x\left(t\right))-\epsilon \left(x\left(t\right)\right)\hfill \\ & ={\tilde{\theta }}^T\left(t\right)\psi \left(x\left(t\right)\right)-\epsilon \left(x\left(t\right)\right)\hfill \end{array}$$

(25)

Then the adaptive fuzzy controller can be constructed as

$$u\left(t\right)={\theta }^T\left(t\right)\psi \left(x\left(t\right)\right)+ke\left(t\right)+bsign\left(e\left(t\right)\right)$$

(26)

where k and b are free positive constants to be designed. Substituting the proposed controller (26) into the tracking error dynamics (19) gives

$$P{D}^{\alpha }e\left(t\right)=\mu \left(x\left(t\right)\right)-{\theta }^T\left(t\right)\psi \left(x\left(t\right)\right)-ke\left(t\right)-bsign\left(e\left(t\right)\right)$$

(27)

Multiplying $e^T\left(t\right)$ to both sides of (27) and applying (25) yields

$$e^T\left(t\right)P{D}^{\alpha }e\left(t\right)=-k{e}^T\left(t\right)e\left(t\right)+\sum _{i=1}^n{e}_i\left(t\right){\epsilon }_i\left(x\left(t\right)\right)-b\sum _{i=1}^n{e}_i\left(t\right){\tilde{\theta }}_i^T\left(t\right){\psi }_i\left(x\left(t\right)\right)-b\sum _{i=1}^n\left|e_i\left(t\right)\right|$$

(28)

The fractional adaptation laws for updating the fuzzy parameters ${\theta }_i\left(t\right)$ are designed as the following fractional-order differential equations

$$D^{\alpha }{\theta }_i\left(t\right)={\gamma }_i{e}_i\left(t\right){\psi }_i\left(x\left(t\right)\right)-{\gamma }_i{\sigma }_i{\theta }_i\left(t\right),i=1,2,\cdots ,n,$$

(29)

where ${\sigma }_i$ and ${\gamma }_i$ are positive design parameters.

Theorem 1. 

Suppose that the controller is designed as (26) and the fractional adaptation laws are defined as (29). Then all signals in the closed-loop system will keep bounded, and the tracking error will eventually be arbitrary small if appropriate control parameters are chosen.

Proof. 

Choose the following quadratic Lyapunov function

$$V\left(t\right)=\frac{1}{2}{e}^T\left(t\right)Pe\left(t\right)+\frac{1}{2}\sum _{i=1}^n\frac{1}{{\gamma }_i}{\tilde{\theta }}_i^T\left(t\right){\tilde{\theta }}_i\left(t\right)$$

(30)

By using Lemma 1, we can obtain

$$D^{\alpha }V\left(t\right)\le e^T\left(t\right)P{D}^{\alpha }e\left(t\right)+\sum _{i=1}^n\frac{1}{{\gamma }_i}{\tilde{\theta }}_i^T\left(t\right)D^{\alpha }{\tilde{\theta }}_i\left(t\right)$$

(31)

Noting that the Caputo derivative of a constant function is 0, we have

$$D^{\alpha }{\tilde{\theta }}_i\left(t\right)=D^{\alpha }{\theta }_i\left(t\right)$$

(32)

Thus, we have

$$D^{\alpha }V\left(t\right)\le e^T\left(t\right)P{D}^{\alpha }e\left(t\right)+\sum _{i=1}^n\frac{1}{{\gamma }_i}{\tilde{\theta }}_i^T\left(t\right)D^{\alpha }{\theta }_i\left(t\right)$$

(33)

Substituting (28) and the fractional adaptation laws (29) into (33), we have

$$D^{\alpha }V\left(t\right)\le -k{e}^T\left(t\right)e\left(t\right)-(b-\overline{\epsilon })\sum _{i=1}^n\left|e_i\left(t\right)\right|-\sum _{i=1}^n{\sigma }_i{\tilde{\theta }}_i^T\left(t\right){\theta }_i\left(t\right)$$

(34)

If b is taken from $(\overline{\epsilon },+\infty )$, then

$$D^{\alpha }V\left(t\right)\le -k{e}^T\left(t\right)e\left(t\right)-\sum _{i=1}^n{\sigma }_i{\tilde{\theta }}_i^T\left(t\right){\theta }_i\left(t\right)$$

(35)

Note that

$$-\sum _{i=1}^n{\sigma }_i{\tilde{\theta }}_i^T\left(t\right){\theta }_i^{*}\le \frac{1}{2}\sum _{i=1}^n{\sigma }_i{\tilde{\theta }}_i^T\left(t\right){\tilde{\theta }}_i\left(t\right)+\frac{1}{2}\sum _{i=1}^n{\sigma }_i{\theta }_i^{*T}{\theta }_i^{*}$$

(36)

Thus we have

$$\begin{array}{cc}\hfill D^{\alpha }V\left(t\right)& \le -k{e}^T\left(t\right)e\left(t\right)-\sum _{i=1}^n{\sigma }_i{\tilde{\theta }}_i^T\left(t\right){\theta }_i\left(t\right)\hfill \\ & =-k{e}^T\left(t\right)e\left(t\right)-\sum _{i=1}^n{\sigma }_i{\tilde{\theta }}_i^T\left(t\right){\tilde{\theta }}_i\left(t\right)-\sum _{i=1}^n{\sigma }_i{\tilde{\theta }}_i^T\left(t\right){\theta }_i^{*}\hfill \\ & \le -k{e}^T\left(t\right)e\left(t\right)-\frac{1}{2}\sum _{i=1}^n{\sigma }_i{\tilde{\theta }}_i^T\left(t\right){\tilde{\theta }}_i\left(t\right)+\frac{1}{2}\sum _{i=1}^n{\sigma }_i{\theta }_i^{*T}{\theta }_i^{*}\hfill \\ & \le -k{e}^T\left(t\right)e\left(t\right)-\frac{\sigma }{2}\sum _{i=1}^n{\tilde{\theta }}_i^T\left(t\right){\tilde{\theta }}_i\left(t\right)+\frac{1}{2}\sum _{i=1}^n{\sigma }_i{\theta }_i^{*T}{\theta }_i^{*}\hfill \\ & \le -\frac{2k}{{\lambda }_{max}\left(P\right)}\frac{1}{2}{e}^T\left(t\right)Pe\left(t\right)-\frac{\sigma \gamma }{2}\sum _{i=1}^n\frac{1}{{\gamma }_i}{\tilde{\theta }}_i^T\left(t\right){\tilde{\theta }}_i\left(t\right)+\frac{1}{2}\sum _{i=1}^n{\sigma }_i{\theta }_i^{*T}{\theta }_i^{*}\hfill \\ & \le -k_{0}V\left(t\right)+\frac{1}{2}\sum _{i=1}^n{\sigma }_i{\theta }_i^{*T}{\theta }_i^{*}\hfill \end{array}$$

(37)

where

$$\begin{array}{cc}\hfill \sigma & =min\{{\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_n\}\hfill \\ \hfill \gamma & =min\{{\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_n\}\hfill \\ \hfill k_0& =min\{\frac{2k}{{\lambda }_{max}\left(P\right)},\sigma \gamma \}\hfill \end{array}$$

Applying Lemma 2, there exists a $t_0>0$ such that

$$\parallel V\left(t\right)\parallel \le \frac{{\sum }_{i=1}^n{\sigma }_i{\theta }_i^{*T}{\theta }_i^{*}}{k_0}$$

(38)

which yields that

$$\parallel e\left(t\right)\parallel \le \sqrt{\frac{2{\sum }_{i=1}^n{\sigma }_i{\theta }_i^{*T}{\theta }_i^{*}}{k_0{\lambda }_{min}\left(P\right)}}$$

(39)

which means $\parallel e\left(t\right)\parallel$ can be arbitrarily small in $(t_0,\infty )$ if the parameters k and ${\gamma }_i$ are chosen large enough. Besides, it can be easily seen that all the signals in the closed-loop system will remain bounded.

5. Numerical Simulations

In this section, an illustrative example is presented to illustrate the effectiveness and applicability of the proposed adaptive fuzzy control approach and to confirm the theoretical results. Consider the following fractional-order rotational mechanical system with model uncertainties and external disturbances [17].

$$\begin{array}{cc}\hfill D^{\alpha }{x}_1=& x_2+\mathrm{\Delta }{f}_1\left(x\right)+d_1\left(t\right)\hfill \\ \hfill D^{\alpha }{x}_2=& 0.25{(x_3+2.4)}^{2}sin(x_1-0.69)cos(x_1-0.69)\hfill \\ & -sin(x_1-0.69)-0.7x_2+\mathrm{\Delta }{f}_2\left(x\right)+d_2\left(t\right)\hfill \\ \hfill D^{\alpha }{x}_3=& 2.8cos(x_1-0.69)-1.942-0.5sin\left(et\right)+\mathrm{\Delta }{f}_3\left(x\right)+d_3\left(t\right)\hfill \end{array}$$

(40)

In the simulation, the uncertainty term and external noise of the system are selected as follows

$$\begin{array}{cc}\hfill \mathrm{\Delta }{f}_1\left(x\right)+d_1\left(t\right)& =-0.15sin\left(2t\right)x_1+0.15sin\left(3t\right)\hfill \\ \hfill \mathrm{\Delta }{f}_2\left(x\right)+d_2\left(t\right)& =0.25cos\left(4t\right)x_2+0.1cos\left(t\right)\hfill \\ \hfill \mathrm{\Delta }{f}_3\left(x\right)+d_3\left(t\right)& =0.2sin\left(3t\right)x_1+0.2sin\left(3t\right)\hfill \end{array}$$

(41)

Initial conditions of the system are selected as $x_1\left(0\right)=-3$, $x_2\left(0\right)=4$, and $x_3\left(0\right)=-2$. The referenced signal is set to be $x_d\left(t\right)={[sin\left(t\right),cos\left(t\right),sin\left(2t\right)]}^T$. Throughout the simulation, the model of the fractional-order nonlinear system (33) is fully unknown. The proposed control methods do not need to the knowledge of the system. The fuzzy systems have $x_1\left(t\right)$, $x_2\left(t\right)$ , and $x_3\left(t\right)$ as the inputs. For each input, we define 11 Gaussian membership functions uniformly distributed on $[-10,10]$. Thus, 121 rules are used. The parameters of the controller are chosen as $k=1,b=1,{\sigma }_1={\sigma }_2={\sigma }_3=0.001,{\gamma }_1,{\gamma }_2,{\gamma }_3$. The initial conditions of the fuzzy systems ${\theta }_1\left(0\right)$, ${\theta }_2\left(0\right)$, and ${\theta }_3\left(0\right)$ are chosen randomly.

The simulation results are shown in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. Figure 1, Figure 2 and Figure 3 give the track performance of the state variables $x_1\left(t\right)$, $x_2\left(t\right)$, and $x_3\left(t\right)$, respectively. Time responses of the tracking errors are shown in Figure 4. We can see the tracking errors have a fast convergence. Figure 5 displays the trajectories of the control inputs. From the simulation results we can say that good control performance has been achieved.

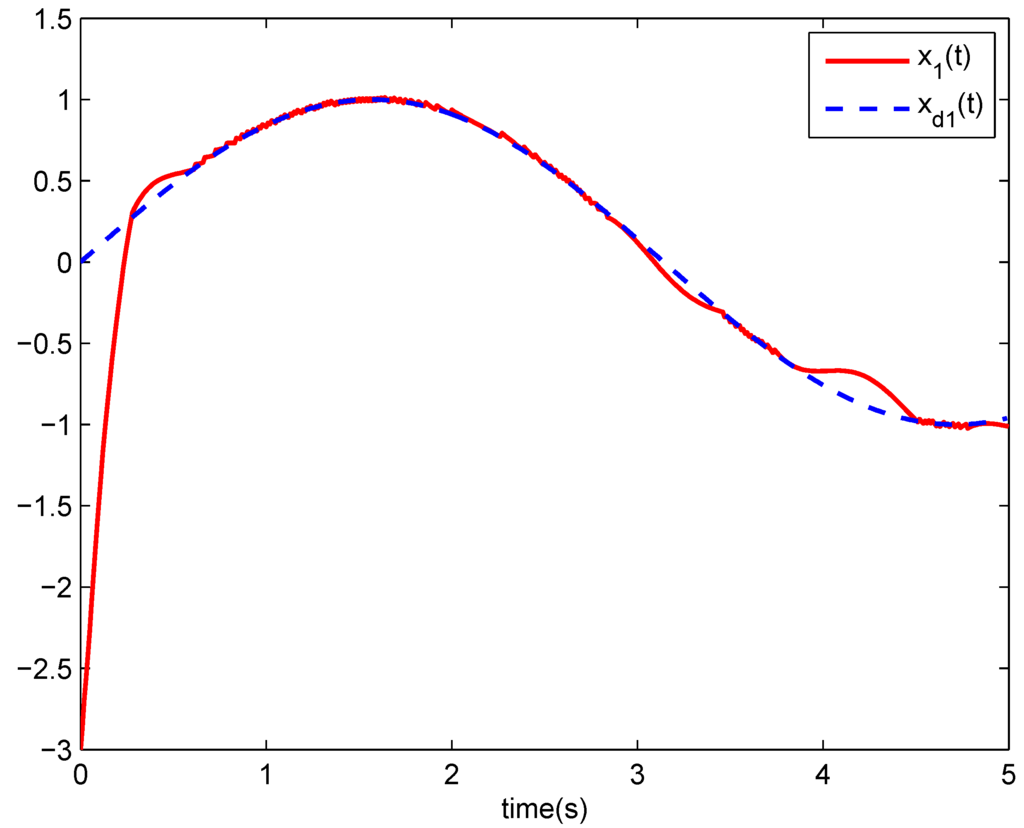
Figure 1. Responses of the system state $x_1\left(t\right)$.

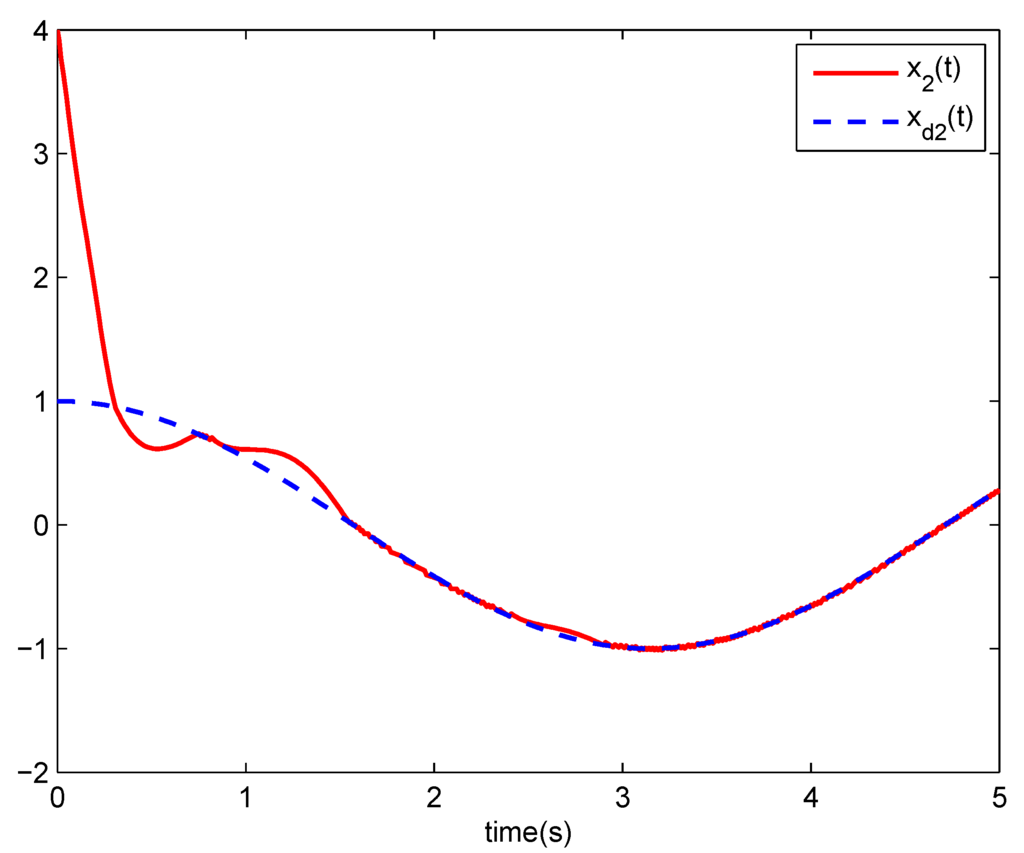
Figure 2. Responses of the system state $x_2\left(t\right)$.

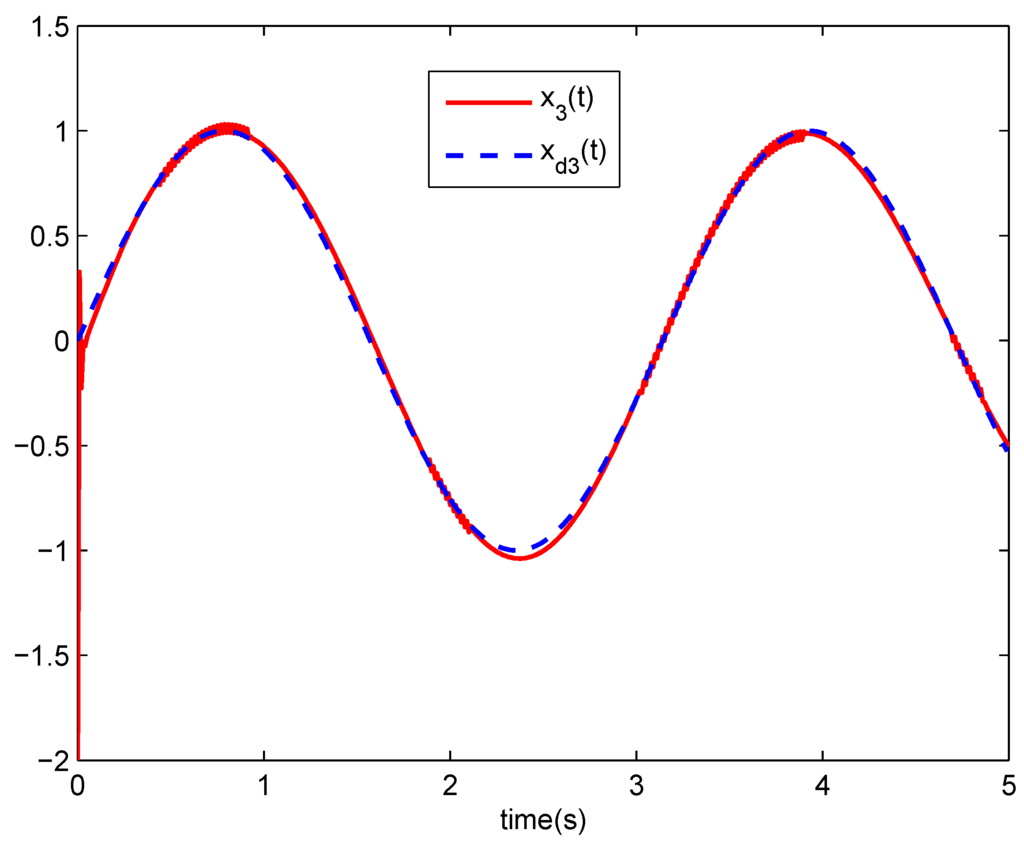
Figure 3. Responses of the system state $x_3\left(t\right)$.

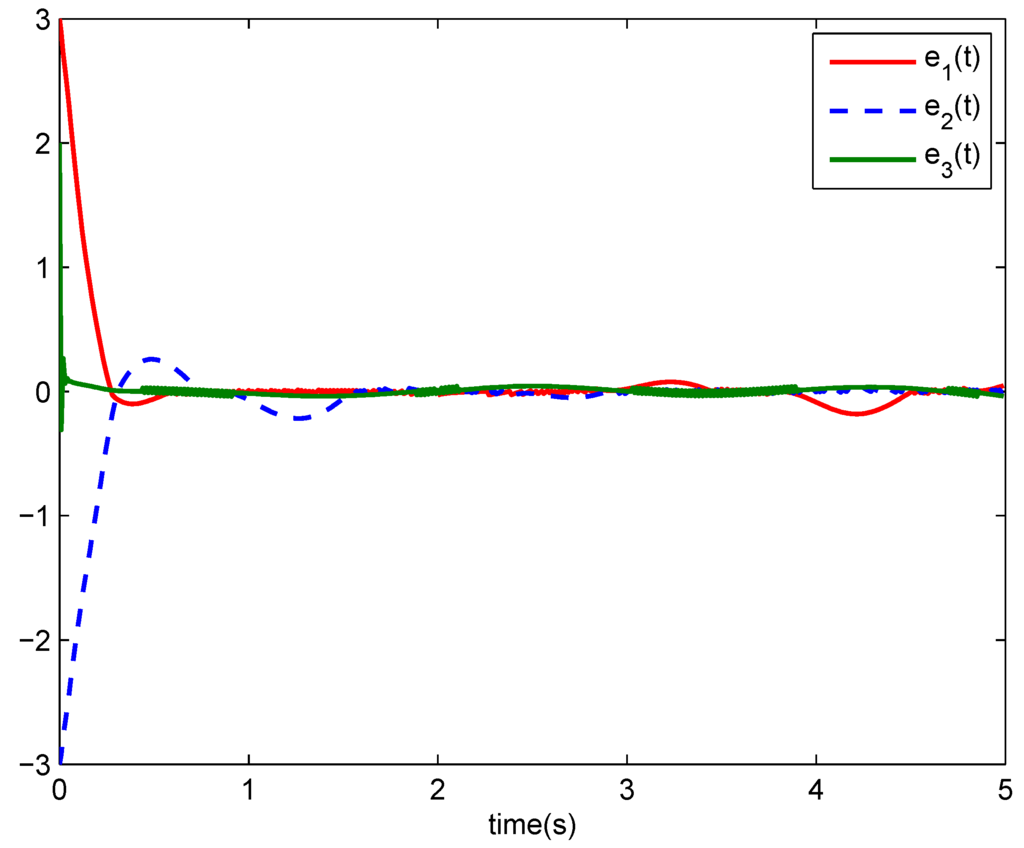
Figure 4. Trajectories of the tracking errors.

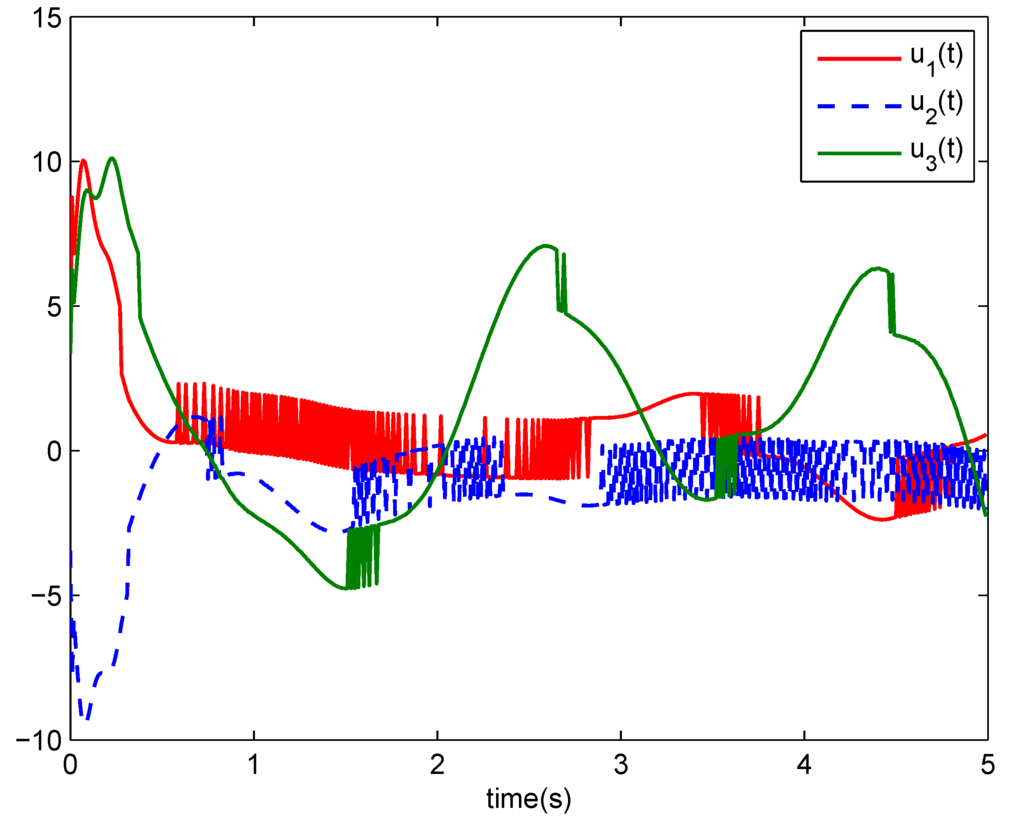
Figure 5. Trajectories of the control inputs.

6. Conclusions

In this paper, an adaptive fuzzy control method for fractional-order nonlinear systems in the presence of model uncertainty and external noises is proposed. Fuzzy logic systems are used for estimating the unknown nonlinear functions. Based on the fractional Lyapunov direct method, an adaptive fuzzy controller is designed. The proposed method can guarantee all the signals in the closed-loop systems remain bounded and the tracking errors converge to an arbitrary small region of the origin. Lastly, an illustrative example is given to demonstrate the effectiveness of the proposed results.