H∞ Control for Markov Jump Systems with Nonlinear Noise Intensity Function and Uncertain Transition Rates
Abstract
:1. Introduction
2. Problem Description
3. Robust Stochastic ∞ Performance Analysis
4. Robust Stochastic ∞ Controller Design
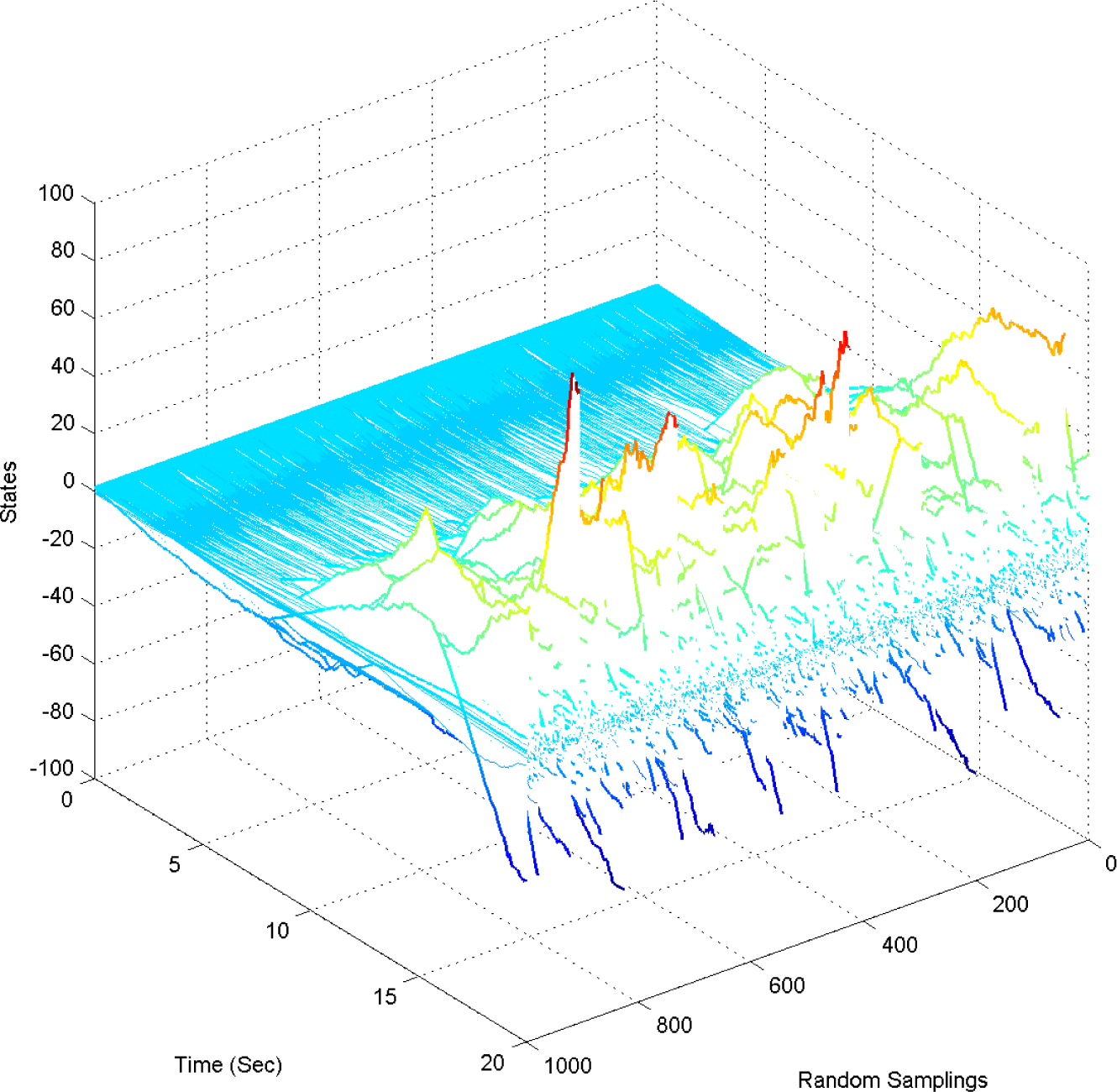
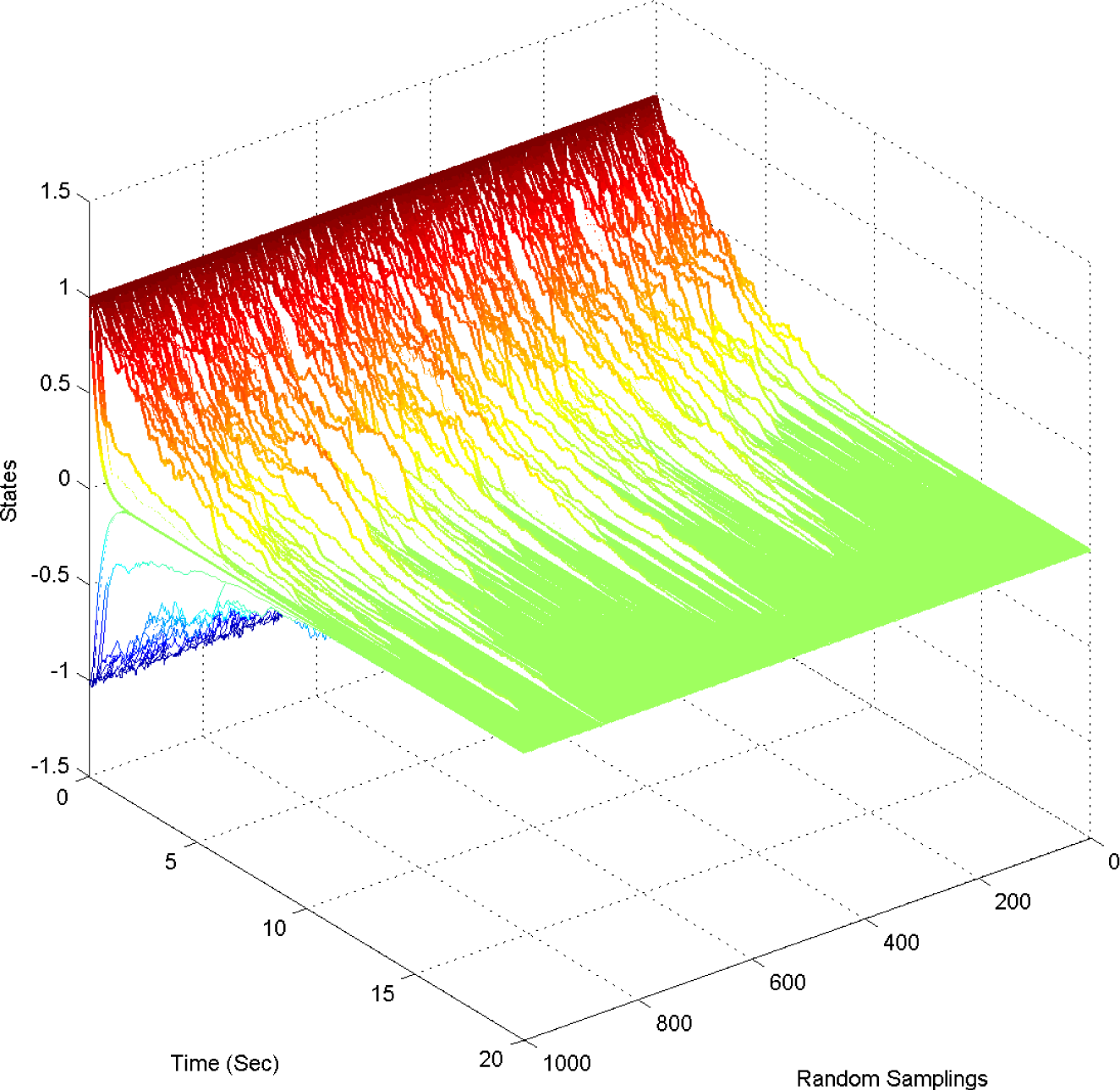
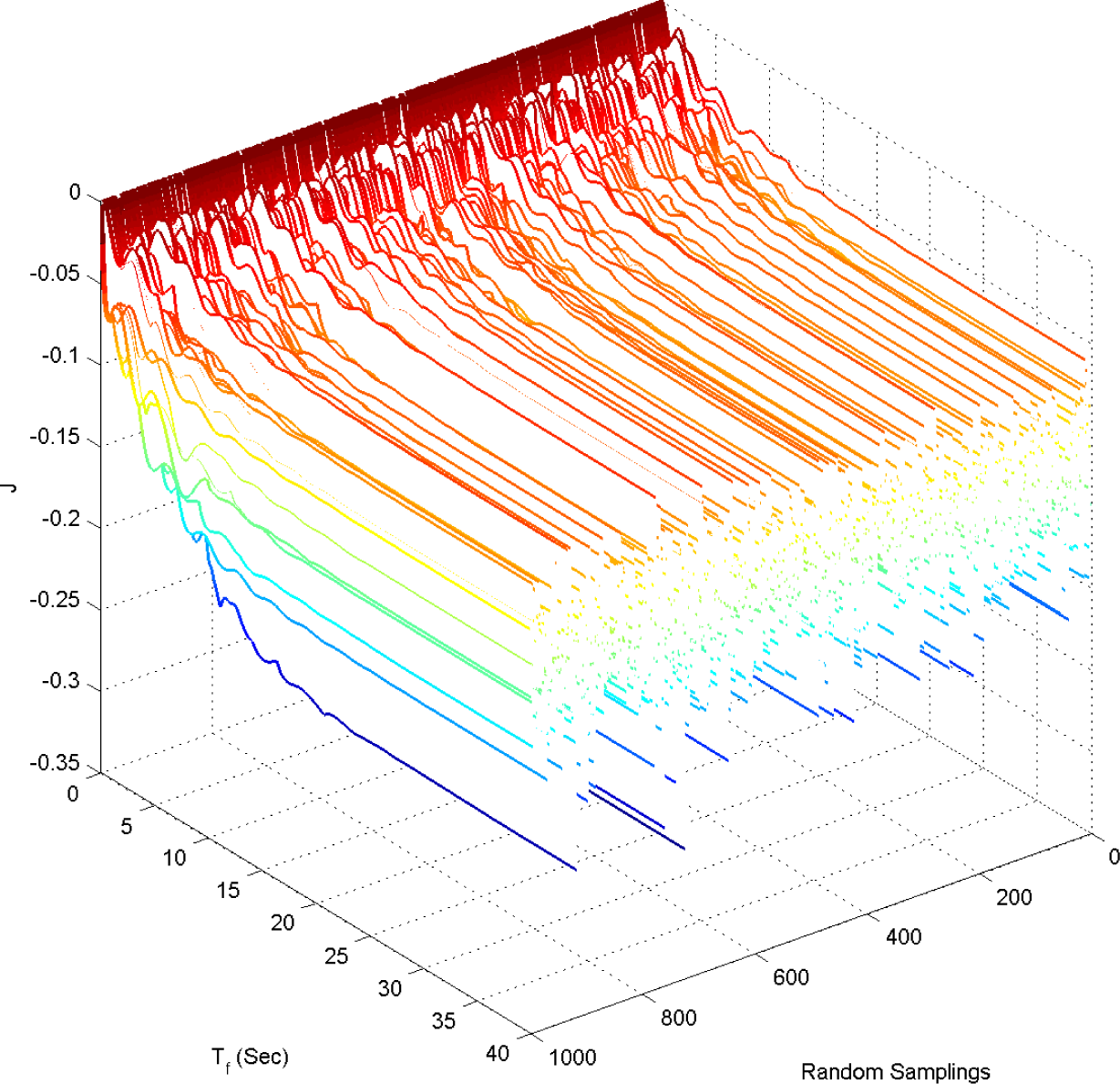
5. Numerical Example
6. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stoica, A.; Yaesh, I. Jump-Markovian based control of wing deployment for an uncrewed air vehicle. J. Guid. Control Dyn. 2002, 25, 407–411. [Google Scholar]
- Sworder, D.D.; Rogers, R.O. An LQG solution to a control problem with solar thermal receiver. IEEE Trans. Autom. Control 1983, 28, 971–978. [Google Scholar]
- Ploplys, N.J.; Kawka, P.A.; Alleyne, A.G. Closed-loop control over wireless networks. IEEE Control Syst. Mag. 2004, 24, 58–71. [Google Scholar]
- Ugrinovskii, V.A.; Pota, H.R. Decentralized control of power systems via robust control of uncertain Markov jump parameter systems. Int. J. Control 2005, 78, 662–677. [Google Scholar]
- Svensson, L.E.O.; Williams, N. Optimal monetary policy under uncertainty: A Markov jump-linear-quadratic approach. Fed. Reserve St. Louis Rev. 2008, 90, 275–293. [Google Scholar]
- Ji, Y.; Chizeck, H.J. Controllability, stabilizability, and continuous-time Markovian jump linear quadratic control. IEEE Trans. Autom. Control 1990, 35, 777–788. [Google Scholar]
- Feng, X.; Loparo, K.A.; Ji, Y.; Chizeck, H.J. Stochastic stability properties of jump linear systems. IEEE Trans. Autom. Control 1992, 37, 38–53. [Google Scholar]
- Costa, O.L.V. do Val, J.B.R.; Geromel, J.C. Continuous-time state-feedback H2-control of Markovian jump linear system via convex analysis. Automatica 1999, 35, 259–268. [Google Scholar]
- Do Val, J.B.R. Geromel, J.C.; Goncalves, A.P.C. The 2-control for jump linear systems: Cluster observations of the Markov state. Automatica 2002, 38, 343–349. [Google Scholar]
- De Farias, D.P.; Geromel, J.C. do Val, J.B.R.; Costa, O.L.V. Output feedback control of Markov jump linear systems in continuous-time. IEEE Trans. Autom. Control 2000, 45, 944–949. [Google Scholar]
- Costa, O.L.V.; Guerra, S. Robust linear filtering for discrete-time hybrid Markov linear systems. Int. J. Control 2002, 75, 712–727. [Google Scholar]
- Costa, O.L.V.; Fragoso, M.D.; Todorov, M.G. Continuous-Time Markov Jump Linear Systems; Asmussen, S., Gani, J., Jagers, P., Kurtz, T.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Yue, D.; Han, Q.-L. Delay-dependent exponential stability of stochastic systems with time-varying delay, nonlinearity, and Markovian switching. IEEE Trans. Autom. Control 2005, 50, 217–222. [Google Scholar]
- Senthilkumar, T.; Balasubramaniam, P. Delay-dependent robust stabilization and ∞ control for nonlinear stochastic systems with Markovian jump parameters and interval time-varying delays. J. Optim. Theory Appl. 2011, 151, 100–120. [Google Scholar]
- Zhang, Y. Stability of discrete-time delay Markovian jump systems with stochastic non-linearity and impulses. IET Control Theory A 2013, 7, 2178–2187. [Google Scholar]
- Xiong, J.; Lam, J.; Gao, H.; Ho, D.W.C. On robust stabilization of Markovian jump systems with uncertain switching probabilities. Automatica 2005, 41, 897–903. [Google Scholar]
- Xiong, J.; Lam, J. Robust 2 control of Markovian jump systems with uncertain switching probabilities. Int. J. Syst. Sci. 2009, 40, 255–265. [Google Scholar]
- Shu, Z.; Lam, J. Static output-feedback stabilization of discrete-time Markovian jump linear systems: A system augmentation approach. Automatica 2010, 46, 687–694. [Google Scholar]
- Xu, S.; Chen, T. Robust ∞ control for uncertain stochastic systems with state delay. IEEE Trans. Autom. Control 2002, 47, 2089–2094. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Pennsylvania, PA, USA, 1994. [Google Scholar]
- Mao, X. Robustness of exponential stability of stochastic differential delay equation. IEEE Trans. Autom. Control 1996, 41, 442–447. [Google Scholar]
- El Ghaoui, L.; Rami, M.A. Robust state-feedback stabilization of jump linear systems via LMIs. Int. J. Robust Nonlinear Control 1996, 6, 1015–1022. [Google Scholar]
- Ugrinovskii, V.A. Randomized algorithms for robust stability and guaranteed cost control of stochastic jump parameters systems with uncertain switching policies. J. Optim. Theory Appl. 2005, 124, 227–245. [Google Scholar]
- Barmish, B.R.; Shcherbakov, P.S. On avoiding vertexization of robustness problems: the approximate feasibility concept. IEEE Trans. Autom. Control 2002, 47, 819–824. [Google Scholar]
- Boukas, E. K.; Shi., P.; Benjelloun, K. On stabilization of uncertain linear systems with jump parameters. Int. J. Control 1999, 72, 842–850. [Google Scholar]
- Wang, G.; Zhang, Q. Robust ∞ control of Markovian jump systems with uncertain switching probabilities. Asian J. Control 2012, 14, 1407–1410. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Guo, Y. H∞ Control for Markov Jump Systems with Nonlinear Noise Intensity Function and Uncertain Transition Rates. Entropy 2015, 17, 4762-4774. https://doi.org/10.3390/e17074762
Wang X, Guo Y. H∞ Control for Markov Jump Systems with Nonlinear Noise Intensity Function and Uncertain Transition Rates. Entropy. 2015; 17(7):4762-4774. https://doi.org/10.3390/e17074762
Chicago/Turabian StyleWang, Xiaonian, and Yafeng Guo. 2015. "H∞ Control for Markov Jump Systems with Nonlinear Noise Intensity Function and Uncertain Transition Rates" Entropy 17, no. 7: 4762-4774. https://doi.org/10.3390/e17074762
APA StyleWang, X., & Guo, Y. (2015). H∞ Control for Markov Jump Systems with Nonlinear Noise Intensity Function and Uncertain Transition Rates. Entropy, 17(7), 4762-4774. https://doi.org/10.3390/e17074762




