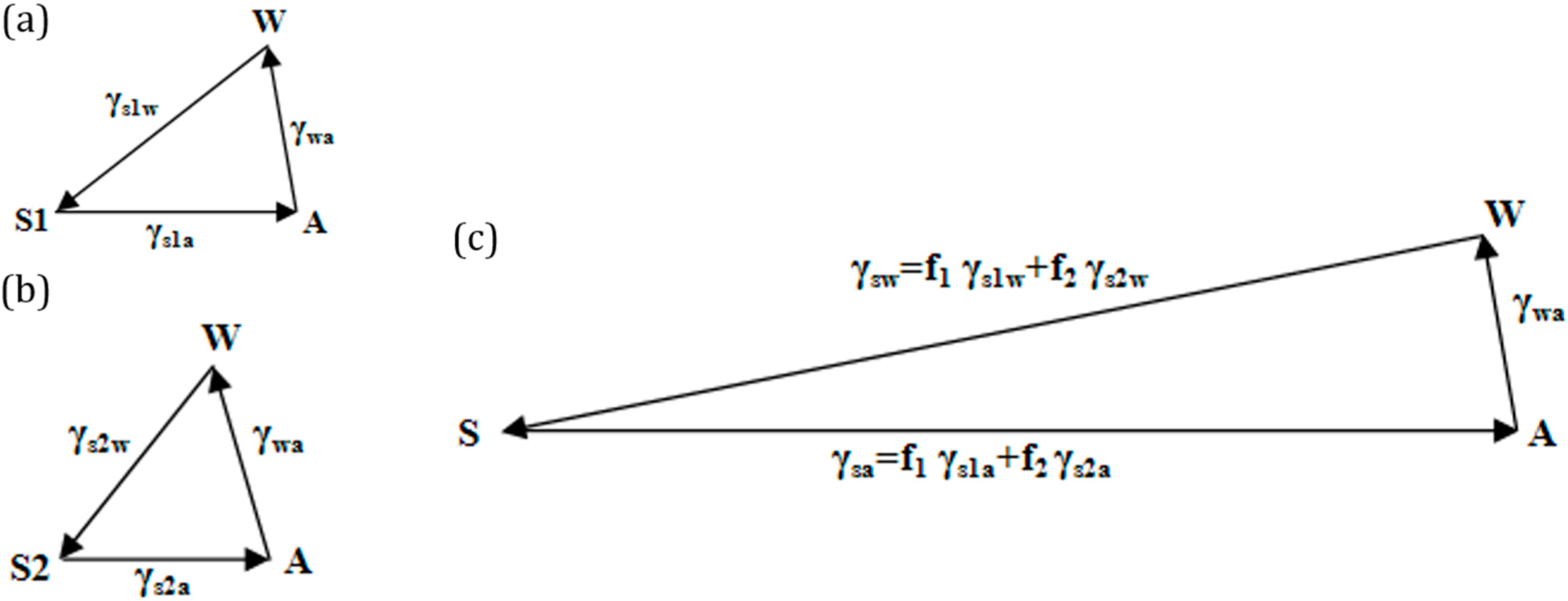1. Introduction
Surface tension is a fundamental concept in surface physics and chemistry, which appears quite simple. However, the concept is much more complex than it seems to a beginning student. The most common definition of surface tension is that it is force acting along a line of unit length parallel to the surface, but perpendicular to the line. The surface tension is often considered equivalent to the surface free energy,
i.e., the energy needed to create a surface with unit area. Related to the surface tension is the concept of the surface stress, defined as the amount of reversible work per unit area needed to stretch the surface, which is identical to the surface free energy for the liquid to liquid and liquid to gas interfaces, but is different for the solid to liquid and solid to gas interfaces [
1].
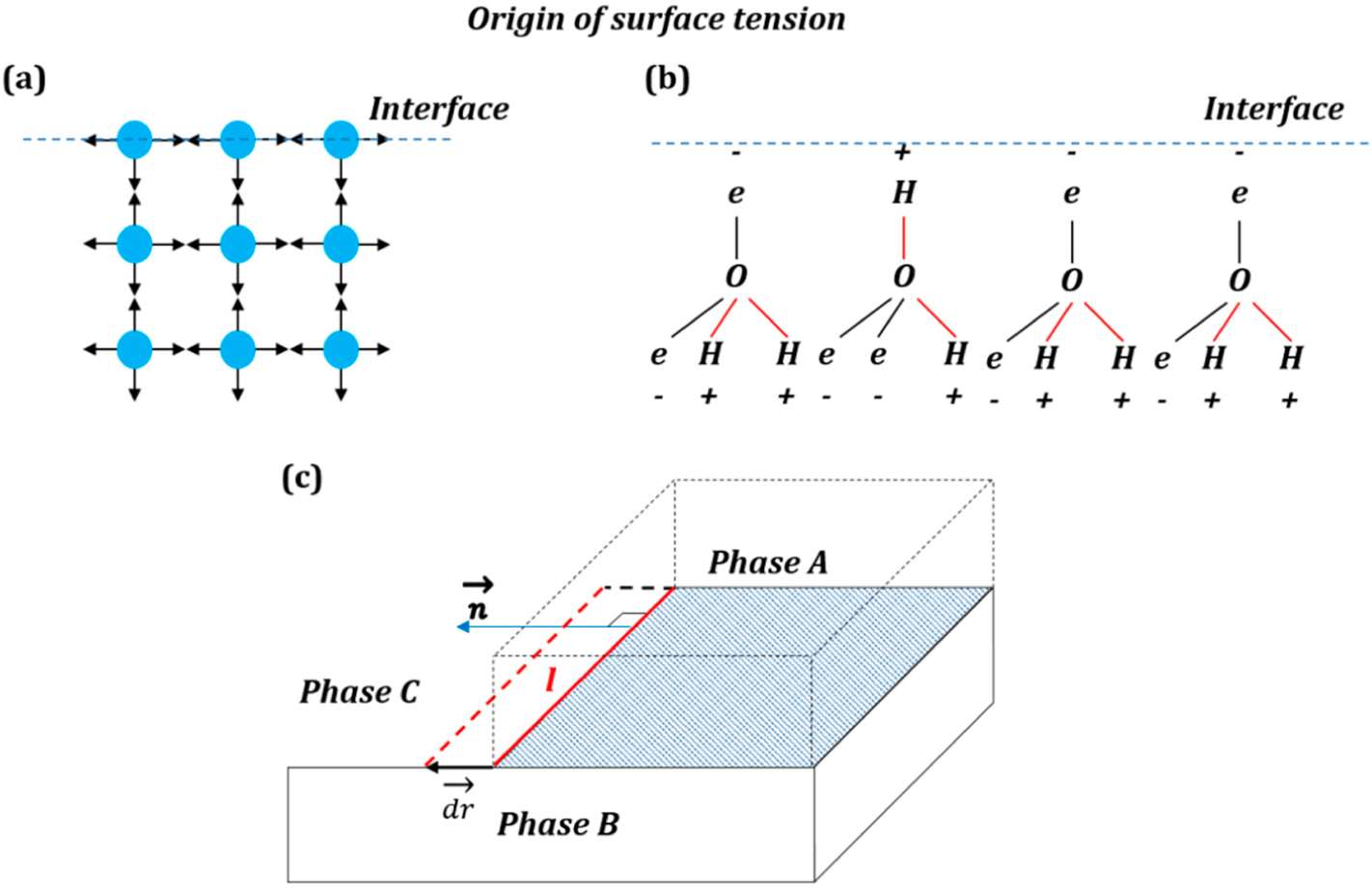
The simplest (and popular in textbooks) explanation of the origin of the surface free energy is that surface atoms and molecules have higher energy than those in the bulk due to lower amount of bonds with neighboring atoms and molecules (
Figure 1a). An explanation of the origin of the interfacial energy is found in the popular textbook by Lautrup [
2], who states that the binding energy per molecule may be estimated as the product of the specific heat of evaporation,
h (evaporation enthalpy per unit of mass), and the mass of a single molecule. The surface tension is then obtained by multiplying the binding energy by the number of molecules in the surface layer,
, where ρ is the density and
l is the molecular separation length. The factor 1/6 is due to the assumption of six bonds per molecule (one per each side). The formula overestimates water surface tension as γ = 0.129 Jm
−2, while the true value is γ = 0.072 Jm
−2.
The naive explanation of
Figure 1a may be valid for non-polar molecules; however, the mechanisms leading to the surface energy can be much more complex in the case of polar molecules (e.g., water), involving reorientation of molecular networks in the surface layer and, thus, an entropic (rather than enthalpic) contribution to the surface energy (
Figure 1b) [
3].
An entropic force acts on the system in its entirety. The change of Gibbs free energy is given by Δ
G = Δ
H −
TΔ
S, where
H,
T and
S are the enthalpy, temperature and entropy of the system. Water molecules form a regular “clathrate cage” around a hydrophobic non-polar (e.g., hydrocarbon) molecule, with an average number of hydrogen bonds in the cage larger than in the bulk volume. For an entropic force, such as the hydrophobic interaction between hydrophobic molecules in water, which prevents their dissolution, the decrease of the enthalpy Δ
H due to the formation of new hydrogen bonds is smaller than the decrease of entropy
TΔ
S due to the formation of a regularly-ordered structure around the hydrocarbon molecule, and thus, clathrate cages are energetically non-profitable, leading to the effective attraction of the hydrophobic molecules in water. It has been argued [
3] that a similar entropic effect occurs at the water to air interface (where the water molecular network is more ordered than in the bulk), and it is responsible for the origin of the surface tension. Consequently, it is not possible often to demonstrate how the vector of the surface tension force results from the summation of the intermolecular forces, and the surface tension is thought of as a result of a complex interaction in the entire system, rather than a sum of forces in the surface layer.
It is noted, however, that unlike most entropic forces, the surface tension decreases with increasing temperature in accordance with the Eötvös rule [
4]. As far as non-polar liquids are concerned, Bormashenko [
5] argued that the surface tension of most organic liquids is governed by London dispersion forces.
Mechanical forces are vectors that are applied to bodies or material points. Unlike conventional mechanical forces, the tension forces are not applied to the three-phase line, which is a geometrical line and not a material object with mass, but rather constitute generalized forces or derivatives of the interfacial energies by the distance for which the three-phase line advances. These forces reflect the tendency of the system to reduce its energy (and increase entropy).
The high solid-vapor energy of an interface causes wetting of the solid surface and spreading of liquid on it (low θ), while low energy produces non-wetting interfaces (high θ). The surface tension force is assumed to be similar to the pressure in the sense that pressure
P is a scalar, which, however, results in a vector force
when applied to an area
A with the normal
. Similarly, the surface tension γ is a scalar that results in the force
when applied to a line
l with the normal
(the normal lies in the plane of the surface), (
Figure 1c).
However, there is a significant difference between the pressure and surface tension due to the fact that the latter results in a concentrated force applied at a line. In mechanics, a concentrated force results in various types of singularities, e.g., infinite strains or accelerations. Thus, when Young’s law for the contact angle is derived, usually the considerations of the balance of three surface tension forces are employed. These forces are thought to be applied to the immaterial three-phase line, which is a geometric concept, rather than a material object with a finite mass.
Another important question in physical and colloidal chemistry is how to predict the value of the surface tension at the interface of two phases when tensions of each of these phases are known. Although in general, this may be an unsolvable task, since many forces of various natures are involved, there are two conflicting approaches that are often used. Antonow [
6] suggested a simple rule based on the idea that the surface free energy is caused by broken molecular bonds at the surface. Therefore, when two substances of a similar nature (e.g., two immiscible liquids) come in contact, they partially compensate for the broken bonds. An alternative theory was developed by Girifalco and Good [
7] on the basis of the assumption that dispersive forces act between the molecules of the substances. The topic has been extensively discussed in the literature and textbooks, although no single answer appropriate for all cases has been given.
In this paper, we suggest to view the surface tension as a generalized force and propose a geometric (vector) interpretation of various equations involving the surface tension at equilibrium (the Young, Wenzel, Cassie, Antonoff and Girifalco–Good equations). We also present some data on surface tension in multiphase systems.
3. Graphical Interpretation of the Surface Tension at Equilibrium
As we have discussed above, the surface tensions at the three-phase line in equilibrium are not forces in the strictly mechanical sense of the word, because they are applied to an imaginary line rather than to a physical body. Instead, we suggest treating tensions as generalized forces,
i.e., the derivative of surface energy by a generalized coordinate, such as the position of a three-phase line. In that case, there is no need to perceive surface tensions as applied to a particular object, but as vector quantities in general. It is known that both Young, Wenzel and Cassie equations can be derived from variational principles [
29].
In this section, we suggest a geometric interpretation of the surface tension balance extending the well-known Neumann’s triangle approach. Phases are represented by points, while tensions are vectors connecting these points. The Young, Wenzel, Cassie, Antonoff and Girifalco–Good equations receive simple interpretations in this approach.
3.1. Three-Phase Systems
When a three-phase line propagates (
Figure 1c) for a short distance
, the change of free energy is given by the interfacial area γ times the scalar product of
by the normal to the three-phase line,
, in the plane of the interface:
. The surface tension vector as a generalized force is a vector given by a derivative:
The only difference of this presentation from the standard one is that it is a generalized force, which is not a mechanical force, and thus, it is not applied to a particular point or a body.
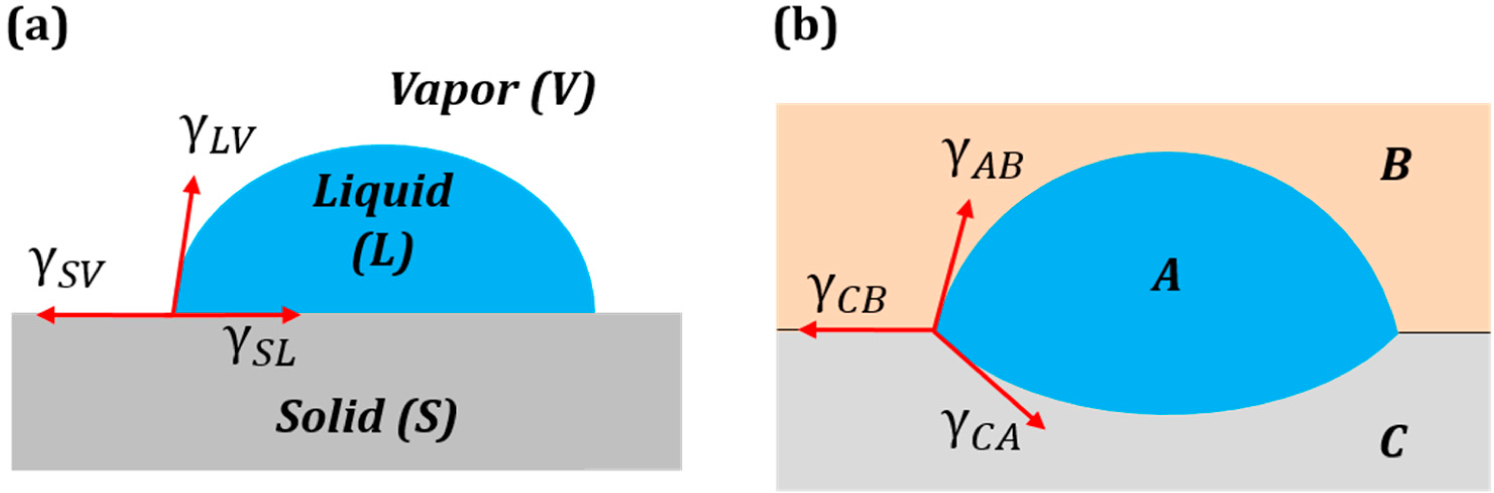
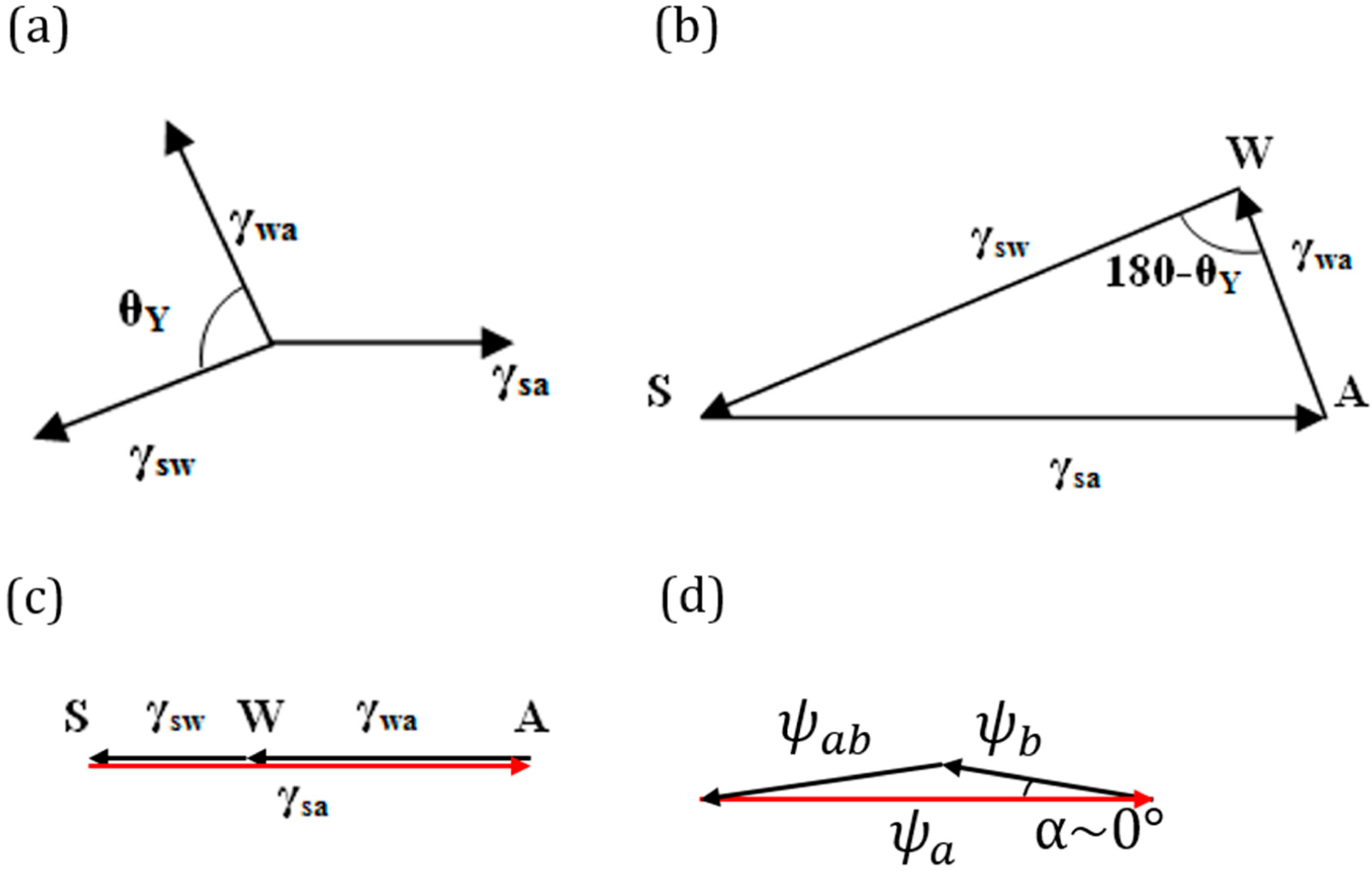
Consider a droplet of water placed on a solid surface in air. Let Points S, A and W denote the three phases solid, air and water, respectively. Let γ
sa, γ
wa and γ
sw denote the surface tensions for the solid to air, water to air and solid to water interfaces, respectively (
Figure 4a.). The surface tensions can be represented as the sides of the triangle with Vertices S, A and W (
Figure 4b). Mechanical equilibrium of the droplet requires that the vector sum of the surface tensions be zero,
i.e.,
.
If Antonoff’s rule (
Equation (2)) were valid as an exact equality,
, then it would mean that the three vectors,
,
and
, lie on the same line.
Figure 4c shows such a case for the three-phase system SAW. Note that this corresponds to the case of complete wetting of the solid. However, if Antonoff’s rule constitutes an inequality, γ
max < γ
med + γ
min, then the rule receives a clear geometric interpretation of the triangle inequality. The contact angle is a measure of the deviation from the equality of
Equation (2).
Antonoff’s rule is intended for immiscible liquids; however, a similar approach can be used for estimates of the surface tension in solid to liquid to vapor systems in equilibrium. Thus, Lautrup [
2] calculates the contact angle of water on ice at 0 °C using the above-mentioned estimate:
where
h is the specific enthalpy of the phase transition, ρ is the density of the phase and
l is the molecular separation length. For liquid water, the molar enthalpy of evaporation is h
evap = 45.051 kJ/mol, whereas for ice, the molar enthalpy of melting is h
melt = 6.010 kJ/mol, and the molar enthalpy of sublimation h
subl = 51.059 kJ/mol. Notice that h
subl = h
melt + h
evap as one would expect. Using the densities ρ
ice = 916.72 kg m
−3 and ρ
water = 1000 kg m
−3 at 0°C, Lautrup [
2] finds γ
sa = 0.138 Jm
−2, γ
sw = 0.016 Jm
−2 and γ
wa = 0.129 Jm
−2 yielding the value of the contact angle
θ = 19° (while the experimentally measured value lies between 12° and 24°).
In accordance with our geometric interpretation, the above discussion by Lautrup means that the equality, h
subl = h
melt + h
evap, when normalized by water and ice density, yields the triangle inequality, h
subl ρ
ice < h
melt ρ
ice + h
evap ρ
water, corresponding to the vector triangle
in
Figure 4b. This triangle inequality is satisfied only because the density of ice is lower than that of water at 0 °C, ρ
ice < ρ
water, which constitutes the famous “water anomaly.” Thus, the 19° contact angle of water on ice is a measure of the water anomaly. Without the water anomaly, a thin water film would completely cover the ice surface with zero contact angle. Additionally, this is indeed the case for most substances, whose liquid phase wets their solid phase with a thin film, rather than forming a droplet.
Interestingly, the effective interfacial energy between two liquids can also be negative, when a chemical reaction between two immiscible liquids creates surfactant molecules [
30]. This means that the interfacial area would tend to increase spontaneously; thus, larger droplets would divide into smaller droplets. However, this corresponds to non-equilibrium situations.
As far as the geometric interpretation of the Girifalco and Good [
7] equation (
Equation (3)),
, we note its striking similarity with the law of cosines,
, where
and
. Thus, we interpret
Equation (3) as the triangle inequality for
,
and
. Furthermore, in the important case of Φ =1 (or
α = 0), which corresponds to only dispersion forces present (non-polar molecules), we obtain the equality
(
Figure 4d). While the physical interpretation of this equality is beyond the scope of this paper, we note that for adhesion energy caused by an electrostatic field, the total energy is proportional to the squares of the electric field intensities, and thus, the equality
could correspond to a simple summation of electric fields of different phases. The value of the angle
α is a quantitative characteristic of the deviation from the pure dispersion force interaction.
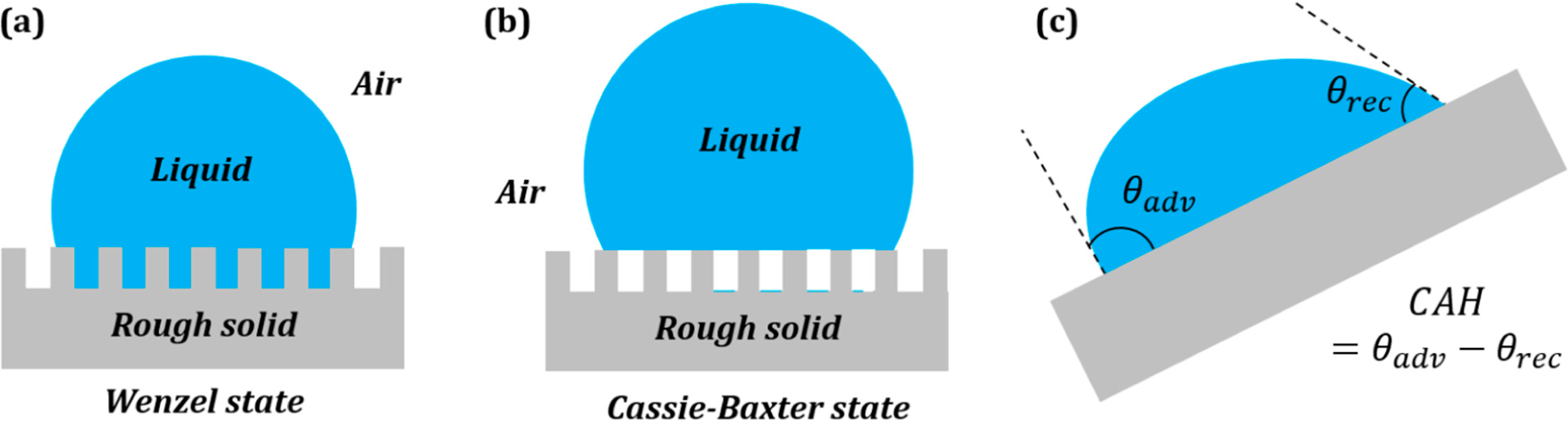
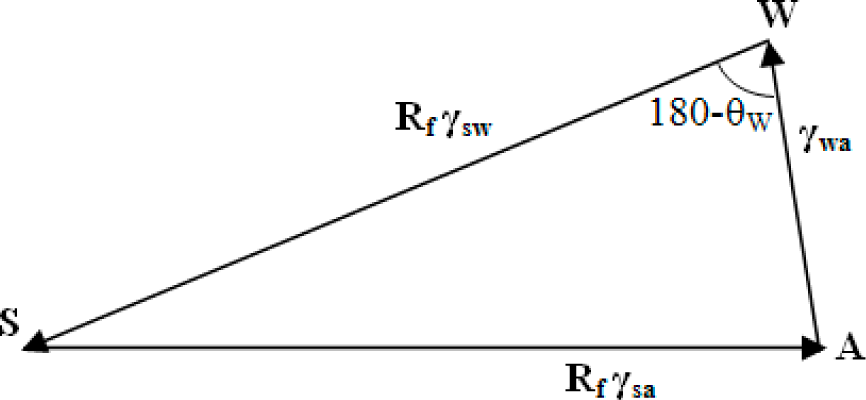
3.2. Wenzel and Cassie States in the Three-Phase System
Surface roughness is known to affect the measured value of the contact angle. The two extreme cases of a droplet on a rough surface are described by the Wenzel state and the Cassie–Baxter state. In the Wenzel state, a homogenous interface is formed between the droplet and the solid. The contact angle for the Wenzel state is given by
Equation (5). Neumann’s vector triangle is shown in
Figure 5. The water to air interface remains unaffected by the roughness, and hence, its surface tension remains the same. The roughness effectively changes the solid to water and solid to air surface tensions by a factor
Rf.
If the solid surface is non-homogenous,
i.e., it consists of two different materials S
1 and S
2, with area fractions
f1 and
f2, then the apparent contact angle given by the Cassie–Baxter equation (
Equation (7)) can be written as:
This is equivalent to writing
, where
and
. The surface tensions can be once again represented by the sides of a vector triangle (
Figure 6). If we consider S
2 as air, then the equation reduces to
.
We interpret the effect of surface roughness as stretching the vectors
and
in the Neumann’s triangle in
Figure 5 by a factor equal to the Wenzel roughness factor. We interpret the effect of surface heterogeneity as a linear combination of vectors
,
and
,
, which correspond to two components of the interface, with the weight factors of
f1 and
f2.
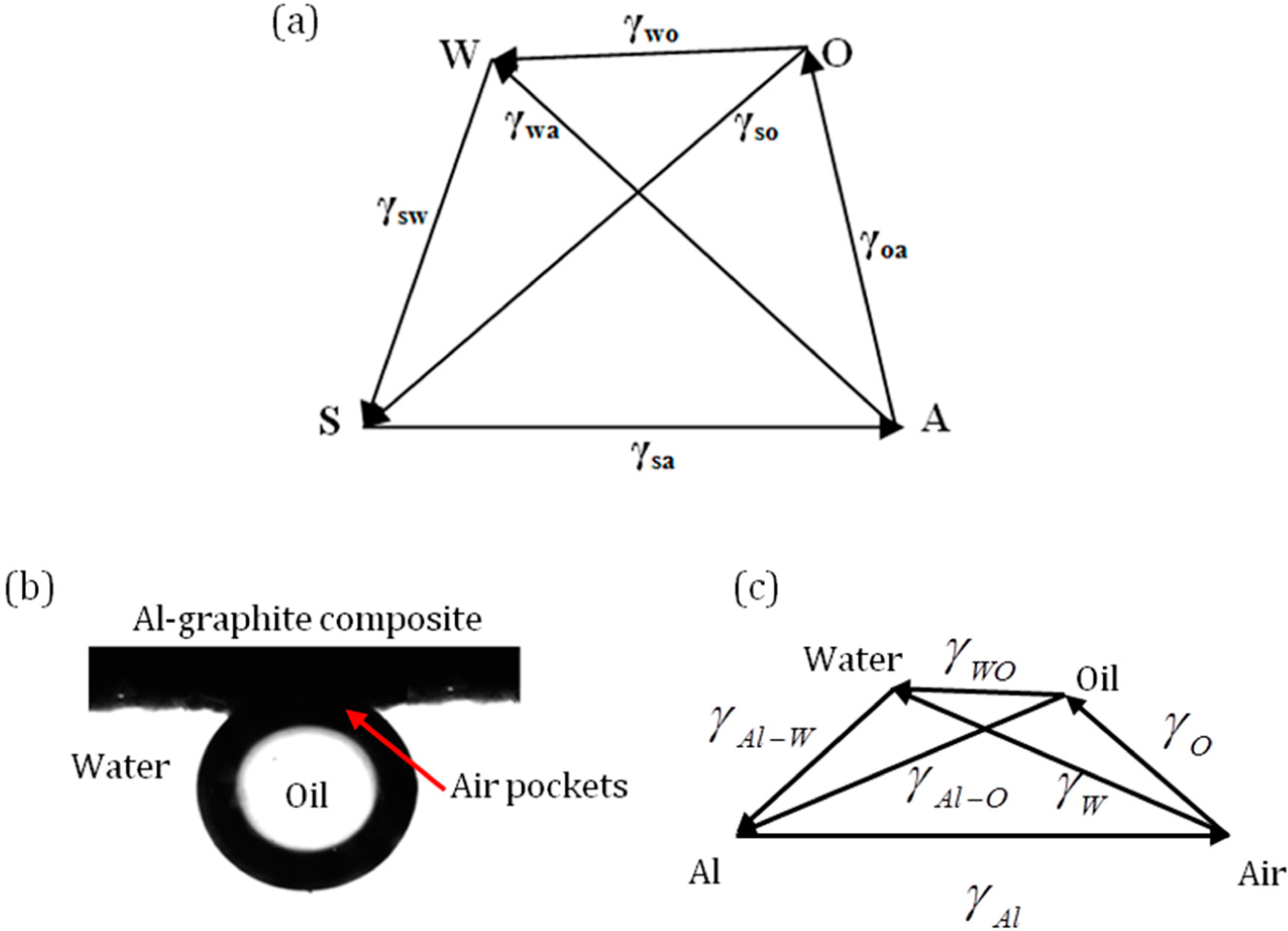
3.4. Four Phase Systems
Consider four phases, namely solid (S), water (W), oil (O) and air (A). The three-phase systems SWO, WOA, SWA and SWA can be represented by four triangles, as discussed above. If the four phases exists in mechanical equilibrium, the pyramid (or tetrahedron) SAOW with the vectors representing the interfacial tensions can be drawn as in
Figure 8a. If the vector triangles SWA and SWO are drawn, the surface tension of the water to oil interface can be inferred from the magnitude of
.
For a four-phase system consisting of an oil droplet on aluminum-graphite composite under water with trapped air pockets is shown in
Figure 8b [
35]. The surface tensions of oil and water are 0.032 Jm
−2, 0.072 Jm
−2. A pyramid with surface tension forces can be drawn as shown in
Figure 8c.
Note that in general, none of the three points among S, W, A and O would lie on the same line, with the exception of the limiting cases when the triangle inequality becomes a strict equality. As a result, the four points do not lie within the same plane. We need a 2D triangle to represent three phases and a 3D pyramid to represent four phases. The dimension will grow with a further increase of the number of phases.
The notion can easily be extended for the Wenzel and Cassie interfaces by stretching of corresponding vectors and for contact angle hysteresis by rotation of the corresponding vectors, as described in the preceding sections.
4. Conclusions
We discussed the concepts of the interfacial energy and surface tension. While it is often assumed that the origin of interfacial energy is in the broken molecular bonds in the surface layer, more sophisticated models imply the entropic effects of molecular reorientation at the surface. The entropic force is a result of molecular interactions in a system as a whole, and it is quite difficult to demonstrate how an entropic force is a result of a net sum of microscopic forces acting on particular molecules. The surface tension is not the same as the interfacial energy, and it can be viewed as a generalized force, i.e., a derivative of the internal energy of the system by a generalized coordinate. The difference between the generalized forces and the conventional mechanical forces is that the latter are applied to certain bodies or material points, whereas the former are vectors without any particular point of application. The traditional interpretation of wetting equilibrium as a balance of three surface tension forces applied to the three-phase line is therefore misleading.
By considering the surface tensions as vectors, which are not applied to a particular point, we developed a simple geometric interpretation of the Young, Wenzel, Cassie, Antonoff and Girifalco–Good equations for the equilibrium during wetting, as well as for contact angle hysteresis. This approach extends the traditional concept of Neumann’s triangle. Substances are presented as points, while tensions are vectors connecting the points, and the equations and inequalities of wetting equilibrium obtain simple geometric meaning. The effect of the surface roughness was interpreted as stretching of the corresponding vectors. The effect of the surface heterogeneity was interpreted as a linear combination of vectors corresponding to the two phases involved. The effect of contact angle hysteresis was interpreted as a rotation of a corresponding vector.