Quantifying Redundant Information in Predicting a Target Random Variable
Abstract
:1. Introduction
2. Background: Partial Information Decomposition
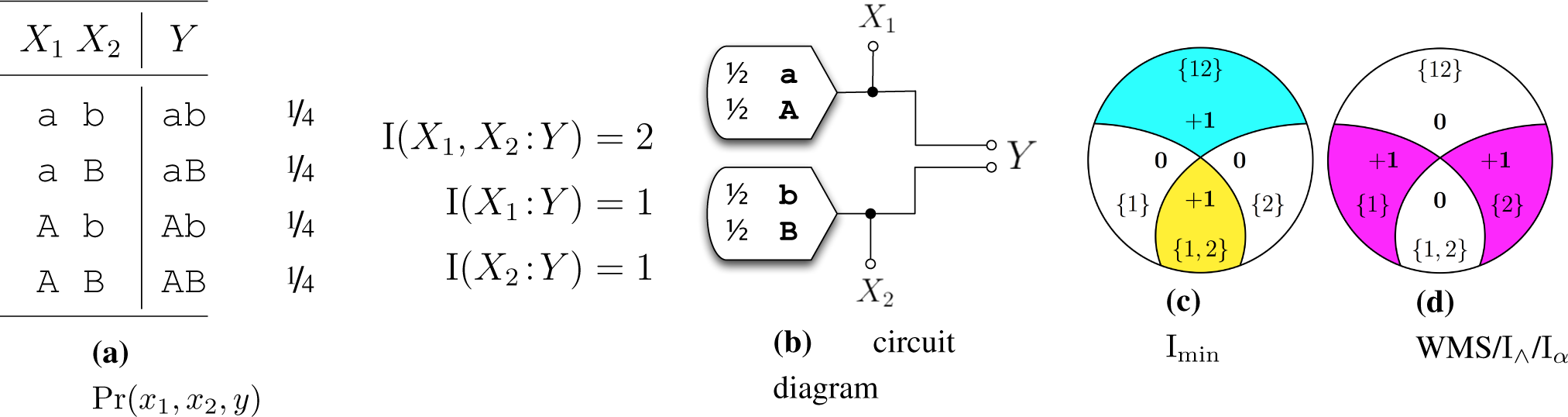
3. Desired I∩ properties and canonical examples
- (So) Weak Symmetry: I∩({X1,…,Xn}:Y) is invariant under reordering of X1,…,Xn.
- (Mo) Weak Monotonicity: I∩({X1,…,Xn, Z}:Y) ≤ I∩({X1,…,Xn}:Y) with equality if there exists Xi ∈ {X1,…,Xn} such that H(Z, Xi) = H(Z).Weak Monotonicity is a natural generalization of the monotonicity property from [13]. Weak monotonicity is inspired by the property of mutual information that if H(X|Z) = 0, then I(X:Y) ≤ I(Z:Y).
- (SR) Self-Redundancy: I∩({X1}:Y) = I(X1:Y). The intersection information a single predictor X1 conveys about the target Y is equal to the mutual information between the X1 and the target Y.
- (M1) Strong Monotonicity: I∩({X1,…,Xn, Z}:Y) ≤ I∩({X1,…,Xn}:Y) with equality if there exists Xi ∈ {X1,…,Xn} such that I(Z,Xi:Y) = I(Z:Y).Strong Monotonicity captures more precisely what is meant by “redundant information”, it says explicitly that it information about Y that is redundant, not just any redundancy among the predictors (weak monotonicity).
- (LP) Local Positivity: For all n, the derived “partial informations” defined in [13] are nonnegative. This is equivalent to requiring that I∩ satisfy total monotonicity, a stronger form of supermodularity. For n = 2 this can be concretized as, I∩({X1, X2}:Y) ≥ I(X1:X2) − I(X1:X2|Y).
- (TM) Target Monotonicity: If H(Y|Z) = 0, then I∩({X1,…,Xn}:Y) ≤ I∩({X1,…,Xn}:Z).
4. Previous candidate measures
5. New candidate measures
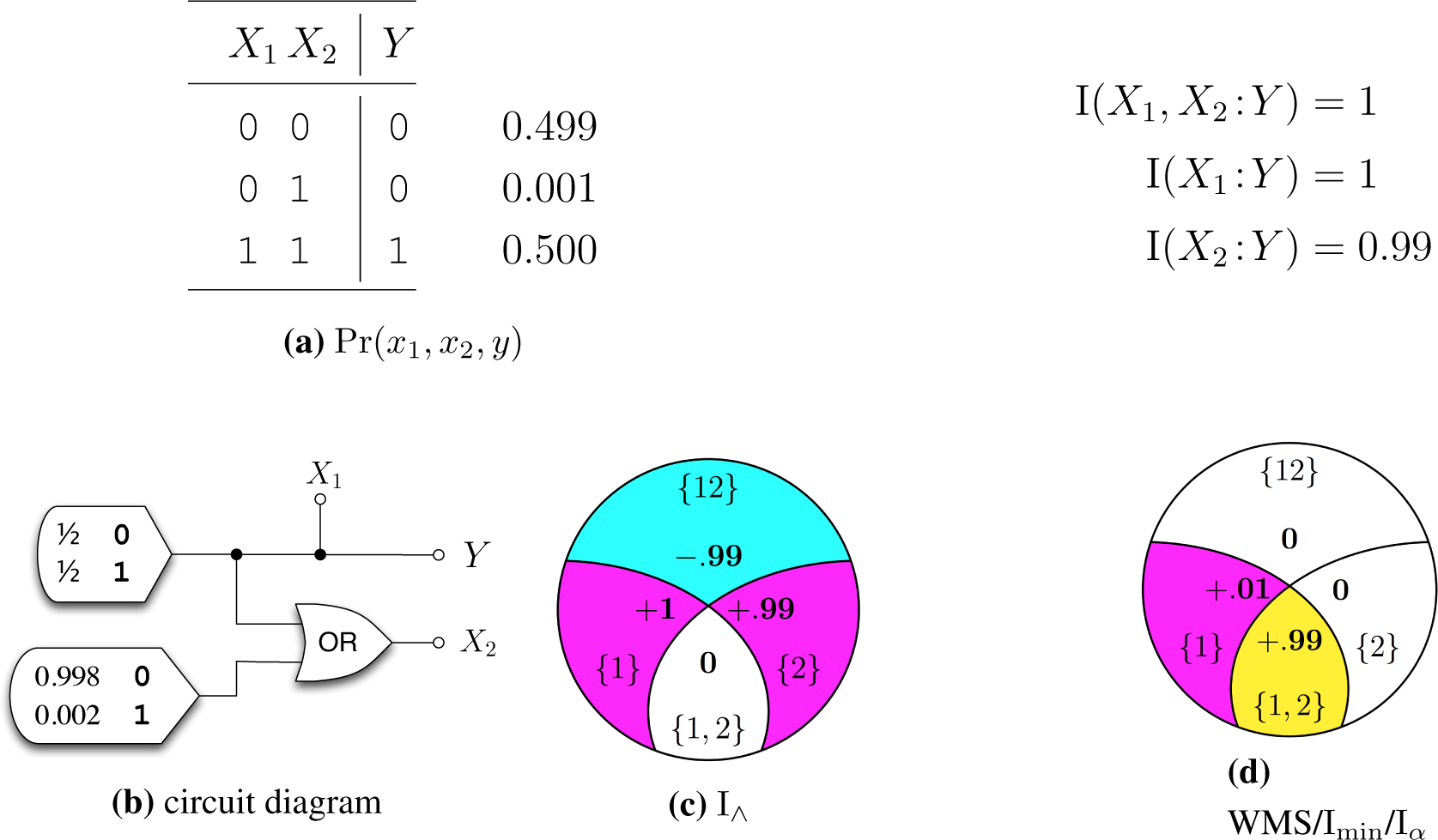
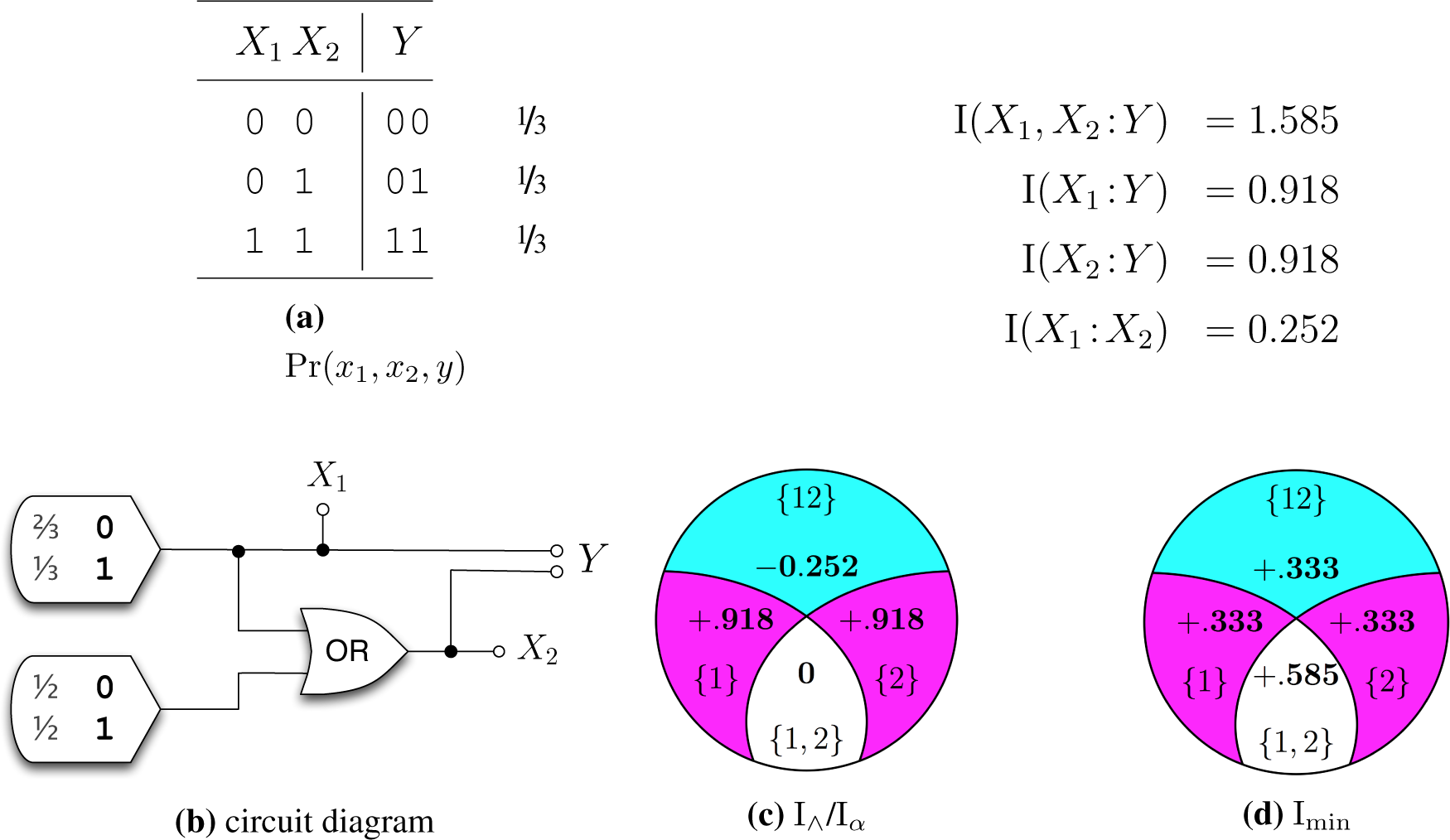
5.1. The IΛ measure
5.2. The Iα measure
6. Conclusion
Acknowledgments
A. Appendix
Author Contributions
Conflicts of Interest
References
- Schneidman, E.; Bialek, W.; Berry, M.J. Synergy, redundancy, and independence in population codes. J. Neurosci. 2003, 23, 11539–11553. [Google Scholar]
- Narayanan, N.S.; Kimchi, E.Y.; Laubach, M. Redundancy and Synergy of Neuronal Ensembles in Motor Cortex. J. Neurosci. 2005, 25, 4207–4216. [Google Scholar]
- Balduzzi, D.; Tononi, G. Integrated information in discrete dynamical systems: Motivation and theoretical framework. PLoS Comput. Biol. 2008, 4, e1000091. [Google Scholar]
- Anastassiou, D. Computational analysis of the synergy among multiple interacting genes. Mol. Syst. Biol. 2007, 3, 83. [Google Scholar]
- Lizier, J.T.; Flecker, B.; Williams, P.L. Towards a Synergy-based Approach to Measuring Information Modification. Proceedings of 2013 IEEE Symposium on Artificial Life (ALIFE), Singapore, Singapore, 16–19 April 2013; pp. 43–51.
- Gács, P.; Körner, J. Common information is far less than mutual information. Prob. Control Inf. Theory. 1973, 2, 149–162. [Google Scholar]
- Wyner, A.D. The common information of two dependent random variables. IEEE Trans. Inf. Theory. 1975, 21, 163–179. [Google Scholar]
- Kumar, G.R.; Li, C.T.; Gamal, A.E. Exact Common Information. Proceedings of 2014 IEEE International Symposium on Information Theory (ISIT), Honolulu, HI, USA, 29 June–4 July 2014; pp. 161–165.
- Griffith, V.; Koch, C. Quantifying synergistic mutual information. In Guided Self-Organization: Inception; Emergence, Complexity and Computation Serie; Volume 9, Springer: Berlin/Heidelberg, Germany, 2014; pp. 159–190. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared Information—New Insights and Problems in Decomposing Information in Complex Systems. In Proceedings of European Conference on Complex Systems 2012; Springer Proceedings in Complexity Serie; Springer; Switzerland, 2013; pp. 251–269. [Google Scholar]
- Griffith, V.; Chong, E.K.P.; James, R.G.; Ellison, C.J.; Crutchfield, J.P. Intersection Information based on Common Randomness. Entropy 2014, 16, 1985–2000. [Google Scholar]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information 2010. arXiv: 1004-2515.
- Weisstein, E.W. Antichain. Available online: http://mathworld.wolfram.com/Antichain.html accessed on 29 June 2015.
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar]
- Schneidman, E.; Still, S.; Berry, M.J.; Bialek, W. Network Information and Connected Correlations. Phys. Rev. Lett. 2003, 91, 238701–238705. [Google Scholar]
- Wolf, S.; Wullschleger, J. Zero-error information and applications in cryptography. Proceedings of IEEE Information Theory Workshop, San Antonio, TX, USA, 24–29 October 2004; pp. 1–6.
- Rauh, J.; Bertschinger, N.; Olbrich, E.; Jost, J. Reconsidering unique information: Towards a multivariate information decomposition. Proceedings of 2014 IEEE International Symposium on Information Theory (ISIT), Honolulu, HI, USA, 29 June–4 July 2014; pp. 2232–2236.



© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Griffith, V.; Ho, T. Quantifying Redundant Information in Predicting a Target Random Variable. Entropy 2015, 17, 4644-4653. https://doi.org/10.3390/e17074644
Griffith V, Ho T. Quantifying Redundant Information in Predicting a Target Random Variable. Entropy. 2015; 17(7):4644-4653. https://doi.org/10.3390/e17074644
Chicago/Turabian StyleGriffith, Virgil, and Tracey Ho. 2015. "Quantifying Redundant Information in Predicting a Target Random Variable" Entropy 17, no. 7: 4644-4653. https://doi.org/10.3390/e17074644
APA StyleGriffith, V., & Ho, T. (2015). Quantifying Redundant Information in Predicting a Target Random Variable. Entropy, 17(7), 4644-4653. https://doi.org/10.3390/e17074644




