Maximum Entropy Rate Reconstruction of Markov Dynamics
Abstract
:1. Introduction
2. Theory
2.1. Unconstrained Case
2.2. Constraints
3. Solving the Equations
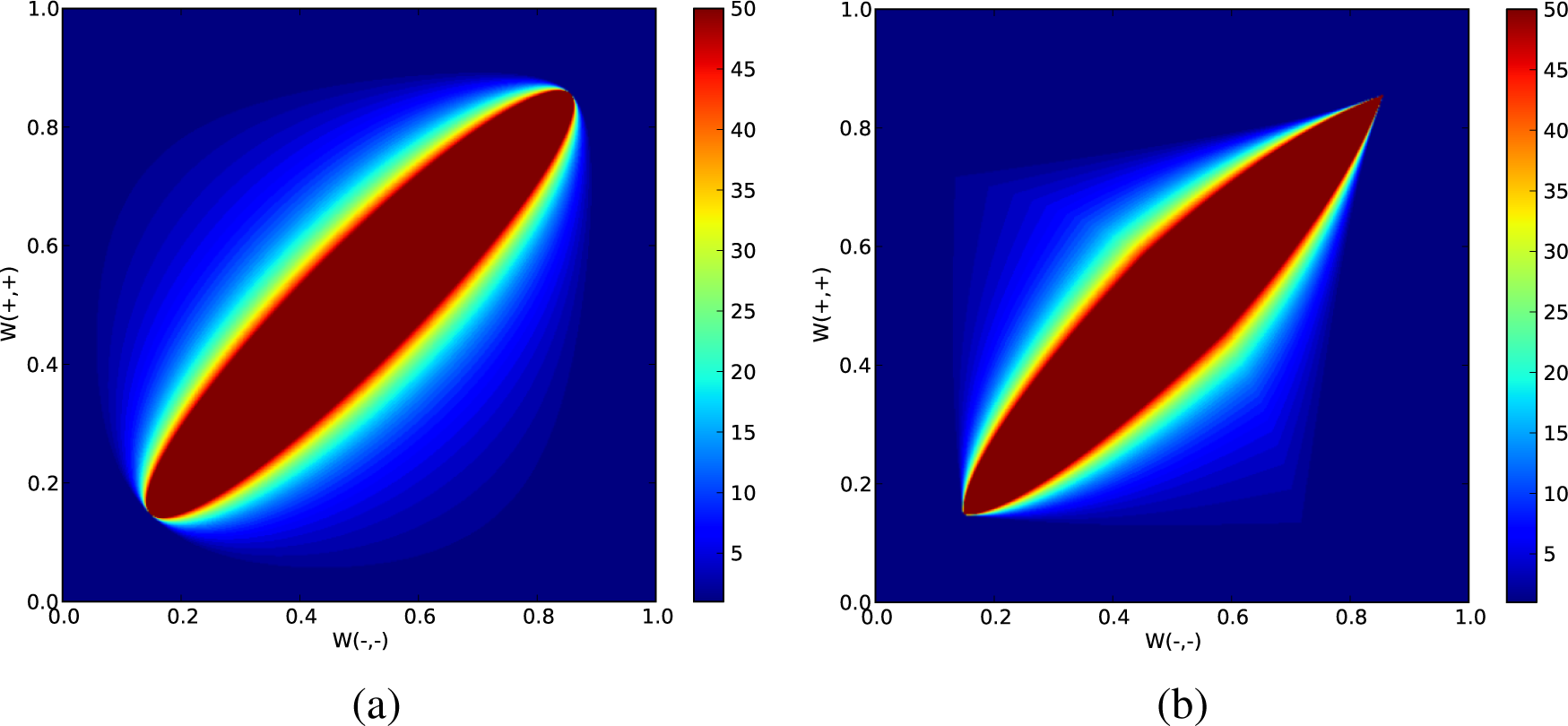
3.1. Two-State Case
3.2. Three-State Case
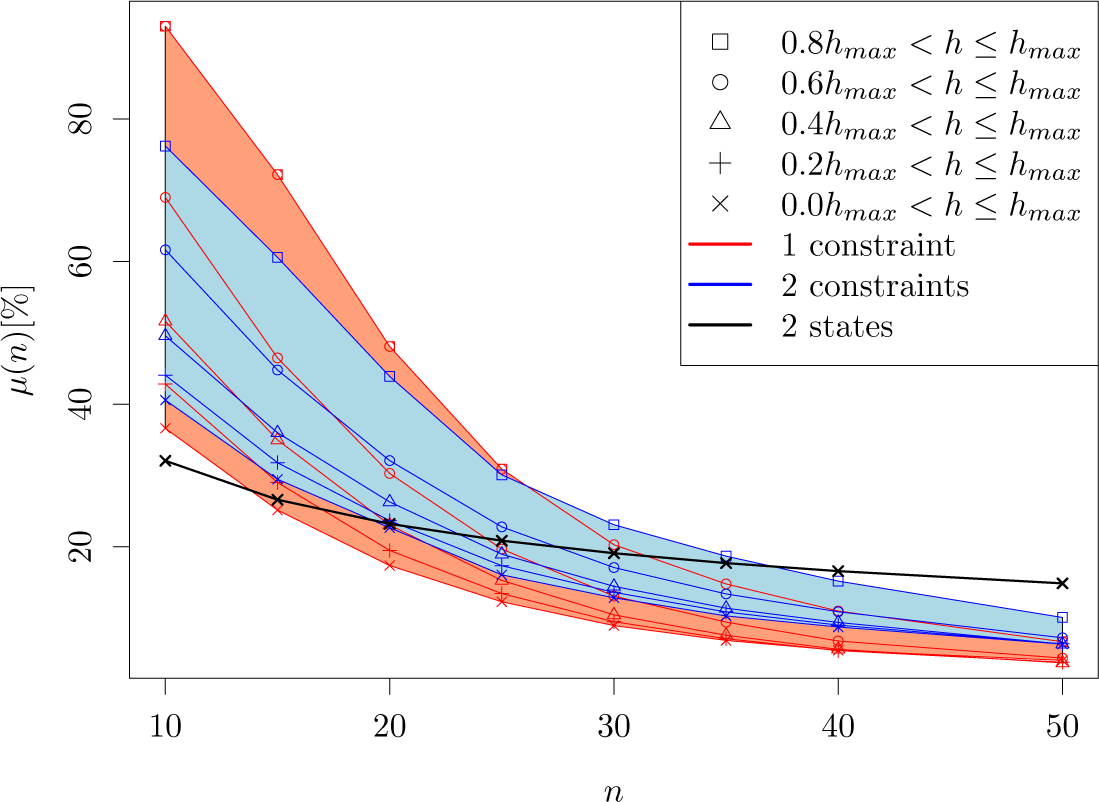
3.3. Algorithm
 |
4. MaxEnt Estimations for Time Series
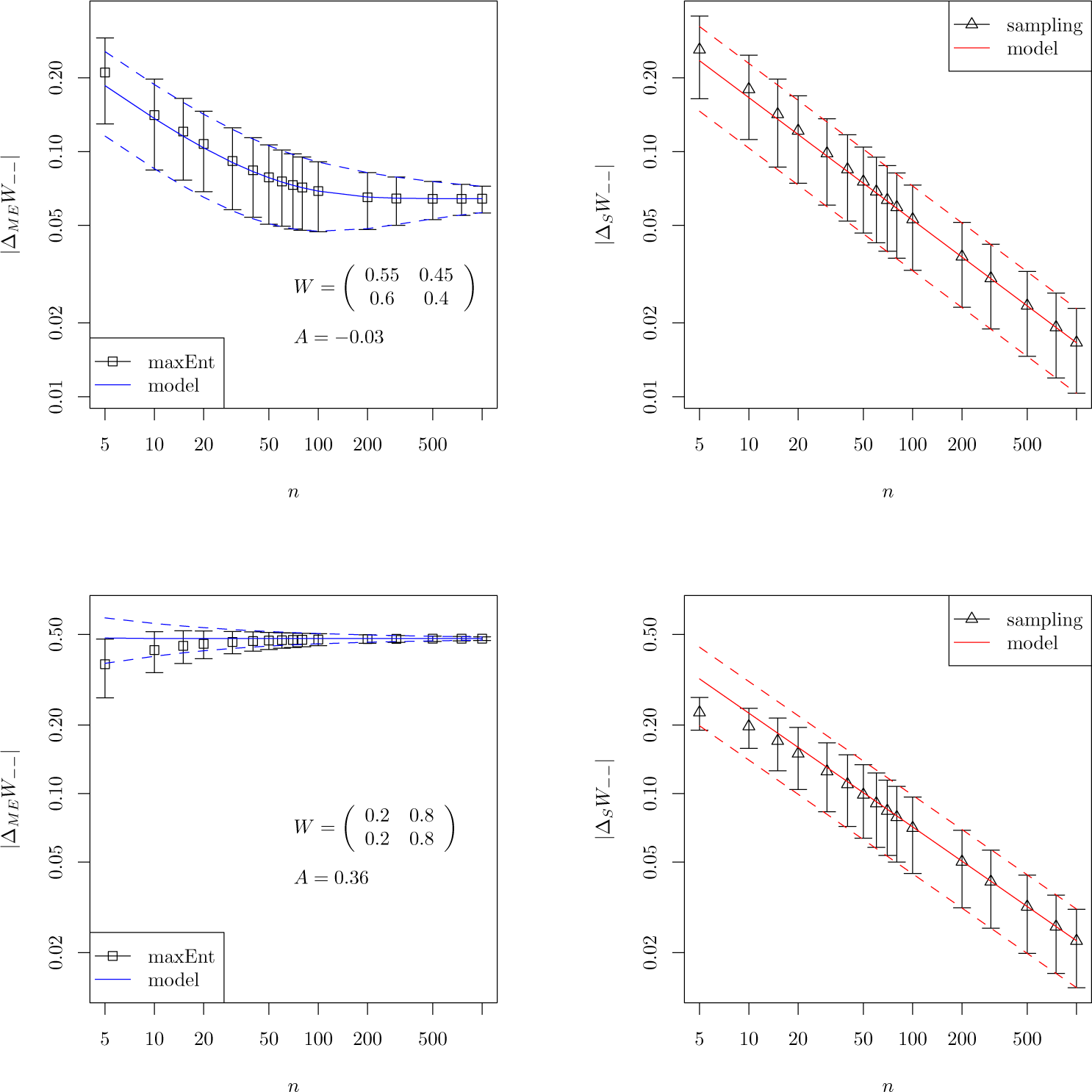
4.1. Stationary Processes
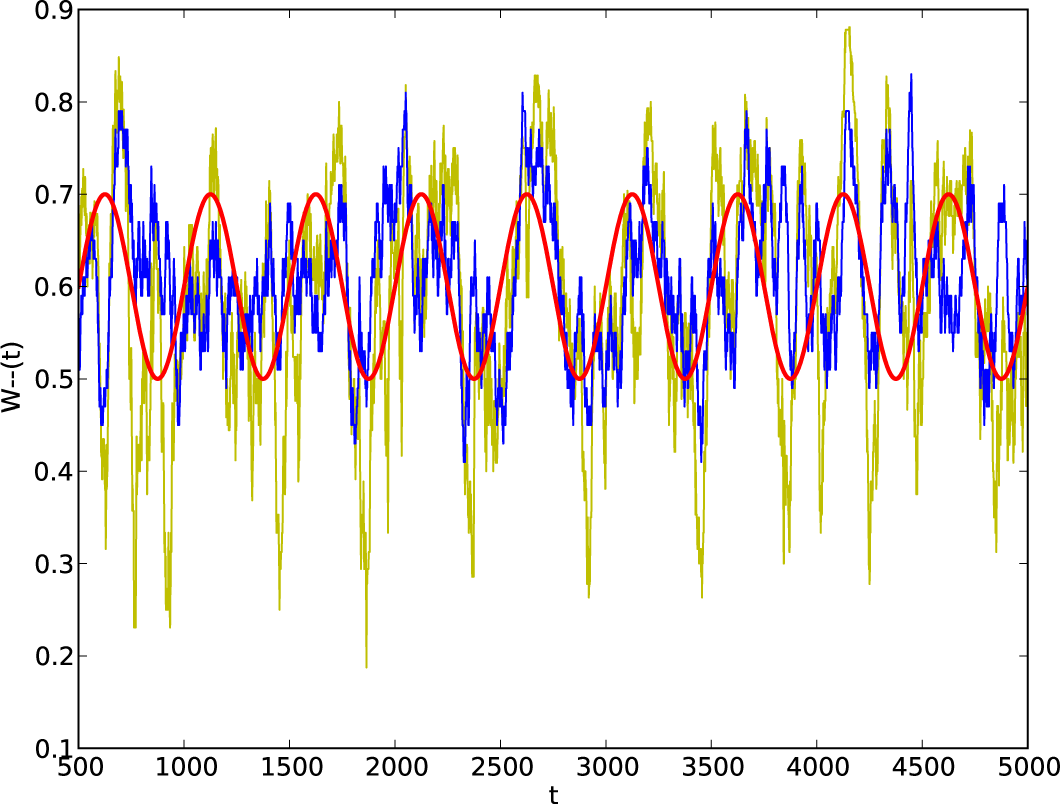
4.2. Non-Stationary Processes
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jaynes, E.T. Information Theory Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar]
- Jaynes, E.T. Information Theory Statistical Mechanics. II. Phys. Rev. 1957, 108, 171–190. [Google Scholar]
- Schneidman, E.; Still, S.; Berry, M.J.; Bialek, W. Network Information and Connected Correlations. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef]
- Stephens, G.J.; Bialek, W. Statistical Mechanics of Letters in Words. Phys. Rev. E 2010, 81. [Google Scholar] [CrossRef]
- Mora, T.; Bialek, W. Are Biological Systems Poised at Criticality. J. Stat. Phys. 2011, 144, 268–302. [Google Scholar]
- Bialek, W.; Cavagna, A.; Giardina, I.; Mora, T.; Silvestri, E.; Viale, M.; Walczak, A. Statistical Mechanics for Natural Flocks of Birds. Proc. Natl. Acad. Sci. USA 2012, 109, 4786–4791. [Google Scholar]
- Stephens, G.J.; Mora, T.; Tkacik, G.; Bialek, W. Statistical Thermodynamics of Natural Images. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef]
- McCallum, A.; Freitag, D.; Pereira, F. Maximum Entropy Markov Models for Information Extraction and Segmentation. Proceedings of the Seventeenth International Conference on Machine Learning, Standord, CA, USA, 29 June–2 July, 2000.
- Marre, O.; El Boustani, S.; Fregnac, Y.; Destexhe, A. Prediction of Spatiotemporal Patterns of Neural Activity from Pairwise Correlations. Phys. Rev. Lett. 2009, 102, 138101. [Google Scholar]
- Biondi, F.; Legay, A.; Nielsen, B.; Wasowski, A. Maximizing Entropy over Markov Processes. Proceedings of the 7th International Conference, Language and Automata Theory and Applications 2013, Bilbao, Spain, 2–5 April 2013; pp. 128–140.
- Cavagna, A.; Giardina, I.; Ginelli, F.; Mora, T.; Piovani, D.; Tavarone, R.; Walczak, A. Dynamical Maximum Entropy Approach to Flocking. Phys. Rev. E 2014, 89, 042707. [Google Scholar]
- Fiedor, P. Maximum Entropy Production Principle for Stock Returns 2014, arXiv, 1408.3728.
- Van der Straeten, E. Maximum Entropy Estimation of Transition Probabilities of Reversible Markov Chains. Entropy. 2009, 11, 867–887. [Google Scholar]
- Chliamovitch, G.; Dupuis, A.; Golub, A.; Chopard, B. Improving Predictability of Time Series Using Maximum Entropy Methods. Europhys. Lett. 2015, 110. [Google Scholar] [CrossRef]
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Malouf, R. A. Comparison of Algorithms for Maximum Entropy Parameter Estimation. Proceedings of the CoNLL-2002, Taipei, Taiwan, 31 August–1 September 2002; pp. 49–55.
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods; Springer: Berlin, Germany, 1991. [Google Scholar]
- Leone, F.C.; Nelson, L.S.; Nottingham, R.B. The Folded Normal Distribution. Technometrics 1961, 3, 867–887. [Google Scholar]
- Brandimarte, P. Handbook in Monte Carlo Simulation: Applications in Financial Engineering, Risk Management, and Economics; Wiley: New York, NY, USA, 2014. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chliamovitch, G.; Dupuis, A.; Chopard, B. Maximum Entropy Rate Reconstruction of Markov Dynamics. Entropy 2015, 17, 3738-3751. https://doi.org/10.3390/e17063738
Chliamovitch G, Dupuis A, Chopard B. Maximum Entropy Rate Reconstruction of Markov Dynamics. Entropy. 2015; 17(6):3738-3751. https://doi.org/10.3390/e17063738
Chicago/Turabian StyleChliamovitch, Gregor, Alexandre Dupuis, and Bastien Chopard. 2015. "Maximum Entropy Rate Reconstruction of Markov Dynamics" Entropy 17, no. 6: 3738-3751. https://doi.org/10.3390/e17063738
APA StyleChliamovitch, G., Dupuis, A., & Chopard, B. (2015). Maximum Entropy Rate Reconstruction of Markov Dynamics. Entropy, 17(6), 3738-3751. https://doi.org/10.3390/e17063738






