Noiseless Linear Amplifiers in Entanglement-Based Continuous-Variable Quantum Key Distribution
Abstract
:1. Introduction
2. Entanglement-Based CV-QKD Protocols
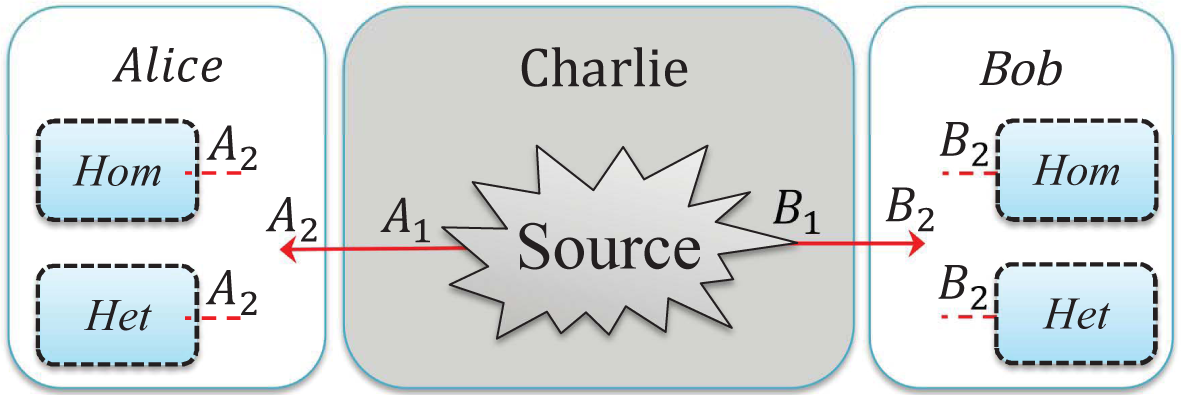
2.1. Entanglement Distribution: Entanglement-Based Protocols with an Untrusted Source
- Step 1: The untrusted third party, Charlie, initially prepares an entangled source. He sends one mode A1 to Alice through Channel 1 and sends the other mode B1 to Bob through Channel 2, where Eve may perform her attack.
- Step 2: Alice and Bob perform either a homodyne (switching) (Hom) or a heterodyne (no switching) (Het) measurement on the received modes A2 and B2. Once Alice and Bob have collected a sufficiently large set of correlated data, they proceed with classical data post-processing, namely error reconciliation and privacy amplification. The reconciliation can be performed in one of two ways: either direct reconciliation (DR) [7] or reverse reconciliation (RR) [8].
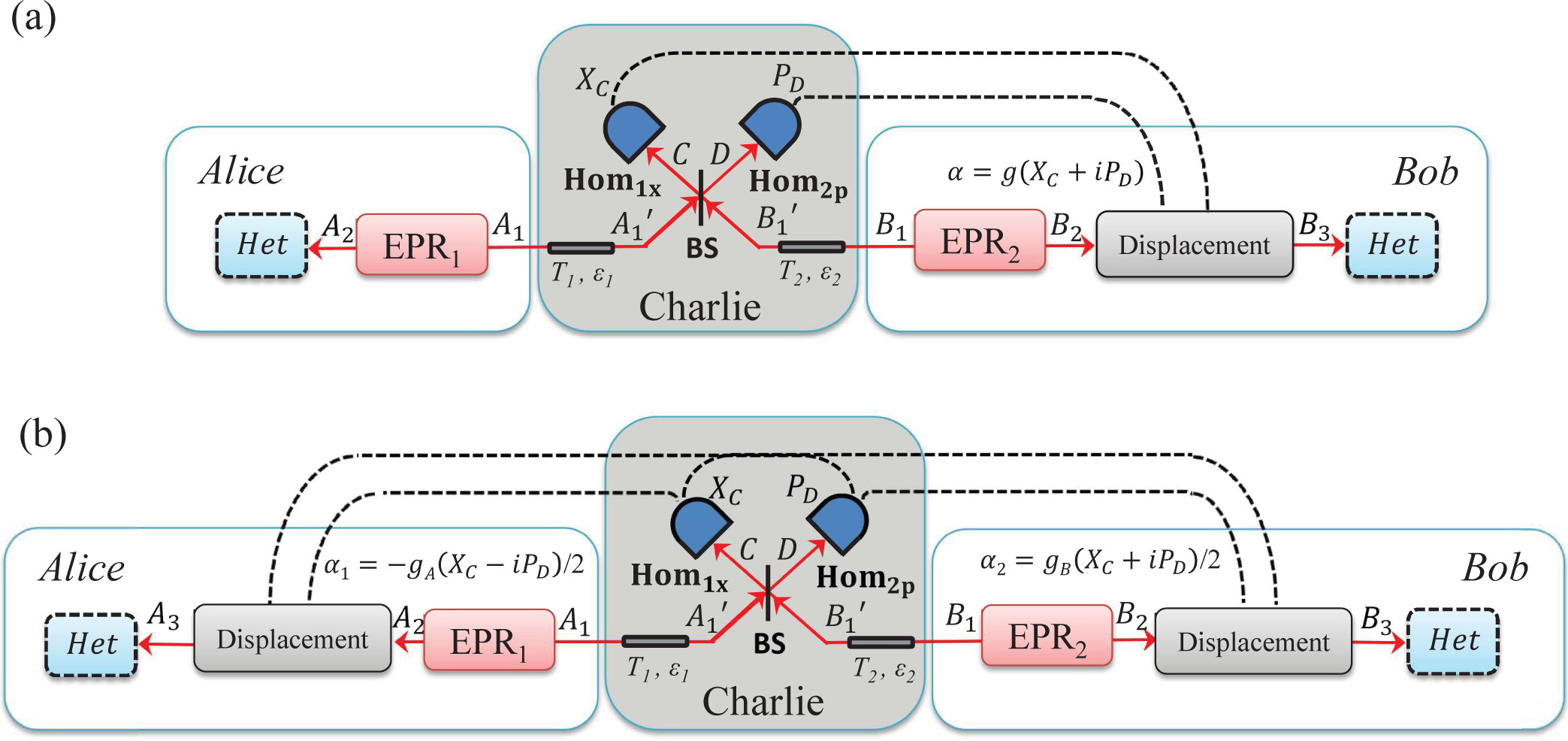
2.2. Entanglement Swapping: Entanglement-Based Protocol with an Untrusted Relay
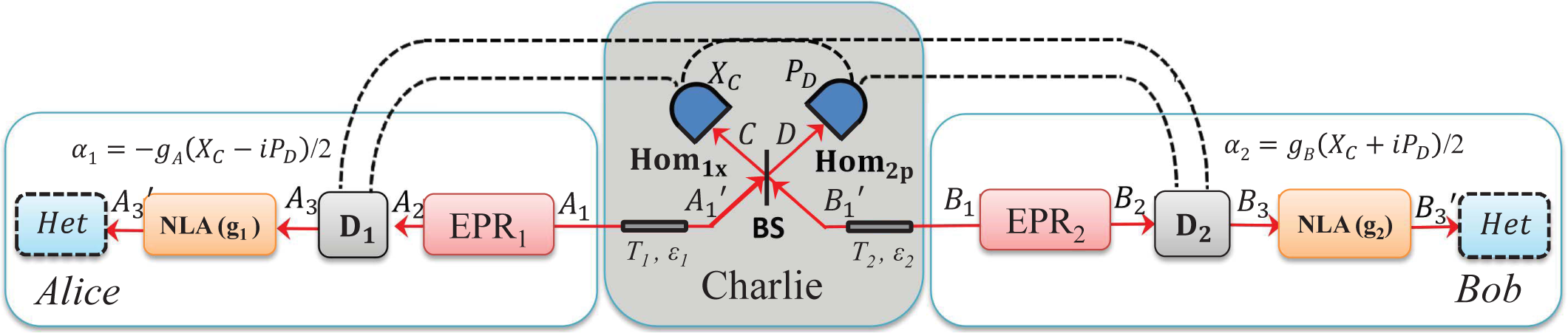
- Step 1: Alice and Bob both generate an Einstein–Podolsky–Rosen (EPR), states EPR1 and EPR2, respectively, with variances VA and VB and they keep modes A2 and B2 at their respective sides. Then, they send their other modes A1 and B1 to the untrusted third party (Charlie) through two different quantum channels with lengths LAC and LBC.
- Step 2: Charlie combines the received two modes and onto a beam splitter (50:50), where we label output modes of the beam splitter as C and D. Charlie then measures the x-quadrature of mode C and the p-quadrature of mode D using homodyne detectors and publicly announces the measurement results xC, pD to Alice and Bob through classical channels. After the measurements of modes C and D, the two initially independent modes A2 and B2 get entangled if channel noise is not too strong.
- Step 3: Bob displaces the mode B2 to B3 by the operation and gets , where represents the density matrix of mode B, β = g (XC + iPD), (↠and â are the creation and annihilation operators, respectively), and g represents the gain of the displacement. Then Bob measures the mode B3 to get the final data {xB, pB} using heterodyne detection. Alice also measures the mode A2 to get the final data {xA, pA}, again using heterodyne detection.
- Step 4: Once Alice and Bob have collected a sufficiently large set of correlated data, they use an authenticated public channel to do parameter estimation from a randomly-chosen sample of final data from {xA, pA} and {xB, pB}. Then, Alice and Bob proceed with classical data post-processing to distil a secret key. The reconciliation can also be done in two ways: either DR or RR.
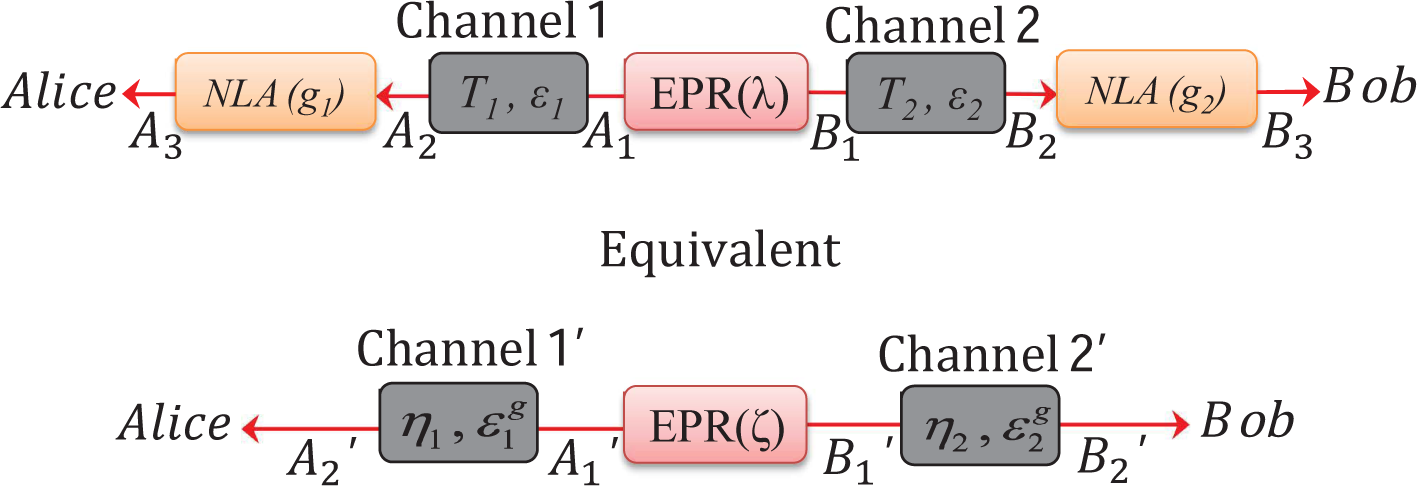
3. Improvement Using Noiseless Linear Amplifiers
3.1. Noiseless Linear Amplifier
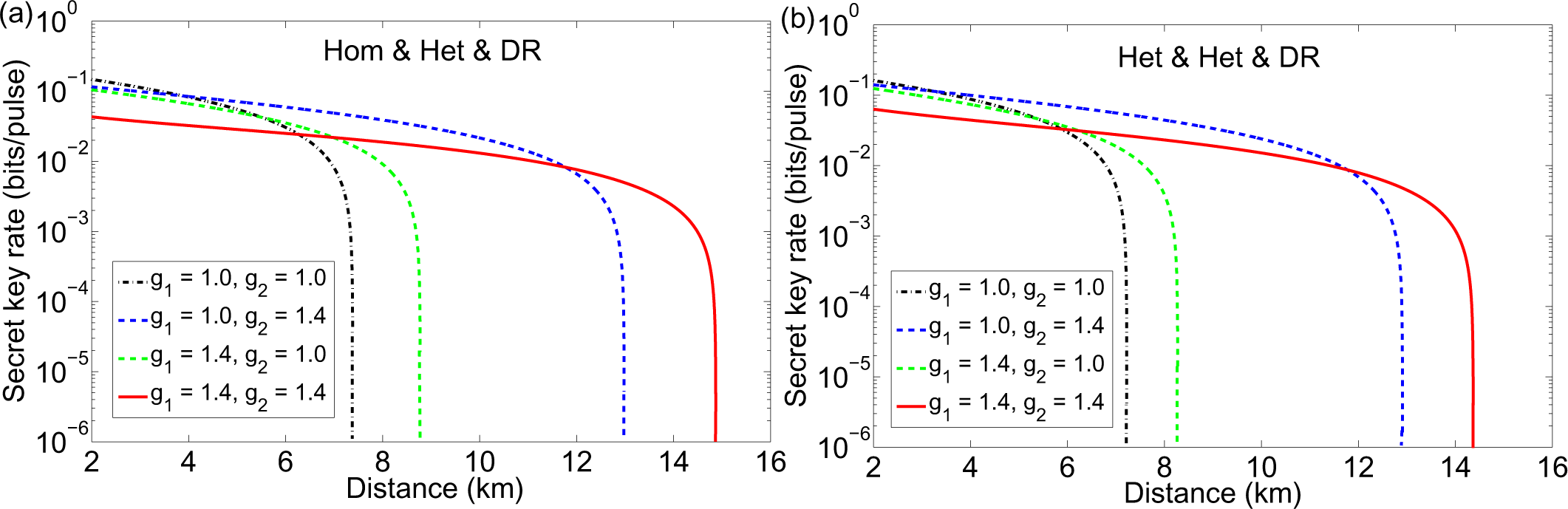
3.2. Entanglement-Based Protocol with an Untrusted Source
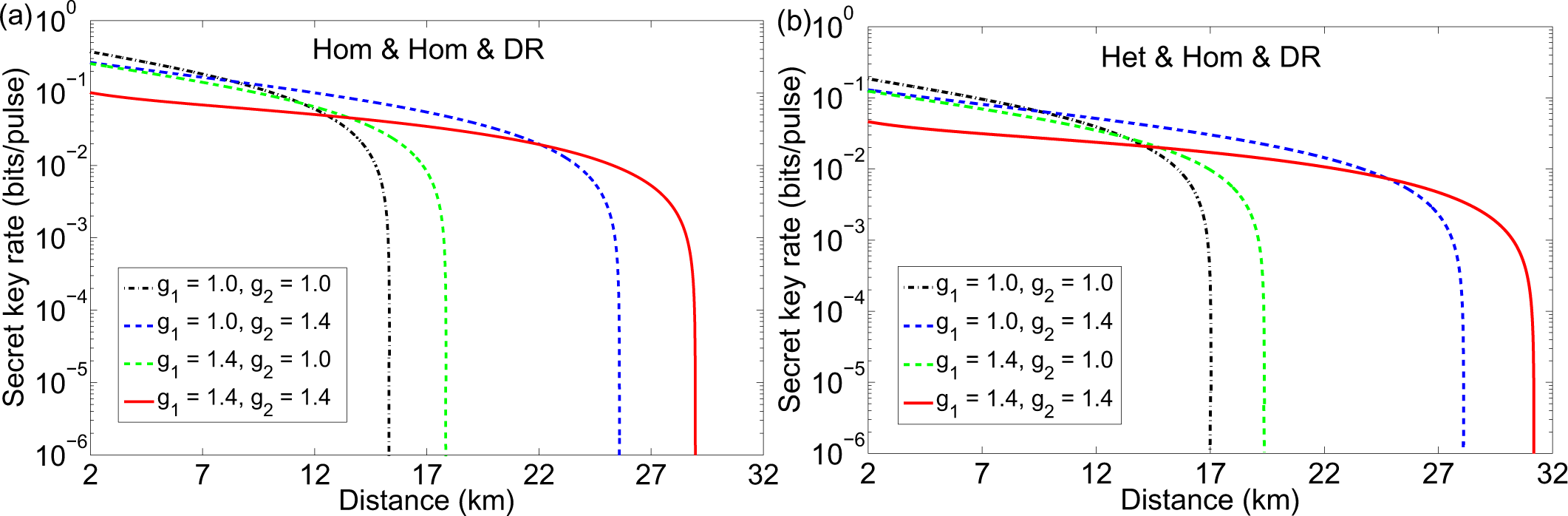
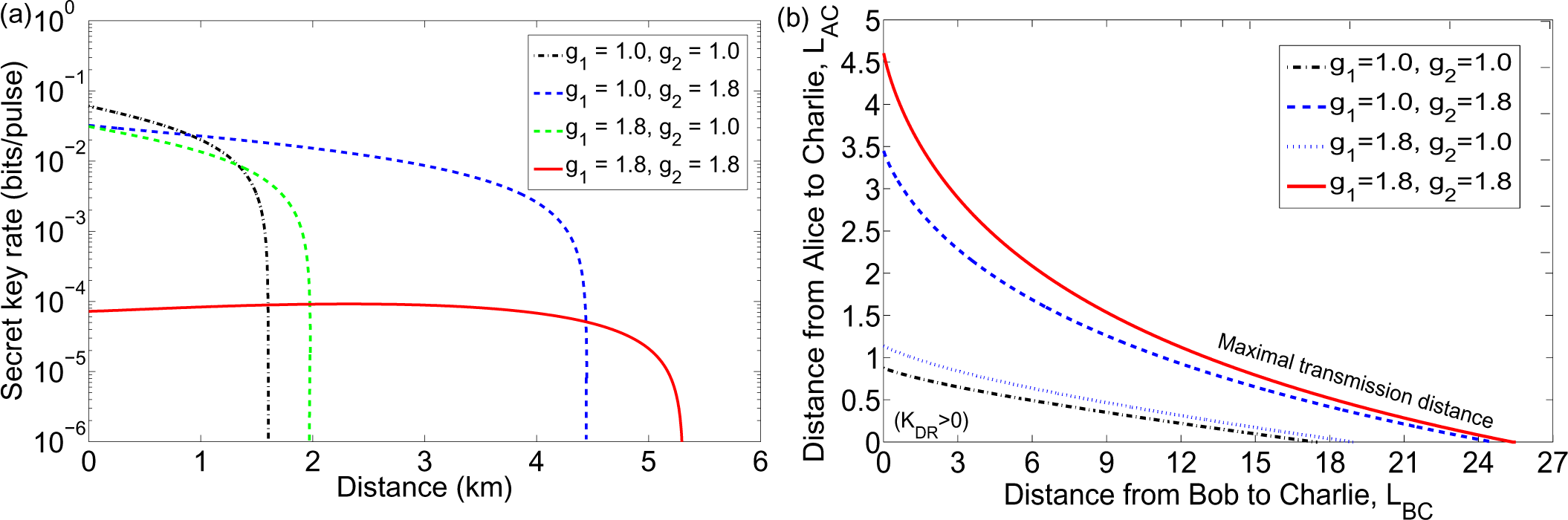
3.3. Entanglement-Based Protocol with an Untrusted Relay
4. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–577. [Google Scholar]
- Wang, X.B.; Hiroshima, T.; Tomita, A.; Hayashi, M. Quantum Information with Gaussian States. Phys. Rep. 2007, 448, 1–111. [Google Scholar]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621–669. [Google Scholar]
- Jouguet, P. Kunz-Jacques,S.; Leverrier, A.; Grangier, P.; Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photon. 2013, 7, 378–381. [Google Scholar]
- Grosshans, F.; Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar]
- Grosshans, F.; van Assche, G.; Wenger, J.; Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using gaussian-modulated coherent states. Nature 2003, 421, 238–241. [Google Scholar]
- Weedbrook, C.; Lance, A.M.; Bowen, W.P.; Symul, T.; Ralph, T.C.; Lam, P.K. Quantum cryptography without switching. Phys. Rev. Lett. 2004, 93, 170504. [Google Scholar]
- Lance, A.M.; Symul, T.; Sharma, V.; Weedbrook, C.; Ralph, T.C.; Lam, P.K. No-switching quantum key distribution using broadband modulated coherent light. Phys. Rev. Lett. 2005, 95, 180503. [Google Scholar]
- Lodewyck, J.; Bloch, M.; García-Patrón, R.; Fossier, S.; Karpov, E.; Diamanti, E.; Debuisschert, T.; Cerf, N.J.; Tualle-Brouri, R.; McLaughlin, S.W.; Grangier, P. Quantum key distribution over 25 km with an all-fiber continuous-variable system. Phys. Rev. A 2007, 76, 042305. [Google Scholar]
- Khan, I.; Wittmann, C.; Jain, N.; Killoran, N.; Lütkenhaus, N.; Marquardt, C.; Leuchs, G. Optimal working points for continuous-variable quantum channels. Phys. Rev. A 2013, 88, 010302. [Google Scholar]
- Renner, R.; Cirac, J.I. de Finetti representation theorem for infinite-dimensional quantum systems and applications to quantum cryptography. Phys. Rev. Lett. 2009, 102, 110504. [Google Scholar]
- Leverrier, A.; García-Patrón, R.; Renner, R.; Cerf, N.J. Security of continuous-variable quantum key distribution against general attacks. Phys. Rev. Lett. 2013, 110, 030502. [Google Scholar]
- Pirandola, S.; Mancini, S.; Lloyd, S.; Braunstein, S.L. Continuous-variable quantum cryptography using two-way quantum communication. Nat. Phys. 2008, 4, 726–730. [Google Scholar]
- Sun, M.; Peng, X.; Shen, Y.; Guo, H. Security of a new two-way continuous-variable quantum key distribution protocol. Int. J. Quantum Inf. 2012, 10, 1250059. [Google Scholar]
- Zhang, Y.-C.; Li, Z.; Weedbrook, C.; Yu, S.; Gu, W.; Sun, M.; Peng, X.; Guo, H. Improvement of two-way continuous-variable quantum key distribution using optical amplifiers. J. Phys. B 2014, 47, 035501. [Google Scholar]
- Weedbrook, C.; Ottaviani, C.; Pirandola, S. Two-way quantum cryptography at different frequencies. Phys. Rev. A 2014, 89, 012309. [Google Scholar]
- Weedbrook, C.; Pirandola, S.; Lloyd, S.; Ralph, T.C. Quantum Cryptography Approaching the Classical Limit. Phys. Rev. Lett. 2010, 105, 110501. [Google Scholar] [Green Version]
- Usenko, V.C.; Filip, R. Feasibility of continuous-variable quantum key distribution with noisy coherent states. Phys. Rev. A 2010, 81, 022318. [Google Scholar]
- Weedbrook, C.; Pirandola, S.; Ralph, T.C. Continuous-Variable Quantum Key Distribution using Thermal States. Phys. Rev. A 2012, 86, 022318. [Google Scholar]
- Ma, X.-C.; Sun, S.-H.; Jiang, M.-S.; Liang, L.-M. Wavelength attack on practical continuous-variable quantum-key-distribution system with a heterodyne protocol. Phys. Rev. A 2013, 87, 052309. [Google Scholar]
- Huang, J.-Z.; Weedbrook, C.; Yin, Z.-Q.; Wang, S.; Li, H.-W.; Chen, W.; Guo, G.-C.; Han, Z.-F. Quantum hacking of a continuous-variable quantum-key-distribution system using a wavelength attack. Phys. Rev. A 2013, 87, 062329. [Google Scholar]
- Huang, J.-Z.; Kunz-Jacques, S.; Jouguet, P.; Weedbrook, C.; Yin, Z.-Q.; Wang, S.; Chen, W.; Guo, G.-C.; Han, Z.-F. Quantum hacking on quantum key distribution using homodyne detection. Phys. Rev. A 2014, 89, 032304. [Google Scholar]
- Jouguet, P.; Kunz-Jacques, S.; Diamanti, E. Preventing calibration attacks on the local oscillator in continuous-variable quantum key distribution. Phys. Rev. A 2013, 87, 062313. [Google Scholar]
- Ma, X.-C.; Sun, S.-H.; Jiang, M.-S.; Liang, L.-M. Local oscillator fluctuation opens a loophole for Eve in practical continuous-variable quantum-key-distribution systems. Phys. Rev. A 2013, 88, 022339. [Google Scholar]
- Acín, A.; Brunner, N.; Gisin, N.; Massar, S.; Pironio, S.; Scarani, V. Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 2007, 98, 230501. [Google Scholar]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419–478. [Google Scholar]
- Walk, N.; Wiseman, H.M.; Ralph, T.C. Continuous variable one-sided device independent quantum key distribution 2014, arXiv, 1405.6593.
- Marshall, K.; Weedbrook, C. Device-independent quantum cryptography for continuous variables. Phys. Rev. A 2014, 90, 042311. [Google Scholar]
- Braunstein, S.L.; Pirandola, S. Side-Channel-Free Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130502. [Google Scholar]
- Li, Z.; Zhang, Y.-C.; Xu, F.; Peng, X.; Guo, H. Continuous-variable measurement-device-independent quantum key distribution. Phys. Rev. A 2014, 89, 052301. [Google Scholar]
- Zhang, Y.-C.; Li, Z.; Yu, S.; Gu, W.; Peng, X.; Guo, H. Continuous-variable measurement-device-independent quantum key distribution using squeezed states. Phys. Rev. A 2014, 90, 052325. [Google Scholar]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate measurement-device-independent quantum cryptography. Nat. Photon. 2015, 397–402. [Google Scholar]
- Ottaviani, C.; Spedalieri, G.; Braunstein, S.L.; Pirandola, S. Continuous-variable quantum cryptography with an untrusted relay: Detailed security analysis of the symmetric conguration. Phys. Rev. A 2015, 91, 022320. [Google Scholar]
- Xiang, G.Y.; Ralph, T.C.; Lund, A.P.; Walk, N.; Pryde, G.J. Heralded noiseless linear amplification and distilation of entanglement. Nat. Photon. 2010, 4, 316–319. [Google Scholar]
- Weedbrook, C. Continuous-variable quantum key distribution with entanglement in the middle. Phys. Rev. A 2013, 87, 022308. [Google Scholar]
- Blandino, R.; Leverrier, A.; Barbieri, M.; Etesse, J.; Grangier, P.; Tualle-Brouri, R. Improving the maximum transmission distance of continuous-variable quantum key distribution using a noiseless amplifier. Phys. Rev. A 2012, 86, 012327. [Google Scholar]
- Fiurášek, J.; Cerf, N.J. Gaussian postselection and virtual noiseless amplification in continuous-variable quantum key distribution. Phys. Rev. A 2012, 86, 060302. [Google Scholar]
- Walk, N.; Ralph, T.C.; Symul, T.; Lam, P.K. Security of continuous-variable quantum cryptography with Gaussian postselection. Phys. Rev. A 2013, 87, 020303. [Google Scholar] [Green Version]
- Devetak, I.; Winter, A. Distillation of secret key and entanglement from quantum states. Proc. R. Soc. London Ser. A 2005, 461, 207–235. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Communication; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Navascués, M.; Grosshans, F.; Acín, A. Optimality of gaussian attacks in continuous-variable quantum cryptography. Phys. Rev. Lett. 2006, 97, 190502. [Google Scholar]
- García-Patrón, R.; Cerf, N.J. Unconditional optimality of gaussian attacks against continuous-variable quantum key distribution. Phys. Rev. Lett. 2006, 97, 190503. [Google Scholar]
- Xu, B.; Tang, C.; Chen, H.; Zhang, W.; Zhu, F. Improving the maximum transmission distance of four-state continuous-variable quantum key distribution by using a noiseless linear amplifier. Phys. Rev. A 2013, 87, 062311. [Google Scholar]
- Wang, T.; Yu, S.; Zhang, Y.-C.; Gu, W.; Guo, H. Improving the maximum transmission distance of continuous-variable quantum key distribution with noisy coherent states using a noiseless amplifier. Phys. Lett. A 2014, 378, 2808–2812. [Google Scholar]
- Walk, N.; Lund, A.P.; Ralph, T.C. Non-deterministic noiseless amplification via non-symplectic phase space transformations. New J. Phys. 2013, 15, 073014. [Google Scholar]
- Bernu, J.; Armstrong, S.; Symul, T.; Ralph, T.C.; Lam, P.K. Theoretical analysis of an ideal noiseless linear amplifier for Einstein-Podolsky-Rosen entanglement distilation. J. Phys. B 2014, 47, 215503. [Google Scholar]
- Eisert, J.; Browne, D.E.; Scheel, S.; Plenio, M.B. Distillation of continuous-variable entanglement with optical means. Ann. Phys. 2004, 311, 431–458. [Google Scholar] [Green Version]
- Pandey, S.; Jiang, Z.; Combes, J.; Caves, C.M. Quantum limits on probabilistic amplifiers. Phys. Rev. A 2013, 88, 033852. [Google Scholar]
- Pirandola, S.; Braunstein, S.L.; Lloyd, S. Characterization of collective gaussian attacks and security of coherent-state quantum cryptography. Phys. Rev. Lett. 2008, 101, 200504. [Google Scholar]
- Chrzanowski, H.M.; Walk, N.; Assad, S.M.; Janousek, J.; Hosseini, S.; Ralph, T.C.; Lam, P.K. Measurement-based noiseless linear amplification for quantum communication. Nat. Photon. 2014, 8, 333–338. [Google Scholar]
- Cerf, N.J.; Levy, M.; van Assche, G. Quantum distribution of Gaussian keys using squeezed states. Phys. Rev. A 2001, 63, 052311. [Google Scholar]
- García-Patrón, R.; Cerf, N.J. Continuous-Variable Quantum Key Distribution Protocols Over Noisy Channels. Phys. Rev. Lett. 2009, 102, 130501. [Google Scholar]
- Pirandola, S.; García-Patrón, R.; Braunstein, S.L.; Lloyd, S. Direct and Reverse Secret-Key Capacities of a Quantum Channel. Phys. Rev. Lett. 2009, 102, 050503. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, Z.; Weedbrook, C.; Marshall, K.; Pirandola, S.; Yu, S.; Guo, H. Noiseless Linear Amplifiers in Entanglement-Based Continuous-Variable Quantum Key Distribution. Entropy 2015, 17, 4547-4562. https://doi.org/10.3390/e17074547
Zhang Y, Li Z, Weedbrook C, Marshall K, Pirandola S, Yu S, Guo H. Noiseless Linear Amplifiers in Entanglement-Based Continuous-Variable Quantum Key Distribution. Entropy. 2015; 17(7):4547-4562. https://doi.org/10.3390/e17074547
Chicago/Turabian StyleZhang, Yichen, Zhengyu Li, Christian Weedbrook, Kevin Marshall, Stefano Pirandola, Song Yu, and Hong Guo. 2015. "Noiseless Linear Amplifiers in Entanglement-Based Continuous-Variable Quantum Key Distribution" Entropy 17, no. 7: 4547-4562. https://doi.org/10.3390/e17074547
APA StyleZhang, Y., Li, Z., Weedbrook, C., Marshall, K., Pirandola, S., Yu, S., & Guo, H. (2015). Noiseless Linear Amplifiers in Entanglement-Based Continuous-Variable Quantum Key Distribution. Entropy, 17(7), 4547-4562. https://doi.org/10.3390/e17074547




