General Approach for Composite Thermoelectric Systems with Thermal Coupling: The Case of a Dual Thermoelectric Cooler
Abstract
:1. Introduction
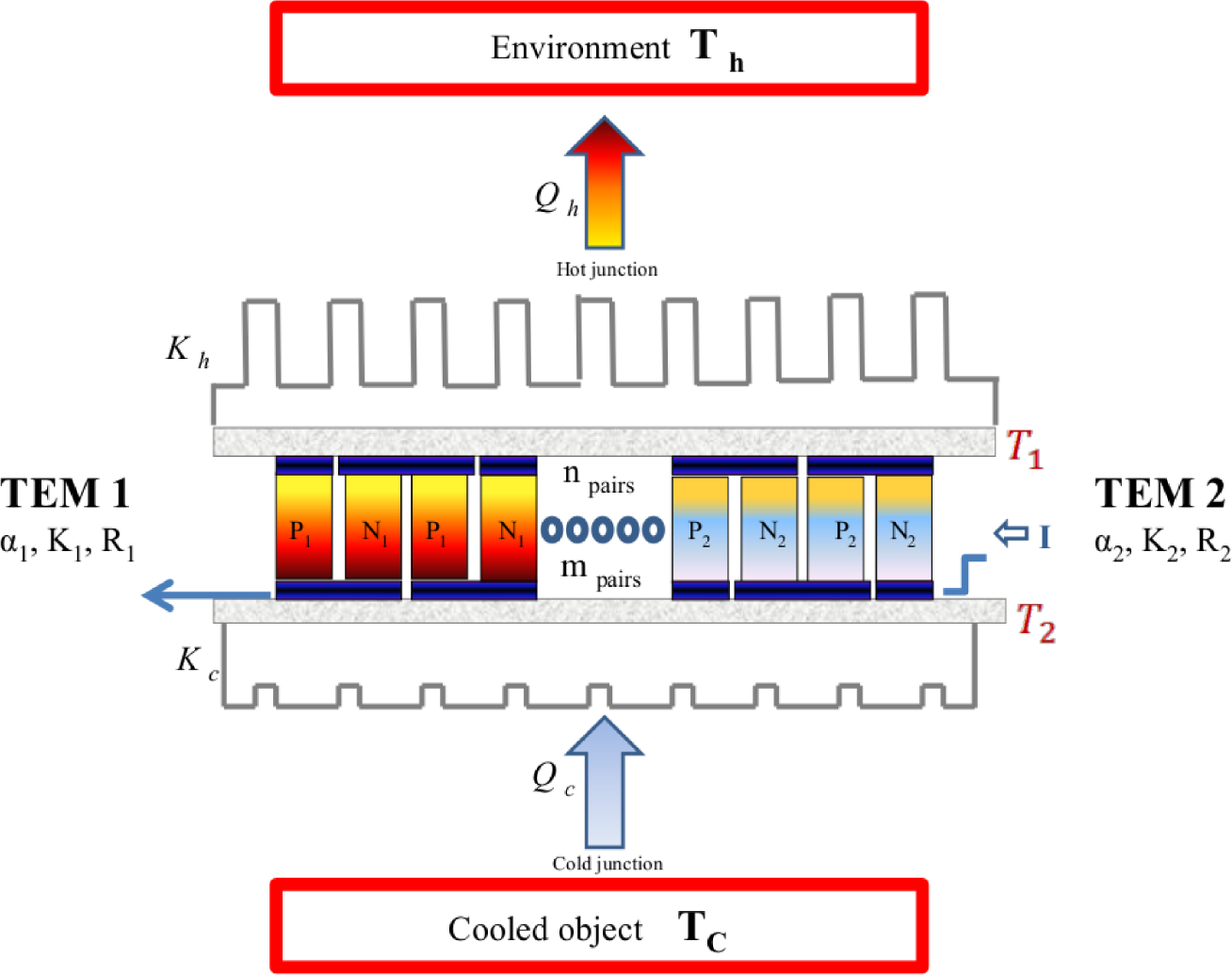
2. Dual Thermoelectric Cooling System
3. Heat Balance Equations
3.1. Equivalent Dual TEC System
3.2. Dimensionless Equivalent Heat Balance Equations
4. Results and Discussion
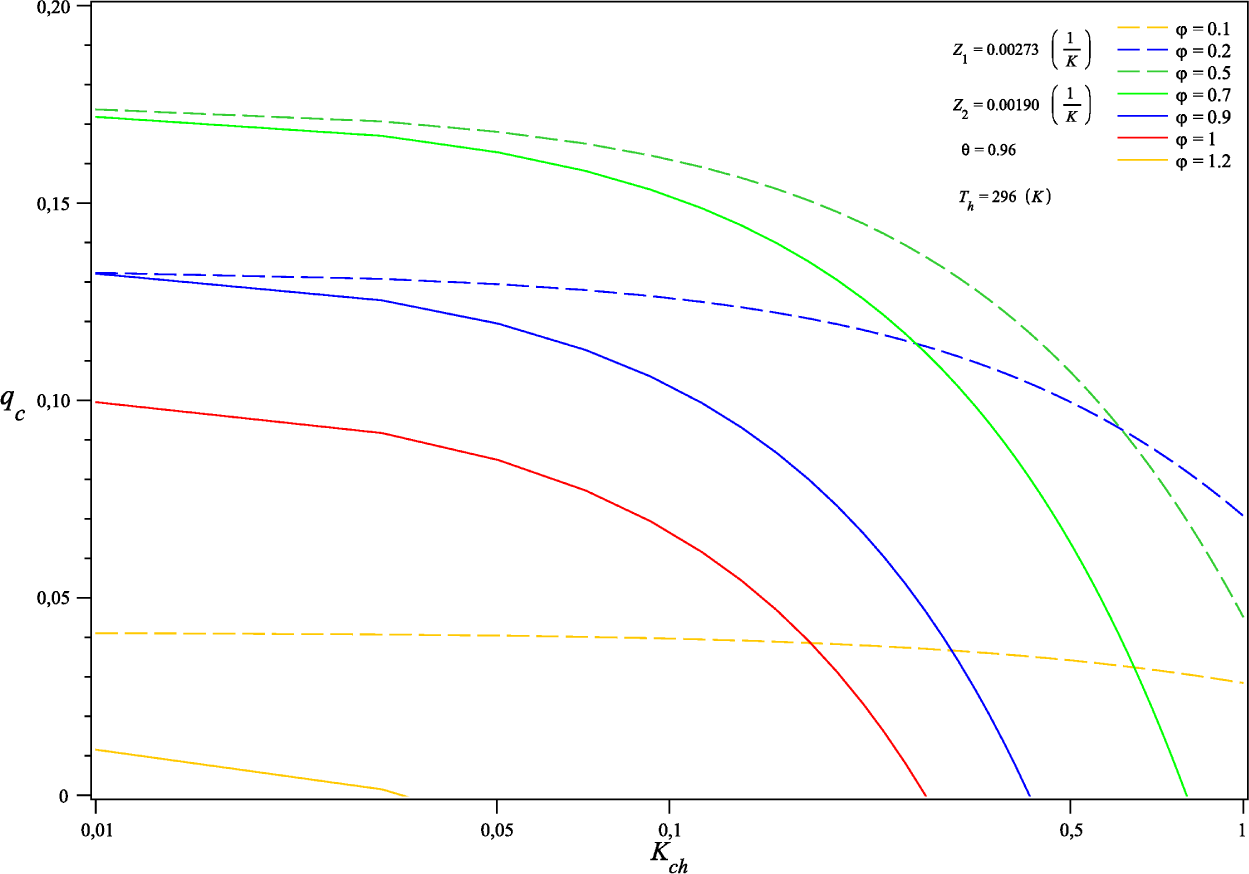
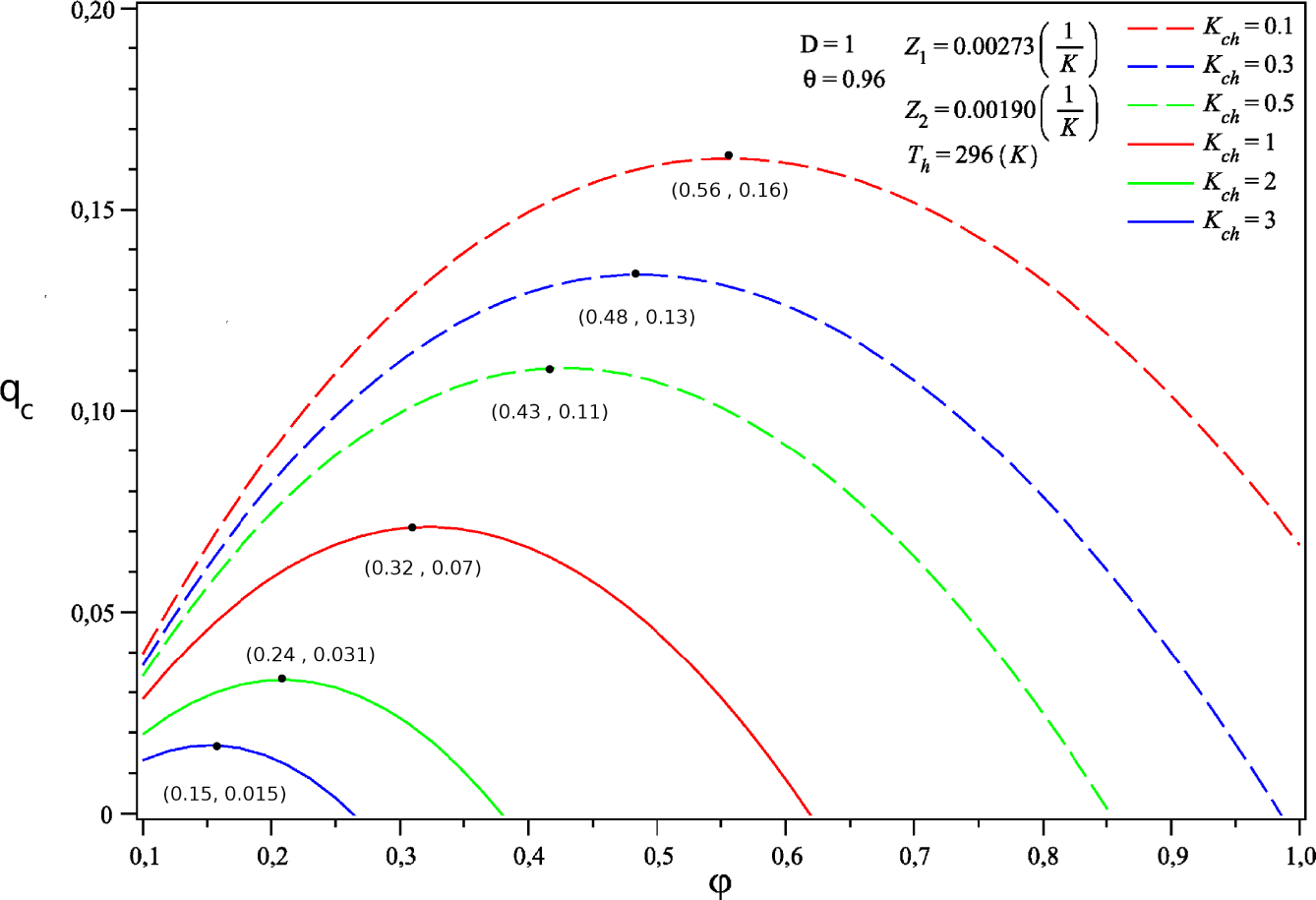
4.1. Cooling Capacity qc: External Conductances Match
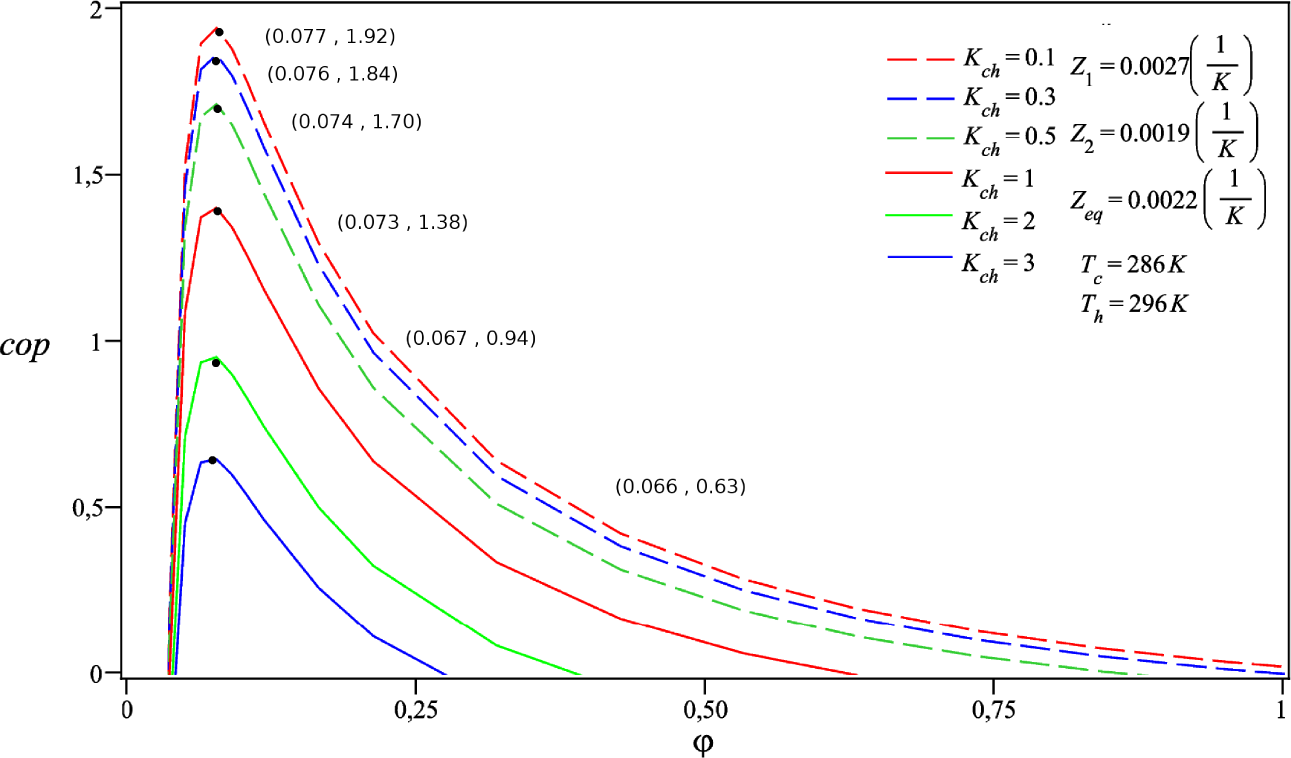
4.2. Coefficient of Performance (COP): External Conductances Match
4.3. Numerical Validation
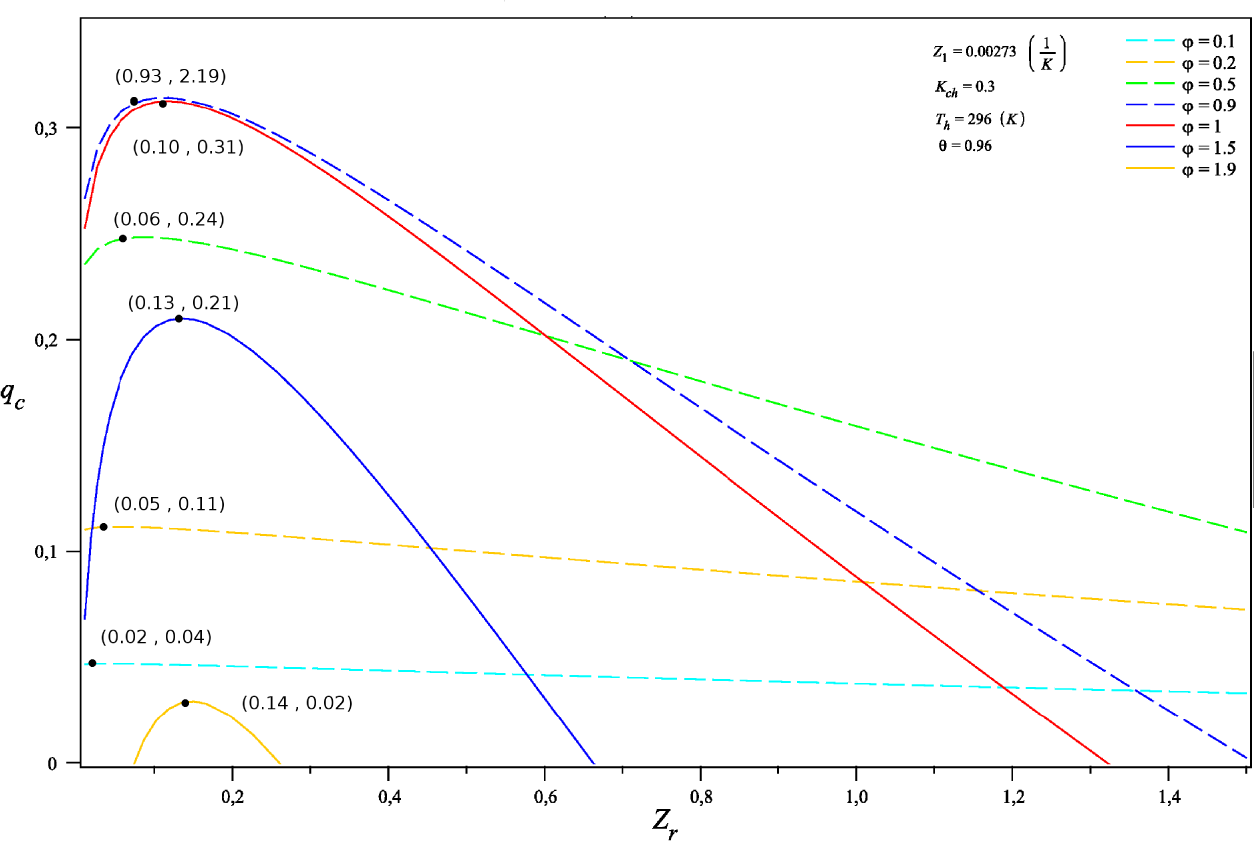
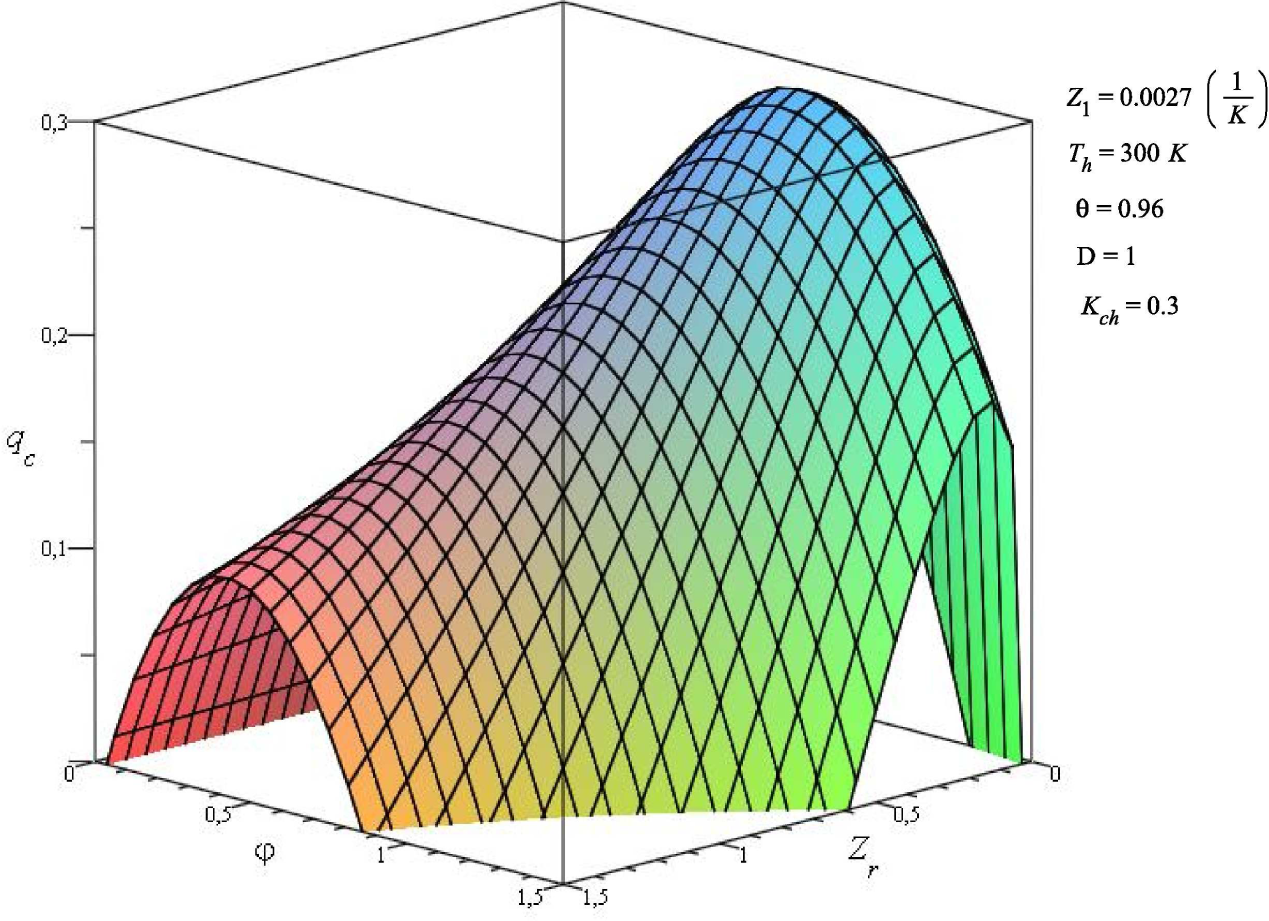
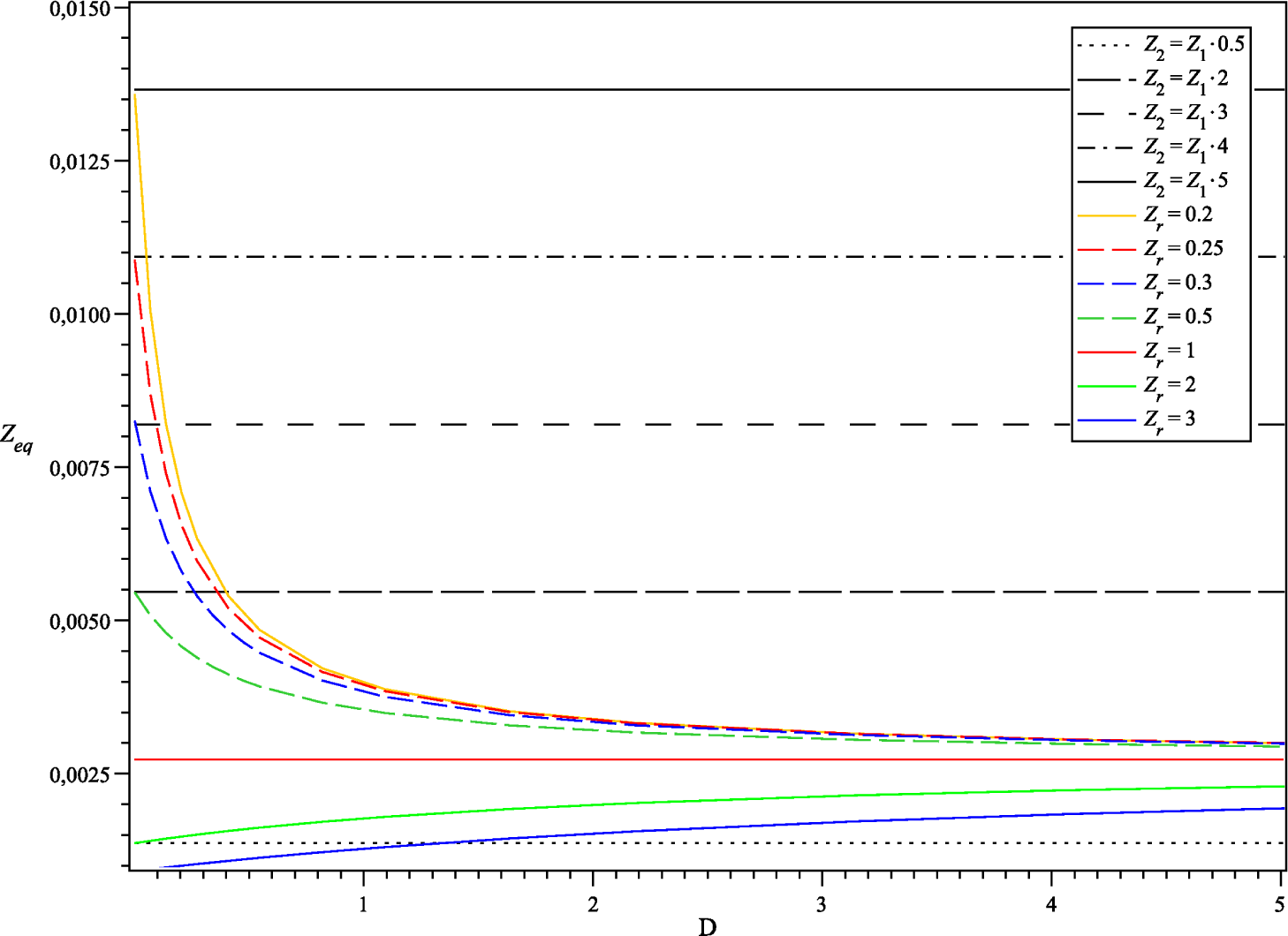
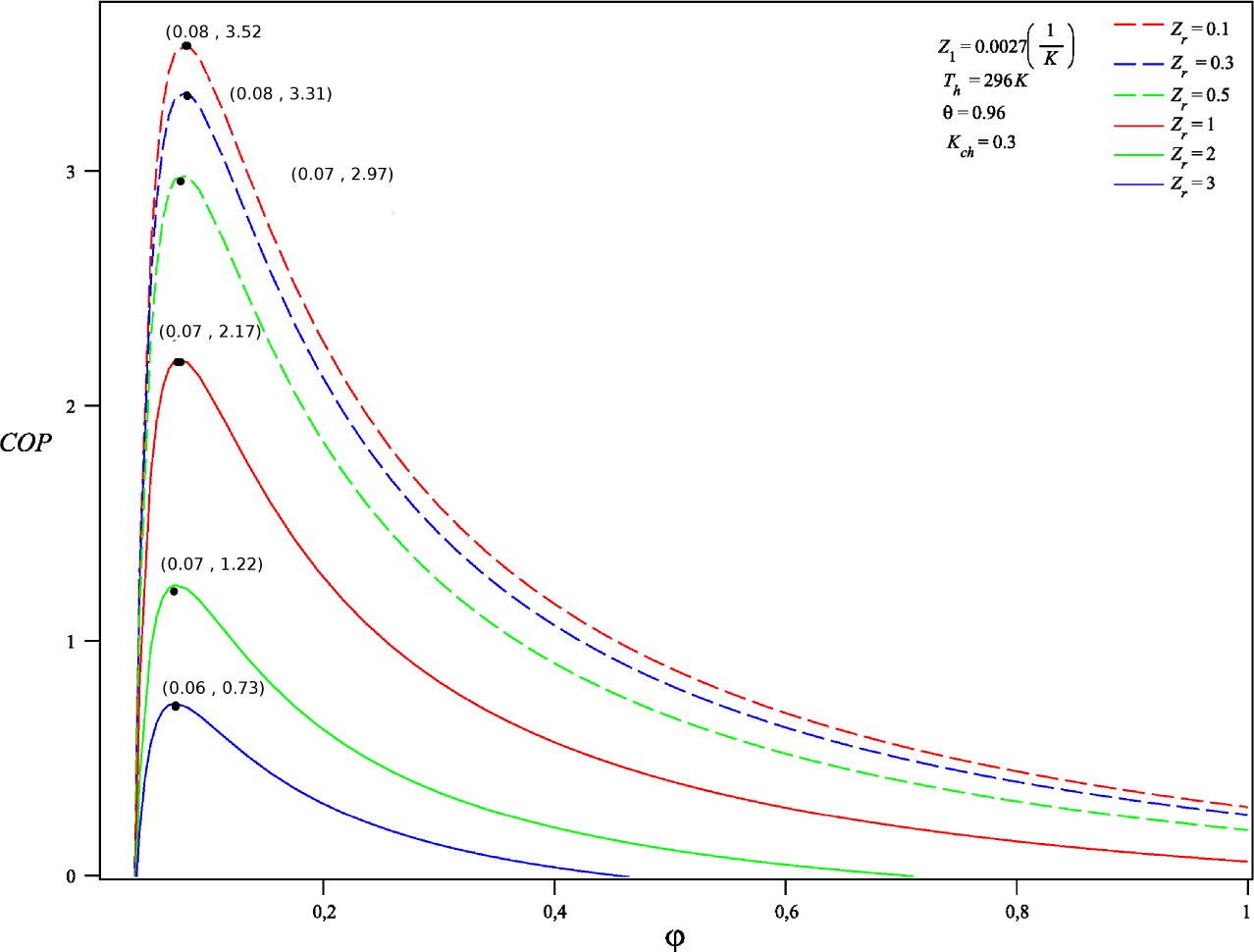
4.4. Role of the Equivalent Figure of Merit
4.5. Simplified Approaches: Previously Considered Cases
5. Conclusions
Acknowledgments
A. Effect of the Thermoelectric Parameters in COP and Qc
A.1. Cooling Capacity qc
A.2. Coefficient of Performance
Author Contributions
Conflicts of Interest
Nomenclature
| COP | Coefficient of performance |
| D | Number of pair ratio |
| I | Electric current through thermoelements (A) |
| K | Thermal conductance of thermoelement |
| Kc | Thermal conductance of cold-end heat exchanger
|
| Kch | Thermal conductance of heat exchangers ratio |
| Kh | Thermal conductance of hot-end heat exchanger
|
| m | Total number of thermoelements at first TEM |
| n | Total number of thermoelements at second TEM |
| qc | Dimensionless cooling capacity |
| qh | Dimensionless heat rejection |
| Qc | Cooling capacity of the TEC system (W) |
| Qh | Heat rejection of the TEC system (W) |
| R | Electric resistance of thermoelement (Ω) |
| T1 | Hot end temperature of TEMs (K) |
| T2 | Cold end temperature of TEMs (K) |
| Tc | Temperature of the cold reservoir (K) |
| Th | Temperature of the hot reservoir (K) |
| V | Input voltage (V) |
| Z | Figure of merit
|
| Zr | Figures of merit ratio |
| Zeq | Equivalent figure of merit |
| Greek Letters | |
|---|---|
| α | Seebeck coefficient of thermoelement
|
| δ | Cold conductance ratio |
| ∆T | Temperature across the TEMs (K) |
| ρ | Hot conductance ratio |
| θ | Temperature of heat reservoirs ratio |
| φ | Dimensionless current |
| µ | Coupling factor |
| Subscripts | |
|---|---|
| 1 | First TEM |
| 2 | Second TEM |
| eqH | Equivalent for hot side |
| eqC | Equivalent for cold side |
| ch | Heat exchangers conductances ratio |
| Lou | Thermoelectric value obtained through Z. Luo’s method |
| r | Ratio |
| max | Maximum |
References
- Rowe, D.M. Thermoelectric Handbook, Macro to Nano; CRC Press: Taylor and Francis Group, Boca Raton, FL, USA, 2006. [Google Scholar]
- Nolas, G.S.; Sharp, J.; Goldsmid, H.J. Thermoelectrics: Basic Principles and New Materials Developments; Springer Verlag: Berlin, Germany, 2001. [Google Scholar]
- Shakouri, A. Recent Development in Semiconductor Thermoelectric Physics and Materials. Ann. Rev. Mater. Res. 2011, 41, 399–431. [Google Scholar]
- Riffat, S.B.; Ma, X. Thermoelectrics: A Review of Present and Potential Applications. Appl. Therm. Eng. 2003, 23, 913–935. [Google Scholar]
- Yamanashi, M. A New Approach to Optimum Design in Thermoelectric Cooling Systems. J. Appl. Phys. 1996, 80, 5494–5502. [Google Scholar]
- Xuan, X.C. Investigation of Thermal Contact Effect on Thermoelectric Coolers. Energ. Convers. Manage. 2003, 44, 399–410. [Google Scholar]
- Pearson, M.R.; Lents, C.E. Dimensionless Optimization of Thermoelectric Cooler Performance when Integrated within a Thermal Resistance Network. Proceedings of the ASME 2013, International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013; pp. V010T11A087–V010T11A087.
- Apertet, Y.; Ouerdane, H.; Goupil, C.; Lecoeur, P. Thermoelectric Internal Loops inside Inhomogeneous System. Phys. Rev. B 2012, 85, 033201. [Google Scholar]
- Apertet, Y.; Ouerdane, H.; Glavatskaya, O.; Goupil, C.; Lecoeur, P. Optimal Working Conditions for Thermoelectric Gnerators with Realistic Thermal Coupling. Europhys. Lett. 2012, 97, 28001. [Google Scholar]
- Vargas-Almeida, A.; Olivares-Robles, M.A.; Camacho-Medina, P. Thermoelectric System in Different Thermal and Electrical Configurations: Its Impact in the Figure of Merit. Entropy 2013, 15, 2162–2180. [Google Scholar]
- Camacho-Medina, P.; Olivares-Robles, M.A.; Vargas-Almeida, A. Maximum Power of Thermally and Electrically Coupled Thermoelectric Generators. Entropy 2014, 16, 2890–2903. [Google Scholar]
- Ioffe, A. Semiconductor Thermoelements and Thermoelectric Cooling; Infosearch: London, UK, 1957. [Google Scholar]
- Home page of TE Technology. Available online: http://tetech.com accessed on 1 February 2015.
- Home page of Thermal Force. Available online: http://thermalforce.de accessed on 1 June 2015.
- Luo, Z. A Simple Method to Estimate the Physical Characteristics of a Thermoelectric Cooler from Vendo Datasheet. Electon. Cool. 2008, 14, 22–27. [Google Scholar]
- Series-Parallel Modules. Available online: https://tetech.com/Peltier-thermoelectric-cooler-modules/series-parallel/ accessed on 5 June 2015.
- Bergman, D.J.; Levy, O. Thermoelectric Properties of a Composite Medium. J. Appl. Phys. 1991, 70, 6821–6833. [Google Scholar]

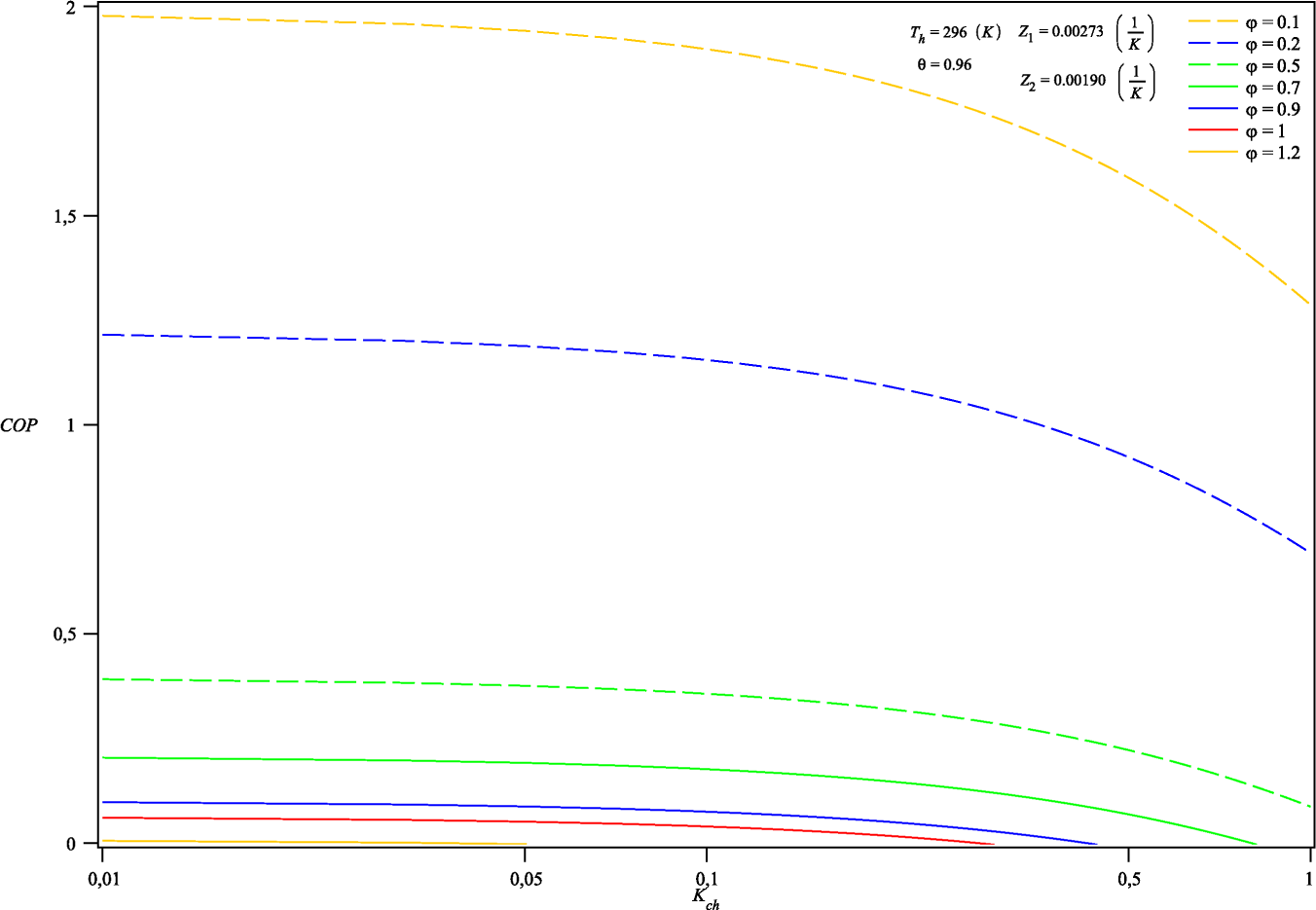
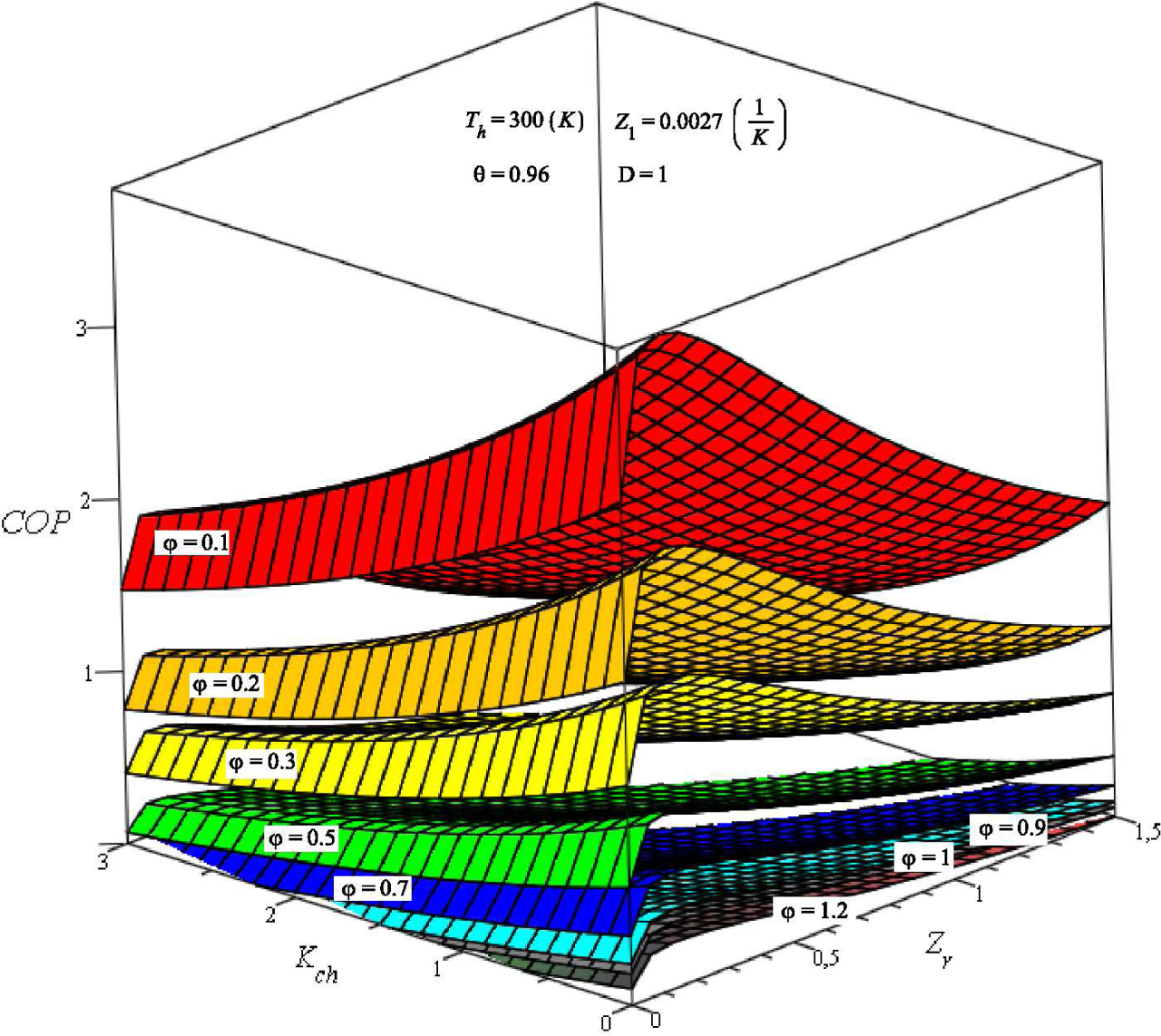
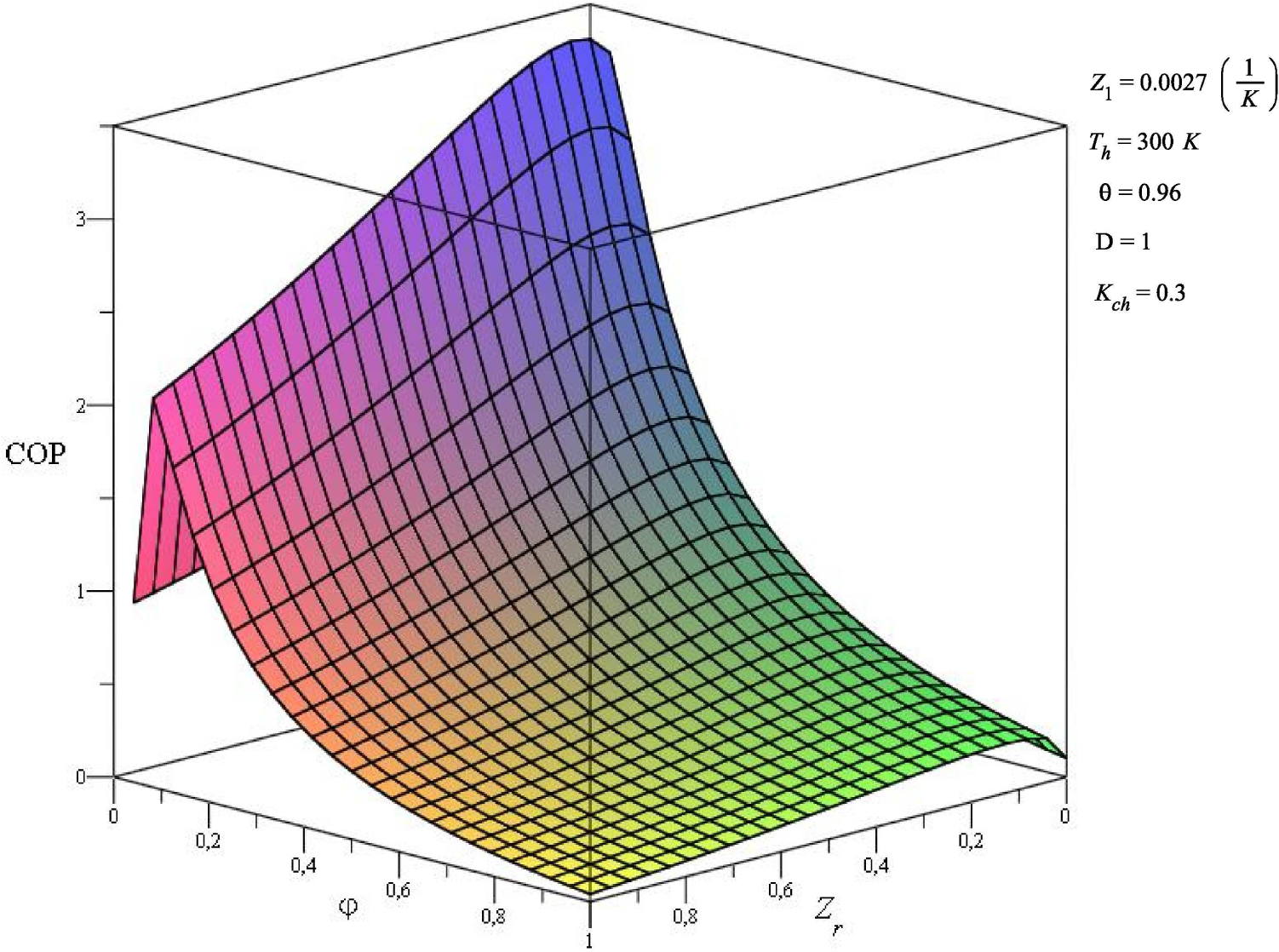
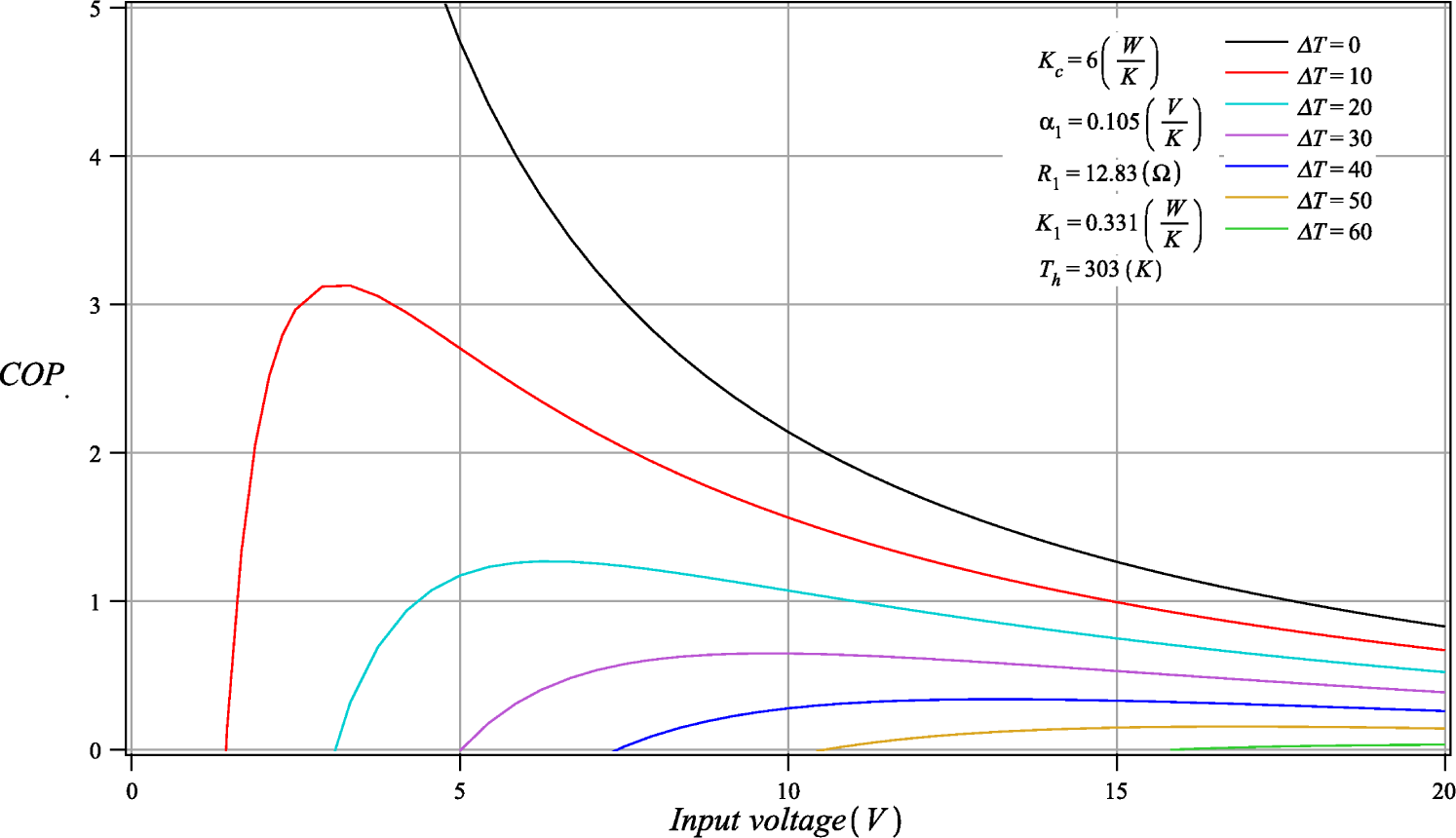


| Kch | COP | ∆COP |
|---|---|---|
| 0 | 1.9866 | 0.045 |
| 0.05 | 1.9416 | 0.0437 |
| 0.10 | 1.8979 | 0.0424 |
| 0.15 | 1.8555 | 0.0412 |
| 0.20 | 1.8143 | 0.0400 |
| 0.25 | 1.7743 | 0.0389 |
| 0.30 | 1.7354 | 0.0378 |
| 0.35 | 1.6976 | 0.0368 |
| 0.40 | 1.6608 | 0.0358 |
| 0.45 | 1.6250 | 0.0349 |
| 0.50 | 1.5901 | 0.0339 |
| 0.55 | 1.5562 | 0.0331 |
| 0.60 | 1.5231 | 0.0322 |
| 0.65 | 1.4909 | 0.0314 |
| 0.70 | 1.4595 | 0.0306 |
| 0.75 | 1.4289 | 0.0298 |
| 0.80 | 1.3991 | 0.0292 |
| 0.85 | 1.3699 | 0.0284 |
| 0.90 | 1.3415 | 0.0278 |
| 0.95 | 1.3137 | 0.0271 |
| Kch | 0.3 | 0.5 | 1 | 2 |
|---|---|---|---|---|
| δ | 0.3522 | 0.3522 | 0.3522 | 0.3522 |
| ρ | 0.10566 | 0.1761 | 0.3522 | 0.7044 |
| Zr | α2 | R2 | K2 | Z2 |
|---|---|---|---|---|
| 0.1 | 0.0170 | 0.341 | 0.0313 | 0.0273 |
| 0.5 | 0.0381 | 1.705 | 0.1565 | 0.0054 |
| 1 | 0.054 | 3.41 | 0.313 | 0.0027 |
| 2 | 0.0766 | 6.82 | 0.626 | 0.0013 |
| 3 | 0.0935 | 10.23 | 0.939 | 0.0009 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flores-Niño, C.Y.; Olivares-Robles, M.A.; Loboda, I. General Approach for Composite Thermoelectric Systems with Thermal Coupling: The Case of a Dual Thermoelectric Cooler. Entropy 2015, 17, 3787-3805. https://doi.org/10.3390/e17063787
Flores-Niño CY, Olivares-Robles MA, Loboda I. General Approach for Composite Thermoelectric Systems with Thermal Coupling: The Case of a Dual Thermoelectric Cooler. Entropy. 2015; 17(6):3787-3805. https://doi.org/10.3390/e17063787
Chicago/Turabian StyleFlores-Niño, Cuautli Yanehowi, Miguel Angel Olivares-Robles, and Igor Loboda. 2015. "General Approach for Composite Thermoelectric Systems with Thermal Coupling: The Case of a Dual Thermoelectric Cooler" Entropy 17, no. 6: 3787-3805. https://doi.org/10.3390/e17063787
APA StyleFlores-Niño, C. Y., Olivares-Robles, M. A., & Loboda, I. (2015). General Approach for Composite Thermoelectric Systems with Thermal Coupling: The Case of a Dual Thermoelectric Cooler. Entropy, 17(6), 3787-3805. https://doi.org/10.3390/e17063787







