Delayed-Compensation Algorithm for Second-Order Leader-Following Consensus Seeking under Communication Delay
Abstract
:1. Introduction
2. Problem Formulation
2.1. Agent’s Dynamics
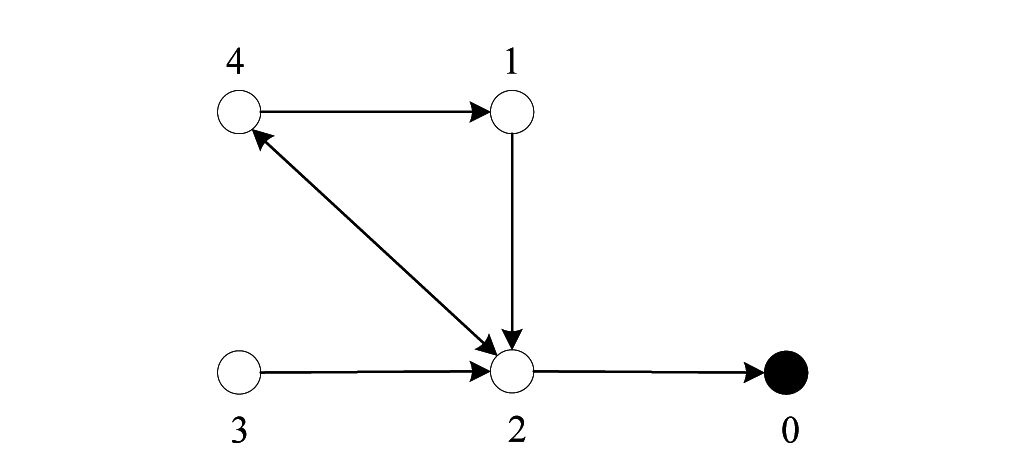
2.2. Interconnection Topology
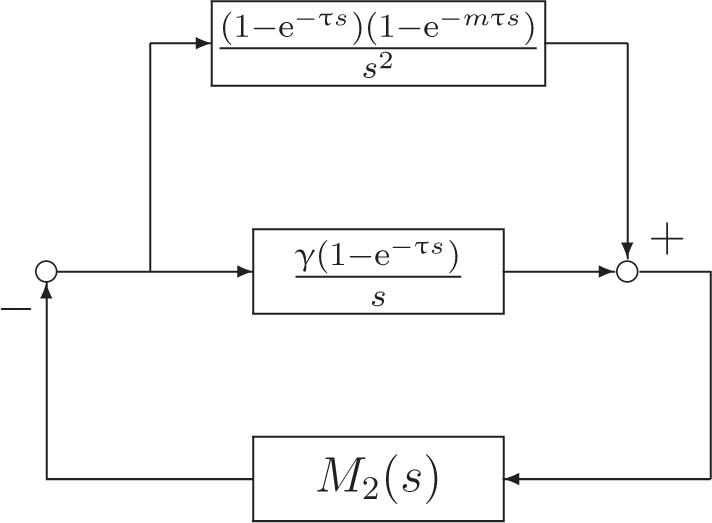
2.3. Delayed-Compensation Consensus Algorithm
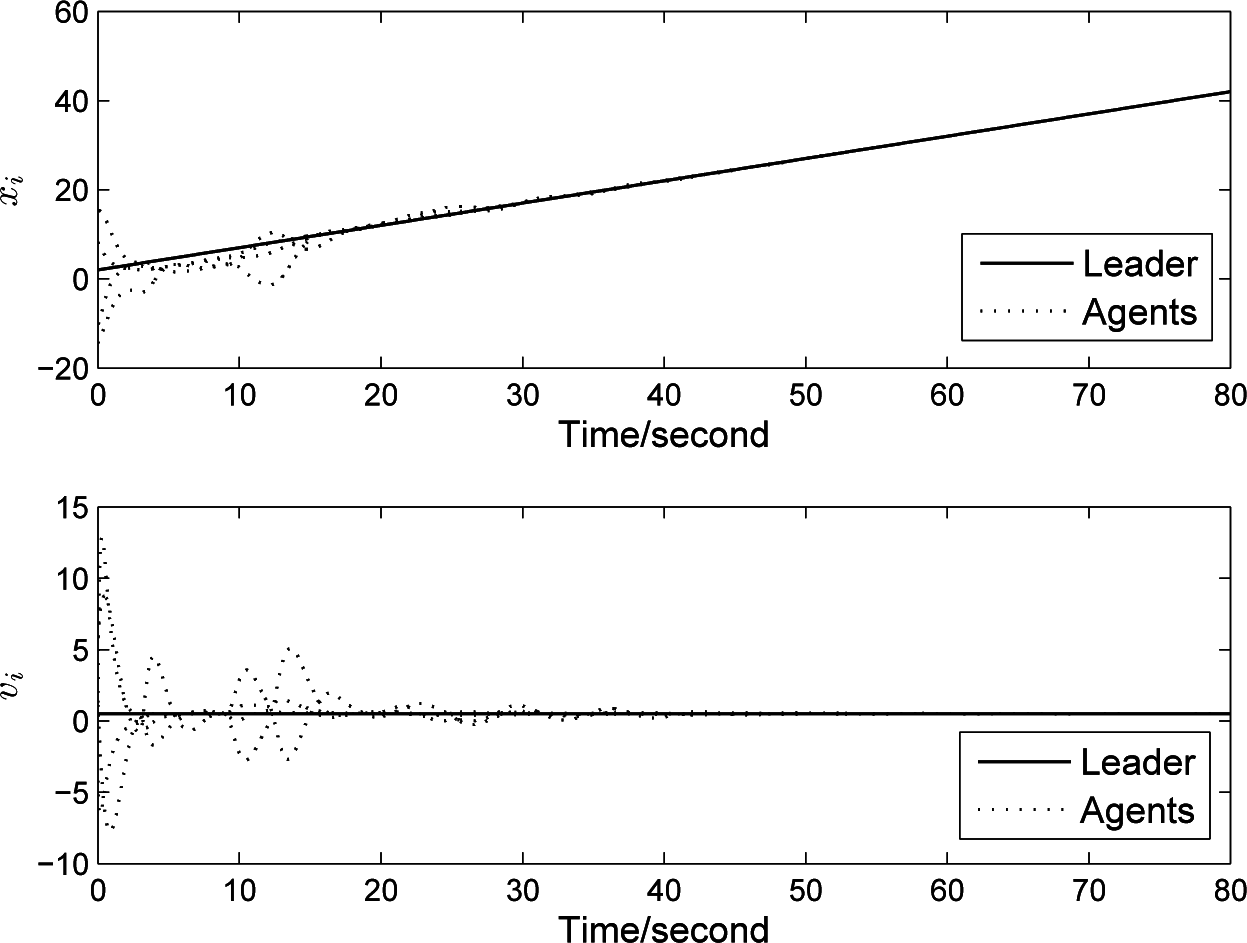
3. Main Results
3.1. Delay-Independent Consensus Criterion
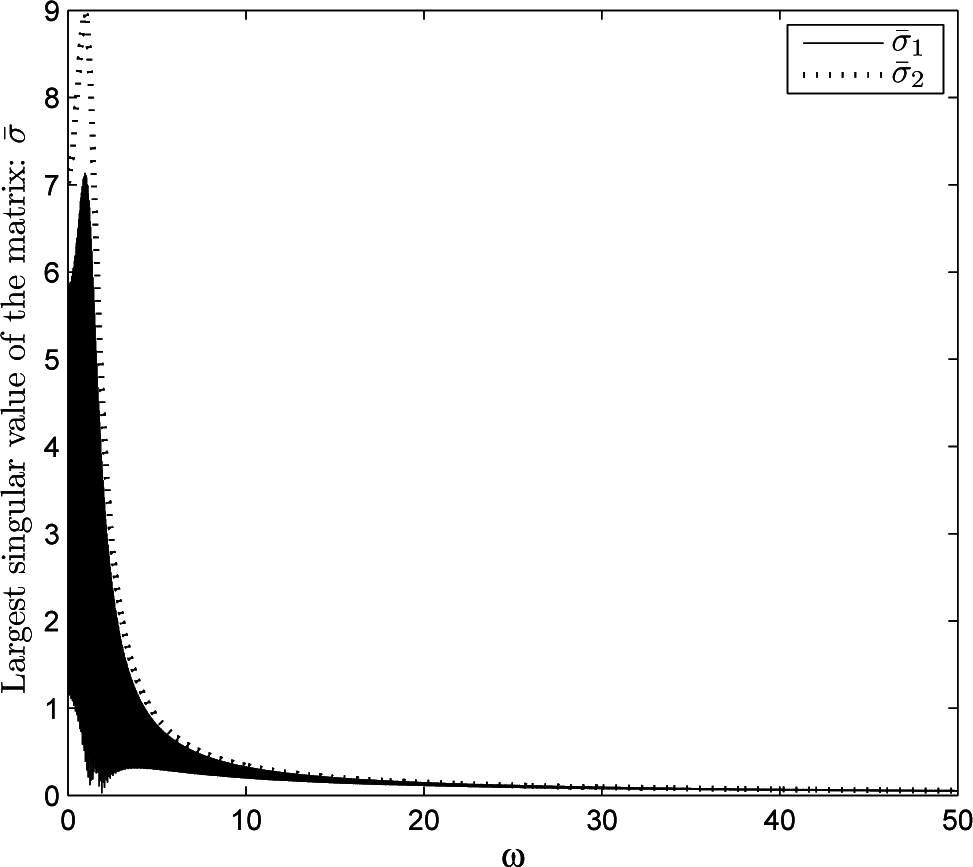
3.2. Delay-Dependent Consensus Criterion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar]
- Lin, P.; Jia, Y.; Du, J.; Yuan, S. Distributed consensus control for second-order agents with fixed topology and time-delay. Proceedings of the 26th Chinese Control Conference, Zhangjiajie, China, 26–31 July 2007; pp. 577–581.
- Yu, W.; Chen, G.; Cao, M. Some necessary and sufficient conditions for second-order consensus in multi-agent dynamical systems. Automatica 2010, 46, 1089–1095. [Google Scholar]
- Munz, U.; Papachristodoulou, A; Allgower, F. Consensus in multi-Agent systems with coupling delays and switching topology. IEEE Trans. Autom. Control 2011, 56, 2976–2982. [Google Scholar]
- Lu, X.; Austin, F; Chen, S. Flocking in multi-agent systems with active virtual leader and time-varying delays coupling. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1014–1026. [Google Scholar]
- Hu, J.; Hong, Y. Leader-following coordination of multi-agent systems with coupling time delays. Physica A 2007, 374, 853–863. [Google Scholar]
- Su, H.; Wang, X. Second-order consensus of multiple agents with coupling delay. Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 7181–7186.
- Lin, P.; Jia, Y. Consensus of a Class of second-order multi-agent systems with time-delay and jointly-connected topologies. IEEE Trans. Autom. Control 2010, 55, 778–784. [Google Scholar]
- Sun, Y.G.; Wang, L.; Xie, G. Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays. Syst. Control Lett. 2008, 57, 175–183. [Google Scholar]
- Qin, J.; Gao, H. A sufficient condition for convergence of sampled-data consensus for double-integrator dynamics with nonuniform and time-varying communication delays. IEEE Trans. Autom. Control. 2012, 57, 2417–2422. [Google Scholar]
- Yu, J.; Wang, L. Group consensus in multi-agent systems with switching topologies and communication delays. Syst. Control Lett. 2010, 59, 340–348. [Google Scholar]
- Sun, Y.G.; Wang, L. Consensus of multi-agent systems in directed networks with nonuniform time-varying delays. IEEE Trans. Autom. Control 2009, 54, 1607–1613. [Google Scholar]
- Zhang, Y.; Tian, Y.P. Allowable delay bound for consensus of linear multi-agent systems with communication delay. Int. J. Syst. Sci. 2014, 45, 2172–2181. [Google Scholar]
- Wang, J.; Elia, N. Consensus over network with dynamic channels. In Proceedomgs of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 2637–2642.
- Lee, D.J.; Spong, M.K. Agreement with non-uniform information delays. Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 756–761.
- Moreau, L. Stability of continuous-time distributed consensus algorithms. Proceedings of the 43rd IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004; pp. 3998–4003.
- Wang, W.; Slotine, J.J.E. Contraction analysis of time-delayed communication delays. IEEE Trans. Autom. Control. 2006, 51, 712–717. [Google Scholar]
- Cao, M.; Morse, A.S.; Anderson, B.D.O. Reaching an agreement using delayed information. Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 3375–3380.
- Wang, L.; Xiao, F. A new approach to consensus problems for discrete-time multiagent systems with time-delays. Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 2118–2123.
- Liu, X.; Lu, W.; Chen, T. Consensus of multi-agent systems with unbounded time-varying delays. IEEE Trans. Autom. Control. 2010, 55, 2396–2401. [Google Scholar]
- Lin, P.; Jia, Y. Consensus of second-order discrete-time multi-agent systems with nonuniform time-delays and dynamically changing topologies. Automatica 2009, 45, 2154–2158. [Google Scholar]
- Liu, C.L.; Liu, F. Stationary consensus of heterogeneous multi-agent systems with bounded communication delays. Automatica 2011, 47, 2130–2133. [Google Scholar]
- Yang, W.; Bertozzi, A.L.; Wang, X.F. Stability of a second order consensus algorithm with time delay. Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2926–2931.
- Liu, C.L.; Liu, F. Consensus analysis for multiple autonomous agents with input delay and communication delay. Int. J. Control Autom. Syst. 2012, 10, 1005–1012. [Google Scholar]
- Liu, C.L.; Tian, Y.P. Formation control of multi-agent systems with heterogeneous communication delays. Int. J. Syst. Sci. 2009, 40, 627–636. [Google Scholar]
- Zhu, W.; Cheng, D. Leader-following consensus of second-order agents with multiple time-varying delays. Automatica 2010, 46, 1994–1999. [Google Scholar]
- Zhu, W. Consensus of multiagent systems with switching jointly reachable interconnection and time delays. IEEE Trans. Syst. Cybern. A 2012, 42, 348–358. [Google Scholar]
- Liu, C.L.; Liu, F. Dynamical consensus seeking of second-order multi-agent systems based on delayed state compensation. Syst. Control Lett. 2012, 61, 1235–1241. [Google Scholar]
- Hong, Y.; Hu, J.; Gao, L. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 2006, 42, 1177–1182. [Google Scholar]
- Tang, Y.; Gao, H.; Zhang, W.; Kurths, J. Leader-following consensus of a class of stochastic delayed multi-agent systems with partial mixed impulses. Automatica 2015, 53, 346–354. [Google Scholar]
- Tang, Y.; Qian, F.; Gao, H.; Kurthsa, J. Synchronization in complex networks and its application—a survey of recent advances and challenges. Ann. Rev. Control. 2014, 38, 184–198. [Google Scholar]
- Lu, X.; Lu, R.; Chen, S.; Lu, J. Finite-time distributed tracking control for multi-agent systems with a virtual leader. IEEE Trans. Circuits Syst. I 2013, 60, 352–362. [Google Scholar]




© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.-L.; Liu, F. Delayed-Compensation Algorithm for Second-Order Leader-Following Consensus Seeking under Communication Delay. Entropy 2015, 17, 3752-3765. https://doi.org/10.3390/e17063752
Liu C-L, Liu F. Delayed-Compensation Algorithm for Second-Order Leader-Following Consensus Seeking under Communication Delay. Entropy. 2015; 17(6):3752-3765. https://doi.org/10.3390/e17063752
Chicago/Turabian StyleLiu, Cheng-Lin, and Fei Liu. 2015. "Delayed-Compensation Algorithm for Second-Order Leader-Following Consensus Seeking under Communication Delay" Entropy 17, no. 6: 3752-3765. https://doi.org/10.3390/e17063752
APA StyleLiu, C.-L., & Liu, F. (2015). Delayed-Compensation Algorithm for Second-Order Leader-Following Consensus Seeking under Communication Delay. Entropy, 17(6), 3752-3765. https://doi.org/10.3390/e17063752




