Abstract
In this paper, the leader-following consensus algorithm, which is accompanied with compensations related to neighboring agents’ delayed states, is constructed for second-order multi-agent systems with communication delay. Using frequency-domain analysis, delay-independent and delay-dependent consensus conditions are obtained for second-order agents respectively to converge to the dynamical leader’s states asymptotically. Simulation illustrates the correctness of the results.
1. Introduction
Coordination control mechanism of distributed multiple autonomous agents exists commonly in social, nature and engineering applications. As one of the hottest issues in multi-agent systems, consensus problem, which requires the several autonomous agents reach a state agreement in a distributed cooperative manner, has stimulated more and more research interests recently in various research fields, such as physics, artificial intelligence, automatic control, etc.
Communication delays related to information transmission cannot be neglected in multi-agent network, and consensus algorithms with communication delays are usually divided into synchronously-coupled and asynchronously-coupled forms. In synchronously-coupled form, each agent introduce self-delays, which equal the corresponding communication delays, in the coordination control part. In asynchronously-coupled form, each agent uses its current state, or its delayed state with the delay different from the corresponding communication delay to compare with its delayed neighboring agents’ states.
Convergence of synchronously-coupled consensus algorithm depends on communication delay strictly for multi-agent systems under fixed [1–5] or switched topologies [6–13]. To our great delight, the first-order and second-order agents with stationary consensus algorithms in the asynchronously-coupled form can be robust to arbitrary communication delays by choosing proper control parameters [14–22]. However, under dynamical consensus algorithm composed of the position and velocity consensus coordination parts, asynchronously-coupled form just drives the second-order agents to achieve a stationary consensus, and the consensus convergence is strictly dependent on the communication delay [23,24].
To make second-order agents with dynamical consensus algorithm in asynchronously-coupled form get the original dynamical consensus, delayed-compensation consensus algorithms have been proposed in [25–28]. Liu et al. designed the delay-dependent compensations based on the information of global desired objective for each agent, and obtained delay-independent consensus condition for second-order multi-agent systems [25–27]. Liu and Liu [28] constructed compensations for normal asynchronously-coupled consensus algorithm based on neighboring agents’ delayed states, and gained delay-dependent sufficient conditions for second-order multi-agent systems with communication delay under a general digraph. The results in [28] have demonstrated that asynchronously-coupled consensus algorithm accompanied with delay-dependent compensations can tolerate higher communication delay than synchronously-coupled consensus algorithm.
In this paper, leader-following consensus algorithm composed of the position and velocity consensus coordination parts is constructed to make second-order agents converge to a dynamical leader. The leader-following algorithm in asynchronously-coupled form is accompanied with compensations on neighboring agents’ delayed states, but does not require each agent to get leader’s states. Using frequency-domain analysis, we obtain delay-independent sufficient condition for second-order agents to converge to the dynamical leader’s states asymptotically. Then, delay-dependent sufficient conditions are obtained for the multi-agent systems with communication delay under general digraph based on linear fractional transformation and small-gain theorem.
2. Problem Formulation
2.1. Agent’s Dynamics
Investigate the second-order dynamic agents:
where xi ∈ R, vi ∈ R, and ui ∈ R denote the position, velocity and acceleration, respectively, of the agent i. In addition, the leader’s dynamics are modelled as
where x0 ∈ R denotes the position, and v0 ∈ R is a constant denoting the desired velocity for all agents (1). As a typical control method, leader-following consensus algorithms have been extensively adopted to solve the stationary and dynamical consensus problems for multi-agent systems, and abundant results have been achieved in the past decade [5,6,25,26,29–32]. Under the leader-following coordination control structure, the agents’ states are required to converge to the leader’s states asymptotically, i.e., limt→∞ xi(t) = x0(t), limt→∞ vi(t) = v0.
2.2. Interconnection Topology
Interconnection topology of multi-agent systems is usually described as a digraph. Agents can be considered as the nodes of a digraph, while the information flow between neighboring agents is regarded as a directed edge between the neighboring nodes of the digraph.
A weighted digraph G = (V, E, A) of order n is composed of a set of vertices V = {1,⋯, n}, a set of edges E ⊆ V × V and a weighted adjacency matrix A = [aij] ∈ Rn×n with aij ≥ 0. The node indexes belong to a finite index set
. A directed edge from the node i to the node j of the diagraph G is denoted by eij = (i, j) ∈ E. We assume that the adjacency elements associated with the edges of the digraph are positive, i.e., aij > 0 ⇔ eij ∈ E. Moreover, we assume aii = 0 for all
. The set of neighbors of node i is denoted by Ni = {j ∈ V : (i, j) ∈ E}. The Laplacian matrix of the weighted digraph G is defined as L = D − A = [lij] ∈ Rn×n, where
is the degree matrix of G.
In the digraph, if there is a path from one node i to another node j, then j is said to be reachable from i. If a node is reachable from every other node in the digraph, then we say it globally reachable.
2.3. Delayed-Compensation Consensus Algorithm
For second-order agents (1), we take following consensus algorithm similar to that in [5,25]
where κ > 0, γ > 0, Ni denotes the neighbors of agent i, aij > 0 is adjacency element of A in the digraph G = (V, E, A), and bi denotes the linking weight from agent i to the leader (2). Assume that bi > 0 if there is a directed edge from agent i to the leader; otherwise, bi = 0. In the rest of the paper, the notation
is used.
With non-negligible communication delay, the algorithm (3) in asynchronously-coupled form becomes
where τ > 0 is the communication delay between neighboring agents.
Remark 1. Used in the stationary consensus problem of multi-agent systems with communication delays [4,22], asynchronously-coupled consensus algorithm has shown its delay-independent consensus convergence property. With regard to the dynamical consensus problem of second-order or high-order multi-agent systems, nevertheless, asynchronously-coupled consensus algorithm changes the final consensus behavior and cannot achieve the original dynamical consensus convergence [24,28]. In the same way, it is evident that the algorithm (4) cannot drive second-order agents (1) to converge to the dynamical leader’s states asymptotically. In this case, several consensus algorithms with compensations related to delayed states of neighboring agents [28], desired target [25] and dynamical leader [26,27] were added to consensus algorithm in order to remain the original control objective. The compensation constructed in this paper is similar to that in [28], but we just add compensation to position coordination part:
where −(xj(t − (m + 1)τ) − xj(t − mτ)) is compensation, and m ≥ 1 is an integer.
Remark 2. The compensation’s form in (5) is more general than that in [28], and we can choose the integer m arbitrarily. Analogous to the delayed-compensation consensus algorithm in [25–28], the new algorithm (5) also requires each agent to know exact value of communication delay. Particularly, the compensations in algorithm (5) is different from the delayed-compensation leader-following consensus algorithm in [26,27], since our proposed algorithm does not require each agent to get the leader’s states.
For leader-following structure, we come to the following property from Lemma 2 in [25] and Lemma 3 in [29].
Lemma 1. Assume that the interconnection topology graph of n agents together with the leader in system (6) has the leader as a globally reachable node. Then, the matrix L + B has no zero eigenvalues, and D+B > µI where µ > 0, and L is the Laplacian matrix of the interconnection topology of n agents without leader.
Define
,
,
, and we get
where
and
. Taking Laplace transform of system (7) yields the characteristic equation on
as follows
3. Main Results
3.1. Delay-Independent Consensus Criterion
Theorem 1. Assume that the interconnection topology of n agents and a leader in system (6) has the leader as a globally reachable node. Then, all the agents in system (6) asymptotically converge to the leader’s state, if
hold for ω ∈ R, where denotes the largest singular value of matrix.
Before proving Theorem 1, we introduce the following lemma firstly.
Lemma 2. If |h1| < |h2|,
, where W ∈ Cn×n, h1 ∈ C, h2 ∈ C, and C denotes the complex number.
Lemma 2 can be easily proved according to the definition of matrix’s singular value. Now, we present the proof of Theorem 1.
The characteristic Equation (8) can be rewritten as
From Lemma 1, we get D + B > µI for some µ > 0, so s2I + κ(D + B)(1 + γs) just has its zeros on the open left half complex plane. According to the generalized Nyquist stability criterion, the roots of characteristic Equation (10) all lie on the open left half complex plane, as long as the eigenloci of
, i.e., λ(M1(jω)), does not enclose the point (−1, j0) for ω ∈ R, where λ(·) denotes the matrix eigenvalue.
Since
hold for ω ∈ (0, ∞), we obtain from Lemma 2 and the condition (9) that
holds for ω ∈ (0, ∞), where ρ(·) denotes matrix spectral radius.
Hence, λ(M1(jω)) does not enclose the point (−1, j0) for all ω ∈ R, i.e., the roots of the characteristic Equation (10) all lie on the open left half of the complex plane. Therefore, the closed-loop system (7) is asymptotically stable, and the agents in (6) converge to the leader’s states asymptotically. Theorem 1 is proved.
Remark 3. The result in Theorem 1 demonstrates that the delay robustness of delayed-compensation leader-following algorithm (5) is much better than that of synchronously-coupled consensus algorithm, since convergence of synchronously-coupled consensus algorithm always depends on communication delay strictly from existing works [2,3,7]. However, the delay-independent sufficient condition (9) is effective for second-order multi-agent systems with proper interconnection topology and coupling weights, but not for all interconnection topologies that have the leader as a globally reachable node.
Remark 4. Assume that the interconnection topology of n agents and a leader in system (6) has the leader as a globally reachable node, and each agent just has one direct path to reach the leader. For simplicity, we can assume that the direct edge from agent i to j satisfies i > j, and we get
Then, we can obtain
since the eigenvalues of A are all equivalent to zero. Therefore, all the agents in system (6) asymptotically converge to the leader’s states, i.e., our proposed algorithm (5) can tolerate arbitrary communication delay without regard to the coupling weights and the control parameters.
From Theorem 1, if interconnection topology has more directed edges from agents to the leader and less links between agents themselves, and the coupling weights between agents and leader are higher, the agents can achieve delay-independent asymptotic consensus more easily.
Example 1. Investigate a multi-agent network with four agents and a leader given by (6), and the interconnection topology is shown in Figure 1. It is obvious that the leader is the globally reachable node. The weights of the directed edges are: a12 = 1.5, a24 = 0.3,a32 = 1.4, a41 = 0.9, a42 = 0.6, b1 = 5, b2 = 8, and the control parameters are chosen as κ = 1.5 and γ = 0.8. Besides, we take m = 3 for the compensations in (6). With given coupling weights and control parameters, two largest singular values and in (11) are shown in Figure 2. From the condition (9) in Theorem 1, the agents converge to the leader’s states without any relationship with the communication delay (see, Figure 3).
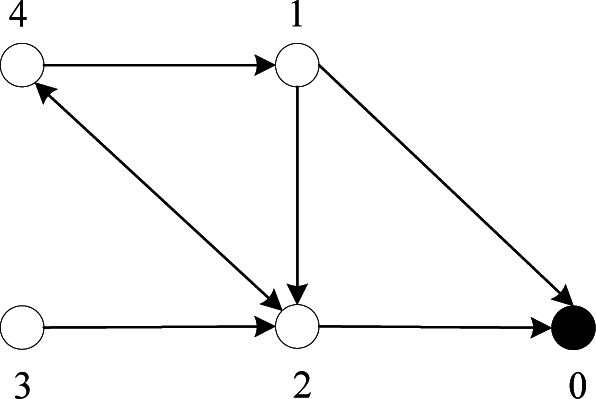
Figure 1.
Topology 1: Network of four agents and a leader.
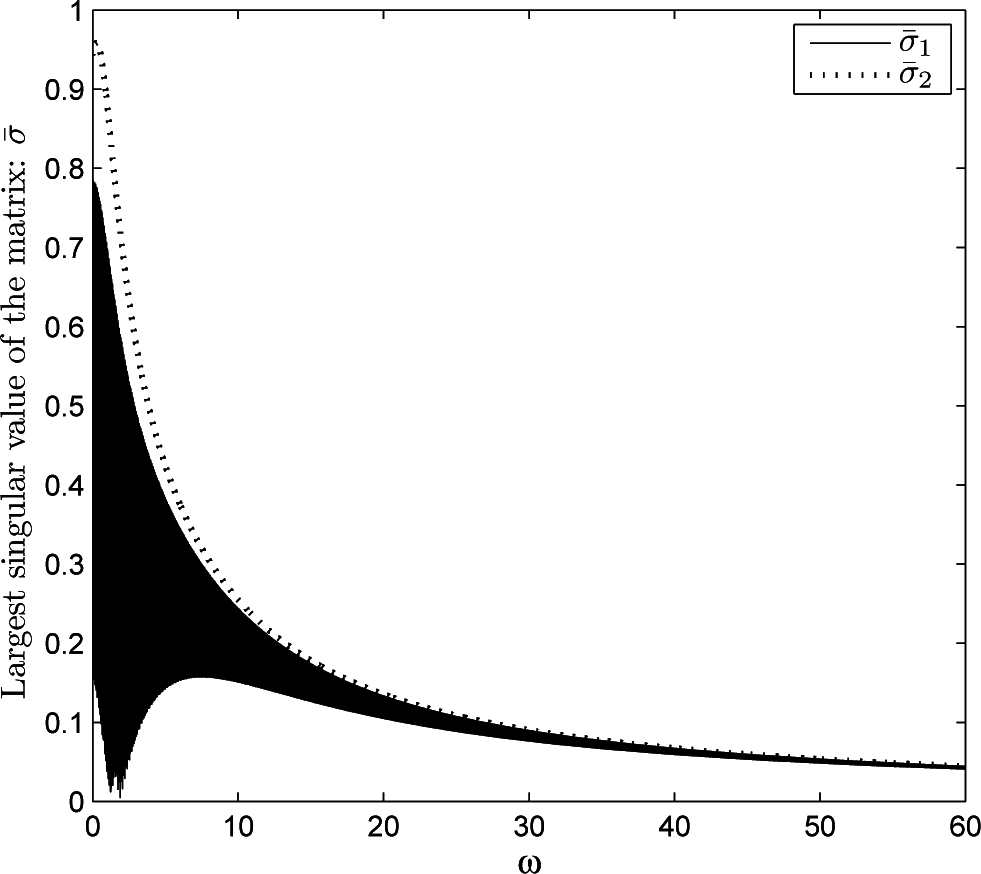
Figure 2.
Largest singular value with b1 = 5 and b2 = 8.
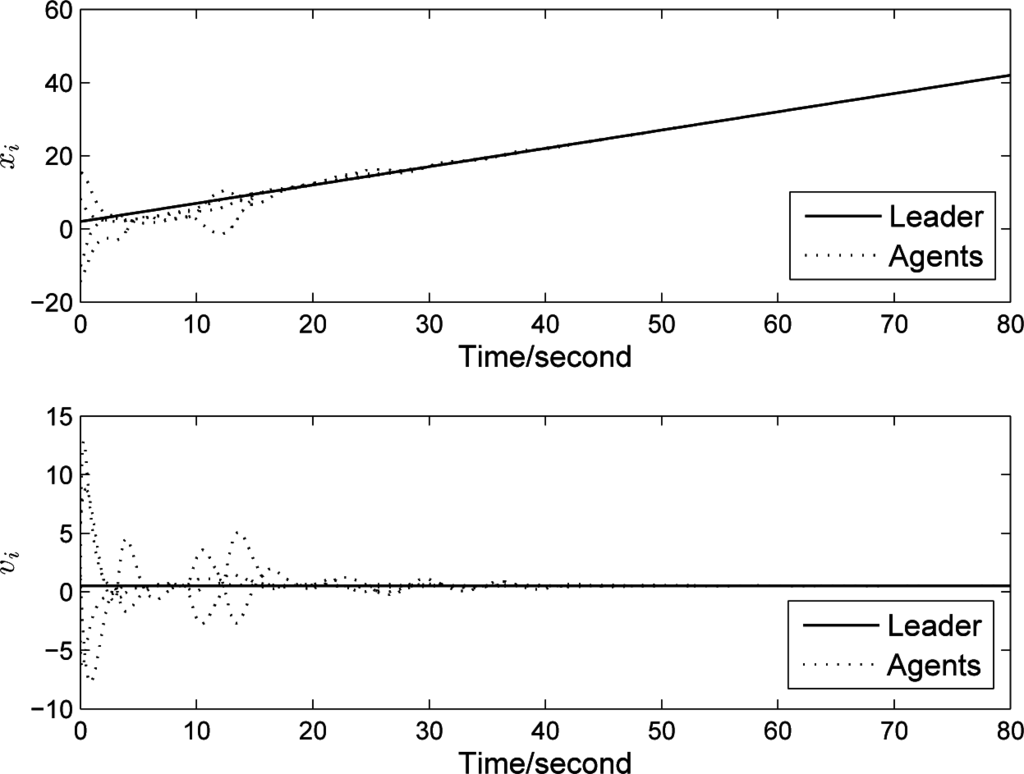
Figure 3.
Delay-independent consensus convergence.
However, the condition (9) does not hold for any coupling weights and interconnection structure. In topology 1, if the coupling weights from agent 1 and agent 2 to the leader are chosen as b1 = 0.5 and b2 = 0.8, and
and
are shown in Figure 4. Obviously, the condition (9) does not hold, and we find that the communication delay that the system (6) can bear now is τ < 1.46(s) through numerical simulation. Moreover, if the interconnection topology of four agents and a leader is described in Figure 5, and we choose the same coupling weights and control parameters as above. Then, it is found that the condition (9) can not hold with arbitrary coupling weight b2.
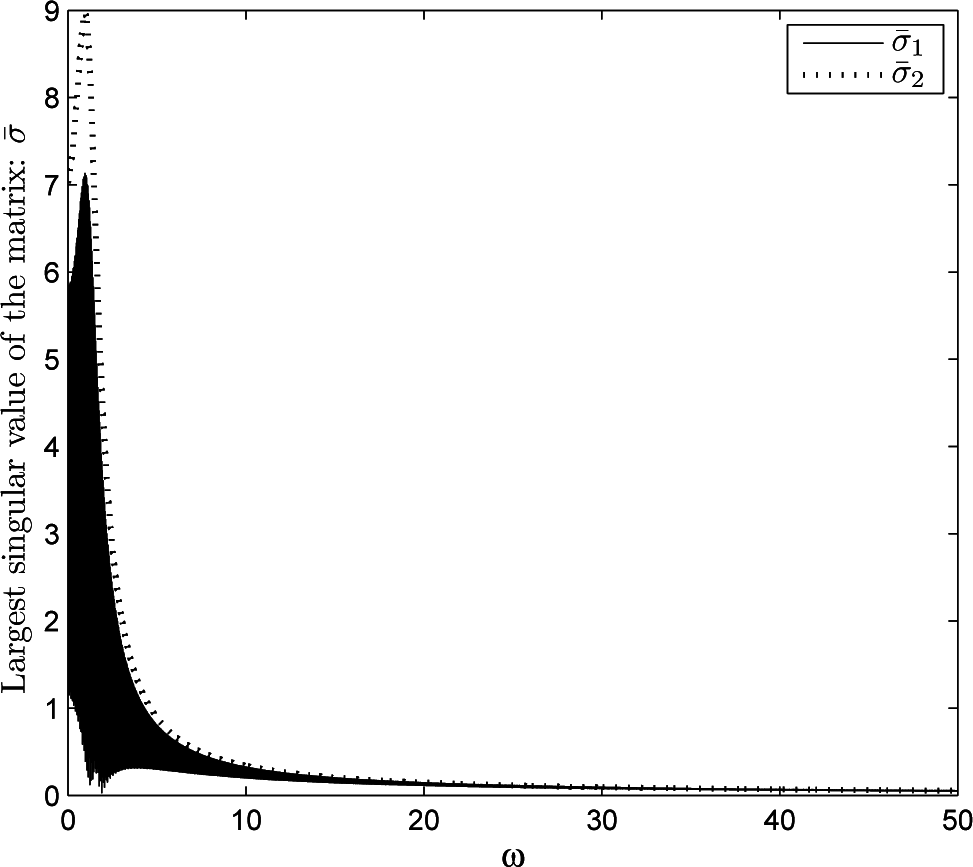
Figure 4.
Largest singular values with b1 = 0.5 and b2 = 0.8.
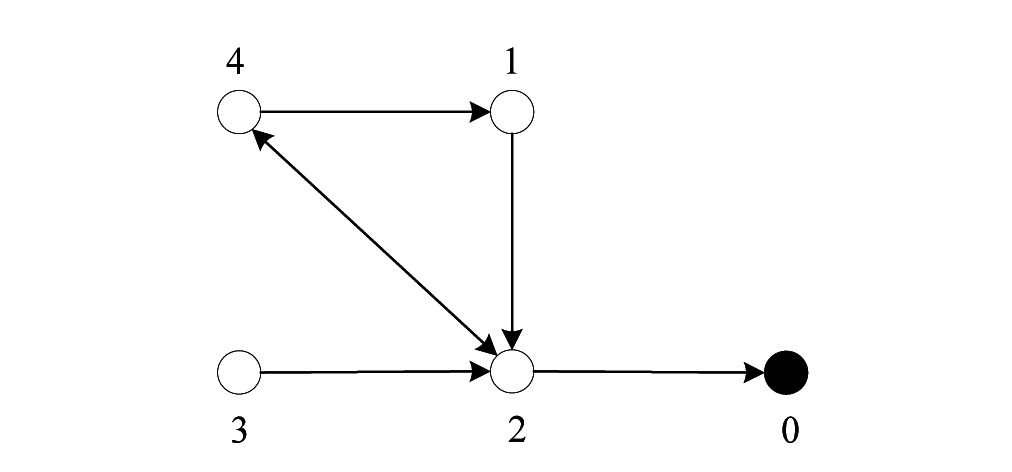
Figure 5.
Topology 2: Network of four agents and a leader.
3.2. Delay-Dependent Consensus Criterion
Theorem 2. Assume that the agents in system (6) without communication delay converges to the leader’s states asymptotically. Let
where.Then, all the agents in system (6) converge to the leader’s states asymptotically, if
i.e.,
holds for ω ∈ R.
Proof. Under the assumption that the agents without communication delay converge to the leader’s states asymptotically, the roots of following equation
all lie on the open left half complex plane, so we obtain rank(L + B) = n.
Rewrite the Equation (8) as follows
Let
When s = 0,
, i.e., p(s) has no zeros at s = 0.
The feedback diagram corresponding to the Equation (16) is illustrated in Figure 6. Using the linear fractional transformation, the diagram in Figure 6 can be equivalently transformed into the form shown in Figure 7, where M2(s) is defined in Equation (12). The characteristic equation of the closed-loop system in Figure 7 is
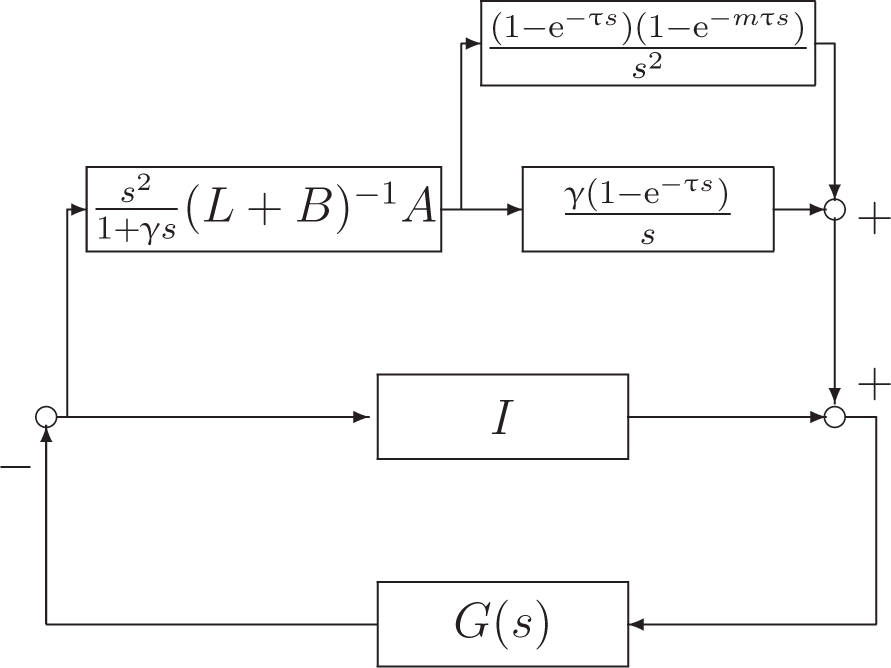
Figure 6.
The diagram of the Equation (16).
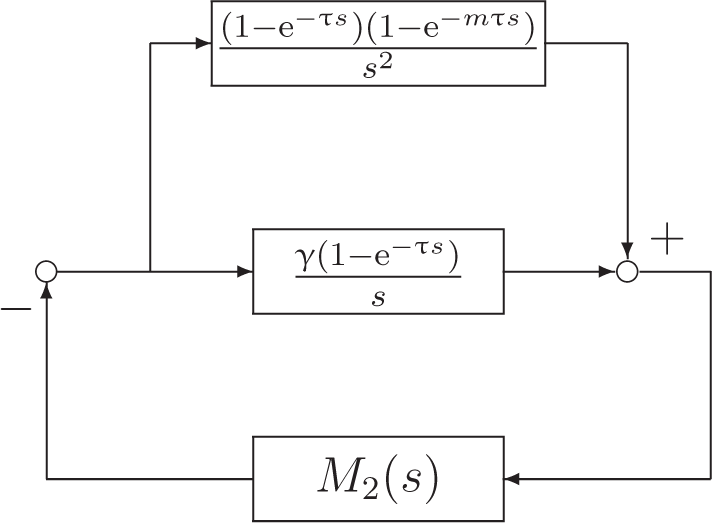
Figure 7.
Equivalent transformation of Figure 6.
Obviously,
,
and M2(s) both have no poles in the open right half complex plane from the assumption in Theorem 2.
By computing, we obtain
Based on small gain theorem, therefore,
is non-singular for Re(s) ≥ 0, i.e., the roots of the characteristic Equation (17) all lie on the open left half complex plane. Hence, the agents in system (6) converge to the leader’s states asymptotically.
Remark 5. For the interconnection topology that has the leader as a globally reachable node, the condition (14) in Theorem 2 always gives a criterion to calculate the delay bound for the multi-agent systems (6), but does not have special requirements on topology structure, coupling weights and control parameters.
Remark 6. Obviously, the positive integer m in the compensations has different impacts on the conditions (9) and (14) respectively. The condition (9) is independent of m, while the largest delay value in (14) decreases when m increases.
Remark 7. For n agents (6), delay-independent condition (9) can be applied firstly. If (9) does not hold, then, we use the delay-dependent condition (14) to obtain an upper bound of the delay value.
Example 2. Consider a multi-agent system composed of four agents and a leader given by (6). For simplicity, we choose the interconnection topology 2 in Figure 5. In addition, coupling weights are a12 = 1.5, a24 = 0.3, a32 = 1.4, a41 = 0.9, a42 = 0.6, b2 = 0.8, the control parameters are κ = 1.5, γ = 0.8, and m = 2. Example 1 has shown that delay-independent condition (9) in Theorem 1 does not hold for the agents under topology 2 with these coupling weights and control parameters. According to the condition (14) in Theorem 2, we get that the agents in system (6) can reach the leader’s states asymptotically if τ < 0.2461(s) (see, Figure 8). To our delight, the leader-following consensus algorithm (5) can tolerate distinct largest communication delay with different m, for example, τmax = 0.705(s) with m = 1, τmax = 0.71(s) with m = 2, τmax = 1.38(s) with m = 3, and τmax = 0.98(s) with m = 4. By choosing proper m, therefore, we can get an algorithm with best delay robustness. Moreover, the largest communication delay the synchronously-coupled consensus algorithm can bear in this case is τmax = 0.32(s), which is much less than our proposed algorithm (5).
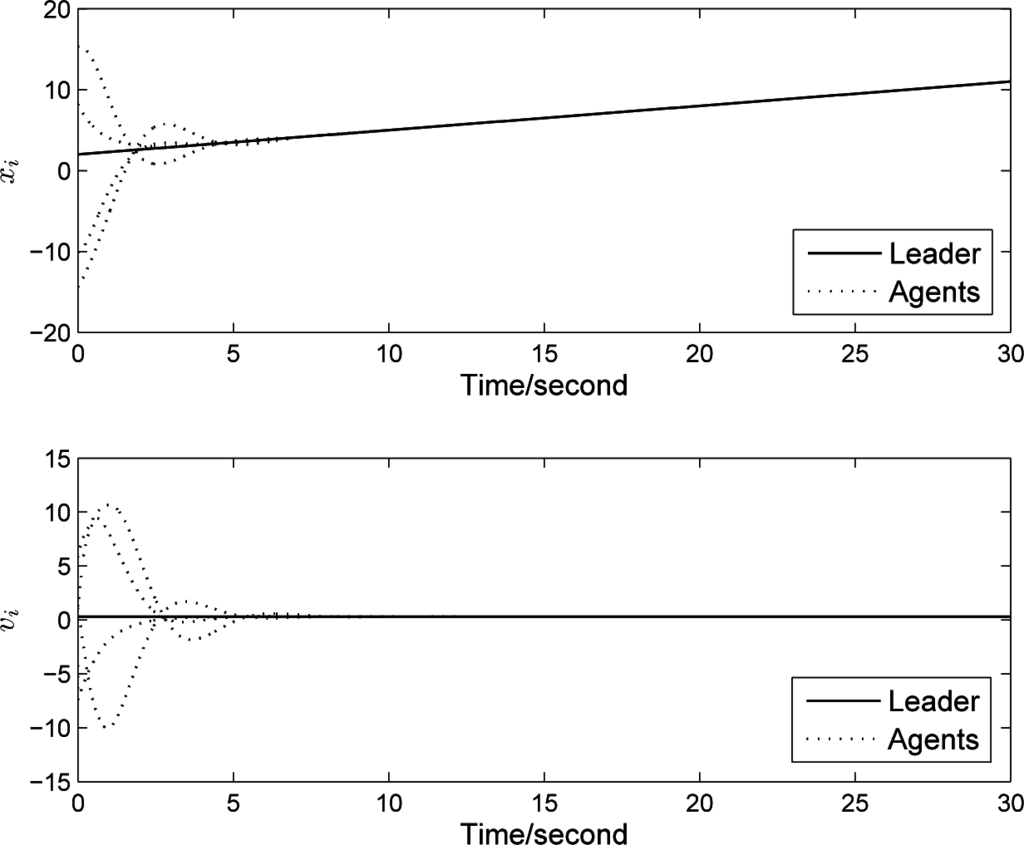
Figure 8.
Delay-independent consensus convergence.
4. Conclusions
In this paper, we propose a delayed-compensation leader-following consensus algorithm for second-order multi-agent systems to track a dynamical leader asymptotically under communication delay. Our proposed algorithm includes the position and velocity consensus coordination parts in asynchronously-coupled form, and the compensations related to the delayed neighboring agents’ states are just added into the position coordination part. Based on frequency-domain analysis, we obtain delay-independent and delay-dependent sufficient conditions, respectively, for the second-order agents converging to the dynamical leader’s states asymptotically. Although the delay-independent condition does not hold for the agents with arbitrary interconnection structure and coupling weights, it sufficiently proves that delayed-compensation algorithm in asynchronously-coupled form can tolerate much higher communication delay than synchronously-coupled algorithm. The delay-dependent sufficient condition provides a criterion to calculate an upper bound of communication delay, and it is very interesting that choosing proper delay value of the compensations can yield different delay robustness for our proposed algorithm. However, the results herein are just for the second-order multi-agent systems with static interconnection topology and identical communication input delay, and the consensus conditions are just sufficient and a little conservative. Hence, our future work will focus on proposing some proper analysis methods to obtain less conservative consensus conditions for the second-order multi-agent systems under switching topologies and distinct communication delays.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 61473138, 61104092, and 61134007), the 111 Project (B12018), and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Author Contributions
Both authors contributed to the initial motivation of the work, to the research and numerical experiments and to the writing. Both authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar]
- Lin, P.; Jia, Y.; Du, J.; Yuan, S. Distributed consensus control for second-order agents with fixed topology and time-delay. Proceedings of the 26th Chinese Control Conference, Zhangjiajie, China, 26–31 July 2007; pp. 577–581.
- Yu, W.; Chen, G.; Cao, M. Some necessary and sufficient conditions for second-order consensus in multi-agent dynamical systems. Automatica 2010, 46, 1089–1095. [Google Scholar]
- Munz, U.; Papachristodoulou, A; Allgower, F. Consensus in multi-Agent systems with coupling delays and switching topology. IEEE Trans. Autom. Control 2011, 56, 2976–2982. [Google Scholar]
- Lu, X.; Austin, F; Chen, S. Flocking in multi-agent systems with active virtual leader and time-varying delays coupling. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1014–1026. [Google Scholar]
- Hu, J.; Hong, Y. Leader-following coordination of multi-agent systems with coupling time delays. Physica A 2007, 374, 853–863. [Google Scholar]
- Su, H.; Wang, X. Second-order consensus of multiple agents with coupling delay. Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 7181–7186.
- Lin, P.; Jia, Y. Consensus of a Class of second-order multi-agent systems with time-delay and jointly-connected topologies. IEEE Trans. Autom. Control 2010, 55, 778–784. [Google Scholar]
- Sun, Y.G.; Wang, L.; Xie, G. Average consensus in networks of dynamic agents with switching topologies and multiple time-varying delays. Syst. Control Lett. 2008, 57, 175–183. [Google Scholar]
- Qin, J.; Gao, H. A sufficient condition for convergence of sampled-data consensus for double-integrator dynamics with nonuniform and time-varying communication delays. IEEE Trans. Autom. Control. 2012, 57, 2417–2422. [Google Scholar]
- Yu, J.; Wang, L. Group consensus in multi-agent systems with switching topologies and communication delays. Syst. Control Lett. 2010, 59, 340–348. [Google Scholar]
- Sun, Y.G.; Wang, L. Consensus of multi-agent systems in directed networks with nonuniform time-varying delays. IEEE Trans. Autom. Control 2009, 54, 1607–1613. [Google Scholar]
- Zhang, Y.; Tian, Y.P. Allowable delay bound for consensus of linear multi-agent systems with communication delay. Int. J. Syst. Sci. 2014, 45, 2172–2181. [Google Scholar]
- Wang, J.; Elia, N. Consensus over network with dynamic channels. In Proceedomgs of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 2637–2642.
- Lee, D.J.; Spong, M.K. Agreement with non-uniform information delays. Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 756–761.
- Moreau, L. Stability of continuous-time distributed consensus algorithms. Proceedings of the 43rd IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004; pp. 3998–4003.
- Wang, W.; Slotine, J.J.E. Contraction analysis of time-delayed communication delays. IEEE Trans. Autom. Control. 2006, 51, 712–717. [Google Scholar]
- Cao, M.; Morse, A.S.; Anderson, B.D.O. Reaching an agreement using delayed information. Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 3375–3380.
- Wang, L.; Xiao, F. A new approach to consensus problems for discrete-time multiagent systems with time-delays. Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 2118–2123.
- Liu, X.; Lu, W.; Chen, T. Consensus of multi-agent systems with unbounded time-varying delays. IEEE Trans. Autom. Control. 2010, 55, 2396–2401. [Google Scholar]
- Lin, P.; Jia, Y. Consensus of second-order discrete-time multi-agent systems with nonuniform time-delays and dynamically changing topologies. Automatica 2009, 45, 2154–2158. [Google Scholar]
- Liu, C.L.; Liu, F. Stationary consensus of heterogeneous multi-agent systems with bounded communication delays. Automatica 2011, 47, 2130–2133. [Google Scholar]
- Yang, W.; Bertozzi, A.L.; Wang, X.F. Stability of a second order consensus algorithm with time delay. Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2926–2931.
- Liu, C.L.; Liu, F. Consensus analysis for multiple autonomous agents with input delay and communication delay. Int. J. Control Autom. Syst. 2012, 10, 1005–1012. [Google Scholar]
- Liu, C.L.; Tian, Y.P. Formation control of multi-agent systems with heterogeneous communication delays. Int. J. Syst. Sci. 2009, 40, 627–636. [Google Scholar]
- Zhu, W.; Cheng, D. Leader-following consensus of second-order agents with multiple time-varying delays. Automatica 2010, 46, 1994–1999. [Google Scholar]
- Zhu, W. Consensus of multiagent systems with switching jointly reachable interconnection and time delays. IEEE Trans. Syst. Cybern. A 2012, 42, 348–358. [Google Scholar]
- Liu, C.L.; Liu, F. Dynamical consensus seeking of second-order multi-agent systems based on delayed state compensation. Syst. Control Lett. 2012, 61, 1235–1241. [Google Scholar]
- Hong, Y.; Hu, J.; Gao, L. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 2006, 42, 1177–1182. [Google Scholar]
- Tang, Y.; Gao, H.; Zhang, W.; Kurths, J. Leader-following consensus of a class of stochastic delayed multi-agent systems with partial mixed impulses. Automatica 2015, 53, 346–354. [Google Scholar]
- Tang, Y.; Qian, F.; Gao, H.; Kurthsa, J. Synchronization in complex networks and its application—a survey of recent advances and challenges. Ann. Rev. Control. 2014, 38, 184–198. [Google Scholar]
- Lu, X.; Lu, R.; Chen, S.; Lu, J. Finite-time distributed tracking control for multi-agent systems with a virtual leader. IEEE Trans. Circuits Syst. I 2013, 60, 352–362. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).