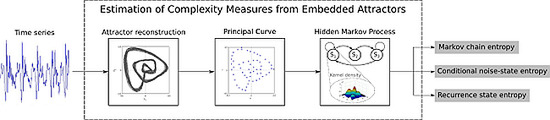
Entropies from Markov Models as Complexity Measures of Embedded Attractors
Abstract
:1. Introduction
2. Attractor Reconstruction
3. Entropy Measures
4. HMM-Based Entropy Measures
- π = {πi}, i = 1, 2, …, m is the stationary distribution, where m is the number of states in the MC and πi = P(Xt = i) as t → ∞ being the probability of ending at the i-th state independent of the initial state.
- K = {Kij}, 1 ≤ i, j ≤ m is the transition kernel of the MC, where Kij = P(Xt+1 = j|Xt = i) is the probability of reaching the j-th state at time t + 1, coming from the i-th state at time t.
4.1. Estimation of the HMM-Based Entropies
- B = {Bij}, i = 1, 2, …, m, j = 1, 2, …, b is the probability distribution of the observation symbols, being Bij = P(Zt = υj|Xt = i), where Zt is the output at time t, υj are different symbols that can be associated with the output and b is the total number of symbols.
5. Experiments and Results
5.1. Results
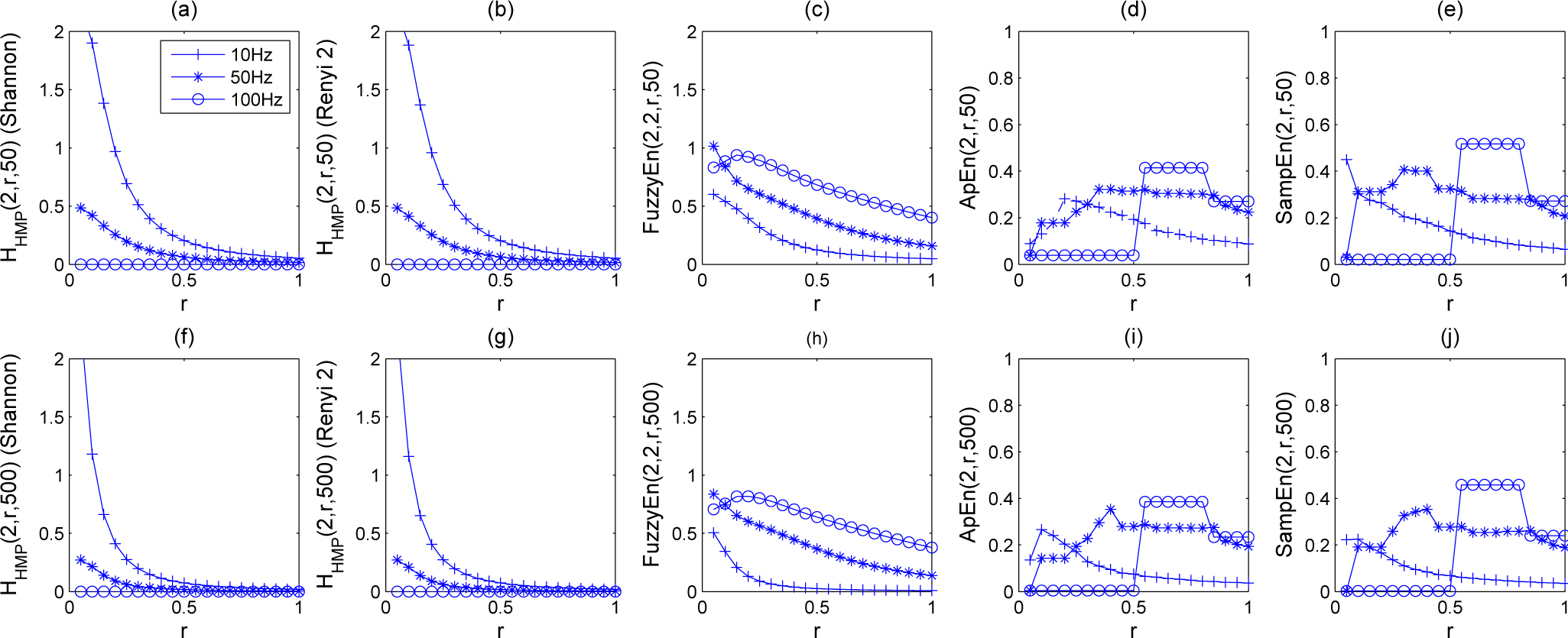
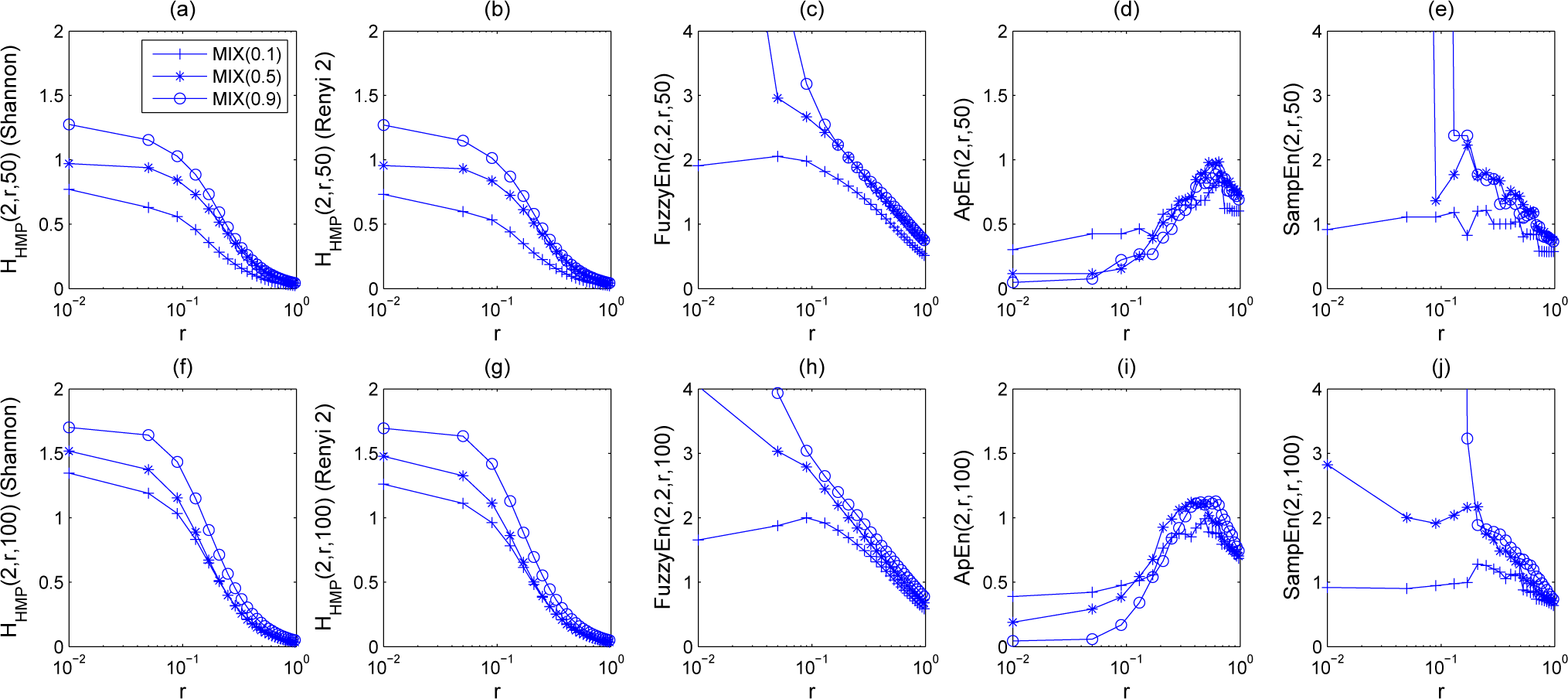
5.1.1. Synthetic Sequences
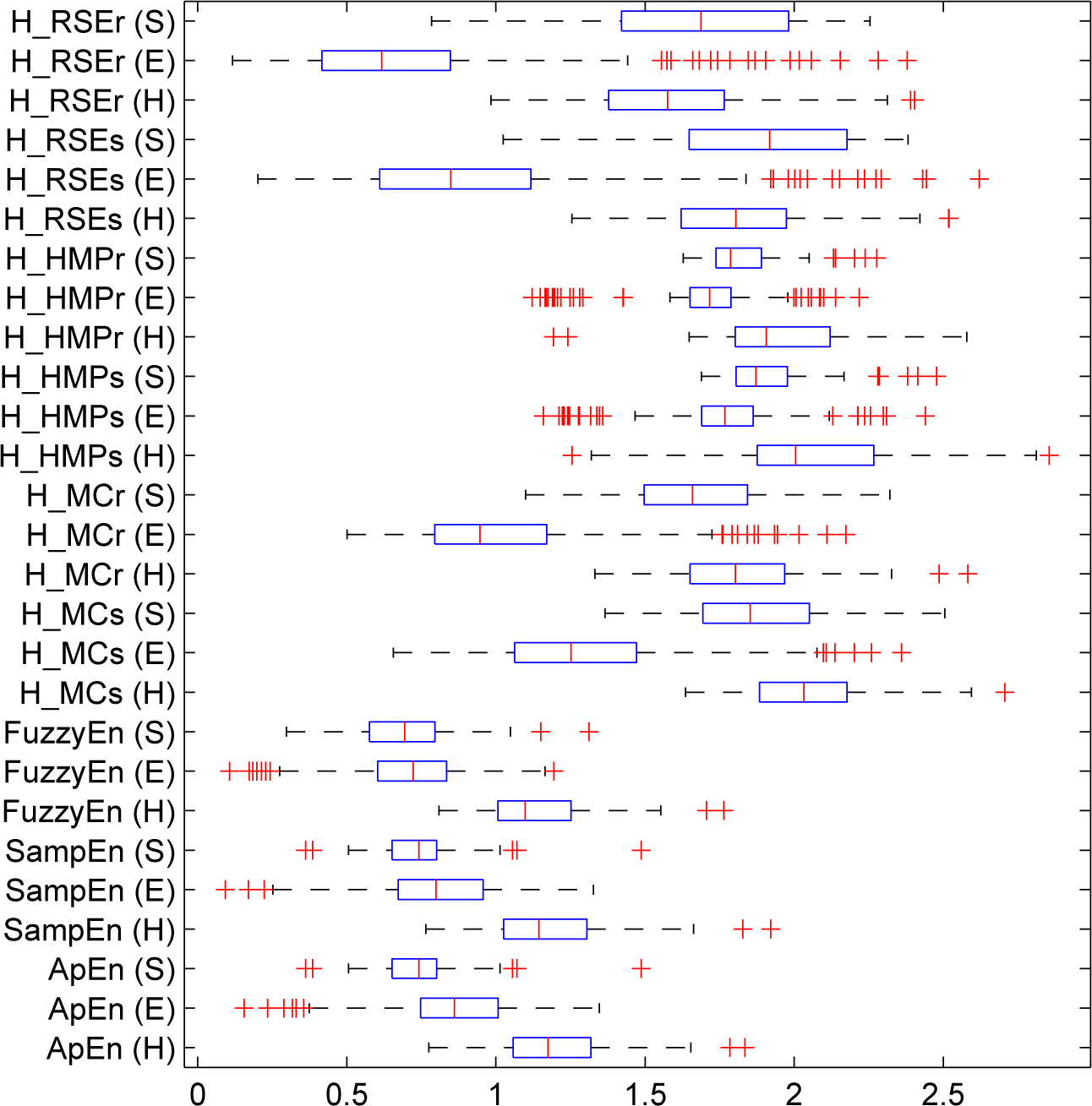
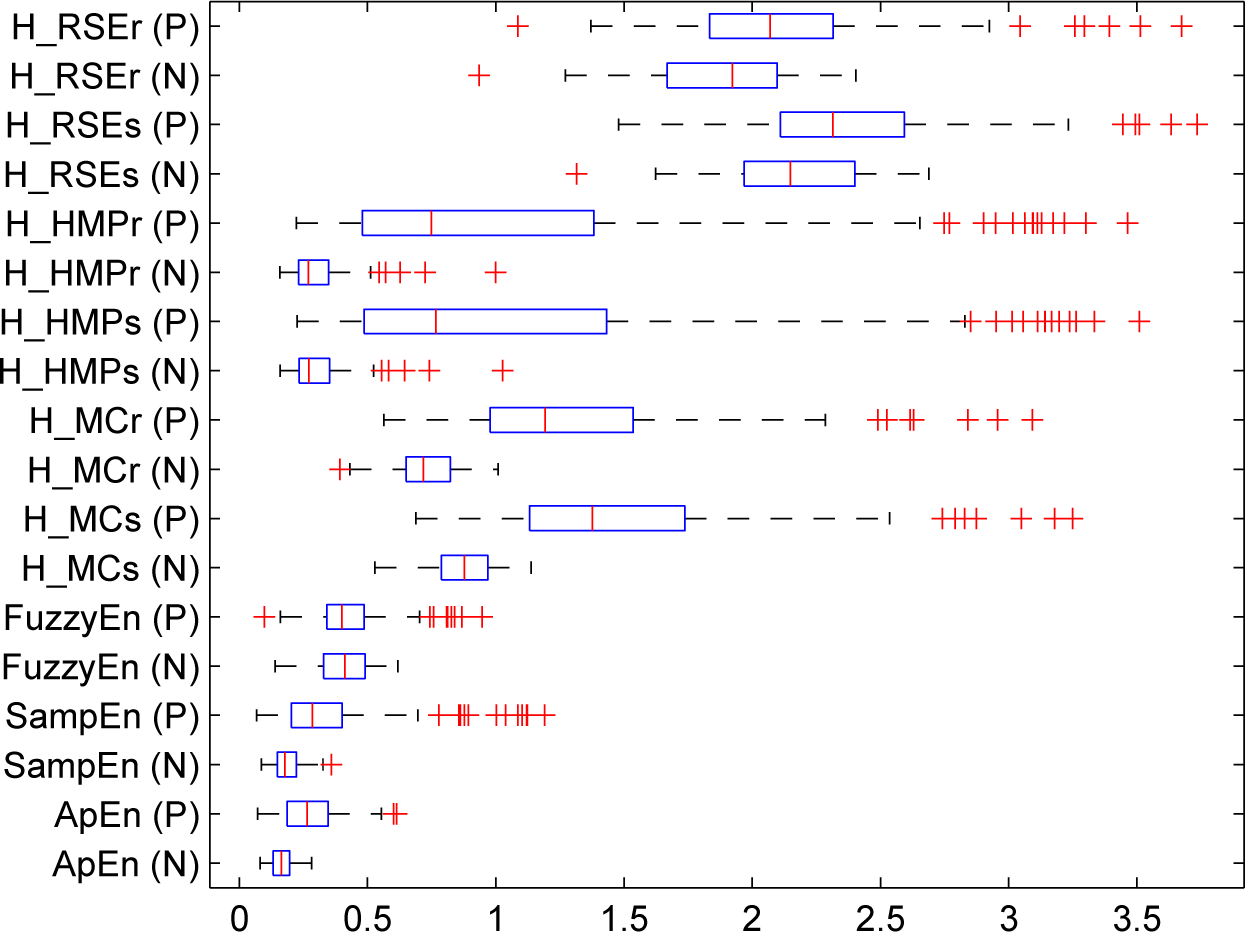
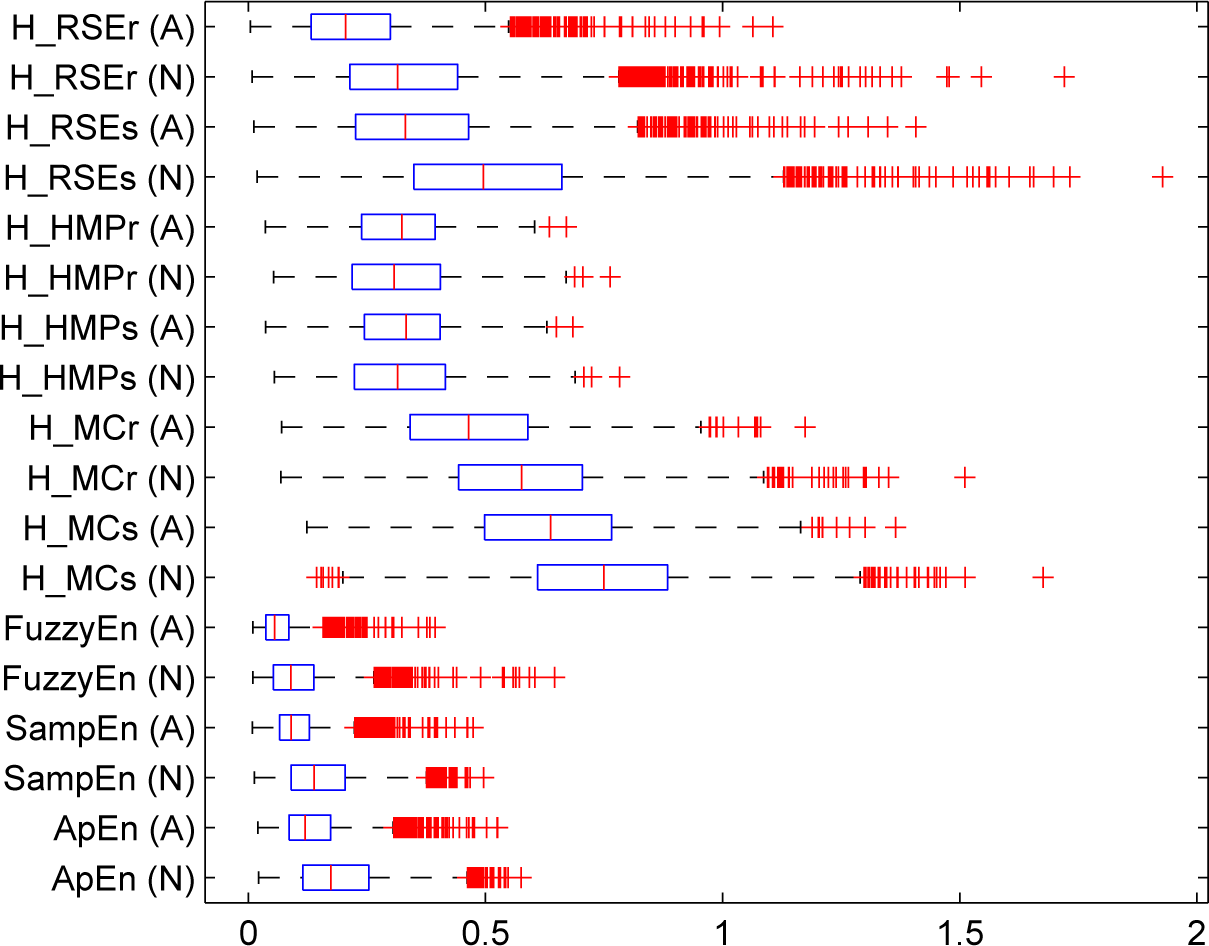
5.1.2. Real-Life Physiological Signals
6. Discussion and Conclusions
Acknowledgments
Appendix
Author Contributions
Conflicts of Interest
References
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis, 2nd ed; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Gao, J.; Hu, J.; Tung, W.W. Entropy measures for biological signal analyses. Nonlinear Dyn. 2012, 68, 431–444. [Google Scholar]
- Yan, R.; Gao, R. Approximate entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process 2007, 21, 824–839. [Google Scholar]
- Balasis, G.; Donner, R.V.; Potirakis, S.M.; Runge, J.; Papadimitriou, C.; Daglis, I.A.; Eftaxias, K.; Kurths, J. Statistical Mechanics and Information-Theoretic Perspectives on Complexity in the Earth System. Entropy 2013, 15, 4844–4888. [Google Scholar] [Green Version]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. 1991, 88, 2297–2301. [Google Scholar]
- Abarbanel, H.D. Analysis of Observed Chaotic Data; Springer: New York, NY, USA, 1996. [Google Scholar]
- Milnor, J. On the concept of attractor. Commum. Math. Phys. 1985, 99, 177–195. [Google Scholar]
- Giovanni, A.; Ouaknine, M.; Triglia, J.M. Determination of Largest Lyapunov Exponents of Vocal Signal: Application to Unilateral Laryngeal Paralysis. J. Voice. 1999, 13, 341–354. [Google Scholar]
- Serletis, A.; Shahmordi, A.; Serletis, D. Effect of noise on estimation of Lyapunov exponents from a time series. Chaos Solutions Fractals 2007, 32, 883–887. [Google Scholar]
- Arias-Londoño, J.; Godino-Llorente, J.; Sáenz-Lechón, N.; Osma-Ruiz, V.; Castellanos-Domínguez, G. Automatic detection of pathological voices using complexity measurements, noise parameters and cepstral coefficients. IEEE Trans. Biomed. Eng. 2011, 58, 370–379. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ Physiol. 2000, 278, H2039–H2049. [Google Scholar]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar]
- Xu, L.S.; Wang, K.Q.; Wang, L. Gaussian kernel approximate entropy algorithm for analyzing irregularity of time series, Proceedings of the Fourth International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; pp. 5605–5608.
- Cappé, O. Inference in Hidden Markon Models; Springer: New York, NY, USA, 2007. [Google Scholar]
- Ozertem, U.; Erdogmus, D. Locally Defined Principal Curves and Surfaces. J. Mach. Learn. Res. 2011, 12, 241–274. [Google Scholar]
- Hastie, T.; Stuetzle, W. Principal curves. J. Am. Stat. Assoc. 1989, 84, 502–516. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of information theory, 2nd ed; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Nonlinear Optimization; Volume 898, Lecture Notes in Mathematics; Springer: Berlin, Germany, 1981; pp. 366–381. [Google Scholar]
- Alligood, K.T.; Sauer, T.D.; Yorke, J.A. CHAOS: An Introduction to Dynamical Systems; Springer: New York, NY, USA, 1996. [Google Scholar]
- Costa, M.; Goldberger, A.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E. 2005, 71, 021906. [Google Scholar]
- Rezek, I.A.; Roberts, S.J. Stochastic complexity measures for physiological signal analysis. IEEE Trans. Biomed. Eng. 1998, 45, 1186–1191. [Google Scholar]
- Woodcock, D.; Nabney, I.T. A new measure based on the Renyi entropy rate using Gaussian kernels; Technical Report; Aston University: Birmingham, UK, 2006. [Google Scholar]
- Murphy, K.P. Machine learning a probabilistic perspective; MIT Press: Cambridge, MA, USA, 2012; Chapter 17. [Google Scholar]
- Fraser, A.M. Hidden Markov Models and Dynamical Systems; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Ephraim, Y.; Merhav, N. Hidden Markov Processes. IEEE Trans. Inf. Theory 2002, 48, 1518–1569. [Google Scholar]
- Ragwitz, M.; Kantz, H. Markov models from data by simple nonlinear time series predictors in delay embedding spaces. Phys. Rev. E. 2002, 65, 1–12. [Google Scholar]
- Sheng, Y. The theory of trackability and robustness for process detection. Ph.D. Thesis; Dartmouth College: Hanover, New Hampshire, NH, USA, 2008. Available online: http://www.ists.dartmouth.edu/library/206.pdf accessed on 2 June 2015.
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications on speech recognition. Proc. IEEE. 1989, 77, 257–286. [Google Scholar]
- Massachusetts Eye and Ear Infirmary, Voice Disorders Database, Version.1.03 [CD-ROM]; Kay Elemetrics Corp; Lincoln Park, NJ, USA, 1994.
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Ghassabeh, Y.; Linder, T.; Takahara, G. On some convergence properties of the subspace constrained mean shift. Pattern Recognit. 2013, 46, 3140–3147. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean Shift: A Robust Approach Toward Feature Space Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar]
- Erdogmus, D.; Hild, K.E.; Principe, J.C.; Lazaro, M.; Santamaria, I. Adaptive Blind Deconvolution of Linear Channels Using Renyi’s Entropy with Parzen Window Estimation. IEEE Trans. Signal Process 2004, 52, 1489–1498. [Google Scholar]
- Rényi, A. On measure of entropy and information, Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Statistical Laboratory of the University of California, Berkeley, CA, USA, 20 June–30 July 1960; pp. 547–561. Available online: http://projecteuclid.org/euclid.bsmsp/1200512181 accessed on 2 June 2015.
- Andrzejak, R.; Lehnertz, K.; Rieke, C.; Mormann, F.; David, P.; Elger, C. Indications of nonlinear deterministic and finite dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E. 2001, 061907. [Google Scholar]
- Parsa, V.; Jamieson, D. Identification of pathological voices using glottal noise measures. J. Speech Lang. Hear. Res. 2000, 43, 469–485. [Google Scholar]
- Goldberger, A.; Amaral, L.; Glass, L.; Hausdorff, J.; Ivanov, P.; Mark, R.; Mietus, J.; Moody, G.; Peng, C.K.; Stanley, H. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar]
- Penzel, T.; Moody, G.; Mark, R.; Goldberger, A.; Peter, J.H. The Apnea-ECG Database, Proceedings of Computers in Cardiology, Cambridge, MA, USA, 24–27 September 2000; pp. 255–258.
- Viertiö-Oja, H.; Maja, V.; Särkelä, M.; Talja, P.; Tenkanen, N.; Tolvanen-Laakso, H.; Paloheimo, M.; Vakkuri, A.; YLi-Hankala, A.; Meriläinen, P. Description of the entropy™ algorithm as applied in the Datex-Ohmeda S/5™ entropy module. Acta Anaesthesiol. Scand. 2004, 48, 154–161. [Google Scholar]
- Kaffashi, F.; Foglyano, R.; Wilson, C.G.; Loparo, K.A. The effect of time delay on Approximate & Sample Entropy calculation. Physica D. 2008, 237, 3069–3074. [Google Scholar]
- Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Physica D. 1997, 110, 43–50. [Google Scholar]
- Morabito, F.C.; Labate, D.; La-Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate Multi-Scale Permutation Entropy for Complexity Analysis of Alzheimer’s Disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar]
- Aboy, M.; Hornero, R.; Abásolo, D.; Álvarez, D. Interpretation of the Lempel-Ziv Complexity Measure in the Context of Biomedical Signal Analysis. IEEE Trans. Biomed. Eng. 2006, 53, 2282–2288. [Google Scholar]


| fi | N | HMC | HHMP | HRSE | ApEn | SampEn | FuzzyEn | |||
|---|---|---|---|---|---|---|---|---|---|---|
| S* | R** | S | R | S | R | |||||
| 10 | 50 | 1.21 | 1.07 | 1.38 | 1.37 | 0.75 | 0.67 | 0.18 | 0.28 | 0.48 |
| 500 | 1.01 | 0.76 | 0.66 | 0.65 | 0.96 | 0.70 | 0.24 | 0.19 | 0.21 | |
| 50 | 50 | 0.30 | 0.28 | 0.33 | 0.33 | 0.26 | 0.23 | 0.18 | 0.31 | 0.72 |
| 500 | 0.12 | 0.10 | 0.14 | 0.14 | 0.11 | 0.09 | 0.14 | 0.19 | 0.65 | |
| 100 | 50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.04 | 0.02 | 0.94 |
| 500 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.82 | |
| ρ | N | HMC | HHMP | HRSE | |||
|---|---|---|---|---|---|---|---|
| S | R | S | R | S | R | ||
| 0.3 | 50 | 0.64 | 0.59 | 0.63 | 0.61 | 0.56 | 0.56 |
| 0.3 | 100 | 0.96 | 0.88 | 0.59 | 0.56 | 0.94 | 0.89 |
| 0.5 | 50 | 0.93 | 0.91 | 0.64 | 0.62 | 0.57 | 0.57 |
| 0.5 | 100 | 1.31 | 1.26 | 0.80 | 0.78 | 1.09 | 1.08 |
| 0.7 | 50 | 0.83 | 0.80 | 0.83 | 0.82 | 0.90 | 0.62 |
| 0.7 | 100 | 1.22 | 1.18 | 0.81 | 0.79 | 1.16 | 1.14 |
| R | NL | HMC | HHMP | HRSE | ApEn | SampEn | FuzzyEn | |||
|---|---|---|---|---|---|---|---|---|---|---|
| S | R | S | R | S | R | |||||
| 3.5 | 0.0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.28 |
| 0.1 | 0.85 | 0.74 | 0.23 | 0.22 | 1.90 | 1.67 | 0.08 | 0.07 | 0.48 | |
| 0.2 | 1.40 | 1.17 | 0.85 | 0.83 | 2.56 | 2.07 | 0.61 | 0.56 | 0.82 | |
| 0.3 | 1.44 | 1.28 | 1.33 | 1.31 | 2.23 | 2.37 | 0.90 | 0.88 | 1.03 | |
| 3.7 | 0.0 | 0.84 | 0.74 | 0.43 | 0.42 | 3.41 | 2.68 | 0.38 | 0.38 | 0.77 |
| 0.1 | 1.10 | 0.95 | 0.67 | 0.66 | 3.38 | 2.73 | 0.49 | 0.49 | 0.89 | |
| 0.2 | 1.58 | 1.43 | 1.54 | 1.51 | 2.83 | 2.98 | 0.86 | 0.81 | 1.10 | |
| 0.3 | 1.77 | 1.63 | 2.65 | 2.02 | 2.74 | 3.11 | 1.10 | 1.13 | 1.29 | |
| 3.8 | 0.0 | 1.10 | 0.98 | 0.40 | 0.39 | 3.63 | 3.28 | 0.47 | 0.47 | 0.99 |
| 0.1 | 1.22 | 1.03 | 0.72 | 0.70 | 3.75 | 3.52 | 0.58 | 0.59 | 1.14 | |
| 0.2 | 1.78 | 1.65 | 1.53 | 1.49 | 3.37 | 3.25 | 0.92 | 0.90 | 1.31 | |
| 0.3 | 1.83 | 1.68 | 2.14 | 2.10 | 2.42 | 2.36 | 1.19 | 1.24 | 1.55 | |
| Measures | Datasets
| |||||||
|---|---|---|---|---|---|---|---|---|
| EEG
| Voice
| ECG
| HRV
| |||||
| FI | ANOVA | FI | ANOVA | FI | ANOVA | FI | ANOVA | |
| ApEn | 0.48 | p < 0.001 | 0.69 | p < 0.001 | 0.64 | p < 0.001 | 0.69 | p < 0.001 |
| SampEn | 0.48 | p < 0.001 | 0.34 | p < 0.001 | 0.08 | v < 0.001 | 0.83 | p < 0.001 |
| FuzzyEn | 0.80 | p < 0.001 | 0.09 | p < 0.001 | 0.03 | p < 0.001 | 0.72 | p < 0.001 |
| HMCr | 1.00 | p < 0.001 | 1.00 | p < 0.001 | 0.37 | p < 0.001 | 0.58 | p < 0.001 |
| HHMPr | 0.24 | p < 0.001 | 0.57 | p < 0.001 | 0.16 | p < 0.001 | 0.01 | p > 0.05 |
| HRSEr | 0.83 | p < 0.001 | 0.20 | p < 0.001 | 1.00 | p < 0.001 | 1.00 | p < 0.001 |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arias-Londoño, J.D.; Godino-Llorente, J.I. Entropies from Markov Models as Complexity Measures of Embedded Attractors. Entropy 2015, 17, 3595-3620. https://doi.org/10.3390/e17063595
Arias-Londoño JD, Godino-Llorente JI. Entropies from Markov Models as Complexity Measures of Embedded Attractors. Entropy. 2015; 17(6):3595-3620. https://doi.org/10.3390/e17063595
Chicago/Turabian StyleArias-Londoño, Julián D., and Juan I. Godino-Llorente. 2015. "Entropies from Markov Models as Complexity Measures of Embedded Attractors" Entropy 17, no. 6: 3595-3620. https://doi.org/10.3390/e17063595
APA StyleArias-Londoño, J. D., & Godino-Llorente, J. I. (2015). Entropies from Markov Models as Complexity Measures of Embedded Attractors. Entropy, 17(6), 3595-3620. https://doi.org/10.3390/e17063595