Probabilistic Teleportation via Quantum Channel with Partial Information

Abstract

Two novel schemes are proposed to teleport an unknown two-level quantum state probabilistically when the sender and the receiver only have partial information about the quantum channel, respectively. This is distinct from the fact that either the sender or the receiver has entire information about the quantum channel in previous schemes for probabilistic teleportation. Theoretical analysis proves that these schemes are straightforward, efficient and cost-saving. The concrete realization procedures of our schemes are presented in detail, and the result shows that our proposals could extend the application range of probabilistic teleportation.

1. Introduction

Quantum teleportation, first proposed by Bennett et al. [1], is the process that transmits an unknown quantum state from a sender to a remote receiver via local operation and classical communication. Quantum teleportation is the basic theory and a crucial task of quantum computation and quantum information [2], and a growing number of theoretical and experimental works [3–10] have appeared in the teleportation in the past years. The quantum entangled state can be viewed as a resource in quantum information science, because it can be used in many information processing schemes. The implementation of teleportation mainly relies on the entanglement state preparation [11], entanglement purification, entanglement concentration [12,13] and its protocols [14,15]. In recent years, teleportation plays an irreplaceable role in many applications including quantum key distribution [16–18], quantum dense coding [7,19–21], quantum secret sharing [22–24], quantum state sharing [25–27], quantum secure direction communication [28–30], quantum repeater [31–34], et al. The mechanism and capability of teleportation will bring fatal influence into these applications. When the teleportation is not up to certain grade, quantum dense coding failed, and the quantum cryptography protocol insecure.

Owing to the development of correlative theory and applications above, a growing number of works have appeared in the teleportation recently. For instance, Lo [5] introduced a concept “remote preparation” and presents a method of teleportation in lower cost. Li et al. [6] proposed a scheme of probabilistic teleportation to transmit an unknown single-qubit when the receiver extracts the quantum information by adopting a general evolution. Teleportation also can be obtained via super-radiance without Hadamard and CNOT transformations by Chen et al. [35]. There are also many proposals using multi-particle entangled states [36,37]. Teleportation in a noisy environment is considered in [38–40]. Wei et al. [8] presented a scheme to teleport an two-level quantum state probabilistically in the situation that quantum channel is only available for the sender. There are many outstanding results have been gotten, whereas we will account for quantum teleportation in another way. In most schemes about probabilistic teleportation about a quantum states using a partially entangled state as quantum channel, either the receiver Bob or the sender Alice needs to fully know the information about the quantum channel to make a corresponding unitary transformation to reconstruct the original quantum state. Evidently, the previous schemes are not valid on the condition that the sender Alice and the receiver Bob only have partial knowledge of the non-maximally entangled state, respectively. To overcome this drawback, two novel protocols are proposed to perform probabilistic teleportation, meantime, the realization procedures of our schemes are presented in detail.

The remainders of this paper are organized as follows: Two different conditions of quantum channel with partial information quantum channel are stated in Section 2. We put forwards to two novel proposals for probabilistic teleportation in Section 3. The first scheme is presented in Section 3.1, and this proposal could be valid when the amplitude factor of quantum channel is only available for the sender, while the receiver only has the phase factor. In Section 3.2, one can make use of the second novel scheme to probabilistically transmit an unknown quantum state under the case that the phase factor of quantum channel is only known for the sender, and the amplitude factor is available for the receiver. In Section 4, the result and advantages of schemes are discussed.

2. Different Conditions of Quantum Channel with Partial Information

Teleportation is a crucial way of transfer information separated spatially by qubit which is an unknown state and could be expressed as Equation (1). Superpositions of |0₁〉 and |1₁〉 are called qubits to signify the new possibilities introduced by quantum physics into information science [41].

$$|{\psi }_1\rangle =\alpha |0_1\rangle +\beta |1_1\rangle$$

(1)

where α is real and β is a complex number, and |α|² + |β|² = 1. The subscript number indicates the owner of given qubit in the context.

To place it in a more general way, the implementation of teleportation recurs to the quantum channel that is composed of a partially entangled two-particle state below.

$$|{\psi }_{23}\rangle =a|0_2{0}_3\rangle +b|1_2{1}_3\rangle =a|0_2{0}_3\rangle +|b|e^{i\varphi }|1_2{1}_3\rangle$$

(2)

where 0 < ϕ ≤ 2π, the real coefficient a and the complex one b satisfy a² + |b|² = 1, and a ≥ |b| > 0. Particle 2 belongs to the sender Alice, while particle 3 belongs to the receiver Bob.

It is worth pointing out that ϕ is known as the (relative) phase of quantum channel shown as Equation (2), and a can be considered as the amplitude factor. Conveniently, |b| will be replaced with $\sqrt{1-a^2}$. According to the kind of quantum channel’s factor information possessed by the sender Alice and the receiver Bob, two cases need to be taken into consideration. Firstly, the sender Alice or the receiver Bob has full information about the quantum channel. Secondly, the sender Alice or the receiver Bob has partial information about the quantum channel. For the first condition, some proposals of probabilistic teleportation have been presented, and the concrete realization procedures of the relative schemes can be obtained in [6,8]. However, the previous proposals are not valid under the second condition. In order to enlarge the application range of probabilistic teleportation, two novel protocols for the second condition would be presented in Section 3.

3. The Teleportation for Partial Information Quantum Channel

Many schemes how to get the amplitude factor or phase factor can be obtained in [42–45]. It should be underlined that one can not make use of the former schemes [6,8] to realize probabilistic teleportation under the case that the sender Alice and the receiver Bob only have partial information about the quantum channel, respectively. In this section, two proposals would be presented for these cases.

3.1. Alice only Knows the Amplitude Factor a, and Bob only Knows the Phase Factor ϕ

In this subsection, a novel scheme to transmit an unknown quantum state is proposed when the amplitude factor a is only available for the sender Alice, and only the receiver Bob has the phase factor ϕ. Moreover, the detailed processes of our proposal are elaborated as follows:

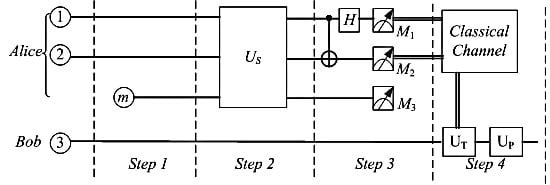
• Step 1: A particle m who plays an auxiliary function in teleportation with an initial state |0_m〉 is introduced by Alice, and then Alice’s state which is composed of particles 1, 2, m and 3 will take the form of the following Equation (3).

  $$\begin{array}{l}|{\psi }_{12m3}^0\rangle =|{\psi }_{12}\rangle \otimes |0_m\rangle \otimes |{\psi }_3\rangle \\ =\alpha a|0_1{0}_2{0}_m{0}_3\rangle +\alpha \sqrt{1-a^2}{e}^{i\varphi }|0_1{1}_2{0}_m{1}_3\rangle +\beta a|1_1{0}_2{0}_m{0}_3\rangle +\beta \sqrt{1-a^2}{e}^{i\varphi }|1_1{1}_2{0}_m{1}_3\rangle \end{array}$$

  (3)
• Step 2: Following on the heels of step 1, an operation named U_S will be performed on all particles including 1, 2 and m by Alice. If the quantum channel is maximal entangle state, the U_S could be bypassed. The U_S operation is an unitary transformation, could be expressed as Equation (4).

  $$U_s=\left(\begin{array}{cccc}A\left(a\right)& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\sigma }_z& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& A\left(a\right)& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& {\sigma }_z\end{array}\right)$$

  (4)

  where 0 is the 2 × 2 zero matrix, σ_z and A(a) could be expressed as

  $${\sigma }_z=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)A\left(a\right)\left(\begin{array}{cc}\sqrt{\frac{1-a^2}{a^2}}& \sqrt{\frac{2a^2-1}{a^2}}\\ \sqrt{\frac{2a^2-1}{a^2}}& -\sqrt{\frac{1-a^2}{a^2}}\end{array}\right)$$

  (5)

  Then the whole system will become

  $$\begin{array}{l}|{\psi }_{12m3}^1\rangle =\left(U_s|{\psi }_{12m}^0\rangle \right)\otimes |{\psi }_3^0\rangle \\ =\sqrt{\frac{1-a^2}{2}}|{\varphi }_{12}^{+}\rangle \otimes |0_m\rangle \otimes \left(\alpha |0_3\rangle +\beta e^{i\varphi }|1_3\rangle \right)+\sqrt{\frac{1-a^2}{2}}|{\varphi }_{12}^{-}\rangle \otimes |0_m\rangle \otimes \left(\alpha |0_3\rangle -\beta e^{i\varphi }|1_3\rangle \right)\\ +\sqrt{\frac{1-a^2}{2}}|{\mathrm{\Psi }}_{12}^{+}\rangle \otimes |0_m\rangle \otimes \left(\alpha |1_3\rangle +\beta e^{i\varphi }|0_3\rangle \right)+\sqrt{\frac{1-a^2}{2}}|{\mathrm{\Psi }}_{12}^{-}\rangle \otimes |0_m\rangle \otimes \left(\alpha |1_3\rangle -\beta e^{i\varphi }|0_3\rangle \right)\\ +\sqrt{2a^2-1}\left(\alpha |0_1{0}_2\rangle +\beta |1_1{0}_2\rangle \right)\otimes |1_m\rangle \otimes |0_3\rangle \end{array}$$

  (6)

  where the Bell-state measurements $|{\varphi }_{12}^{\pm }\rangle$and $|{\mathrm{\Psi }}_{12}^{\pm }\rangle$ are given by

  $$|{\varphi }_{12}^{\pm }\rangle =\frac{1}{\sqrt{2}}\left(|0_1{0}_2\rangle \pm |1_1{1}_2\rangle \right)$$

  (7)

  $$|{\mathrm{\Psi }}_{12}^{\pm }\rangle =\frac{1}{\sqrt{2}}\left(|0_1{1}_2\rangle \pm |1_1{0}_2\rangle \right)$$

  (8)
• Step 3: Subsequently, the auxiliary particle m is measured and particles 1 and 2 are performed in the form of the Bell-state measurements. Then, Alice transmits measurement results information to Bob in the manner of classical channel.
• Step 4: Bob will perform two continuous unitary operators U_P and U_T on particle 3 to obtain the original state according to the information including the information received from Alice via classical channel and the local phase factor.

  Table 1. The unitary transformation U_T based on Alice’s measurements results.

  Measurement results		State of Particles 3	Probabilities	UT
  Particle m	Particles 1, 2
  |0m〉	$|{\varphi }_{12}^{+}\rangle$	α∣03〉 + ∣βeiϕ∣13〉	$\frac{1-{\alpha }^2}{2}$	I
  	$|{\varphi }_{12}^{-}\rangle$	α∣03〉 − βeiϕ∣13〉	$\frac{1-{\alpha }^2}{2}$	σz
  	$|{\mathrm{\Psi }}_{12}^{+}\rangle$	α∣13〉 + βeiϕ∣03〉	$\frac{1-{\alpha }^2}{2}$	σx
  	$|{\mathrm{\Psi }}_{12}^{-}\rangle$	α∣13〉 − βeiϕ∣03〉	$\frac{1-{\alpha }^2}{2}$	iσy
  |1m〉	–	–	2a2−1	–

  shows the corresponding relations between the outcomes of measurement and the unitary transformation U_T for particle 3. The unitary operation U_P, relative to the phase factor ϕ of Equation (2), is described as Equation (9).

  $$U_P=\left(\begin{array}{cc}1& 0\\ 0& e^{-i\varphi }\end{array}\right)$$

  (9)

The whole probabilistic teleportaton processes are depicted in Figure 1. It should be emphasized that the unitary operations U_S performed by the sender Alice is only relative with the amplitude factor a, and U_P can be finished on the condition that the receiver Bob has the phase factor ϕ. Hence, as long as Alice has the amplitude factor a, and Bob has the phase factor ϕ, the probabilistic teleportation could be successfully obtained. On the other hand, the success probability of the teleportation has significant positive correlation with the fidelity of entangle channel, that is to say, the higher of fidelity, the teleportation will be obtained in higher probability. The success probability could be expressed as 2−2a². If quantum channel is a maximally entangled state, $|a|=\frac{1}{\sqrt{2}}$, the teleportation will be successful at all times. This result is in agreement with the success probability in [1].

3.2. Alice only Knows the Phase Factor ϕ, and Bob only Knows the Amplitude Factor a

To teleport an unknown quantum state probabilistically when the amplitude factor a of quantum channel is only available for the receiver Bob, and the sender Alice has the phase parameter ϕ, a new scheme would be presented in this subsection. The concrete realization procedures of the novel schemes are presented as follows:

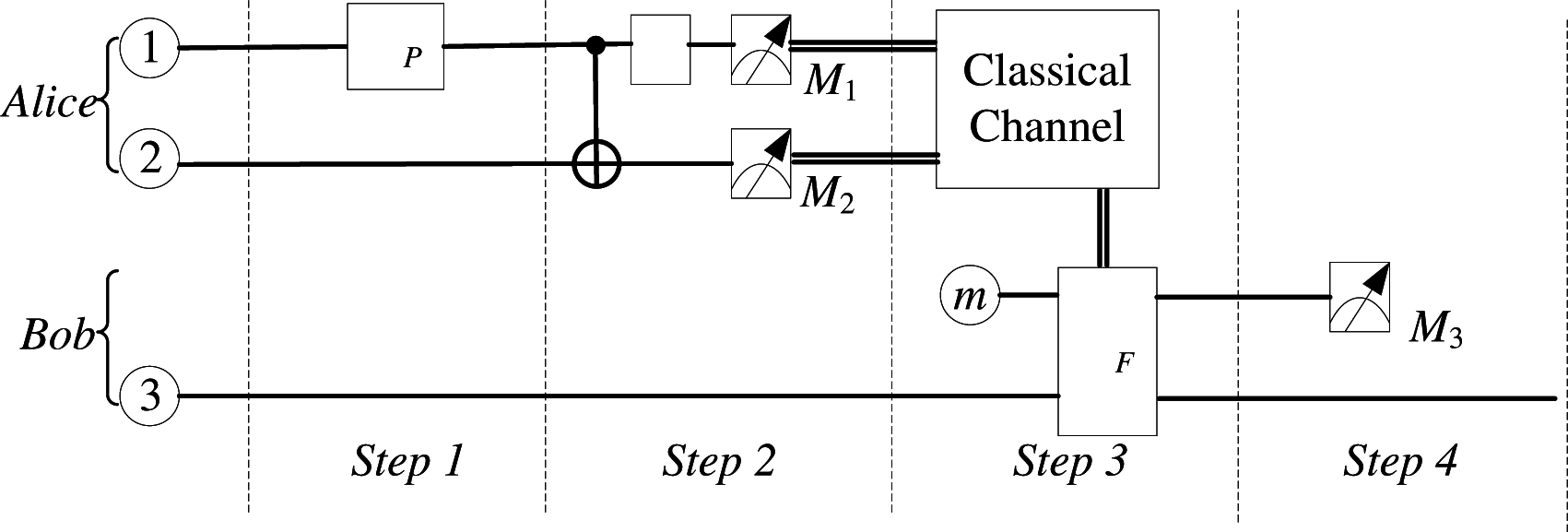
• Step 1: Alice performs the unitary operation U_P on particle 1 shown as Equation (9) using the phase information owned by herself, as a consequence, the total system can be expressed as

  $$\begin{array}{l}|{\psi }_{123}^1\rangle =|{\psi }_1\rangle \otimes (U_P|{\psi }_2\rangle )\otimes |{\psi }_3\rangle \\ =\frac{1}{\sqrt{2}}|{\varphi }_{12}^{+}\rangle \otimes (\alpha a|0_3\rangle +\beta \sqrt{1-a^2}|1_3\rangle )+\frac{1}{\sqrt{2}}|{\varphi }_{12}^{-}\rangle \otimes (\alpha a|0_3\rangle -\beta \sqrt{1-a^2}|1_3\rangle )\\ +\frac{1}{\sqrt{2}}|{\mathrm{\Psi }}_{12}^{+}\rangle \otimes (\alpha a|1_3\rangle +\beta \sqrt{1-a^2}|0_3\rangle )+\frac{1}{\sqrt{2}}|{\mathrm{\Psi }}_{12}^{-}\rangle \otimes (\alpha a|1_3\rangle -\beta \sqrt{1-a^2}|0_3\rangle )\end{array}$$

  (10)

  where $|{\varphi }_{12}^{\pm }\rangle$and $|{\mathrm{\Psi }}_{12}^{\pm }\rangle$ are given by Equations (7) and (8), respectively.
• Step 2: Alice performs the Bell-state measurements on particles 1 and 2. Subsequently, Alice informs Bob of her measurement results using classical channel.
• Step 3: Similar to the condition presented in previous subsection, an auxiliary particle which could be marked as m is introduced necessarily. Then, an unitary transformation U_F which can be written as Equation (11) will be performed on particles 3 and m depending on the remote and local information. The unitary transformations $U_F^i\left(i=0,1,2,3\right)$in

  Table 2. The Bell-state measurement results(BMRs) and the unitary transformation U_F.

  BMRs on particles 1, 2	UF	Results after the transformation UF
  		Particle m	Particle 3	Probabilities
  $|{\varphi }_{12}^{+}\rangle$	$U_F^0$	∣0m〉	α∣03〉 + β∣13〉	$\frac{1-{\alpha }^2}{2}$
  		∣1m〉	∣03〉	$\frac{|\alpha {|}^2}{2}(2{\alpha }^2-1)$
  $|{\varphi }_{12}^{-}\rangle$	$U_F^1$	∣0m〉	α∣03〉 + β∣13〉	$\frac{1-{\alpha }^2}{2}$
  		∣1m〉	∣13〉	$\frac{|\alpha {|}^2}{2}(2{\alpha }^2-1)$
  $|{\mathrm{\Psi }}_{12}^{+}\rangle$	$U_F^2$	∣0m〉	α∣03〉 + β∣13〉	$\frac{1-{\alpha }^2}{2}$
  		∣1m〉	∣13〉	$\frac{|\alpha {|}^2}{2}(2{\alpha }^2-1)$
  $|{\mathrm{\Psi }}_{12}^{-}\rangle$	$U_F^3$		α∣03〉 + β∣13〉	$\frac{1-{\alpha }^2}{2}$
  			∣13〉	$\frac{|\alpha {|}^2}{2}(2{\alpha }^2-1)$

  are the 2 × 2 matrix. Table 2 shows the corresponding relations between the measurement results on particles 1, 2 and the unitary transformation U_F on particles 3 and m, and then the origin state is appeared.

  $$\begin{array}{l}{U}_F^{\mathbf{0}}=\left(\begin{array}{cc}A\left(a\right)& \mathbf{0}\\ \mathbf{0}& {\sigma }_z\end{array}\right)U_F^1=\left(\begin{array}{cc}A\left(a\right)& \mathbf{0}\\ \mathbf{0}& -{\sigma }_z\end{array}\right)\\ U_F^2=\left(\begin{array}{cc}\mathbf{0}& {\sigma }_z\\ A\left(a\right)& \mathbf{0}\end{array}\right)U_F^3=\left(\begin{array}{cc}\mathbf{0}& -{\sigma }_z\\ A\left(a\right)& \mathbf{0}\end{array}\right)\end{array}$$

  (11)

  where σ_z and A(a) could be expressed as Equation (5).
• Step 4: Subsequently, To obtain the origin state of qubit, only one measurement result of particle m is in need. There are two cases for the result. In case of that the state of m is |1_m〉, quantum teleportation fails. In the other case that the state of m is |0_mi, the teleportation will be realized with the same probability of $\frac{1-a^2}{2}$ for four different kinds showed in Table 2, and then the sum of success probability is 2 − 2a². To put it in another way, the success probability is decided by the entangle state as discussed in Section 3.1.

The whole probabilistic teleportaton processes are presented in Figure 2. It can be found that if the receiver Bob has the amplitude factor a of quantum channel, while the phase parameter ϕ is available for the sender Alice, thus the unitary operations U_P and U_F can be performed by Alice and Bob, respectively. Therefore, the novel scheme of this section is effective.

4. Discussion and Conclusions

The total cost of schemes presented in this paper are almost the same as previous schemes [6,8], including quantum entangle, an auxiliary particle and classic communication. The essential difference is that the sender or the receiver has partial independent information and operations, respectively. Based on anatomizing schemes above, it can be found that schemes decompose a complicated physical manipulation which is performed by Alice or Bob into many interdependent and simple operations by Alice and Bob. It distributes the complexity of operations to the sender and the receiver rather than the only one of them, and then the system will be implemented in a relative simple way.

Our proposals can get equivalent success probability that is a paramount parameter but not the only evaluation parameter with previous schemes [6,8]. The success probability is 2 − 2a², also could be expressed as 2|b|² in our proposals. It is determined by the fidelity of entangle channel which could be realized in various ways, to name only a few, photon polarization, super-radiance, collective spontaneous emission. Proposals mentioned in this paper mainly focus on the mechanism of Alice and Bob without regard to the fidelity entangle channel. Many outstanding proposals [12,13,35,46] could improve the fidelity of entangle channel, and could be joined with our proposals.

The other advantage of our schemes are beneficial to security in the applications implemented by teleportation, i.e., quantum key distribution, quantum secret sharing, quantum secure direction communication. If a spy named Charlie exist in the process of teleportation, he could not know whether the total probabilistic teleportation is successful or not. It attributes to the fact that there is an ambiguous transformation has been done by Alice or Bob.

In summary, two novel schemes are proposed to teleport an unknown two-level quantum state with the help of auxiliary particles and appropriate local unitary operations when the sender and the receiver only have partial information about quantum, respectively. The first scheme can be used to perform the probabilistic teleportation when the phase factor of quantum channel is only known for the receiver, and the amplitude factor is available for the sender. Meantime, one can make use of the second novel scheme to probabilistic teleport an unknown two-level quantum state under the condition that the amplitude factor of quantum channel is only available for the receiver, while the sender has the phase factor. Additionally, the detailed realization procedures of the novel schemes are elaborated, and the results show that our proposals could be used to extend the applied range of probabilistic teleportation.