Log-Determinant Divergences Revisited: Alpha-Beta and Gamma Log-Det Divergences
Abstract
:1. Introduction
1.1. Preliminaries
- D(P ║ Q) ≥ 0, where the equality holds if and only if P = Q (nonnegativity and positive definiteness).
- D(P ║ Q) = D(Q ║ P) (symmetry).
- D(P ║ Z) ≤ D(P ║ Q) + D(Q ║ Z) (subaddivity/triangle inequality).
2. Basic Alpha-Beta Log-Determinant Divergence
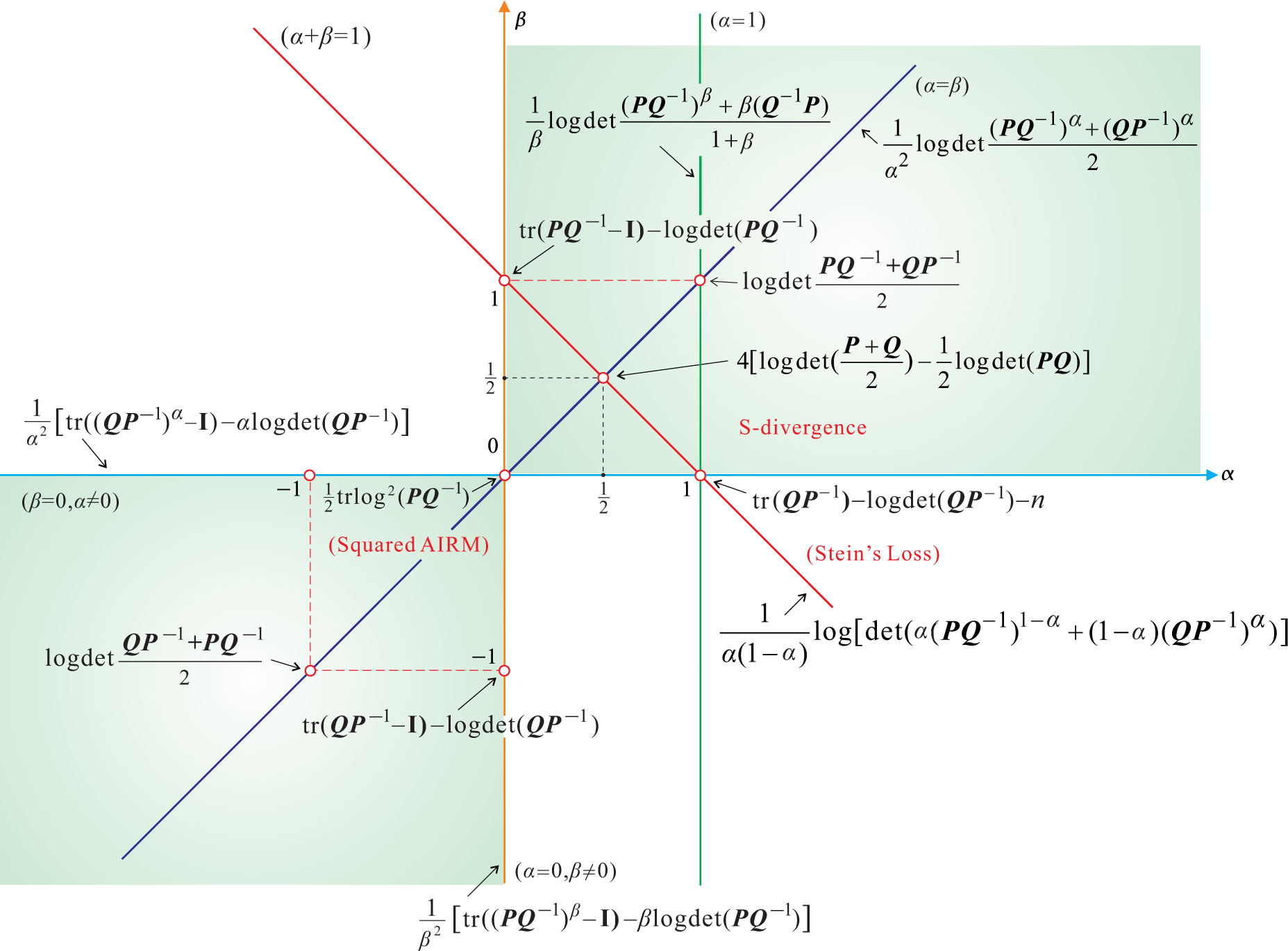
3. Special Cases of the AB Log-Det Divergence
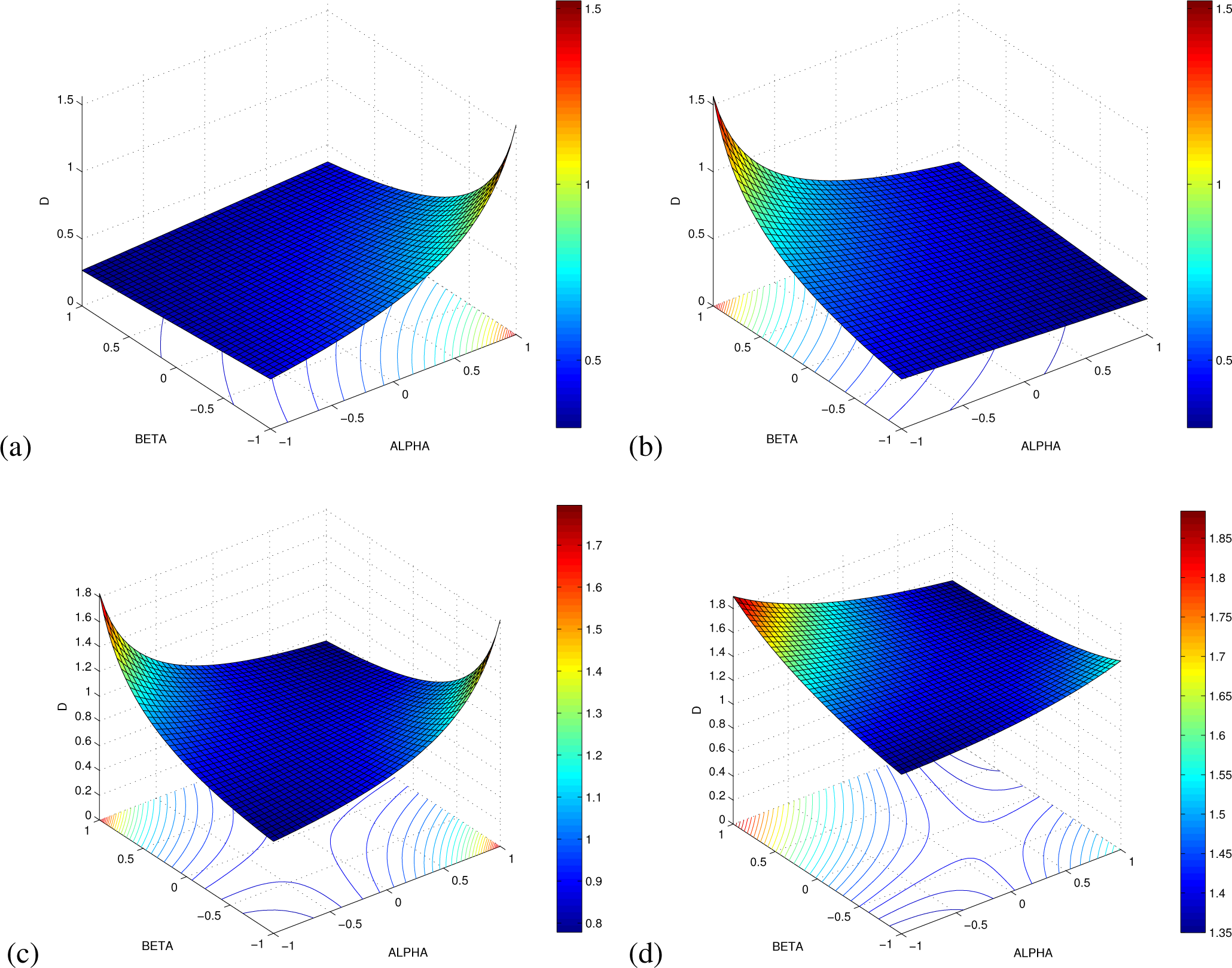
4. Properties of the AB Log-Det Divergence
- Nonnegativity; given by
- Identity of indiscernibles (see Theorems 1 and 2); given by
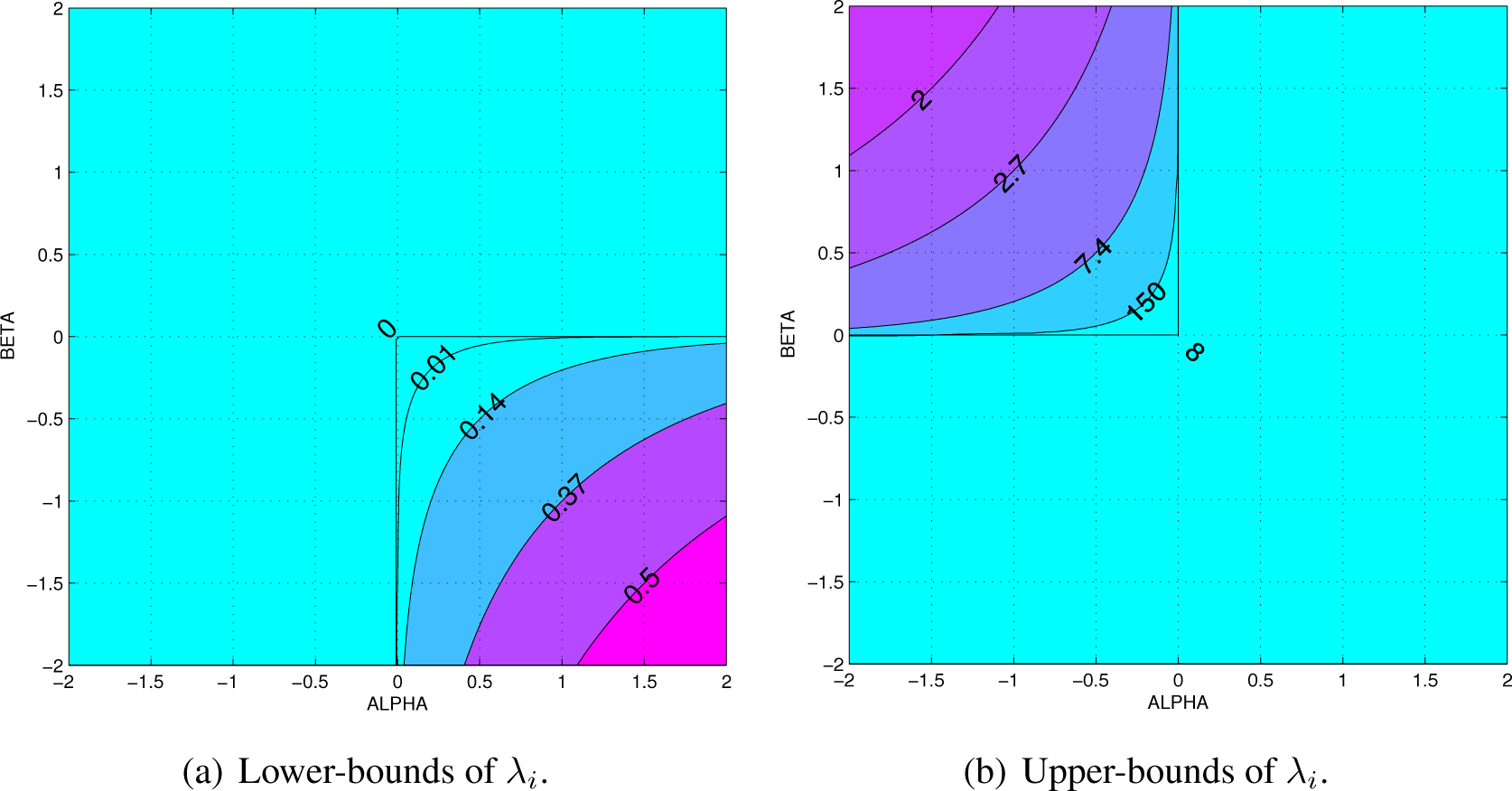
- Continuity and smoothness of as a function of α ∈ ℝ and β ∈ ℝ, including the singular cases when α = 0 or β = 0, and when α = −β (see Figure 2).
- The divergence can be expressed in terms of the diagonal matrix Λ = diag{λ1, λ2, …, λn} with the eigenvalues of PQ−1, in the form
- Scaling invariance; given byfor any c > 0.
- Relative invariance for scale transformation: For given α and β and nonzero scaling factor ω ≠ 0, we have
- Dual-invariance under inversion (for ω = −1); given by
- Dual symmetry; given by
- Affine invariance (invariance under congruence transformations); given byfor any nonsingular matrix A ∈ ℝn×n
- Divergence lower-bound; given byfor any full-column rank matrix X ∈ ℝn×m with n ≤ m.
- Scaling invariance under the Kronecker product; given byfor any symmetric and positive definite matrix Z of rank n.
- Double Sided Orthogonal Procrustes property. Consider an orthogonal matrix and two symmetric positive definite matrices P and Q, with respective eigenvalue matrices ΛP and ΛQ which elements are sorted in descending order. The AB log-det divergence between ΩTPΩ and Q is globally minimized when their eigenspaces are aligned, i.e.,
- Triangle Inequality-Metric Distance Condition, for α = β ∈ ℝ. The previous property implies the validity of the triangle inequality for arbitrary positive definite matrices, i.e.,The proof of this property exploits the metric characterization of the square root of the S-divergence proposed first by S. Sra in [6,17] for arbitrary SPD matrices.
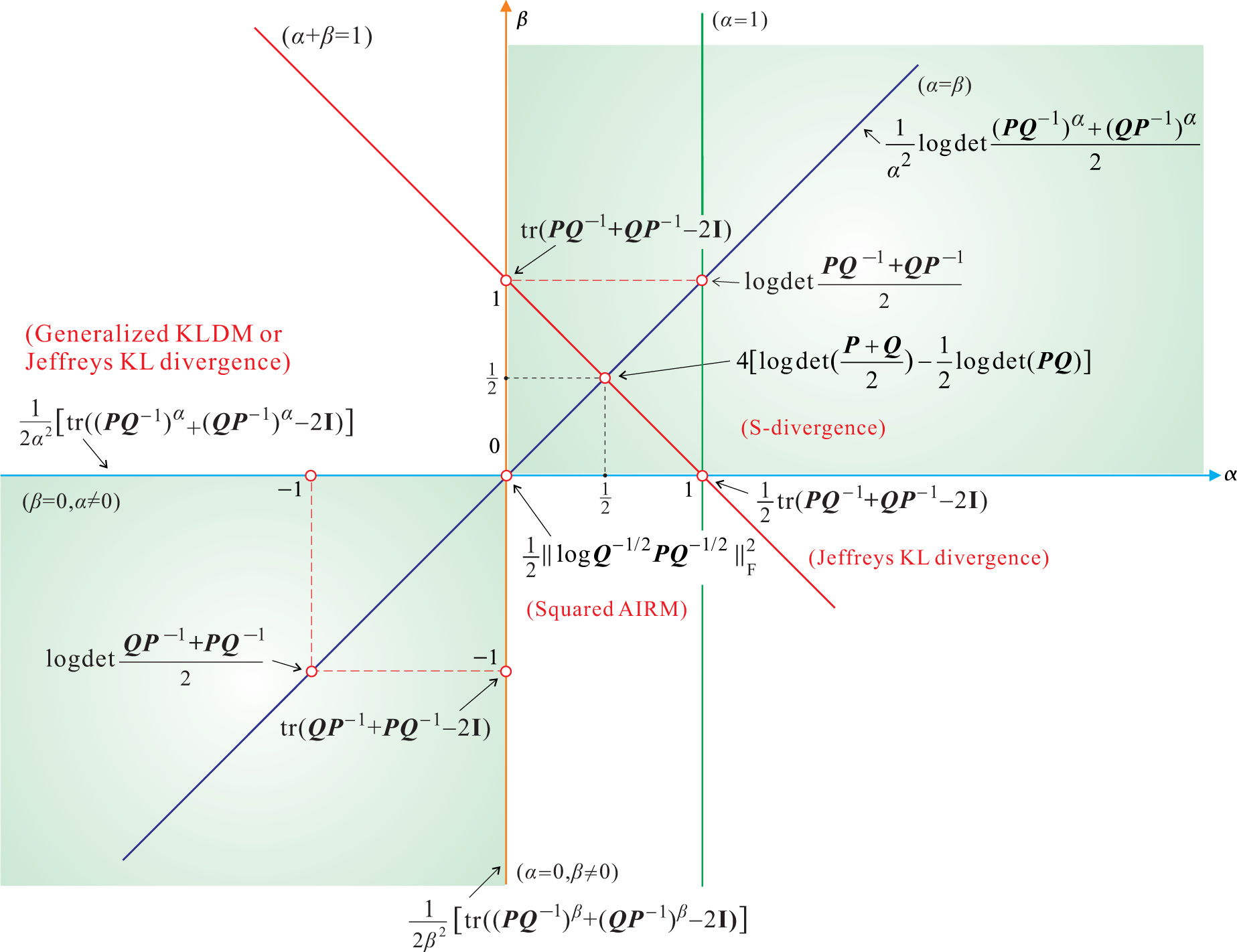
5. Symmetrized AB Log-Det Divergences
- For α = 0 and β = ±1 or for β = 0 and α = ±1, we obtain the KLDM (symmetrized KL Density Metric), also known as the symmetric Stein’s loss or Jeffreys KL divergence [3]:
6. Similarity Measures for Semidefinite Covariance Matrices in Reproducing Kernel Hilbert Spaces
6.1. Measuring the Dissimilarity with a Divergence Lower-Bound
6.2. Similarity Measures Between Regularized Covariance Descriptors
7. Modifications and Generalizations of AB Log-Det Divergences and Gamma Matrix Divergences
- Nonnegativity, dH(P ║ Q) ≥ 0, and definiteness, dH(P ║ Q) = 0, if and only if there exists a c > 0 such that Q = cP.
- Invariance to scaling:for any c1, c2 > 0.
- Symmetry:
- Invariance under inversion:
- Invariance under congruence transformations:for any invertible matrix A.
- Separability of divergence for the Kronecker product of SPD matrices:
- Scaling of power of SPD matrices:for any ω ≠ 0.Hence, for 0 < |ω1| ≤ 1 ≤ |ω2| we have
- Scaling under the weighted geometric mean:for any u, s ≠ 0, where
- Triangular inequality: .
7.1. The AB Log-Det Divergence for Noisy and Ill-Conditioned Covariance Matrices
8. Divergences of Multivariate Gaussian Densities and Differential Relative Entropies of Multivariate Normal Distributions
- For α = β = 1, the Gamma-divergences reduce to the Cauchy-Schwartz divergence:
8.1. Multiway Divergences for Multivariate Normal Distributions with Separable Covariance Matrices
9. Conclusions
Acknowledgments
Appendices
A. Basic operations for positive definite matrices
B. Extension of for (α, β) ∈ ℝ2
C. Eigenvalues Domain for Finite
D. Proof of the Nonnegativity of
E. Derivation of the Riemannian Metric
F. Proof of the Properties of the AB Log-Det Divergence
- Nonnegativity; given byThe proof of this property is presented in Appendix D.
- Identity of indiscernibles; given bySee Appendix D for its proof.
- Continuity and smoothness of as a function of α ∈ ℝ and β ∈ ℝ, including the singular cases when α = 0 or β = 0, and when α = −β (see Figure 2).
- The divergence can be explicitly expressed in terms of Λ = diag{λ1, λ2, …, λn}, the diagonal matrix with the eigenvalues of Q−1 P; in the formProof. From the definition of divergence and taking into account the eigenvalue decomposition PQ−1 = VΛ V−1, we can write
- Scaling invariance; given byfor any c > 0.
- For a given α and β and nonzero scaling factor ω 6= 0, we haveProof. From the definition of divergence, we writeHence, the additional inequalityis obtained for |ω| ≤ 1.
- Dual-invariance under inversion (for ω = −1); given by
- Dual symmetry; given by
- Affine invariance (invariance under congruence transformations); given byfor any nonsingular matrix A ∈ ℝn×n.Proof.
- Divergence lower-bound; given byfor any full-column rank matrix X ∈ ℝn×m with n ≤ m.This result has been already proved for some special cases of α and β, especially these that lead to the S-divergence and the Riemannian metric [6]. Next, we present a different argument to prove it for any α, β ∈ ℝ.Proof. As already discussed, the divergence depends on the generalized eigenvalues of the matrix pencil (P, Q), which have been denoted by λi, i = 1, …, n. Similarly, the presumed lower-bound is determined by µi, i = 1, …, m, the eigenvalues of the matrix pencil (XT PX, XT QX). Assuming that both sets of eigenvalues are arranged in decreasing order, the Cauchy interlacing inequalities [29] provide the following upper and lower-bounds for µj in terms of the eigenvalues of the first matrix pencil,We classify the eigenvalues µj on three sets , and , according to the sign of (µj − 1). By the affine invariance we can writewhere the eigenvalues µj ∈ have been excluded since for them .With the help of (178), the first group of eigenvalues µj ∈ (which are smaller than one) are one-to-one mapped with their lower-bounds λj, which we include in the set . Also those µj ∈ (which are greater than one) are mapped with their upper-bounds λn−m+j, which we group in . It is shown in Appendix D that the scalar divergence is strictly monotone descending for λ < 1, zero for λ = 1 and strictly monotone ascending for λ > 1. This allows one to upperbound (180) as followsobtaining the desired property.
- Scaling invariance under the Kronecker product; given byfor any symmetric and positive definite matrix Z of rank n.Proof. This property was obtained in [6] for the S-divergence and the Riemannian metric. With the help of the properties of the Kronecker product of matrices, the desired equality is obtained:
- Double Sided Orthogonal Procrustes property. Consider an orthogonal matrix and two symmetric positive definite matrices P and Q, with respective eigenvalue matrices ΛP and ΛQ, which elements are sorted in descending order. The AB log-det divergence between ΩT PΩ and Q is globally minimized when their eigenspaces are aligned, i.e.,Proof. Let Λ denote the matrix of eigenvalues of ΩT PΩQ−1 with its elements sorted in descending order. We start showing that for ∆ = log Λ, the function is convex. Its Hessian matrix is diagonal and positive definite, i.e., with non-negative diagonal elementswhereSince is strictly convex and non-negative, we are in the conditions of the Corollary 6.15 in [47]. This result states that for two symmetric positive definite matrices A and B, which vectors of eigenvalues are respectively denoted by (when sorted in descending order) and (when sorted in ascending order), the function is submajorized by . By choosing A = ΩT PΩ, B = Q−1, and applying the corollary, we obtainwhere the equality is only reached when the eigendecompositions of the matrices ΩT PΩ = VΛP VTand Q = VΛQVT, share the same matrix of eigenvectors V.
- Triangle Inequality-Metric Distance Condition, for α = β ∈ ℝ; given byProof. The proof of this property exploits the recent result that the square root of the S-divergenceis a metric [17]. Given three arbitrary symmetric positive definite matrices P, Q, Z, with common dimensions, consider the following eigenvalue decompositionsand assume that the diagonal matrices Λ1 and Λ2 have the eigenvalues sorted in a descending order.For a given value of α in the divergence, we define ω = 2α ≠ 0 and use properties 6 and 9 (see Equations (168) and (175)) to obtain the equivalenceSince the S-divergence satisfies the triangle inequality for diagonal matrices [5,6,17]from (196), this implies thatIn similarity with the proof of the metric condition for S-divergence [6], we can use property 12 to bound above the first term in the right-hand-side of the equation bywhereas the second term satisfiesAfter bounding the right-hand-side of (198) with the help of (199) and (200), the divergence satisfies the desired triangle inequality (192) for α ≠ 0.On the other hand, as α → 0 converges to the Riemannian metricwhich concludes the proof of the metric condition of for any α ∈ ℝ
G. Proof of Theorem 3
H. Gamma Divergence for Multivariate Gaussian Densities
Author Contributions
Conflicts of Interest
References
- Amari, S. Information geometry of positive measures and positive-definite matrices: Decomposable dually flat structure. Entropy 2014, 16, 2131–2145. [Google Scholar]
- Basseville, M. Divergence measures for statistical data processing—An annotated bibliography. Signal Process 2013, 93, 621–633. [Google Scholar]
- Moakher, M.; Batchelor, P.G. Symmetric Positive—Definite Matrices: From Geometry to Applications and Visualization. In Chapter 17 in the Book: Visualization and Processing of Tensor Fields; Weickert, J., Hagen, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 285–298. [Google Scholar]
- Amari, S. Information geometry and its applications: Convex function and dually flat manifold. In Emerging Trends in Visual Computing; Nielsen, F., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 75–102. [Google Scholar]
- Chebbi, Z.; Moakher, M. Means of Hermitian positive-definite matrices based on the log-determinant α-divergence function. Linear Algebra Appl 2012, 436, 1872–1889. [Google Scholar]
- Sra, S. Positive definite matrices and the S-divergence 2013. arXiv:1110.1773.
- Nielsen, F.; Bhatia, R. Matrix Information Geometry; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Amari, S. Alpha-divergence is unique, belonging to both f-divergence and Bregman divergence classes. IEEE Trans. Inf. Theory 2009, 55, 4925–4931. [Google Scholar]
- Zhang, J. Divergence function, duality, and convex analysis. Neural Comput 2004, 16, 159–195. [Google Scholar]
- Amari, S.; Cichocki, A. Information geometry of divergence functions. Bull. Polish Acad. Sci 2010, 58, 183–195. [Google Scholar]
- Cichocki, A.; Amari, S. Families of Alpha- Beta- and Gamma- divergences: Flexible and robust measures of similarities. Entropy 2010, 12, 1532–1568. [Google Scholar]
- Cichocki, A.; Cruces, S.; Amari, S. Generalized alpha-beta divergences and their application to robust nonnegative matrix factorization. Entropy 2011, 13, 134–170. [Google Scholar]
- Cichocki, A.; Zdunek, R.; Phan, A.-H.; Amari, S. Nonnegative Matrix and Tensor Factorizations; John Wiley & Sons Ltd: Chichester, UK, 2009. [Google Scholar]
- Cherian, A.; Sra, S.; Banerjee, A.; Papanikolopoulos, N. Jensen-Bregman logdet divergence with application to efficient similarity search for covariance matrices. IEEE Trans. Pattern Anal. Mach. Intell 2013, 35, 2161–2174. [Google Scholar]
- Cherian, A.; Sra, S. Riemannian sparse coding for positive definite matrices. Proceedings of the Computer Vision—ECCV 2014—13th European Conference, Zurich, Switzerland, September 6–12 2014; 8691, pp. 299–314.
- Olszewski, D.; Ster, B. Asymmetric clustering using the alpha-beta divergence. Pattern Recognit 2014, 47, 2031–2041. [Google Scholar]
- Sra, S. A new metric on the manifold of kernel matrices with application to matrix geometric mean. Proceedings of the 26th Annual Conference on Neural Information Processing Systems 2012, Lake Tahoe, Nevada, USA, 3–6 December 2012; pp. 144–152.
- Nielsen, F.; Liu, M.; Vemuri, B. Jensen divergence-based means of SPD Matrices. In Matrix Information Geometry; Springer: Berlin/Heidelberg, Germany, 2013; pp. 111–122. [Google Scholar]
- Hsieh, C.; Sustik, M.A.; Dhillon, I.; Ravikumar, P.; Poldrack, R. BIG & QUIC: Sparse inverse covariance estimation for a million variables. Proceedings of the 27th Annual Conference on Neural Information Processing Systems 2013, Lake Tahoe, Nevada, USA, 5–8 December 2013; pp. 3165–3173.
- Nielsen, F.; Nock, R. A closed-form expression for the Sharma-Mittal entropy of exponential families. CoRR. 2011. arXiv:1112.4221v1 [cs.IT]. Available online: http://arxiv.org/abs/1112.4221 accessed on 4 May 2015.
- Fujisawa, H.; Eguchi, S. Robust parameter estimation with a small bias against heavy contamination. Multivar. Anal 2008, 99, 2053–2081. [Google Scholar]
- Kulis, B.; Sustik, M.; Dhillon, I. Learning low-rank kernel matrices. Proceedings of the Twenty-third International Conference on Machine Learning (ICML06), Pittsburgh, PA, USA, 25–29 July 2006; pp. 505–512.
- Cherian, A.; Sra, S.; Banerjee, A.; Papanikolopoulos, N. Efficient similarity search for covariance matrices via the jensen-bregman logdet divergence. Proceedings of the IEEE International Conference on Computer Vision, ICCV 2011, Barcelona, Spain, 6–13 November 2011; pp. 2399–2406.
- Österreicher, F. Csiszár’s f-divergences-basic properties. RGMIA Res. Rep. Collect. 2002. Available online: http://rgmia.vu.edu.au/monographs/csiszar.htm accessed on 6 May 2015.
- Cichocki, A.; Zdunek, R.; Amari, S. Csiszár’s divergences for nonnegative matrix factorization: Family of new algorithms. Independent Component Analysis and Blind Signal Separation, Proceedings of 6th International Conference on Independent Component Analysis and Blind Signal Separation (ICA 2006), Charleston, SC, USA, 5–8 March 2006; 3889, pp. 32–39.
- Reeb, D.; Kastoryano, M.J.; Wolf, M.M. Hilbert’s projective metric in quantum information theory. J. Math. Phys 2011, 52, 082201. [Google Scholar]
- Kim, S.; Kim, S.; Lee, H. Factorizations of invertible density matrices. Linear Algebra Appl 2014, 463, 190–204. [Google Scholar]
- Bhatia, R. Positive Definite Matrices; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Li, R.-C. Rayleigh Quotient Based Optimization Methods For Eigenvalue Problems. In Summary of Lectures Delivered at Gene Golub SIAM Summer School 2013; Fudan University: Shanghai, China, 2013. [Google Scholar]
- De Moor, B.L.R. On the Structure and Geometry of the Product Singular Value Decomposition; Numerical Analysis Project NA-89-06; Stanford University: Stanford, CA, USA, 1989; pp. 1–52. [Google Scholar]
- Golub, G.H.; van Loan, C.F. Matrix Computations, 3rd ed; Johns Hopkins University Press: Baltimore, MD, USA, 1996; pp. 555–571. [Google Scholar]
- Zhou, S.K.; Chellappa, R. From Sample Similarity to Ensemble Similarity: Probabilistic Distance Measures in Reproducing Kernel Hilbert Space. IEEE Trans. Pattern Anal. Mach. Intell 2006, 28, 917–929. [Google Scholar]
- Harandi, M.; Salzmann, M.; Porikli, F. Bregman Divergences for Infinite Dimensional Covariance Matrices. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1003–1010.
- Minh, H.Q.; Biagio, M.S.; Murino, V. Log-Hilbert-Schmidt metric between positive definite operators on Hilbert spaces. Adv. Neural Inf. Process. Syst 2014, 27, 388–396. [Google Scholar]
- Josse, J.; Sardy, S. Adaptive Shrinkage of singular values 2013. arXiv:1310.6602.
- Donoho, D.L.; Gavish, M.; Johnstone, I.M. Optimal Shrinkage of Eigenvalues in the Spiked Covariance Model 2013. arXiv:1311.0851.
- Gavish, M.; Donoho, D. Optimal shrinkage of singular values 2014. arXiv:1405.7511.
- Davis, J.; Dhillon, I. Differential entropic clustering of multivariate gaussians. Proceedings of the Twentieth Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006; pp. 337–344.
- Abou-Moustafa, K.; Ferrie, F. Modified divergences for Gaussian densities. Proceedings of the Structural, Syntactic, and Statistical Pattern Recognition, Hiroshima, Japan, 7–9 November 2012; pp. 426–436.
- Burbea, J.; Rao, C. Entropy differential metric, distance and divergence measures in probability spaces: A unified approach. J. Multi. Anal 1982, 12, 575–596. [Google Scholar]
- Hosseini, R.; Sra, S.; Theis, L.; Bethge, M. Statistical inference with the Elliptical Gamma Distribution 2014. arXiv:1410.4812.
- Manceur, A.; Dutilleul, P. Maximum likelihood estimation for the tensor normal distribution: Algorithm, minimum sample size, and empirical bias and dispersion. J. Comput. Appl. Math 2013, 239, 37–49. [Google Scholar]
- Akdemir, D.; Gupta, A. Array variate random variables with multiway Kronecker delta covariance matrix structure. J. Algebr. Stat 2011, 2, 98–112. [Google Scholar]
- PHoff, P.D. Separable covariance arrays via the Tucker product, with applications to multivariate relational data. Bayesian Anal 2011, 6, 179–196. [Google Scholar]
- Gerard, D.; Hoff, P. Equivariant minimax dominators of the MLE in the array normal model 2014. arXiv:1408.0424.
- Ohlson, M.; Ahmad, M.; von Rosen, D. The Multilinear Normal Distribution: Introduction and Some Basic Properties. J. Multivar. Anal 2013, 113, 37–47. [Google Scholar]
- Ando, T. Majorization, doubly stochastic matrices, and comparison of eigenvalues. Linear Algebra Appl 1989, 118, 163–248. [Google Scholar]
| Geodesic Distance (AIRM) (α = β = 0) |
| S-divergence (Squared Bhattacharyya Distance) (α = β = 0.5) |
| Power divergence (α = β ≠ 0) |
| Generalized Burg divergence (Stein’s Loss) (α =0, β ≠ 0) |
| Generalized Itakura-Saito log-det divergence (α =−β ≠ 0) |
| Alpha log-det divergence (0 < α < 1, β = 1 − α) |
| Beta log-det divergence (α =1, β ≥ 0) , Ω = {i= λi > 1} |
| Symmetric Jeffrey KL divergence (α =1, β = 0) |
| Generalized Hilbert metrics |
| Riemannian (geodesic) metric | LogDet Zero (Bhattacharyya) div. | Hilbert projective metric |
| dR(P║Q) = ║log(Q−1/2PQ−1/2)║F | ||
| dR(P║Q) = dR(Q ║ P) | dBh(P║Q) = dBh(Q ║ P) | dH(P║Q) = dH(Q ║ P) |
| dR(cP ║ cQ) = dR(P ║ Q) | dBh(cP ║ cQ) = dBh(P ║Q) | dH(c1P ║ c2Q) = dH(P ║Q) |
| dR(APAT║AQAT) = dR(P ║Q) | dBh(APAT║AQAT) = dBh(P ║Q) | dH(APAT║AQAT) = dH(P ║Q) |
| dR(P−1║Q−1) = dR(P ║ Q) | dBh (P−1║Q−1) dBh (P ║ Q) | dH (P−1║Q−1) = dH (P ║ Q) |
| dR (Pω ║ Qω) ≤ ω dR(P ║ Q) | dH (Pω ║ Qω) ≤ ω dH (P ║ Q) | |
| dR(P ║ P#ωQ) = ω dR(P ║ Q) | dH (P ║ P#ωQ) = ω dH (P ║ Q) | |
| dR (Z#ωP ║ Z#ωQ) ≤ ω dR (P ║ Q) | dH (Z#ωP ║ Z#ωQ) ≤ ω dH (P ║ Q) | |
| dR (P#sQ ║ P#uQ) = ψ dR (P ║ Q)) | dH (P#sQ ║ P#uQ) = ψ dH (P ║ Q) | |
| dR (P ║ P#Q) = dR (Q ║ P# Q) | dBh (P ║ P#Q) = dR (Q ║ P# Q) | dH (P ║ P#Q) = dH (Q ║ P# Q) |
| dR (XTPX ║ XTQX) ≤ dR (P ║ Q) | dBh (XTPX ║ XTQX) ≤ dBh (P ║ Q) | dH (XTPX ║ XTQX) ≤ dH (P ║ Q) |
| dH (Z ⊗ P ║ Z ⊗ Q) = dH (P ║ Q) | ||
| dBh (P1⊗ P2 ║ Q1⊗ Q2) ≥ dBh (P1○ P2 ║ Q1○ Q2) | dH(P1⊗ P2 ║ Q1⊗ Q2) = dH (P1║ Q1) +dH (P2║ Q2) | |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cichocki, A.; Cruces, S.; Amari, S.-i. Log-Determinant Divergences Revisited: Alpha-Beta and Gamma Log-Det Divergences. Entropy 2015, 17, 2988-3034. https://doi.org/10.3390/e17052988
Cichocki A, Cruces S, Amari S-i. Log-Determinant Divergences Revisited: Alpha-Beta and Gamma Log-Det Divergences. Entropy. 2015; 17(5):2988-3034. https://doi.org/10.3390/e17052988
Chicago/Turabian StyleCichocki, Andrzej, Sergio Cruces, and Shun-ichi Amari. 2015. "Log-Determinant Divergences Revisited: Alpha-Beta and Gamma Log-Det Divergences" Entropy 17, no. 5: 2988-3034. https://doi.org/10.3390/e17052988
APA StyleCichocki, A., Cruces, S., & Amari, S.-i. (2015). Log-Determinant Divergences Revisited: Alpha-Beta and Gamma Log-Det Divergences. Entropy, 17(5), 2988-3034. https://doi.org/10.3390/e17052988







