On the κ-Deformed Cyclic Functions and the Generalized Fourier Series in the Framework of the κ-Algebra
Abstract
:1. Introduction
2. κ-Mathematics Formalism
2.1. κ-Algebra
2.2. κ-Calculus
3. Euler Formula and κ-Cyclic Trigonometric Functions
3.1. First Case
3.2. Second Case
4. Orthogonality and Completeness Relations
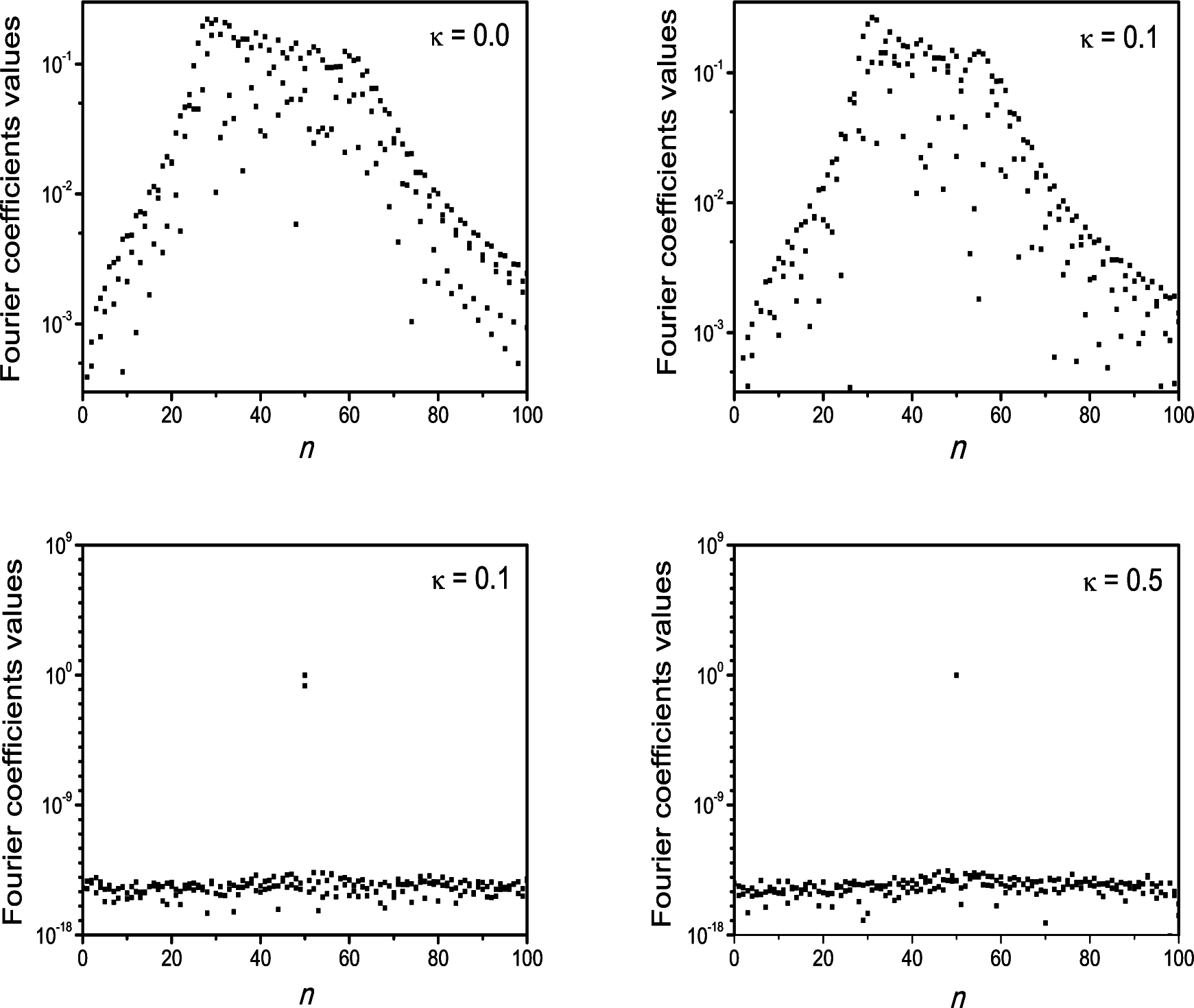
5. Generalized Fourier Series
6. Final Remarks
Conflicts of Interest
References
- Kaniadakis, G. Non-linear kinetics underlying generalized statistics. Physica A 2001, 296, 405–425. [Google Scholar]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. Phys. Rev. E 2002, 66, 056125. [Google Scholar]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. II. Phys. Rev. E 2005, 72, 036108. [Google Scholar]
- Silva, R. The H-theorem in κ-statistics: Influence on the molecular chaos hypothesis. Phys. Lett. A 2006, 352, 17–20. [Google Scholar]
- Wada, T. Thermodynamic stability conditions for nonadditive composable entropies. Cont. Mech. Thermodyn 2004, 16, 263–267. [Google Scholar]
- Kaniadakis, G.; Scarfone, A.M. Lesche stability of κ-entropy. Physica A 2004, 340, 102–109. [Google Scholar]
- Kaniadakis, G. Maximum entropy principle and power-law tailed distributions. Eur. Phys. J. B 2009, 70, 3–13. [Google Scholar]
- Kaniadakis, G. Relativistic entropy and related Boltzmann kinetics. Eur. Phys. J. A 2009, 40, 275–287. [Google Scholar]
- Naudts, J. Continuity of a class of entropies and relative entropies. Rev. Math. Phys 2004, 16, 809–822. [Google Scholar]
- Scarfone, A.M.; Wada, T. Canonical partition function for anomalous systems described by the κ-entropy. Prog. Theor. Phys. Suppl 2006, 162, 45–52. [Google Scholar]
- Scarfone, A.M.; Wada, T. Thermodynamic equilibrium and its stability for microcanonical systems described by the Sharma-Taneja-Mittal entropy. Phys. Rev. E 2005, 72, 026123. [Google Scholar]
- Santos, A.P.; Silva, R.; Alcaniz, J.S.; Anselmo, D.H.A.L. Non-Gaussian effects on quantum entropies. Physica A 2012, 391, 2182–2192. [Google Scholar]
- Guo, L.; Du, J. The κ-parameter and κ-distribution in κ-deformed statistics for the systems in an external field. Phys. Lett. A 2007, 362, 368–370. [Google Scholar]
- Wada, T.; Suyari, H. kappa-generalization of Gauss’ law of error. Phys. Lett. A 2006, 348, 89–93. [Google Scholar]
- Wada, T.; Scarfone, A.M. Asymptotic solutions of a nonlinear diffusive equation in the framework of κ-generalized statistical mechanics. Eur. Phys. J. B 2009, 70, 65–71. [Google Scholar]
- Wada, T. A nonlinear drift which leads to kappa-generalized distributions. Eur. Phys. J. B 2010, 73, 287–291. [Google Scholar]
- Lapenta, G.; Markidis, S.; Kaniadakis, G. Computer experiments on the relaxation of collisionless plasmas. J. Stat. Mech. Theory Exp 2009, 2009. [Google Scholar] [CrossRef]
- Lapenta, G.; Markidis, S.; Marocchino, A.; Kaniadakis, G. Relaxion of relativistic plasmas under the effect of wave-particle interactions. Astrophys. J 2007, 666, 949–954. [Google Scholar]
- Rossani, A.; Scarfone, A.M. Generalized kinetic equations for a system of interacting atoms and photons: Theory and simulations. J. Phys. A Math. Theor 2004, 37, 4955–4975. [Google Scholar]
- Carvalho, J.C.; Silva, R.; do Nascimento, J.D., Jr.; Soares, B.B.; de Medeiros, J.R. Observational measurement of open stellar clusters: A test of Kaniadakis and Tsallis statistics. Europhys. Lett 2010, 91. [Google Scholar] [CrossRef]
- Pereira, F.I.M.; Silva, R.; Alcaniz, J.S. Non-Gaussian statistics and the relativistic nuclear equation of state. Nucl. Phys. A 2009, 828, 136–148. [Google Scholar]
- Olemskoi, A.I.; Borysov, S.S.; Shuda, I.A. Statistical field theories deformed within different calculi. Eur. Phys. J. B 2010, 77, 219–231. [Google Scholar]
- Abul-Magd, A.Y.; Abdel-Mageed, M. Kappa-deformed random-matrix theory based on Kaniadakis statistics. Mod. Phys. Lett. B 2012, 26, 1250059. [Google Scholar]
- Clementi, F.; Gallegati, M.; Kaniadakis, G. κ-generalized statistical mechanics approach to income analysis. J. Stat. Mech 2009, 02037. [Google Scholar]
- Clementi, F.; Gallegati, M.; Kaniadakis, G. Model of personal income distribution with application to Italian data. Empir. Econ 2011, 39, 559–591. [Google Scholar]
- Clementi, F.; Gallegati, M.; Kaniadakis, G. New model of income distribution: The kappa-generalized distribution. J. Econ 2012, 105, 63–91. [Google Scholar]
- Clementi, F.; Gallegati, M.; Kaniadakis, G. A generalized statistical model for the size distribution of wealth. J. Stat. Mech. Theory Exp 2012, 2012. [Google Scholar] [CrossRef]
- Trivellato, B. Deformed exponentials and applications to finance. Entropy 2013, 15, 3471–3489. [Google Scholar]
- Trivellato, B. The minimal κ-entropy martingale measure. Int. J. Theor. Appl. Finan 2012, 15, 1250038. [Google Scholar]
- Tapiero, O.J. A maximum (non-extensive) entropy approach to equity options bid-ask spread. Physica A 2013, 392, 3051–3060. [Google Scholar]
- Bertotti, M.L.; Modenese, G. Exploiting the flexibility of a family of models for taxation and redistribution. Eur. Phys. J. B 2012, 85, 261–270. [Google Scholar]
- Kaniadakis, G. Theoretical foundations and mathematical formalism of the power-law tailed statistical distributions. Entropy 2013, 15, 3983–4010. [Google Scholar]
- Kaniadakis, G.; Scarfone, A.M. A new one-parameter deformation of the exponential function. Physica A 2002, 305, 69–75. [Google Scholar]
- Scarfone, A.M. Entropic forms and related algebras. Entropy 2013, 15, 624–649. [Google Scholar]
- Yang, X.-J.; Baleanu, D.; Tenreiro Machado, J.A. Mathematical aspects of the Heisenberg uncertainty principle within local fractional Fourier analysis. Bound. Value Probl 2013, 2013, 1–16. [Google Scholar]
- Yang, X.-J.; Baleanu, D.; Tenreiro Machado, J.A. Application of the local fractional Fourier series to fractal signals. Disc. Complex. Nonlinear Phys. Syst 2014, 6, 63–89. [Google Scholar]
- Yang, X.-J. Local fractional integral transforms. Prog. Nonlin. Sci 2011, 4, 1–225. [Google Scholar]
- Yang, X.-J. Fast Yang-Fourier transforms in fractal space. Adv. Intell. Trans. Sys 2012, 1, 15–28. [Google Scholar]
- Sornette, D. Discrete-scale invariance and complex dimensions. Phys. Rep 1998, 297, 239–270. [Google Scholar]
- Kutnjak-Urbanc, B.; Zapperi, S.; Milosevic, S.; Stanley, H.E. Sandpile model on the Sierpinski gasket fractal. Phys. Rev. E 1996, 54, 272–277. [Google Scholar]
- Berche, P.E.; Berche, B. Aperiodic spin chain in the mean field approximation. J. Phys. A 1997, 30, 1347–1362. [Google Scholar]
- Doucot, B.; Wang, W.; Chaussy, J.; Pannetier, B.; Rammal, R.; Vareille, A.; Henry, D. Observation of the Universal Periodic Corrections to Scaling: Magnetoresistance of Normal-Metal Self-Similar Networks. Phys. Rev. Lett 1986, 57, 1235–1238. [Google Scholar]



© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scarfone, A.M. On the κ-Deformed Cyclic Functions and the Generalized Fourier Series in the Framework of the κ-Algebra. Entropy 2015, 17, 2812-2833. https://doi.org/10.3390/e17052812
Scarfone AM. On the κ-Deformed Cyclic Functions and the Generalized Fourier Series in the Framework of the κ-Algebra. Entropy. 2015; 17(5):2812-2833. https://doi.org/10.3390/e17052812
Chicago/Turabian StyleScarfone, Antonio Maria. 2015. "On the κ-Deformed Cyclic Functions and the Generalized Fourier Series in the Framework of the κ-Algebra" Entropy 17, no. 5: 2812-2833. https://doi.org/10.3390/e17052812
APA StyleScarfone, A. M. (2015). On the κ-Deformed Cyclic Functions and the Generalized Fourier Series in the Framework of the κ-Algebra. Entropy, 17(5), 2812-2833. https://doi.org/10.3390/e17052812





