A Novel Risk Metric for Staff Turnover in a Software Project Based on Information Entropy

1. Introduction

2. Related Research

3. A Novel Risk Metric Based on Information Entropy Theory

3.2. Five Aspects of Risk Level Influence

This paper considers that the risk level of staff turnover in a software project has five aspects, namely, staff turnover probability, turnover type, staff level, software project complexity, and staff order degree. The first item refers to the uncertainty of turnover, namely, P in Section 3.1, while the remaining four items denote the degree of loss caused by the risk; they fall within the ambit of C in Section 3.1. The analysis is demonstrated as follows:

• Staff turnover probability

Generally, a higher risk probability and stronger influence of the project correspond to a greater risk. Therefore, a reasonable metric model should include staff turnover probability. In current studies, the probability is always estimated subjectively by experts. An objective and quantitative method in calculating the probability will be proposed in the next section of this paper.

• Turnover type

Staff turnover is frequent and uncertain in a software project, and has the following two types (Table 1):

Table 1. Two types of staff turnover.

The first case poses the highest risk because rehiring or training a new employee increases costs and disrupts the project schedule. Moreover, losing key staff can threaten a project as he may disclose business secrets. In the second case, even though the replacement occurred within the company, the replaced employee needs time to become familiar with new tasks, which can compromise the schedule and software quality. Therefore, both resignation and replacement pose risks to software project, and risk level varies among different turnover types. In this paper, T expresses turnover type, T = T(T₁,T₂), where, T₁ denotes resignation and T₂ represents replacement.

• Staff level

The effects of turnover on a project vary depending on different staff levels, which indicates different risk levels. A larger risk loss and stronger influence on the project corresponds to greater risk. Risk of key staff turnover is evidently higher than that of other staff. A key staff is the most important employee because he possesses strong technical knowledge and skill, extensive experience, and excellent management skills, and is crucial to a company’s production operations. The resignation of a key staff significantly influences the project, and finding a replacement is challenging. In this paper, the staff of a software project is divided into four levels in order of importance, namely, key, important, ordinary, and subordinate staff. Staff level is recorded as L = L(L₁, L₂, L₃, L₄).

• Software project complexity

A more complex software project relies heavily on key staff, which is why such a project is affected negatively and may even be discontinued if the key staff resigns. Less complex projects rely less on key staff. Accordingly, the complexity of a software project should be considered when measuring risk.

• Staff order degree

In systems science theory, order exists when a partial order relation exists among subsystems; otherwise, disorder or chaos exists. Order degree is the opposite of balance degree. The former is the distribution of the contribution of the part to the whole, that is, the contribution comes mainly from one part of the system or an average contribution comes from all parts. A more uniform contribution of each subsystem corresponds to a more disorganized system and vice versa. Dissipative structure theory is one of the important theories in systems science, while fluctuation is an important concept in dissipative structure theory. If each staff contributes uniformly to the software project, that is, the order degree of the system is low, then the fluctuation caused by staff turnover is small, and the fluctuation will be dissipated easily by the system. Thus, the software project faces low risks despite staff turnover. On the contrary, if some employees contribute significantly to the project, then the system depends on only a few staff members, which indicates that a high order degree of the system. Thus, the resignation or replacement of these employees will cause a large fluctuation in the system. The system would encounter difficulties in dissipating this fluctuation, hence the high risk. Consequently, the risk level and staff order degree are directly related.

3.3. Novel Risk Metric Model Based on Information Entropy

Based on the above analysis, this section proposes a novel information-entropy-based risk metric, which includes five aspects, namely, staff turnover probability, turnover type, staff level, software project complexity, and staff order degree, to measure the risk of staff turnover in a software project.

Staff turnover risk in a software project can be defined as Risk = (M, P,C), where represents M staff, P is the risk probability, C is the risk loss. As mentioned in Section 4.1, staff turnover has two types, T₁ and T₂, represent resignation and replacement, and risk level varies among different turnover types. Likewise, turnover of different people have different risk impacted on the project, the staff of a software project is divided into four levels, L₁, L₂, L₃ and L₄ in Section 4.1, represent key, important, ordinary, and subordinate staff, separately. In order to accurately measure the risk, every case must be subdivided, C = C(C₁,C₂), and

$$\begin{array}{cc}{C}_1=\left(T_1,L\right)=\{\begin{array}{c}{T}_1•L_1\\ T_1•L_2\\ T_1•L_3\\ T_1•L_4,\end{array}& C_2=\left(T_2,L\right)=\{\begin{array}{c}{T}_2•L_1\\ T_2•L_2\\ T_2•L_3\\ T_2•L_4.\end{array}\end{array}$$

In which, T₁ • L₂ represents L₂ level staff has a T₁ event, namely, an important staff has a resignation event, the other items are similar.

Suppose n staff exist in a software project M₁,M₂,…,M_n, and C₁₁,C₁₂,…,C_1n is the resignation risk loss, where C_1i = (T₁, L)_i, i =1,…,n, P₁₁, P₁₂,…, P_1n is the probability, and C₂₁,C₂₂,…,C_2n is the replacement risk loss, where C_2i = (T₂, L)_i, i =1,…,n, and P₂₁, P₂₂,…, P_2n is the probability. The loss degree of each staff is A₁, A₂,…, A_n, where

$$A_i=C_{1i}\times P_{1i}+C_{2i}\times P_{2i},i=1,\dots ,n$$

(1)

Make a normalization processing for A_i then

$${\rho }_i=\frac{A_i}{{\displaystyle \sum _{j=1}^n{A}_j}}=\frac{C_{1i}\times P_{1i}+C_{2i}\times P_{2i}}{{\displaystyle \sum _{j=1}^n\left(C_{1i}\times P_{1i}+C_{2i}\times P_{2i}\right)}}$$

(2)

where i = 1,…,n, 0 ≤ ρ_i ≤ 1, ${\displaystyle \sum _{i=1}^n{\rho }_i=1}$.

According to information entropy theory,

$$H=-{\displaystyle \sum _{i=1}^n{\rho }_i\ln {\rho }_i}$$

(3)

A more symmetrical ρ_i corresponds to a larger entropy value H. When absolute uniformity ${\rho }_i={\rho }_2=\dots ={\rho }_n=\frac{1}{n}$, the entropy value is the largest, $H_{\max }=H(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n})=\ln n$.

In Formula (3), maybe H is larger than one, therefore, make a normalization processing for convenient measurement. Then

$$H^{*}=\frac{H}{H_{\max }}$$

(4)

where 0 ≤ H* ≤1.

The more symmetrical ρ_i is, the larger entropy value H is, the smaller the risk is, and then,

$$Risk=CF\times \left(1-H^{*}\right)=CF\times \left(1-\frac{H}{H_{\max }}\right)=CF\times \left(1+\frac{{\displaystyle \sum _{i=1}^n{\rho }_i\ln {\rho }_i}}{\ln n}\right)$$

(5)

where 0 ≤ Risk ≤ 1, CF is complexity degree factor of a software project, 0 ≤ CF ≤ 1. This paper does not focus on calculation of CF, which is explained in [20,21]. [20] considers software project complexity includes project environment complexity and software product complexity, it presents a software project complexity evaluation method based on evidence reasoning. The authors of [21] mention technical complexity factor and environment complexity factor and also lists 14 technical complexity factors as well as proposes a technical complexity calculation formula.

According to Section 4.1 and the above analysis, the following preparatory model is obtained based on the information entropy theory for measuring staff turnover risk in a software project.

$$Risk=CF\times \left(1+\frac{{\displaystyle \sum _{i=1}^n\frac{C_{1i}\times P_{1i}+C_{2i}\times P_{2i}}{{\displaystyle \sum _{j=1}^n\left(C_{1i}\times P_{1i}+C_{2i}\times P_{2i}\right)}}\ln \frac{C_{1i}\times P_{1i}+C_{2i}\times P_{2i}}{{\displaystyle \sum _{j=1}^n\left(C_{1i}\times P_{1i}+C_{2i}\times P_{2i}\right)}}}}{\ln n}\right)$$

(6)

The probability is the required data in this model. Reference [16] adopts the expert estimation method, which is expanded in this paper to include a more objective probability calculation. The reason for staff turnover needs to be analyzed; in this paper, this reason pertains to why employees resign. The most well-known staff turnover theories are shown in Table 2.

Table 2. Three famous staff turnover theories.

These theories explain the inevitability and necessity of staff turnover from the aspect of personal growth and stimulation of creativity. Other scholars present other explanations for staff turnover. The authors of [12] suggest that staff turnover depends on job satisfaction. According to [25], the prospect of a bleak future, disorganized internal management, poor working conditions, unreasonable pay, and high job pressure, among others, cause core technicians to resign. The authors of [26] state that a collective turnover reason involves the salary system, professional career planning and training, interpersonal relationships, values conception and mode of thinking, and business competition, etc. The authors of [27] state that staff turnover reasons include the personal characteristics of the staff, the management system, and job market competition. The authors of [13] and [28] categorize the reasons for staff turnover as follows: (1) internal factors such as unfair salary, poor career prospects, and inability to fulfill promises which indicate a lack of acknowledgment of efforts and contributions; (2) external factors such as staff supply and demand; and (3) individual factors such as lifestyle, regional preferences, and interests.

In this section, staff turnover mainly refers to resignation, which occurs because of job dissatisfaction. Turnover probability is inversely proportional to satisfaction, as shown in Figure 1. Higher dissatisfaction results in higher turnover probability, and vice versa.

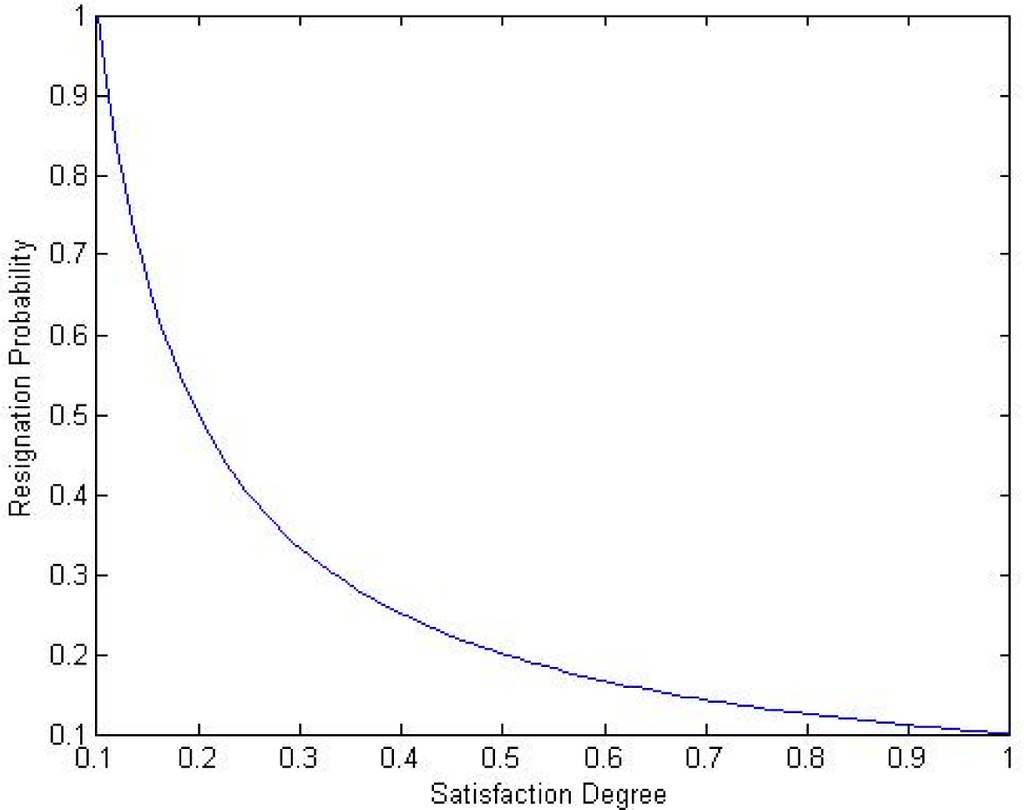
Figure 1. Resignation probability and satisfaction degree.

Based on the existing studies (especially field theory, equity theory and goal congruence theory) as well as fully integrating the characteristic of a software project, this section presents a job satisfaction questionnaire, shown in Table 3.

Table 3. Job satisfaction questionnaire.

According to Table 3, job satisfaction is measured as follows:

$$|S_i|=\frac{{\displaystyle \sum _{j=1}^m{f}_{ij}}}{2m}$$

(7)

where f_ij ∈ {0,1,2}, i =1,…,n, j = 1,…,m. Obviously, 0 ≤| S_i |≤1. n is the number of project staff, and m is the number of resignation risk items.

Given that resignation probability is inversely related to job satisfaction, the probability is calculated as follows:

$$P_{1i}=1-|S_i|=1-\frac{{\displaystyle \sum _{j=1}^m{f}_{ij}}}{2m}$$

(8)

where f_ij ∈ {0,1,2}, i = 1,…,n, j = 1,…,m, and 0 ≤ P_1i ≤1. n is the number of project staff, and m is the number of resignation risk items.

According to the analysis in Section 3.2, replacing staff presents risks, except in cases in which the staff resigned. The replacement probability is negatively correlated with the suited and the unsubstitutable degrees for the job, as shown in Figure 2.

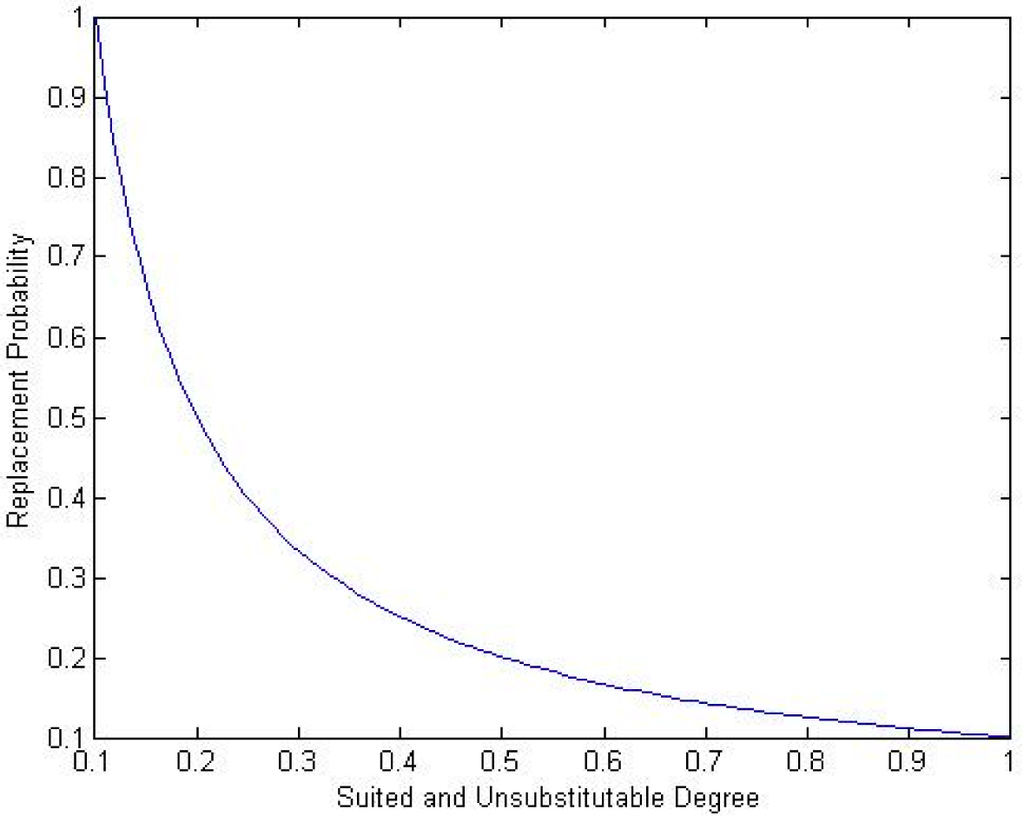
Figure 2. Replacement probability and suited and unsubstitutable degree.

A questionnaire on potential replacement risk is shown in Table 4.

Table 4. Replacement risk questionnaire.

Risk items are summarized in Table 4. The formula that can be used to calculate the probability of replacing staff is given as

$$P_{2i}=\frac{{\displaystyle \sum _{j=1}^k{g}_{ij}}}{2k}$$

(9)

where g_ij ∈{0,1,2}, i = 1,…,n, j =1,…,k, and 0 ≤ P_2i ≤1. n is the number of project staff, and k is the number of replacing risk items.

Equations (8) and (9) are substituted into Equation (6), and a new staff turnover risk metric model (10) is shown as follows:

$$Risk=CF\times \left(1+\frac{{\displaystyle \sum _{i=1}^n\frac{C_{1i}\times \left(1-\frac{{\displaystyle \sum _{j=1}^m{f}_{ij}}}{2m}\right)+C_{2i}\times \frac{{\displaystyle \sum _{j=1}^k{g}_{ij}}}{2k}}{{\displaystyle \sum _{j=1}^n\left(C_{1i}\times \left(1-\frac{{\displaystyle \sum _{j=1}^n{f}_{ij}}}{2m}\right)+C_{2i}\times \frac{{\displaystyle \sum _{j=1}^k{g}_{ij}}}{2k}\right)}}\ln \frac{C_{1i}\times \left(1-\frac{{\displaystyle \sum _{j=1}^m{f}_{ij}}}{2m}\right)+C_{2i}\times \frac{{\displaystyle \sum _{j=1}^k{g}_{ij}}}{2k}}{{\displaystyle \sum _{j=1}^n\left(C_{1i}\times \left(1-\frac{{\displaystyle \sum _{j=1}^m{f}_{ij}}}{2m}\right)+C_{2i}\times \frac{{\displaystyle \sum _{j=1}^k{g}_{ij}}}{2k}\right)}}}}{\ln n}\right)$$

(10)

where C_1i,C_2i can be obtained from statistical or historical data in the enterprise; f_ij, g_ij are the values from Tables 3 and 4; m and k represent entries in Tables 3 and 4, respectively; n is the number of staff; and CF is the complexity degree factor of a software project, which can be obtained from [20,21], CF ∈ [0,1], Risk ∈[0,1].

4. Case Study

4.1. Case 1

Kunming Shunning Technology Company, herein after referred to as KSTC, mainly engages in software development. KSTC contracts for a software development project X. The project team has 20 members, namely, M = {M₁,M₂,…,M₂₀}, and the number of L₁, L₂, L₃, L₄ is 2, 5, 8 and 5, respectively. Risk probability is a major problem for risk measurement. The model (10) developed in this paper effectively solves the problem. To accurately measure the risk, the personnel manager asked the staff to fill in the questionnaires according to Tables 3 and 4. Staff turnover risk probability is quantitatively calculated in Tables 3 and 4. The data as follows:

$$\begin{array}{cc}\hfill f_{ij}=\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{32}\\ A_{31}& A_{32}\end{array}\right)\hfill & \hfill g_{ij}=\left(\begin{array}{cc}{B}_{11}& B_{12}\end{array}\right)\hfill \\ A_{11}=\left(\begin{array}{cccccccccc}0& 0& 1& 0& 2& 1& 1& 2& 0& 2\\ 2& 1& 1& 1& 1& 1& 1& 0& 2& 0\\ 0& 2& 0& 1& 2& 1& 2& 2& 2& 2\\ 2& 0& 0& 1& 1& 1& 1& 2& 0& 0\\ 2& 1& 2& 0& 0& 0& 2& 0& 1& 1\\ 2& 1& 0& 0& 1& 0& 0& 2& 2& 1\\ 1& 2& 2& 0& 2& 0& 2& 0& 1& 1\\ 0& 2& 2& 1& 2& 1& 2& 0& 0& 1\\ 2& 2& 1& 0& 0& 0& 0& 0& 2& 1\\ 1& 2& 1& 1& 2& 0& 0& 0& 1& 1\end{array}\right)& A_{12}=\left(\begin{array}{cccccccccc}2& 0& 2& 1& 0& 0& 2& 2& 2& 0\\ 0& 0& 1& 2& 0& 2& 0& 1& 0& 1\\ 0& 2& 0& 1& 1& 1& 2& 1& 1& 0\\ 2& 2& 0& 2& 0& 1& 1& 1& 2& 2\\ 0& 2& 2& 0& 2& 1& 0& 1& 1& 1\\ 0& 2& 2& 1& 2& 2& 0& 0& 1& 1\\ 0& 1& 0& 0& 1& 0& 1& 0& 2& 0\\ 2& 0& 0& 0& 1& 2& 1& 1& 2& 0\\ 2& 0& 0& 0& 2& 1& 1& 2& 0& 2\\ 2& 1& 1& 1& 1& 1& 2& 1& 1& 2\end{array}\right)\\ A_{21}=\left(\begin{array}{cccccccccc}1& 2& 1& 1& 2& 1& 2& 0& 2& 0\\ 2& 0& 0& 0& 0& 0& 1& 1& 1& 1\\ 2& 1& 1& 0& 2& 2& 1& 2& 1& 1\\ 0& 1& 2& 2& 1& 2& 1& 2& 2& 0\\ 0& 2& 2& 1& 0& 1& 1& 1& 1& 1\\ 2& 2& 0& 0& 0& 2& 2& 1& 1& 1\\ 1& 0& 1& 1& 1& 2& 1& 2& 0& 1\\ 0& 0& 0& 2& 0& 1& 1& 0& 2& 2\\ 1& 0& 2& 2& 2& 2& 1& 0& 1& 2\\ 1& 0& 0& 1& 1& 1& 2& 1& 2& 2\end{array}\right)& A_{22}=\left(\begin{array}{cccccccccc}2& 1& 0& 1& 0& 0& 1& 1& 2& 0\\ 2& 1& 1& 0& 2& 2& 2& 0& 1& 1\\ 2& 2& 1& 2& 1& 0& 1& 0& 2& 1\\ 0& 1& 2& 0& 0& 0& 0& 1& 2& 1\\ 1& 2& 2& 1& 0& 0& 1& 0& 1& 2\\ 1& 2& 0& 2& 2& 1& 1& 2& 2& 0\\ 0& 0& 1& 0& 1& 0& 2& 1& 0& 0\\ 2& 1& 2& 2& 1& 0& 0& 2& 2& 2\\ 0& 2& 2& 0& 2& 1& 1& 0& 1& 2\\ 0& 2& 1& 0& 2& 1& 2& 0& 0& 1\end{array}\right)\\ A_{31}=\left(\begin{array}{cccccccccc}1& 1& 2& 2& 1& 2& 1& 0& 0& 2\\ 0& 1& 0& 2& 1& 0& 0& 1& 1& 0\\ 0& 0& 1& 2& 2& 2& 0& 1& 1& 0\\ 1& 1& 0& 0& 2& 1& 2& 2& 0& 2\\ 1& 0& 0& 1& 2& 1& 0& 2& 2& 0\\ 1& 2& 1& 0& 2& 1& 2& 2& 0& 2\\ 2& 1& 1& 1& 1& 2& 1& 0& 0& 1\\ 2& 2& 1& 1& 1& 1& 0& 0& 2& 2\\ 0& 2& 2& 0& 2& 2& 2& 0& 1& 2\\ 0& 2& 2& 1& 2& 1& 1& 1& 1& 0\end{array}\right)& A_{32}=\left(\begin{array}{cccccccccc}1& 0& 0& 2& 2& 0& 2& 0& 2& 0\\ 1& 0& 1& 2& 1& 0& 0& 2& 2& 0\\ 2& 2& 2& 0& 2& 2& 0& 2& 2& 0\\ 2& 2& 1& 1& 2& 1& 1& 1& 2& 2\\ 1& 1& 1& 0& 1& 0& 0& 0& 1& 0\\ 1& 2& 0& 1& 0& 0& 0& 1& 2& 0\\ 2& 2& 0& 1& 1& 2& 1& 0& 0& 1\\ 2& 1& 2& 0& 1& 0& 1& 0& 1& 1\\ 0& 0& 0& 1& 1& 2& 2& 2& 1& 1\\ 1& 2& 1& 1& 0& 1& 2& 0& 0& 2\end{array}\right)\\ B_{11}=\left(\begin{array}{cccccccccc}2& 0& 2& 2& 0& 1& 0& 1& 1& 0\\ 1& 2& 0& 2& 2& 2& 0& 0& 1& 1\\ 1& 0& 0& 0& 0& 2& 0& 2& 1& 0\\ 0& 1& 1& 2& 0& 1& 2& 1& 2& 2\\ 2& 0& 2& 2& 2& 1& 1& 1& 2& 0\\ 0& 1& 2& 0& 1& 0& 0& 2& 1& 1\\ 2& 1& 1& 2& 1& 2& 2& 2& 2& 1\end{array}\right)& B_{11}=\left(\begin{array}{cccccccccc}0& 0& 1& 1& 2& 0& 0& 1& 0& 1\\ 2& 1& 0& 2& 2& 1& 2& 0& 1& 1\\ 0& 2& 1& 1& 1& 1& 1& 1& 2& 2\\ 0& 2& 2& 1& 0& 1& 1& 0& 1& 2\\ 1& 1& 1& 2& 1& 1& 2& 1& 1& 2\\ 1& 2& 1& 1& 1& 0& 2& 0& 2& 0\\ 1& 0& 1& 0& 2& 0& 1& 2& 0& 1\end{array}\right)\end{array}$$

The turnover of L₁, L₂, L₃, L₄ is divided into two types, namely, T₁ resignation and T₂ replacement. The resignation risk loss can be calculated both through the culture fee of the staff given by the company and the direct project loss caused by the resignation. The replacement risk loss can be determined based on the costs of selecting and training another employee as well as through the direct loss caused by the replacement. Based on historical and statistical data, risk loss is shown in Table 5.

Table 5. Risk loss for staff turnover.

According to formula (10), Risk₁ = 0.262281316, (for convenient calculation, take CF = 1, same as below).

4.2. Comparative Analysis within Seven Different Cases

Risk variation was observed through a comparative analysis of seven different cases.

Figure 3 and Table 6 indicate that risk increases as the probability increases, and vice versa. Figure 4 and Table 6 indicate that risk decreases as the risk loss decreases, and vice versa. Figure 5 and Table 6 indicate that if one project depends primarily on a few people, turnover will pose a major risk to the project once resignation or replacement occurs. Staff order degree will decrease by adding a number of key staff, thereby decreasing the risk. On the contrary, if only one key staff exists, the order degree and the risk will be significantly high.

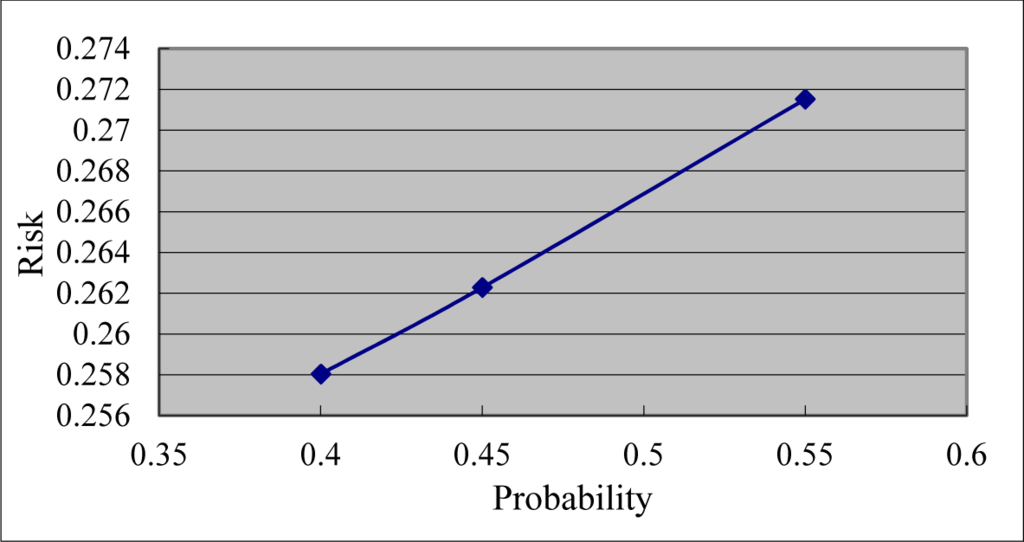
Figure 3. Probability and risk.

Table 6. Comparison of seven cases.

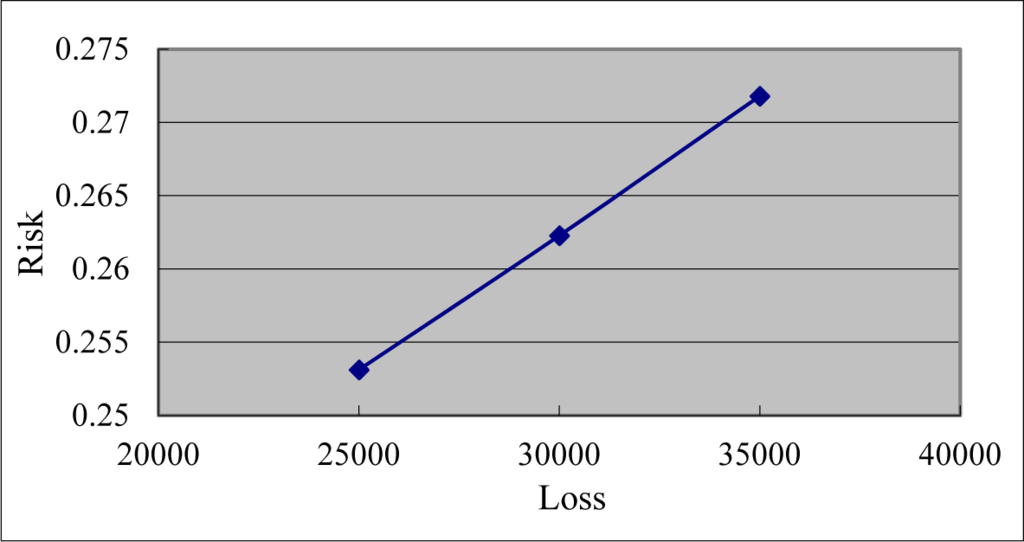
Figure 4. Loss and risk.

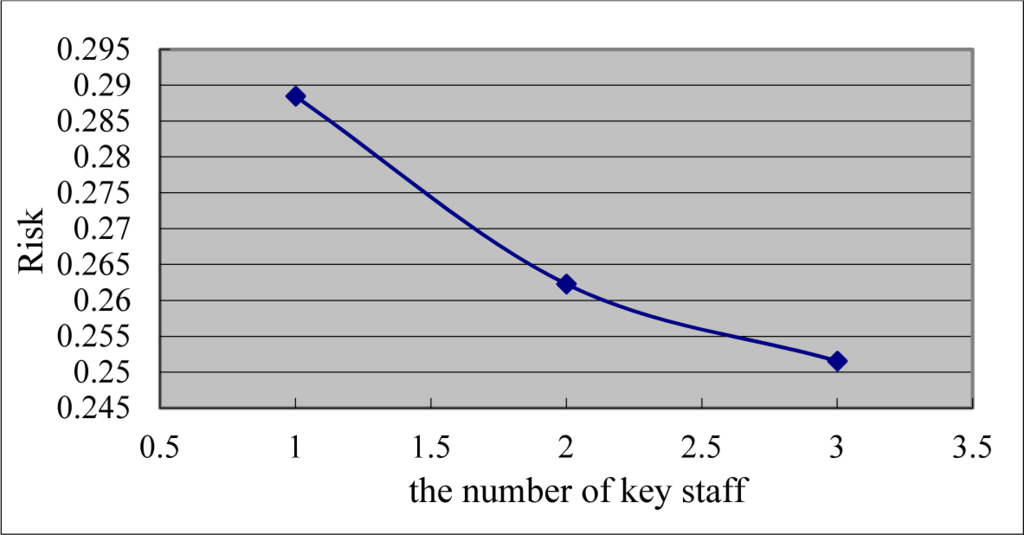
Figure 5. The number of key staff and risk.

This observation is consistent with the findings of qualitative risk analysis. Thus, the model (10) can be used to effectively measure staff turnover risk in a software project.

5. Discussion

5.2. Advantages over Other Studies

The significance of the results of a study depends on its advantage over other studies or its ability to address the deficiency of existing studies. Therefore, the findings of this paper are compared with those of other research.

This paper’s advantages are illustrated mainly in two aspects as follows.

• More Objective

Risk probability is a major difficulty in risk metric field and determined directly by expert’s estimation in current literature, such as [16], etc. In the proposed model in this paper, risk probability is calculated via formulas (8) and (9), which avoids subjective estimation risk probability of traditional research. Accordingly, the model is superior to the existing study obviously.

Quantitative risk research on staff turnover rarely focuses on software projects. Given that [11] is the only relevant paper, its findings are compared with those of this paper. The details are shown in Table 7.

Table 7. Advantages over Reference [11].

Eight parameters exist in the proposed model, and twelve parameters exist in the model of [11]; six and seven are objective parameters, and two parameters are historical and statistical data, respectively. No parameters are determined through expert evaluation in the former. However, three parameters, namely, α_j, β_j, ϕ_j, are determined by expert evaluation in the latter. Therefore, our proposed model is more objective and superior than the model of [11], which ensures that subjective evaluation parameters are avoided.

• More Comprehensive

As mentioned earlier in this paper, generally, risk can be defined as the product of P and C. Usually, they are determined directly by expert’s estimation, e.g., [16], which lead to coarse and imprecise metric. Differently, in this paper, risk level is not decided directly by expert’s estimation and the factors that influence risk level are deeply analyzed. The proposed model contains fully various factors that affect risk level, including staff turnover probability, turnover type, staff level, software project complexity, and staff order degree. It is a pioneering work and more comprehensive, reasonable and refined than existing risk metric research.

6. Results and Conclusions

References

1. Blackburn, J.; Scudder, G.S.; van Wassenhove, L.N. Improving Speed and Productivity of Software Development: A Global Survey of Software Developers. IEEE Trans. Softw. Eng 1996, 22, 875–885. [Google Scholar]
2. Boehm, B.W. Software risk management: Principles and practices. IEEE Softw 1991, 81, 32–41. [Google Scholar]
3. De Marco, T.; Lister, T. Waltzing with Bear: Managing Risk on Software Projects; Dorset House Publishing: New York, NY, USA, 2003. [Google Scholar]
4. Raspotnig, C.; Opdahl, A. Comparing risk identification techniques for safety and security requirements. J. Syst. Softw 2013, 86, 1124–1151. [Google Scholar]
5. Jørgensen, M. Identification of more risks can lead to increased over-optimism of and overconfidence in software development effort estimates. Inf. Softw. Technol 2010, 52, 506–516. [Google Scholar]
6. Huang, J.S.; Han, W.M. Exploring the relationship between software project duration and risk exposure: A cluster analysis. Inf. Manag 2008, 45, 175–182. [Google Scholar]
7. Kulk, G.P.; Peters, R.J.; Verhoef, C. Quantifying IT estimation risks. Sci. Comput. Program 2009, 74, 900–933. [Google Scholar]
8. Bannerman, P.L. Risk and Risk Management in Software Projects: A Reassessment. J. Syst. Softw 2008, 81, 2118–2133. [Google Scholar]
9. Yang, L.; Jones, B.F.; Yang, S.H. Genetic algorithm based software integration with minimum software risk. Inf. Softw. Technol 2006, 48, 133–141. [Google Scholar]
10. Song, H.; We, D.; Li, M.; Cai, C.; Li, J. An Entropy Based Approach for Software Risk Assessment: A Perspective of Trustworthiness Enhancement. Proceedings of the 2nd International Conference on Software Engineering and Data Mining (SEDM), Chengdu, China, 23–25 June 2010; pp. 575–578.
11. Chen, R.; Xie, G.G.; Zhang, D.F.; Wang, R.D. Quantitative Assessment and Analysis of Turnover Risk on Software Project. Appl. Res. Comput 2006, 2, 38–41. [Google Scholar]
12. Emberland, J.S.; Rundmo, T. Implications of job insecurity perceptions and job insecurity responses for psychological well-being, turnover intentions and reported risk behavior. Saf. Sci 2010, 48, 452–459. [Google Scholar]
13. Zhang, Y.L.; Yang, N.D. Analysis and Control for staff turnover risk. Sci. Sci. Mang. Sci. Technol 2000, 21, 42–44, in Chinese. [Google Scholar]
14. Hou, X.; Zhu, H. Precaution and resolution of risk in collectivity staff turnover. Special Area Economy 2004, 12, 149–150, in Chinese. [Google Scholar]
15. Wang, M.X. Risk management of staff turnover on software project. Commer. Res 2004, 52–53, in Chinese. [Google Scholar]
16. Jiang, R.; Liao, H.Z.; Yu, J.K.; Feng, T.; Zhao, C.G.; Li, J.L. A model based on information entropy to measure developer turnover risk on software project. Proceedings of the 2009 2nd IEEE International Conference on Computer Science and Information Technology, Beijing, China, 8–11 August 2009; pp. 419–422.
17. Özmen, A. An entropy-based algorithm for data elimination in time-driven software instrumentation. J. Syst. Softw 2009, 82, 907–913. [Google Scholar]
18. Nicolaou, N.; Georgiou, J. Detection of epileptic electroencephalogram based on Permutation Entropy and Support Vector Machines. Expert Syst. Appl 2012, 39, 202–209. [Google Scholar]
19. Qin, Z.; Xu, W.H.; Han, Y.; Tang, J. Software Project Management, 2nd ed; Tsinghua University Press: Beijing, China, 2009; in Chinese. [Google Scholar]
20. Jiang, G.P.; Chen, Y.W. Software Project Complexity Evaluation Based on Evidence Reasoning. Comput. Eng. Appl 2005, 2, 4–7, in Chinese. [Google Scholar]
21. Han, W.J.; Jiang, L.X. A Cases Course for Software Project Management, 2nd ed; China Machine Press: Beijing, China, 2010; in Chinese. [Google Scholar]
22. Tedford, K.; Baker, D.; Lewin, Kurt. Work Teams: Past, Present and Future; Springer: Berlin/Heidelberg, Germany, 2000; Volume 6, pp. 107–114. [Google Scholar]
23. Denhardt, R.B. Managing Human Behavior in Public and Non-Profit Organizations, 3rd ed; Sage Publications: Thousand Oaks, CA, USA, 2013. [Google Scholar]
24. Zhao, F.; Lu, J.; Xing, X. Review of Turnover for Creative Talent: Base on the Perspective of Organizational View. Sci. Manag. Res 2012, 30, 87–91, In Chinese. [Google Scholar]
25. Guan, Y.M. Risk and Prevention of Key Technician Turnover in a Small Enterprise of Hign Technology. Market Modernization 2006, 316–317, in Chinese. [Google Scholar]
26. Hou, X.; Zhu, H. Risk Prevention and Dissolution for Collective Turnover. Spec. Zones Econ 2004, 149–150, in Chinese. [Google Scholar]
27. Zhang, Q. Risks and Guard of Knowledge Staff’Outflow in Enterprises. Technol. Innov. Manag 2009, 30, 506–509, in Chinese. [Google Scholar]
28. Yao, K.; Cao, J.L. A Prelim inary Probe into the Management of Knowledge Staff Dra in Risk. High-Technol. Ind 2007, 28, 106–109, in Chinese. [Google Scholar]