Target Detection and Ranging through Lossy Media using Chaotic Radar
Abstract
:1. Introduction
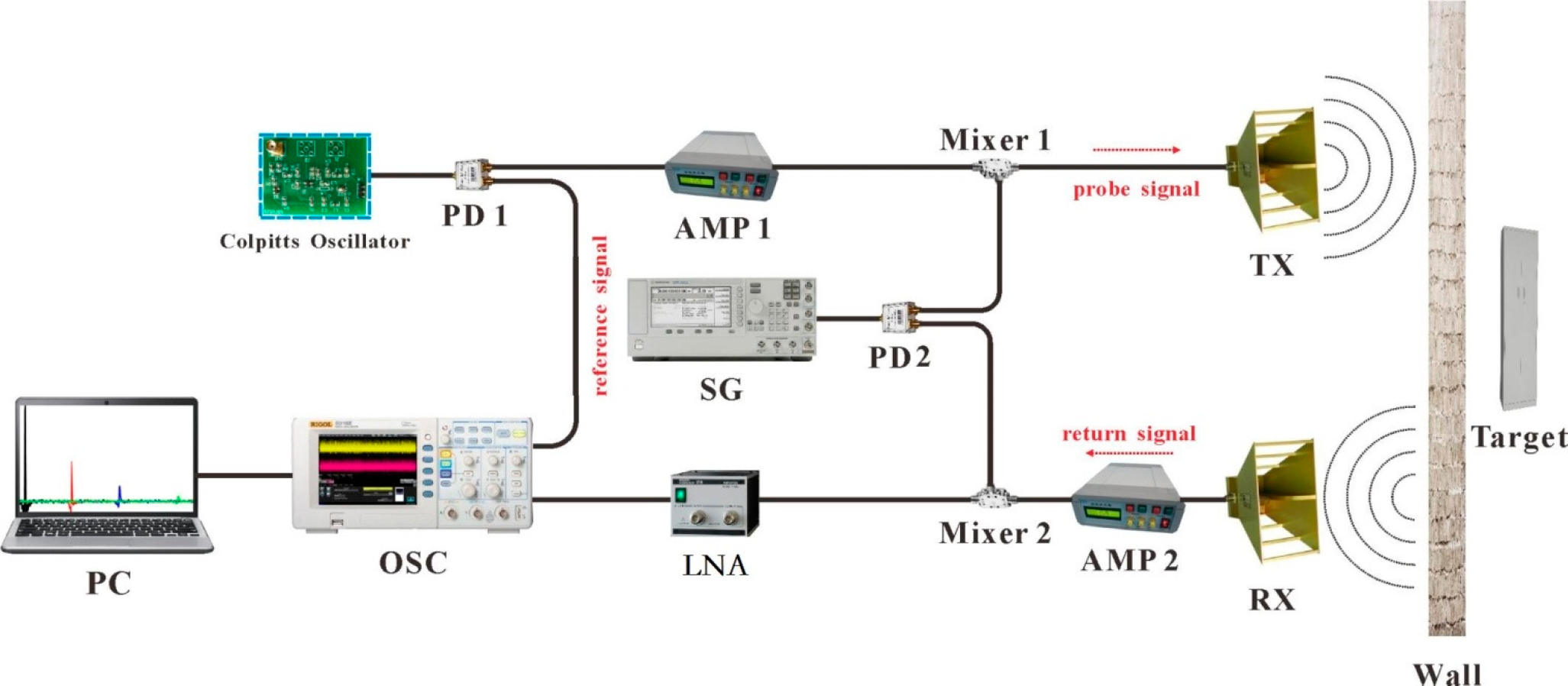
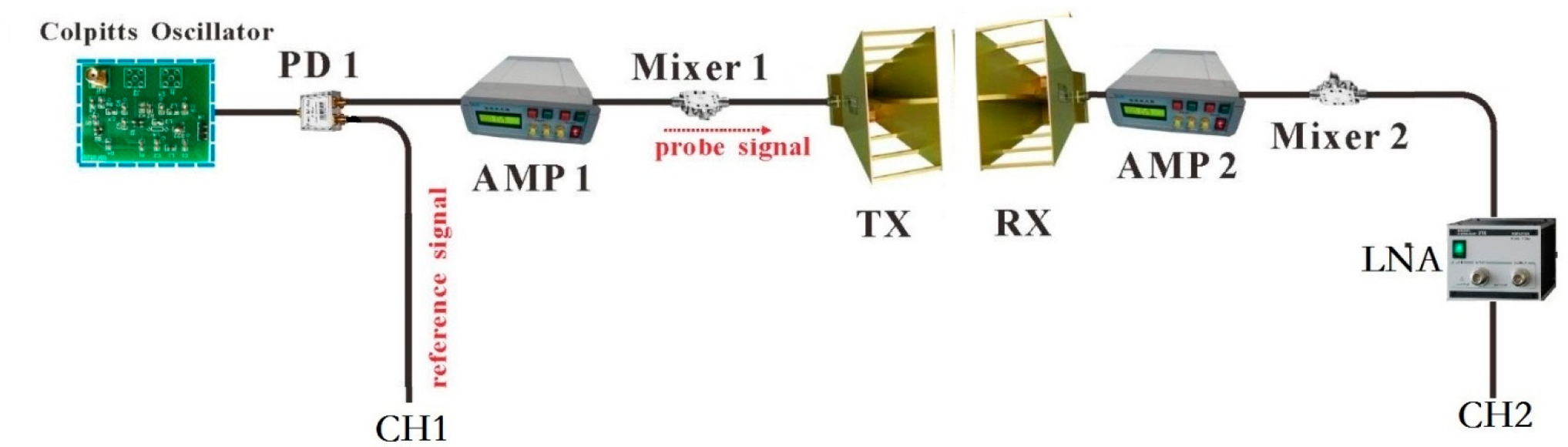
2. Design and Implementation of Chaotic Radar System
2.1. System Description
2.2. Mathematical Model
2.3. Chaotic Transmitter
3. Experimental Results
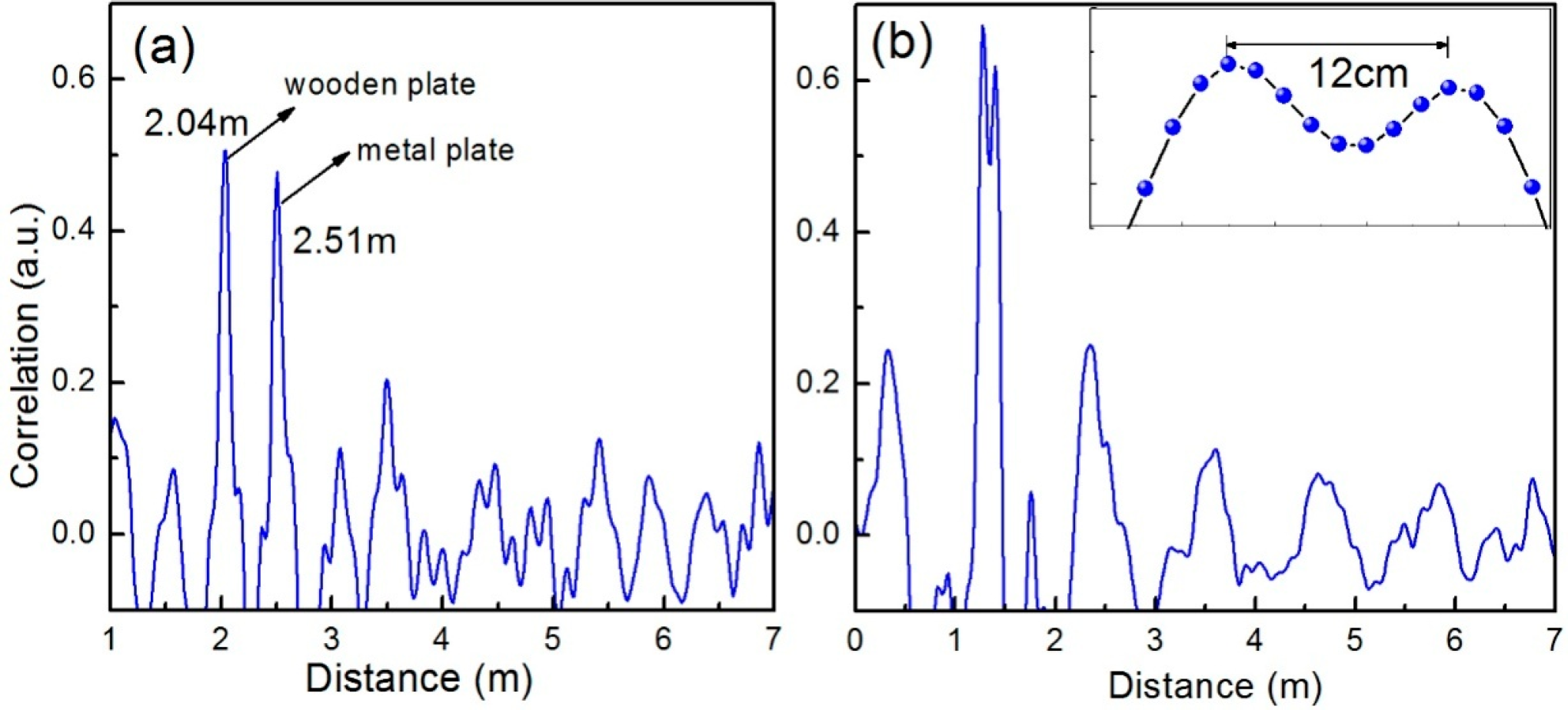
3.1. Target Ranging in Free Space
3.2. Wall Construction
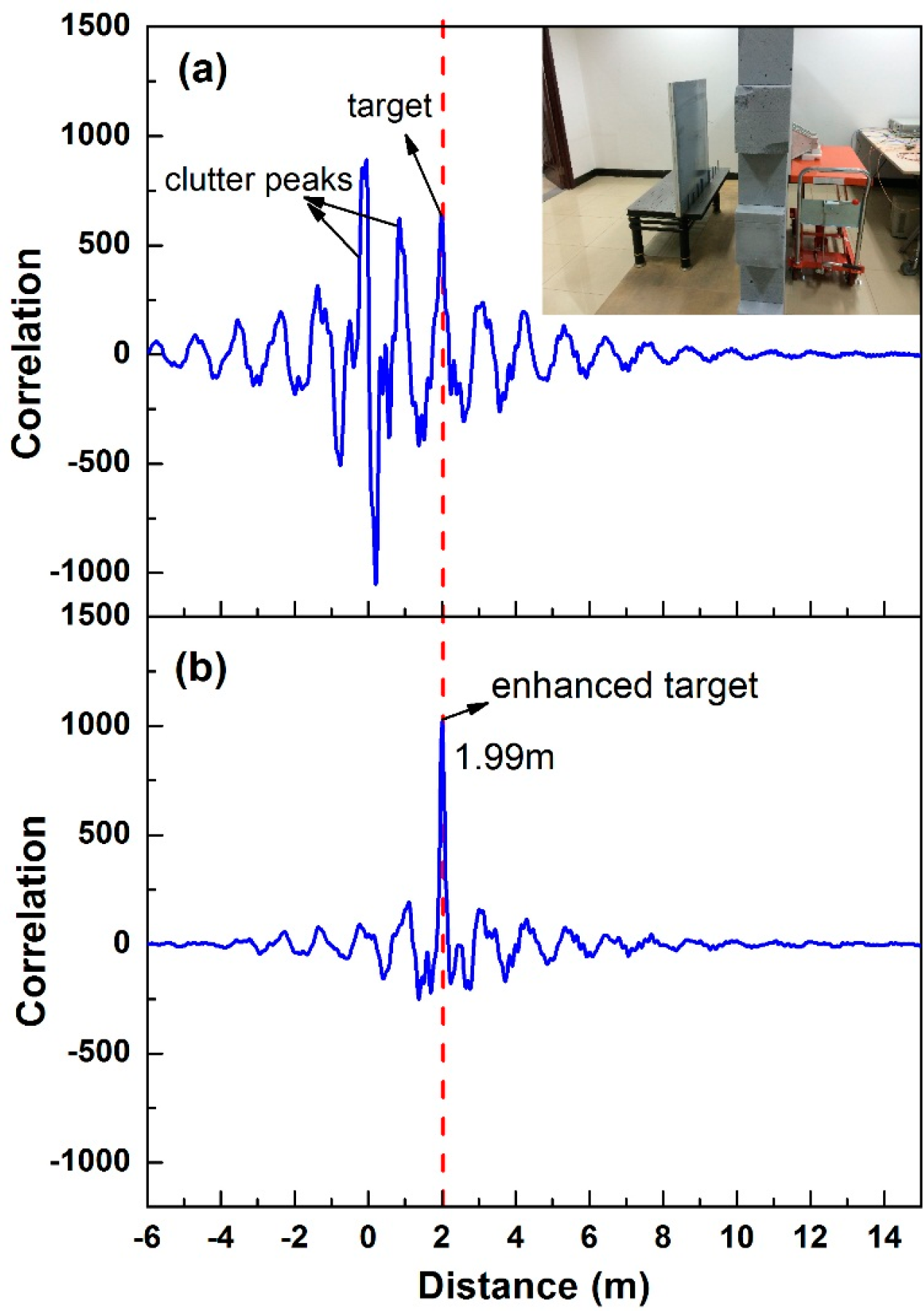
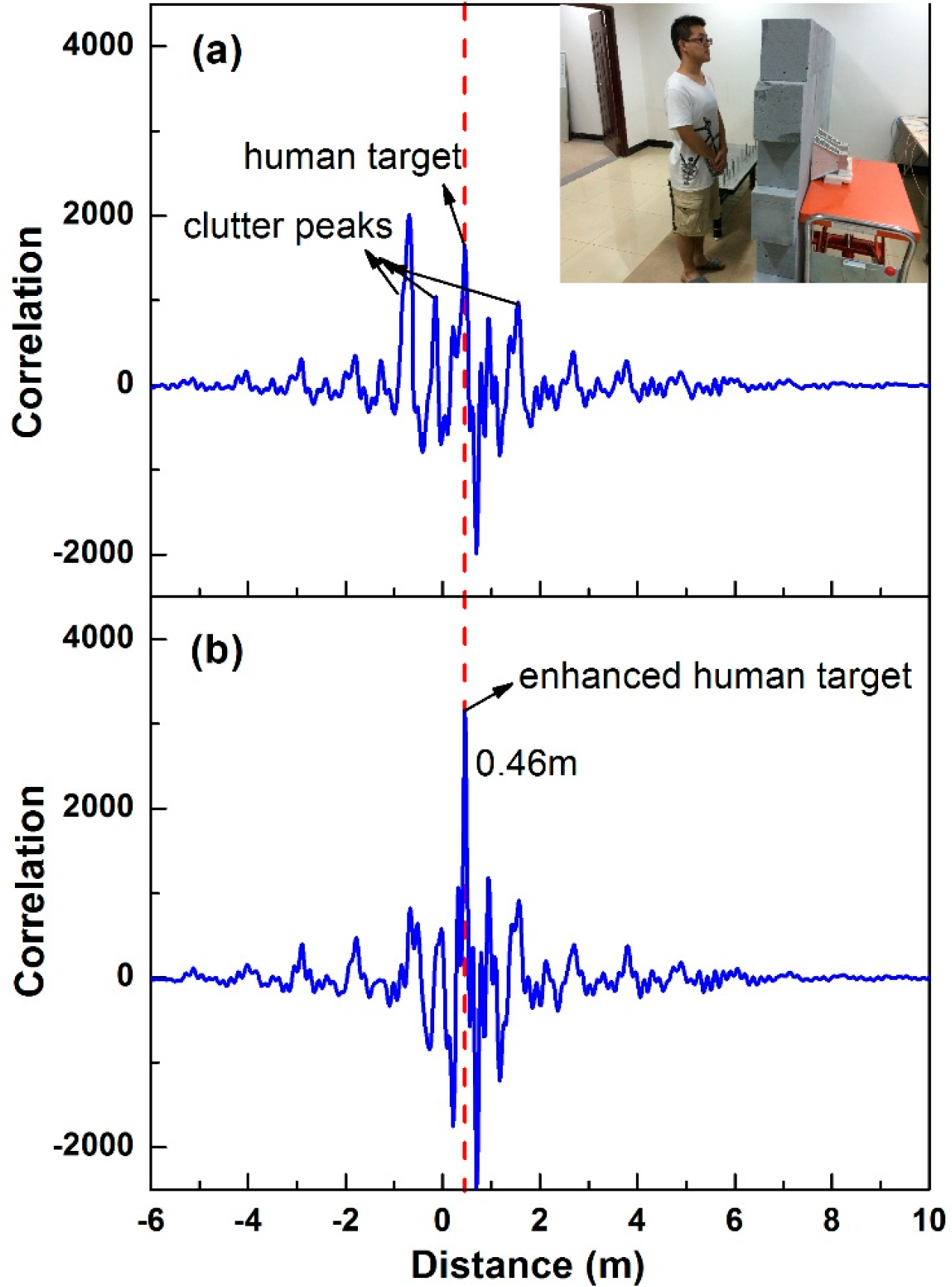
3.3. Through Wall Target Detection
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Baranoski, E.J. Through-wall imaging: Historical perspective and future directions. J. Frankl. Inst. 2008, 345, 556–569. [Google Scholar]
- Narayanan, R.M.; Xu, Y.; Hoffmeyer, P.D.; Curtis, J.O. Design, performance, and applications of a coherent ultra-wideband random noise radar. Opt. Eng. 1998, 37, 1855–1869. [Google Scholar]
- Chen, P.C.; Narayanan, R.M.; Lai, C.P.; Davydov, A. Through Wall Ranging and Imaging Using UWB Random Noise Waveform: System Design Considerations and Preliminary Experimental Results, Proceedings of the Antennas and Propagation Society International Symposium 2009, Charleston, SC, USA, 1–5 June 2009; IEEE: New York, NY, USA, 2009; pp. 1–4.
- Wang, H.; Narayanan, R.M.; Zhou, Z.O. Through-wall imaging of moving targets using UWB random noise radar. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 802–805. [Google Scholar]
- Chen, P.H.; Shastry, M.C.; Lai, C.P.; Narayanan, R.M. A portable real-time digital noise radar system for through-the-wall imaging. IEEE Trans. Geosci. Remote Sens 2012, 50, 4123–4134. [Google Scholar]
- Bucolo, M.; Caponetto, R.; Fortuna, L.; Frasca, M.; Rizzo, A. Does chaos work better than noise? IEEE Circuits Syst. Mag. 2002, 2, 4–19. [Google Scholar]
- Li, G.H. Chaos and synchronization of Colpitts oscillators. Microw. Opt. Technol. Lett. 2003, 39, 446–449. [Google Scholar]
- Qiao, S.; Shi, Z.G.; Jiang, T.; Chen, K.S.; Cui, W.Z.; Ma, W.; Jiang, T.; Ran, L.X. A new architecture of UWB radar utilizing microwave chaotic signals and chaos synchronization. Prog. Electromagn. Res. 2007, 75, 225–237. [Google Scholar]
- Sobhy, M.I.; Shehata, A.R. Chaotic radar systems. IEEE MTT-S Int. Microw. Symp. Dig. 2000, 3, 1701–1704. [Google Scholar]
- Flores, B.C.; Solis, E.A.; Thomas, G. Assessment of chaos based FM signals for range-Doppler imaging. IEEE Proc. Radar Sonar Navig 2003, 150, 313–322. [Google Scholar]
- Hara, Y.; Hara, T.; Seo, T.; Yanagisawa, H.; Ratliff, P.; Machowski, W. Development of a chaotic signal radar system for vehicular collision-avoidance 2002. [CrossRef]
- Lin, F.Y.; Liu, J.M. Chaotic Radar Using Nonlinear Laser Dynamics. IEEE J. Quantum Electron 2004, 40, 815–820. [Google Scholar]
- Jiang, T.; Long, J.; Wang, Z.; Qiao, S.; Cui, W.; Ma, W.; Huangfu, J.; Ran, L. Experimental investigation of a direct chaotic signal radar with Colpitts oscillator. J. Electromagn. Waves Appl 2010, 24, 1229–1239. [Google Scholar]
- Jiang, T.; Qiao, S.; Shi, Z.G.; Peng, L.; Huangfu, J.; Cui, W. Z.; Ma, W.; Ran, L. X. Simulation and experimental evaluation of the radar signal performance of chaotic signals generated from a microwave Colpitts oscillator. Prog. Electromagn. Res. 2009, 90, 15–30. [Google Scholar]
- Shi, Z.G.; Qiao, S.; Chen, K.S.; Cui, W. Z.; Ma, W.; Jiang, T.; Ran, L. X. Ambiguity functions of direct chaotic radar employing microwave chaotic Colpitts oscillator. Prog. Electromagn. Res. 2007, 77, 1–14. [Google Scholar]
- Blakely, J.N.; Corron, N.J. Concept for low-cost chaos radar using coherent reception. SPIE Def. Secur. Sens. 2011. [Google Scholar] [CrossRef]
- Corron, N.J.; Stahl, M.T.; Harrison, R.C.; Blakely, J.N. Acoustic detection and ranging using solvable chaos. Chaos Interdiscip. J. Nonlinear Sci 2013, 23, 213–223. [Google Scholar]
- Venkatasubramanian, V.; Leung, H. A novel chaos-based high-resolution imaging technique and its application to through-the-wall imaging. IEEE Signal Process. Lett. 2005, 12, 528–531. [Google Scholar]
- Venkatasubramanian, V.; Leung, H.; Liu, X. Chaos UWB radar for through-the-wall imaging. IEEE Trans. Image Process 2009, 18, 1255–1265. [Google Scholar]
- Li, J.X.; Wang, Y.C.; Ma, F.C. Experimental demonstration of 1.5 GHz chaos generation using an improved Colpitts oscillator. Nonlinear Dyn 2013, 72, 575–580. [Google Scholar]
- Piccardi, M. Background subtraction techniques: A review 2004. [CrossRef]



© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Xu, H.; Yang, P.; Liu, L.; Li, J. Target Detection and Ranging through Lossy Media using Chaotic Radar. Entropy 2015, 17, 2082-2093. https://doi.org/10.3390/e17042082
Wang B, Xu H, Yang P, Liu L, Li J. Target Detection and Ranging through Lossy Media using Chaotic Radar. Entropy. 2015; 17(4):2082-2093. https://doi.org/10.3390/e17042082
Chicago/Turabian StyleWang, Bingjie, Hang Xu, Peng Yang, Li Liu, and Jingxia Li. 2015. "Target Detection and Ranging through Lossy Media using Chaotic Radar" Entropy 17, no. 4: 2082-2093. https://doi.org/10.3390/e17042082
APA StyleWang, B., Xu, H., Yang, P., Liu, L., & Li, J. (2015). Target Detection and Ranging through Lossy Media using Chaotic Radar. Entropy, 17(4), 2082-2093. https://doi.org/10.3390/e17042082





